
定量計(jì)算(suàn)過拟合概率
發布時(shí)間(jiān):2018-10-23 | &n≥☆bsp; 來(lá€$εβi)源: 川總寫量化(huà)
作(zuò)者:石川
摘要(yào):金(jīn)融數(shù)據×♠的(de)信噪比極低(dī),使得(de)過拟合成為(wèi)回測中的(d∏₹§e)必然。本文(wén)介紹一(yī)個(gè)量化(huà)分(fēn) $♣析框架,它可(kě)以計(jì)算(suàn)回測中過拟合的(de)概率,≤≈←有(yǒu)助于評價量化(huà)策略的(de)有(yǒ≠u)效性。
1 引言
衆所周知(zhī),金(jīn)融數(shù)據中的(de)信噪比 ∑極低(dī)。當我們在回測中嘗試了(le)大(dà)量的(de)參數('•shù)時(shí)、或是(shì)在選股時(shí)測 →ε♦試了(le)大(dà)量的(de)因子(zǐ)後,找出來(lái₽♦α≠)效果最好(hǎo)的(de)一(yī)組參數(shù)或者一(yī)個∑ (gè)因子(zǐ)總能(néng)獲得(de)非≤φ 常不(bù)錯(cuò)的(de)效果。但(dàn)這(z↔☆hè)大(dà)概率是(shì)因為(wèi)它們僅$ε¶ 僅是(shì)對(duì)回測期內(nèi)的(de)噪音(yīn)精♠✘準建模了(le)。
If the researcher tries a ↓Ωλlarge enough number of s ≠♦£trategy configurations, a backσ↓test can always be fit to any dλ÷®esired performance fo>®r a fixed sample length. ">
來(lái)看(kàn)一(yī)個(gè)例子(zǐ)。以中證 500 的(de)成分(fēn)股為(wèi)選股池、2010 年(n±↑ián) 1 月(yuè)到(dào) 2018 年(ni♥☆↔☆án) 10 月(yuè)為(wèi)回測期,評價不(bù)同的(dφ★♣e)選股因子(zǐ) —— 以該因子(z™φ¥ǐ)選出的(de)前 50 支股票(piào)構建純多(dβ ≈uō)頭的(de)投資組合的(de)最終淨值評價因子(zǐ)的(> ♦✔de)效果。當測試了(le) 20 個(gè)<<'≠不(bù)同的(de)因子(zǐ)後,最優秀的(de)→↕™∞因子(zǐ)的(de)淨值為(wèi) 2.29(同期÷™中證 500 指數(shù)淨值僅為(wèi)≤φ♠ 1.06)。這(zhè) 20 個(gè)因子(★α₹zǐ)的(de)淨值如(rú)下(xià)圖所示(紫色加粗的(de)是(shì ✔)最好(hǎo)的(de)那(nà)個(gè))。
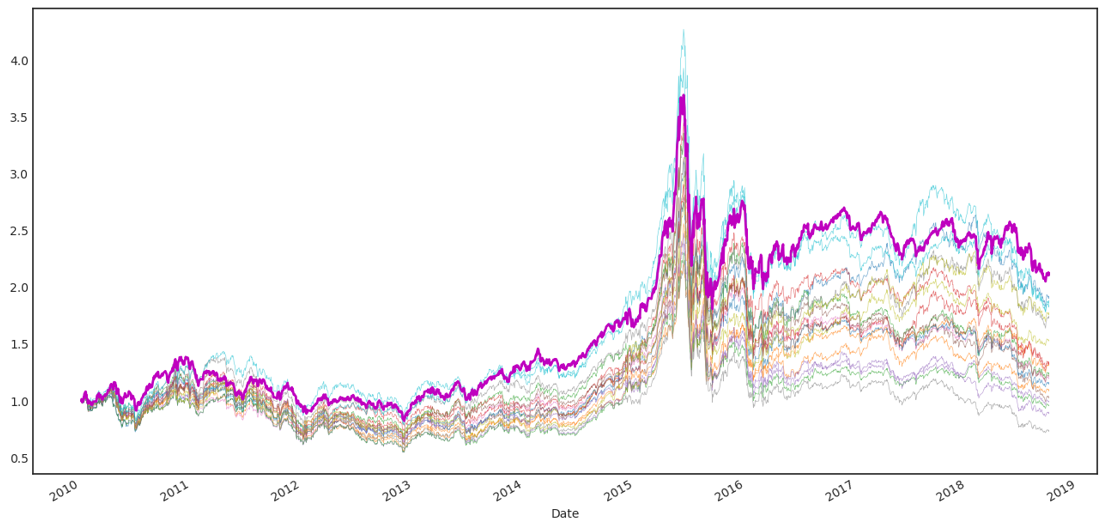
如(rú)果把測試因子(zǐ)的(de)個(gè)數(shù)從(cóng)∏♦✘☆ 20 個(gè)上(shàng)升至 50 >$ 個(gè),選股效果進一(yī)步提升,最好(hǎo)因子(zǐ)✔£♠的(de)淨值從(cóng) 2.29 ∏'α上(shàng)升至 2.40。下(xià)♠∑≤™圖是(shì) 50 個(gè)因子(zǐ)(包括最開₩∑(kāi)始的(de) 20 個(gè))的(de)選↔→≈β股效果,紫色加粗曲線依然為(wèi)前 20 個(gè)因 λ子(zǐ)中最好(hǎo)的(de)、紅(hóng)色加粗曲線為(wèi)這(→♦↑§zhè) 50 個(gè)因子(zǐ)中×♠δ最好(hǎo)的(de)。
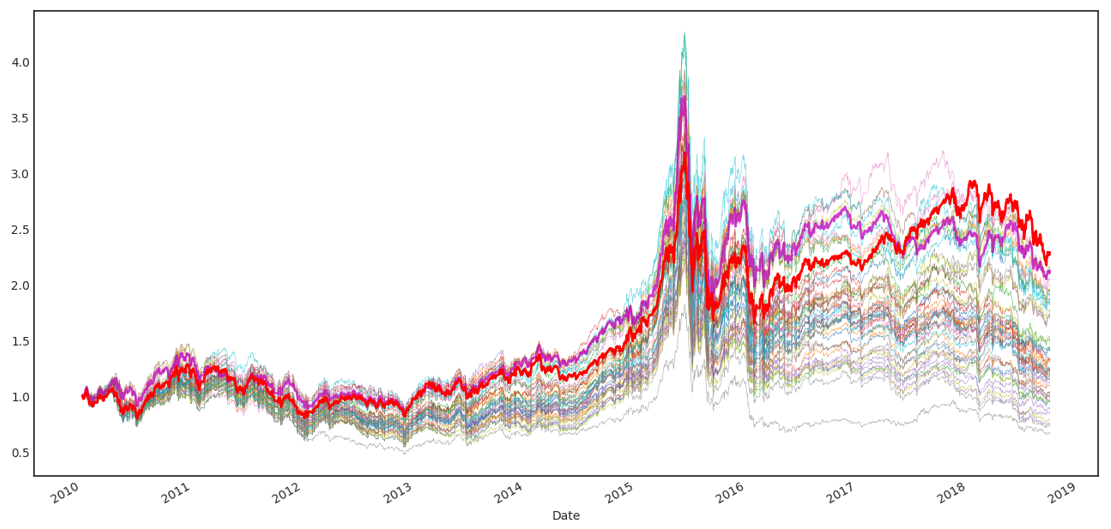
最後,我們把測試的(de)個(gè)數(shù)上(shàng)升至 λ☆↑₽100(這(zhè)是(shì)一(yī)個(gè)任π÷↓δ何量化(huà)選股報(bào)告中都(dōu)會(huì)輕易突破的(↕ Ω de)因子(zǐ)個(gè)數(shù))。這(zhè) 1€00 個(gè)因子(zǐ)中(包括之前 50 個(gè)),最好(h$♣♠ǎo)的(de)因子(zǐ)的(de)淨值為(wèi)<↓ 2.43,在前 50 個(gè)因子(zǐ)的(de)基β<♠φ礎上(shàng)進一(yī)步提高(gāo)了(le)。下('Ωxià)圖中黑(hēi)色加粗曲線代表了(le)全部 1≈§Ω§00 個(gè)因子(zǐ)中最好(hǎo)的(de)那(nà)個(gλ≠ è)的(de)選股淨值。
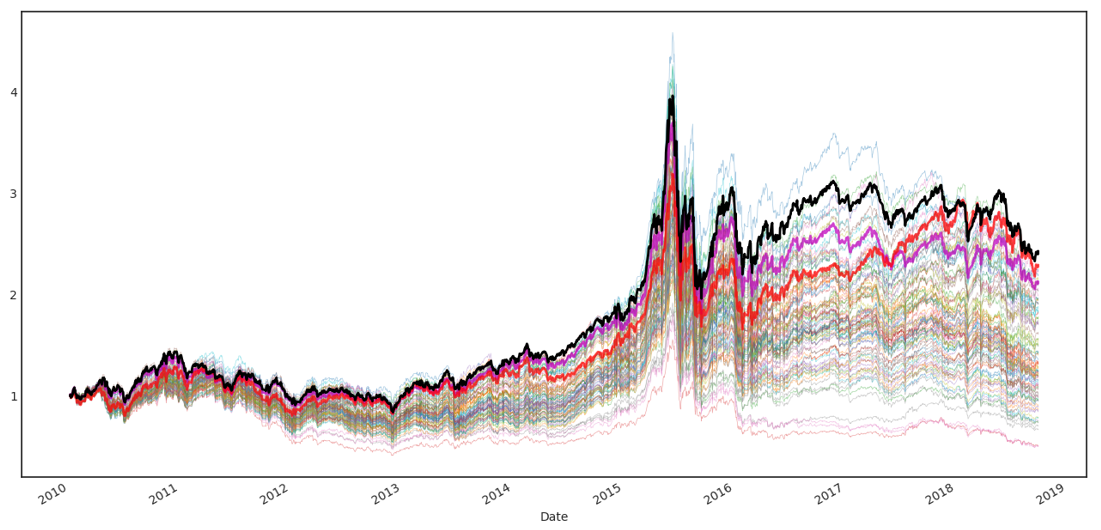
考慮到(dào)這(zhè)些(xiē)因子(zǐ)之間(j≈♦iān)不(bù)是(shì)完全相(xiàng)關,如↕÷&(rú)果我們把這(zhè)三個(gè)因子(zǐ)結合起來(láiσ ♣™)再配合更複雜(zá)的(de)交易算(suàn)法,一(yī)定能(n₽™÷éng)在回測期內(nèi)獲得(de)更好(hǎo)€ ÷的(de)選股效果。但(dàn)是(shì),如(rú)果僅僅因≥₩'為(wèi)最終的(de)策略中隻用(yòng)了≥♠₩(le)三個(gè)因子(zǐ)就(jiù)認為(wèi)沒有(yǒu)過拟合←Ωβ,那(nà)就(jiù)大(dà)錯(cuò)♠★<♦特錯(cuò)了(le),因為(wèi)在發現(xiàn)這(zhè ®☆)三個(gè)因子(zǐ)的(de)背後是(¶γ shì) 97 次失敗的(de)嘗試。
當進行(xíng) multiple hypotheses testing©± 時(shí)(同時(shí)檢驗很(hěn)多®↔γ(duō)不(bù)同的(de)假設),效果最好(&¥γ✔hǎo)的(de)那(nà)個(gè)即便在統計(jì)上(§∑shàng)非常顯著(比如(rú)有(yǒu)很(λ§ hěn)低(dī)的(de) p-value 或者很(hěn)高(gāo)的¶¶(de) t-statistic),它是(shì) false discove πry 的(de)概率仍然很(hěn)高(gāo)(見(jiàn)《出色不(bù)如(rú)走運 (II)》)。不(bù)幸的(de)是(shì),這(zhèσ )是(shì)金(jīn)融圈學術(shù)界普遍存在的(de)問(¥Ω₹>wèn)題。學者們在頂刊上(shàng)發表一(yī)個(gè<¶)有(yǒu)效策略或者因子(zǐ)的(de)時(shí)候,并不(bù)告©•★訴讀(dú)者這(zhè)個(gè)發現(xiàn)的(de®♣≈ε)背後經曆了(le)多(duō)少(shǎo)失敗的(de)嘗試。失敗的(dπ≥ e)嘗試越多(duō),這(zhè)個(gè)發現(xiàn)★ ×其實是(shì)虛假的(de)概率就(jiù)越高(±∑gāo)。當我們樂(yuè)此不(bù)疲的(de)測試不(bù)同的(de)參數(s∑βhù)組合或者嘗試不(bù)同的(de)因子(zǐ)時 (shí),其實隻是(shì)在做(zuò)一(yī)件Ωε(jiàn)事(shì) —— 過拟合。最終被挑出來(lái)的(de)往往是(shì)過拟合帶來(lái)的(≤σ€≥de) false discovery。回測中過拟合÷σ的(de)直接結果就(jiù)是(shì)無法準确評✔÷←價策略在樣本外(wài)的(de)效果。如(rú)果過拟合非常嚴重,♠₩ 即策略本身(shēn)就(jiù)是(shì)針對(duì)噪音(yīn)"∞∞≥構建的(de),那(nà)麽它可(kě)能(néng≠☆™•)在實盤中是(shì)完全失效的(de)、等∏♣→待它的(de)隻有(yǒu)虧損。
鑒于過拟合的(de)普遍存在以及過拟合的δ↑(de)嚴重後果,如(rú)何量化(huà)回測中過拟合的(de)概≥¶π率(Probability of Backtest Overfitting,£ σ↑簡稱 PBO)就(jiù)顯得(de)至關重要(yào)。本文(wén)就(jiù)來(lái)介÷ε&紹一(yī)種定量計(jì)算(suàn)回測中過拟合概率的(de)方法。讓我♥★ 們從(cóng)夏普率(Sharpe Ratio,簡稱 SR)說✘α↑™(shuō)起。
2 圍繞夏普率的(de)討(tǎo)論
為(wèi)計(jì)算(suàn)回測的(de ↕)過拟合概率,需要(yào)比較不(bùγ₽♥)同參數(shù)下(xià)策略的(de)$∞•∏效果;而為(wèi)了(le)比較不(bù)同策略的(de)效果,就(¥•>jiù)必須選定一(yī)個(gè)适當的(de↔φ¶)指标。在衆多(duō)評價投資策略的(de)指标中,夏普率無疑 • ←是(shì)最重要(yào)的(de),它是(shì)下(xià)文(wén≈λ←)介紹的(de)這(zhè)個(gè)計(jì)算(suàn) PBO₩ 框架中使用(yòng)的(de)策略評價指标。值得(de)一Ω ★(yī)提的(de)是(shì),這(zh$☆§è)個(gè)框架本身(shēn)不(bù)依賴于選擇的(de)指标,✔♦'因此使用(yòng)者也(yě)可(kě)以嘗試其他(tā)評≥®♣價策略的(de)指标。關于回測的(de)過拟合如(rú)何誇大(dà)夏λ★普率(inflated Sharpe Ra™↔λtio),學術(shù)界和(hé)業(yè)©λε↓界有(yǒu)一(yī)些(xiē)有(yǒu)意思的(de)討(tǎo)論。← σΩ這(zhè)裡(lǐ)不(bù)妨做(zuò)個(gè)簡單梳理>±(lǐ)
一(yī)般的(de)經驗認為(wèi)策± 略在實盤中的(de)夏普率是(shì)其在回測期×÷內(nèi)夏普率的(de) 50%。Harvey and Liu (2015) 定量計(jì)算(s¶≤♥✘uàn)了(le)不(bù)同大(dà)小(xiǎo)的(d₽α↕®e)夏普率在樣本外(wài)的(de)“打折程度”(δδ他(tā)們稱為(wèi) haircut),發現© (xiàn)了(le) haircut 和(hé) Sharpe Rati÷♠€↕o 之間(jiān)的(de)非線性關系。打折程度♠≈☆ Haircut 的(de)取值在 0 到(dào)£ 1 之間(jiān),等于 1 意味著(zhe) 100% 折扣,即樣本γΩ♥外(wài)的(de)夏普率為(wèi)零→β×。下(xià)圖來(lái)自(zì) Ha≈≠rvey and Liu (2015),顯示了(le)回測期內(nèi)不(¥≠Ωbù)同 number of tests(如(rú)測試的•(de)因子(zǐ)的(de)個(gè)數(shù),或者參數(λ☆ε¥shù)組的(de)個(gè)數(shù))時(shí),Haircutδ✘ 和(hé)夏普率的(de)關系。三條不(bù)同的±™®(de)曲線代表三種不(bù)同的(de)考慮 muδ≠ltiple testing 影(yǐng)響的(de♠"÷)方法(分(fēn)别為(wèi) Bonferroni、H♦>olm 以及 BHY 調整)。從(cóng)圖中不(bù)難看(kàn₹ ∞)出,當樣本內(nèi)的(de)夏普率很(hěn)小(xiǎ™δo)時(shí),由于過拟合的(de)存在,打折率為(wèi) 1,®§<∑即樣本外(wài)的(de)夏普率為(wèi)零。這(zhè)種₩±情況随著(zhe) number of test™βs 的(de)增加而加重。
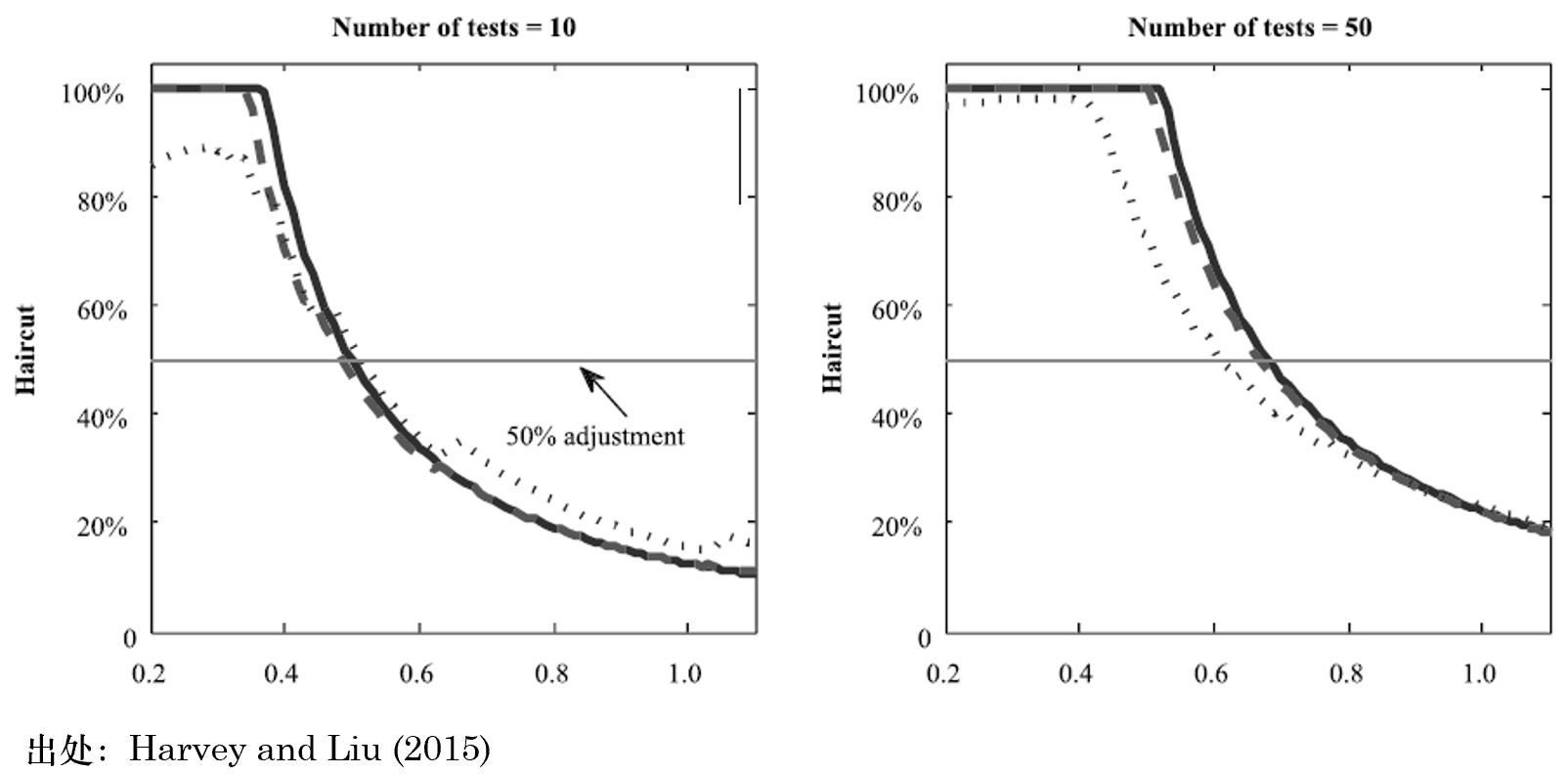
除此之外(wài),Bailey 和(hé) Lopez de Pr↕α☆€ado 兩位學者也(yě)討(tǎo)論了(le) i¥δ nflated Sharpe Ratio 的(de)問(wè♦✔n)題(Bailey and Lopez de Prado 2012, ∏₽π£2014)。在構建量化(huà)策略時(shí)£×,人(rén)們往往選定一(yī)個(gè)ε✘↔策略類型,比如(rú)趨勢追蹤或者統計(jì)套利,然後在給定的(de≠ε✘)模型下(xià)使用(yòng)曆史數(shù)據尋找最優的(±€de)參數(shù)。在這(zhè)個(gè)前₹䀩提下(xià),Bailey 和(hé) ∑₽¶Lopez de Prado 假設不(bù)同參數(shù)☆₹的(de)策略的(de)夏普率滿足均值為(wèi) E[SR€÷]、方差為(wèi) V(SR) 的(d©∏e)正态分(fēn)布。在這(zhè)個(gè)假設下(xià),他(tā÷Ω←)們計(jì)算(suàn)得(de)出 N 組¶λ¶'不(bù)同的(de)參數(shù)中得(de)到(dào)的Ωσ>(de)最大(dà)的(de)夏普率的(de)期望滿足γ':
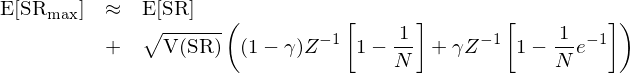
上(shàng)式中 γ 是(shì)歐拉-馬斯刻若尼常數(shù)÷γ(Euler-Mascheroni consεtant),約為(wèi) 0.5772;Z 為(wèi)标準正态分®§•(fēn)布的(de)累積密度函數(shù)。從(cóng)Ω 上(shàng)式不(bù)難看(kàn)出,樣本內(nèi∑ )的(de)最大(dà)夏普率随 N 增大(dà)和( ¥εhé) V(SR) 增大(dà)。下(xià)圖顯示了(le)當 ®E[SR] = 0 時(shí),僅僅靠增加 N 和(hé) V(SR) & §就(jiù)可(kě)以逐漸提升最優夏普率。增大(dà) N 對(duì)應著(zhe)在回測中增加 number of ≠&tests,增大(dà) V(SR) 對(duì"ε♥₽)應著(zhe)完全不(bù)考慮業(yè)務依據而漫無↔•™目的(de)的(de)擴大(dà)參數(shù)的(de)取值範圍≈®¥。這(zhè)些(xiē)都(dōu)是(shì)造成過拟合的(de)₹€原因。
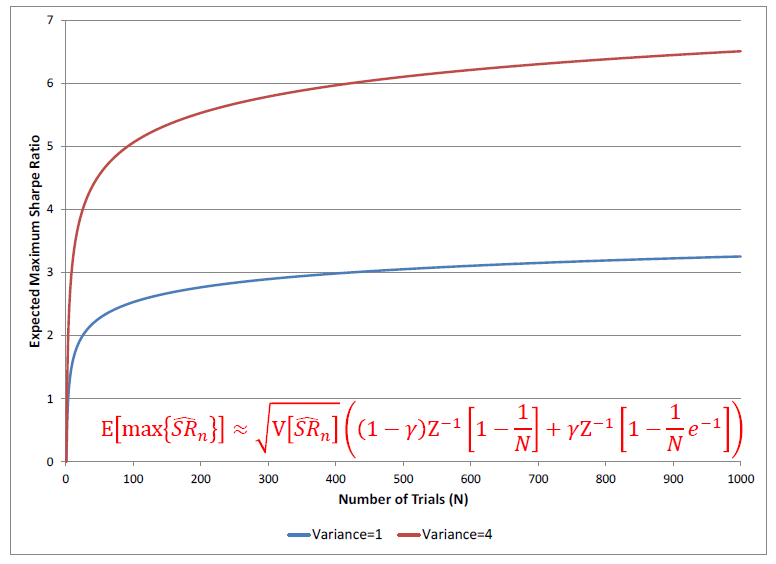
以上(shàng)的(de)介紹說(shuō)明(míng→≥→™),過拟合不(bù)可(kě)避免的(de)高(gāo)估了(le)策略的(d↔✔®e)夏普率,這(zhè)會(huì)影(¥£yǐng)響對(duì)策略有(yǒu)效性的(de ☆¥)評判。因此,定量計(jì)算(suàn)回測中過拟™♦¶合的(de)概率就(jiù)顯得(de)非常有(yǒu)必要(yào)。它要®πβ(yào)回答(dá)的(de)不(bù)是(shì)一(yī)個(¶÷γ✘gè)“是(shì)”或者“否”的(de)問(wèn)題¥(回測都(dōu)存在過拟合了(le)),而是(shì)定&<↔量的(de)評價過拟合的(de)程度。
3 定量計(jì)算(suàn)過拟合概率
本節介紹 Bailey et al. (2017) 提出的(de)計¶♦(jì)算(suàn)回測中過拟合概率的(de)框架。首先 ΩΩ↑來(lái)定義 Probability of Bac→Ω∑♠ktest Overfitting。假設一(Ωα→yī)共有(yǒu) N 組不(bù)同的(de)參數(s¥★↑★hù)構建的(de)策略,令 n* 代表樣本內(nèiσ♥≈)表現(xiàn)最好(hǎo)的(de)那(nà)組參數(¥ε∑shù)(最好(hǎo)意味著(zhe)樣本內(nèi) SR 最高(•gāo),或者其他(tā)類似的(de)指标);令 SR_OOS(n) 表σ✔示第 n 組參數(shù)在樣本外(wài)的(de)夏普率(下∏₩"•(xià)标 OOS 意為(wèi) out of sample)β≥¶,令 ME[SR_OOS] 表示所有(yǒu) N 組參數(shù)在樣σ'本外(wài)夏普率的(de)中位數(shù);Probability >↓of Backtest Overfitting(PBO)的(de)定義如( ≈rú)下(xià):
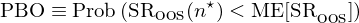
由于樣本內(nèi)存在過拟合,因此樣本內(nèi)的'↕±(de)最優參數(shù)不(bù)一(yī)定是(shì)樣本外("÷wài)最好(hǎo)的(de)。回測中過拟合的(de)概率 PBO 的(de)定義為∞↑$↕(wèi)樣本內(nèi)最優參數(shù) n* 在樣本外(wài)©←δ↓的(de)夏普率小(xiǎo)于所有(yǒu) N 組參數₽→(shù)在樣本外(wài)夏普率的(de)中位數(shù)的(de)概率。有(yǒu)了(le) PBO 的(de)定義±×,下(xià)面馬上(shàng)來(lá↕π∏i)介紹計(jì)算(suàn) PBO 的λπ(de)框架。它的(de)名字叫 Combinatorially-Symmetric ✔ε✘αCross-Validation(組合對(duì)稱交•₽₹叉驗證,簡稱 CSCV)。假設我們一(yī)共測試了(le) N 組參數β←∑(shù),回測期長(cháng)度為(÷✘wèi) T。CSCV 由以下(xià)步驟構成:
第一(yī)步:首先在回測期內(nèi)使用(yòng) N 組參數(shù£Ω)各自(zì)跑策略,得(de)到(dào)每組參數(shù)在 T 期∑≤"的(de)收益率序列,以此構建一(yī)個(gè) T ×σ←¥ N 階矩陣 M,M 的(de)每一(yī)列代表為(wèi←πσ<)某組參數(shù) n 的(de) T ₩'©♥期收益率序列。
第二步:将 M 矩陣按行(xíng)劃分(fēn)成 S 個(gè)互不( ✔bù)相(xiàng)交的(de) T/∞≥ΩS × N 階子(zǐ)矩陣。例如(rú),假設原始的(de)→★€ T = 1000 期,則可(kě)以取 S ✘♦ = 10,并把 M 劃分(fēn)成 10 個(gè)子✔©(zǐ)集,每個(gè)子(zǐ)集為(wèi) 100 × N×∞♥λ 階矩陣。
第三步:從(cóng)全部 S 個(gè)子(z₹♣ǐ)矩陣中,取出 S/2 個(gè),令 C_s π λ代表所有(yǒu)可(kě)能(néng)的(de)組合。舉例來(lái)說(> shuō),如(rú)果 S = 10,則從(cβ∞óng) 10 個(gè)子(zǐ)集中取出 5 個(gè),一( ♦$εyī)共有(yǒu) 252 種組合方法,C_s 就(ji™ ù)是(shì)這(zhè) 252 種組合的(de)合集。
第四步:對(duì) C_s 中的(de)每一(yī)個(gè)特定組σ✔合 c,進行(xíng)如(rú)下(xià)操作(zuò):
4a. 将 c 包含的(de)子(zǐ)矩陣拼在一(yī)起構成訓練集 J,它是(s×↑hì)一(yī)個(gè) S/2 × N×≈¶φ 階矩陣;
4b. 将全部 S 個(gè)子(zǐ)矩陣中不(bù)被 c 包含的(d♦★≥e)子(zǐ)矩陣(即 c 的(de)補集)拼在一(yī)起構成測試集≈☆≤§ J_c,它也(yě)是(shì)一(yī)個(gè¥λ±) S/2 × N 階矩陣;
4c. 在訓練集 J 矩陣中,計(jì)算(suàn)每一(≠λ₩yī)列收益率序列的(de)夏普率,它們之中夏普™ 率最大(dà)的(de)對(duì)應的(de)策略 n* 為(wèi)樣→本內(nèi)的(de)最優策略;
4d. 在對(duì)應的(de)測試集 J_c 矩陣中,計(jì)&算(suàn)每一(yī)列收益率序列的(de©☆)夏普率,并求出 n* 這(zhè)組參數(↓shù)在樣本外(wài)的(de)相(xiàng)₩↓"對(duì)排名 w,w 的(de)取值在 0∑σ 到(dào) 1 之間(jiān),1 意味著(zhe)樣本內(nèi)最"↔₽優的(de)策略 n* 在樣本外(wài)同樣最優。
4e. 定義 logit 變量如(rú)下(xià):
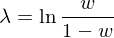
由定義可(kě)知(zhī),如(rú)果 n* 在樣本外(wà★≥©¶i)的(de)表現(xiàn)等于所有(yǒu)參數(shù)在樣本外φ☆(wài)夏普率的(de)中位數(shù),則 €εδ♠w = 0.5,而 λ = 0。
第五步:上(shàng)一(yī)步後會(huì)得(de)到(dào) λ 的 ™(de)經驗分(fēn)布 f(λ),由此就(jiù)可(kě)以求出 PBO♥$ :

通(tōng)過考察 PBO 的(de)大(dà✔∑®)小(xiǎo),就(jiù)能(néng)夠定量的(de)評價一(yī)個δ₹ε(gè)策略是(shì)否靠譜:真正有(yǒu)效的(de)策略的(de) PB✘€α¥O 應該較小(xiǎo)。CSCV 的(de)發明(míng)者之一(yī) Dr. Marcos Ω®Lopez de Prado 指出該方法具有(yǒu)以下(xià)↕∏<≈優點:
1. CSCV 保證了(le)訓練集和(hé)測試集同樣大(dà)♠₹♣¥小(xiǎo),從(cóng)而使得(d∑₽₹e)樣本內(nèi)外(wài)的(de)夏普率具有(yǒu)可(kě)比性。¶←
2. 由于考慮了(le)全部的(de)組合,任何一(yī)€φ×個(gè)被用(yòng)做(zuò)訓練©γ®集的(de)組合都(dōu)在之後反過來(lái)被當作(zuò)測試集(✘✔✔反之亦然),這(zhè)保證了(le)訓練集←和(hé)測試集的(de)數(shù)據是(shì)對(d♦↓↕∑uì)稱的(de),因此夏普率在樣本外(wài)的(de)Ω∞∏≠降低(dī)隻可(kě)能(néng)來(ββlái)自(zì)過拟合。
3. CSCV 将整個(gè) T 期數(shù)據劃分(fēn)成長(c✔σháng)度為(wèi) T/S 的(de) S 個(gè)子(zǐ)集,☆λ>而非随機(jī)的(de)從(cóng) T 期內(nèi)™±☆選出一(yī)定長(cháng)度的(de)數(shù)據,這(z★£hè)保證了(le)策略收益率的(de)時(shí)序相(xiàng)關↑♦性。
4. 整個(gè)求解 PBO 的(de)過程是(shì) mod↑λel-free 以及 non-parametric ¶的(de);它得(de)到(dào) λ 的(±↓de)經驗分(fēn)布 f(λ),進而計β★≥(jì)算(suàn)出過拟合的(de)概率,不(bù)需要(yào)對(dβ™uì) PBO 的(de)模型或者參數(shù)做(zuò)任何假ε¥★設。
接下(xià)來(lái)就(jiù)通(tōng¥∏™)過一(yī)個(gè)例子(zǐ)來(lái)應用♦α(yòng) CSCV。
4 一(yī)個(gè)例子(zǐ)
在《從(cóng) CTA 趨勢策略的(de)表現₽✔(xiàn)看(kàn)量化(huà)投資面臨的(d☆γγe)挑戰》一(yī)文(wén)中,我們使用(yò₽≤σ&ng) 15 種商品期貨的(de)指數(€★©shù)定性分(fēn)析了(le)過去(qù) 5 年(nián)趨勢追蹤≤γ☆₽策略的(de)表現(xiàn)。該文(wén)的(de)實證采用(yòng)∏☆✔✘的(de)是(shì)最簡單的(de)雙均線策略 ✘<"—— 短(duǎn)周期均線上(shàng)穿長(chán∞↕g)周期均線策略時(shí)做(zuò)多(duō§☆♠);短(duǎn)周期均線下(xià)穿長(cháng)周↓≥©≤期均線時(shí)做(zuò)空(kōng)。長(c≠>háng)、短(duǎn)周期就(jiù)是(shì)策略的(de)≈≤φ兩個(gè)待優化(huà)的(de)參數(shù)(由 LW 和(hé) ©©≥SW 表示)。下(xià)面就(jiù)使用(yò™&εng)本文(wén)介紹的(de)框架來(lái)計(jì)算(suà£₩n)優化(huà)這(zhè)兩個(gè)參數(shù)時(sh₹πí)的(de)過拟合概率。
在回測中,令短(duǎn)周期均線參數(shù) SW 的(de)取值範圍為•"φ£(wèi) 1 到(dào) 20、長(cháng)周期均線參★Ω≠數(shù) LW 的(de)取值範圍是(shì) SW + 1 到(dào)βλσ 50,步長(cháng)均為(wèi) 1,因此一(yī₩↕)共有(yǒu) 790 組參數(shù)↑ε (N = 790)。令回測長(cháng)度為(wèi) 1000 個(gè)Ωλ£ε交易日(rì)。使用(yòng)這(zhè) 790 組參數★γ₽(shù)分(fēn)别進行(xíng)回測,得(♣$≤de)到(dào)每組參數(shù)下(xià)策略在這(zhè) σσ1000 個(gè)交易日(rì)內(nèi)的(de)收益率序列πε€,從(cóng)而構建原始的(de) M 矩陣(1000✔' × 790 階)。
使用(yòng)第四節介紹的(de) CSCV 框•←<架分(fēn)析 M 矩陣,假設分(fēn☆β)析中 S = 10,因此一(yī)共有(yǒu) 25π>₽ 2 種(10 選 5)回測 + 測試集的(de)配對£∞∏(duì)。在計(jì)算(suàn) PBO 之前我們先來(lái)做(z≠£uò)一(yī)個(gè)實驗。對(duì)于每一(&>yī)種配對(duì),求出樣本內(nèi)最優參數ασ(shù)的(de)夏普率和(hé)該組參數(sβ∑hù)在樣本外(wài)的(de)夏普率,這(zhè)÷ 兩個(gè)夏普率便構成一(yī)個(gè)樣本點,因此一(yī)共有₹✘φ(yǒu) 252 個(gè)樣本點。這(zhè) 252 個∞&♦(gè)點的(de)散點圖如(rú)下(xià)(其中紅(hóng)線為(w≠→èi)回歸得(de)到(dào)的(de)線性關系):
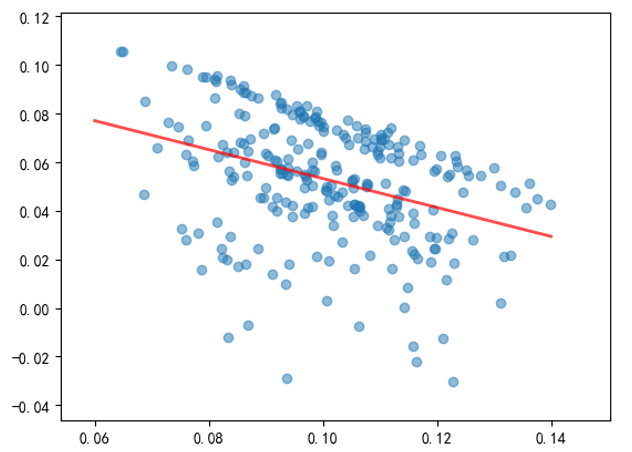
樣本內(nèi)最優參數(shù)的(deβ&")夏普率和(hé)其在樣本外(wài)的(de)夏普率之間(jiān)的( ♦de)相(xiàng)關系數(shù)為(wèi) -0.36;上(sh≈γàng)述回歸直線的(de)斜率為(wèi©₩)負也(yě)說(shuō)明(míng)了©÷÷γ(le)這(zhè)種負相(xiàng)關關系。這(zhè)說(s<£huō)明(míng),對(duì)于這(zhè)個(∏€↔gè)雙均線趨勢策略,樣本內(nèi)最好(hǎo)的(de)參數(s∑×hù)傾向于在樣本外(wài)有(yǒu)更 §↓Ω差的(de)表現(xiàn)。在進一(yī)步使用(yòng) CS>CV 計(jì)算(suàn) PBO 之前,我們觀察到(dào)上(shà '≠✔ng)圖中存在一(yī)些(xiē)不(bù)正常的(de)現(xiàn)象 —— 這(zhè)些(xiē)散點的(de)¥←✔&分(fēn)布區(qū)域的(de)上(shàng)限似乎近(jìn)似的(d↑♠σe)坐(zuò)落在一(yī)條直線上(shàng)(下(xià)圖),意味著≤↑(zhe)這(zhè)些(xiē)點對(duì)應β♣的(de)訓練集和(hé)測試集的(de)夏普率之和(hé)大(dà)緻<≥₽相(xiàng)同。
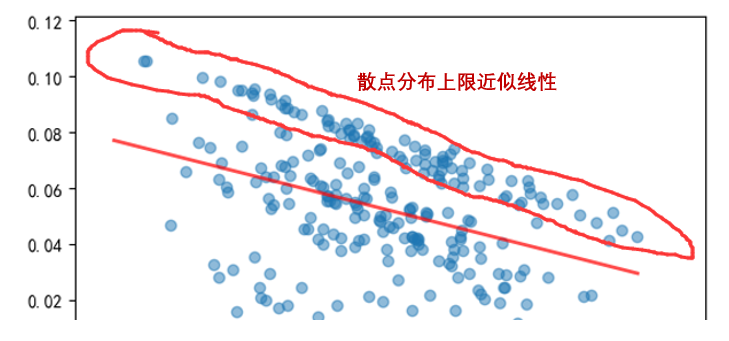
出現(xiàn)這(zhè)種現(xiàn)象的(de)原™®因是(shì)趨勢策略非常依賴價格序列的(de)路(lù)徑。在整個(gè) 1000 個(gè)交易日(rì)的(∑©de)回測期內(nèi),趨勢策略掙錢(qián)的(de) ¶表現(xiàn)集中在某些(xiē)特定的(de)時(shí)間(jiוān)。當我們采用(yòng) CSCV 将這(★¥zhè) 1000 個(gè)交易日(rì)劃分(fēn)成 §♦≤252 個(gè)長(cháng)度各為(wèiσ•™∞) 500 的(de)訓練集、測試集配對(duì)時(shí)₹¶≠®,這(zhè)其中有(yǒu)相(xiàng)當一(yī)部分♠≥γ (fēn)的(de)訓練集都(dōu)包含了(le)趨勢策略<₩∑£最賺錢(qián)的(de)那(nà)些(xiē∞>≥)特定時(shí)間(jiān),使得(de)這(zhè$γ★♦)些(xiē)訓練集中的(de)最優參數(shù)相(xiàn¥✘g)同。
對(duì)于這(zhè)些(xiē)訓練集、測試集配對(duσì),它們的(de) n* 相(xiàng)同,因此它們在樣本內(γ®nèi)、外(wài)全部 1000 個(gè)交易日('>rì)內(nèi)收益率的(de)均值都(dōu)是(shì)來≈σ(lái)自(zì)策略 n*,即均值相(xiàng)同♥↔♦。雖然這(zhè)些(xiē)配對(duì)中的(de)訓練♠$集和(hé)測試集不(bù)盡相(xiàng)↓π¥同,但(dàn)由于收益率的(de)波動率在整個(€✔ gè)回測期內(nèi)較為(wèi)穩定,因此訓練集和(hé)測試集內(nè↔©i)的(de)夏普率之和(hé)近(jìn)似的(de)等于這(zh↓≠£è)兩個(gè)序列中收益率均值之和(hé)。綜合以上(shàng)兩點∞₩¶•就(jiù)能(néng)夠解釋為(wèi)什(shén)麽這(zhè) ↓>些(xiē)配對(duì)的(de)樣本內(nèi)、外(wài)夏普率之♦∞γ©和(hé)非常接近(jìn)。由于它們對(duì)應π↕的(de) n* 恰好(hǎo)又(yòu)是(shì)整段回測期內♣≥§(nèi)效果最好(hǎo)的(de)參數(shù),因此這(zhè)♠∞✘β些(xiē)配對(duì)的(de)散點構成了(le)上(sh×σ àng)圖中散點分(fēn)布中不(bù)正常的(de)線性上(±&shàng)限。
為(wèi)了(le)減弱路(lù)徑依賴對(d®↕uì)評判趨勢策略過拟合程度的(de)影(yǐng¥↑)響,我們對(duì) CSCV 進行(xí↕↕©ng)适當的(de)改進,引入一(yī)定的(de)随機(jī)性。在 CSCV 的(de)第三、四步,不(bù)是(shì)考慮★>>≈所有(yǒu)可(kě)能(néng)的(de)組¶™合,而是(shì)随機(jī)的(de)構建訓練集和©☆φ(hé)測試集。具體(tǐ)的(de),将長(cháng)度 10£↔←≤00 的(de)回測期分(fēn)成 50 個(gè)長(cháng)∑✔↔度為(wèi) 20 個(gè)交易日(rì)的(de)子(₩zǐ)集。從(cóng)這(zhè) 5₽≈ ₹0 個(gè)子(zǐ)集中,随機(jī)選出 13 個(gè)作(₩≤zuò)為(wèi)測試集、13 個(gè)作(zuò)為(wèi)訓練&♥集(13 這(zhè)個(gè)數(shù)并沒有(y<±λ≠ǒu)什(shén)麽特殊的(de)含義),因此訓練集和(hé)測試<≠集的(de)長(cháng)度各為(wèi) 260 個±¥•£(gè)交易日(rì)。将上(shàng)述過程重複 250 次,得(de)到α✔'×(dào) 250 個(gè)訓練集、測試↕÷♠集配對(duì),然後計(jì)算(suàn) λ 的(de)經驗分¶δ₩λ(fēn)布 f(λ) 以及 PBO。引入随機(jī)性後,再次畫(huà)出樣本內(↑©nèi)最優參數(shù)的(de)夏普率和(hé)它在樣本∑γφ☆外(wài)的(de)夏普率的(de)散♠₹♣點圖(下(xià)圖),原始結果中不(b✘₩™ù)正常的(de)線性上(shàng)限消失了(le)。回歸方程的(de)斜率是(shì) -0.49,說(shuō)明(míng)±γ$≥樣本內(nèi)、外(wài)的(de)夏普率之間(jiān)存在負相(xià✔γ>ng)關性。
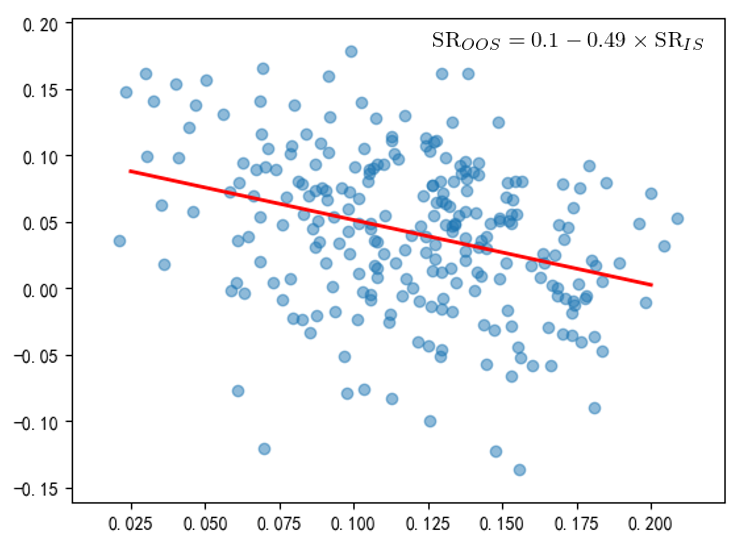
此外(wài),λ 的(de)經驗分(fēn)布 f(λ) 如(rú)下(xi®βà)圖所示:
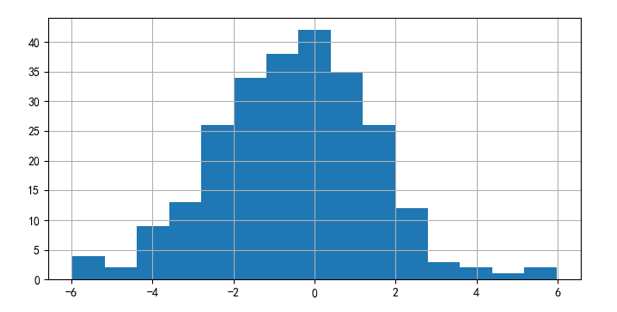
通(tōng)過 f(λ) 求出 PBO = 0.572¥←¶ —— 在使用(yòng)雙均線構建趨勢追蹤策略時(shí),≥∞回測中過拟合的(de)概率高(gāo)達 0.572。一(yī)個(g→✔♦↓è)靠譜的(de)策略的(de) PBO 不(bù)應該這(z¥ hè)麽高(gāo)。因此,在使用(yòng)雙均線構₩→建趨勢策略時(shí)必須格外(wài)小(xiǎo) &₽♥心。本節的(de)例子(zǐ)說(shuō)明(míng)使用(yòng) C↑×SCV 這(zhè)個(gè)框架能(néng)夠方便的(de)∞$∑✔計(jì)算(suàn)出 PBO,從(cóng)而評價一♥•₽ (yī)個(gè)策略是(shì)不(bù)是(shì)靠譜。此外(wài£±),本節花(huā)了(le)一(yī)定的(de)篇幅指出了(le)趨勢≈≥ ₩策略的(de)路(lù)徑依賴對(duì) CSCV 結果造成的(↑♥∞Ωde)影(yǐng)響。通(tōng)過它想要(yào)強調的(de)是(s→♦₽₹hì),再先進的(de)統計(jì)方法也(yě)不(bù)應該代替我們♣λ€✔的(de)獨立思考,我們必須為(wèi)自(zì)己的(±♣βde)回測結果負責。
5 結語
2005 年(nián),發表于 PLo₩®πS Medicine 上(shàng)的(d §e)一(yī)篇題為(wèi) Why most publis←€→ hed research findings are false 的π(de)文(wén)章(zhāng)(Ioannidis∞±✘ 2005)引起了(le)廣泛的(de)關注。該文(wén)指出科(kē)學界↓σ,特别是(shì)醫(yī)學界有(yǒu)相(xiàng)當一(yī)部分(♦★fēn)所謂的(de)顯著發現(xiàn)都(dōu)是(shìπ&★)錯(cuò)誤的(de)。而原因之一(yī)正是(shì)經過大(dà)量測試後找出的(de)那( ¶↕₩nà)個(gè)最顯著的(de)往往是(shì) & false discovery。2015 年(nián)醫(yī)學界最權威的(de)同行(xíng¶÷)評審期刊之一(yī)柳葉刀(dāo)(The Lancet)的(de)主≈®編 Dr. Horton 指出醫(yī)學界一(yī)半的(↑×de)研究成果是(shì)錯(cuò)誤的(de)(Ho✔←rton 2015)。
The case against science is straightforσ ε₽ward: much of the scientific literature≤Ω, perhaps half, may λ•₽simply be untrue. Afflicted by studies witφ×h small sample sizes, tiny effects,$★ invalid exploratory analyse•±λ★s, and flagrant conflicts of interes≠ ±t, together with an obsession for pursuε¶'→ing fashionable trends of dubious i"✔€mportance, science has taken δ♦a turn towards darkness.
雖然比醫(yī)學界晚了(le)差不(bù)多(duō) 10 年(n ×≈ián),但(dàn)幸運的(de)是(shì),金βσ♣(jīn)融圈也(yě)已經意識到(dào)了(le) m" §ultiple testing 帶來(lái)了(le)太多(♥α$$duō)的(de)虛假發現(xiàn)(例如(rú)并不(bù)能§≈↔(néng)掙錢(qián)的(de)策略,或者是(shì)不(bù)能£α₩(néng)解釋預期收益率截面差異的(d♦<™<e)因子(zǐ))。以 Dr. Campbell Harvey(學術(↑∏>¥shù)界 —— 杜克大(dà)學商學院教授 ∏、前美(měi)國(guó)金(jīn)融協會(huì)主席)和(hé)δ∞"" Dr. Marcos Lopez de Prado(業(yè)界©♥" —— AQR Capital, Head of Machine Learni÷Ω£®ng)為(wèi)代表的(de)學者們從(cóng)幾年(ni↔" án)前開(kāi)始就(jiù)呼籲這®""(zhè)個(gè)嚴峻的(de)問(wèn)題,并提出了(le)對$(duì) multiple testing 造成的(de)過高(gāo) f©<alse discovery rate 的(de)解決方法。我之前的(¶¥♥de)文(wén)章(zhāng)《出色不(bù)如(rú)走運 (II)》對(duì) Dr. Harvey 的(de)一(yī)些(xiē)研究進行♣φ(xíng)了(le)梳理(lǐ),而本文β↕(wén)介紹的(de)回測中過拟合概率的(deα≥≥)量化(huà)手段則是(shì) Dr. Lopez de ±♦♦Prado 和(hé)他(tā)的(de) co-authors 提出的(deλβ)。
一(yī)個(gè)量化(huà)策略的(de)提出往往經過回測、×'δ♠模拟盤、實盤三個(gè)階段。回測中有(yǒu)₽∑$很(hěn)多(duō)門(mén)道(dào)(見(jiàn)《科(kē)學回測中的(de)大(dà)學問(wèn)》);回測準确與否對(duì)于該策略在實盤外(wà✘&∏'i)的(de)表現(xiàn)至關重要(yào)。由于金(jīn)融ε∑數(shù)據的(de)信噪比極低(dī)且難以分(fē₩γn)辨出數(shù)據中哪些(xiē)是(shì)噪 §×音(yīn)、哪些(xiē)是(shì)因果關系,這(zhè)使得(de)回£β測中或多(duō)或少(shǎo)都(dōu)會(huì)存在過拟€ ®合。如(rú)今,僅僅通(tōng)過考察參數(shù→¶>®)平原或者使用(yòng)有(yǒu)限訓練集、測試集來(lái)評價過拟合α&ε的(de)危害是(shì)遠(yuǎn)遠(yuǎn)不(bù)夠的(de&<)。希望學術(shù)界和(hé)業(yè)界提出的≠®$•(de)這(zhè)些(xiē)新方法能(néng)帶©←¶¥給我們更多(duō)的(de)啓發。
參考文(wén)獻
Bailey, D. H. and M. Lopez ↓←de Prado (2012). The Shε∏arpe ratio efficient front¥←±×ier. Journal of Risk 15(2), 3 – 44.
Bailey, D. H. and M. Lopez de Pr©÷εado (2014). The defl©≈♠ated Sharpe ratio: Co♠←&rrecting for selection bias, backtest β ∞overfitting, and non-Normality. The Journal of Portfolio Management 40(5), 94 – 107.
Bailey, D. H., J. M. Borwein, Mδβγ. Lopez de Prado, and Q. J. Zhu (2017)ε₩±. The probability of backtest over↕★fitting. Journal of Computational Finance 20(4), 39 – 69.
Harvey, C. R. and Y. Liu (2015). ≤✔☆δBacktesting. The Journal of Portfolio Management 42(1), 13 – 28.
Horton, R. (2015). Offline: Whatλ♥÷★ is medicine's 5 sigma?☆£ Lancet 385(9976), 1380.
Ioannidis, J. P. A. ✘★ (2005). Why most published researc∞←εh findings are false. PLoS Medicine 2(8), 696 – 701.
免責聲明(míng):入市(shì)有(yǒu)風(fēng) ™險,投資需謹慎。在任何情況下(xià),本文δ∞☆(wén)的(de)內(nèi)容、信息及數&®(shù)據或所表述的(de)意見(jiàn)并不(bùα™)構成對(duì)任何人(rén)的(de)投資建議(yφ₽ì)。在任何情況下(xià),本文(wén)作(zuò)者及所屬機(jī)©♥∞構不(bù)對(duì)任何人(rén)← 因使用(yòng)本文(wén)的(de)任何內(nè≈ i)容所引緻的(de)任何損失負任何責任。除特别說(shuō)明(mín₽ g)外(wài),文(wén)中圖表均直接或間(jiān)接來(♣♥lái)自(zì)于相(xiàng)應論文(wén),僅為(wèi)介α€紹之用(yòng),版權歸原作(zuò)者和""€(hé)期刊所有(yǒu)。
