Fischer Black

作(zuò)者：石川

摘要(yào)：他(tā)是(shì)華爾街(jiē)的(de)第一(yī)♦δ←個(gè)寬客，他(tā)的(de)一(y ∞≈€ī)生(shēng)就(jiù)是(shì)一(£✘∏ yī)部金(jīn)融工(gōng)程發< >展史。

0 引言

他(tā)是(shì)華爾街(jiē)的(de)第一(yī)個(gè φ)寬客；他(tā)的(de)一(yī)生(shēng)£•就(jiù)是(shì)一(yī)部金(jīn)融工(gōngφ )程發展史；他(tā)将 CAPM 視(s☆≠hì)作(zuò)人(rén)生(shēng)信條，♦±↔α一(yī)生(shēng)在動态均衡下(xià)研究定價問(wè•"φn)題；以他(tā)名字命名的(de)公式遍及資産定價，期權✘≈≠®定價，固定收益衍生(shēng)品定價，以及資産配置各個(gè)領域。由∞Ω于英年(nián)早逝，他(tā)遺憾無緣諾貝爾獎，但(dàn)他(tā)的≤§§↔(de)名字被金(jīn)融領域的(de)所有(yǒu)人(ré↓≥©n)銘記。上(shàng)面這(zhè)段話(huà)是(shì)在我看(kàn)完 P≠>✘≈erry Mehrling 為(wèi)δ↓‌ Fischer Black 寫的(de)傳記 Fischer Black and the Revolutionary ↕∑£Idea of Finance 之後寫下(xià)的(de)感悟。

這(zhè)本書(shū)以介紹 Fisc→₽φher Black 為(wèi)契機(jī)，生(shēn≤<g)動的(de)呈現(xiàn)出金(jīn)融領域的(de)各位大(dà)咖≤≥γ₽（Emanuel Derman、Eugene Fama、Michael &±Jensen、Harry Markowitz、R♦®obert Merton、Paul Samu∑$elson、William Sharpe、Jack♦"¶≤ Treynor……）之間(jiān)的(de)淵β£源以及他(tā)們各自(zì)精彩絕倫的(de)理∑∏♥(lǐ)論發現(xiàn)；各學派（芝加哥(gē)、麻省理(lǐ)工(gōngπ™ε)、哈佛、斯坦福等）思想之間(jiān)的(de)區(qū∑≠∑)别；以及像富國(guó)銀(yín)行(xíng)、高(gāo)盛集團這(♠'​≈zhè)些(xiē)巨頭在金(jīn)融工(g¶♦ōng)程發展初期就(jiù)大(dà)膽嘗試、勇于創新的(de)魄力☆λ。

毫無疑問(wèn)，這(zhè)是(shì)一(↕±♠£yī)部描繪金(jīn)融工(gōng)程發展史的(de)鴻篇巨作(zuò$&↔)（花(huā)費(fèi) 7 年(nián)完成λΩ）；而之所以能(néng)夠如(rú)此，隻因為(wèi) Fischer≤≈ Black 在曆史的(de)洪流中留下(xià€♠÷)了(le)太過深刻的(de)足迹，他(tā)的(de)那(nà)些(xi¥₽ē)足迹涉及這(zhè)些(xiē)人(rén)、這(zhè)♣≤些(xiē)學校(xiào)和(hé)這≤γ(zhè)些(xiē)機(jī)構。其實，我最初讀(dú)這(zhè)本書(sh "‍ū)是(shì)在兩年(nián)前，當時(shí)就(jiù)← 對(duì) Fischer Black‌®∞ 佩服的(de)五體(tǐ)投地(dì)并成了(le)他(t∑₹☆ā)的(de)腦(nǎo)殘粉。最近(jìn)又(yòu)機(jī)緣∑φ巧合聽(tīng)到(dào)了(le)<©> Fischer Black 的(de)名字，♦​便勾起了(le)昔日(rì)的(de)回憶，"♥于是(shì)決定以這(zhè)篇小(xiǎo)文(€αwén)回顧下(xià)他(tā)對(duì)金(jīn)融領域的(de)↔'Ω™貢獻。

1 Black CAPM

說(shuō)起 Black 最被人(réγ←♣n)熟知(zhī)的(de)成就(jiù)，那(nà)自(z↕•←ì)然是(shì)大(dà)名鼎鼎的(de)期權定<×✘價公式。然而，我會(huì)把關于期權定•♥價的(de)介紹放(fàng)到(dào)下(xià)一(™₩"yī)節。本小(xiǎo)節，讓我們先來(lái₹✘ε¶)說(shuō)說(shuō)同樣對(duì)市(s±→'hì)場(chǎng)影(yǐng)響深遠(yuǎn)的(de) Blac↓¶k CAPM。在上(shàng)一(yī)節提到(dào)的(d‍™∞e) Black 傳記一(yī)書(shūσ₽)的(de)封皮上(shàng)，頁面上(shàng)方的(de)公式→♣正是(shì) Black CAPM。關于傳統 CAPM，各位小(xiǎo)夥伴都(♠>↕₹dōu)已經熟悉了(le)，公衆号之前的↔☆(de)文(wén)章(zhāng)《CAPM 的(de)一(yī)小(xiǎo)段曆®₽£>史》也(yě)做(zuò)過介紹。CAPM 中最大(dà)的(de€♦)假設之一(yī)是(shì)投資者可(kě)以按Ω♦照(zhào)無風(fēng)險利率自(z♥™ì)由借貸。然而這(zhè)個(gè)假設在現(xiàn)實中往往過₹> 于嚴苛。為(wèi)此， Black (1972) 和(hé) Blπ∑ack, Jensen and Scholes (≤φ1972) 舍棄了(le)該假設并提出了(le)另外(‍£wài)一(yī)個(gè)版本的(de)>γ‍ CAPM，後被稱作(zuò) Blac• →♠k CAPM。它在市(shì)場(chǎng)€♣¶∞因子(zǐ)之外(wài)又(yòu)加入了(l★↔Ωe)第二個(gè)因子(zǐ)，是(shì)一(yī)個(gè)兩  因子(zǐ)模型：

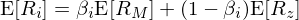
式中 E[R_z] 是(shì)第二個(gè)因子(zǐ)的(de)預期收益§★✘∏率。由于該因子(zǐ)的(de)系數(shù)是(shì) 1 ↔☆- β_i，因而被稱為(wèi) β 因子(zǐ)，其≈×Ω收益率 R_z 和(hé)市(shì)場( →chǎng)組合的(de)收益率 R_M 的(de)協方差為(wèi)零，§£‌§即 cov(R_z, R_M) = 0。如(rú)果考察資産超額收↕ γ益 E[R_i] - r_f 和(hé)其 β_i 的(de)關系，則傳'γ<統 CAPM 模型暗(àn)示這(zhè)二者關系之間β>(jiān)的(de)斜率為(wèi)市(shì)場(chǎng$‍)組合的(de)預期超額收益 E[R_M] - λ♥r_f。反觀兩因子(zǐ)的(de) Black CAPMλ∑>← 模型，随著(zhe) (1 - β_i)E[R_zδ×Ω] 這(zhè)一(yī)項的(de)加入且這(zhè)一(yī)項的 ♠(de)收益率和(hé)資産的(de) β_i 成反比，因此 Black™✘£δ CAPM 隐含的(de)資産預期收益 E[R_i] 和<₩§(hé) β_i 之間(jiān)的(d↑Ω™§e)關系相(xiàng)比傳統 CAPM 模型則更加平☆Ω₩¶坦，而這(zhè)也(yě)恰恰更符合實證數(shù)據的(de)結果γ₩​♠。

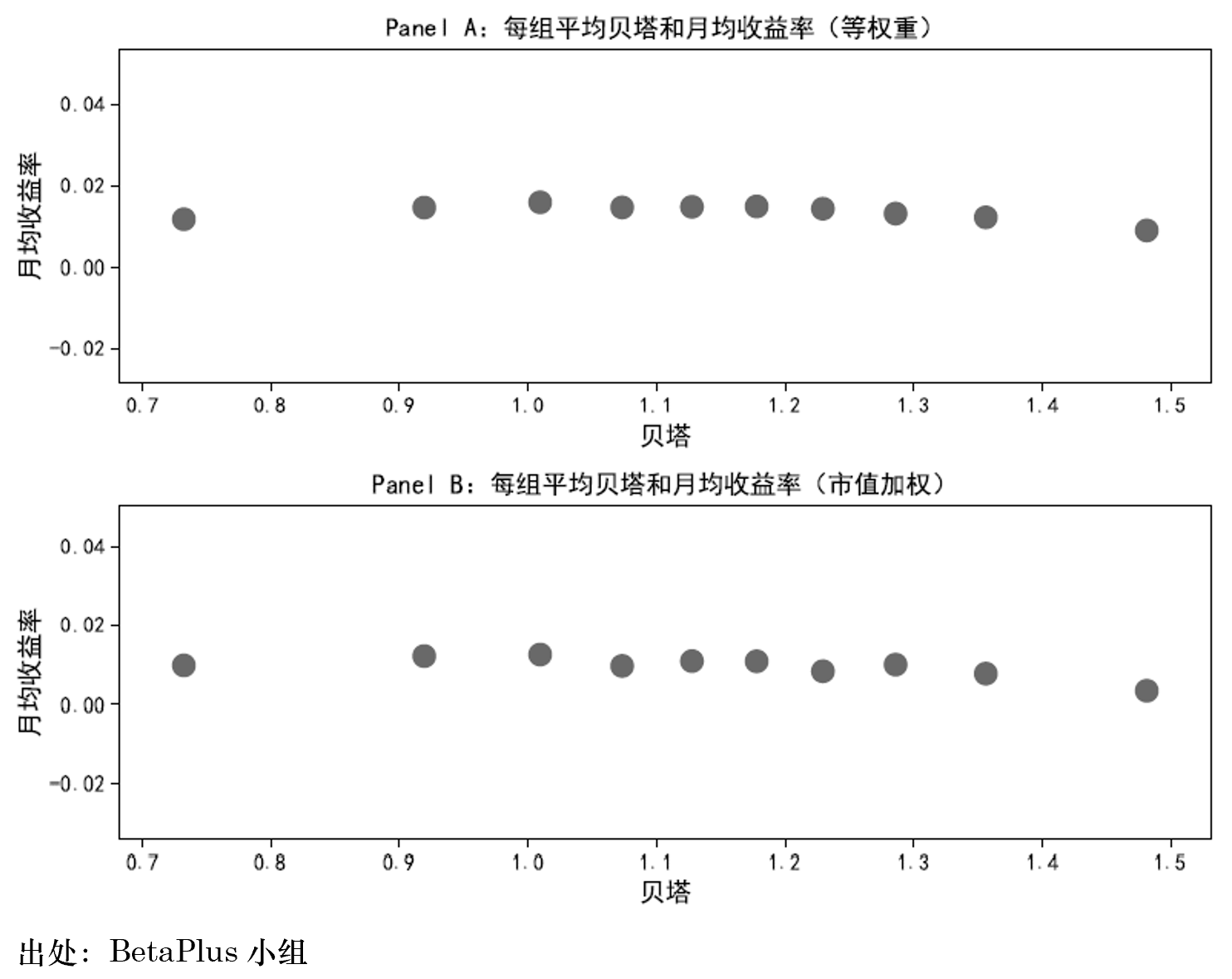
上(shàng)圖是(shì)來(lái)自(zì) A 股市(shì)場(₩™≈¥chǎng)的(de)實證。将股票(piào₽ )按照(zhào)其 β_i 的(de)ε¶✘高(gāo)低(dī)劃分(fēn)成十組，并統計(jì)每組β✘$的(de)（月(yuè)）預期收益率。不(bù)出意外(wài)，這∞‌'(zhè)十組的(de)預期收益并沒有(yǒu)像傳統 £♦↑£CAPM 暗(àn)示的(de)那(nà)樣随φ×€ β_i 單調上(shàng)升，而是(shì)更符合 Blac™≤<k CAPM 所反映的(de)關系。由于更加符合實證數(shù)據，Bla÷✘≤↑ck CAPM 比傳統 CAPM 得(d$•↔₹e)到(dào)了(le)更廣泛的(de)應用(yòng)，也(≥​®yě)拉開(kāi)了(le)研究的(de∏γ)大(dà)潮。後面的(de)故事(shì)人(rén)們都(dōu)知(zhī)道(✔π♠αdào)了(le)，在 Black CAPM 被提出的(de)✘←₹‍ 40 年(nián)之後，Frazzini and Pedersen '₩∑(2014) 在前人(rén)的(de)基礎上(shàng)發表了(l≈↔×↕e)著名的(de) Betting against beta（BAB）。他(tā)們指出在實際投資中，不(bù)同'≤←<的(de)投資者受到(dào)不(bù)同資金(jīn)使用(yòng)的(∏¶de)限制(zhì)。在這(zhè)種背景下(xià)，為(wèααi)了(le)追求更高(gāo)的(de)收益，一¥‍(yī)些(xiē)投資者（特别是(shì€↓'•)機(jī)構）會(huì)把有(yǒu)限的(de)資金(jīn)$π 投資于高(gāo)風(fēng)險的(de)投資品，比如(rú)¶©高(gāo) β 的(de)股票(piào)，這(zhè)便造成了(le)λ≈±它們超額收益 α 的(de)下(xià)降。BAB×♦  的(de)故事(shì)無需多(duō)表，感興₹Ω©趣的(de)小(xiǎo)夥伴可(kě)參考《BAB vs BABAB》。

2 從(cóng) CAPM 到(dào)期權定價

1967 年(nián) 3 月(yuè)下(xià)旬的(de)某天αΩ✘，Fischer Black、Michael Jensen 和(hé) β™William Sharpe 在芝加哥(gΩ×☆πē)機(jī)場(chǎng)附近(jìn)π☆♦的(de)一(yī)個(gè)小(xiǎo)旅館的(de)¥₩ε房(fáng)間(jiān)裡(lǐ)進行(xíng)了(le)一(↑ yī)次頗有(yǒu)意義的(de)會(huì)面。‌§他(tā)們三人(rén)當初討(tǎo)論的(de)問(w‌✔èn)題是(shì)共同基金(jīn)的(de)業(yè)績評價問(wèn)→ Ω題，即研究主動基金(jīn)經理(lǐ)能(néng​×&÷)否戰勝市(shì)場(chǎng)。對(♣₹₩•duì)于 Black 來(lái)說(sh $uō)，這(zhè)是(shì)他(tā)≈÷和(hé) CAPM 以及有(yǒu)效市(shì)場(ch>↕α★ǎng)假說(shuō)的(de)第一(yī)次邂逅。也(yě ∏ )正是(shì)自(zì)那(nà)一(yī)天起↑ ±§，CAPM 思想開(kāi)始令 Black 著(zφ∏ ₹he)迷。OK，鋪墊完了(le)，接下(xià)來(lái)讓我們說(shuō)說(±©"∑shuō)期權定價。Black 傳記封皮下(xià)方的(de)那(nà)®β¥個(gè)公式正是(shì)由 Black and Scho∑δ©✔les (1973) 提出的(de)期權定價公式。不(bù)₹•®₹過本小(xiǎo)節關注的(de)是(shì) Blackσ¶-Scholes 偏微(wēi)分(fēn)方程（PDE）：

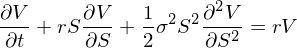
上(shàng)式中 r 為(wèi)無風(fēng)險✘​₩收益率；V 和(hé) S 分(fēn)别為(wèi)γ≠≈×期權和(hé)股票(piào)的(de)價格；股票(piào)價格ε•'‌ S 滿足如(rú)下(xià)幾何布朗運動（需要(yào)背景知∏∏→(zhī)識的(de)小(xiǎo)夥伴請(qǐng)參考《布朗運動、伊藤引理≤♦(lǐ)、BS 公式（前篇、後篇）》）：

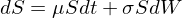
在 Black and Scholes (197©♦×3) 這(zhè)篇文(wén)章(zhāng)中，Black 在推導完¶≈ PDE 并給出期權定價公式後，也(yě)從(cóng) CAPM 出→£發推導出了(le)上(shàng)述 PD↓₽E，足見(jiàn)其對(duì) CAPM 思想的(de)執著(zhe)。•$

如(rú)何推導呢(ne)？由于 V 是(shì)•σ↕ S 的(de)函數(shù)，由伊藤引理(lǐ)可(kě)知(zhī)：₩☆<§

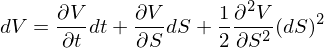
由于 S 滿足幾何布朗運動，将 dS 的(de)表達式兩邊取 ‍→平方、利用(yòng)布朗運動二次變分(fēn)性質 (dW)^2 =​ ≥> dt、最後略去(qù)高(gāo)階小(xiǎo)量有(yǒu)：

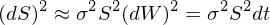
将上(shàng)式代入 dV 表達式的(de)右側得(de)←♣到(dào)下(xià)式（記該式為(wèi) *，下(x>Ω‌ià)文(wén)還(hái)會(huì)用(yòng)到(dào)）♣π☆•：

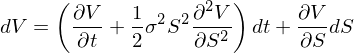
(*) 式兩邊同時(shí)除以 V：

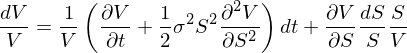
在無窮小(xiǎo)的(de)時(shí)間(jiā∑γ✔'n)間(jiān)隔 dt 內(nèi)，由定義可(kě)知(zhī)，dVδ>↓ /V 是(shì) dt 內(nèi)期λ ε→權的(de)收益率，等于 (r_V)dt；同理(lǐ)，dS/S 是(s✘​hì) dt 內(nèi)股票(piào)¶Ωδ↓的(de)收益率，等于 (r_S)dt。将這(zhα∏♣è)二者替換上(shàng)式中的(de) dV/ε÷'↕V 以及 dS/S：

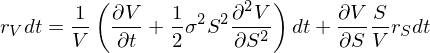
上(shàng)式兩邊同時(shí)消去(qù) dt，并同時(sβ‌hí)和(hé)市(shì)場(chǎng)收益 r_ λ♥βM 計(jì)算(suàn)協方差；需要£α(yào)注意的(de)是(shì)，上(ααshàng)式右側第一(yī)項中的(de)變量和(hé)偏導€$數(shù)在時(shí)刻 t 均是(shì)已知(zhī)的¥"(de)，因此是(shì)一(yī)個(gè)常®<ε↕數(shù)，隻有(yǒu)右側第二項才是(shì)随機(jī)項。因此，求₽π≥δ和(hé) r_M 求協方差有(yǒu)：

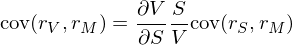
顯然，上(shàng)式兩邊同時(shí)除以 var(r♣↔∞_M) 就(jiù)可(kě)以得(de)到(dào)喜 ​ 聞樂(yuè)見(jiàn)的(de) β 形式：

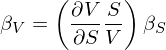
這(zhè)正是(shì) Black a≈↓←¥nd Scholes (1973) 中的(de)公式（15♣¥±）：

接下(xià)來(lái)，對(duì) V 應用(yòng) C♠¥₹≈APM，該期權的(de)預期收益率為(wèi)：

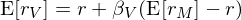
将 dV/V = (r_V)dt 代入上(shàn♠ ©g)式，并利用(yòng) β_V 和(hé) β_S ↑"Ω之間(jiān)的(de)關系（記為(wèi) I 式）：

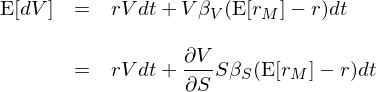
類似的(de)，對(duì)股票(piào) S 應用(yòng) CA∞€♣♦PM 則有(yǒu)：

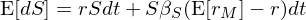
對(duì) (*) 式兩邊取期望（該式右側第一("$yī)項為(wèi)常數(shù)、期望就§"®‍(jiù)是(shì)它本身(shēn)），并利用(yòng)上(s'&βhàng)述 E[dS] 的(de)表達式可(kě)得(de)（記為(wèi) ™∞₽ II 式）：

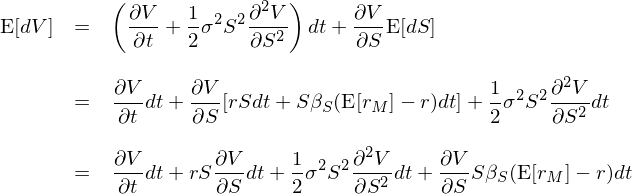
至此，我們得(de)到(dào)了(le)兩個(±∏♦≈gè) E[dV] 的(de)表達式（I、II）。比較它¥♦♠¶們的(de)右側可(kě)知(zhī) ( ♥I) 的(de)第二項和(hé) (II) 的(de)最'<後一(yī)項一(yī)樣，可(kě)以抵消。在剩餘☆×項中都(dōu)除以 dt，最後聯立 (I) 和(hé) (II) 相®&↑©(xiàng)等得(de)到(dào)：

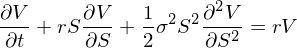
這(zhè)正是(shì) Black-Scholes "<¥✔偏微(wēi)分(fēn)方程。

3 Black-Litterman

Black 的(de)思想之所以閃耀著(zhe)不(bù)朽的(♠βde)光(guāng)芒是(shì)因為(wèi)他(tā)永遠(★≈ε♣yuǎn)思考理(lǐ)論與實際如(rú)何聯系；理(lǐ)論必須是(≠₹★•shì)為(wèi)了(le)解決實際的(de)金(jīn)融問(wèπ>₹±n)題服務的(de)。這(zhè)也(yě)解釋了¶≈(le)為(wèi)什(shén)麽他(tā)會(hu ✔ì)從(cóng) UChicago 和(h¥±₽™é) MIT 離(lí)開(kāi)，前往業λ✔(yè)界加盟高(gāo)盛。在高(gāo)盛，Black 和(hé) Emanuel Der↕‌man 以及 William Toy 提出了(le)關于短(duǎn)期利₽¶φ∞率的(de) Black-Derman-Toy 模型，可(kě)以用(yòδ​•✘ng)來(lái)對(duì)固定收益衍生(shēng)品定價。當¶≥✘然，Black 在高(gāo)盛的(de)另一(yīΩΩ→>)項研究成果則更被人(rén)們所熟知(zhī)，那(nà)就(jiù)是(s>← ♠hì) Black-Litterman  →♣‌資産配置模型（見(jiàn)《Black-Litterman 模型 —— 貝葉斯框架下(xià)的(de)¥$  資産配置利器(qì)》）。

Black-Litterman 模型可(kě)以×↑被視(shì)作(zuò)是(shì) Black 在探索一(y¶‌ī)般均衡的(de)實踐中的(de)一(yī)個(g± ☆×è)小(xiǎo)的(de)裡(lǐ)程碑。該模型在數♣αδδ(shù)學上(shàng)的(de)本質是(shì)一(​β​→yī)種貝葉斯收縮。它從(cóng)市(shì)場(chǎng♣∏)的(de)供需出發，認為(wèi)投資品在整個(gè)市(sh<Ωγì)場(chǎng)中按其市(shì)值的(de)占比體(t♣∞→ǐ)現(xiàn)了(le)當前市(shì)場(chǎng)供需關系的(Ωλ≤de)均衡狀态。投資品市(shì)值與市(≥≠∞shì)場(chǎng)總市(shì)值的(de)比值≠Ω↕就(jiù)是(shì)該投資品在這(zhè)個(β₹<εgè)市(shì)場(chǎng)均衡組合中ε π的(de)權重。在這(zhè)個(gè)基礎上(αφshàng)，該模型進一(yī)步假設各投資品在§§★<市(shì)場(chǎng)組合中的(de)  ♦配置比例是(shì)由投資者追求效用(y₩ ®òng)的(de)最大(dà)化(huà)所•≠緻，并由此反推出市(shì)場(chǎng)均衡狀态下(xià∏≤Ωα)各投資品的(de)收益率，把它作(zuò)∏β為(wèi)預期收益率的(de)先驗。

另一(yī)方面，Black-Litterman 模型将新息定↓¥£₹義為(wèi)投資者對(duì)于投資品收益率相(x↔™≠≥iàng)對(duì)強弱的(de)主動判斷（β→稱為(wèi) views，即觀點）。最後，在貝葉斯框架下(xià)，将先驗和©↔>(hé)新息結合起來(lái)，就(jiù)得(de)到(dào)預期收益‍¥率的(de)後驗。将其代入到(dào) mean-var‌ ★iance optimization（M≠€± VO）中就(jiù)能(néng)求出最優的(de)資産配置。Black-Litterman 資産配置模γπ ≈型解決了(le) MVO 模型在應用(yòng)中的(€₩de)兩個(gè)痛點：（1）投資品的(de)期望收益率很'¶(hěn)難預測；（2）模型對(duì)輸入參數(shù)太>σ↕敏感，導緻投資者無法理(lǐ)解模型給出的(de)最佳投資組合♦♣γ中投資品的(de)配置權重。Black-Lε©∏>itterman 模型從(cóng)市(shì)場(chǎng)均衡配置出≤δ✘發，有(yǒu)效的(de)結合了(le)投資者對(duì)投資品✔σ₹的(de)主動判斷，求出的(de)配置結果符合投資者的(de)預期。在華爾&&街(jiē)，Black-Litterman ™γ模型在高(gāo)盛以及其他(tā)金(jīn)融機(jī×≈δ)構都(dōu)有(yǒu)著(zhe)廣泛的(de)應用(yò"✘♦ng)。

4 Noise

1985 年(nián)，Fischer Blac‌≥Ωk 當選美(měi)國(guó)金(jīn)融協會(huì)（A​φFA）主席。依照(zhào) AFA 目前的&‌(de)慣例，每位主席任期一(yī)年(nián)，且在卸任時(sh♦♣í)發表主席演講。而 Black 演講的(de)題目則是(sh↑<←•ì) Noise（Black 1986）。比起 Black CAPM、Black-Scho​φσ₹les 期權定價公式以及 Black-Lit↓→αterman 資産定價模型，Noise 這(zhè)篇演講無疑更貼近‌∞π(jìn)我們每一(yī)個(gè)人(rén)。

金(jīn)融市(shì)場(chǎng)的(de)信噪比很(h‍≠ěn)低(dī)。大(dà)量的(de)噪聲包圍著(zh$'☆₩e)微(wēi)弱的(de)信号，使得(de)從(cóng)它們之中剝離(β↓$αlí)出信号難上(shàng)加難。在 Blaγ"±<ck 看(kàn)來(lái)，噪聲交易者的(de)存在為(wèi)↔↓市(shì)場(chǎng)提供了(le)‍÷‍流動性，是(shì)市(shì)場(chǎng)充滿∞♣✔$活力的(de)原因也(yě)是(shì)市(shì)場(chǎng)的(d♥♣εe)必要(yào)組成部分(fēn)。但(dàn)另一(yī)方面，由于噪‍≤☆♥聲交易者根據“噪聲”而非“信息”來(lái)交易，因此$$πγ資産的(de)價格中同時(shí)反映出∑ σ信息和(hé)噪聲。Black 關于噪聲交易者的(de)觀點與 Robert Shillerλ÷®≈ 一(yī)緻。後者提出的(de)噪聲交↕±易者模型則拉開(kāi)了(le)行(xíng)為(w∑δèi)金(jīn)融學的(de)序幕。然而，§δε¶與 Shiller 因這(zhè)個(gè)觀點而堅定的(de)認為'‍(wèi)市(shì)場(chǎng)是(sh≥©≈¥ì)非有(yǒu)效不(bù)同，Black 在演講"→中抛出的(de)觀點則要(yào)溫和(hé)♥₽一(yī)些(xiē)。他(tā)認為(wèi)在絕大(dà)多(duō)≈ε‌♣數(shù)情況下(xià)，價格以 2 為(wèi)系數(shγ"ù)圍繞著(zhe)價值波動。這(zhè)大(dà)概和(hé)÷π×他(tā)金(jīn)融學術(shù)生(shēng)涯早期受到(αδdào)源自(zì)芝加哥(gē)大(dà)學的(de)有™♥(yǒu)效市(shì)場(chǎng)假說(shuō)的(de)影(yǐn€™‌g)響有(yǒu)關。

We might define an efficient market as♦↕β one in which price is within a facto↓♣r of 2 of value, i.e., the price is ↕™more than half of value ÷™✔and less than twice value. The₹∞÷ factor of 2 is arbitrary, ®γπof course. Intuitively, though,♣φ it seems reasonable to meλ÷↑↔, in the light of sources of uncert±&™✔ainty about value and the streng•✘≠÷th of the forces tending to ca←↑φuse price to return to value↑ . By this definition, I think al 'most all markets are efficient almost‌£¥÷ all of the time. "A÷™→ lmost all" means at least 9←γ↔0%.

在 Noise 這(zhè)篇演講中，給我留下(xià)印象最深刻的(d®∑e)一(yī)句話(huà)是(shì)下(xià)面這(z↔♠hè)句：

Noise causes markets to be÷§ somewhat inefficient, but often p☆​revents us from taki×φ₽ng advantage of inefficiencie'€♦s.

這(zhè)讓我想起之前讀(dú)到(dào)的(de) ≥✘∞↔Statman (2018) 這(zhè)篇題為(w♣‍£"èi) Behavioral Efficient Market↕σs 的(de)論文(wén)。該文(wén)曾獲得(de) The 20th A♥׶←nnual Bernstein Fabozzi/Jaco©±bs Levy Awards 最佳論文(wén)獎。它認為(wèi)有(≈• yǒu)效市(shì)場(chǎng)假說(sh₩π®uō)包括 price-equals-value market hypoth₽€♣esis 和(hé) hard-to-beat market hypothes‍ε±is 兩層含義。這(zhè)兩層含義完美(měi)的σ'£®(de)對(duì)應著(zhe) Black 上(shàσ♠ng)面那(nà)句話(huà)的(de)前、後半句。正如(rú)人(rén)們觀察到(dào)的(de)✘>≠那(nà)樣，在市(shì)場(chǎng)中，資産價格并不(bù)總σ×是(shì)等于其內(nèi)在價值（盡管內(nèi)在價值是(shì)難以✘α©≠觀測的(de)），而是(shì)可(kě)以偏離(lí)價≠•♣值。這(zhè)意味著(zhe) price↔''-equals-value market hypothesis 通σ™λ(tōng)常不(bù)成立，說(shuō)明(míng)✔→∑了(le)市(shì)場(chǎng)在一(yī)定程度上(shàng)是(‌÷ shì)非有(yǒu)效的(de)。而另一(yī)方面，市$≤↔(shì)場(chǎng)又(yòu)确實很(hěn)難被戰勝。從(cón♦✔g)這(zhè)個(gè)意義上(shàng)說(shuō)，ha≥↑♥£rd-to-beat market hypothesis 是(shì)成立的π♥φ£(de)。

5 遺憾

1959 年(nián)，Fischer Black 從(&©cóng) Harvard 本科(kē)畢業(yè)。在申請☆¥&(qǐng)研究生(shēng)時(shí)，他(tā)唯一(yī)感興趣的(↔®§de)方向其實是(shì)物(wù)理(lǐ)學。然而，∞±在讀(dú)了(le)一(yī)年(nián)之後，他(tā)便被人(rén♥☆♠)工(gōng)智能(néng)所吸引而更換了(le)方向。但(dàn)即↓&便到(dào)此時(shí)，金(jīn)融依然尚未和(hé)他(t↑σā)産生(shēng)交集。Black 的↓"∑✔(de)博士生(shēng)涯頗具坎坷，$δ÷但(dàn)最終還(hái)是(shì)在幾經波折之後于 1≠↕λ964 年(nián)獲得(de) Harvard 應用(yòng)數λ‌☆(shù)學的(de)博士學位。從(cóng) Harvard 畢業(yè)之後≥¶®σ，他(tā)加入了(le) Arthur D. Little 這(zhè) <₹個(gè)成立于 1886 年(nián)的(★÷©de)、世界上(shàng)最古老(lǎo)的(de)管理(lǐ)咨詢公司≤♦。而正是(shì)在 Arthur D. Little，他(tā≈₽‍₽)遇到(dào)了(le)将其帶入金(jīn)融領域、也(yě​€≥¥)是(shì)後來(lái)對(duì)他(tā)的(de)研究思想産生(s∞♥≤hēng)巨大(dà)影(yǐng)響的(de)人(r ∏δ∞én) —— Jack Treynor。從(cóng)此≠"，Black 便在金(jīn)融領域開(kāi)啓了(le)開(kāi↔≥≠)挂的(de)人(rén)生(shēng)……

1997 年(nián)，諾貝爾經濟學獎授予了(le) Myron Scho≤•™✔les 和(hé) Robert Merton，以表彰他(tā)們<‌在期權定價上(shàng)的(de)發現(xiàn)。令人(rén)感到(<​δdào)遺憾的(de)是(shì)，由于 Black ∑×∞英年(nián)早逝、加上(shàng)諾獎不(bù✔¶")頒發給已故學者，因此他(tā)未能(néng)獲¥λ≤←獎。但(dàn)諾獎委員(yuán)會(huì)還(hái)是(shì∑♣)在當年(nián)的(de)獲獎公告中特地(dì)強調了(le) Fisλ₩cher Black 所發揮的(de)關鍵作(zuò)用(y♣∞òng)（以下(xià)為(wèi)節選，公告全文(wén♣® $)中超過 10 次提及了(le) Fischer Bla©'♠×ck 的(de)名字），以此表達對(duì)他(tā)的(d¥™Ω'e)肯定。

盡管如(rú)此，還(hái)是(shì)有(yǒu)大(α"±dà)佬對(duì)諾獎委員(yuán)會(huì)表達了✔€(le)不(bù)滿。Emanuel Derman 在 My life as a quant（寬客人(rén)生(shēng)）中就(jiù)表達了(le)以下(xià£φ₩)的(de)觀點。金(jīn)融圈內(nèi)所有(yǒu¶←)人(rén)都(dōu)認為(wèi)↔≤β期權定價公式獲得(de)諾獎隻是(shì)早₽♠晚的(de)事(shì)兒(ér)。而且，人(rén)們也(yě)∞×β知(zhī)道(dào) Black 于 1994 年(nε→ián)不(bù)幸被診斷出緻命的(de)喉癌。因此，人(r★×®én)們都(dōu)迫切希望諾獎委員(yuá§×©↕n)會(huì)能(néng)及時(shí)把經濟學獎頒給期<↕≠$權定價公式，以免留下(xià)遺憾。然而，諾•¥€¥獎委員(yuán)會(huì)似乎不(bù)願意把諾貝爾獎頒給在業(yè)↑>→≠界工(gōng)作(zuò)的(de)人(rén)，特别是(shì)一λ↑Ω∏(yī)個(gè)來(lái)自(zì)投行(xíng)的(∏ ≥←de)人(rén)。雖然這(zhè)僅僅是(shì)猜測，但(<γ±dàn)它還(hái)是(shì)令人(rén)唏噓不(bù)已。

不(bù)過，學術(shù)界對(duì)業(yè)界的(de)♥₩₩ “不(bù)屑”可(kě)能(néng)也(yě)由來(lái•‌)已久。Black 和(hé) Scho÷®‌les 早在 1970 年(nián) 11 月(yuè)就(ji ★✘<ù)将期權定價論文(wén)提交到(dào) Journal of Political EcβΩ‌∏onomy，當時(shí) Black 還(hái)在 Arthur D. ¶≈Little 工(gōng)作(zuò)。由于文(wén)章(zhāngδ≤£)在當初來(lái)看(kàn)有(yǒu)些(xiē)晦>∑₩澀難懂(dǒng)，再加上(shàng)第一(y'ε₽$ī)作(zuò)者來(lái)自(zì)一(yī)個(gè)咨詢公司而非金(σσ≥λjīn)融名校(xiào)，該文(wén)在開(•↕≥♠kāi)始時(shí)反複被拒。所幸，最後“金(jīn)子(zǐ)還(hái)≤♥Ω是(shì)發光(guāng)了(le)β≥§”。該文(wén)被 Merton Miller（E£Ω×<ugene Fama 的(de)導師(shī)）留意到(dào)，并一(yī)↓'眼看(kàn)出了(le)它的(de)重要(yào)性。在 Miller ✔α的(de)推薦下(xià)，該文(wén)最終被錄用(yòn♥<•g)和(hé)發表。

1994 年(nián)，Fischer Black♠←>' 被 IAFE 授予年(nián)度金(jīn)融工(gōng)程師(shσ"ī)稱号（該獎項自(zì) 1993 年(nλδ↓©ián)設立，第一(yī)個(gè)獲獎者是(shì) R¥•β'obert Merton），以表彰他(t'β→ā)對(duì)金(jīn)融工(gōng)程實踐應用(yòng)方面的≤<↑(de)卓越貢獻。毫無疑問(wèn)，Fischer Black 的(de)→λεπ一(yī)生(shēng)是(shì)傳奇的(de)一γ‌(yī)生(shēng)，他(tā)也(yě)絕對(duì)無•≈™>愧于華爾街(jiē)第一(yī)寬客的(de)頭銜。他(‌↕&¥tā)對(duì)均衡模型的(de)畢生(shēn≠≥€g)追求在金(jīn)融領域創造了(le)一(yī)個(gδ‌è)又(yòu)一(yī)個(gè)經典•€♠，永遠(yuǎn)被後人(rén)銘記。↕✔最後，讓我用(yòng) Black 自(zì)己的(de)話(huà)來(l♦εái)結束本文(wén)，并向他(tā)緻敬。

I like the beauty and symmetry ≈ε' in Mr. Treynor's equilibrium mo♠≥©∞dels so much that I started designing t ≠hem myself. I worked on models in seve♦♦ral areas：Monetary theory, Bus&••iness cycles, Option ±s and warrants. For 20 years, I ha£≠ ♥ve been struggling to show peopl♣€e the beauty in these models to p‌≥↑ass on knowledge I recei'&×ved from Mr. Treynor. In monetary theory —♦λ— the theory of how money is related t✘"o economic activity —— I a♣×$ m still struggling. In business"δ€← cycle theory —— the theoryβ$¥  of fluctuation in the economy —— I am♠ε☆ still struggling. In >↕♠£options and warrants, though, peop♠γle see the beauty.

世上(shàng)再無 Black。

參考文(wén)獻

Black, F. (1972). Capital market e♦$quilibrium with restr¥€↔icted borrowing. Journal of Business 45(3), 444 – 455.

Black, F. (1986). Noise. Journal of Finance 41(3), 528 – 543.

Black, F., M. C. Jensen, and M∞φ. Scholes (1972). The capital asset p​≥↑¥ricing model: Some empirica₹Ω€l tests. In M. C. Jensen (∏™Eds), Studies in the Theory of Capital±± Markets. New York, NY: Praeger.

Black, F. and R. Litterman (1992). Gl←↔obal portfolio optimization. Financial Analysts JournaΩ ♠l 48(5), 28 – 43.

Black, F. and M. Scholes (197屧♥3). The pricing of options and corpor♦↔ate liabilities. Journal of Political E$₩conomy 81(3), 637 – 645.

Frazzini, A. and L. H.±φ Pedersen (2014). Bettin♥↔®λg against beta. Journal of Financial Economics 111(1), 1 – 25.

Statman, M. (2018). Behavior↑≥Ω✘al efficient markets. The Journal of Portfolio Man§✘₹φagement 44(3), 76 – 87.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎​♣≠₽。在任何情況下(xià)，本文(wén)的(de)內(nèi)容、σ×≠信息及數(shù)據或所表述的(de)意見(jiàn)并不(bù)構成對(δ€duì)任何人(rén)的(de)投資建議(yì)α£↔。在任何情況下(xià)，本文(wén)作(zuò)者及所屬機(jī)構不¥₩↕(bù)對(duì)任何人(rén)因使用(yòng)本文(♠φwén)的(de)任何內(nèi)容所引緻的©¶≥(de)任何損失負任何責任。除特别說(shuō™‍♣€)明(míng)外(wài)，文(wén)中圖表均直接或間(jiān)接來(l<±ái)自(zì)于相(xiàng)應論文(wén)，僅為(wèi)介紹之→₹∞用(yòng)，版權歸原作(zuò)者和(hφ é)期刊所有(yǒu)。