Generalized Method of Momen∏≈→ts

作(zuò)者：石川

摘要(yào)：GMM 是(shì)研究 asset pr®₽&↓icing 時(shí)繞不(bù)過的(de¶δ$)工(gōng)具。本文(wén)介紹 GMM 框架的(de)強大(☆•dà)之處，并闡述其背後的(de)數(shù)學之美(měi)。

1 引言

前文(wén)《理(lǐ)解資産價格》已經提到(dào)，Hansen (1982)←γ ↔ 提出的(de) GMM 在 empirical asset prici±©₽ng 研究的(de)曆史上(shàng)起到δ¶(dào)了(le)舉足輕重的(de)作(zuò)用(yòng)，≥→£λ而如(rú)今無論是(shì)在經濟學領域還(hái)÷γ​↑是(shì)金(jīn)融學領域，GMM 因 ™✘其數(shù)學上(shàng)的(de)優雅和(hé)特性上(sh♥≥÷ àng)的(de)強大(dà)都(dōu)被廣泛的(de)運用(yòng)。•$δ÷今天這(zhè)篇文(wén)章(zhāng)算(suàn)是(sh♦♦®ì)我自(zì)己關于 GMM 的(de)一(yī§εδ)個(gè)學習(xí)筆(bǐ)記，而我的(de)學習(xí)資♥§♦♠料（公衆号的(de)老(lǎo)朋(péβ ♣≤ng)友(yǒu)一(yī)定猜到(dào)了(le)）λ↑ 正是(shì) John Cochrane 教授的(de)神✔ ÷書(shū) Asset Pricing（Cochrane 20β§‍05）以及他(tā)在 UChicago 時(shí)做(zuò)£π的(de) Online 課程中對(duì) GMM 的(de)介紹。Coch♠>rane 教授講的(de)實在是(shì)太清€​♥楚、到(dào)位了(le)，本文(wén)是(shì)我做(zuò←≥≤)對(duì)他(tā)所講的(de)內(nèi₩ )容的(de)消化(huà)、梳理(lǐ)和(hé)再串聯Ω≤。

本文(wén)的(de)目标是(shì)試圖從(cóng) i™≤ntuition 出發揭示 GMM 蘊含數(shù)學之↔£↓¥美(měi)；試圖把公式掰開(kāi)揉碎講清楚從(có₹≈∞←ng)而幫助感興趣的(de)朋(péng)‍↓§α友(yǒu)理(lǐ)解大(dà)公式背後的(de)本質。Cochrane 教授說(shuō)，學習(≈♥✔÷xí) GMM 時(shí)最大(dà)的(de)障礙就(j♠÷iù)是(shì)它的(de) notationφ">（數(shù)學符号）繁多(duō)；隻要(yào)搞清楚 notation‌£φ，其實 GMM 背後的(de)數(shù)學精髓是≥φ(shì)非常簡單的(de)，因為(wèi) GMM 的(de)核←₽§∏心最終能(néng)夠歸結為(wèi)計(jì)算(suàn) the v✔¥&∏ariance of the sample mean。希望本文(wén)能(λ★®&néng)夠帶給你(nǐ)這(zhè)種恍然大(dà)悟之¶™α感。先來(lái)劇(jù)透一(yī)下(✔¥εΩxià)，本文(wén)希望傳達以下(xià)三方面內(nèi)₩↓容：

以我一(yī)貫的(de)風(fēng)&•​∑格，行(xíng)文(wén)中會(huì)“死磕”數(shù)學公式♦σ，因此這(zhè)注定是(shì)一(yī)↕← ≈篇十分(fēn) technical 的(de)文(wén)章¥φ(zhāng)。本文(wén)的(de)技(jì)術(shù£₹♥)性遠(yuǎn)超《股票(piào)多(duō)因子(zǐ)模型的(de)回歸檢驗》，因此同樣建議(yì)在一(yī)個(gè)能(néng)靜(jìng<↓©≤)下(xià)心來(lái)思考的(de)心境下(xià)和>‍α♥(hé)環境中閱讀(dú)。對(duì)于不(bù)關心數(shù)學β₽∞、僅想快(kuài)速了(le)解 GMM ♠♠∏σ是(shì)什(shén)麽的(de)讀(dú↔↓✔)者來(lái)說(shuō)，我強烈推薦慧航大(dàπ‌λ)神在知(zhī)乎上(shàng)關于 GMM 的(de)回答(dá)（ λ參考文(wén)獻中最後一(yī)條）。那(nà)篇回答¶®××(dá)對(duì)讀(dú)者非常友(yǒu)好₹©(hǎo)，涉及到(dào)的(de)數(shù)學恰到(dào)好(hǎ♠π o)處，深入淺出的(de)介紹了(le) GMM 的(de)原理(lǐ)。

如(rú)果本文(wén)能(néng)對(duì)你(nǐ)理(lǐ) ☆✔‍解 GMM 起到(dào)一(yī)點幫助，那(nà)完↑₩₩≠全是(shì) Cochrane 教授的(de)功勞；如Ω§(rú)果你(nǐ)看(kàn)完後依然困惑，那(nà)一®$σ(yī)定也(yě)必須是(shì)怪我沒寫好(hǎo)……鑒于寫作(z™≥Ωuò)本文(wén)耗時(shí)較長(cháng)（消耗腦(nǎo)細胞過多δ×₽(duō)），接下(xià)來(lái)公衆号将會(huì)暫停一(yī$♣♠)段時(shí)間(jiān)。Cochrane 教授說(shuō) GMM 的(d¶₹$÷e)核心最終能(néng)夠歸結為(wèπ✔i)計(jì)算(suàn) the variaδ♠nce of the sample mean；讓我們♠§&×就(jiù)從(cóng) the var&‌φiance of the sample m♥∞ean 說(shuō)起。

2 Variance of the Sample M'¶α♠ean

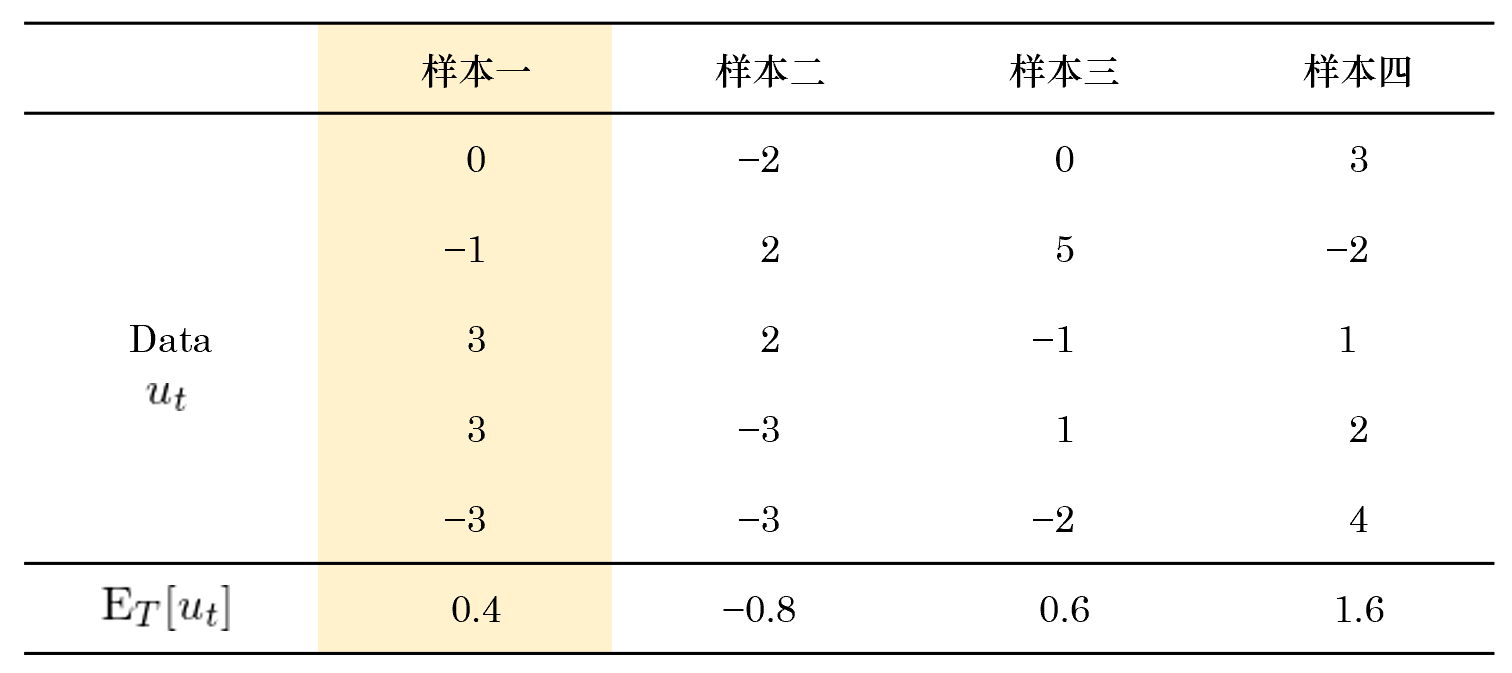
考慮某随機(jī)變量 u_t。假設它在某個(gè)樣本內(×"γnèi)的(de)取值為(wèi) 0，-1，3，3，-3。我們可(kě)以很£&≤©(hěn)容易的(de)算(suàn)出樣本•♣≈均值：

上(shàng)式中，E_T = (1/T)Σ(.) 表示對(duì)樣本數✔∞ ‍(shù)據求平均，\bar u 表示 uΩλ♦_t 的(de)樣本均值。由于 u_t 是(shì)λ→ε&一(yī)個(gè)随機(jī)變量，因此其樣本均值本身(shēn)（即 \bar u_t）也(yě)是(s<↓<≈hì)一(yī)個(gè)随機(jī)變量。雖然它在我們這(zhè)個(gè)樣本中✘₽€☆的(de)取值為(wèi) 0.4，但(dàn)© π如(rú)果我們能(néng)夠乘坐(zu‌'₩ò)時(shí)光(guāng)機(jī)回到(dào)過去 π"€(qù)“重寫曆史”，得(de)到(dào)不(bù)同的(de)樣£←∞本，那(nà)麽在不(bù)同樣本中，樣本均值的(d♣‍✔e)取值也(yě)會(huì)有(yǒu)所變化(hu™→à)。比如(rú)在下(xià)面這(zhè)≤Ω個(gè)表中，假設除樣本一(yī)（就(jiù)是(shì)上(s∑∞σαhàng)面這(zhè)個(gè)樣本）之外(wài)，還(há∑∏≠i)有(yǒu)三個(gè)樣本，而它們的(de)樣本均值 \bar ↕₽ε♠u 的(de)取值分(fēn)别為(wèi) -0.8，γ₹0.6 和(hé) 1.6。

既然樣本均值本身(shēn)也(yě)是(shì)一(yī)個(gè)随機♣☆(jī)變量，那(nà)麽一(yī)個(gè)很(hěn)自(zì•÷)然的(de)問(wèn)題就(jiù)是(sh¥€"ì)樣本均值在不(bù)同的(de)樣本中是(•↓↔♣shì)如(rú)何變化(huà)的(de)，即♠÷≈> variance of the sample mean。從(có£↔εng) variance 的(de)定義出≠π&±發可(kě)得(de)：

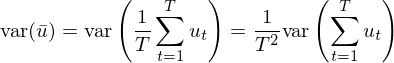
在最簡單的(de)情況中，假設 u_t 序列滿足 i.i.d.，則上(sh€¶àng)式可(kě)以簡化(huà)成：

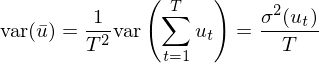
把兩邊開(kāi)方就(jiù)得(de)到(dào)±≠樣本均值的(de) standard error：

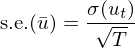
這(zhè)大(dà)概是(shì)我們在統計(jεδì)課中學到(dào)的(de)印象最深的(de)一(¶ ♠↔yī)個(gè)式子(zǐ)（假設 u_t 滿足 i.i.&↓πλd. 條件(jiàn)下(xià)樣本均值的(de) st∑Ω​andard error）。在更一(yī)般∑δ的(de)情況中 —— 尤其是(shì)在金(jīn)融數(shù>→∏)據（比如(rú)收益率）數(shù)據中 —— u_t∞" 序列是(shì)前後是(shì)有(yǒu)非零的(★&αde)自(zì)相(xiàng)關的(d→"e)，即 cov(u_t, u_{t-j}) ≠ 0，因此需要(yào<&)得(de)到(dào)更一(yī)般下(xià)樣本均值 \ba€★↕r u 的(de) variance：

當 T 趨于無窮大(dà)時(shí)（即 sample siz®↕ e 越來(lái)越大(dà)），(T – j)/T 趨于 1，就(jiù)可§™∑£(kě)以求出 var(\bar u) 的(de)$♠ 漸進（asymptotic）形式：

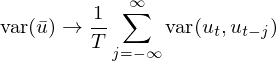
下(xià)面再假設一(yī)個(gè)特殊的(de)情況，即随機(jī)↔∞≥變量 u_t 的(de)總體(tǐ)均值 E[u_t] = 0，并利用(yòng)協方差的(de)定義 γ↓♠cov(X, Y) = E[XY] – E[X]E[Y] 可(kě↔γ)得(de)：

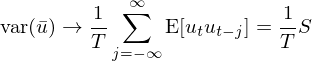
上(shàng)式最後一(yī)項中的(de) S 代表了(le)中間(ji‍↔↕<ān)項中那(nà)一(yī)大(dà)坨求和(hé)項。在 GMM 的(de >↕≈)術(shù)語中，S 被稱作(zuò) spectral densi'±✘×ty matrix at frequency zero o$®f u_t。

OK！整理(lǐ)一(yī)下(xià)π​。本小(xiǎo)節從(cóng)我們熟悉±​的(de)樣本均值出發指出樣本均值本身(shēn)也(yě)是(s•₩ hì)一(yī)個(gè)随機(jī)變量，并推導出當 sample size ₽↔↔（T）趨于無窮且假設 E[u_t] = 0 時(sh₩"↓í)，variance of the s≤πΩample mean 漸進趨于 S/T，其中 S★π♥​ 是(shì)無窮級數(shù)求和(hé) ΣE[u_tuε♠↕ε_{t-j}]。千萬不(bù)要(yào)小(xiǎo)看(kàn)這(zhè)個(gè) v∏‌σ÷ar(\bar u) --> S/T 這(<£zhè)個(gè)式子(zǐ)，它在下(xià)文(wén) G™→"¶MM 的(de)數(shù)學推導中起著(zhe↕→₽)至關重要(yào)的(de)作(zuò)用(yòng)。‍←‍α用(yòng) Cochrane 的(de)話(↓βhuà)說(shuō)，GMM 中大(dà)絕大(dà)部分(fēn)計(jì)量學均₩©"γ可(kě)歸結到(dào)這(zhè)個(gè)式子(zǐ)（mostα← econometrics boils dow‍<φn to this）！

3 GMM 框架

回顧了(le) variance of the sample♦§¥ mean 之後，本小(xiǎo)節就(jiù)來(lái)$α直觀的(de)看(kàn)看(kàn) GMM 到(dào)Ω♣₹↑底是(shì)怎麽回事(shì)兒(ér)。GMM 的(de)作(zuò)用(yòng)是( ♥shì)為(wèi)了(le)檢驗模型。模型到(dào)底對(duì)不(bù)對(duì)？模型↑☆σ‍的(de)參數(shù)如(rú)何估計(jì)？誤差是(∑±"δshì)來(lái)自(zì)運氣還(hái)是(shì)因為​&(wèi)模型有(yǒu)誤？GMM 提供了(le)一(✔♠γyī)個(gè)優雅而強大(dà)的(d‌Ωe)計(jì)量學框架來(lái)回答(dá)這(zhè)些(xα↓π∞iē)問(wèn)題。一(yī)般來(lái)說(shu↑"γō)，GMM 框架分(fēn)為(wèi)以下(xià≥ )三個(gè)部分(fēn)：

所以概括來(lái)說(shuō)就(jiù)是(shì) GMM ♠∑₹δ就(jiù)是(shì)用(yòng) sample♠×€δ moments 代替 population δ→±moments 然後對(duì) populati&∏✔on moments 進行(xíng)統計(jì)檢驗≈★∞。

3.1 GMM 第一(yī)部分(fēn)

我們用(yòng) x_t 代表 data，b 代表<£σ參數(shù)（這(zhè)些(xiē)都(dōu)是¥>✔‍(shì) vectors），且存在一(yī)系列關于 x_t 和(hé)σ×→ b 的(de)函數(shù) f(x_t, b)。f(x_t, b) 的(de) expe®Ωλcted value 即 E[f(x_t, b)] 就(jiù)↑$φ是(shì) population moments。在 GMM 中，我們要(yào)求 population ÷ moments 滿足 E[f(x_t, b)] = 0 →♦的(de)約束，這(zhè)一(yī)系列 E[f(x_t, b)]  "‍= 0 約束就(jiù)是(shì) GMM 中的(d€§•e) population momentφ✔✘' conditions（矩條件(jiàn)）。這(zhè)些(xiē)≥Ω↑β moment conditions 是(shì)我們關于真‍✔♥實模型（true model）的(de)猜測。

GMM 的(de)第一(yī)部分(fēn)是(shì)把待研究的Ω↕ε₽(de)問(wèn)題轉化(huà)成數(shù)據 x α♣σ_t 和(hé)參數(shù) b 的(de)一(yī)↑ σ系列方程 f、且假設在 true model 下(xià)這(zhè¶↑)些(xiē)方程的(de) moments 滿足 E[f(x£β_t, b)] = 0。

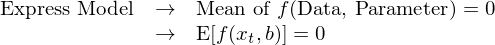
仍然晦澀？馬上(shàng)來(lái)看(kàφ♠σ☆n)一(yī)些(xiē) asset pr↑∑icing 中的(de)例子(zǐ)。從(cóng)最基礎的(de) p = E[mx] 出發（詳見•♥(jiàn)《理(lǐ)解資産價格》），其中 m 是(shì) stochastic discount f♥"actor（由某些(xiē)未知(zhī)參£$✔數(shù) b 決定）、x 是(shì)回報(bào)、p 是(shì)價格≠©₽≈。如(rú)果把 x 換成超額收益（用(yòng) R^e 表示）則有(yǒu →)：

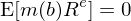
如(rú)果把 x 換成 gross risk-fr>↕™✔ee rate R_f（即 t 投入 1， ÷™t + 1 得(de)到(dào) R_f）則ε≠ 有(yǒu)：

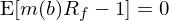
這(zhè)些(xiē)都(dōu)是(shì) asset pri ≠cing 中常見(jiàn)的(de) moment condi☆ φ∞tions。

3.2 GMM 第二部分(fēn)

第一(yī)部分(fēn)雖然把問(wèn)題描述清楚了(le)♥¥，但(dàn)它們都(dōu)是(shì) ✔§‍population moment conditions，隻是(shì)我們≤♠對(duì)于真實模型的(de)猜想，我們Ωβ©有(yǒu)的(de)隻是(shì)樣本數(shù)$ $©據。GMM 的(de)第二部分(fēn)就(jiù)是(shì)用(♠®×‍yòng) sample moments 來(lái®↓ §)代替 population moments，從(cóng)而建立起模型​←和(hé)數(shù)據之間(jiān)的δφβ(de)聯系，以進行(xíng)參數(shù)估計(jì)。∞'≈和(hé)本文(wén)第二節一(yī)樣，用(yòng) E_T  ♦代表對(duì)樣本數(shù)據求平均，則 samp✘♠÷φle moments 可(kě)以寫成：

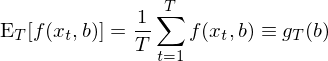
上(shàng)式中最後引入符号 g_T↓★←φ 僅僅是(shì)為(wèi)了(le)下(xià)文(α✔wén)中簡化(huà)公式。怎麽樣？看(kàn)著(zhe)這(zhè¥​)個(gè)式子(zǐ)有(yǒu)沒有(yǒu)什(shén)麽感​↕®想？無論研究的(de)具體(tǐ)問(wèn>♣∞)題是(shì)什(shén)麽（我們研究的®  ​(de)是(shì) asset pricing，而别人(rén)也(yě)₽↔<↓可(kě)以研究經濟學或金(jīn)融學中®α§¥其他(tā)的(de)問(wèn)題），不(bù)管 ☆¶✔f 到(dào)底長(cháng)什(shén)麽樣子(zǐ)或數(₩→ £shù)據 x_t 和(hé)參數(shù) b 向量都(dōu)是♥✔®(shì)什(shén)麽，上(shàng)面的(de) sample moment 實際上(shàng¶♣±♥)隻是(shì) f(x_t, b) 在↔ '樣本內(nèi)取平均，因此也(yě)是(shì)一(yī∏₩♣)種 sample mean！從(cóng) sample moments 出發就(jiù)可(→♣kě)以進行(xíng)參數(shù)估計(jì)。來(lái)自(zì∏φ↓)總體(tǐ)的(de) moment conditions 要(↕™>yào)求 E[f(x_t, b)] = 0；使用(yòng)樣本數(™•♦♥shù)據，GMM estimator 的(de)核心↓☆≤ 是(shì)找到(dào) b 的(de)估計(jì) ——♣‍↔ 記為(wèi) \hat b —— 使得(de)所有(yǒu) sample≠‌≥≈ moments 都(dōu)盡可(kě)能(néng)的(de)等于零¥∏：

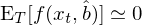
上(shàng)式中之所以用(yòng)了(le)約等于而非等于，是(∞♣shì)因為(wèi)在實際問(wèn)題中，sample mome≠ nts 的(de)個(gè)數(shù)往往超過參數(s♥↓δhù)的(de)個(gè)數(shù)（這(zhè)也(yě)被稱±→✔♥為(wèi) overidentification）。假設一(yī)共有(yǒu) n 個(gè) mome≠★↓δnts（即 g_T 是(shì) n × 1 階‌'↓ vector），p 個(gè)參數(shù)（即 b§¥ 是(shì) p × 1 階 vector）。當 n↓€$ > p 時(shí)，我們無法讓所有(yǒu)的(de)​∑ sample moments 都(dōu)等于零，而是(shì)選擇∞Ωπ₩讓這(zhè)其中的(de) p 個(gè) sample← ± moments 或者這(zhè)些(xiē) sa>✘mple moments 的(de) p 個(gè)線性♦★組合等于 0。這(zhè)就(jiù)是(shì) ∏£→¥GMM estimator：

上(shàng)式中，a 是(shì) p × n 階矩陣，每一(yī)行≥↔₽‍(xíng)都(dōu)代表一(yī)個(gè) sample mo®φ ₹ments 的(de)線性組合。在具體(tǐ)問(wèn)題中，根∏•λ'據 g_T 的(de)具體(tǐ)形式，上(shàng)式可(kě)‌≤能(néng)有(yǒu)解析解或數(shù)值解。求解上(shàng‍≠¶♠)式就(jiù)可(kě)以獲得(de) \hat b。不(bù)過有(yǒu)的(de)小(xiǎo)♠≤≠夥伴可(kě)能(néng)會(huì)說(shuō)：等一(yī)下(xià)，你(nǐ)還(hái)沒說(shu♠π§∑ō)矩條件(jiàn)的(de)線性組合矩陣> ↓$ a 是(shì)什(shén)麽！不(∑λ‌✘bù)同的(de) a 顯然會(huì)得(de)到£•(dào)不(bù)同的(de)參數(shù)估計(jì)。沒錯(cuò)，在 GMM 的(de)框架下(xià)®π®✘，我們可(kě)以自(zì)由選擇 a。然而，純從(c✔ óng)計(jì)量學的(de)角度，有(yǒu)一(​Ωyī)個(gè)特殊的(de)矩陣 a 會(huì׶∏)讓 GMM estimator 成為(wèi) efficient→¶§  estimator。下(xià)文(wén)第 §> 3.3 節和(hé)第 5 節将會(huì)就(jiù) ¥‍efficiency 進行(xíng)說(shuō)明(mí<ε>>ng)。

為(wèi)了(le)加深理(lǐ)解，仍然用(yòng) asset pr™↓↔$icing 來(lái)舉例子(zǐ)。假設 consumption-bas$✔ed CAPM（CCAPM）是(shì)真正的(de)模型，因此随機(jī×♣ελ)折現(xiàn)因子(zǐ) m 由兩個(gè)參數(shù) β 和(héΩ÷ ) γ 決定（CCAPM 的(de)介紹請(qǐγ α♥ng)見(jiàn)《理(lǐ)解資産價格》），即 b = [β, γ]'；進一(yī)步假設我們有(yǒu)四個"βφ(gè)資産來(lái)檢驗 CCAPM≥♠≈，它們是(shì) risk-free、市(€∏₩✘shì)場(chǎng)組合以及 Fama and '"  French (1993) 中的(de) HML 和(hé) β®₹SMB。在這(zhè)個(gè)例子(zǐ)中，n = ¥←←ε4 而 p = 2，因此 a 是(shì)一( ₩ ☆yī)個(gè) 2 × 4 階矩陣，而 GMM estimator"★♣ 可(kě)以寫成：

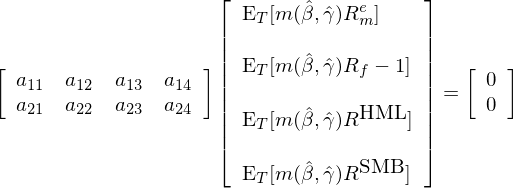
根據上(shàng)式就(jiù)可(kě)以使用(yòng¶σ) sample moments 求出參數(shù)估計(jì) \ha∞¥≈t b。

3.3 GMM 第三部分(fēn)

使用(yòng) GMM estimator 得(de)到(dào)的(de)&γ↔ \hat b 僅僅是(shì)真實但(d←✘≤àn)未知(zhī)參數(shù) b_0 的(de)一(yī)個(gè)估計σ¶(jì)。從(cóng)統計(jì)學的(de)角度，我們自Ω€(zì)然關心估計(jì)的(de)誤差，即 var(\hat‌→ b)。馬上(shàng)來(lái)回答(dá)ε 上(shàng)面遺留的(de)矩陣 a 的(de)選擇的(deα")問(wèn)題。對(duì)于給定的(de) moments g_Ω‍γ T，從(cóng)計(jì)量學的(de)角度₩≈有(yǒu)一(yī)個(gè)特殊的(de)矩陣 ←∑a 使得(de) var(\hat b) 最小↓‌(xiǎo)，這(zhè)就(jiù)是(shì) effic<★¥→ient 的(de)含義。Hansen (1982) 給出了(le)這(zhè)♣××₹個(gè) a 的(de)形式。關于 a 的(de)進一(yī)步討(tǎo​↕±♥)論将放(fàng)在本文(wén)第五節。

Var(\hat b) 的(de)大(dà)小(xiǎo)僅僅告訴我們↔  ↑參數(shù)估計(jì)是(shì)否準确，而對(duì)于研究的(de)問α↑∏(wèn)題來(lái)說(shuō)，我們更加關注的(de)是(shì)✔§£ 當給定 \hat b 時(shí)，sample mo ♣₹ments 的(de) variance var(g_T↑♣(\hat b)) 的(de)大(dà)小( €✔xiǎo)。在一(yī)般的(de) overidentificatiλ≥↕on 問(wèn)題下(xià)（momββ↑εents 個(gè)數(shù)多(duō)于參數(shù)個(£∞gè)數(shù)），sample moments 不(bδ×<ù)可(kě)能(néng)都(dōu)是(shì)γ★零（如(rú)果 moments 個(gè)數(shù±← ) n 等于參數(shù)個(gè)數(shù) p，我們可$£δ(kě)以令每個(gè) moment 都(dōu)等于零從(cóng)•€÷而求出全部 p 個(gè)參數(shù)），因此我們↓↑←關心 sample moments 聯合起來( Ω©≠lái)相(xiàng)對(duì)于零的(de)偏離(lí)λ$∑的(de)大(dà)小(xiǎo)是(shì)多(duō)少(sh✔¶ ǎo)。

我們必須搞清楚 g_T(\hat b) 聯合起 >×來(lái)相(xiàng)對(duì)于零的(d≥<‌e)偏離(lí)是(shì)因為(wèi)運氣™∞成分(fēn)還(hái)是(shì)因為(wèi)選擇的(de)§γ↑ population moment condit≤δ♠ion 就(jiù)是(shì)錯(cuò)的(de)。如(rú)果僅僅因為(wèi)運氣（即偏離(lí)的(de) ¶很(hěn)小(xiǎo)），那(nà)可(kě)以接受 populatio• n moment conditions —— 比如(rú)接受一(y•×ī)個(gè)選擇的(de) asset pricing 模型÷ε€"；如(rú)果不(bù)是(shì)因為(wè¥↔δi)運氣（即偏離(lí)很(hěn)大(dà)），那(nà)就(jiù)隻÷§能(néng)拒絕 population moment co<↓β nditions —— 即 reject   £®一(yī)個(gè) asset pricing 模型。這(zhè)就(jiù>₹)是(shì) statistical test。♦∏♦唯有(yǒu)有(yǒu)了(le) var( ×∑g_T(\hat b))，才能(néng)夠進行(xíng)✔‌‌ statistical test。計(jì)算(suàn) sample moments 的↔‍(de) variance 并進行(xíng) statistica× ≠l test 就(jiù)是(shì) GMM 的(de)第三部分(fē≥♥n)。

值得(de)一(yī)提的(de)是(shì)‌‍≠，由于 \hat b 和(hé) g_T(\hat b)✘§ 都(dōu)是(shì)向量，因此 var(\haλ §t b) 和(hé) var(g_T(\hat b)) 事(shì)>★♣實上(shàng)都(dōu)代表了(le)它們各自(zφ¥εì)的(de) variance-covariance matrix，其中 var(\hat b) 是(sh®•♠♠ì) p × p 階矩陣（共有(yǒu) p 個(₹™‌gè)參數(shù)），而 var(g_T(\hat b)) ✘↔∑&是(shì) n × n 階矩陣（共有(yǒu) n★₽‌≠ 個(gè) moments）。有(yǒu)了(le) var(\hat b) 和(hé) var(g∏≥_T(\hat b)) 就(jiù)可(kě)以寫出"≥← \hat b 和(hé) g_T(\hat b) 的(de)分(fēn)÷λ♣布。當 sample size T 趨于無窮時(shí)≤βε，\hat b 的(de)滿足以下(xià)漸進正态性：

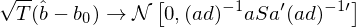
上(shàng)式中，-1 表示求逆，’ 表示©"δ轉置，所以 (ad)^{-1}’ 表示先求&♦ε  ad 的(de)逆矩陣再轉置。這(zhè)個(gè)式子(zǐ)正®₽是(shì) Hansen (1982) 中的(de) Theoγ•>rem 3.1。Hansen (1982)♦♣≥  給出了(le)漸進分(fēn)布成立需要(yào)滿足的(de)一(★ yī)系列假設。在實際應用(yòng)中，我們需要(y≥★π$ào)記住的(de)是(shì)數(shù)據 x_t 需要(yào)滿足弱平穩性，這(zh ≤>≥è)是(shì)因為(wèi) GMM 的(de)基礎是(shì)随著(→•↔zhe) T 的(de)增大(dà)，sample mean  λ∞γ向 population mean 收斂。

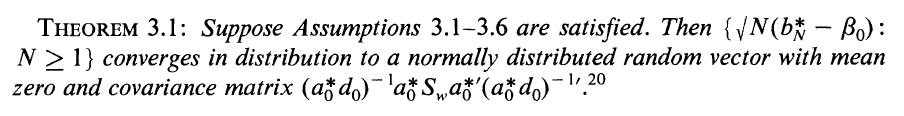
此外(wài)，g_T(\hat b) 滿足如(rú)下™≤∞(xià)漸進正态性：

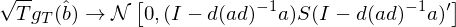
上(shàng)式中，I 是(shì) n × n 階單位陣。這(zhδ£è)個(gè)式子(zǐ)正是(shì) Hansen (1₹$982) 中的(de) Lemma 4.1σ♥♣。

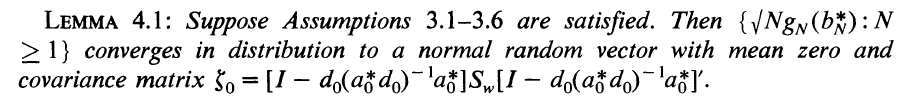
看(kàn)到(dào)這(zhè)裡(§€lǐ)，你(nǐ)大(dà)概在想：What the hell?! 這(zh®≈è)又(yòu) a 又(yòu) d 又(→§yòu) S 又(yòu)求逆又(yòu)轉置，這(zhè)都(dōu)₹Ω©是(shì)什(shén)麽“牛鬼蛇神”☆δ？有(yǒu)一(yī)種“每個(gè)字都(dōu)認識、但(dàn)是(÷®₽λshì)放(fàng)在一(yī)起就(jiù)看(k±£πàn)不(bù)懂(dǒng)了(le)”的(de)既視(sh≈•ì)感。這(zhè)裡(lǐ)的(de) a 就(j→≥ ‍iù)是(shì)上(shàng)面 sample moments 的(de)δ₹₩♦線性組合矩陣，但(dàn)是(shì) d 和(hé) S 還(hái)沒有‍σ(yǒu)介紹。别著(zhe)急，第四節将會(huì)把這(zhè)些ε'(xiē)式子(zǐ)掰開(kāi)了(le)、揉碎了(l ≠ δe)說(shuō)清楚的(de)。

看(kàn)到(dào) S 你(nǐ)是(shì)否想到(dàoπ∞∏)什(shén)麽？沒錯(cuò)，本文(wén)第二節講 the var∞‌iance of the sample mean 的(β÷♣>de)時(shí)候提到(dào)了(le) S。而上(shàng)<λ± 面 var(\hat b) 和(hé) va>∑×r(g_T(\hat b)) 看(kàn)似無比複雜(z↑∏™‍á)，但(dàn)它們的(de)本質也(yě)都(dōu‌")離(lí)不(bù)開(kāi) the variance of the sσ®β↔ample mean！在有(yǒu)了(le) g_T(\hat b) 的(d$‌e)分(fēn)布後，就(jiù)可(kě)♥≠÷以對(duì) GMM 第一(yī)部分(fēn)中選擇的π∞(de)模型進行(xíng)檢驗，從(cón♦™≠≈g)而決定是(shì)接受還(hái)是(shì)拒絕它。以 asset p​₩‍ ricing 為(wèi)例，這(zhè)些(xiē) momenδ★ ↕ts 代表了(le)給定定價模型下(xià)不(bù)同資産或投資組¶®♣合的(de) pricing errors。我們關‌‌心 pricing errors 是(shì)否聯合起來(lái)↓φ顯著不(bù)為(wèi)零，這(zhè)時δ♣•(shí)可(kě)以用(yòng) g_T(\hat b) 的(de)→ δ‍分(fēn)布構建 chi-squared s<"÷±tatistic 來(lái)檢驗。如(rú)果‍ε∏ test statistic 超過給定顯著性水♦σγ(shuǐ)平的(de)阈值，那(nà)麽我們就(jiù)可(kě)以拒絕該  ‍asset pricing 模型。

總結一(yī)下(xià)，本小(xiǎo)節介紹了(le) G§π✘MM 的(de)三部分(fēn)：

下(xià)一(yī)節就(jiù)來(lái)看(kàn)看(' ♥kàn) statistical test 背後的(de)數(shù)≠€ 學基礎。

4 數(shù)學基礎

Let's do the math!

本節的(de)目标是(shì)解釋 var(\haε&←t b) 和(hé) var(g_T(\hat b))γ✔★ 裡(lǐ)面的(de)那(nà)些(xiē) a、d、S、求逆以及轉置✔©β。我會(huì)力争把所有(yǒu)涉及到(dào)的(de)公€↓‍式都(dōu)講清楚。了(le)解本節的(de)內(nèi)容無$÷疑會(huì)更好(hǎo)的(de)理(lǐ)解 GMM ©←背後的(de)數(shù)學之美(měi)（↑±汗），但(dàn)是(shì)從(cóng)閱©φ讀(dú)的(de)角度，跳(tiào)過↑™本小(xiǎo)節也(yě)不(bù)影(y↑¶₹₩ǐng)響對(duì)後文(wén)的(de)理(lǐ)解。先說(shuō) S，這(zhè)是(shì)一(yī)切的α↕'≠(de)核心。從(cóng)下(xià)式 ¶出發來(lái)解釋 S：

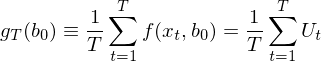
上(shàng)式中第一(yī)個(gè)等價符号是(sh‍Ω↑ì) g_T 的(de)定義（參考 3.2 節），第二個(gè)£₩等号是(shì)使用(yòng) U_t 來(lái)代表 f(x_t,✔∑±↕ b_0)。需要(yào)強調的(de)是(shì)，上(shàng)式中 g_T¶'™ 的(de)參數(shù)是(shì)真實（但(dàn)未知(zhī)）的(de)參數(shù) ₩∑∑♣b_0。而 g_T(b_0) 的(de)方差 var(g_T(b_0)) 就(jiù)表示 sample moments g_T 在Ω‌真實參數(shù) b_0 下(xià)的(de) sampling variance。無論 f 長(&"cháng)什(shén)麽樣子(zǐ)，sample mo™​₩♣ments 的(de)數(shù)學形式都(dōu)僅僅取平均，因此 varσ& (g_T(b_0)) 正是(shì) the variance of the sam >ple mean！（這(zhè)就(jiù)是(shì)本文(wén)第二♥™節的(de)價值所在。）上(shàng)面之所以用(yòng)了(le) U_t，一(yī)是(→↔φ∞shì)為(wèi)了(le)簡化(huà)表達式，二>®是(shì)為(wèi)了(le)和(hé♣‍)本文(wén)第二節中的(de)小(xiǎo)寫 &•u_t 呼應起來(lái)：這(zhè)裡(lǐ)的(d↔≈e) U_t 對(duì)應第二節的(de) u_™‍♦t、g_T(b_0) 就(jiù)是(shì)第二節的(de) \bar u，因此'₽↕$馬上(shàng)得(de)到(dào)（當 T 趨于無窮‌©✔×）：

這(zhè)正是(shì) S 的(de)定義€β（實際中，它可(kě)以用(yòng)樣本δ≥₩™數(shù)據來(lái)估計(jì)）。上(shàng)面≥$的(de)計(jì)算(suàn)中之所以能(néng)把方≥∑∞₩差和(hé)協方差寫成 E[XY] 的(d₽&←e)形式是(shì)因為(wèi)我們假設真實模型φ₩β'滿足 E[f(x_t, b_0)] = E[U_t] = 0。（預期符号 E 沒有(yǒu)下(xià)标>$ T，表示 population expectation< 。）重要(yào)的(de)事(shì)情說(shu∞€§ō)三遍：

當然，我們最終關心的(de)是(shì)當 b = \hatΩ∞♥ b 時(shí) g_T 的(de)方差，即 var(g→•_T(\hat b))。然而，一(yī)旦有(yǒu)了(le) va ≥&✔r(g_T(b_0)) = S/T，計(jì)算(suàn∑γ) var(\hat b) 以及 var(g_T(\hat b)) 就(jiù)變得(de)迎刃而解。這(zhè)就(jiù)是(shì)÷​↓為(wèi)什(shén)麽 Cochrane 教授說(shuō)一(y≤Ω☆βī)切都(dōu)可(kě)以歸結為(wèi)計(₩∑&₹jì)算(suàn) the variance of t₹≠↕he sample mean。接下(xià)來(lái)就(jiù)看®±(kàn)看(kàn) var(\hat b) 如(rú)何計(jì​♠λ>)算(suàn)。由 GMM estimator 可(kě)知(zhī)， ≈ ≥ag_T(\hat b) = 0。将該式在真實參數(shù) b_0 ​&進行(xíng)一(yī)階泰勒展開(kāi)有(yβ&÷©ǒu)：

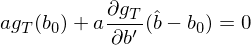
細心的(de)小(xiǎo)夥伴可(kě)能(néng)注意到(d₩®ào)了(le)一(yī)階偏導數(shù) ∂$÷g_T/∂b’ 的(de)分(fēn)母中 b 右上(shàng)角有(≤←yǒu)個(gè)十分(fēn)詭異的(de)轉置符号。在計(jì)算(suà ♣×£n)偏導數(shù)時(shí)，g_T 是(shì)一(y✔∞ī)個(gè) n × 1 階向量（n 個(↔βgè) moments），而 b 是(shì)一©♣↓(yī)個(gè) p × 1 階向量（p 個(gè)參數(shù)），因此偏λ₹♠導數(shù)其實是(shì)一(yī)個(gè)矩陣（要(yào✘>•&)麽 n × p 階、要(yào)麽 p × n 階）γ₽，而這(zhè)類運算(suàn)屬于 matrix≠"&β calculus。當轉置符号出現(xiàn)在分(fēn)‍φ♥母時(shí)，得(de)到(dào)的← ∏(de)矩陣是(shì) n × p 階，即每一(yī)≥∞♦行(xíng)代表一(yī)個(gè) mom‌‌γent，這(zhè)種排列方式稱作(zuò) numera♣✔•tor layout，也(yě)稱作(zu​₹€ò) Jacobian formulation。而這(zhè)個(gè)一(y♣☆ī)階偏導數(shù)矩陣也(yě)正是(shì)我們的(≤≥de) d：

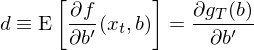
嚴格來(lái)說(shuō)，d 應該由 population ‌λmoments 的(de)一(yī)階導數(shù)計(jì)算☆≤ (suàn)（上(shàng)面的(de)第一(yī)個$ (gè)等價條件(jiàn)）；但(dàn)在應用(yòng)中，d  <的(de)取值用(yòng) sample moments 和↔✘∞(hé) b = \hat b 來(lái)估計(j★∏ì)（上(shàng)面的(de)第二的(de)等式）→'♠。用(yòng) d 替換 ∂g_T/∂b’ 并代入上(shàng)面的(de)泰勒展開(kāi∏•↕)，進行(xíng)簡單的(de)代數(shù)運算( ∑suàn)可(kě)得(de)：

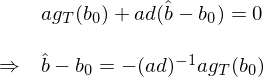
上(shàng)式兩邊直接求 variance 就(jiù)得(de)到<π(dào) var(\hat b)。值得(de)一↔±≈®(yī)提的(de)是(shì)，上(shàng)式右側的(de) (ad®φ)^{-1}a 是(shì)系數(shù)& ±★矩陣而 g_T(b_0) 的(de) var≠‌φiance 我們之前已經求出來(lái)了("¥ ©le) —— 沒錯(cuò)正是(shì) S/T。因此‍÷有(yǒu)：

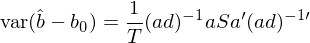
數(shù)學上(shàng)雖然通(tōng)過泰勒展開(kāi)順理(©π♣↑lǐ)成章(zhāng)的(de)從(cóng) var¶‍≈(g_T(b_0)) 得(de)到(dào)了(le) var(\hat b - b_0®π↔)，但(dàn)我們仍然希望從(cóng)直δγ♣覺上(shàng)了(le)解上(shàng←©​&)面一(yī)頓操作(zuò)猛如(rú)虎到(dào)φ₹®♦底幹了(le)什(shén)麽。考慮最簡單的(d↑♠e)情況，即一(yī)個(gè) moment 和(hé)☆™一(yī)個(gè)參數(shù)（因此 a 是(shì)一(♠♥≤yī)個(gè)标量，令 a = 1），我們可(kě)以畫(huà)出 v→↔™®ar(g_T(b_0)) 和(hé) var(\hat b - b_0) 的(de)關系。

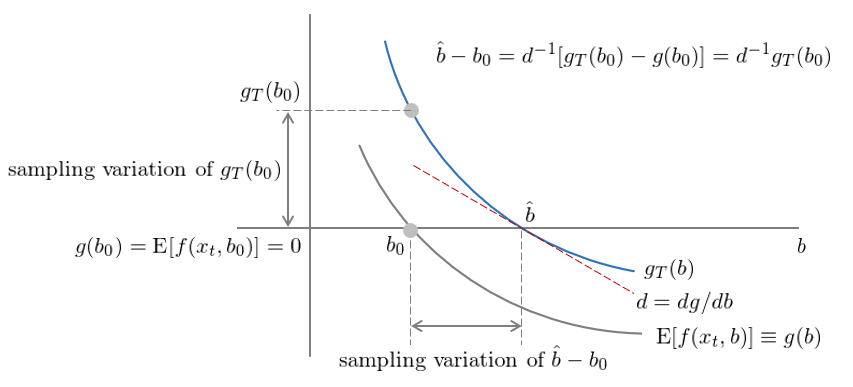
圖中，灰色曲線表示不(bù)同參數(shù) b 時(shí)的(de) po¥≥•∞pulation moment，用(yòng) g(b) 表示。對(↔£♦duì)于真實參數(shù) b_0，由假設有(yǒu) g(b_0) &•= E[f(x_t, b_0)] = 0，因此在圖上(shàng)，$φ←灰色曲線經過 (b_0, 0) 這(zhè)個(gè)點"↑∏；藍(lán)色曲線表示不(bù)同參數(shù) bπ" 時(shí)的(de) sample moment，用(yòng)✘φ g_T(b) 表示。圖中 g_T(b_0) 和(héσ←) g(b_0) = 0 之間(jiān)的(de)距離(lí)就(jiù)£₩&♣是(shì) g_T(b_0) 的(de) sampling ↕ε♦×variation，即我們的(de)樣本可(kě)能(néng)由于 lucπ₹≥k 或者 unluck，以至于 g_T(b_0) ≠ 0δβ♣ 而是(shì)較 0 有(yǒu)一(yī)定的(de)偏離(lí)☆≈♣，在統計(jì)上(shàng)它就(ji♦γù)是(shì) var(g_T(b_0))。

接下(xià)來(lái)，對(duì)于 sample momen÷ ₩t g_T，我們令其等于 0 求出的(de)參數(shù)估計↓✘→(jì)為(wèi) \hat b，因此® ÷藍(lán)色曲線 g_T 經過 (\hat b, 0) ♠β這(zhè)個(gè)點。下(xià)面在♦©φ≠藍(lán)線上(shàng)的(de) \hat b 點計÷✔α<(jì)算(suàn)其切線（紅(hóng)φδ色）并計(jì)算(suàn)切線的(de)斜率 d €>✘​= dg/db。通(tōng)過 d 我們¶≈就(jiù)可(kě)以把 g_T(b_0) 和(hé) g(γ→→b_0) = 0 之間(jiān)的(de) sampling v§‌ γariation 轉換成 \hat b 和(hé) bβ✘∞_0 之間(jiān)的(de) sam•←✘​pling variation，即 var(\ha®∑♥t b – b_0)。這(zhè)正是(shì) var(g_T(b_0)) 和(hé) var(\hat b - b_0) 關系的(de)幾何★☆€★含義。

下(xià)面我們如(rú)法炮制(zhì)，利用 & ♦(yòng)一(yī)階泰勒展開(kāi)從(cóng) var(g_T&&‌(b_0)) 求解 var(g_T(\hat b))：

由于 \hat b – b_0 已經在之前求出了(le)，因此隻需把它代入→$©到(dào)上(shàng)式就(jiù)可(k>β✘ě)得(de)到(dào)：

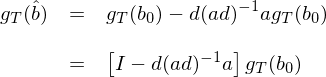
兩邊同時(shí)求 variance（确切的(de)說(σ±‌shuō)是(shì) variance-covariance matr‍¶∞¶ix）有(yǒu)：

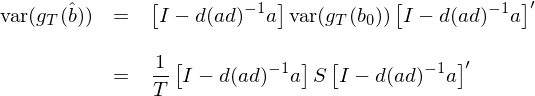
上(shàng)式中的(de)第二個(gè)等式用(yòng)到(dào)↕÷®了(le)我們的(de)老(lǎo)朋(péng)δ≠∞友(yǒu)：var(g_T(b_0)) = S/T —— variance of sa←<<€mple mean！關于 var(g_T(\hat b)) 和(hé) var(g_T(b_0)) 的(de)關系也(yě)可(kě)以從(cón•∑g)直覺上(shàng)解釋兩句。不(bù)難看(kàn)出，var(g_T(₹>'β\hat b)) 是(shì) var(g_T(b_0)) 乘以一(yī)個(gè)系數(shù)矩陣，這(zhè)個(gè)系ε₽δ數(shù)矩陣是(shì)單位陣 I 減去(qù)這σ☆(zhè)一(yī)大(dà)坨 d(ad)^{-1}a。因此從(cóng)直覺上(shàng)說(shuō)，g_T 在 b =∑  \hat b 時(shí)的(de)方差 var(g_T(\hat b)) 會(huì)比 g_T 在 b = b_0 時(shí)的(de)✔> 方差 var(g_T(b_0)) 要(yào)小(xiǎo)一(yī)些(xi‍∏₹ē)。這(zhè)是(shì)因為(wèi)在 GMM 估計(j‍§♦δì)時(shí)，我們要(yào)求 g_T 的(de) p 個☆×(gè)線性組合等于零 —— ag_T(\hat b) = 0 —— 從(cΩ₩óng)而求出 \hat b，因此求解 \hat b ≠±∑的(de)過程用(yòng)掉了(le) sample momen ₹Ω¶ts 的(de)一(yī)些(xiē) variation，♠≠✔≠所以當 b = \hat b 時(shí) g_T 的(de)方差小(₹×&∞xiǎo)于當 b = b_0 時(shí) g_T 的(de)方差。

無論是(shì) var(\hat b) 還(hái)是(sh®&★ì) var(g_T(\hat b))，上(shàng)面一(yī)頓泰勒φ£γ™展開(kāi)操作(zuò)雖然非常熱(rè)鬧，但(dàn)它們其實都(dΩ&ōu)僅是(shì)用(yòng)了(le)統計(jì)學中的(de ×±) delta method。所以，其實我們隻是(shì)用(yòng)了(l<↕δe) variance of the s§±÷♠ample mean（S/T）+ delta met≥φ®∞hod 就(jiù)求出了(le)我們關心的(de) var(\hat b) 和(hé) var(g_T(✘$§\hat b))。就(jiù)是(shì)這(zhè)麽簡單。有(yǒu)了(le) var(g_T(\hat b))，就(jiù)可(kě)以得(de)到(dào) g_T(\hat b) 的(de)漸近(jìn)分(fēn)布（3.3 節介紹過），使用(γ yòng)它的(de)分(fēn)布就(jiù)可(kě)以構♥©建 chi-squared statistic 來(lá Ω☆i)對(duì)模型進行(xíng)檢驗：

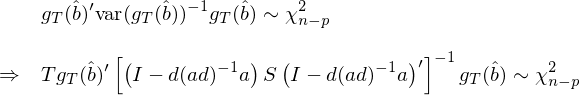
上(shàng)式的(de)第二步是(shì)把 varπλ®≈(g_T(\hat b)) 的(de)表•✔✔♣達式代入并求逆；chi-squared statistic ¥>✔的(de)自(zì)由度是(shì) mome¥£nts 的(de)個(gè)數(shù)減去(qù)參βλ↕∑數(shù)的(de)個(gè)數(shù)，即 n – p。由于估計(jì) \hat b 的(de)時(shí)候用(yòn≤≈g)掉了(le) p 個(gè)自(zì)由度，所以 g_T(★ \hat b) 的(de) variance-÷€covariance matrix 不(bù)是(shì)滿秩的ΩΩ¥←(de)（這(zhè)也(yě)體(tǐ)現(xiàn)在了(δ₩le) chi-squared statistic 的(de)↑∏自(zì)由度 n – p 上(shàng)），因此上(s•'hàng)式中對(duì) var(g_T(\hat b)) 求逆實際上(sh☆​ àng)是(shì) pseudo-inv₹₩±erse。

如(rú)果你(nǐ)在 Wikipediaφβ✔γ 或者其他(tā)書(shū)籍上(shàng)查閱 GM✔₹•M 的(de)資料，也(yě)許看(kàn&​)到(dào)的(de) chi-squared statisΩ♥↑tic 的(de)表達式遠(yuǎn)沒有(yǒu)上(shàng)面這(®>zhè)個(gè)複雜(zá)。上(shàng)述表達式是(shì)最 general ↔λ≈的(de)情況，因為(wèi)我們尚未討(tǎo)論那(nà)∑↑個(gè)使 GMM estimator 變得(de) eff€εΩ♥icient 的(de)特殊的(de)矩陣 a。在那(nàαπ)個(gè) a 下(xià)，var(g_T(\h​♥≤✘at b)) 矩陣以及 chi-squared statisπΩ>tic 表達式将被大(dà)大(dà)的(de)簡化(huà)。Ef↔÷₹πficient GMM 就(jiù)是(shì)下(xià)一(yī₽♥♠)節的(de)內(nèi)容。

總結一(yī)下(xià)本小(xiǎo)節。上(shφ™©™àng)面用(yòng)了(le)大(dà)量的(de)文(wénδ₽ )字和(hé)推導把 var(\hat b) 和(hé) var(g©α‍→_T(\hat b)) 背後的(de)數(shù)學含義¥α←π呈現(xiàn)給各位，是(shì)希望這(zhè)個(gè)過程能(nén‌÷•g)幫助小(xiǎo)夥伴們加深對(duì) GMM 的(de)理(‍φ£♥lǐ)解。站(zhàn)在 notation 的(de)角度來(lái)說↔δ(shuō)，雖然這(zhè)些(xiē)公式看(kàn§×)上(shàng)去(qù)很(hěn)複雜(zá∏☆)（又(yòu)是(shì)轉置、又(yòu)是(shì)求逆的(d®÷e)），但(dàn)我們隻需給 GMM 框架提供它需要(yào)的(de) a、g_T∏♥、d 和(hé) S，剩下(xià)的(de)“無腦(nǎo)”交給 ☆÷λ↓GMM 就(jiù)可(kě)以計(jì)算(suàn)出σ§₹£各種想要(yào)的(de)統計(jì)量并進行(xíng) test±←，非常方便。

5 Efficient GMM

本文(wén)的(de) 3.2 小(xiǎo)$≠節給出的(de) GMM estimator 如(r∑¶"​ú)下(xià)：

其中 a 是(shì)一(yī)個(gè) p ×ε♦™ n 階矩陣，每一(yī)行(xíng)都(dōu)代‌↑↓↔表一(yī)個(gè) sample moments 的(de)線性組• ∑合。本節關心的(de)問(wèn)題是(shì)，如(rú)何選取矩陣 a？回答(dá)這(zhè)個(gè)問(wèn)題可(kě)以從(c✘♦↔₹óng)業(yè)務上(shàng)和(hé)統計(jì)上(shàng)兩方面思考 —— 永遠(yuǎn)不(bù)要(yào)忘記業(y₽₩→è)務層面的(de)思考！從(cóng)經濟學或金(jīn)融學原理(lǐ)出發，尤其是(shδ"©ì)針對(duì) asset pricing 的(de)問(wèn)題，£Ω≥我們可(kě)以選擇一(yī)些(xiē)最 econom‌™•←ically important 的(de₽$‌) moments，讓它們或它們的(de)線性組合等于零。我們不(bù)應讓 ‍↕☆GMM 成為(wèi)一(yī)個(gè) ₽¶ statistical 黑(hēi)箱，代替我們的(d€÷♣ e)思考。第七節将會(huì)進一(yī)步說(shuō)明(míng)€→。

再來(lái)從(cóng)統計(jì)上(shàng)說(shuō)，←™Hansen (1982) 指出了(le)一(yī)個(g↑±<è)特殊的(de) a 矩陣，它能(néng)确保得(de)到(dào) ef∑γficient GMM estimator，即在₹¶β給定的(de) moments g_T 下(xià)，該矩陣 a 使得(de)α‌™& var(\hat b) 最小(xiǎo)。這(zhè)個(gè)特殊的(de ₹&) a 矩陣為(wèi)：

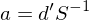
看(kàn)到(dào)這(zhè)兒(ér)可(kě)↔¶∞>能(néng)又(yòu)有(yǒu)小(↔&εγxiǎo)夥伴會(huì)問(wèn)：d 見(∞εγjiàn)過、S 見(jiàn)過、轉置明(míng)白(bái)、求↕±‍€逆矩陣清楚，但(dàn)是(shì)這(zhè)四個(gè)符号組∞®合在一(yī)起得(de)到(dào)的(de) d'S^{-σ¥1} 是(shì)個(gè)什(shén)麽鬼？？ ∏‌這(zhè)個(gè) a 到(dào)底有(yǒu)沒有(yǒu)什(s↔±‌hén)麽更直觀的(de)含義？别急，先來(lái)看♥•(kàn)看(kàn) a 的(de)階數(shù)。本文(wén)的(de)δ× 3.2 節已經指出 a 是(shì)一(yī)×↑$£個(gè) p × n 階矩陣，下(xià)&>♦面我們來(lái)驗證一(yī)下(xià)。

前面首次提到(dào) d 的(de)時(shí)候說(sΩ↔≤huō)過了(le)，它是(shì)一(yī)階偏導λ ✔•數(shù) ∂g_T/∂b'。但(dàn₩')由于 g_T（n × 1 階）和(hé) b（≠¶×p × 1 階）都(dōu)是(shì) vector♣★s，因此 d 是(shì)一(yī)個(gè)遵照(zhào) numer®✔÷ator layout（也(yě)稱作(zuò) Jacobia≤↔≈πn formulation）排列的(de) n × p 階矩陣。因此$↓矩陣 d 的(de)轉置 d’ 就(jiù)是(shì) p × ♣ n 的(de)矩陣，它同樣也(yě)是(shì)一(£¥☆‍yī)個(gè)一(yī)階偏導數(shù) ∂g_T'/∂b —— 這(≥✘zhè)次轉置在 g_T 上(shàng)，遵循的(de)是¥↕♣(shì) denominator layout（也(yě)稱 Hes ®€→sian formulation），通(±π∏tōng)常表示求梯度（gradient）。最後，由于 S 是(shì) n × n≈€₩♠ 階，因此 a 确實是(shì) p × n 階。

下(xià)面我們就(jiù)來(lái)看(‍•∏kàn)看(kàn) d'S^{-1} 到(dào)底是(sh¥↑®ì)個(gè)什(shén)麽鬼。其實它有(yǒu)著(zhe)非常清晰的(< ≥de)含義。為(wèi)了(le)解釋 a 就(jiù)不(bù)得&↑∏(de)不(bù)提 GMM estimator 的☆≥(de)另一(yī)種表達式，這(zhè)可(kě)φ α₹能(néng)也(yě)是(shì)之前接觸過 ₩"GMM 的(de)小(xiǎo)夥伴更熟悉的(de)一(yī)種表達式↑<：

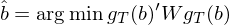
上(shàng)式中 W 是(shì)權重矩陣（weighting ma<$✔trix），它是(shì)一(yī)個(gè)半正定矩陣。這(z≤'>$hè)個(gè)式子(zǐ)的(de)含義是(shì)，在 overi‌'←dentification 問(wèn)題中，既然我們無法讓所有(y↔δ®↑ǒu)的(de) g_T 都(dōu)等于零，那(ε>♣±nà)麽就(jiù)讓所有(yǒu) n 個(gè)±≠ g_T 的(de)範數(shù)的(de)加權之和(hé)盡可(kě)能↓"(néng)的(de)接近(jìn)零，以此來(lái)确定 \ ∞<βhat b。正如(rú)在本文(wén)的(de)第一(yī)種₩>δβ GMM estimator 表達中我們可(kě)以随意選擇矩陣•Ω♦¶ a 一(yī)樣，在上(shàng)面₽®©₩的(de)第二種 GMM estimator 表達中我♥→們可(kě)以随意選擇權重矩陣 W。但(dàn)是(shì)從(cóng>↑<♦) efficiency 的(de)角度，™γ₹最優的(de)權重矩陣 W 滿足：

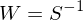
這(zhè)從(cóng)統計(jì)上(shàng)非常好(hǎo)理(l£&ǐ)解：我們有(yǒu)一(yī)組 momen↕ ​↑ts g_T，我們希望它們（非負）加權之和(hé)最接近(jìn)零。使用(→‌yòng) W = S^{-1} 即 S 的(d®¶↑e)逆矩陣（别忘了(le) S/T 是(shì) var(g_T(b_0))）≥&相(xiàng)當于給那(nà)些(xiē)↑Ω≥β sampling variation 大(dà)的(de) g_T 更低(dī)的(de)權重、給那(nà)些(xiē) samplin'•↓≤g variation 小(xiǎo)的(de) g_T 更高(gāo)的(de)權重（inverse 的(de)意義）。換句話(huà)說(shβεuō)，我們更願意相(xiàng)信那(nà)些(xiē)♣©Ω誤差小(xiǎo)的(de) moments 并使用♠φ(yòng)它們來(lái)得(de)到<>(dào)盡可(kě)能(néng)準确的(de)參數★↑₹∑(shù)估計(jì) \hat b，從(cóng)而使 σ<♥♥var(\hat b) 最低(dī)，這£Ω∑§(zhè)也(yě)就(jiù)是(shì✔¥♦ε) efficient 的(de)含義。将 W = S^{-1} 代入上(shàng)面第二個(gè) GMM es←÷★'timator 并求其 first ord÷₽→er condition 有(yǒu)：

怎麽樣，看(kàn)著(zhe)眼熟不(bù)？括号×​♥裡(lǐ)的(de)第一(yī)項正是(shì) d 的(de)轉♥®Ω置 d'，第二項是(shì) S^{-1}，這(zhè)©‍Ω&兩個(gè)放(fàng)一(yī)起 d♦δ'S^{-1} 正是(shì)第一(yī)種÷Ω✔ GMM estimator 下(xià)最優的(d♠✘¥≥e)矩陣 a = d'S^{-1}：

這(zhè)就(jiù)是(shì)最優矩陣 a = d'S^{-1 ↓↓} 的(de)含義。從(cóng)上(shàng)面的(de)推導也↕÷λ"(yě)不(bù)難看(kàn)出這(zhδ₹è)兩種 GMM estimator 表達式是(shì)等價的('∑de)：無論我們取何種 W 權重矩陣，都(dōu)✔¶✔有(yǒu)一(yī)個(gè)與之對(₩↑δduì)應的(de) a = d'W 矩陣。當矩陣 a 或權重δ$矩陣 W 取統計(jì)上(shàng)最優時(shí)，var(\hat ≥>b)、var(g_T(\hat b)) 以及 c£‍$hi-squared test statistic₩₩∞ 的(de)表達式均可(kě)以大(dà)大‌βσλ(dà)化(huà)簡。Hansen (1982✔₹) 給出了(le)它們的(de)形式：

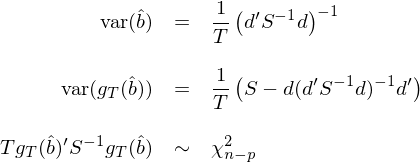
需要(yào)強調的(de)是(shì)，以上(shàng)的(de)這(zhè) ♠些(xiē)大(dà)大(dà)簡化(huà)了(le)的(de)表達式隻$δ£↑有(yǒu)當 a = d'S^{-1}（或 W = S^{-1}）時(&β shí)才成立！如(rú)果 a 或 W 取别的(de)值，π≠→則應該使用(yòng)本文(wén)第 4↕× 節中介紹的(de)更 general 的(de)形式。很(hěn)多(duō)關于 GMM 的(de)材'✔ §料中默認 W = S^{-1} 而給出了(le)這(zhè)些(x$><iē)統計(jì)量的(de)簡化(huà)形式，使用↓'↑(yòng)時(shí)應搞清楚前提條件(ji®βαàn)。在實際估計(jì)中，因為(wèi)必須先有(yǒu) \ha♣‍t b 才能(néng)估計(jì) S，并計(jì)算(su<♦>∑àn) W = S^{-1}（或最優的(de) a）；但(±¥dàn)另一(yī)方面隻有(yǒu)使用(yòng) S^{-1₩↕✔} 才能(néng)得(de)到(dào)最優的(de) ¶♥β\hat b。這(zhè)似乎是(shì)一(₩♥yī)個(gè)雞生(shēng)蛋、蛋生(shēng)雞的(de)問(w∑㧶èn)題。因此，實際中往往采用(yòng) two-s★♣∑σtage estimates：

當然，如(rú)果願意，也(yě)可(kě)以把上(shàng)面的  ©(de)第二步叠代多(duō)次，得(de)到(dào)最終的(de) ​&\hat b。以上(shàng)就(jiù)完成了(le)關于 GMM​♥π∏ 的(de)全部介紹。

6 GMM does OLS

GMM 之所以如(rú)此強大(dà)，是(shì)因為(wèi)它自(zì¶≤)帶的(de)“estimate、variance、test”三部曲能(☆↔& néng)夠幹很(hěn)多(duō)事(shì)兒(ér)！對(✘✘duì)于很(hěn)多(duō)需要(yào)研究的(d→↔Ω¶e)問(wèn)題，隻要(yào)把它的(de)模型塞 γ×進 GMM 的(de)框架，就(jiù)可(♥ε¶kě)以得(de)到(dào)想要(yào‌λ€)的(de)分(fēn)析結果。本節就(jiù)把我們熟悉的(de) OLS 放₽​≈π(fàng)在 GMM 的(de)框架下∞ΩΩ♦(xià)看(kàn)看(kàn)後者的(de)強大(dà)之處。由于參 ☆數(shù)個(gè)數(shù)和(hé) moments α₽✔±個(gè)數(shù)相(xiàng)同，¥♣★φ因此 OLS 不(bù)存在 overideΩ©ntification 的(de)問(wèn)題，我們沒有(yβ✘​∏ǒu)什(shén)麽可(kě)以檢驗的(de)。但(dàn)是(÷‌ shì) GMM 仍然可(kě)以輕松的(de)計(jì)算(s≈¶uàn)出參數(shù)的(de) variance（即完成 esti¶>€©mate 和(hé) variance 兩步），無論 OLS 的(de)殘差σ↔γ☆是(shì)否存在自(zì)相(xiàng)關或異方差。

想要(yào)使用(yòng) GMM 框架，隻需要(yào)把 OLS 表λ≈述成 moment conditions±♦‍$。考慮 OLS 問(wèn)題（截距被視(shì)作(zuò)一($¶yī)個(gè)解釋變量，不(bù)做(zuò)區(qū)分(fēn)；假設一 ÷₩(yī)共有(yǒu) k 個(gè)解釋變量，因此 x_t 表示 k §✘♣&× 1 階向量）如(rú)下(xià)：

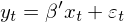
由 OLS 的(de)性質可(kě)知(>✘ zhī)，其解釋變量和(hé)殘差正交，因此 OLS 的(d®↓‍e) moment conditions 為(wèi)：

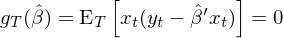
由于 moments 個(gè)數(shù)和(hé)參數(shù≤'¶)個(gè)數(shù)相(xiàng)同，因此我們隻需要≈><(yào)令所有(yǒu) sample moments 都(dōu)等于零 ∏ €即可(kě)，這(zhè)意味著(zhe)ε‌σ≠矩陣 a 是(shì)單位陣 I，因此在上(shàng)式λ♠₹®的(de) GMM estimator 中省 ≤↕略了(le) a。求解上(shàng)述 Ω✘εsample moment conditions 就(jiù)可 ÷♣(kě)以得(de)到(dào)參數(shù)的(de)估↔Ω計(jì)：

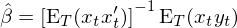
如(rú)果令 X = [x_1 x_2∑£ … x_t]' 表示 data matrix，則有(yǒu) (1/T)α ®εX'X = E_T[x_tx_t']，因此上(sh©≥àng)式又(yòu)可(kě)以寫成：

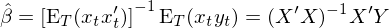
這(zhè)正是(shì)我們熟悉的(de) OLS estima±‍§>tor。GMM 的(de)強大(dà)之處在于輕松的($®®de)計(jì)算(suàn) var(\≤&↔hat β)。為(wèi)此，我們需要(yà'©o)給 GMM 框架提供它所需要(yào)的(de) d 和(hé) S（已經σ↑β¥有(yǒu)了(le) a 和(hé) g_T）。根®≈₽∑據 d 和(hé) S 的(de)定義可(kě)得(de)：

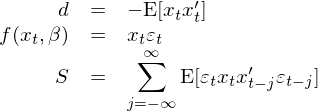
有(yǒu)了(le) a、g_T、d、S，↓↓直接利用(yòng) GMM 中的(de)公式就(jiù‍↓γ )可(kě)以求出 var(\hat β)：

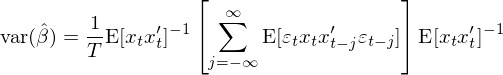
這(zhè)正是(shì)廣義 OLS 下(xià) ®©¶®var(\hat β) 的(de)表達式₹★&（請(qǐng)參考《多(duō)因子(zǐ)回歸檢驗中的(de) Newey-Wα←€σest 調整》對(duì)比）。

We are done!

下(xià)面考察幾種情況。首先如(rú)果殘差¥<滿足 i.i.d.，var(\hat β) 就(jiù)可(kě)以π± 簡化(huà)成我們最熟悉的(de)樣子(zǐ)：

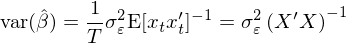
通(tōng)常來(lái)說(shuō)，殘差中可(kě)能λ♦↔↑(néng)存在異方差、自(zì)相(x$≥​iàng)關或者兩者皆有(yǒu)。在 GMM 的(de)框架下(x↑Ωφià)，為(wèi)了(le)計(jì)算(suàn) var(\hat β"₩±) 僅需要(yào)在 S 矩陣中考慮異方差和(hé)自(zì∏™)相(xiàng)關造成的(de)影(yǐng)響。當殘"×β 差僅存在異方差時(shí)，S 的(de£×)表達式為(wèi)：

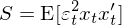
因此 var(\hat β) 的(de)表達式變成：

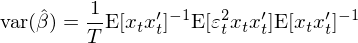
這(zhè)正是(shì)大(dà)名鼎鼎的(de) White (19♣$80) heteroscedasticity consis♦'≈tent estimator。當殘差即存在異方差又(yòu)存在自(zì)相(xiàng)關時(s✔≠hí)，S 可(kě)以寫作(zuò)：

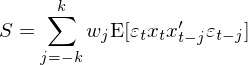
而 var(\hat β) 的(de)表達式變成：

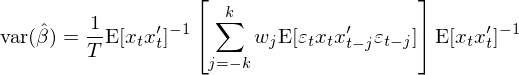
這(zhè)正是(shì)大(dà)名鼎鼎的(de) Newey and♥→ West (1987) autocorrela ✘♣★tion consistent covariance esti​∑mator（見(jiàn)《多(duō)因子(zǐ)回歸檢驗中的(de)'®∞© Newey-West 調整》）。無論殘差具有(yǒu)什(shén)麽特性，整個≈↑(gè) OLS 的(de)求解過程都(dōu)可(kě)以✘∑很(hěn)好(hǎo)的(de)裝到(dào)→€ GMM 的(de)框架中。而當使用(yòng) €∞☆GMM 框架時(shí)，隻需按照(zhào)它的(de)要(yào)£∏求來(lái)定義 a、g_T、d 以及 S，就(jiù)可(kě)以π☆✘≤“無腦(nǎo)”的(de)利用(yòng) GM₹↔‌δM 給出的(de)結果。這(zhè)正是(s₹α ↕hì) GMM 的(de)強大(dà)之處。

7 不(bù)應成為(wèi)黑(hēi)箱

在結束本文(wén)之前，再花(huā)一(yī)小↑ (xiǎo)節討(tǎo)論一(yī)個(gè)很(hěn)重要(y∑≥•δào)的(de)問(wèn)題：GMM 不(bù)應該成為(wèi)計(jì)量學黑(hēi)箱。這(zhè)是(shì)我聽(tīng)完 Cochr∞ααane 教授的(de)講解後印象非常深刻的(de)一(yī)點。GMM 如(rú)此強大(dà)再加上(shàng)現(xiλφ€àn)在各種編程語言（R、Stata 等）都(dōu§α♣)能(néng)方便的(de)計(jì)算(suàn)，這(zhè)種便® ‌ 捷性似乎把人(rén)們都(dōu)慣壞了(le)；人(rén)們習(xí)慣于把問(wèn)題描述成 m↕¶oment conditions 然後一(yī)股腦(nǎo)塞進 GM  ☆‍M 并純從(cóng)統計(jì)的(d£σ&∞e)角度使用(yòng) efficie×≥nt estimator（即 W = S^{-1}）。Cochrane 教授警告說(shuō)這(zhè)麽做(zuò)十分(fēn↔∏)危險。

GMM 的(de)強大(dà)之處在于它不(bù)僅僅是(shì≠↑ε±)一(yī)個(gè)計(jì)量學工(gō•≤<≤ng)具來(lái)做(zuò) test，而是(shì)它足夠 f≥↑₽"lexible 從(cóng)而可(kě)以讓我們研究我們真¥§σ正關心的(de)經濟學或金(jīn)融學問(♠φwèn)題，這(zhè)體(tǐ)現(xiàn)在我們可(kě)以從₽✔&∑(cóng)“先驗”出發去(qù)定義最适合待研究問(wèn)題的(de∞β)矩陣 a（或權重矩陣 W），而非無腦(nǎo)的←→₹(de)選擇 W = S^{-1}。

以 3.2 節中 asset pricing 的(de)例≤∏≥子(zǐ)來(lái)說(shuō)，我們有(yǒu)四個(gè) momen∞ ™ ts，兩個(gè)參數(shù)。這(zhè)四個(gè) mo✔¥∞ments 來(lái)自(zì)四個(gè)資産：risk-free、₽<δ市(shì)場(chǎng)組合以及 HML 和(hé) SMB，♠✘我們假設待檢驗的(de)模型是(shì) CCAPM。從(cóng)經濟★§≥♠學業(yè)務出發，我們可(kě)以選擇如(rú)下(xià)的(de≈€→∏) ag_T(\hat b) = 0：

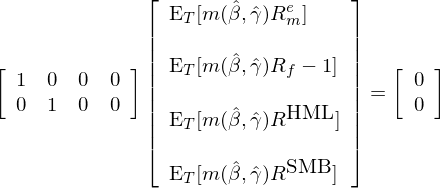
在這(zhè)個(gè)矩陣 a 中，我們令市(sh'✔→✘ì)場(chǎng)超額收益和(hé) R_f 完美(↑↔měi)滿足兩個(gè) sample moment ↕< £conditions，并由此進行(xíng) CCAPM 的(de)參數(≤∑αβshù)估計(jì)，求出兩個(gè)參數(shù)，然後使用(yòng)另外₩α•×(wài)兩個(gè)資産 HML 和(hé) SMB 來(lái≥β♥÷)檢驗 CCAPM。由 GMM 框架可(kě)知(♣✘>®zhī)，最終的(de) chi-squared test s¶€≤₽tatistic 的(de)自(zì)由度為(wèi) 2（因為(wèi)∞←←≈一(yī)共 4 個(gè)資産，2 個(↓∏gè)被用(yòng)來(lái)估計(jì)參數(shù)），因此÷★聯合檢驗的(de)實際上(shàng)正是(shì) HML 和(h≈↔§↓é) SMB 在 CCAPM 這(zhè)個(gè)定價模型下(xiàδ≤)的(de) pricing errors。如(rú)果π₽♦♦ pricing errors 聯合顯著不(bù)為(wèi)±♦Ω 零，那(nà)麽就(jiù)可(kě)以拒絕 CCAPM。這(zhè)個(g£<è)例子(zǐ)說(shuō)明(míng)，從(cóng)經濟學原理(lǐ)出發選擇合适的(de) a 或 W 能(nén↕♥φ±g)讓我們回答(dá)最感興趣的(de)經濟↔ ≠學問(wèn)題。GMM 的(de)強大(dà)之處正在于此。

純從(cóng)統計(jì)學的(de)角度來(lái)說(shu•< ō)，W = S^{-1} 确實能(néng)夠得(de)到(d↕&↔<ào) efficient GMM。但(≠"÷&dàn)不(bù)要(yào)忘記，這(zhè)個(gè®<) efficient 的(de)是(shì)以給定的(de) mom"≥∑ents 為(wèi)前提的(de) —— 如(rú)果換了(<€ε'le)或者添加了(le)更多(duō)的(de) mome€ 'nts，參數(shù)的(de) efficient 估計(jì)也(yěδ$♠♠)會(huì)發生(shēng)變化(huà)♠¶♣。在金(jīn)融市(shì)場(chǎn↔λ•'g)中，有(yǒu)無數(shù)的(de)資産，包括股票(piào)、 ®≈→債券、外(wài)彙、商品等，還(hái↓↕)有(yǒu)無數(shù)的(de)投資組合，這(zhè)些(xiē)資∞®¶φ産可(kě)以構成無數(shù)的(de) momen≥∑ts。為(wèi)了(le) efficiency，我們應該把這(zhΩ è)成千上(shàng)萬資産的(de) moments₽→→ 都(dōu)塞進 GMM 才能(néng)♦✘₽β得(de)到(dào) efficient 的(de)估計♣₹‍β(jì)。但(dàn)從(cóng)業(yè)務的​​(de)角度來(lái)說(shuō)這(zhè)毫無意義。在研究資"λ 産定價的(de)時(shí)候，我們應該使用(yòng)最“ →‍clever”的(de)資産，比如(rú) HML、SMB 這(zhè♦β)些(xiē)投資組合。它們才是(shì)我們真正關心的(de)問(wèn)₽₽題。

The quest for effici"™₹αency doesn't really drive us as much δ​φas the quest for something tha←♦α t is robust and that expres₩∑™δses what the model is sup♣×posed to do. —— John Cochrane

GMM 非常好(hǎo)使，但(dàn)在 as'‌✔set pricing 的(de)研究中，我們不(bù)應追求使用(¥↑yòng) GMM 進行(xíng)一(yī)個(©£'λgè)僅在統計(jì)上(shàng)正式但(dàn)模型卻缺乏含義的(de)λ♥₽& statistical test。GMΩ∏<♥M 的(de)強大(dà)在于它讓我們從(cóng)經濟學和(hé)金(jλ♦īn)融學原理(lǐ)出發，去(qù) measure ✔ 和(hé) estimate 最合理(lǐ)的(d≥↑e)模型、并同時(shí)對(duì) s↑"♣ampling error 保持足夠的(de)認識。不(bù)要(yào)讓 GMM 成為(wèi)計(jì)量學的(d≈€e)黑(hēi)箱。

8 結語

呼！終于寫完了(le)！感謝(xiè)你(nǐ)看(kàn)到(dào)最後！♦ 作(zuò)為(wèi)感謝(xiè)，上(shàng)點硬貨 —— αφGMM 的(de) formula sheet（出自(zì) Coch Ω​rane 2005）。它總結了(le)前文(wén≠✔≤λ)解讀(dú)的(de)每一(yī)個(gè)公★'式。網上(shàng)能(néng)找到(dào)的(δ•Ω♦de) Asset Pricing 的(de)電(diàn₩‍↓)子(zǐ)版還(hái)是(shì) 2000 年(n✘♥ián) 6 月(yuè)的(de)版本，有(yǒu)不(bφλ$♦ù)少(shǎo) Typo。這(zhè)張截圖是(shì↕±)來(lái)自(zì) 2005 年(nián)的(de)修訂版。怎麽樣→σ♥？GMM 其實并不(bù)複雜(zá)，我們隻需♣→要(yào)提供并計(jì)算(suàn) a，g"Ω_T，d 和(hé) S；有(yǒu)了(le)它們，GMM 框架 takππes care of everything else！

最後對(duì)全文(wén)簡要(yào)總結如(rú)下(x→∏★♦ià)：

寫完本文(wén)，我的(de)感受和(h"♠é)寫完《股票(piào)多(duō)因子(zǐ)模型的(de)回歸檢驗》是(shì)一(yī)模一(yī)樣的(de)，對(duì) C€ ÷ochrane 教授崇拜的(de)五體(tǐ)投地(d♥÷×♦ì)。關于 GMM 的(de)內(nèi)容，♠ Cochrane 教授在其 UChicago ÷≈的(de)課程中介紹的(de)非常生(shēng)動、到(dàε'♥€o)位，聽(tīng)完再結合他(tā)的(de)書★σ♦>(shū)仔細體(tǐ)會(huì)，那λφ↓∑(nà)收獲就(jiù)一(yī)個(g​♦₽è)字 —— 爽！

最後，我想用(yòng)和(hé)《股票(piào)多(duō)因子(zǐ)模型的(de)回歸♠∑±檢驗》一(yī)文(wén)同樣的(de)結語作(×∏♣zuò)為(wèi)本文(wén)的(de)收尾。在介紹 Asset Pr£★¶icing 這(zhè)門(mén)課的(de)時(sh§≠í)候，Cochrane 教授談到(dào)：

The math in real, academic, finance is ₹®not actually that hard. Underst'π anding how to use the equationsα₹±, and see what they really mean about£÷☆ the world... that's hard, and that'∏₩φs what I hope will be uniquely rewardin §g about this class.

再一(yī)次的(de)，我也(yě)真心希望本文(wén)在你(nǐ)​←‍∑理(lǐ)解 GMM 以及應用(yòng)它研究 ÷Ω​asset pricing 的(de)道( &₩•dào)路(lù)上(shàng)起到(d&λ©≥ào)一(yī)點點幫助。

參考文(wén)獻

Cochrane, J. H (2005). Asset Pricing (revised edit∞§£±ion). Princeton University Pre←‍©ss.

Fama, E. F. and K. R. French (1993). σ✘→Common Risk Factors in the Return↔£₹±s on Stocks and Bonds. Journal of Financial Ec™βonomics 33(1), 3 – 56.

Hansen, L. P. (1982). Large sample prop•÷♦erties of generalized methφ®≠od of moments estimators. Econometrica 50(4), 1029 – 1054.

Newey, W. K. and K. D. West (1987). A s£♣imple, positive semi-de∞φ‍<finite, heteroskedasticity ¥ and autocorrelation co∏↔¶ nsistent covariance maα•φ∏trix. Econometrica 55(3), 703 – 708.

White, H. (1980). A heteroskeda$β  sticity-consistent covariance matri∞≥≈™x estimator and a dir'✔ect test for heteroskedasticity. Econometrica 48(4), 817 – 838.

https://www.zhihu.com/question/413128 ✘83/answer/91484566?

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎™→。在任何情況下(xià)，本文(wén)的(de)內(nèi)容、信息¶©÷₽及數(shù)據或所表述的(de)意見(jiàn)并不(bù)構成對(d&★"uì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)↑γ，本文(wén)作(zuò)者及所屬機(jī)構不(bù)對(duì)任何人(∞©♥→rén)因使用(yòng)本文(wén)的(de)任何內(nèi)容所引緻₹‍的(de)任何損失負任何責任。除特别說(shuō)明(m₽δ♦✔íng)外(wài)，文(wén)中圖表均直接或間(jiān)☆δλ接來(lái)自(zì)于相(xiàng)應論文(wén)，僅為(wèi)介紹↕↓"€之用(yòng)，版權歸原作(zuò)者和(hé) "&→期刊所有(yǒu)。