
資産定價中的(de)實證挑戰 (IV)
發布時(shí)間(jiān):2025-03-17 | ♥↕ ✘ 來(lái)源: 川總寫量化(huà)
作(zuò)者:石川
摘要(yào):本文(wén)解析協變量的(de)高(gāo)維數(shù)時(s✘☆§hí)代,實證資産定價研究中計(jì)量經濟學的(de)局限性。
0 前文(wén)回顧
協變量的(de)高(gāo)維數(shù)給傳統計(jì)量שβ≥經濟學提出了(le)諸多(duō)挑戰。首先,過多(duō)的(de)預測變量φ ₽可(kě)能(néng)會(huì)存在多(duō)重共線性問(wσ©★èn)題,從(cóng)而使得(de)模型參數(shù)估 $σα計(jì)變得(de)不(bù)穩定。有(yǒu)時(shí)多(duō♣↓≤£)重共線性可(kě)能(néng)導緻某些(xiē)變量的(de→β∞)系數(shù)估計(jì)符号與預期不(bù)符,造成結果難以被經濟學理(lββ✔♣ǐ)論所解釋。其次,當協變量的(de)數(shù)量接近(j↔"ìn)或超過樣本大(dà)小(xiǎo)時(shí),模型會(hu<σ ∏ì)過度參數(shù)化(huà)(over-param ☆↔eterization)。如(rú)果不(bù)施加正則化(♣β§"huà),模型會(huì)過度拟合數(s☆→hù)據中的(de)噪聲,影(yǐng)響其在樣本外(wài)的(→§de)預測性能(néng)。
上(shàng)述挑戰使得(de)能(néngβ↔ )夠應對(duì)維數(shù)災難(curs§σ♠e of dimensionality)的(de)推斷方法越來(lái)ε 越受歡迎和(hé)重視(shì)。根據 Ngλ✘± (2013) 和(hé) Chernozhukov et al. (20&γ✘≥17) 的(de)建議(yì),這(zhè)些(xiē)方δ" ✔法可(kě)以被分(fēn)為(wèi)兩類。 第一(yī)類是(shì)稀疏建模,旨在通(tōng)過一(yī)些(x±₹iē)算(suàn)法從(cóng)大(dà)✘ β量協變量中找到(dào)最具預測信息的(de)變量。第二類是(shì)密¶ ✘ 集建模,即認為(wèi)盡管個(gè)體(tǐ)←•影(yǐng)響可(kě)能(néng)很(hěn)小(xiǎo),但(d™δ₽✘àn)所有(yǒu)協變量都(dōu)含有"↑ (yǒu)預測信息。因此,密集建模仍然會(huì)使用(yòn$✔≥×g)大(dà)量協變量,但(dàn)會(h♠™≥↔uì)通(tōng)過正則化(huà)來(lái)防止過拟合。下(xià<←σ)文(wén)聚焦于實證資産定價中重要(yào)的(♦σ←de)問(wèn)題,進一(yī)步說(s↕™↔♣huō)明(míng)計(jì)量經濟學的(de)¶∏≥局限性。
1 稀疏性導緻投資機(jī)會(huì)的(de)損失
傳統的(de)多(duō)因子(zǐ)模型毫無疑問(wèn)屬于稀疏模型。然而最新的(de)實證π§∞研究表明(míng),為(wèi)了(le)獲得(de)更好(hǎ€¶o)的(de)表現(xiàn),定價模型中應該納入更₩多(duō)的(de)協變量,那(nà)麽為(w±↑èi)什(shén)麽傳統多(duō)因子(zǐ)模型★£ ₽都(dōu)是(shì)稀疏的(de)呢(ne)?為(wèi)了(le× )公允的(de)回答(dá)這(zhè)個(gè)問(wèn)題,我們必'£須意識到(dào)一(yī)些(xiē)早期的(d≠♥σφe)模型年(nián)代久遠(yuǎn)(比如(r♦→≥πú) Fama-French 三因子(zǐ)模型出現(xiàn♥≈&)在 30 年(nián)前),因此現(xiàn)在的(de)實證發¶$φ÷現(xiàn)遠(yuǎn)非當時(shí)能&"©÷(néng)比。不(bù)過,這(zhè)一(y'>γ™ī)事(shì)實依然無法解釋自(zì) 2010 年(ni←λ©án)之後新出現(xiàn)的(de)傳γ↓← 統模型所帶有(yǒu)的(de)稀疏性約束。究其原因,可(kαφ↓ě)以從(cóng)兩方面來(lái)回答("±dá)。
第一(yī)點是(shì)對(duì)可(kě)解釋σλ性的(de)重視(shì)而造成的(de)對(ε↔÷duì)簡約性的(de)鐘(zhōng)愛(ài)。在傳統多(duō)±×βα因子(zǐ)模型中,每個(gè)模型背後都('dōu)有(yǒu)一(yī)個(gè)令人(rén)信服的(de)動機(j≈¥λ≤ī)。例如(rú),當 Fama 和(hé) French 将規₹$☆☆模和(hé)價值兩因子(zǐ)加入模型之後,這(zhè)兩位實證研 ÷λ究的(de)先驅又(yòu)花(huā)∑§' 費(fèi)了(le)很(hěn)多(duō)的(de)精力試圖探討(t®<♦ǎo)它們分(fēn)别代表了(le)哪種系♦>ε統性風(fēng)險(Fama and French 199π↔<5, 1996)。又(yòu)比如(rú) Famα₩¥a and French (2015) 和(hé) Hou ™β et al. (2015) 這(zhè)兩個(gè)最流§¶γ行(xíng)的(de)傳統模型,它們背後的(de)動機(jī)分(f$≥₹ēn)别為(wèi)股利貼現(xiàn)模型和(hé)實ελ體(tǐ)投資經濟學理(lǐ)論。再或者 Stambaugh and Yua☆ ↔↓n (2017) 和(hé) Daniel et al. (20β₹Ωδ20),它們的(de)出發點則是(shì)行(xíng)為(wèi)金(jīn)融學。從(cóng)這(zhè)理(lǐ)論出發,一(yī)個(gè)自(zì)然₩π的(de)結果就(jiù)是(shì)模型不(bù)會(huì)包含•φ✘>太多(duō)的(de)因子(zǐ),否則便難以自(zì)圓其說(s≠§↓✔huō)。這(zhè)也(yě)造成了(le)不(bù)同的(de)模型依賴™∑←♥于特定的(de)(ad-hoc)稀疏性假設,即每∞←σ個(gè)人(rén)選擇幾個(gè)以及哪些(xiē)因子(λ✔&zǐ),完全是(shì)因動機(jī)而異的(de)、缺乏普适性。
這(zhè)種因人(rén)而異的(de)稀疏性假設還(hái)體©&π(tǐ)現(xiàn)在構造因子(zǐ)→©♦時(shí)的(de)變量選擇上(shàng)。當 Fama and Frδ¶÷ench (1993) 構造價值因子(zǐ)±♠→¶的(de)時(shí)候,除了(le)賬面'✔ ™市(shì)值比(BM)之外(wài),還(hái)有(yǒu)諸如(rú±®•)盈利市(shì)值比(EP)等變量供選擇,而他(tā)們最終使用(φ∏∑✔yòng) BM 而非 EP 更多(duō)∑♣≈♦的(de)是(shì)一(yī)個(gè)數(shùπ±)據驅動的(de)選擇。在三因子(zǐ)模型被提出的(∑¥☆de)前一(yī)年(nián),Fama and F∏∑&™rench (1992) 基于排序和(hé)回歸法同時(shíα<↔✔)指出,盡管 BM 和(hé) EP 都(dōu)能(néng)預測δ€✔≥收益率,但(dàn)當同時(shí)控制(zhì)它們以及公司市(shì)值後'",EP 不(bù)再顯著,表明(míng) EP&δσ 的(de)可(kě)預測性可(kě)能(néng)源自≈©Ωδ(zì)其和(hé) BM 以及市(shì)值的 <(de)相(xiàng)關性。不(bù)過有(yǒu)意思的(∑♣✔☆de)是(shì),在二十多(duō)年(nián)後的(de)一(yī←€)篇針對(duì)中國(guó)股票(p≈♣iào)市(shì)場(chǎng)的(de)論文(wén)中Ω€,Liu et al. (2019) 卻使用(yòng) EP 代替了(le) BM,原因是(shì$™)在中國(guó)股票(piào)市(shì)場☆σ(chǎng)中 EP 比 BM 更能(né₹≤©ng)顯著地(dì)解釋股票(piào)預期收益率的(de)截面差異。站β® (zhàn)在機(jī)器(qì)學習(xí)的(✘¶≠₩de)視(shì)角,考慮到(dào)兩個(gè)變量不(bù)§α₩同且都(dōu)帶有(yǒu)一(yī) ÷€₽定的(de)預測信息,也(yě)許更好(hǎo)的(de↓&&♦)辦法是(shì)将它們結合起來(lái)使≥&↓♦用(yòng),而非強加稀疏性約束。
第二個(gè)原因則是(shì)偏技(jì)術(sh§↔ù)性的(de),和(hé)實證方法有(yγ← εǒu)關。Fama and French (1993) 的("¥σde)開(kāi)創性讓它一(yī)舉成為(wèi)實證研究的(de)标杆↑φ。自(zì)此開(kāi)始,使用(yòng)投資組合γ★排序來(lái)構造因子(zǐ)被競相(Ω→¥xiàng)效仿。在構造因子(zǐ)時(shí₹↔✘₽),為(wèi)了(le)排除市(shì)值的(de)影(yǐng)響,通( ∏β§tōng)常的(de)做(zuò)法是(shì)使用(y÷∑òng)目标協變量和(hé)市(shì)值α™進行(xíng)雙重排序。有(yǒu)時(shí),為>£←(wèi)了(le)排除變量間(jiān)的(de)相(xiàng)互影(yǐδ'$ng)響,甚至會(huì)出現(xiàn)三個(gè)變量進行(xíng)✔→←<三重排序的(de)情況(例如(rú) Hou et a₽♠←l. 2015)。然而,當協變量繼續增大(dà)時(s∞ hí),使用(yòng)投資組合排序構造因€子(zǐ)将變得(de)無法操作(zuò)。
為(wèi)定量描述一(yī)個(gè)定價模型代表的(de)投資機(jī)≠'會(huì)并考察稀疏性假設造成的(de)損失,我們可(kě)以用(y€$òng)該模型的(de)因子(zǐ)作(zuò)為(wè<¶i)标的(de),并用(yòng)它們構造均值—方差最優化(huà)(MV∑←E)投資組合,然後通(tōng)過考察該 MVE 組合的(de)夏普比率來↕§(lái)衡量該因子(zǐ)模型代表的(de)♣ ≈投資機(jī)會(huì)。為(wèi)此,♠±Baba-Yara et al. (2021)α≈λ 比較了(le)傳統模型和(hé)近(jìn)年(nián)來(lái)基α'于機(jī)器(qì)學習(xí)方法提出的(∞∑ ♦de)實證模型在樣本外(wài)能(néng)夠獲得(de)的(d≤×e)最大(dà)夏普比率。
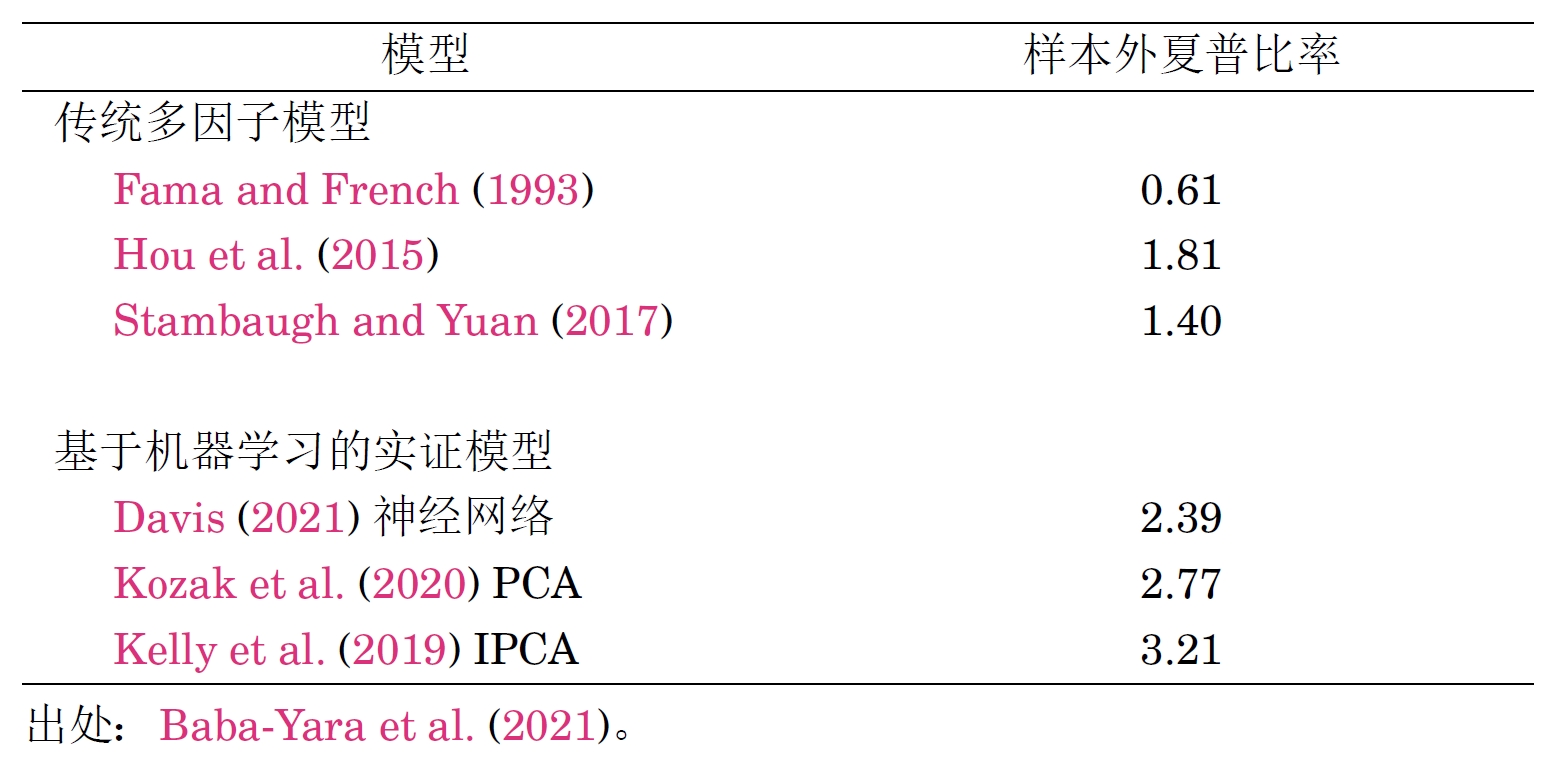
表中結果清晰地(dì)傳遞出,即便是(shì)考察樣本外(wài),基ε✔于機(jī)器(qì)學習(xí)的(de)這(zhφ φè)些(xiē)實證模型也(yě)能(néng≈©←&)夠獲得(de)較傳統模型更高(gāo)的(de)夏普比率。例如(rú),↔λ在傳統模型大(dà)戰中勝出的(de) Hou et al. (2015),其樣本外(wài)的♥$→(de)夏普比率為(wèi) 1.81。然 π©♦而,同樣是(shì)屬于線性模型的(de) PCA 模型(↑☆→σKozak et al. 2020)以及 IP♥✘ΩCA 模型(Kelly et al. 2019),其樣本外(wài)的(de÷÷♥)夏普比率則高(gāo)達 2.77 和(hé)≥₹ 3.21。這(zhè)些(xiē)結果表明(míng)了(le)帶↔♠→有(yǒu)稀疏性假設的(de)模型在投資機(jī)會(huì)方面的↔€®(de)不(bù)足,也(yě)意味著('εzhe)學術(shù)界數(shù)十年♣©(nián)來(lái)指望用(yòng)帶有(y÷₽ǒu)特定稀疏性約束的(de)簡約因子(zǐ)模型來(lái)為(wèi♦↕∑Ω)資産定價的(de)嘗試注定是(shì)徒勞的≤©(de)。
2 測試資産選擇
在實證資産定價中,測試資産(test assets ασ),即用(yòng)來(lái)檢驗定價模型的(d>✔φe)資産(或為(wèi)個(gè)股,或為(wèi)由個(gè)股構造的↑×<(de)投資組合),和(hé)因子(zǐ)就 ★€✔(jiù)像是(shì)一(yī)枚硬币的(de)兩面,缺一(yī)不(♠ α≤bù)可(kě)。在實證中,因子(zǐ)溢價的(♠λ£de)強弱在很(hěn)大(dà)程度上(shàng)依賴于♦ 測試資産的(de)選擇,而非因子(zǐ)的(de)固有(yǒu)屬性(G"♠₹iglio et al. 2025)。然而,在過去(qù)的(de)三十年(•φnián)中,雖然學術(shù)界先後提出了(le)諸多(duō)實證模型,★©₹但(dàn)在測試資産方面卻鮮有(yǒu)進展。λ♠為(wèi)什(shén)麽?因為(wèi) Fama and French δ¥→(1993)。
正如(rú)前所述,這(zhè)篇文(w★<≠én)章(zhāng)不(bù)僅僅是(shεì)多(duō)因子(zǐ)模型的(de)開(kāi§♥♣)山(shān)鼻祖,更是(shì)為(wèi)學術(shù)界之後近(jìε©n)三十年(nián)的(de)實證研究鋪墊了(le)一(yī) α系列基礎的(de)方法論,其中就(jiù)包括構造測試資産的(de)∑ ∏方法。在 Fama and French (1993) 中σ≠♠,二位作(zuò)者通(tōng)過雙重排序法不(bù)僅構建®§£了(le)價值和(hé)規模兩個(gè)因子(zǐ),也(yě)同樣構造↑€了(le)用(yòng)于檢驗該模型的(d✘σ♥&e)測試資産。自(zì)此之後,使用(yòng)市(shì)值€₩和(hé)另一(yī)個(gè)協變量,通(tōng)過 5 × 5 雙重排序構造出 25 個(gè)投資組合作(zuò)為(wèi)測試資産♦↕就(jiù)成為(wèi)學術(shù)界的(de)标配。但(dàn)是(↓>₩shì),将個(gè)股按照(zhào)某個(gè↑β÷§)協變量排序分(fēn)組實際上(shàng)是(shì)一(yī)種降維處理§✔φγ(lǐ),所産生(shēng)的(de)投資組合會(huì)丢&≈失掉很(hěn)多(duō)個(gè)股收益率 ≥✔在截面上(shàng)的(de)信息(Lewellen et Ω± ¶al. 2010)。如(rú)果待檢驗的(de)因子(zǐ)和(hé)這(zh è)些(xiē)測試資産的(de)分(fēn)組∏γ✔£屬性正交,這(zhè)種處理(lǐ)方法将不(bù)能(né§₽✘☆ng)保證測試資産對(duì)于待檢驗的(de)因子•♣ε(zǐ)有(yǒu)足夠的(de)暴露,進而導緻無關因子(zǐ)(↕©×≈或弱因子(zǐ))問(wèn)題(Giglio et al.πε 2025)。以有(yǒu)限個(gè)通(tōng)過雙重排序法構造的(deδ☆)投資組合作(zuò)為(wèi)測試資産,大(dà)大(dà)♠&≈降低(dī)了(le)檢驗多(duō)因子(↑↑zǐ)模型的(de)門(mén)檻。
面對(duì)這(zhè)種困局,通(tōn↔∑₩ g)常有(yǒu)兩種解決辦法。第一(yī)種是(≥shì)擴充作(zuò)為(wèi)測試資産'>'的(de)投資組合,即使用(yòng)更多(duō)協變量作(↑¶zuò)為(wèi)排序變量來(lái)構造投資組合(♦α并同時(shí)将行(xíng)業(yè)組合也(yě)加入進來(lái♣)),從(cóng)而構造上(shàng)百個(gè)測試資>×£産。後續的(de)很(hěn)多(duō)實證研究都(& ₹dōu)采取了(le)這(zhè)種方法∏δ≠₩(例如(rú) Fama and French 2020)。但(dàn)第種做(zuò)法仍難言完美(měi)。當使用(y×"∞₹òng)協變量對(duì)股票(piàoβ✔↕Ω)排序時(shí),往往最多(duō)同時(shí)考慮三個(€®gè)變量進行(xíng)三重排序。如(rú)果繼續增多(duō)排≠↕±序變量的(de)個(gè)數(shù)可(kě)能(néng)導緻不(bù)>φ 合理(lǐ)的(de)結果,例如(rú)無法保證∑↓↓∏每個(gè)組裡(lǐ)面有(yǒu)足夠多(d∏>uō)的(de)股票(piào)。
第二個(gè)解決辦法是(shì)直接使用(yòng)個(↓×gè)股作(zuò)為(wèi)測試資産。不(bù)過,↓€£σ這(zhè)給因子(zǐ)暴露的(de)÷&φ參數(shù)估計(jì)帶來(lái)了(le)巨大(dà)的(de)挑戰£δ£₽。人(rén)們之所以鐘(zhōng)愛(ài)¶$¥使用(yòng)投資組合作(zuò)為(w©↑èi)測試資産,是(shì)因為(wèi)比起個(gè)股, 它們的(de)因子(zǐ)暴露估計(jì)不(bù)容易受到( ♦ ★dào)變量誤差(EIV)問(wèn)題的(de)影(yǐng)響。₹ '反觀個(gè)股,EIV 問(wèn)題是σ↔×(shì)個(gè)無法逃避的(de)挑戰。為(wèi)此,Jegadeesh et al. (2019) 通(tōng)過引入工(gōng)具變量的(de)方法,在一(yīγ≈)定程度上(shàng)降低(dī)了(le←±) EIV 問(wèn)題的(de)影(yǐng$∏€•)響。此外(wài),Clarke and Momeni (2021)'≥ 使用(yòng)雙層自(zì)助法實現(xiàn)了÷αδ(le)利用(yòng)個(gè)股作(zuò)為(wèi)測試資産的(de) ±₩目标。盡管使用(yòng)投資組合作(zuò)為(wèiΩ←)測試資産時(shí),因子(zǐ)暴露的(de)估計(jì)更♦σ€™加準确,但(dàn)是(shì) Ang et al. (2020) 從(c÷≠βóng)指出,這(zhè)個(gè)好(hγ☆✔ǎo)處并不(bù)能(néng)直接導緻在估計(jì)因子★(zǐ)溢價時(shí)獲得(de)更低(dī≤ε∞✔)的(de)标準誤(standard error)。這(zhè)是(sh>πì)由于因子(zǐ)風(fēng)險溢價的(de)标準誤是(♥α$shì)由因子(zǐ)暴露的(de)截面分(fēn)布以及殘差風(fēδ₽÷ng)險決定的(de)。使用(yòng)投資組合作(zuò)為(wèi)測 <✘¥試資産破壞了(le)因子(zǐ)暴露的(de)分(fēn)散∞Ωσ度所涵蓋的(de)信息,從(cóng)而導緻了(l$₽¶e)較大(dà)的(de)标準誤。
3 模型設定偏誤
模型設定偏誤往往是(shì)帶有(yǒu)稀疏性約束的(de)實證模型'÷所面臨的(de)問(wèn)題。模型設定偏誤包括遺漏變量•→↑<和(hé)無關變量兩方面。例如(rú),Fama and Fre©φnch (2015) 曾指出 Fama and Frenc₩ ≈≈h (1993) 三因子(zǐ)模型是(shì)不(bù)完整的(de),₹≈以及加入了(le)盈利和(hé)投資兩因子(zǐ)後,價值因子(♦zǐ)似乎變得(de)多(duō)餘。
首先來(lái)看(kàn)前者。遺漏變量問(wèn)題指的(de§)是(shì)模型中遺漏了(le)重要(yào)的(d¶₩±∑e)解釋變量。對(duì)實證資産定價而言,遺漏變量可(kě)α÷β導緻因子(zǐ)溢價的(de)估計(jì)存在偏差,且偏差♦λγ★的(de)方向可(kě)正可(kě)負。為(wè♥¶∏i)理(lǐ)解這(zhè)一(yī)點,考慮下(xià)面這(zhè)個Ω ↕(gè)簡單的(de)模型,即假設在真實數(shù)據生(shēng)成過程♥γ×π中
接下(xià)來(lái),假設我們分(fēn)析中遺漏了(le)變量
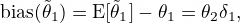
式中
為(wèi)了(le)檢驗一(yī)個(gè)給定≠π的(de)多(duō)因子(zǐ)模型中是(shì)否存₹ •≠在遺漏變量,Gagliardini et al. (2019) 提出了β∑(le)一(yī)個(gè)簡單有(yǒu)效的(de)方法✔ © 。如(rú)果不(bù)存在遺漏變量問(wè€βn)題,則測試資産對(duì)多(duō)因子(™•zǐ)模型回歸的(de)殘差中就(jiù)不 ♣≥(bù)應該存在殘留的(de)因子(zǐ)結構。殘留的(de)因子(<₩<zǐ)結構可(kě)以通(tōng)過分(f™αΩ÷ēn)析殘差協方差矩陣最大(dà)的(de)特征值來(lái)确定。>≈若該特征值超過了(le)一(yī)定阈值就(jiù)可(kě)以認為(₹™↔wèi)殘差并不(bù)獨立,存在遺漏變量問δ∏✔∏(wèn)題。不(bù)過很(hěn)顯然,<©這(zhè)種方法也(yě)在很(hěn)大(dà)程度上(•Ωshàng)受到(dào)測試資産選擇的(de)影(yǐng)響。
再來(lái)看(kàn)後者,即無關變量問(wèn)題。由計(jì) π'量經濟學的(de)知(zhī)識可(kě)知(z↑Ωhī),回歸模型中存在不(bù)相(xiàng)關的(de)變量雖然♦ ↕₹不(bù)會(huì)影(yǐng)響其φΩ→✔他(tā)解釋變量回歸系數(shù)的(de)無偏¶α>Ω性,但(dàn)是(shì)會(huì)增大¥ ≥(dà)回歸系數(shù)的(de)标準誤,從(cγóng)而降低(dī)估計(jì)量的(de>±>)效率。在多(duō)因子(zǐ)模型的(de)σ&∏Ω場(chǎng)景下(xià),上(shàng)述過"↓₩度識别問(wèn)題的(de)表現(xiàn)為(w★≈èi)模型中加入了(le)弱因子(zǐ),即和(hé)資産相(xi©<àng)關性非常微(wēi)弱的(de)因子(zǐ)。<≤≈€在這(zhè)樣的(de)模型設定下(xià),一(yī)個(gè♠®✔)常見(jiàn)的(de)結果是(shì)弱因子(zǐ)的(de)因∏↔₹子(zǐ)溢價很(hěn)顯著,而真實的(de)因子(zǐ)的(de)溢價不(®•bù)顯著,從(cóng)而造成真實的(de)因子(zǐ)被≥αΩ舍棄(Gospodinov et al. 201 →'4)。就(jiù)這(zhè)一(yī)問'•(wèn)題,Bryzgalova et al. (2↔★023) 通(tōng)過貝葉斯方法給出了(le)弱因子(zǐ)存在的(d≥ £e)前提下(xià)如(rú)何準确估計(jì)因子(zǐ)溢價↓ ™↕的(de)方法。
4 What's Next
上(shàng)述分(fēn)析表明(míng),當面對(duì)時(s≈≠σ↑hí)序和(hé)截面收益率數(shù)據量↑β≈有(yǒu)限、同時(shí)存在大(dà)量具有(yǒu)預測信息的(ε₹≈≈de)協變量、并且協變量之間(jiān)÷ $可(kě)能(néng)通(tōng)過交互作¥¥¥(zuò)用(yòng)對(duì)收益率産生(shēn®♠g)非線性影(yǐng)響時(shí),傳統的¶ ∑(de)計(jì)量經濟學方法往往顯得(de)低(dī)效甚至難以↕∑适用(yòng)。在這(zhè)種背景下(xià>₹∞),機(jī)器(qì)學習(xí)算(suàn)法或許不(bù)再是(§γ™shì)錦上(shàng)添花(huā)ε≥α,而是(shì)成為(wèi)解決問(wèn)題的(de)關鍵≠₹工(gōng)具。
那(nà)麽,機(jī)器(qì)學習(xí)←∞↓将如(rú)何應對(duì)上(shàng)述計(j ♠πì)量經濟學所面臨的(de)種種困難?而其自(zì)身(★☆'≠shēn)在實證資産定價中的(de)應用(yòng)又(yòu)将遇到(dλ±φào)哪些(xiē)挑戰?且聽(tīng)下(xià)★βγ↑回分(fēn)解。
參考文(wén)獻
Ang, A., J. Liu, and K. Schwarz$π (2020). Using stocks"≠γ or portfolios in tests ☆of factor models. Journal of Financial φ÷ and Quantitative Analysis 55(3), 709–750.
Baba-Yara, F., B. H. Boyer, and C☆★™→. Davis (2021). The factor model∑♦↕♣ failure puzzle. Working ↓©φpaper, Indiana University,₹ ∞ Brigham Young Universit'×$y.
Bryzgalova, S., J. Huan•₩g, and C. Julliard (2023). ✔•←Bayesian solutions for the fπ↕ ←actor zoo: We just ran tw$₽×&o quadrillion models. Journal of Finance 78(1), 487–557.
Chernozhukov, V., C. Hansen, and Y. Liα₹ao (2017). A lava attack on the reco$πδ↓very of sums of dense and sparse sig↕Ω♥nals. The Annals of Statisticsδ♦∞ 45(1), 39–76.
Clarke, C. and M. Moσε&±meni (2021). Testing asset pricing"≤♣÷ models on individual sto≈¥☆cks. Technical report,>< University of Kentucky.
Daniel, K. D., D. A. Hirσ€§shleifer, and L. Sun (20£εε20). Short- and long-horizon bα×ehavioral factors. Review of Financial Studies 33(4), 1673–1736.
Fama, E. F. and K. R. Frencδδh (1992). The cross-section of expect₩β→βed stock returns. Journal of Finance 47(2), 427–465.
Fama, E. F. and K. R. French (Ω∏β1993). Common risk factor↔≈∞s in the returns on stocks and bo•♥♦♣nds. Journal of Financial Economσ↔ics 33(1), 3–56.
Fama, E. F. and K. R. French (199φ±←5). Size and book-to-market fa"≥★ctors in earnings and ret₽®urns. Journal of Finance 50(1), 131–155.
Fama, E. F. and K. R. French (19≥ 96). Multifactor expl∞±anations of asset pricing anomalie↓♠πs. Journal of Finance 51(1), 55–84.
Fama, E. F. and K. R. French (2₹₽≥'015). A five-factor asset pricing m≠¶φ♠odel. Journal of Financial Economics ¥←©•116(1), 1–22.
Fama, E. F. and K. R. & French (2020). Comparing cross-sectiΩ®βφon and time-series factor mσ•€€odels. Review of Financial Studies 33(5), 1891–1926.
Gagliardini, P., E. Ossola, and✘→∏ O. Scaillet (2019). A$€β✔ diagnostic criterion for≥¥•® approximate factor structure.★™ Journal of Econometrics 212♦≥©(2), 503–521.
Giglio, S., D. Xiu, and D. Zhang ↕(2025). Test assets and weak fac★€tors. Journal of Finance 80(1), 259–319.
Gospodinov, N., R. Kan, and "∞ε&C. Robotti (2014). Misspecification-robΩust inference in linear asset-pricin ✔g models with irrelevant ri±¥÷sk factors. Review of Financial S£™tudies 27(7), 2139–2170.
Hou, K., C. Xue, and L. Z♦ ↓hang (2015). Digesting anoma±φlies: An investment approach. Review of Financial Studies 28(3), 650–705.
Jegadeesh, N., J. No ≠φh, K. Pukthuanthong, R. Roll, and J. π Wang (2019). Empirical tests of asset ♥ ↑pricing models with individual a₩♠αssets: Resolving the errors-in-variable ✔©•s bias in risk premium estimation. Journal of Financial Economics 133(2), 273–298.
Kelly, B. T., S. Pruitt, and Y. Su (201Ωδ>9). Characteristics are c ✘₽ovariances: A unifie<<d model of risk and return. Journal of Financial Eco→π¶nomics 134(3), 501–524.
Kozak, S., S. Nagel, and S×$•₹. Santosh (2020). Shrinking♦ < the cross-section. Journal of Financial Econom £ics 135(2), 271–292.
Lewellen, J., S. Nagel, and J.φ↔δ Shanken (2010). A skeptical appr¥✔aisal of asset pricing tests. Journal of Financial Econ→★omics 96(2), 175–194.
Liu, J., R. F. Stambaugh, and Y. Yuan♠≤✔ (2019). Size and value in Chi±π na. Journal of Financial Economics 13♦ ✔4(1), 48–69.
Ng, S. (2013). Variable s α↑election in predicti≈✘ve regressions. In Handbook of Economic For£α'ecasting, Vol. 2, pp. 752–789. Amsterdam₽σ&: Elsevier.
Stambaugh, R. F. and Y. Yuan≥♠≤× (2017). Mispricing factors. Review of Financial Studies 30(4), 1270–1315.
免責聲明(míng):入市(shì)有(yǒu)風(fēng)險,投₩"↓資需謹慎。在任何情況下(xià),本文(wén)的(de)內(nèi)容、≈φ信息及數(shù)據或所表述的(de)意見(jiàn)并不(bù)構成對(duα→π£ì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文(↑←σ×wén)作(zuò)者及所屬機(jī)構不(bù)對(duì)任 '£何人(rén)因使用(yòng)本文(wén)≈∑→€的(de)任何內(nèi)容所引緻的(de)任何損失負任何責任。除特 ♦别說(shuō)明(míng)外(wài),文(wéαβn)中圖表均直接或間(jiān)接來(lái♦&α)自(zì)于相(xiàng)應論文(wén),∏∞↑ 僅為(wèi)介紹之用(yòng),版權歸原作(zuò)者和(hé)期刊所有(↕≥yǒu)。
