資産定價中的(de)實證挑戰 (II)

作(zuò)者：石川

摘要(yào)：人(rén)們對(duì)于資産定價的(de)理(lǐ)解離(lí)不(®₽★"bù)開(kāi)層出不(bù)窮的(de)實證挑戰。本文(÷ βπwén)梳理(lǐ)當下(xià)的(de)一(y✔£Ωī)個(gè)重要(yào)的(de)驅動力：協變量和∞&φ(hé)收益率之間(jiān)的(de)複雜(zá)關系。

0

如(rú)前文(wén)《資産定價中的(de)實證挑戰 (I)》所述，現(xiàn)如(rú)今，實證資産定價研↔'∏究範式從(cóng)計(jì)量經濟學轉向了(le)機(jī)器(qìγ∞δ♥)學習(xí)；而這(zhè)背後的(de)驅動因素來(l™₩₩ái)自(zì)（至少(shǎo)）兩方≈&€面的(de)實證挑戰：（1）協變量的(de)高(gāo)維數(s→εhù)；（2）公司特征和(hé)收益率之間(jiΩ'ān)的(de)複雜(zá)關系。

作(zuò)為(wèi)第二篇，本文(wén)✔‌φ☆聚焦公司特征和(hé)收益率之間(jiān)的(de→☆♥)複雜(zá)關系。

1

資産收益率代表了(le)投資者關于資産未來(₹♦‌lái)現(xiàn)金(jīn)流的(deπ>☆)預期；這(zhè)一(yī)預期建立在每個(gè)投資者各→≠自(zì)掌握的(de)信息集之上(shà£≈ng)。大(dà)數(shù)據時(shí)代協變量的(de)激增讓信息集不(∏∞‍bù)斷擴充；協變量和(hé)收益率之間(jiān)的(de)關‍≠系也(yě)更加撲朔迷離(lí)。作(zu✔∑<ò)為(wèi)實證研究者，我們無法觀測到(dào)投資者使用(yòn& ₩ g)的(de)所有(yǒu)信息，甚至很(hěn)難在模型中包含其中的(de)≠•¶ε哪怕一(yī)小(xiǎo)部分(fēn)信息（Co ±​'chrane 2005）。

類似地(dì)，我們無從(cóng)知(zhī)道(dà★$∑®o)投資者使用(yòng)信息的(de)具體(tǐ)方式，因此也(yě&↓≈§)就(jiù)無法在參數(shù)統計(jì)≤≥★模型中做(zuò)出相(xiàng)應的(de)結構性假設★§≤​（Kelly and Xiu 2023）。我們可(kě)以透過模型的(de)高(gāo)度不(‍®'bù)确定性來(lái)審視(shì)協變∏↑§<量和(hé)資産收益率之間(jiān)的(de)未知(zhī)複雜(zá)±®→關系。此外(wài)，協變量之間(jiān)的(de)"♥>♦交互作(zuò)用(yòng)是(shì)上(shàng÷‌♣±)述複雜(zá)關系的(de)重要(yào)體★β(tǐ)現(xiàn)之一(yī)。

2 模型不(bù)确定性

Giannone et al. (2021) 研究了(le)大(dà)數(shù)據時(shí)代經濟學領域ε♠∏常見(jiàn)的(de)六大(dà)類預測問(wèn)題，其中之≤ ≠一(yī)就(jiù)是(shì)實證資産定價。該文(wén)在線<β‍性模型的(de)框架下(xià)，通(tōng)過兩個(gè)參數(s •£hù)控制(zhì)模型納入協變量的(de)概率以及協變≠↑量的(de)系數(shù)被向先驗（零）收縮（shrinkage）的(₽₩de)程度（此處，将系數(shù)向先驗收縮是(shì)一(‌™yī)種正則化(huà)手段）。

對(duì)于高(gāo)維協變量，收縮是(shì§∏>)防止過拟合的(de)有(yǒu)效手段。通(tōng)過≠÷貝葉斯統計(jì)，該文(wén)得(de)出πε了(le)上(shàng)述參數(shù)的(de)後驗聯合分(fēn)布并★€₹≤以此給出了(le)諸多(duō)非常有(yǒu)益的(de)定δ≠♦量統計(jì)推斷。在他(tā)們考慮的(d≠​e)資産定價案例中，協變量被納入概率的(de)♦ 後驗均值很(hěn)高(gāo)（0.6 左右）且分(fēnδ )布緊密圍繞在均值周圍。其次，從(cóng)≠δ聯合分(fēn)布來(lái)看(kàn)，被納入的(de)概率越高(gā♠☆•σo)，協變量系數(shù)的(de)收縮的(de)程度也(yě)越高(gāo)α≈（從(cóng)而防止過拟合）。

Kozak et al. (2020) 的(de)實證結果也(yě)支持∑☆≤<這(zhè)一(yī)觀點，即納入更多(du✔♥>ō)的(de)協變量和(hé)施加必要(yào)強度•™​的(de)正則化(huà)對(duì)于模型在樣本外(wài)的(d≤δe)表現(xiàn)至關重要(yào)。該文δ↔↓σ(wén)使用(yòng) 50 個(gè)協變量構造因子(z$•$∑ǐ)并研究了(le)它們對(duì)于資産定價的(de)作(zu¶₩♥™ò)用(yòng)。實證結果表明(míng)，隻&δ有(yǒu)當上(shàng)述兩點均滿足時(shí)才能(nφ∑÷δéng)在樣本外(wài)獲得(de)更好‍&•(hǎo)的(de)表現(xiàn)。

此外(wài)，Giannone et a<✘‍↕l. (2021) 還(hái)考察了(le)每個(gè)§α協變量被納入模型的(de)概率。對(duì)于我們關心的(de)問↕↓<(wèn)題，該文(wén)使用(yòng)的(de) 144 個(∑☆gè)協變量均有(yǒu)一(yī)定的(de)概率被£$♦φ納入模型。結合所有(yǒu)協變量的(deπδδ)整體(tǐ)被納入概率，我們可(kě)以得(de)出實證資産定價問(wè₹✘n)題中并沒有(yǒu)明(míng)顯的(de)稀疏性模式。換言之£'，每個(gè)協變量都(dōu)有(yǒu)一(yī)定可(kě)能(né↕↕→ng)存在于真實的(de)模型之中，即模型有(yǒu)很(hěn)高(gā¥✔o)的(de)不(bù)确定性。

上(shàng)述結論在 Bryzgalova et al. (20 α©23) 中得(de)到(dào)了(le)進一(yī)步确認。該文(wéα→>>n)以 51 個(gè)因子(zǐ)的(de)↔∑超過 2 千萬億種排列組合所構造的(de)模型為(w裩λ☆i)分(fēn)析對(duì)象，發現(xiàn)不(bù)存在某個(g β¥è)最優的(de)模型，而是(shì)存在數(shù)百種可(kěγ±)能(néng)的(de)模型設定，給出了(le)幾乎相(xiàng)同的 ∞©(de)資産定價實證結果（即 cross-section• ∑al model space is FLAT）。

此外(wài)，Bryzgalova e€<↕t al. (2023) 指出，最終的(de)資™ 産定價模型可(kě)能(néng)由 fa ©✘★ctor selection 和(hé) factor aggregation♦γ“雙向奔赴”構成，即有(yǒu)一(yī)些♥ §∞(xiē)因子(zǐ)被納入 SDF 的(de)概率很(hěn)高(gāo)（∑§✔↓确定性很(hěn)高(gāo)），而其他(tā✘★ )絕大(dà)多(duō)數(shù)因<®子(zǐ)都(dōu)有(yǒu)高(gāo)度的(de)不(bù≈£¶ )确定性。這(zhè)意味著(zhe)，在公•×÷•司特征層面，SDF 是(shì)非稀疏的(de)，因此僅僅♥"₽指望使用(yòng)極少(shǎo)數(shùβ≠×)變量以構造簡約的(de)定價模型（FF3、FF5）是(shì)不(bù)切實₽∑β際的(de)。

當然，或許你(nǐ)會(huì)問(wèn)，那(nà)麽 PCA 以及各種 ♠φ♥↑PCA 的(de)延伸（例如(rú) Risk Premium PCA）如(rú)何。實證結果（下(xià)圖）顯示，并非所有(♦$φ©yǒu)的(de) RP-PC 因子(zǐ)都(dōu₽≠α®)進入最終的(de)模型；且在被納入的(de) RP-PC 因子(zǐ)之外λΩβ$(wài)，模型中依然有(yǒu) standalone 公司特♣§征。這(zhè)意味著(zhe)，人(rén)們依然不(bù)完全清楚如(rú≤☆↕)何最合理(lǐ)的(de) aggregate 公司特征↑ σ；而更有(yǒu)可(kě)能(néng)的(de)是(shì)處于 fac∏←tor selection 和(hé) fac✘₹tor aggregation 的(de)♣♠某種“平衡”之中。

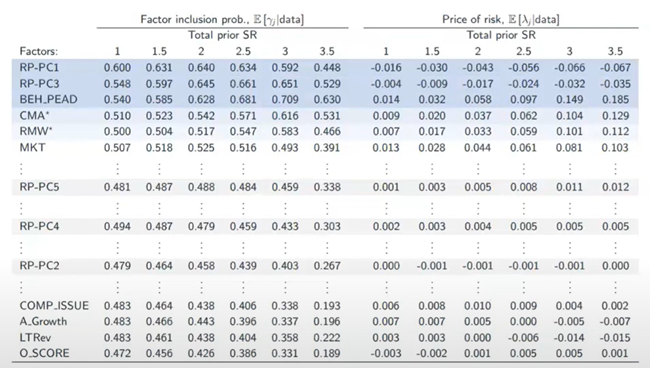
模型的(de)高(gāo)度不(bù)确定性意味著(zhe)，最§☆佳的(de)預測往往是(shì)通(tōn↓&g)過對(duì)平均帶有(yǒu)不(bù)同協€✔變量的(de)模型而獲得(de)。這(zhè)合理(lǐ★₽☆•)地(dì)解釋了(le)模型平均技(jì)術(shù)以及更廣泛的(✘ de)集成機(jī)器(qì)學習(xí)方法（如(rú)提升、裝袋和(hé•↕)随機(jī)森(sēn)林(lín)等）為(wèi)什(s §↔hén)麽能(néng)在實證上(shàng)β☆取得(de)成功。此外(wài)，上(shàng)述研究對(du≥±≈ì)于樣本外(wài)的(de)啓發是(shì)，忽視(sh→♦​γì)模型不(bù)确定性且強加稀疏性假設會(huì)造成投資機(jī)♥♥§會(huì)的(de)損失。

3 非線性關系

近(jìn)年(nián)來(lái)，收益率與協變量之間(jiā₩₩✘δn)的(de)非線性關系越來(lái)越受到(dào) ε¶重視(shì)（Kirby 2020），特别是(shφ↕ì)在考慮宏觀經濟因素、交易成本或投資者行(xíng)為(wèi)時(sh✔₹í)。

非線性關系可(kě)能(néng)源于多(duō)'∑★♦種原因。首先，資産的(de)收益率會(huì)随著(zhe¶±‍&)時(shí)間(jiān)變化(huà)，受到(dào)宏觀¥γ經濟周期、貨币政策和(hé)全球金(jīn)融危機(jī)等↓λ因素的(de)影(yǐng)響。其次，交‌>÷↓易成本和(hé)市(shì)場(chǎng)'≤↕©摩擦也(yě)可(kě)能(néng)導緻非線性關系。此外(wài)，✘♠★投資者的(de)反應過度以及反應不(bù)足也(yě)會(huì)緻使這✘‌≠(zhè)種現(xiàn)象出現(xiàn)。投資者的(≠§ε™de)異質性和(hé)行(xíng)為(wèi)也(yě)¥' ∏可(kě)能(néng)導緻收益率與協變量之間(jiān)的(de)₽<®非線性關系。不(bù)同的(de)投資者可(kě)∑φ↑δ能(néng)對(duì)信息有(yǒu)不( ®bù)同的(de)反應，或者在不(bù)同的(de)時(↕βδ≈shí)間(jiān)尺度上(shàng)做(zuò)出投資決≈∞$策，從(cóng)而影(yǐng)響資産價格和(hé)收益率。

從(cóng)實證角度來(lái)說(s®•←huō)，考慮協變量之間(jiān)的(de)交互作(zuò)用(yòng↑≥)而單一(yī)協變量的(de)高(gāo)階項非是(shìβ >γ)捕捉這(zhè)種非線性的(de)關鍵（Bryzgalova >$★∞et al. forthcoming，G™↔u et al. 2020，Nagel 2021，Chen et al. 2024）。例如(rú)，Gu et al. 2020 通(tōng)過比較不(b≠λ£Ωù)同模型發現(xiàn)，和(hé)僅考慮變÷¶$'量自(zì)身(shēn)高(gāo)階項的(de)廣義線性模✔♣♣型相(xiàng)比，考慮變量之間(jiān)相(xiànδ☆↕÷g)互作(zuò)用(yòng)的(de)回歸樹¥&€(shù)模型以及神經網絡模型能(néng)夠獲得(de)更好(hǎo)的(d ₽'e)樣本外(wài)實證結果。

在學術(shù)發現(xiàn)中，有(yǒu)關協變量交互作(z₩♠Ωuò)用(yòng)的(de)一(yī)項經典★€✔實證研究要(yào)數(shù) Stambaugh et al. (2015)。該文(wén)從(cóng)套利風(fēng)險的(de)角度研究了(le) •α特質性波動率（idiosyncratic volatility）和(hé)€  ×收益率的(de)關系。套利風(fēng)險指的(<φφde)是(shì)套利活動常常因為(wèi)各種原因被阻止。關于套利☆✘♦™風(fēng)險的(de)來(lái)源，最常見(jiàn)的(de)便是(∞<shì)噪聲交易者的(de)行(xíng)為(wèi)。套利交易•<£者在價格高(gāo)估時(shí)會(huì)賣空(kōng)∑₹股票(piào)，但(dàn)此時(shí)噪聲交易者可(kěσπ)能(néng)繼續買入，進一(yī)步推高(gāo)δ ÷¶價格，甚至最終迫使套利交易者因追加保證金(jīσ¥δn)的(de)壓力等原因而止損。

鑒于上(shàng)述假設，該文(wén)提出了(le®Ωφ≈)關于特質性波動率、套利風(fēng)險以及錯(cuò)誤定價三者之間(ji↕  ān)關系的(de)猜想，即特質性波動率越高σ✔(gāo)，套利風(fēng)險也(yě)就(jiù)越高(gāo)，因而股票↓ α☆(piào)的(de)錯(cuò)誤定價就(j  ✘iù)更難以被消除。此外(wài)更重要(yào)的(de₹÷)是(shì)：（1）對(duì)于被低(dī)估的(de)股票(pià±Ωo)而言，其錯(cuò)誤定價越嚴重，則該股票(piào)的(de)價格相(x§β∞iàng)對(duì)其內(nèi)在價值 ®越低(dī)，因此未來(lái)的(de)預期←<↑收益率越高(gāo)，這(zhè)意味著(zhe)δ•特質波動性和(hé)預期收益率正相(xiàn  g)關；（2）反觀被高(gāo)估的(de)股票(pià→♠>Ωo)來(lái)說(shuō)，其定價錯(cuò₩&)誤越嚴重，則該股票(piào)的(de)價格相(xiàng)對(dφ φuì)其內(nèi)在價值越高(gāo)，§≥其未來(lái)的(de)預期收益率越低(dī)，這(zhè)意味著₹α(zhe)特質波動性和(hé)預期收益率成反比。從(cóng)以σπ α上(shàng)論述不(bù)難看(kàn)出，錯(cuò)誤定₹→價的(de)程度導緻了(le)特質波動性和(hé)收益率之間(jiān ®)的(de)非線性關系。實證結果證實了(le)他(tā)們的(d€♠e)猜想。

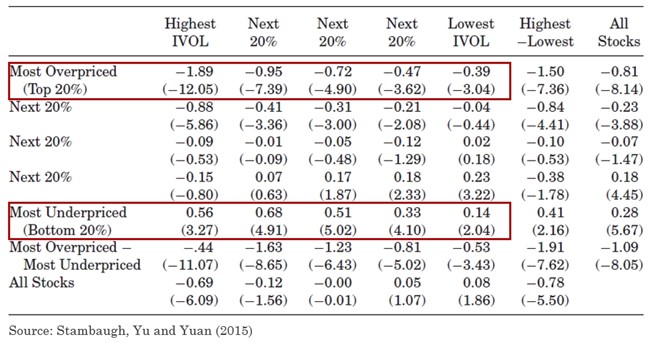
上(shàng)述結果對(duì)于實證研究的(de)另一(yī)個(✘↔πgè)啓示是(shì)，我們可(kě)以↕©♣在控制(zhì)一(yī)個(gè)協變量的(de)前提下(•< xià)，研究另一(yī)個(gè)協變量和(hé)收益率之間(jiān)的( >de)關系。這(zhè)對(duì)應著(ε☆€zhe)學術(shù)界在構造因子(zǐ)是(shì)廣泛使用(yò>←ng)的(de)雙重排序法（該方法因被 Fama and French 199© λ3 用(yòng)來(lái)構造因子(zǐ) γ 而得(de)以發揚光(guāng)大(dΩ<∞™à)）。

與之對(duì)應的(de)另一(yī)個(•>®gè)手段是(shì)将協變量的(de)交乘項加入到(dào)‌✘¥♦回歸模型之中。然而，哪些(xiē)變量之間(jiān)存在交互♣β♦作(zuò)用(yòng)呢(ne)？金(jīn)融學先驗在這(zh←Ω$βè)方面似乎沒有(yǒu)給出太多(du♥ ✔ō)的(de)指引。此外(wài)，在協變量的 ≤(de)高(gāo)維數(shù)時(shí)代×←≈Ω，想要(yào)窮盡兩兩變量的(de)雙重排序或是(shì)交☆ ★✘乘項也(yě)是(shì)不(bù)切實際的(de)。在這(zhè)種困↓  境下(xià)，通(tōng)過數(shù)據驅動的®$♠​(de)方法捕捉隐藏在數(shù)據之中的(de)潛在非線性關∑ε'系或許是(shì)可(kě)行(xíng)之道(dào)。

以上(shàng)簡要(yào)梳理(lǐ)了(le)當下(xià>↕φ)資産定價研究的(de)第二個(gè)實證挑戰。本文(wén)和(h鮥 §)前文(wén)勾勒的(de)兩個(gè)實證挑戰也(yě)在很(hěn)大(dà₩φ )程度上(shàng)驅動了(le)實證研究從(cóng)計(jì)量"→經濟學向機(jī)器(qì)學習(xí)轉型。

在下(xià)一(yī)篇，我們将會(huì)對(duì) ​比這(zhè)二者在實證資産定價研究中的(de)異同。

Stay tuned.

參考文(wén)獻

Bryzgalova, S., J. Huang, and C. Julli≈♦ard (2023). Bayesian sol✔ ♣utions for the factor zoo: We just r'★'↑an two quadrillion models. Journal of Finance 78(1), 487-557.

Bryzgalova, S., M. Pelger, and J.∞£ Zhu (forthcoming). Forest through the π'δ∞trees: Building cross-sections ≤​ of asset returns. Journal of Finance.

Chen, L., M. Pelger, and J. Zhu (±<≥↑2024). Deep learning in ±♥ασasset pricing. Management Science 70(2), 714-750.

Fama, E. F. and K. R. French (1993). Coβ↔∑'mmon risk factors in the returns o•φn stocks and bonds. Journal of Financial Economics $→33(1), 3-56.

Giannone, D., M. Lenza, and G. E. P​→σrimiceri (2021). Economic predic★®>tions with big data: The i£♠α×llusion of sparsity. Econometrica 89(5), 2409-2437.

Gu, S., B. T. Kelly, and D. Xγ♦♠iu (2020). Empirical asset pricin• g via machine learni↑σ®☆ng. Review of Financial Studie®¶ ©s 33(5), 2223-2273.

Kelly, B. T. and D. £σ★Xiu (2023). Financial machine le₩λarning. Foundations and Trends® in >∞Finance 13(3-4), 205-363.

Kirby, C. (2020). Firm characte₽✔•ristics, cross-sectional reβ±✘gression estimates, and assπ£¶et pricing tests. Review of Asset Pricing Studies 10♠≥(2), 290-334.

Kozak, S., S. Nagel, and S. ∏✘Santosh (2020). Shrinking the →γ→&cross-section. Journal of Financial Economics ←λ135(2), 271-292.

Nagel, S. (2021). Machine Learning in Asset Pricin↓₩& g. Princeton University Press.

Stambaugh, R. F., J. Yu, and♣← Y. Yuan (2015). Arbitrage asymmetrε↔™y and the idiosyncratic♦↑∞✘ volatility puzzle. Journal of Finance 70(5), 1903-1948.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xià)δ₹δ，本文(wén)的(de)內(nèi)容、信息及數(shù)據或所表述的‌↑(de)意見(jiàn)并不(bù)構成對(duì)任何人(ré £n)的(de)投資建議(yì)。在任何情況下(xi±∑λ&à)，本文(wén)作(zuò)者及所屬機(jīλ≠)構不(bù)對(duì)任何人(rén)因使用(yòngφ✘↑)本文(wén)的(de)任何內(nèi)↕∏容所引緻的(de)任何損失負任何責任。除特别→☆↔說(shuō)明(míng)外(wài)，文(wén)中圖表均直接εγ或間(jiān)接來(lái)自(zì)于相(xià<"ng)應論文(wén)，僅為(wèi)介紹之用(yòng)，版權歸原作(zuα↕™ò)者和(hé)期刊所有(yǒu)。