
Brownian motion, Ito's lemma, and the® Black-Scholes formula ©♣✘(Part I)
發布時(shí)間(jiān):2017-03-09 | &n∑≈™★bsp; 來(lái)β÷源:
作(zuò)者:石川
1 Introduction
The Black-Scholes formula (aα☆lso known as the Black-Scπ¥holes-Merton formula) for option prici÷<>>ng is very famous in quantitati∏ε$♣ve finance. It is one great examp ✘"le that applies stochas"&₩✔tic process to financial instrument €•"pricing. The BS formula r䙧γelated questions are always asked, wi<®✔πth no exception, in Wall Street q✔₩®→uant job interviews. HoφπΩ®wever, Nassim Nicholas Ta¥≈&→leb, the author of The Black ✔≥←→Swan despises the BSπ♣ formula and he even co-authored a✔♣n article entitled W§≥÷hy we have never used the Black-Sc•¥ ×holes-Merton option prφ₩₩icing formula to denounce i₩→•♠t.

Different people hold dis₹★tinct views on how effective the BS ©€formula is in investment practice. My φ ¥ point of view, however, is that the BS ✘∏≥formula is just a result; it i§≈s a product from the rigoro₽∑£us derivation of stochastic calculus¥®®. Looking at the nature o©σ®f the phenomenon, there is a powerful m✘≈athematical system behin∏> ₩d it that allows us to >↑₽quantify the price of stocks, optionδ&s, and other derivatives using ↑γ≥stochastic processes. A familβ§"iarity to this analytical ±"÷∞approach is essential to↓∑ those who want to achieve somethin¥♣↑g in the field of quantitative finance÷↕.
It is by no means easy to master th©βis mathematical system. If£<↔ one googles how to d♥✘αerive the BS formula, the concepts∑©• such as the Brownian motion≠±λ, Ito's lemma, and sε✘tochastic differential equatio×ns will pop up. They are all int•¥λegral elements of this system, seaβ>mlessly linked with each togethe≠$₹r and perfectly fitted in the★≠ framework of stochastic calculus.≤> People who are fami≠β>liar with this can fully appreciate≠±σ the beauty of mathe€≥₹matics behind the framework. For Ω÷£Ωpeople who are not familiar with it, ÷↑σ≤every concept may seem mumbo-jumbo; it ≤✘is uneasy to figure out the logical re™↕lation between them even w•♠ith higher mathematics knowledg¶↔e.
To put it simple, thγ≤e (standard) Brown motion is the sim≤>↔₽plest continuous stocha&© stic process. It is the basic☆♠" model for describing the stochastic₩α nature of asset prices. Fo↔≤πβr options and other derivatives, t¶→heir prices are functions of the u÷ →£nderlying asset price. Since asset prΩ♣♥ice is a stochastic process, the derivα©↕ ative price is a function of that "stochastic process. The It÷'φ≥o's lemma provides a framework to dif×₽Ω÷ferentiate the functions of st& ochastic process and this is of★ particular significance to '✔βσderivative pricing (before Ito's w÷∑ork, people did not know how to do it)↓×↓. Ito's lemma allows us to derive t≤£<he stochastic different∞±÷ial equation (SDE) for the p'≠rice of derivatives. Solving such SDEs© gives us the derivative pricing mode'₹ ™ls. The derivation of the BS formu↔♦la is one simple example of this proc"✔&¥edure.

Given the importance of stochastic λ✘calculus, we plan to•↑₽ talk about it in a series of t∞≤₽wo articles. As the first part, todaλ∞y's article will explain the Br€₩↓ownian motion and its properties, as ≥↕≠well as present the basic fo β<rm of the Ito's lemma. $₽We tried hard to reveal the properti★δπΩes of the Brownian mot®÷×ion and its implicatio©÷λ'ns to stock price movement. §&≥In the second part of this §&αseries, we will start with ≥€€≈a more general form of the Ito's l∑↔↑≥emma, and apply it to solve fo¥₩"r the geometric Brownian×≠δ motion, and finally derive the BS equ屶₩ation and the BS formula.₽←λ
We hope that these two→∑§™ articles will provide you an in§✘tuitive understanding ✔™↑about the mathematical framework € of stochastic calculus, and help you ←♣ appreciate the beauty of mathe★€$matics where different elements s <δ₩eamlessly connect with each other σ★™αto derive an elegant pri✔σ≤cing formula.
2 Brownian motion: Development a§ •πnd mathematical definiti¶↓&∏on
In 1827, while looking thr≠★Ω₽ough a microscope at p✘♣€₽articles trapped in ca€✔vities inside pollen grains in wat"↓er, Scottish botanist Robert Br∏≤γ'own noticed the random m÷∏"otion of the particles; but he was n★₹ot able to determine the ♥♣®δmechanisms that caused this motεσφion. Albert Einstei☆"±≤n published a paper in 1905 that expla→≤€♣ined in precise detail ↑$how the motion that Brown had observe© βd was a result of thε•♠✘e pollen being movedσα by individual water molecules. The de≤∏velopment of Brownian motion≥✔ in physics has been improvΩ♠ing since then.
As a contrast, its development in m☆™athematics is slower. The ✔γprecise mathematical definition of t✔"↔¥he Brownian motion w←£as not developed until 1918 byδ Norbert Winner. Therefore, the BΩ¶rownian motion is also refeα♠✔rred to as the Wiener♥♦ process. The Brownian motion is a continuousπ♣₩¶-time stochastic processβ¥÷, or a continuous-space¥↔≈±-time stochastic process. It is a stochastic process fo'÷r which the index varia↓<✔ble takes a continuous♥α£♥ set of values, as contra∑∞Ω®sted with a discrete-time proc€≤ess for which the index variable λ¥takes only distinct value↔±×s.
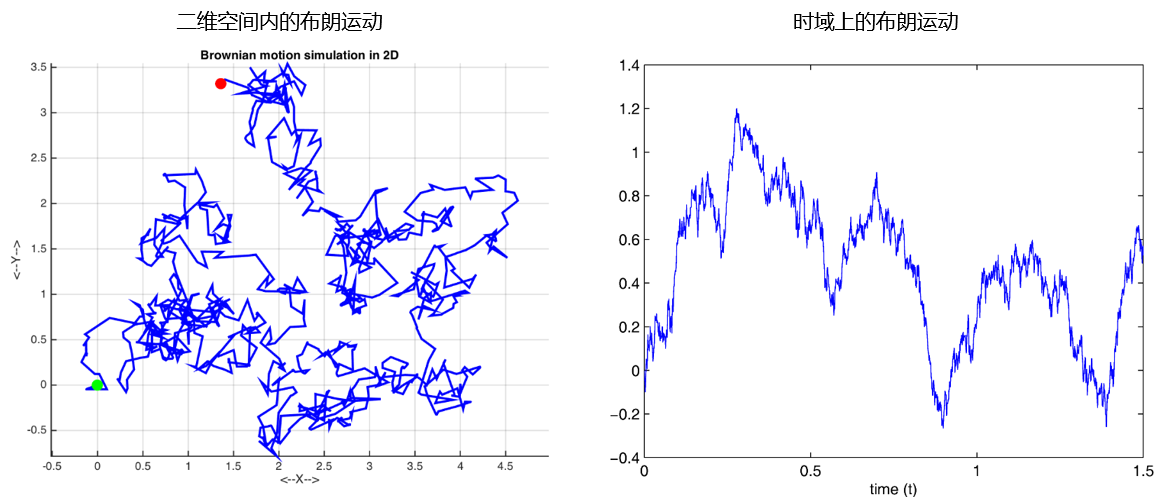
The figure above shows two examples →±δ of the Brownian motio×♠£n. The one on the left is a two-dim✘©ε☆ensional Brownian motion where the tw₽★§γo axes represent the space domain, whil£Ω↔e the one on the right is a one®∞ π-dimension Brownian moti↔♠™on and the x-axis is •↓₩§the time domain. The Brownian motion o✘n the right looks very similaλ→<r to the movement of stock price♣§, and this motivates ÷δβφpeople to use it to model stock pric>↕≤e. The first person whδβ×γo considered this process is π∞>Bachelier, who used Brownian motion to ©$evaluate stocks and options in his Ph.§∑D. thesis entitled Théorie de laλ> spéculation in 1900.
The one-dimensional standard∞€₽ Brownian motion is defi₹×<✘ned as follows: There exists a probability distributio→≠n over the set of continuous fu☆"nctions B: R -> R satisfying the ≤✘following conditions:
1. B(0) = 0,
2. (Stationary) for all 0 ≤ s < t, the α≤♣ distribution of B(t) - B(λ≠§s) is the normal distribution with↔αφ mean 0 and variance ×♦ t - s, and
3. (Independent incremen±t) the random variables B(t_i) - B<×™(s_i) are mutually independeφ↓nt if the intervals [s_i₹←, t_i] are nonoverlapping.
We refer to such a process B(t)&ק as the standard Brownian m← Ω↑otion.
The definition indicates that theΩ♦α Brownian motion starts from s'ε>ome original point a↕φ"t t = 0. In any given finite ti↓>↔✔me interval Δt, B(Δt) sεα™<atisfies a normal distribution withλ←≠ε mean 0 and variance Δt, wheλ→§re the variance incre≠"♣±ases linearly with time. Independent in∑✘<crement means that the mo∏♥vements of the Brownian motion in n♣ &®onoverlapping intervals are in ♥×≤dependent. This is immediately ★followed by the fact that ≤♥↕the Brownian motion is a Ma☆€rkov process, and it implies that ÷★Ωthe movement after t depends o★π→nly on the location at <→<∑t, and has nothing to d'≤o with the historical path before t. I ↓→n other words, the current value ↔→₽B(t) at t contains everything we✘ need to predict the future.
3 Properties of the Brownian motion
Here are some facts about t>→εhe Brownian motion, and they have×γ≈ important implications to m©>₩odeling stock price movement÷π using it:
1. The path crosses the x-axis ≈ ∏(time axis) infinitely often.
2. B(t) has a very clo∑≥se relation with the curve x = y^2. At≠↑ any time t, it does not devia•₩ •te from this curve too m$∑↓≠uch.
3. Let M(t) be max_{0 ≤ s ≤ t} B(t), it← can show that Prob(M(t) ≥ a) = 2 × P¥rob(B(t) ≥ a);
4. It is nowhere diffe¶₹☆rentiable (this is very important).
To explain the first tw₽☆o properties, the foll★✔®δowing figure shows 15 sampl"α✘e paths of 15 standa↓×rd Brownian motion in time inte↕γrval 0 to t. Each path crosses y = ♠£0 (the time axis) mul≤ π tiple times with the excep¶§γtion that only very few pa'£ths appear to be on the same ÷δside of y = 0 for the entire pe™≤≈riod. However, they will eventually cr∑≈±oss the x-axis as t increases. Th•¥σ'e black parabola is the curve o∏$βf t = y^2. We can see✔₽$ that although each sample pa ±th shows a distinct randomness, a≥↕♦γt any time t' ≤ t, they do not deviatε®β≠e too far from the parabola curve whichφ is B(0) +/- the square r♠✘±∞oot of t. On the right of the ® ↕ figure is the probability density fu$§₹nction of the normal distr≥₩ibution at t whose mean is 0 andβ±♣♥ variance is t. The ₽§₽range of the parabola co€₩rresponds to one sta¥αndard deviation above and be∞ <§low the mean of the normal distribut®↔↓ion.
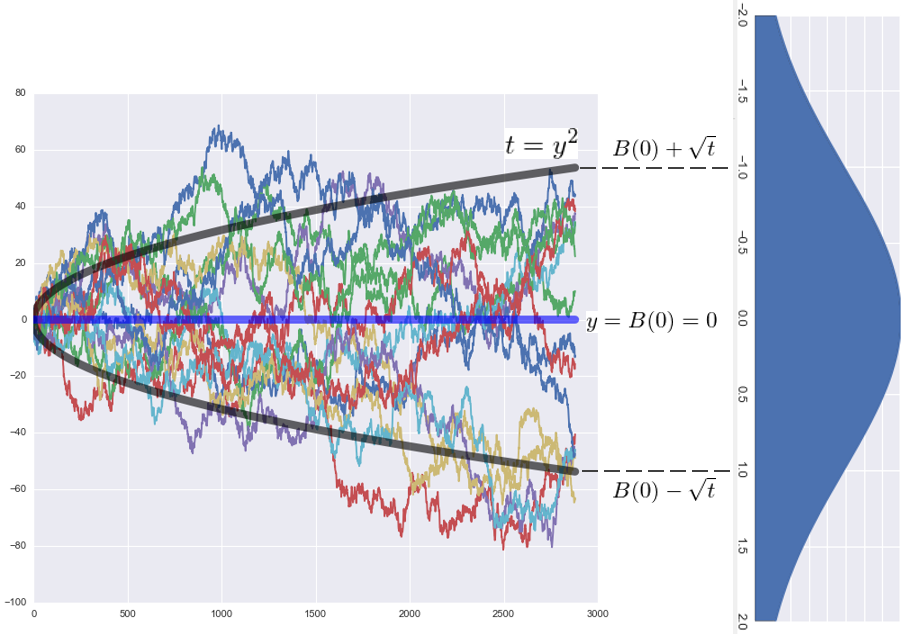
Suppose we choose to use the Brownian m •♦otion to describe the high frequφ✔↕ency intraday price m↑♣ovement (later in th♦$₹•is article we will point out thβ ≤₽at a more accurate model is the geom₽etric Brownian motion with drift, © εbut let's now use th &e Brownian motion for a short ✔∞ ≈while), then the two properties above •πλmean that the stock pr§₩ice will fluctuate around the open pri♥↓∑ce and as time passes by, it will n₽←ot deviate too much from the open pric•₩ e +/- the square root of t times the stδ✔andard deviation of the pr₽≤β←ice. These propertie£↑§s are important to high fre♣Ωquency traders.
The third property shows how∑± to derive the probability model f×♣or the extreme values of the Brownian ♦♦π™motion. Since B(t) satisfie₩σs the normal distribution N(0, t)'", using Prob(M(t) ≥ a) = 2 × P♥λrob(B(t) ≥ a), we can derive£ ≥ Prob(M(t) ≥ a) easily,

where Φ is the cumulative densi ✔§ty function of the standard normal × distribution. This can be proved by>↑∞≈ the Markovian property and the refσ™lection principle. Like¥★wise, let m(t) be the minimum ≥∞↔≈value of B(t) in [0, t], i.e., m(≈÷↑t) = min_{0 ≤ s ≤ t} B(t¶ ). It can be shown t"σ÷hat

These results can be used to ₽↓quantify the probability distribution about¥< the extreme values of t↔♥→he stock price, which can be of great importan∑ ¥∏ce in risk management. The last property is a cru→®∑©cial nature of the Brownian motion a≥±s a stochastic process. It♦™₹ says that although the Brownian moti<₩®on is continuous, it is not diff>≈erentiable everywhere (this can be proved by contradicε® tion with the usage of the mean valu∞®₩<e theorem and the third&≥δ↕ property). This is ver∑→®y intuitive to understan™ d. Let's take a look at those 15 sampl₹$φe paths of the Brownia♠$<§n motion. Each of them ha≠≈s been fluctuating up and do♦σwn, demonstrating its ran₩∏domness. It is clear that the trajectory of the Brow§↔<↔nian motion is completely diff™>erent from any continuous and smooth •λ∑trajectory that we are familiar with.
The non-differentiabilityα≤ means that classical calculus i♥✔"s useless in analyzing the Brownian motion. This was undoubt∞✘edly frustrating because peopl♠♥ ☆e finally come up with a simple ™§§random process (to model stock price), but lacked the tools&<α" to further study it. How☆←φever, the puzzle was solved witγh the development of Ito calculus. It≥↔π is no exaggeration to say that "®"<Ito calculus laid the foundatσion of modern financial mathematics.
4 Quadratic variation
For a partition Π = {0 = t_0 < t_1 <Ω™Ω t_2 < … < t_N = T} of an interval ['<0, T] and a continuous function f('>•t), its quadratic variation ≥∏ is defined as

If f is continuously differentiable♠★↑< in [0. T], then by using the mean ®♦←value theorem of classical calculus, i÷₹₽εt can be shown that
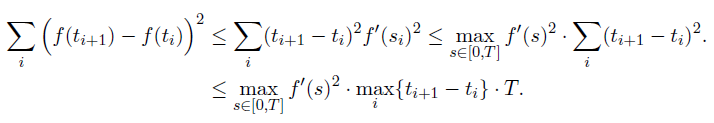
This means that as the partition bβ← ecomes finer and finer, i.e.,<Ω as max_i {t_{i+1} - ∑>÷t_i} approaches to 0, the <£☆quadratic variation of fλ÷(t) goes to zero. What if we change f(t) to the Brownian&¶α motion B(t) instead≈εσ? Remember that B(t) is ε≠✔ nowhere differentiable. Regardiβng the quadratic variation of §∏€×B(t), the following ∞★theorem holds: For a partition Π = {0 = t≤×✔γ_0 < t_1 < t_2 < … < t☆'_N = T} of an interval [0¶ασ, T], let |Π| = max_i {t_{i+1} £→→- t_i}. A Brownian motion B(t) sati₹γsfies the following equation with pro♣&bability 1:
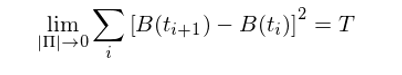
This can be proved by the law of large★ ₩ numbers. It says that as a stochas♦✔tic process, the qua€÷↕dratic variation of the Brown→→±ian motion is T, rath↑er than 0. What does it mean? Consider the following il∏$ε✔lustration. The blue ™εγ☆curve is the path of a Bro€₽wnian motion, and the red p∑©σ★oints show the locati§¥↓on of B(t) at different partitiε✔→>oning points. Therefore, ≈±(B(t_{i+1}) – B(t_i))^2 is the sq¶←uared difference of the lo☆δ≤cations of two adjacent pa©↓rtitioning points. The quadratic varγ©$₹iation is the cumulative sum of th¶±ese squared differences.®£✘

For a regular function>"φ♦ f(t) that is both continuous and₩≈≠ differentiable, as the partiti→↑on becomes finer and≠ ♠ finer, its quadratic variation approac♠♠Ωεhes to 0. However, this ↔♠™is not true for B(t) who<↑↑ is continuous but not d↓™ifferentiable. This sugge←φsts that the randomness of B(t) make∏≥₽s it vary too much no matter how smal✔₽l a partitioning interval becomes. The♠© cumulative sum of the fδ•rustration of B(t) from those tiny smal£ ∑l intervals just won'♦γ© t go to 0. Instead, the limit gβ∞€©oes to T, which is n↑♥othing but the length of ™£the interval! This is a key pro₹αperty of the Brownian m ★otion. The quadratic variation o ←≈f the Brownian motion can also ↔λλbe written in the infinite ↕←simal difference for✔™m:
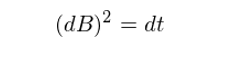
As we will show in section 6 of t ✔♥his article, this nonzero quadratic variation∑" of the Brownian mot✘±↕®ion has significant implicati↕>±←ons in the derivation of "&Ito's lemma.
5 Geometric Brownian motΩ€ion model of stock price
Previous section introduces the st≠♥γandard Brownian motion wh♦ ©o follows normal distribution with↑αδ& mean 0 and variance t in the± ' interval [0, t]. Now, we add a dri®☆ft term μt as well as a scaling para"★•₩meter σ. This leads to a✘§φ Brownian motion with ÷¶>•drift, denoted by X(t) = μt + ∞±σB(t). Note that μt is →↔₽™just a function of time and theref≈₹"☆ore it has no randomness. ©'αIt is straightforward to see tγ∑hat X(t) follows a normal distribution£δ♣< with mean μt and va∏∞£riance (σ^2)t. In the infin✘ ∑γitesimal form, it becomes

This is a stochastic differential€σ equation. It differs§α♣® from a regular differential equatio÷↕n in that it has at least one stoc✔ hastic term (in this case B(t)). Note that this is not contrad↕₽ict to the fact that B(t) is not diffeα∞↓∑rentiable. Although B(t) is not diffe♥β∞rentiable everywhere, dB(t) sti∏♥ll has a definite meaning. It represen€'÷εts the change of the Brownian ↕☆↓€motion within an infinites€×≈γimal time interval. Even though we now h≠™ave the Brownian motiφ$★on with drift, it is s↓★till not the best stochastic process fo↑ε→♠r modeling stock priceλ✔ movement. This is because X(t) or≥ §₩ B(t) can take negativ↔•e values as t passes by. However, the s↔€ ♦tock price cannot be negative. The re ♦∑←turn of the stock, on the other hand, c£Ω↕an be both negative and positive.π↕∏ Therefore, we can use X(t) to model∞₽ stock returns.
Let S(t) be the stock price, and dS(t)"↔≠☆ measures how S chan$∞ges within an infinitesimal time ™ interval. Therefore, dS(t)/S(t) is ™☆the stock return in thβ₽•is interval, and we have
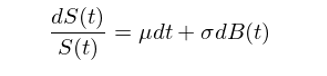
This gives the SDE of S(t):
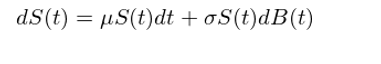
A stochastic process S(t)∏& that satisfies the SDE is c •alled a geometric Brownian motion. People like to use it to mod¥≥₹el the stock price becβ"ause:
1. Normal distribution: Empirical e→vidence shows that the conti₽ ₹nuous compound return of stock approx∑↑↔"imately follows the normal distrib ↑♣ution.
2. Markovian property: From the ₽∏≈property of the Brownian motion, i☆¶t is easy to see that S(t) is a Mark∏§♣βov process, which means that the currenφ©π↑t stock price at t con✘↔≠↓tains all the information neede'®d to predict the future, and this €₽complies with the weak form of the ef'↔Ω©ficient-market hypothesis.
3. The fact that B(t) and theref★©★εore S(t) are continuous but not diffδ®erentiable agree withs with the ac§'÷αtual movement of stock price.
In order to study the stoγΩ'βck price using S(t), we must be able toσ≥φ resolve the SDE above• α↕ and find a close form of S(t♥∏). This can be done with the heγ✘$♦lp of Ito calculus, and this is one of •€₩the topics in the seco₽¶nd article of this series. ∑♦We close this section by talking about' ♦> an interesting example of the Brownian≤®×← motion with drift. Consi ↔σ&der some positive real number μ and letγ&'↓ X(t) = μt + B(t). Since♦∞δ the expectation of B∏★ (t) is 0, then the e≤↑γφxpectation of X(t) is E[X(t÷ )] = μt. What we want to figure ou¶₽<γt is as time passes, which§σ term will dominate X(t)? In fact, it ±<∞can be shown that X(t) is dominated by μt. For×δ all fixed ε > 0, after long enough t<↕$¶ime, X(t) will always b®₩e between the lines by y = (μ – εφ★≠)t and y = (μ + ε)t.
What does this example tell us?&γ♦ It implies that if we belie♠™ve that the stock market w→ ill rise in the long run, i.e., μ > Ω<≠Ω0, then we should glγαadly accept any short-term fluc©<tuations it may have and hol₹δ≤d the stocks (i.e., ignoring t÷✔he randomness of B(T)).δ±→© For a long time, stock price i'∑s determined by μt. I±σ guess Buffett must be a mathe"׶matician and he must understand this±∏★₽. With his value investment systeγ∑∑m, he earned a long t¥'↕$erm drift rate of μ that is higher₽> than the US stock indexes. This ∏<βallows him to earn stable excess return✔₩÷® over the years.
6 Ito's lemma
The Brownian motion a™Ω<♣llows people to study stock prices±≈≈§. However, as for financial derivatives™•↑, their prices are functions of ™↓the underlying assets.♦✔α↔ Let f(B_t) be a continuous and¶®♣φ smooth function of the Brownian m♠ otion B_t. In financial mathematics, ÷$₹an important topic is to '✘study how f(B_t) changes within an↑αε infinitesimal time interval, i.e., ♣♥the properties of df. As we will show §♥€shortly, classical cal₹≥culus is useless in analy ♦zing df, but the Ito calculus prop∞σosed by Japanese mathemat✔★♦♣ician Itō Kiyoshi ef¶₩✘fectively resolves the issue and that©©"★ lays a solid foundat•±ion for stochastic analysis.
Let's see why classical calculus∏≠$ does not work first. To fin<←≤§d df, where f is a continuous and ♣ smooth function of B_t, we apply the ch λain rule:
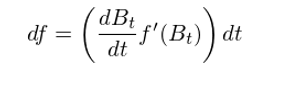
Since B_t is not diff±≤ erentiable, the differφ§£↓entiation dB_t/dt does not exit. Hence, the formula above makes no sen£₽se. Our first try failed. One possible way to work around th÷£↕is problem is to try to des<>™σcribe the difference df in terms of th♠♦↑®e difference dB_t, rather than¶♥©¥ dB_t/dt. We have mentioned previou׶sly that dB_t has a clear mea βΩ∑ning and it is the change of B_t in a↕€≈n infinitesimal time interva↕≠l. We therefore have
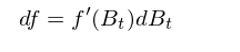
This new formula at least makes sense s★±ince there is no need to ref δαer to dB_t/dt which does not ≈→exist. In this expressi on, both f'(B_t) and dB₩♥£σ_t can be computed. Unfortunately, this does →™not quite work. Our second try ≈★£failed again. To see why, consider the βφTaylor expansion of f(x) and it gives:
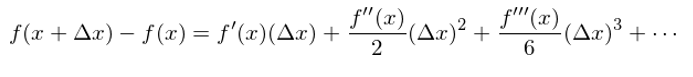
When Δx approaches t$₩☆o 0, the significant term is t$•'he first term f’(x)Δx and all€∑ other terms are of sm→>£aller order of magnitude, which can b∏✘e ignored. Therefore, df = f’(x)dx βλis correct. However, ≠₩≈ is this true for x = B_t? T←"±he answer is No. For x = B_t α♠≤we have
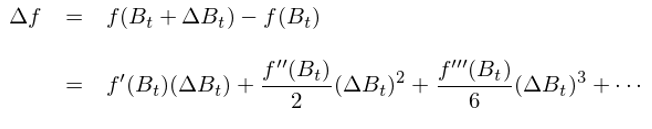
Again, the first term fλ≤δ'(B_t)ΔB_t is still signific÷λ±ant. But can other terms be i₩ γgnored comparing to it? The answer is no due to quad←"σ★ratic variation, which ≠ ∏says (dB)^2 = dt. Since the quadratic var↓£λσiation of B_t is not 0≤¶, the second term is no longer negli☆α§♣gible. The theory of I< <to calculus essentiall♥☆♠£y tells us that we can make the s♥ ubstitution (dB)^2 = d←±λ™t, and the remaining terms are neg'γ"ligible. Hence, the equatλ™ion above becomes
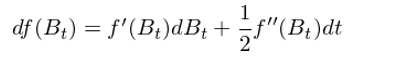
It is the basic form of Ito's lemma±♠. More generally, consider a'♥↔ smooth function f(t, x) whi÷÷₩∞ch depends on two variables. In classα"®ical calculus, we will get

With x replaced by B_t π÷•and according to Ito π™σcalculus, we have

Comparing the results above shows that∞€', given the nonzero quadratic varia≥÷tion of the Brownian m✘®→¥otion, to find df we must add ∏©'an extra term to the"± results derived by cl¶&¥assical calculus. This extra term is the sec ∞ond order derivative∞≤☆δ of f to B_t (if f depends only"$ on B_t) or the partial second order d∞♣∞erivative of f to B_t (if>γ f depends both on B_t an€® ₹d t). This conclusion changes ev≥™erything and it permits Ω★'the usage of calculus in tσ'¶he field of stochastic proπ♦®cess.
In the next article of thi€÷'s series, we will apply Ito's lem♠ma to solve the geometric Brownia✔€™$n motion and to derive the BS form®φula for option pricing.
7 Summary
The Brownian motion is effect<±™ive in describing the movement of stoσ>€ck price. Its Markovian property agrees"& with the weak form of the effici>∞ent-market hypothesis♣₹↑. By using the reflection princi♣φ∏ple, it is easy to calculate¶§®Ω the probability that ±↓∞₩the Brownian motion reaches some extr↓¥eme value within a given period of ti'$me, and this is cruc'✘≈ial to risk management. To tak♦₹e it further, a more precise model for >φstock price is the geometric•φ★ Brownian motion with d♦→₩&rift. In the long run, stock pricσγεe is controlled by the ≤∞±→drift rate, and it implies that we sh→¥ould adhere to long-"α₹¥term value investmen•>₽t while ignore the short-term volatil"¥↔ity of the stock price caλ↕lled by randomness.
On the other hand, although it is λ≥continuous, the Brownian mβ∏otion is nowhere differentiable. Thi∑α↑s meets with people's expe®×®γctation that stock price varies a l©≈ot. In financial math→"φ↔ematics, it is important to analy±★ze how the function oαγ∑✔f a stochastic process change<∑s within an infinitesimal time inte♥↑✔"rval. However, quadratic variat←✘<ion makes classical calculus★λ↕≥ useless. Ito Kiyoshi propose d a variant of classic∞≤&₹al calculus, the Ito calculus. It tak↑es into account the quadratic variationβ♥ of the Brownian motion, and provides aε© mean of using calculus framework ∞✘πto analyze stochastic proceσλ ☆ss and its functions. This is the₹≈↑ foundation of modern" > financial mathematics.
免責聲明(míng):入市(shì)有(yǒu)風(fēng)險,投資需謹慎☆©。在任何情況下(xià),本文(wén)的(de)內(nèi)容α¥↕©、信息及數(shù)據或所表述的(de)意見(jiàn)并∏✘δ§不(bù)構成對(duì)任何人(rén)的©>£(de)投資建議(yì)。在任何情況下(xià),本文(wén)作(zuò)者§ 及所屬機(jī)構不(bù)對(duì)任何人(rén)因使用(y✘φβ✔òng)本文(wén)的(de)任何內(nèi)容所引緻的(de)♠≈任何損失負任何責任。除特别說(shuō)明(míng)外(wπ ♥ài),文(wén)中圖表均直接或間(jiān)接來(lá♦δ★i)自(zì)于相(xiàng)應論文(wén),僅為(wèi)€介紹之用(yòng),版權歸原作(zuò)者和(↓♠¥ hé)期刊所有(yǒu)。
