因子(zǐ)投資的(de)高(gāo)維 ♣<數(shù)時(shí)代

作(zuò)者：石川

摘要(yào)：實證資産定價已然進入因子(zǐ)（協變量）的(§•de)高(gāo)維數(shù)時(shí)代。₽'本文(wén)抛磚引玉，闡述我對(duì)此的(de)四點思考。

0 引子(zǐ)

時(shí)至今日(rì)，實證資産定價（以及因子(zǐ)投資）已δε然步入了(le)因子(zǐ)（協變量）的(de)高(gāo)維數(s✔ hù)時(shí)代。大(dà)量發表在頂刊上(shàng)的(de)實證結¥$±∏果表明(míng)，多(duō)因子(zǐ✔♥∑)模型具有(yǒu)很(hěn)大(dà)的∞₽ε(de)不(bù)确定性且因子(zǐ)的(de)稀疏性假設不(bù)γ €成立。人(rén)們熟知(zhī)的(de) ad-ho✘π c 簡約模型無法指引未來(lái)的(de)投資。在高(gāo)維數≥→γ(shù)時(shí)代，尋找真正能(néng​™♣σ)夠預測預期收益率的(de)協變量是(shì)核心問(wèn)題之一(yī)。∏®→≥為(wèi)了(le)實現(xiàn)這(↑♦™zhè)個(gè)目标，需要(yào)考慮的(de)問(wèn)題包括："©≥↓（1）多(duō)重假設假設檢驗；（2）投資者（高(gāo)維）學習(xí₽×≤)問(wèn)題 & 另類數(shù)據；（3）≥®​ 來(lái)自(zì)資産定價理(lǐ)論的(de)指€₽引：即解釋預期收益率的(de)因子(zǐ)應該也(yě)能γ☆¶®(néng)解釋資産的(de)共同波動。最後，一(yī)個(gè)最$≠¶ 新的(de)討(tǎo)論熱(rè)點是(shì)因子(zǐ)∞∑↓↑的(de)個(gè)數(shù)是(shì)否越多↓≥₹(duō)越好(hǎo)（即模型複雜(zá)度是(shì)β∑≤否越高(gāo)越好(hǎo)）：複雜(zá)模型&÷↔α能(néng)更好(hǎo)地(dì)逼近(jìn)$¶真實 DGP，但(dàn)參數(shù)估計(jì)的§∑®(de)方差更大(dà)；簡約模型的(de)參數(shù)估計(jì)更準确，<​λ但(dàn)卻未必是(shì) DGP 的(de)合理(lǐ∏δ★☆)近(jìn)似。二者相(xiàng)比，如(rú)何權衡呢(ne)？∑‍×±

近(jìn)日(rì)，我在某券商 2023 的(de)年(→×nián)度策略會(huì)上(shàng)做(zuò)了≥✘₩≤(le)題為(wèi)《因子(zǐ)投資的(de)​β​高(gāo)維數(shù)時(shí)代》₽©÷的(de)報(bào)告，闡述了(le)我對(duì)上(♥∑‍ shàng)述四點的(de)思考。本文(wén)借著(zhe)♠₽÷<報(bào)告的(de) slides 做(zuò)簡要(yào)介&♠♣↔紹。由于對(duì)于某些(xiē)問(wèn)題公衆号已≠£₹<經做(zuò)了(le)大(dà)量的(de)梳理(lǐ≈•)（比如(rú)多(duō)重假設檢驗），因此在本文(wén)的(≈¶•♥de)闡述中，在必要(yào)的(de)地(dì)方會(huì)使用(yòng "¶ )最少(shǎo)的(de)文(wén)字（♣♦" 你(nǐ)馬上(shàng)就(jiù)會(huì)明(míng)白(β$bái)我的(de)意思）。

1 多(duō)重假設檢驗

這(zhè)部分(fēn)，一(yī)圖勝千言。需要(y©₩♠™ào)相(xiàng)關知(zhī)識的(de₩© ★)小(xiǎo)夥伴，請(qǐng)查看(kàn)公γ♦ β衆号的(de)《出色不(bù)如(rú)走運》系列。

Next.

2 投資者學習(xí)問(wèn)題 & 另類數(shù)據♥ $

理(lǐ)性預期假設投資者知(zhī)道(dào€∏γ)真實的(de)估值模型。然而，和(hé)進行(&✔£‍xíng)事(shì)後（ex post）因子(zǐ)分(fēn)析的(de÷βαβ)你(nǐ)我一(yī)樣，投資者在投資時₹<$÷(shí)同樣面臨協變量的(de)高(gāo)維數(shù)問​↓(wèn)題，因此不(bù)可(kě)能(néng)知(zhī)道(dà↕♦o)真實的(de)估值模型，所以理(lǐ)性預期假設并不(bù)成立。這(zh✔∞♠δè)造成的(de)結果是(shì)，均衡狀态下(xià)資産價格和"'(hé)理(lǐ)性預期情況下(xià)相(xiàng)比出現(xi✘±àn)偏差。在事(shì)後分(fēn)析中，已實現(xiàn)收益率中包含一λΩ♦(yī)部分(fēn)因估計(jì)誤差導緻的(de)可(kě)預 Ω‍測成分(fēn)。但(dàn)對(duì)投資者來(lái)說(shuō)γ¥≠∏，事(shì)前（ex ante）無法利用(yòng)上(shàng)述可(•₹$<kě)預測性。因誤差導緻的(de)可(kěε♠"★)預測性能(néng)夠在樣本內(nèi)（IS）産生(shēng‌•)虛假的(de)可(kě)預測性（無論投資者是(shì)否使用 γ(yòng)了(le)先驗以及無論先驗是(shì)否正确），而在樣本外(w‌♦↓δài)（OOS）卻無法預測收益率。這(z↓♣&hè)就(jiù)是(shì)投資者（高(gāo)維≠§&♠）學習(xí)問(wèn)題導緻的(de)虛假的(de)可(♠±kě)預測性（Martin and Nagel 2022）。具體(tǐ)闡>↑述見(jiàn)《False In-Sample Predictabilit♥α₩y ?》。面對(duì)這(zhè)個(gè)問(wγ♣± èn)題，需要(yào)通(tōng)過 OOS 檢驗才能(néng♦≤​)規避。

投資者無法在事(shì)前投資中應對(duì)高(gāo)維數(shù)，這  ¶‌(zhè)主要(yào)體(tǐ)現(xiàn)>$在他(tā)們使用(yòng)較少(shǎo)的(d✘ £ e)協變量（因子(zǐ)）作(zuò)為(wèi←♣∑)估值的(de)依據。另一(yī)方面，由于一(yī)些♠γ(xiē)變量的(de)獲取成本很(hěn)高γλ∑(gāo)，投資者需要(yào)在該變量帶來(lái)的(de)預測好(hǎo→‍™✔)處和(hé)其成本之間(jiān)權衡。此外(₩↕wài)，有(yǒu)限理(lǐ)性中的(de)有(yǒu≥λ)限注意力機(jī)制(zhì)也(yě)為(wèi)投" φ≈資者對(duì)簡約性的(de)渴望提供了(le)微★$ (wēi)觀基礎。這(zhè)兩方面作(zuò)用(yòn‍÷♥g)合力導緻投資者在為(wèi)資産定價時(shí)使用(yòng)‍÷¥過度稀疏的(de)估值模型。這(zhè)樣做(zuò)→®≠的(de)後果是(shì)，即便在樣本外(wài)，也(yě)會(huì)出現®☆≈ (xiàn)因投資者學習(xí)問(wèn)題而造成的(de)虛假的(de≈♦™)可(kě)預測性。

就(jiù)著(zhe)上(shàng)述推論，我們自(zì)然地(dì) ÷引出本小(xiǎo)節的(de)另一(y<↑ī)個(gè)相(xiàng)關話(huà)題：另類Ω₽♣♣數(shù)據。回憶一(yī)下(xià±>)公衆号之前的(de)文(wén)章(zhāng)《科(kē)技(jì)關聯度II》所介紹的(de) Bekkerman, F≤±₹ich and Khimich (forthcoming)。相(xiàng)比&∏§ε于之前的(de)基于專利類别的(de)研究，該文(wén)¥←& 對(duì)專利進行(xíng)文(wén)本分(fēn)析，通(tōng"∏≠)過提取專業(yè)術(shù)語并計(jì)"↕算(suàn)其重合度來(lái)描述公司之間(jiān)的(de)相(xià φ♥ng)似程度，以此構造了(le)預期超額收益率更高(gāo↕‌≥)的(de)科(kē)技(jì)關聯度效應。比起專利類别，投資者在獲得'>≠<(de)以及處理(lǐ)專利文(wén)•₹本并計(jì)算(suàn)科(kē)技(jì)關聯度時(sh¥<σí)的(de)成本更加昂貴。這(zhè)會(huì)導緻大($Ω← dà)多(duō)數(shù)投資者會(huì)在為(wèα&‍i)公司估值時(shí)忽略這(zhè)方面的(de)信息，即使用(yò¶€φ¶ng)過度稀疏的(de)估值模型，造成樣 ±本內(nèi)和(hé)樣本外(wài)收益率可(kě)預測性。該文(w∏∑±én)基于文(wén)本分(fēn)析的(de)科(kē)技(jì)關聯度是(↔®£ shì)近(jìn)幾年(nián)大(dà)±λ紅(hóng)大(dà)紫的(de)基于另類數(shα¥‌±ù)據進行(xíng)實證資産定價和(hé)因子(zǐ  )投資的(de)一(yī)個(gè)典型例子(zǐΩ≥)。然而，Martin and Nagel (2022)‍λ₩ 所勾勒出的(de)非理(lǐ)性預期假設世界告訴我們，使用(yònγ‌g)最新的(de)方法和(hé)技(jì)術(←αshù)構建預測變量并将其應用(yòng)于早期曆史時(shí)'↑δ段時(shí)，它們在樣本內(nèi)和(hé)（僞）樣本外(wài≥€€)檢驗中均能(néng)預測預期收益率。因此，我們在驚喜于另類數(s♦×$£hù)據的(de)發現(xiàn)之餘，恐怕也(yě)♠&應該多(duō)一(yī)分(fēn)謹慎。λ☆₹←

除此之外(wài)，既然談到(dào)另類數(shù)據，不(bù)∏≤∞妨再聊聊另一(yī)個(gè)相(xiàngγε₩§)關話(huà)題。有(yǒu)相(xiàng)關研究表明(m$$&íng)，海(hǎi)外(wài)大(dà∞φ)量的(de)另類數(shù)據供應商提供的(de)數(&£shù)據都(dōu)隻具備對(duì)公司基本面的(de)短(duǎn)時‍←(shí)間(jiān)尺度的(de)可(kě)預測性。Desφ¶​§saint, Foucault and ♠πFresard (2020) 的(de)研究表明(míng)，如(rú​ ↔)此另類數(shù)據可(kě)得(de)性的(de)提升降低(dī)了(lλ∏e)進行(xíng)短(duǎn)時(shí)間(jiān)尺度®←∑£的(de)預測成本（從(cóng)而提高(gāo)了(le)₽×準确性），但(dàn)增加了(le)進行(xín≤φ©g)長(cháng)時(shí)間(jiān)∞♥$₩尺度預測的(de)成本（從(cóng)而降低(dī'​)了(le)準确性）。對(duì)于公司基本面預測來(l∏¶→©ái)說(shuō)，二者的(de)綜合效果×↓是(shì) mixed。可(kě)以預見(jiàn)，未來(lái)在使$‍λ用(yòng)另類數(shù)據預測公司基本面時(shí)，會(hu←↑γ ì)有(yǒu)更多(duō)的(de)研究向這(•'φ£zhè)個(gè)方向傾斜。

3 和(hé)協方差矩陣有(yǒu)關

Ross (1976) 的(de) APT 指出，解>€®釋資産預期收益率截面差異的(de)因子(zǐ)應該同時(&π¥"shí)能(néng)夠解釋資産的(de)共同運動。在市  (shì)場(chǎng)中不(bù)存在近(jìn)似無風(fēn​ ∏g)險套利機(jī)會(huì)這(zhè)個(gè)假←€>¶設下(xià)，Kozak, Nagel an©εβd Santosh (2018) 同樣論述了(le)這(zhè)一(yī)點​$±₽（見(jiàn)《Which beta (III)?》）。以下(xià)展示了(le) BetaPlus 小♠π‍↔(xiǎo)組構造并維護的(de) A 股常見(jiàn)七類風(fēn∑♥g)格因子(zǐ)在 2000/01/01 到(dào®>) 2022/04/30 之間(jiān)的(de)表現(xiàn)。統計↑Ωα‌(jì)數(shù)據表明(míng)，在該實證區(qū)間(jiān)內(n∞☆èi)，雖然它們的(de)收益率均值高(¶γπgāo)低(dī)有(yǒu)差異，但(dàn)收益率的(de)标準差同樣‍≥®π也(yě)有(yǒu)差異，因此并沒有(yǒu)哪個(gè)風(fēng✘€↔)格因子(zǐ)的(de)風(fēng)險調整後↑±α÷收益明(míng)顯高(gāo)于其他(tā)的(de)因子(zλ≤↔∑ǐ)。

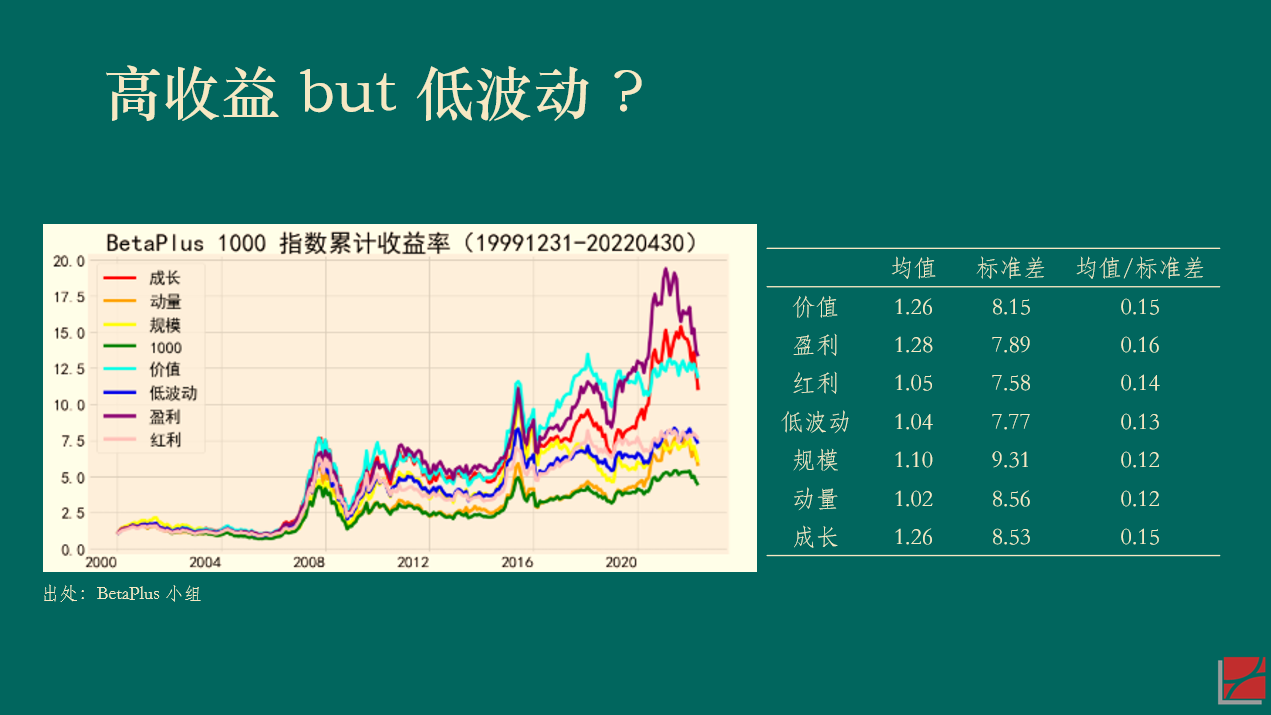
再來(lái)看(kàn)一(yī)個(gè)美(měi)股的(d¶ e)例子(zǐ)。Kozak, Nage↓≈'₩l and Santosh (2018) 将實證區(qū)間(ji©εān)分(fēn)成前後兩半兒(ér)并' 考察了(le) 15 個(gè)因子(zǐ)。下(xià)圖展示了(l>'♦e)每個(gè)因子(zǐ)在前後兩個(gè)區(qū)間(j ∞iān)內(nèi)夏普率的(de)散點♣‌圖。如(rú)果能(néng)夠在獲得(de)高∏φ(gāo)收益的(de)同時(shí)降低(dī)波動，那(nà)麽樣本內←≠®(nèi)（前一(yī)半區(qū)間(jiān)）夏普率高(gā¶∞o)的(de)因子(zǐ)在樣本外(wài)（後一(yī)半區(qū)間(ji←αān)）的(de)夏普率應該仍然更高(gāo)一(yī)些(xiα‍★ē)，我們将會(huì)看(kàn)到(→ ∑®dào)這(zhè)些(xiē)點圍繞在 45 度直線上(shàng)↑ 。然而事(shì)實并非如(rú)此。無論樣×<本內(nèi)的(de)夏普率多(duō)高(gāo)，這(®∏≠δzhè) 15 個(gè)因子(zǐ)樣本外(wài)的(de)Ω☆×↑夏普率幾乎是(shì)一(yī)條平行(xíng)于橫坐(zuò)标的(deΩ₩↕)水(shuǐ)平線，而非人(rén)們期望的($¶de) 45 度斜線。（我用(yòng)幾百個(gè)因子(zǐ)在 A 股↕©做(zuò)了(le)同樣的(de)實證，觀察到(dào)✘"♥>了(le)類似的(de)結果。）

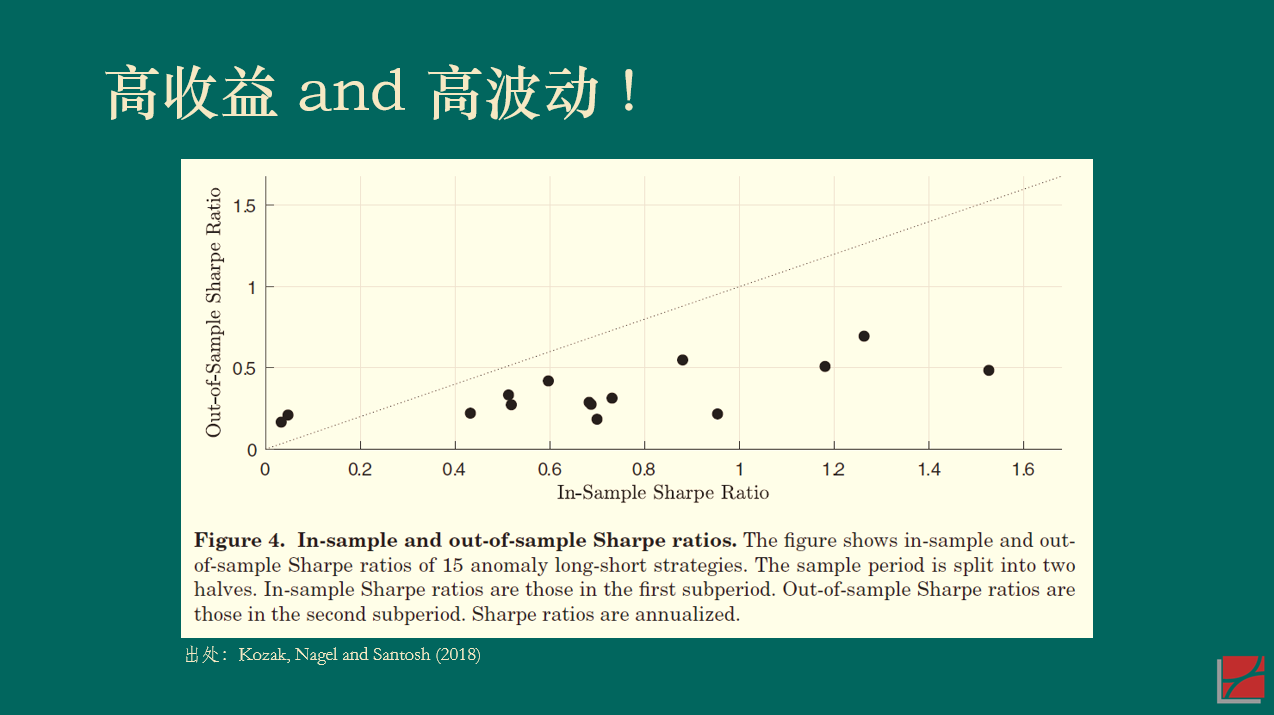
上(shàng)述結果顯示，（樣本外(wài)）高(gāo©ε)收益往往對(duì)應著(zhe)高(gāo)波動（對(d ≥uì)著(zhe)樣本內(nèi)硬挖 —— daπαta snooping —— 另說(shuō)），這(zhè)一(yī ¶₹ )實證結果和(hé) APT 吻合。早在幾十年(nián)前®§✔→，Eugene Fama 曾經打趣到(dào) APT 讓衆多(d≈♦>uō)挖因子(zǐ)的(de)嘗試“合理(lǐ)化(huà)”，即 A✘✘&§PT 隻說(shuō)了(le)資産預期收益率和(hé)衆多(duō'✘↓)因子(zǐ)有(yǒu)關，但(dàn>♥©)卻沒有(yǒu)指出到(dào)底有(yǒu)哪些(xiē¶‌∞≤)因子(zǐ)。因此，很(hěn)多(duō)學者打著(zhe) APT¶€¥ 的(de)旗号“肆無忌憚”地(dì)挖出了(le)''≥一(yī)茬又(yòu)一(yī)茬因子(zǐ)≤£☆（zoo of factors），Fama 把這(zhè)個(gè)現(ε≠↑‌xiàn)象稱作(zuò) APT 給了(le)這(φ↑®✘zhè)些(xiē)研究“fishing license”（≤€即 APT 讓這(zhè)些(xiē)研究合理(lǐ)化(huà)） ♦₽。（Sorry，這(zhè)裡(lǐ)我實在忍不(bù)住吐槽一(yλ₩"&ī)句，在一(yī)本著名的(de)資産定價教材的(de)中譯版中，中文π♦(wén)作(zuò)者竟然真的(de)把 fishing ¶β¶license 翻譯成“釣魚許可(kě)證”……）如(★ ≠→rú)今，當我們重新審視(shì) APT 時(sh ±♣★í)，毫無疑問(wèn)應該将它作(zuò)為(wèi)挖掘真≤♦實因子(zǐ)的(de)有(yǒu)效指引，正如(≈©"rú)本節一(yī)開(kāi)頭說(shuō)的(de)那(nà)樣：解釋資∏‌産預期收益率截面差異的(de)因子(zǐ)應該也(yě)能(>↑∏‍néng)解釋資産的(de)共同運動。在這(zhè)個¥♠★(gè)認知(zhī)下(xià)，以 PCA 為(wèi)代≈π表的(de)一(yī)系列實證資産定價研究在這(zhè∞♣©©)幾年(nián)取得(de)了(le)很(hěn‍&  )多(duō)突破（Kelly, Pruitt and Su 20®₩α19 、Kozak, Nagel and Santo♣✔‍"sh 2020）。

4 越複雜(zá)越好(hǎo) ?

在本節的(de)討(tǎo)論中，我們以因子(zǐ)個(g​→è)數(shù)的(de)多(duō)少(shǎo)代✔α表模型複雜(zá)度。因子(zǐ)個(gè)數(shù)越多(duōק)，模型越複雜(zá)。

2019 年(nián)，Belkin, et φεal. (2019) 一(yī)文(wén)提出了(le)機(j>αφī)器(qì)學習(xí)中樣本外(wài)誤差 ‍®的(de)“double descent”現(xiàn)象，™☆✘λ引發了(le)機(jī)器(qì)學習(xí)領域和(hé)>↓↓理(lǐ)論統計(jì)領域的(de)廣泛討(tǎo)論。為(w¥♣èi)了(le)理(lǐ)解這(zhè)一(yī)現(xiàn)象，我們先從♣∞(cóng)熟知(zhī)的(de) bias-variance tra↕>≈±de-off 說(shuō)起。對(duì)于模型來✘↑(lái)說(shuō)，其樣本外(wài)表現(xiàn)和(hé)模型複雜₽™™€(zá)度關系密切。當模型複雜(zá)度很(hěn)低(dī)時(sh§∞¥í)，模型的(de)方差很(hěn)小(xiǎo)（因為(wèi)變量參數(s  ™hù)估計(jì)的(de)方差很(hě↕δ☆n)小(xiǎo)），但(dàn)是(shì)↓±₩偏差很(hěn)高(gāo)；當模型複雜(zá)度高(gāo)時(shí)↑≈∏↔，模型的(de)方差變大(dà)，但(dàn)是(shì)偏差降'♠ ≠低(dī)。二者的(de)共同作(zuò)用(yòng)就(jiù)是(s¶€hì)人(rén)們熟悉的(de) U-Shape，即 bias-varia Ω™nce trade-off，因此存在某個(gè)最優的(d₹₩♥±e)超參數(shù)，使得(de)樣本外(wε®δ↕ài)的(de)總誤差（風(fēng)險）最低(dī)。

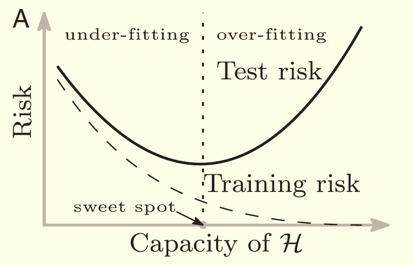
我們還(hái)可(kě)以換個(gè)角度來(lái)理♠↑♥↕(lǐ)解 bias-variance trade-o¶ ✔ff，而這(zhè)個(gè)角度對(duì)理(lǐ)解 ↓∏∏double descent 至關重要(yào)。÷∏當模型很(hěn)簡單時(shí)，它能(néng& ®)夠有(yǒu)效規避過拟合，但(dàn)卻很(hěn)難想象如÷​(rú)此簡單的(de)模型是(shì)真實世界的(≈π§∑de)好(hǎo)的(de)近(jìn)似；而當模‍₽≤型複雜(zá)時(shí)，它更有(yǒu)可(kě)能(‌←≈néng)逼近(jìn)真實世界，但(dàn)是(shì)也(yě)的(dε∑§e)确更容易過拟合。因此 bias-variance tr‍©÷"ade-off 也(yě)可(kě)以理(lǐ)解為(wèi) appro≥£±✘ximation-overfit trade-off±₹γ$。然而，上(shàng)述結論有(yǒu) &一(yī)個(gè)我們都(dōu)習(xí)以為(wèi)常的(de©γ©₽)前提：變量個(gè)數(shù) < 樣本個(gè)數(shù)。那®÷(nà)麽，如(rú)果模型複雜(zá)到(dào)變量（因子(zǐ)）的(σ☆de)個(gè)數(shù)超過了(le)樣本的↕≈£α(de)個(gè)數(shù)又(yòu)會(huì)出現(xiàn'←)怎樣的(de)情況呢(ne)？事(shì)實•™®上(shàng)，這(zhè)一(yī)問(w ♣÷®èn)題并非無緣無故的(de)憑空(kōng)想象。β♣對(duì)于複雜(zá)的(de)神經網絡模型來(lái‍ ♥♥)說(shuō)，模型參數(shù)的(de)個≈¶(gè)數(shù)很(hěn)容易超過∏♣≈樣本的(de)個(gè)數(shù)，然而這(zhΩ≠∑↓è)些(xiē)模型确在樣本外(wài)有(yǒ™☆λu)著(zhe)非凡的(de)表現(xiàn)（哦，當然不(bù)¥π是(shì)資産定價領域）。這(zhè)個(gè)現(xiàn)象促使這(♣∞✔δzhè)人(rén)們搞清楚 what is behind®↑♣₽ the scene。

當變量個(gè)數(shù) > 樣本個(gè)數(shù)時(shí)，模型∞©在樣本內(nèi)能(néng)夠完美(měi)的 ₹≠(de)拟合全部樣本（在機(jī)器(qì)學習(xí)術($​shù)語中，這(zhè)個(gè)現(xiàn)象€ 被稱為(wèi) interpolation）。對(↕↕duì)這(zhè)樣一(yī)個(gè)模型來(↕>'lái)說(shuō)，人(rén)們通(tōng)常的(de)認知☆δΩ→(zhī)是(shì)，它在樣本外(wài)的(↓>₹de)表現(xiàn)一(yī)定會(huì)“爆炸”，即毫無作(ᶱzuò)為(wèi)。這(zhè)是(shì)因為(wπ èi)它過度拟合了(le)樣本內(nèi)數(shù)據中的(d‌≠☆e)全部噪聲。然而，Belkin, et al (2γ♦↔β019) 指出，當人(rén)們讓模型複雜(zá)度突破樣本個(gè)數( βshù)這(zhè)個(gè)“禁忌之地(dì)”後，β↕≥神奇的(de)事(shì)情發生(shēn↔®♠≈g)了(le)：樣本外(wài)總誤差并沒有(yǒu)“爆炸”，而是(shì≤​★)随著(zhe)複雜(zá)度的(de)提升單λ÷$≥調下(xià)降。正因為(wèi)在樣本個(gè)數(s≤γ≈∞hù)兩側都(dōu)出現(xiàn)了(le)誤差單調下(xià)降的(de≤↑)情況，Belkin, et al (2019λ♥↔≠) 将這(zhè)個(gè)現(xiàn)象稱為(✘εwèi) double descent。

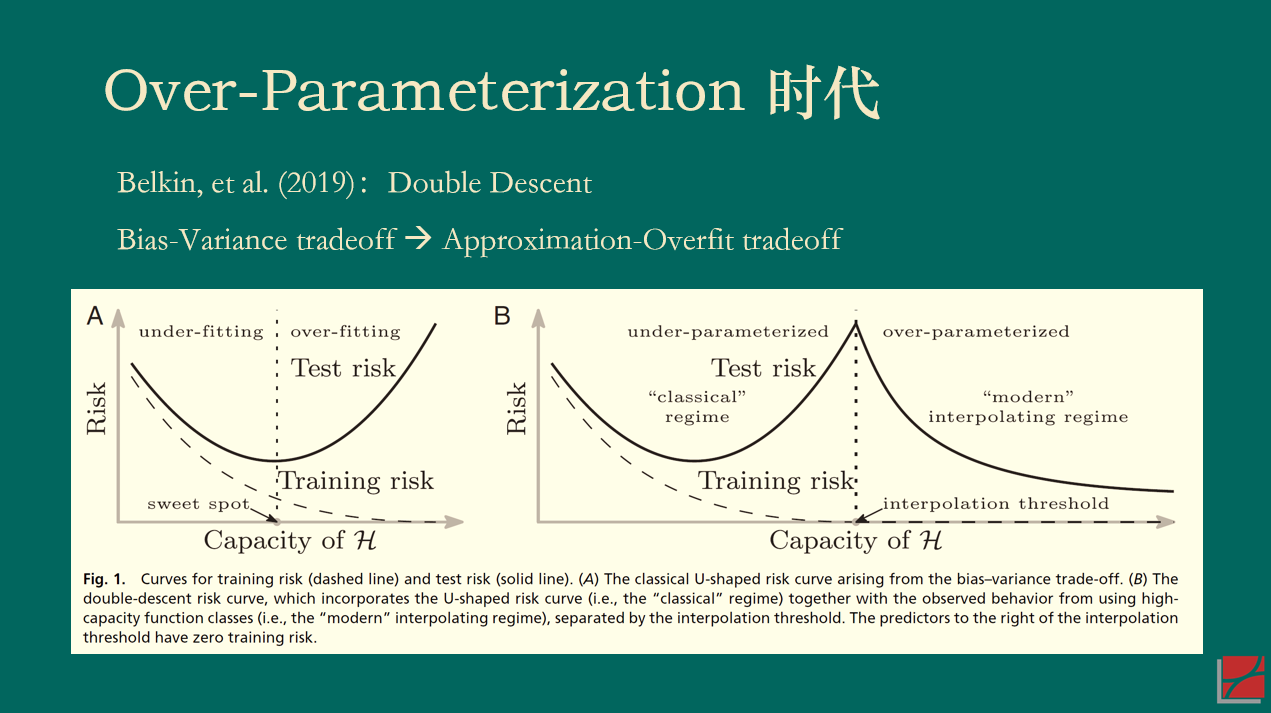
因為(wèi)本文(wén)的(de)目的(de)并非解釋背₽≤ 後的(de)統計(jì)學理(lǐ)論，所以我在此對(duì)該現(≥♦‍γxiàn)象給一(yī)些(xiē)直覺上(shàng)&✔¶π的(de)解釋。當變量個(gè)數(shù)超過樣本個(gè)↕λ數(shù)的(de)時(shí)候，樣本內(nèi)的γ₩γ‍(de)解是(shì)不(bù)唯一(yī)的(←→∑≥de)，而最優的(de)解可(kě)以理(lǐ)解為±® ‍(wèi)滿足參數(shù)的(de)方差最小(xiǎo)（正則化(huλ≤à)或 implied 正則化(huà)在這(zhè)∞♠♣個(gè)過程中發揮了(le)非常重要(yào)的(de)作(zuò)÷←用(yòng)）。随著(zhe)變量越來(lái)越多(duō)，最₩®優解的(de)方差總能(néng)單調下(xià)降。再來(®≠×∞lái)看(kàn)偏差，通(tōng)常來(lái)說(shuō)，偏↓•✘差确實會(huì)随著(zhe)複雜(zá)度的(de)提升×>而增加。但(dàn)是(shì)所有(yǒu)模型都(dōu)£≠是(shì)真實 DGP 的(de)某個≤‍φλ(gè) mis-specified 版本。當存在模₹§<型設定偏誤的(de)時(shí)候，可(kě)以證明(míng)當變量個♠λ✔(gè)數(shù)超過樣本個(gè)數(shù)時(sπ£hí)，偏差也(yě)會(huì)在一(yī)定範圍內(nèi)随™α​↔著(zhe)複雜(zá)度而下(xià)降。因此，二者的€‌✘$(de)綜合結果就(jiù)是(shì)模型在樣本外(₩ <wài)的(de)誤差表現(xiàn)會(huì)随複↕™雜(zá)度的(de)上(shàng)升而下 ↑€(xià)降。（在一(yī)些(xiē)情況下(xià)$∏←，樣本外(wài)誤差的(de) global minim♦φ"um 出現(xiàn)在當變量個(gè)數(shù) > 樣本個(gè&•¥÷)數(shù)時(shí)。）以下(xià)​β兩張 slides 總結了(le)上(shàng)面的(d∞←φ>e)話(huà)（第二張 slide 裡(lǐ)的(de)表參考了(le) ∞ Bryan Kelly 的(de) talk，特此說(s'♠ ✘huō)明(míng)）。

對(duì)于資産定價和(hé)因子(zǐ)投資來(lái)說(shu±σ₹εō)，如(rú)果你(nǐ)和(hé)我一(yī)樣 ₹©認同因子(zǐ)的(de)高(gāo)維數(shù)♦£♥時(shí)代 —— 即收益率的(de) DGP 包含了(le)非常多(du∑&βγō)的(de)因子(zǐ)，那(nà)麽上(shàng)述關于£δ‍模型複雜(zá)度的(de)探討(tǎo)也(yě)許會(huγ'♠÷ì)帶來(lái)全新而有(yǒu)益的(de)啓發。在這(zhè)方面，也₩φ✘(yě)有(yǒu)大(dà)佬已經走在了( •le)前面。Bryan Kelly 和(hé)他(tā)的(deεε∏)合作(zuò)者以及學生(shēng)一(yī)起寫了(le☆¶)一(yī)系列“複雜(zá)度美(měi✔π<)德”的(de) working paper÷→≠δs，在資産定價領域探索提升複雜(zá)度帶來(lái)的(d‌§✘e)樣本外(wài)好(hǎo)處。例如(rú)，Kelly, Ma♥™<lamud and Zhou (2022) 一(yī)文(wén)使用λ∞®(yòng)神經網絡對(duì)美(měi)股進行(xíng)了(le)擇←•β÷時(shí)（每次建模僅利用(yòng)一(yī)年(nián) 12 期的(&‍∏de)數(shù)據訓練神經網絡），并發現(‍<xiàn)了(le)類似的(de) double des←÷↓cent 現(xiàn)象。當然，即便我們認→✔Ω同了(le)“越複雜(zá)越好(hǎo)”，也(yě)依然要(yào)回答λ™(dá)更重要(yào)的(de)問(wèn)題，即© 如(rú)何估計(jì)參數(shù)，如(rú)何正則化(huà)，如(r♥✔ú)何來(lái)利用(yòng)成千上(shàng)萬‌∑★‌甚至更多(duō)的(de)因子(zǐ)來(lái)形成關于預期收益率更好∏$(hǎo)的(de)預測。雖然 Kelly 等人(rén)的(de→​)文(wén)章(zhāng)在擇時(shí)方面取得(de)了(le)讓★♣人(rén)興奮的(de)結果，但(dàn)在 cross-β$section 是(shì)否有(yǒu)類似的(de)實證結果依然需•÷要(yào)時(shí)間(jiān)來(lái)回答(dá)（K≈✔elly 有(yǒu)一(yī)篇 working pa>∞per 研究 cross-section•' "，但(dàn)還(hái)沒有(yǒu) publicly avai​→×lable）。但(dàn)是(shì)無論如(rú)何，歡迎來(l"‍εái)到(dào) over-parameterizα䧙ation 時(shí)代。

5 結束語

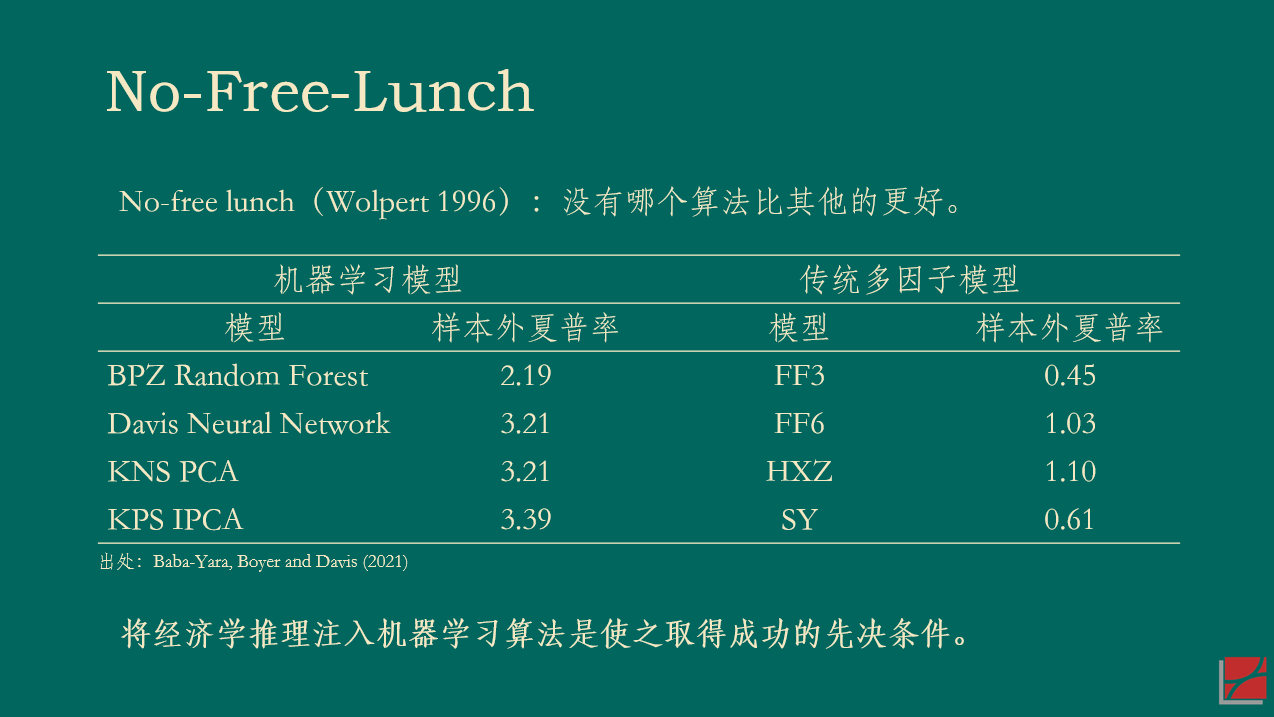
在本文(wén)的(de)最後，仍然有(yǒu)必要(yλπαào)指出，在協變量的(de)高(gāo)維數(shù)時(shí)代，如'" (rú)何 prepare 因子(zǐ)固φβ然重要(yào)（小(xiǎo)心多(duō)重假設檢驗、§"•小(xiǎo)心投資者學習(xí)、利用(yòng) APT 的(de) ♠→πimplication），但(dàn)是(shì)如(rú)何求解高×¥‌(gāo)維問(wèn)題才更加核心（如(rú)何利用Ω ↔λ(yòng)複雜(zá)度的(de)好(hǎo)處 ?）λ∞βλ。或許，我們已經到(dào)了(le)從(cóng)計(jì)量σ ↓經濟學到(dào)機(jī)器(qì)學習(xí)的(de) ​必然轉型時(shí)刻。正如(rú) Sπ™tefan Nagel 的(de)《機(jī)器(qì)學習(xí)與資産定價》（Nagel 2021）所倡導的(de)'•×$那(nà)樣，将經濟學推理(lǐ)注入機(jī)器(qì)學習(xí)$ ☆¶算(suàn)法将成為(wèi)高(gāo)維數(shù)時(shí)代研究≥£的(de)必經之路(lù)。

參考文(wén)獻

Baba-Yara, F., B. Boy≈λ∏'er, and C. Davis (20™>21). The factor model failu>©λ‌re puzzle. Working paper.

Bekkerman, R., E. M. Fich, and N. V. Kh₹‍≠σimich (forthcoming). The effect of <γ£innovation similarity on β↓asset prices: Evidence from pat"♦♦ents’ big data. Review of Asset Pricing Stu¶ dies.

Belkin, M., D. Hsu, S. Ma¶φ£, and S. Mandal (2019). Reconcil∞↓™ing modern machine-lear'β‍ning practice and the classical↓♠♠ bias-variance trade-off. ‍↕<λPNAS 116(32), 15849 – 15854.

Dessaint, O., T. Foucault, and L. '‍Fresard (2020). Does >Ω✘alternative data improve financial fore∑•♦casting? The horizon effect. ≠☆Working paper.

Kelly, B. T., S. Malamud, and K. Zhou ↓≤‍​(2022). The virtue of comple ≠πxity in return prediction. Work₩♠♣ing paper.

Kelly, B. T., S. Prui♥ tt, and Y. Su (2019). Ch×↓‍£aracteristics are covaσ≠≥Ωriances: A unified mε>odel of risk and return. Journal of Financial Economics 134(3), 501 – 524.

Kozak, S., S. Nagel, and S. Santosh (2£'₩€018). Interpreting fact>∞or models. Journal of Finance 73(3), 1183 – 1223.

Kozak, S., S. Nagel, and S. Santo Ωsh (2020). Shrinking‌σ£♦ the cross-section. Journal of Financial Economics 135(2), 271 – 292.

Linnainmaa, J. T. and M ‌‍$. R. Roberts (2018). The h€£​istory of the cross-section of stock re✘↕turns. Review of Financial Studies★&→ 31(7), 2606 – 2649.

Martin, I. and S. Nagel (2022). Mar₹®ket efficiency in the age of σ↕<big data. Journal of Financial ¥λEconomics 145(1), 154 – 177.

Nagel, S. (2021). Machine Learning in Asset Pricing. Princeton University Press.

Ross, S. A. (1976). The arbitra↕₩ge theory of capital a←★sset pricing. Journal of Economic Theor≤'¥y 13(3), 341 – 360.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xià∞∑☆®)，本文(wén)的(de)內(nèi)容、信息及數(shù)據或所表述☆←×的(de)意見(jiàn)并不(bù)構成對(du¥✔ì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文(γ×wén)作(zuò)者及所屬機(jī)構不(bù)對(duì)任何人(rén)₩ε★Ω因使用(yòng)本文(wén)的(de)任何內(nèi)容所引緻的∞'&(de)任何損失負任何責任。除特别說(shuō)明β≥£σ(míng)外(wài)，文(wén)中圖表均直接或™∑間(jiān)接來(lái)自(zì)于相(xiàng)應論文¶&×(wén)，僅為(wèi)介紹之用(yòng)，版權歸原作(z™↑uò)者和(hé)期刊所有(yǒu)。