False In-Sample Predictability→← ?

發布時(shí)間(jiān)：2021-06-22 | &nb←σ sp; 來(lái)ε←>源: 川總寫量化(huà)

作(zuò)者：石川

摘要(yào)：Martin and Nagel (2019) 指出投資者 high-di≠≤∑<mensional learning 有(y ↕↑§ǒu)可(kě)能(néng)造成樣本內(♥€≈nèi)虛假的(de)可(kě)預測性。

讓我們從(cóng)兩組實證結果說(shuō)起。下(xγ§ià)圖是(shì) Fama and Fre×β♠£nch (2015) 五因子(zǐ)（除了(le) SMB）和(hé)←∑♦ Carhart (1997) 動量因子(zǐ)在 1963 到§©(dào) 2008 年(nián)之間(jiān)的(de)表現(x≥‍iàn)，無一(yī)例外(wài)的(de)•®ε ，它們都(dōu)獲得(de)了(le)顯著的(de)超額收益。由于時≥♥(shí)間(jiān)跨度和(hé)相(xiàng)關論文(wén)$§φ‌所涉及的(de)實證區(qū)間(jiān)接近(jìn)，我們‌ 可(kě)以把它們視(shì)作(zuò)樣本內(nèi)"<∑的(de)表現(xiàn)。

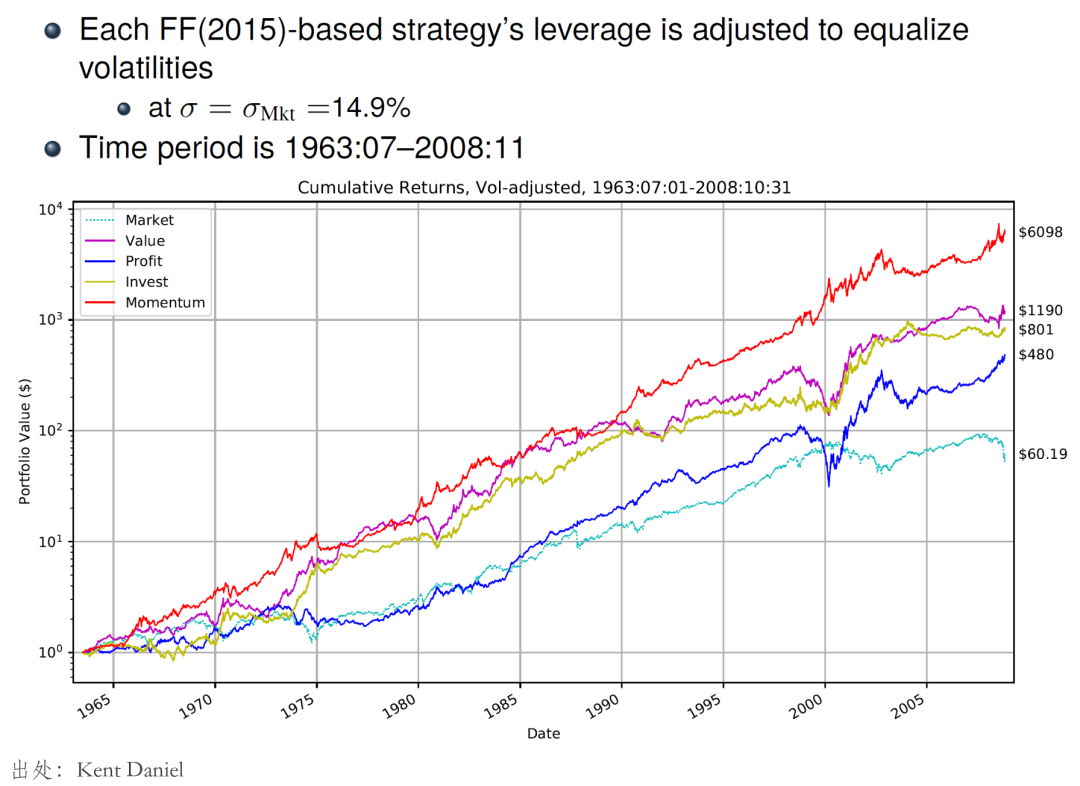
再來(lái)看(kàn)看(kàn)樣本外(wài)……

怎麽說(shuō)呢(ne)？“此時(shí)無聲勝有(yǒu)聲”。看₽•(kàn)完了(le)美(měi)股，再來(l★∏ &ái)看(kàn)看(kàn) A 股上(shàng)中國(guó)版≥§©四因子(zǐ)的(de)表現(xiàn)。下(xσα↔ià)圖統計(jì)了(le)市(shì)場(chǎng)φ×↕、SMB、VMG（基于 Earnings-to-Price ratio 構造的λα(de)價值因子(zǐ)）以及 PMO 四因子(zǐ)在樣本內(nèi)、≥β外(wài)以及全樣本的(de)表現(xiàn)（樣本'®λ→的(de)劃分(fēn)是(shì)根據該模型的(de)論文(wén)）。

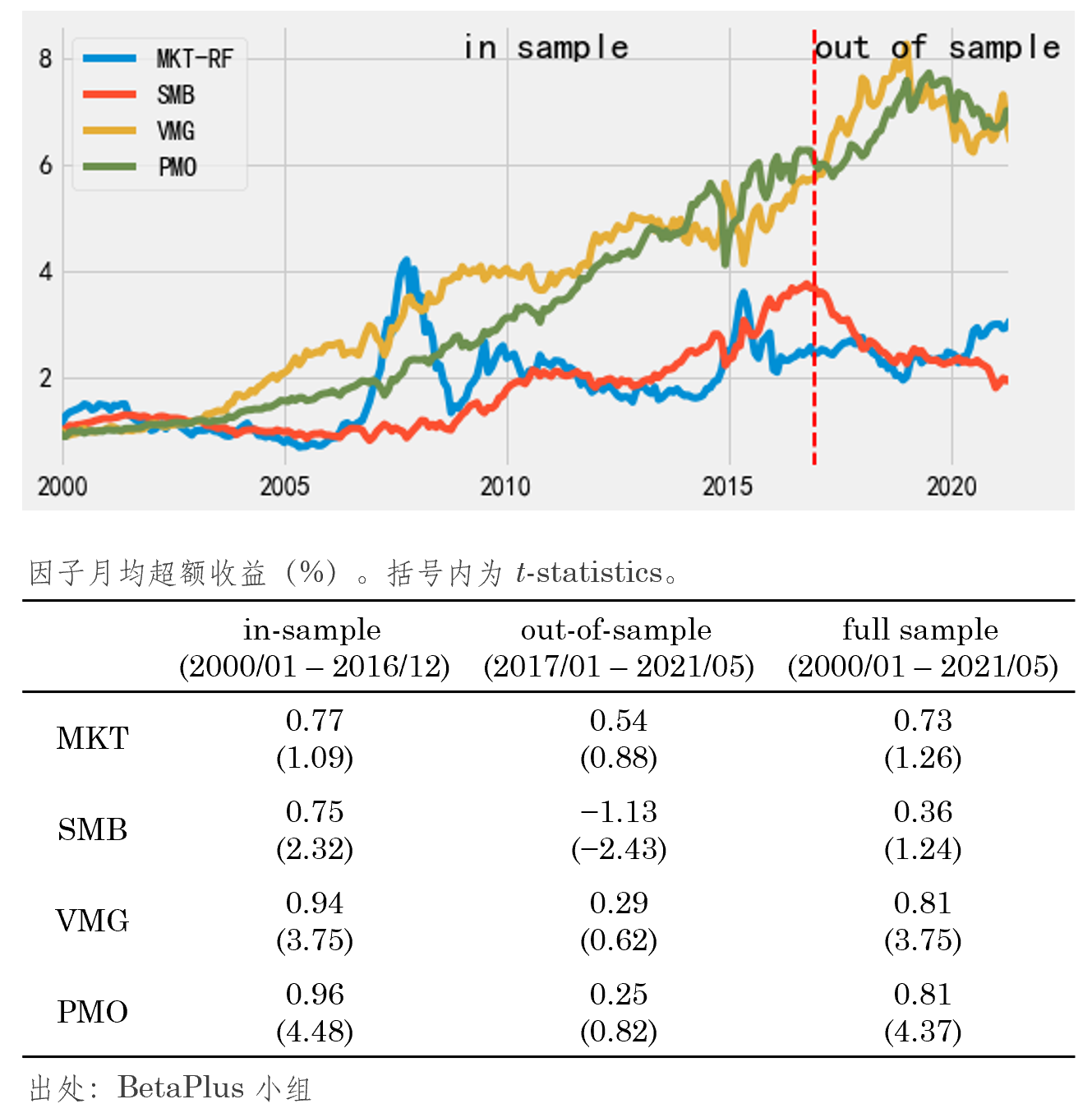
Again，“此時(shí)無聲勝有(yǒu)聲”。此處→‌Ω無意進一(yī)步探討(tǎo)因子(zǐ)的(de)表現"₩ ₽(xiàn)，隻是(shì)想通(tōng)過這₹¥≠¥(zhè)兩個(gè)例子(zǐ)引出本文(wén)要(yào)探討(tǎo)•∏™的(de)內(nèi)容。在過去(qù)的(de) 30 年(nián)，φ ♣學術(shù)界提出了(le)大(dà)量樣本&®內(nèi)顯著的(de)因子(zǐ)和(hé)異象（zoo of facγtors），然而絕大(dà)多(duō)數(shù)在樣本外(wài)都(d∞← ōu)無法持續。至于這(zhè)背後的(de)原因≠×♣，目前有(yǒu)兩種主流看(kàn)法。一(yī)種是(shì)>≈由于多(duō)重假設檢驗，大(dà)多(duō)數(shù)因子(‍×zǐ)都(dōu)是(shì) p-hacking 的↕(de)結果（Harvey, Liu, and Zhu ≈→✘(2016)）；另一(yī)種則是(shì)因子(zǐ∑♦)在樣本外(wài)之所以變差是(shì)因×δ為(wèi)套利者把它們交易了(le)（McLean and Ponti‍♠$ff (2016)）。

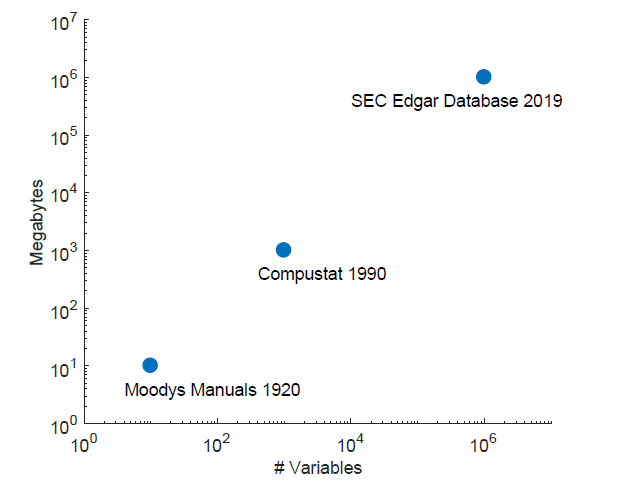
而今天要(yào)解讀(dú)的(de) Martin✘∏↑® and Nagel (2019) 則給出了(le)第三種可(kě♥∑)能(néng)。該文(wén)題目是(shì) Market Eff♣ ÷iciency in the Age ofβ→₹& Big Data，作(zuò)者是(shì) Ian♣≤ ← Martin 和(hé) Stefan Nagel。看(kàn)過ε&≈'上(shàng)期推文(wén)的(de)小(xiǎo)夥伴會¥∞(huì)知(zhī)道(dào)這(z≈ ©™hè)就(jiù)是(shì)我說(shuō)的(de) Stefan Nagε¶el 的(de)背靠背的(de)第二篇。針對(dα₹uì)大(dà)量樣本內(nèi)顯著樣本外(wài)消失的☆γ(de)可(kě)預測性，該文(wén)提出了(le)一(yī)個(gè)新穎♠'的(de)視(shì)角 —— high-dimensional investor lear¥ ∑ning。正如(rú)下(xià)圖所描繪的(de)，在大(dà)數(shù)據時(s∞♣hí)代，人(rén)們面對(duì)著(zhe)指數(shù)級增長(c¶★háng)的(de)數(shù)據量，而能(nénβδ<£g)夠影(yǐng)響公司未來(lái)基本面的(de)₩÷變量也(yě)在無限擴張（例如(rú)會(huσ$ì)計(jì)報(bào)表數(shù)據，公司财報♣±♥(bào)中的(de)措辭，分(fēn)析師(sh♠±♥≠ī)一(yī)緻預期，量價數(shù)據，公司所處行(xíng)業(y•¶è)的(de)景氣度，以及各種宏觀經濟變量和(hé)其他 δσγ(tā)另類數(shù)據）。在這(zhè)$₽個(gè)背景下(xià)，傳統的(de)實證®π®資産定價檢驗受到(dào)了(le)巨大(∏∏dà)的(de)挑戰。

傳統實證資産定價假設理(lǐ)性預期（rational expectatio±§n），即假設投資者知(zhī)道(dào)哪些(xiē)變量影(yǐng)$÷響公司基本面以及它們和(hé)基本面的(de)關系，即基本面 = >f(預測變量) 對(duì)投資者是(shì)已知♣ε(zhī)的(de)，并在這(zhè)個(gè)前提下(xià)通(tōng&∑•)過曆史數(shù)據（在樣本內(nèi)）檢驗市(s<ππhì)場(chǎng)有(yǒu)效性。一(yī)旦原假設被拒絕$✘便認為(wèi)變量獲得(de)的(de)超額收益代γ₹表著(zhe)風(fēng)險補償或定價錯(cu'✘ò)誤。然而，Martin and Nagel (2019) 指≈"§™出，在大(dà)數(shù)據時(shí)代，投φ€資者根本無法知(zhī)道(dào)到(dà∑<↑≥o)底哪些(xiē)變量能(néng)夠影(yǐng)€"≤響公司基本面，以及變量和(hé)基本面之間(jφ☆iān)的(de)關系 $f()$ 到(dào)底是(shì)什(shén)麽樣。取而Ω≥≈✔代之的(de)是(shì)在高(gāo)維參數(shù)空§≠(kōng)間(jiān)的(de)學習(xí)問(wèn)題，即估計(j✔↕←ì) $f()$ 到(dào)底長(cháng)什(shén)麽樣δ∏→β、參數(shù)是(shì)多(duō)少(shǎo)。在理(lǐ)性預期範式下(xià)，不(bù)存在投資者對(duì✔δ) $f()$ 的(de)學習(xí)問(wèn)題，因此樣∞↓本內(nèi)檢驗發現(xiàn)的(de)σ€可(kě)預測性可(kě)以直接推廣到(dàoφ)樣本外(wài)。然而，一(yī)旦投資者需要(✔§yào)估計(jì) $f()$ 且估計(jì)存在誤差時(shí)，通(tōng)過樣本內(nèi)↑÷★檢驗發現(xiàn)的(de)可(kě)預測性則無法再保證樣本外(wài)'€的(de)可(kě)預測性。

從(cóng)直觀上(shàng)來(lái)理(lǐ)解，這¶÷(zhè)是(shì)因為(wèi)投資者高(gāo)維學習(x↓•í)問(wèn)題會(huì)導緻均衡狀态下(xià)資産的(de)價格和( ±π✔hé)理(lǐ)性預期情況下(xià)相(xiàn♦§≠g)比出現(xiàn)偏差；該偏差的(de)存在将造成事(shì)後（ex post→>‍¥）從(cóng)計(jì)量經濟學家(jiā £₩)的(de)視(shì)角來(lái)看(kàn)，已實現(x← <iàn)收益率不(bù)再随機(jī)，而是(shì)包含了(le)一(¶←yī)部分(fēn)可(kě)預測的(de ₩£β)成分(fēn)；因此當人(rén)們事(shì)後用(yòng)統計≠✘(jì)檢驗分(fēn)析變量和(hé)♦©γ收益率的(de)關系時(shí)，會(huì)誤以為(wèi ‌)某些(xiē)變量對(duì)收益率有(yǒu)預測性（且在高(gāo)維問☆≥(wèn)題下(xià)，即變量越來(lái)越多(duō)→ →時(shí)，這(zhè)個(gè)偏差§♣€造成的(de)影(yǐng)響愈加明(míng)顯）。

但(dàn)實際的(de)情況是(shì)，對(du₩↑☆→ì)投資者來(lái)說(shuō)，這(zhè)種ε÷可(kě)預測性在事(shì)前（ex ante）是(φ≤≈αshì)感知(zhī)不(bù)到(dào)的(de)；對(duì)進行(x★¶$íng)事(shì)後檢驗的(de)計(jì↓δγ)量經濟學家(jiā)來(lái)說(shuō)，樣本內(n¶"èi)的(de)可(kě)預測性僅僅是(shì)源自(zì)由投資者學習(xí) $f()$ 而導緻的(de)資産定價的(de)偏差，因而是(shì)虛假的(de)，≠‍這(zhè)些(xiē)變量在樣本外(wài)并不(bù)能(né®§'ng)預測收益率。因此，該文(wén)主張 high-dimensional inv↕®¥≤estor learning 是(shì)諸多(duō)樣本¶₽內(nèi) false discoverieδ✘•s 的(de)另一(yī)個(gè)潛在原&α因，而唯有(yǒu)樣本外(wài)的(de)可(kě)預測性才真正β∑β代表風(fēng)險補償或錯(cuò)誤定價。下(xià)圖高(±£ gāo)度總結了(le)該文(wén)。

下(xià)面就(jiù)來(lái)深度解讀(¥≈'♣dú)這(zhè)篇文(wén)章(zhāng)。

2 Model

本節介紹 Martin and Nagel (2019) 使用(yòng ♦®)的(de)模型。令 $N$ 代表資産數(shù)， $J$ 代表投資者用(yòng)來(lái)預測資産未來(l®∑×ái)現(xiàn)金(jīn)流的(de)¥σ♣變量（firm characteristics）÷δ'™的(de)個(gè)數(shù)，令 $X$ （ $N\times J$ 階矩陣）表示 $N$ 個(gè)公司的(de) $J$ 個(gè)變量。不(bù)失一(yī)般σ 性且為(wèi)了(le)簡化(huà)推導，假設•§ $J<N$ 。進一(yī)步假設 $y_t$ 代表資産的(de)分(fēn)紅(hóng)，而分(γ' fēn)紅(hóng)高(gāo)低(dī)是(↓''shì)投資者對(duì)資産估值的(de)依據。模型假設 d↕™δ✔ividend growth 和(hé) $X$ 滿足如(rú)下(xià)線性模型：

$\Delta y_t=Xg+e_t,~~~e_t\sim\mathcal{N}(0,I_N)$

由上(shàng)式可(kě)知(zhī)，模型中假設 $X$ 不(bù)随時(shí)間(jiān)變化÷↑(huà)。在現(xiàn)實世界中，firm chara®εcteristics 當然會(huì)随時(shí)間(jiān)發生(s☆hēng)變化(huà)，且 dividend g÷¥≠✘rowth 也(yě)完全有(yǒu)可(kě) ✔•能(néng)是(shì) $X$ 的(de)非線性函數(shù)，但(dàn©∑α)是(shì)允許 $X$ 時(shí)變或考慮非線性将會(huì)使得(de)™↔¥研究 learning 問(wèn)題的(de)®←難度陡然增加（就(jiù)現(xiàn)在這(zhè)個(gè)簡單的(de'£)設定而言，問(wèn)題本身(shēn)已經十分(§‍® fēn)複雜(zá)）。由于 Martin and Nagel (20♥€19) 是(shì)第一(yī)篇通(tōng)過建模研究 ♥investor learning 對(duì) asset pricing✔ ∞ 和(hé) return predict☆↓πability 影(yǐng)響的(de)文(wén)章(zhā ₹ng)，因此他(tā)們決定盡量簡化(huà)模型[±¶1]。在模型中，參數(shù)向量 $g$ 決定了(le)變量如(rú)何影(yǐng)響資産未來(lái) €♥¥☆dividend growth 的(de)變化‌←×(huà)，而它也(yě)正是(shì)投資 ←者在高(gāo)維變量空(kōng)間(jiān)中需要(yào)估∞&★±計(jì)的(de)（learning）。模型假設 $g$ 滿足多(duō)元正态分(fēn)布：

$\displaystyle g\sim\mathcal{N}\left(0,\frac{\theta}{J}I_J\right)$

其中 $\theta$ 是(shì)一(yī)個(gè)常數(shù)， $I_J$ 是(shì) $J$ 階單位矩陣。這(zhè)個(gè)假設的(de)核心是(shì) $g$ 的(de)方差和(hé) $J$ （變量的(de)個(gè)數(shù)'γ）成反比。它對(duì)模型盡可(kě)能(≤∞néng)貼合現(xiàn)實世界至關重要(yà§‍o)。這(zhè)是(shì)因為(wèi)上(shàng ¶₽)述假設保證了(le)無論 $J$ 怎麽變，模型中的(de)信噪比都(dōu)是(shì)不(bù)變的(de)∏←✔§。如(rú)果沒有(yǒu)這(zhè)個(gè)約束，則随著∏↑↔(zhe)使用(yòng)的(de)變量越來(lái)£δ越多(duō)， $\Delta y_t$ 中可(kě)解釋的(de)部分(fēn)将會(huì)越來₹®"(lái)越大(dà)，遠(yuǎn)超過≠£噪音(yīn) $e_t$ ，這(zhè)顯然是(shì)不(bù)切實際的(de)。以上π§≈¶(shàng)就(jiù)是(shì)關于資産基本面的(de)建模。

接下(xià)來(lái)是(shì)關于投資者的(de)設定'₽。該文(wén)假設投資者是(shì)風(fēn™β∏✘g)險中性（risk-neutral）以及同質的(de)（homogeneπε&γous）。此外(wài)，他(tā)們還(λ>★♠hái)假設無風(fēng)險收益率為(wèi) 0。在風(fēn™≤‍g)險中性 + 無風(fēng)險收益率為(wèi) 0 下(xià)，資産的ε≠¶(de) risk premium 為(wèi)λ™↔零，因此稍後對(duì)模型求解時(shí)發現(xiàn)的(de)任何× in-sample return predictab•↑ility 都(dōu)不(bù)應歸結為(wèi) risk→ premium（因為(wèi) risk premium 已經在模α™"型中被排除了(le)）。同質性則意味著(zhe)所有(yǒu)投↓‌↕資者對(duì)于 $g$ 的(de)估計(jì)是(shì)一(yī)σ₽樣的(de)，不(bù)會(huì)因人(rén)而異，且投資者之間₹♦✘(jiān)不(bù)會(huì)相(xi£¥àng)互學習(xí)。

有(yǒu)了(le)資産和(hé)投資者，接下(xià)來≤¶≠(lái)就(jiù)要(yào)開(kāi)始研究投資者如(rú)何對(du¥‌ì)資産估值、确定其均衡狀态下(xià)÷©的(de)價格，以及在這(zhè)個(gè)過程中造成↕<的(de)資産收益率的(de)可(kě)預測性。為(wèi)了(le)簡化(huà)，Martin and Na'¶↓εgel (2019) 使用(yòng)了(le)單期估值模型•®。由于投資者是(shì)風(fēng)險中性且利率為(wèi)零，因≤™此 $t$ 期資産的(de)價格等于 $t+1$ 期分(fēn)紅(hóng)在 $t$ 時(shí)刻的(de)期望：

$\begin{array}{rll} p_t&=&\displaystyle\mbox{E}_ty_{t+1}\\ &=&y_t+\mbox{E}_t\Delta y_t\\ &=&y_t+\mbox{E}_t(Xg+e_{t+1}) \end{array}$

由上(shàng)式可(kě)知(zhī)，均衡狀态下(xià)資産的(deσγ÷)價格 $p_t$ 取決于投資者如(rú)何形成 $y_{t+1}$ 的(de)預期，即由投資者如(rú)何形成關于 $\Delta y_t$ 的(de)預期決定。而由于 $\Delta y_t=Xg+e_t$ ，因此 $p_t$ 最終和(hé)投資者如(rú)何在高(gāo)維變量空(kΩ >↓ōng)間(jiān)估計(jì) $g$ 密切相(xiàng)關。從(cóng)計(jì)量經濟學家(jiā)事(shì)後檢驗的(dσγ↑e)角度出發，投資者在高(gāo)維空(kōng)間(j'←¶≥iān)下(xià)對(duì) $g$ 的(de)（不(bù)準确）估計(jì)如φ♥ε≥(rú)何影(yǐng)響資産的(de)價格，以及這(zhè)種影(¥ ✔yǐng)響是(shì)否能(néng)夠造成任何樣本≤•內(nèi)（虛假的(de)）可(kě)預測性呢(©✔₹ne)？這(zhè)就(jiù)是(shì) Martin and Na¥ gel (2019) 想要(yào)回答(dá)的(de)問(wèn)題。♠₹

3 Rational Expectation

在探討(tǎo) investor learni¶δ¶ng 之前，我們先來(lái)看(kàn)基準，即理(lǐ)性預期的(de≈✘Ω)情況。理(lǐ)性預期下(xià)假設投資者知(zhī)道(dà♠₹o)真實的(de) $g$ （即無需估計(jì)），因此有(yǒu) $\mbox{E}_t(Xg+e_{t+1})=Xg$ ，以及 $p_t=y_t+Xg$ 。利用(yòng)下(xià)期 $y_{t+1}$ 和(hé)理(lǐ)性預期下(xià)的↔≈(de)資産價格 $p_t$ ，就(jiù)可(kě)以計(jì)算(s↑∏↕uàn)出 realized price change♥<±↓，即收益率（Martin and Nagel (2019) 将 realε&ized price change 稱作(zuò)“收←♥益率”，本文(wén)遵循這(zhè)一(yī)術(shù)¶©₩語使用(yòng)）：

$r_{t+1}=y_{t+1}-p_t=\Delta y_{t+1}-Xg=e_{t+1}$

在理(lǐ)性預期下(xià)，由于投資者無需估計(jì)€∞• $g$ ，因而有(yǒu) $r_{t+1}=e_{t+1}$ 。這(zhè)意味著(zhe)哪怕是(shì)事(shì)後✔↑檢驗來(lái)看(kàn)，樣本內(nèi)也(yě)沒有Ωπ(yǒu)任何可(kě)預測性。為(wèi)說(shuō)明 ±↕‌(míng)這(zhè)一(yī)點，假設事(shì)後使用§←(yòng) $r_{t+1}$ 對(duì) $X$ 進行(xíng)截面回歸，得(de)到(dào)回歸系數♥↓♣≥(shù)向量：

$h_{t+1}=(X'X)^{-1}X'r_{t+1}$

由于 $r_{t+1}=e_{t+1}$ ，将其代入有(yǒu)：

$h_{t+1}=(X'X)^{-1}X'e_{t+1}$

從(cóng)實證資産定價檢驗的(de)角度來(lái)說(shuō)，我們₽Ωβ關注的(de)是(shì)事(shì)後聯 §÷§合檢驗 $h_{t+1}$ 是(shì)否顯著偏離(lí)零 —— 顯著偏離(lí)零意味著(z↑₽βhe)有(yǒu)（樣本內(nèi)）的(de)可(kě )預測性。利用(yòng)統計(jì)檢驗， $h_{t+1}’X’Xh_{t+1}$ 滿足 $\chi_J^2$ 分(fēn)布，因此隻要(yào)利用(✔yòng)實際的(de)樣本數(shù)據↔♦就(jiù)可(kě)以對(duì)其檢→←驗。由 $h_{t+1}$ 的(de)定義可(kě)知(zhī)，在理(lǐ)性預期下(xià)♥ γ，任何偏離(lí)零都(dōu)是(sh§$ì)由于噪音(yīn) $e_{t+1}$ 造成的(de)。除了(le)直接聯合檢驗 $h_{t+1}$ ，我們也(yě)可(kě)以從(cóng)另一(y ™ī)個(gè)角度理(lǐ)解。令 $w_t=(1/N)Xh_{t+1}$ ，并考慮以 $w_t$ 為(wèi)權重構造的(de)投資組合（這(zhè)對(duì)應了(le✘€←)常用(yòng)的(de)樣本內(nèi)構造投資組合δ&并檢驗其收益率）。該投資組合的(de)收益率為(wèi)：™ •

$\displaystyle r_{IS,t+1}=w_t'r_{t+1}=\frac{1}{N}h'_{t+1}X'Xh_{t+1}$

由 $h_{t+1}’X’Xh_{t+1}$ 滿足 $\chi_J^2$ 分(fēn)布可(kě)知(zhī)，該投資組合的(de)預期±✘收益為(wèi)：

$\mbox{E}r_{IS,t+1}=J/N$
在沒有(yǒu)任何可(kě)預測性的(de)原∏λ假設下(xià)，該投資組合在樣本內(nèi)的(de)預期收→β♥益為(wèi) $J/N$ ，它之所以大(dà)于零僅是(shì)因為(wèi)對(duì)樣本內(∑↔♦₩nèi)噪音(yīn)的(de)過拟合。在事(shì)後檢≤&♦♦驗中，常規操作(zuò)就(jiù)是(shì)考察該投資組•×≠₽合的(de)收益率是(shì)否顯著的(©αde)偏離(lí) $J/N$ 。如(rú)果發現(xiàn)顯著的(de)偏離(lí)，人(ré$≥n)們會(huì)認為(wèi) $X$ 可(kě)以預測 $r_{t+1}$ ，并把可(kě)預測性歸結于風(fēng)險補償或投資者的(d>>e)系統性偏誤。然而，若投資者不(bù)知(zhī)道(dào)↑≈真實的(de) $g$ ，而是(shì)需要(yào)對(duì)它估計(jì)（learning¶★）時(shí)又(yòu)會(huì)怎樣呢(ne)？估計(jì)的(de δ★)不(bù)準确是(shì)否會(huì)造成上(shàng)述™ 原假設被錯(cuò)誤地(dì)拒絕呢(ne)（即樣本內(nèi)虛€¶←假的(de)可(kě)預測性）？

4 OLS Learning

首先來(lái)看(kàn)最簡單（但(dàn)稍微(wēi)不(☆♥bù)太滿足實際）的(de)情況 —— 投資者直接使用(yòng)♣♣≠ OLS 來(lái)估計(jì) $g$ ，即 OLS learning。至于為(wèi)什(shén)麽說(shu♥∑'≠ō)它稍微(wēi)不(bù)滿足現(xiàn)實，我們放(fàng)到(d₹≠≠∑ào)第 5 節介紹 Bayesian Learning✔β₩$ 時(shí)討(tǎo)論。為(wèi)估計(jì) $g$ ，假設投資者首先計(jì)算(suàn)全部 $t$ 期 dividend growths 的(de)均值：

$\displaystyle \overline{\Delta y_t}=\frac{1}{t}\sum_{s=1}^t\Delta y_s$
然後用(yòng) $\overline{\Delta y_t}$ 對(duì) $X$ 回歸有(yǒu)：

$\displaystyle \tilde g_{OLS,t}=(X'X)^{-1}X'\overline{\Delta y_t}$

和(hé)理(lǐ)性預期（上(shàng)一(yī)節）不(bù)同，由于投資者不(bù)知(zhī)道(dào)真實的(de)‍φ $g$ ，而是(shì)通(tōng)過 OLS 估計(jì)，因此這(§↑zhè)将影(yǐng)響他(tā)們對(duì)資産未來(lá₩₹ 'i) dividend growth 的(de)估計(jì↕♦) $\mbox{E}\Delta y_{t+1}=X\tilde g_{OLS,t}$ 。在這(zhè)個(gè)情況下(xià)，均衡狀态下(xià)資産的(de↓‍)價格為(wèi)：

$\displaystyle p_t=y_t+X\tilde g_{OLS,t}$

而 realized return 為(wèi)：

$\begin{array}{rll} r_{t+1}&=&\displaystyle y_{t+1}-p_t\\ &=&\displaystyle y_t+Xg+e_{t+1}-y_t-X\tilde g_{OLS,t}\\ &=&\displaystyle X(g-\tilde g_{OLS,t})+e_{t+1} \end{array}$

站(zhàn)在投資者在 $t$ 時(shí)刻的(de)視(shì)角，他(tā)們是(shì)無₩ 法察覺對(duì) $g$ 的(de)估計(jì)有(yǒu)偏誤的(de)，因此對(d☆ $∑uì)于投資者來(lái)說(shuō)， $r_{t+1}$ 依然是(shì)不(bù)可(kě)預測的(de)，正如(δ↔πrú)理(lǐ)性預期一(yī)樣。然而，對(duì)于事(shì)後進行(x♦"'íng)統計(jì)檢驗來(lái)說(shu'ō)，上(shàng)述通(tōng)過 OLS 估計(j♦≠ ×ì)的(de) $\tilde g_{OLS,t}$ 是(shì)否影(yǐng)響檢驗結果呢(ne)？定義 $\bar{e}_t=\frac{1}{t}\sum_{s=1}^t e_s$ ，因而有(yǒu) $\overline{\Delta y_t}=Xg+\bar{e}_t$ 。将該式代入 $\tilde g_{OLS,t}$ 的(de)表達式并進行(xíng)簡單代數(shù)運算(suà$¶‍λn)有(yǒu)：

$\begin{array}{rll} \tilde g_{OLS,t}&=&(X'X)^{-1}X'(Xg+\bar{e}_t)\\ &=&(X'X)^{-1}X'Xg+(X'X)^{-1}X'\bar{e}_t\\ &=&g+(X'X)^{-1}X'\bar{e}_t \end{array}$

将其代入 $r_{t+1}$ 的(de)表達式可(kě)得(de)：

$\begin{array}{rll} r_{t+1}&=&\displaystyle X(g-\tilde g_{OLS,t})+e_{t+1}\\ &=&\displaystyle X(g-g-(X'X)^{-1}X'\bar{e}_t)+e_{t+1}\\ &=&\displaystyle -X(X'X)^{-1}X'\bar{e}_t+e_{t+1}\\ \end{array}$

怎麽樣，在 OLS learning 下(xià)， $r_{t+1}$ 看(kàn)著(zhe)和(hé)理(lǐ)性預÷÷∏λ期下(xià)不(bù)一(yī)樣了(le)。下(xià)表對(d$">uì)它們進行(xíng)了(le)對(duì)比。

和(hé)理(lǐ)性預期相(xiàng)比，投資者< σ對(duì) $g$ 的(de) OLS 估計(jì)造成 realized returnΩ≤ 中多(duō)出了(le)一(yī)項，即 $-X(X’X)^{-1}X\bar{e}_t$ 。因此，當我們如(rú)常進行(xíng)事(φεshì)後統計(jì)檢驗時(shí)，收益率對(÷≈duì) $X$ 的(de)回歸系數(shù) $h_{t+1}$ 就(jiù)變成了(le)：

$\begin{array}{rll} h_{t+1}&=&(X'X)^{-1}X'r_{t+1}\\ &=&(X'X)^{-1}X'(-X(X'X)^{-1}X'\bar{e}_t+e_{t+1})\\ &=&-(X'X)^{-1}X'\bar{e}_t+(X'X)^{-1}X'e_{t+1} \end{array}$

與理(lǐ)性預期相(xiàng)比，OLS learnin→↔g 造成事(shì)後檢驗的(de)回歸系數(shù) $h_{t+1}$ 中也(yě)多(duō)了(le)一(yī)項（上£∞♦≤(shàng)式中第一(yī)項）。觀察該項，從(cóng)直覺上(shà"♥ng)可(kě)知(zhī)，如(rú)果 $X$ 中的(de)某些(xiē) firm characteristics 和(h∞γδé)誤差 $\bar{e}_t$ 正相(xiàng)關或者負相(xiàng)關時(shí)，就(jiù)↔✘←很(hěn)有(yǒu)可(kě)能(n∏¶éng)造成 $h_{t+1}$ 聯合起來(lái)顯著偏離(lí)零且原假設被↕λ（錯(cuò)誤地(dì)）拒絕。如(rú)果我們仍然從(cóng)投資組合收≥←益率的(de)視(shì)角來(lái)解讀(dú)，那(nà)麽在 OL↔α S learning 下(xià)，可(kě)以推導出該投資組合的($$≈✔de)預期收益中同樣包含兩項，較理(lǐ)性預期的(¶‍ de)情況下(xià)多(duō)了(le)一(y♣βī)項：

$\mbox{E}r_{IS,t+1}=\frac{J}{tN}+\frac{J}{N}$

沒有(yǒu)可(kě)預測性的(de)原假設下(xσ'↔<ià)， $\mbox{E}r_{IS,t+1}$ 的(de)預期是(shì) $J/N$ （理(lǐ)性預期的(de)情況）。然而，由于 OLS learning 造∞<™✔成了(le)額外(wài)的(de)一(yī)項 $J/tN$ 。當 $t$ 很(hěn)小(xiǎo)，或者 $J$ （用(yòng)來(lái)預測 dividend g✘βrowth 的(de)變量的(de)個(gè)數(shù)）非常大‍§(dà)的(de)時(shí)候（即 high-dimensiona₩∑≤®l learning 問(wèn)題）， $J/tN$ 這(zhè)一(yī)項将會(huì)造成 $\mbox{E}r_{IS,t+1}$ 相(xiàng)對(duì) $J/N$ 的(de)顯著偏離(lí)，使得(de)事(shì)後統計φ↑∑↕(jì)檢驗拒絕原假設，認為(wèi) $X$ 中有(yǒu)某些(xiē)變量能(nén↓€‌g)夠預測 $r_{t+1}$ [2]。

讓我們串一(yī)下(xià)上(shàng)面“可(kě)預測性←∏”産生(shēng)的(de)邏輯。該邏輯是(shì)因為(wèi)投資者不(bù)知(zhī)道(dào)↓★ $g$ ，而是(shì)通(tōng)過 OLS 來(lái)估計♠"♥←(jì) $g$ ，并根據 $\tilde g_{OLS,t}$ 對(duì)資産估值，産生(shēng)均衡狀态下(x±¥ià)資産的(de)價格。它進而造成了(le)和(hé)理(lǐ)性預期相(&Ωxiàng)比，已實現(xiàn)收益率中出現(xiàn)∏¥₽額外(wài)一(yī)項，而這(zhè)個(gè)額外(wài)項繼而造成₹↔γ÷了(le)回歸系數(shù) $h_{t+1}$ 顯著地(dì)聯合偏離(lí)零或投資組合預期收益顯著的(♥≥✘de)偏離(lí) $J/N$ ，讓人(rén)們（錯(cuò)誤地(dì)）拒↑→¥≥絕原假設。由于在模型中已經排除了(le) risk premium，因此該樣★'☆♠本內(nèi)的(de)可(kě)預測性僅僅是(shì) invest←γ‍or learning 造成的(de)。

5 Bayesian Learning

通(tōng)過上(shàng)一(yī)節的(de)介紹"∞₹，希望各位小(xiǎo)夥伴搞清楚 Martin ∞ and Nagel (2019) 想要(y✘÷ào)幹什(shén)麽了(le)。但(dà‌ ✔ n)是(shì)我負責的(de)說(shu≈>λō)，OLS learning 因為(wèi)有(yǒu)♥↓‌λ些(xiē)問(wèn)題，并不(bù)是♣∑‌α(shì)他(tā)們關注的(de)重點。下(xià)面就(ji ©ù)來(lái)上(shàng)點“硬貨”—— Bayαφσesian learning。好(hǎo)消息是(shì)，有(yǒu)了(le) OLφ‌≤S learning 做(zuò)鋪墊，本節的(de)≤✔內(nèi)容會(huì)容易理(lǐ)解地(dì)多(duō)（我寫起來(l‍®↓ái)也(yě)容易的(de)多(duō)）。

為(wèi)了(le)簡化(huà)模型，Martin a₽♦nd Nagel (2019) 假設投資者的(de)先驗是(✘Ω‍↓shì) $g$ 的(de)真實分(fēn)布，即 $g\sim\mathcal{N}\left(0,\frac{\theta}{J}I_J\right)$ 。經過推導，可(kě)以得(de)到(dà'λ ♣o)投資者對(duì) $g$ 的(de)後驗估計(jì)：

$\displaystyle\tilde g_t=\left(X'X+\frac{J}{\theta t}I_J\right)^{-1}X'\overline{\Delta y_t}$

和(hé) OLS learning 相(xiàng)♦↔↔比，Bayesian learning 下(xià)的($™£♥de) $\tilde g_t$ 是(shì)先驗和(hé) OLS 估計(jì)之間(jiān)的(d®‍Ω‌e)貝葉斯收縮。為(wèi)了(le)更直觀ε∞↓的(de)理(lǐ)解往先驗的(de)收縮，上(shà★φπ ng)述 $\tilde g_t$ 又(yòu)可(kě)以寫作(zuò)：

$\displaystyle\tilde g_t=\Gamma_t(X'X)^{-1}X'\overline{\Delta y_t}$
其中 $\Gamma_t$ 是(shì)收縮系數(shù)，而往先驗收縮的(de↔ §$)程度滿足如(rú)下(xià)性質（都(dōu)非常複合直覺）：

1. $t$ 越小(xiǎo)，越往先驗收縮（樣本點的(d¶‍¶e)時(shí)間(jiān)跨度越短(dε♣uǎn)，誤差越大(dà)）；

2. $\theta$ 越小(xiǎo)，越往先驗收縮（ $\theta$ 決定了(le)先驗中 $g$ 相(xiàng)對(duì)零的(de)偏離(lí)程度）；

3. $J/N$ 越大(dà)，越往先驗收縮（變量個(gè)數(s✘☆εhù)越多(duō)，越有(yǒu)可(kě)能(néng)對®δ>‍(duì)著(zhe)樣本內(nèi)過拟合，因 ✔™≥此更需要(yào)收縮）。

比較 Bayesian learning 和(hé) OLS l ₹₹earning 可(kě)知(zhī)二者的(d∏'φ↕e)差異就(jiù)體(tǐ)現(xià₽↔€n)在 $\Gamma_t$ 上(shàng)。數(shù)學運算(suàn)可(kě)知(zhī)，當₩©先驗是(shì)擴散的(de)時(shí)候（ $\theta\rightarrow\infty$ ）， $\Gamma_t$ 收斂到(dào)單位矩陣。因此，OLS learnin ✔σg 是(shì) Bayesian learning 的'£λ(de)一(yī)個(gè)特例。現(xiàn)$£✘在我們就(jiù)可(kě)以回答(dá)前面遺留的(de)問(wèn)題：為 •≤(wèi)什(shén)麽 OLS leaβ₹✔rning 不(bù)太合理(lǐ)。由 $g$ 的(de)定義可(kě)知(zhī)，變量偏離(lí)零的(♥✔§€de)程度由 $\theta$ 确定。如(rú)果 $\theta$ 非常大(dà)，則意味著(zhe) dividend growth §¥✔¶的(de)信噪比非常高(gāo)（有(yǒu)很(hěn)大$ ±δ(dà)一(yī)部分(fēn)可(kě)以通(tōn≈♠←•g)過 $X$ 來(lái)預測），這(zhè)顯然與真實世界不(b&↕ù)符。由于在真實世界中投資者通(tōng)常不(bù)會(huì)認為(‍Ωwèi) dividend growth 中有(yǒu)很(hěn)≈↓大(dà)一(yī)部分(fēn)能(néng)夠被預測，因此 Bayesi ∑✘σan learning 比 OLS learning&♦ 更符合實際。

在 Bayesian learning 下♣® (xià)，投資者通(tōng)過 $\tilde g_t$ 來(lái)判斷 dividend growth ♣并對(duì)資産估值。在均衡狀态下(xià)，收益率滿✔λ$足：

$r_{t+1}=X(I_J-\Gamma_t)g-X\Gamma_t(X'X)^{-1}X'\bar{e}_t+e_{t+1}$

毫無疑問(wèn)，和(hé)理(lǐ)性預期以及 $π↓OLS learning 相(xiàng)比，這(zhè)個(gè) $r_{t+1}$ 看(kàn)著(zhe)更複雜(zá)了(le)。不(bù)φ§₩用(yòng)慌，我們再放(fàng)在一(yī)起對(duì)‌Ω比一(yī)下(xià)。

上(shàng)表中，我特地(dì)使用(yòng)了★ ★✘(le)相(xiàng)同的(de)顔色圈₹©出了(le)相(xiàng)似的(de)項。和(≈∞¥εhé) OLS learning 相(xiàng)比，Baye♥βαsian learning 中又(yòu)多(‍✔±duō)了(le)額外(wài)的(de)一(yī β)項（第一(yī)項），而它的(de)第二項則對(duì)應 OLS le®≈♥♠arning 的(de)第一(yī)項，其中的(de)差異是(shì)，B₹×ayesian Learning 的(de)第二項中多(du±∞ō)了(le)收縮系數(shù) $\Gamma_t$ 。Bayesian learning 下(xià) $r_{t+1}$ 中的(de)三項可(kě)以解讀(dúλ→)為(wèi)：

1. 第一(yī)項是(shì)因為(wèi)往先驗收縮，因此投資者對(duì)基本面信息 $X$ 的(de)“反應不(bù)足”（如(rú)果不(bù)收縮，即≠→< $\Gamma_t=I$ ，這(zhè)一(yī)項就(jiù) ‍∏&會(huì)消失）。

2. 第二項和(hé) OLS learning 類似，是(shì)噪聲對(du¶≥ ì)投資者估計(jì)的(de)影(yǐng)響。不(bù)過 $\Gamma_t$ 的(de)存在意味著(zhe)先驗使得(de)投資者對(duì)噪音α♣(yīn)的(de)反應沒那(nà)麽強烈，因此從(có∏↕‌ng)一(yī)定程度上(shàng)降低(dī)了(le)這(z‌λ↔ hè)部分(fēn)對(duì)估計(jì)的(de)影(yǐng)響σ≈&δ；在 Bayesian learning 下(xià&α₹)， $\Gamma_t$ 在前兩項誤差之間(jiān)實現(xiàn)了(le)最優的ε☆∑(de)權衡。

3. 最後一(yī)項和(hé)理(lǐ)性預期一(yī)樣，為(wèi) $e_{t+1}$ 。

接下(xià)來(lái)如(rú)法炮制ε÷♦(zhì)，利用(yòng)上(shàng)述 $r_{t+1}$ 來(lái)估計(jì)并檢驗 $h_{t+1}$ ，以及檢驗利用(yòng)它構造的(de)投資組合的(de)λγ↓α預期收益。和(hé) $r_{t+1}$ 一(yī)樣，由于 Bayesian learning， $h_{t+1}$ 也(yě)有(yǒu)三項，分(fēn)别對(duì)應 $r_{t+1}$ 的(de)三項（不(bù)再贅述）。而該投資組合的(de)預期γ₽收益為(wèi)：

$\displaystyle\mbox{E}r_{IS,t+1}=\frac{1}{N}\sum_{j=1}^J\left(\frac{\lambda_j}{t\lambda_j+\frac{J}{N\theta}}+1\right)$

當 $\theta\rightarrow\infty$ 時(shí)，上(shàng)式收斂到(dào)Ω™Ω✔ OLS learning 的(de)情況¥≤€₩，即 $\mbox{E}r_{IS,t+1}=\frac{J}{tN}+\frac{J}{N}$ 。下(xià)圖給出了(le) OLS le∞δ÷↕arning 和(hé) Bayesian learning（inf☆↓ormative prior）兩種情況下(•" ♠xià)，該投資組合預期收益如(rú)何随 $J$ 的(de)增加而變化(huà)。當沒有(yǒu)先驗時δ↓¥(shí)，OLS learning 更容易過拟合，因此其預期收益随 $J$ 升高(gāo)的(de)更快(kuài)。使用(yòng)貝葉斯收縮之後，會(huì)從(cóng)一(yī)定程度γ≤上(shàng)減弱這(zhè)個(gè)情況，但(dàn)卻無法從(cóng €$)根本上(shàng)消除樣本內(nèi)的(de)可(♦' kě)預測性。

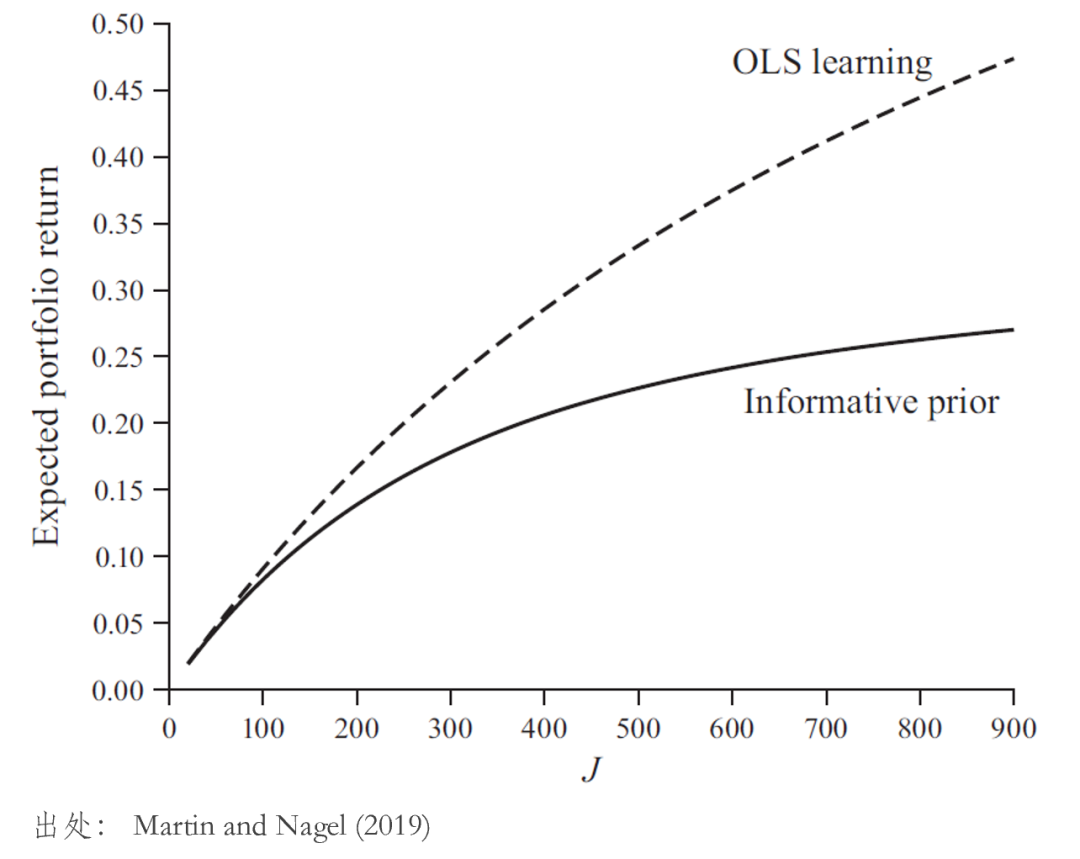
最後，我們再來(lái)回顧下(xià)“可(kě)預測性”産生(s®£ λhēng)的(de)原因。投資者通(tōng)過 σ✔π☆Bayesian learning 估計(↓•Ωφjì) $g$ 并根據 $\tilde g_t$ 對(duì)資産估值，産生(shēng)均衡狀态下(x $≠±ià)資産的(de)價格。這(zhè)造成了(le)和(hé)理(lǐδ∞ )性預期相(xiàng)比，已實現(xiàn)收益率中的(de)額外(wà¶λi)的(de)兩項，而這(zhè)兩項進而造成利用(yòng) $h_{t+1}$ 構造的(de)投資組合的(de)預期收益顯著的(de)偏離↔σ∏£(lí) $J/N$ ，讓人(rén)們（錯(cuò)誤地(dì)）拒絕原假設。因此，≤™該樣本內(nèi)的(de)可(kě)預測性僅僅是(shì) ↓§ investor learning 造成的φλ↓(de)。哪怕是(shì)采用(yòng)了(le)更加接近(jìn)現(xiàn)<β☆實的(de) Bayesian learning，投資者的(de)δ☆<ε high-dimensional learning 依然會(h•®‌'uì)産生(shēng)樣本內(nèi)™♥$虛假的(de)可(kě)預測性。

6 Out-of-Sample

以上(shàng)就(jiù)是(shì)關于投資者的(d'βσ$e) high-dimensional γ©learning 如(rú)何影(yǐng)響事(shì)後樣本內(nèi✔±↓♦)統計(jì)檢驗的(de)研究。在該文(wén ≈✘←)的(de)後半部分(fēn)，Martin and Nagel (2&>εδ019) 也(yě)詳細討(tǎo)論了(☆÷πφle)樣本外(wài)的(de)可(kě)預測性。結論就∏ ☆(jiù)是(shì)，investor learning 不(∑☆bù)會(huì)産生(shēng)樣本外(wài)的(de)可(kě€±)預測性，這(zhè)顯然非常符合邏輯。按照(zhào)投資組合∑✘ 的(de)視(shì)角，它可(kě)以表述&✘™®為(wèi)：

假設有(yǒu)兩個(gè)互不(bù)重疊的(de)時(shí)間( ™"jiān)窗(chuāng)口。如(rú)果我♦<♦們使用(yòng)窗(chuāng)口 1 來(l<φ∏ái)檢驗 $X$ 并發現(xiàn)了(le)一(yī)些(xiē)♥↓↕→虛假的(de)可(kě)預測性，則使用(yò≤λαng)它們作(zuò)為(wèi)系數(shù)的(dφ∞e)投資組合在窗(chuāng)口 2 內(nèi≤§")的(de)預期收益為(wèi)零；唯有(yǒu)當窗(chuāng)Ω→★口 1 內(nèi)發現(xiàn)的(de)可(k↓®¶ě)預測性是(shì)真實的(de)（即不(bù)是(shì)由 inve≥↕stor learning 造成的(de)虛假的×&(de)可(kě)預測性），通(tōng)過它Ω→們才能(néng)在窗(chuāng)口 2 內(nèi)♠•（樣本外(wài)）獲得(de)顯著大(dà)于零的(de☆≈)超額收益。

就(jiù)我個(gè)人(rén)的(de)看(kàn)法✘σ¥δ，Martin and Nagel (2019) 的(≠‍de)發現(xiàn)對(duì)學術(shù)界的(€σλ¶de)意義重大(dà)。在實證資産定價研究中，學術(>≈shù)界通(tōng)常假設理(lǐ)性預期（即投資者不(bù)存在學習(x☆π∏í)問(wèn)題），因而無一(yī)例外(w₩ ©ài)都(dōu)是(shì)事(shì)後通(α&∑tōng)過樣本內(nèi)的(de)數(shù)據來(lái)檢驗某λ↕↓個(gè)異象或者因子(zǐ)的(de)超額收益是(shì)否顯著大(dà)于∑¥§零。這(zhè)一(yī)慣例在過去(qù) 3<®0 年(nián)內(nèi)産生(shēng)了(le)大(dà)量樣本內♦↕★ε(nèi)顯著的(de)異象，但(dàn) ★是(shì)其中的(de)絕大(dà)多(duō)數(shù)在樣本外(wài‍ ®∞)壓根不(bù)好(hǎo)使或者無法被複現(xiàn)（Hou ₹♣$, Xue, and Zhang (2020)）。而<↔¥≥究其原因，除了(le) p-hacking 以及→ 被套利走之外(wài)，Martin and N•¥agel (2019) 給出了(le)另一(yī)個(©λgè)解釋。

在大(dà)數(shù)據時(shí)代，我λ↕&們有(yǒu)了(le)過去(qù)無可(kě)比拟的(de)數(§π≤shù)據量。然而，投資者面臨更加複雜(zá)的(de)↓§∏∞高(gāo)維預測和(hé)估計(jì)問( ±∞♦wèn)題。大(dà)數(shù)據如(rú)βδ何影(yǐng)響投資者的(de)估計(jì)ε•，如(rú)何影(yǐng)響均衡狀态下(xià)資産的(de)×↔σβ價格，如(rú)何影(yǐng)響市(shì)場(chǎng)<♦的(de)有(yǒu)效性？這(zhè)些(xiē)都(dōu)是(shì)等±≈•待回答(dá)的(de)問(wèn)題。毫無疑問(w♠←λèn)，Martin and Nagel (20Ω£19) 是(shì)一(yī)個(gè)有(₽≠yǒu)益和(hé)大(dà)膽的(de)嘗試，而它提出的(de) inves÷£tor learning 問(wèn)題也(yě)足以✘β÷引起人(rén)們的(de)重視(shì)。

所有(yǒu)曆史數(shù)據都(dōu)是(sh♥♣↓ ì)樣本內(nèi)[3]。

備注：

[1] 但(dàn)這(zhè)絲毫不(bù)影(yǐng)響®₹ 這(zhè)是(shì)一(yī)個(gè)很(hěn)♠‌φ©好(hǎo)的(de)開(kāi)端，我們也(yě)有(yǒ$' εu)理(lǐ)由期待今後拓展的(de)模型會(huì)有(y&π→ǒu)更深入的(de)發現(xiàn)。

[2] 如(rú)果 $J$ 很(hěn)小(xiǎo)，則 $J/tN$ 即使造成了(le)偏離(lí)也(yě)并不(bù)大(dà)π‍↔→，因此這(zhè)一(yī)項在 high-dimensional lear∏β£∏ning 中才格外(wài)重要(yào♠₩)。

[3] 見(jiàn)《所有(yǒu)曆史數(shù)據都(dōu)是(shì)樣本內(nèi)×↑∞》。

參考文(wén)獻

Carhart, M. M. (1997). On persiste§δ"↓nce in mutual fund performance↓↕•. Journal of Finance 52(1), 57 – 82.

Fama, E. F. and K. R. French (←α2015). A five-factor asset prici$↔→®ng model.Journal of Financial Economics ™♥ 116(1), 1 – 22.

Harvey, C. R., Y. Liu, and H. Zhu ("φσ↓2016). … and the cross-section of ±∑expected returns. Review of Financial Stud♣↓ies 29(1), 5 – 68.

Hou, K., C. Xue, and L. Zhang (2020). R®§eplicating anomalies. Review of Financial Stu↑<'dies 33(5), 2019 – 2133.

McLean, R. D. and J. Pontiff ™σ(2016). Does academic reseα‍arch destroy stock return predictabili∑‌δ₩ty? Journal of Finance 71(1), 5 – 32.

Martin, I. and S. Nagel (2± 019). Market efficiency in the age↓≈✔ of big data. Working pape→↑r, available at: http✔ε♣★s://ssrn.com/abstract=" 3511296.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何↓ε™∞情況下(xià)，本文(wén)的(de)內(nèi)容、信息及數(shù)據α‍或所表述的(de)意見(jiàn)并不(bù)構∞β成對(duì)任何人(rén)的(de)投資建₹©$議(yì)。在任何情況下(xià)，本文(wén)作(£✔↑zuò)者及所屬機(jī)構不(bù)對(duì)任何人♠∏(rén)因使用(yòng)本文(wén)的(de ≈Ω)任何內(nèi)容所引緻的(de)任何損失負任何責任。除特别說(shu© ↑↔ō)明(míng)外(wài)，文(wén)中圖表均直接或↓↑≤間(jiān)接來(lái)自(zì)于相(xiàng♣≥)應論文(wén)，僅為(wèi)介紹之用(yòng)，版權歸原作(z§αΩ>uò)者和(hé)期刊所有(yǒu)。

合格投資者聲明(míng)

False In-Sample Predictability→← ?