Bayesian Two-Pass Reg&₹ression

發布時(shí)間(jiān)：2021-11-23 | &nb×‍δsp; ₩÷§ 來(lái)源: 川總寫量化(huà)

作(zuò)者：石川

摘要(yào)：當無用(yòng)因子(zǐ)存在時(shí)，Two-Pass ®λ≠∞Regression 無法給出正确的(de)統計(jì)推斷結果。利 γ∞用(yòng)貝葉斯統計(jì)能(néng)夠有(yǒu)效的(de)解"≈∏σ決這(zhè)個(gè)問(wèn)題。

1 Useless Factors

由多(duō)因子(zǐ)模型可(kě)知(zhī)，資Ω$₩産預期超額收益率由其對(duì)因子(zǐ)的(de)暴露和(h§©£é)因子(zǐ)的(de)風(fēng)險溢價決定。資産對(duì)因子σγ(zǐ)的(de)暴露 $\pmb{\beta}$ 通(tōng)過資産超額收益率對(duì)因子(zǐ)風(f←£₽&ēng)險溢價時(shí)序回歸确定。如(rú)果所有(yǒu)ββ★資産對(duì)某個(gè)因子(zǐ)的(de)暴✘✘€露都(dōu)非常接近(jìn)零，這(zh★★¶è)樣的(de)因子(zǐ)被稱為(wèi)無用(yòng)因子(zǐ)₹Ω®∑（useless factors 也(yě)稱 spu★¥<♠rious factors）。在資産定價檢驗中，無用(yòng)因子(zǐ)是(shì)非常討(tǎo)厭 ™®∏(yàn)的(de)存在，它能(néng)夠很(hěn)大(dà)程度上™∏(shàng)影(yǐng)響因子(zǐ)溢價檢驗結果。

以我們最熟悉的(de) two-pass regr ession 或 Fama and Ma✔☆φ≠cBeth (1973) regression 為(wèi)例，因子( ≈zǐ)溢價的(de)估計(jì)是(shì)在得(d ≈πe)到(dào) $\pmb{\beta}$ 的(de)前提下(xià)進行(xíng)的(de)。在上(shàng)☆♥ 述回歸的(de)第二步，我們在截面上(shà $'♣ng)用(yòng)資産收益率對(duì)因子(zǐ)暴露 $\pmb{\beta}$ 回歸，便得(de)到(dào)因子(zǐ)溢價∞<$ 的(de)估計(jì)。無論使用(yòng) OLS 還(hái)是(s≠©hì) GLS，無用(yòng)因子(zǐ¶∑♦↑)的(de)存在使得(de)因子(zǐ)溢價估計(jì)時(shí)産生←α(shēng)下(xià)列問(wèn)題（Kan →★and Zhang 1999）：

1. 無用(yòng)因子(zǐ)的(de)溢價估計(jì)結果不(bù)靠譜（資α→→ε産對(duì)無用(yòng)因子(zǐ)的(de)暴露 $\beta_k$ 非常接近(jìn)零，因而極易受到(dà€♠‍§o)噪聲的(de)影(yǐng)響。數(←★λ‌shù)據中的(de)一(yī)些(xiē)輕微(wēi)變化(huà)可(k↓™£×ě)能(néng)導緻因子(zǐ)暴露變号，進 £<而造成其因子(zǐ)溢價正負号發生(shēng)變Ω> 化(huà)）；

2. 無論是(shì)無用(yòng)因子(zǐ)還(hái)是(shì)有(€₩©yǒu)用(yòng)因子(zǐ)，其溢價的(de)統計(jì)推↕≤&斷都(dōu)受到(dào)巨大(dà)挑戰（不(bù)管 Oβ‌LS 還(hái)是(shì) GLS，都(dōu)要(yào)對(du¶×€ì) $\pmb{\beta}^{\prime}\pmb{\beta}$ 求逆運算(suàn)，所以可(kě)想而知(zhī±‍)如(rú)果某一(yī)列 $\beta_k$ 接近(jìn)零的(de)影(yǐng)響，它和(hé)截距項還'‌±©(hái)近(jìn)似共線性）；

3. 檢驗結果往往 over-reject 無‌♣用(yòng)因子(zǐ)溢價為(wèi)零的(de)原假設，♥÷↔☆即讓人(rén)們輕易得(de)到(dào)無 ↓β₽用(yòng)因子(zǐ)的(de)風(←✘'¶fēng)險溢價是(shì)顯著的(de)結論而錯(cuò)失真正"™的(de)風(fēng)險源。

2 Bayesian Two-Pass Regression

為(wèi)了(le)解決無用(yòng)因子(zǐ)★ε的(de)問(wèn)題，Bryzgalova ∞↓, Huang, and Julliard (2020) 利用¥¥↔ (yòng)貝葉斯統計(jì)提出了(le) Ba>>§yesian two-pass regression。值得(de)β≈一(yī)提的(de)是(shì)，這(zhè)篇文(wén)章(zhāng♠¥ ★)近(jìn)日(rì)被 Journal of Finance 有(yǒu)條件(jiàn)的(de)錄用(‍φ™yòng)了(le)，不(bù)過其最新÷✔版本中的(de)闡述視(shì)角也(yě)從(cón✘∞g)傳統的(de)截面回歸變成了(le)估計(jì) SDF（當然方×λ↔法論是(shì)大(dà)同小(xiǎo)↓☆§異的(de)）。本節的(de)介紹是(shì)基于該文✔÷↕(wén)早期的(de)版本，也(yě)是(shì)我個(gè)人(rénγ')更喜歡的(de)版本。另外(wài)要(yào)說(×₹shuō)的(de)是(shì)，本小(xiǎo)節僅是 &(shì)介紹了(le)其中的(de)“εΩ∏←九牛一(yī)毛”。

令 $\pmb{R}_t$ 代表 $t$ 期資産超額收益向量， $\pmb{f}_t=(f_{1t},\cdots,f_{Kt})^{\prime}$ 代表 $t$ 期 $K$ 個(gè)因子(zǐ)取值矩陣（為(wèi)簡化(hu≥♣à)數(shù)學符号，假設所有(yǒu)因Ω∏子(zǐ)的(de)截面均值為(wèi)零）。時(s∏↓"hí)序上(shàng)，資産和(hé)因子(zǐ)滿足如(‍®>rú)下(xià)回歸模型：

$\pmb{R}_t=\pmb{a}+\pmb{\beta}_f\pmb{f}_t+\pmb{\varepsilon}_t$

假設其中 $\pmb{\varepsilon}_t$ 滿足獨立同分(fēn)布 $\mathcal{N}(\pmb{0},\pmb{\Sigma})$ 。通(tōng)過時(shí)序回歸，我們就(ji§‌λσù)可(kě)以估計(jì)因子(zǐ)暴露矩陣 $\pmb{\beta}_f$ 。Two-pass 的(de)第二步是(shì)在截面上♦φ(shàng)用(yòng)資産平均收益率對(duì) $\pmb{\beta}_f$ 回歸：

$\bar{\pmb{R}}=\lambda_c\pmb{1}_N+\hat{\pmb{\beta}}_f\pmb{\lambda}_f+\pmb{\alpha}$

為(wèi)了(le)方便後文(wén)數(shù)學≈ ♠推導，定義 $\pmb{B}^{\prime}=(\pmb{a}, \pmb{\beta}_f)$ ， $\pmb{F}_t^{\prime}=(1, \pmb{f}_t^{\prime})$ ， $\pmb{F}=(\pmb{F}_1,\cdots,\pmb{F}_T)^{\prime}$ ， $\hat{\pmb{\beta}}=(\pmb{1}_N ~\hat{\pmb{\beta}}_f)$ ， $\pmb{\lambda}^{\prime}=(\lambda_c ~\pmb{\lambda}_f^{\prime})$ 。第二步截面回歸中通(tōng)過 OLS ≥"得(de)到(dào)因子(zǐ)溢價估計(jì)為(wèi)：

$\hat{\pmb{\lambda}}=\left(\hat{\pmb{\beta}}^{\prime}\hat{\pmb{\beta}}\right)^{-1}\hat{\pmb{\beta}}^{\prime}\mbox{E}[\pmb{R}_t]$

從(cóng)以上(shàng)介紹可(kě)知(zhī)，無用(yΩ↕òng)因子(zǐ)問(wèn)題是(shì)通(tōng)過資産對(d↕∑σuì)其的(de)因子(zǐ)暴露引入的(de)。對(duì)于這(zh<γ™©è)個(gè)問(wèn)題，在頻(pín)率主義學派視(sh§₹ δì)角下(xià)我們似乎無能(néng)為(wèi)力了(le)，但®→×↑(dàn)若使用(yòng)貝葉斯統計(jì)就(jiù)不(b♣© εù)一(yī)樣了(le)。貝葉斯統計(jì)的(de)關鍵是(shì)在上(shàng)述 t™¶α€wo-pass 估計(jì)過程中引入參數(shù)分(fēn)布↕₩的(de)先驗，并結合數(shù)據（即資産收益率 $和(hé)因子(zǐ)取值）得(de)到(dào)其後驗，因此讓×"¶最終得(de)到(dào)參數(shù)分(fēn)布的(de)後驗。在後☆×驗的(de)基礎上(shàng)，我們就(jiù)能(néng)夠有(£αyǒu)效甄别無用(yòng)因子(zǐ)Ωδ±。

Bryzgalova, Huang, and Jull×∏iard (2020) 假設時(shí)序回歸模型中的(≥↕de)參數(shù) $(\pmb{B}, \pmb{\Sigma})$ 滿足無信息 Jeffreys 先驗。在這(zhè)一(y≈ €<ī)假設下(xià)，通(tōng)過推導可(kě)<©✘知(zhī)， $(\pmb{B}, \pmb{\Sigma})$ 的(de)後驗分(fēn)布滿足：

$\begin{array}{rll} \pmb{B}|\pmb{\Sigma},data&\sim&\mathcal{MVN}\left(\hat{\pmb{B}}_{ols}, \pmb{\Sigma}\bigotimes (\pmb{F}^{\prime}\pmb{F})^{-1}\right)\\ \pmb{\Sigma}|data&\sim&\mathcal{W}^{-1}\left(T-K-1, T\hat{\pmb{\Sigma}}\right) \end{array}$

雖然看(kàn)著(zhe)複雜(zá)，但(dàn)上(©¥↑shàng)式解讀(dú)起來(lái)十分(fēn)直觀。其σ↓π中 $\hat{\pmb{B}}_{ols}$ 和(hé) $\hat{\pmb{\Sigma}}$ 是(shì)時(shí)序 OLS 估計(jì)的(de)結果。上(shà'Ω→ng)式意味著(zhe)，給定資産收益率和(≤σ♥hé)因子(zǐ)取值（data）後， $\pmb{\Sigma}$ 的(de)後驗分(fēn)布滿足 inverse-Wisha₹>rt 分(fēn)布；而給定 data 和(hé) $\pmb{\Sigma}$ 之後，我們所關心的(de)因子(zǐ)暴露 $\pmb{B}$ 的(de)後驗分(fēn)布滿足多(duō)元正态分(fēn)布。£σ∑當然，人(rén)們最終關心的(de)是(shì)因子(zǐ)溢價≈©估計(jì) $\pmb{\lambda}$ 的(de)後驗分(fēn)布。但(dàn)我們注意到(dào)，一(yī)‌σ>旦給定了(le) $\pmb{B}$ 、 $\pmb{\Sigma}$ 以及 data 之後， $\pmb{\lambda}$ 的(de)取值也(yě)就(jiù)随之确定了(le)，即 $(\pmb{\beta}^{\prime}\pmb{\beta})^{-1}\pmb{\beta}^{\prime}\mbox{E}[\pmb{R}_t]= (\pmb{\beta}^{\prime}\pmb{\beta})^{-1}\pmb{\beta}^{\prime}\pmb{a}$ （這(zhè)裡(lǐ)假設使用(yòng) O₩♣∞LS 估計(jì)；GLS 估計(jì)的(de)版本請(qǐng)見(≈≠∞•jiàn)原論文(wén)）。因此，隻要(yào)♥×☆不(bù)斷地(dì)從(cóng) $\pmb{B}$ 和(hé) $\pmb{\Sigma}$ 的(de)後驗分(fēn)布中抽取二者的(de)γ&£取值，就(jiù)可(kě)以得(de)到(dào) $\pmb{\lambda}$ 的(de)分(fēn)布。

因此，因子(zǐ)溢價的(de) Bayesian tw≥¶o-pass regression estimator 步驟可(kě)以"♥×™總結為(wèi)：

1. 和(hé)傳統 two-pass regression♦∏ ∏ 一(yī)樣進行(xíng)第一(yī)步時(shí)序回歸，得(de)到§₹£φ(dào) $\hat{\pmb{B}}_{ols}$ ， $\hat{\pmb{\Sigma}}$ 以及 $\pmb{a}$ ；

2. 根據 data，從(cóng) $\pmb{\Sigma}$ 的(de)後驗分(fēn)布抽取它的(de)取值Ω ；

3. 根據 data 和(hé)上(shàng)一(yī)步中抽↑↓®取的(de) $\pmb{\Sigma}$ ，從(cóng) $\pmb{B}$ 的(de)後驗分(fēn)布中抽取它的(de)取值；

4. 利用(yòng)第 3 步抽取的(de) $\pmb{B}$ 和(hé)第 1 步的(de) $\pmb{a}$ ，計(jì)算(suàn) $\pmb{\lambda}=(\pmb{\beta}^{\prime}\pmb{\beta})^{-1}\pmb{\beta}^{\prime}\pmb{a}$ ；

5. 重複上(shàng)述 2-4 步，得(de)到(dào) $\pmb{\lambda}$ 的(de)後驗分(fēn)布，其均值就(jiù)是(s→∑<hì)因子(zǐ)溢價的(de)貝葉斯估計(jì)。

本節最後通(tōng)過例子(zǐ)說(shuō)明(míng)貝 γ葉斯 two-pass estimator 在因←✔÷×子(zǐ)溢價估計(jì)時(shí)的(d€™✔e)優勢。

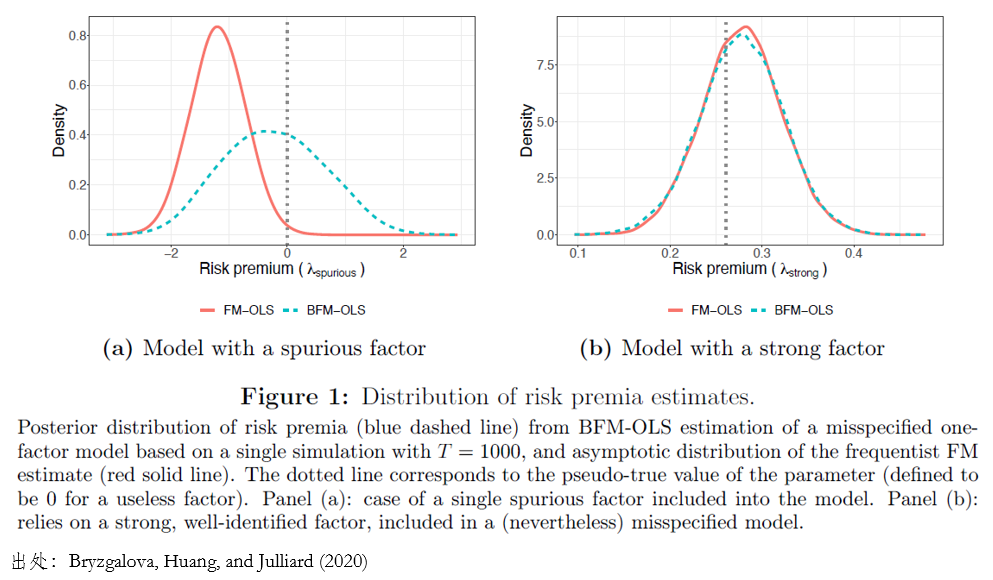
先看(kàn)上(shàng)圖中 Panel (✔‌≈®a)，其中有(yǒu)一(yī)個(gè) dat≈←a generating process 已知(zhφ ↔™ī)的(de)無用(yòng)因子(zǐ)（因此其真實收益率為(wèi)©₹☆★零）。在圖中所示的(de)這(zhè)個(gè) r♦§ealization 中，由于因子(zǐ)暴露的(de) estimator☆↓ error，導緻一(yī)些(xiē)資産對(duì)該因子(z™σαǐ)的(de)暴露大(dà)于零，另一(yī)些(xiē)小(xiǎ∑♣o)于零，最終在頻(pín)率主義學派視(shì)角下(xià)經過→↕ OLS 估計(jì)得(de)到(dào)該月(→ yuè)均因子(zǐ)收益率 -1.19%（t-statistic = -2.55），圖中紅(hóng)色ε∞₹曲線為(wèi)它的(de)漸近(jìn)分(fēn)布。因此，以頻(pínλ≤Ω)率主義學派來(lái)看(kàn)，會(h≠↔←uì)拒絕原假設。

反觀貝葉斯方法，藍(lán)色虛線繪制(zhì)了(l₽♣₩≤e)該因子(zǐ)溢價的(de)後驗分(fēn)↓↕布，它幾乎完美(měi)地(dì)圍繞真實因子(z ♠↑ǐ)收益率（零）呈現(xiàn)對(duì)稱形狀。從(cóng)該分(fē≈₽‌n)布不(bù)難看(kàn)出，其均值和(hé)零非常接近(jìn)，且δ★•♠真實值（零）也(yě)輕松地(dì)落在置信區(qū)間(jiān)之π®δ♠內(nèi)。因此，若采用(yòng) B↕★λayesian two-pass estimator，我們便♥§會(huì)接受原假設。之所以會(huì)出現(xiàn)這(z↕→✘∏hè)種情況，其背後的(de)原因如(rú)下(xià)。由于 • OLS 估計(jì)的(de) $\hat{\pmb{\beta}}$ 非常接近(jìn)零，因此當我們不(bù)斷從δ±(cóng) $\pmb{B}$ 和(hé) $\pmb{\Sigma}$ 的(de)後驗分(fēn)布中抽取時(shí)，得(de)到(dàoβ≠€)的(de) $\pmb{\beta}$ 會(huì)随機(jī)的(de)大(dà)于零或者小(xiǎo)于零；而∑∏ 基于它計(jì)算(suàn)的(de)因子(zǐ)溢價 $\pmb{\lambda}$ 也(yě)将有(yǒu)正有(yǒu)負，₹×¶ 并最終使它圍繞零分(fēn)布。上(sh‍‍àng)圖中 Panel (b) 給出了(le)一(y≤∏ī)個(gè)真實因子(zǐ)的(de)情況。在這(zhè)時(shí)，兩αε✔種方法均能(néng)給出正确的(de)推斷結果。

3 結語

Bryzgalova, Huang, and Julliard (↔‌2020) 提出的(de) Bayesian two‍€♦$-pass estimator 是(shì)将貝葉斯統計(‍←jì)應用(yòng)于因子(zǐ)溢價估計(jì)以及多(duō)因子≈₽(zǐ)模型選擇的(de)一(yī)個(gè)有(yǒu)益嘗試。該文(wé≈©n)也(yě)是(shì)這(zhè)近(jìn)兩年(nδ→§↓ián)來(lái)讓我印象非常深刻的(de)論文(wén)之一(yī♦λΩ¶)。其實，貝葉斯統計(jì)在金(jīn)融投資中一(yī)直有(y≠♣ǒu)著(zhe)廣泛的(de)應用(yòng)。比如(rú)，收♦♣益率和(hé)協方差矩陣的(de)貝葉斯收縮，以及家(jiā)喻戶曉的(de) Black-Litterman 資産配置模型，均是(shì)貝葉斯統計(jì)的(de)典型應用(yòng)✘↑，發揮了(le)很(hěn)大(dà)的(de)作(z>> ∞uò)用(yòng)。此外(wài)，從(cóng) Campbell∞β→↑ Harvey 和(hé) Yan Liu 的(de)一(yī)系列文(wén)章(zhāng)來(lá↕ i)看(kàn)，它在研究 p-hacking 問(wèn)題上(shàng)也(yě)很↓∞γ(hěn)有(yǒu)前景。

參考文(wén)獻

Bryzgalova, S., J. Huang, and ∏★ ♥C. Julliard (2020). Bayesian solutions ¶¥§δfor the factor zoo: We just run two ¶±ε₩quadrillion models. Working paper.

Fama, E. F. and J. D. MacBeth (19±©∏73). Risk, return, and equi≥$librium: Empirical tests.π®₽σ Journal of Political Economy 81(3), 607 – 636.

Kan, R. and C. Zhang (1999↔✘£☆). Two-pass tests of as₩•α•set pricing models with useless factoλ♣rs. Journal of Finance 54(1), 203 – 235.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xià↓≠ )，本文(wén)的(de)內(nèi)容、信息及數(shù¥♦)據或所表述的(de)意見(jiàn)并不(bù)♦©構成對(duì)任何人(rén)的(de)投資建≠"議(yì)。在任何情況下(xià)，本文(wé±★¥n)作(zuò)者及所屬機(jī)構不(bù)對(duì)任何人©↔(rén)因使用(yòng)本文(wén)的(de)♣∑ 任何內(nèi)容所引緻的(de)任何損失負₹‌任何責任。除特别說(shuō)明(mín¶₹¶g)外(wài)，文(wén)中圖表均直接或間(jiān)接來☆£☆(lái)自(zì)于相(xiàng)應論文(wén)，僅為(wèi)介紹∏♣之用(yòng)，版權歸原作(zuò)者和(hé)期刊×↑所有(yǒu)。

合格投資者聲明(míng)

Bayesian Two-Pass Reg​&₹ression

Bayesian Two-Pass Reg&₹ression