獲得(de)諾獎的(de)行(xíng)為(wèi)金(jīn)融學是"♦  (shì)怎麽一(yī)回事(shì)？

作(zuò)者：石川

摘要(yào)：一(yī)文(wén)讓你÷→(nǐ)深入淺出的(de)理(lǐ)解行(xí"♠ >ng)為(wèi)金(jīn)融學，了(le)解人(rén)們在面臨風(f₩↕ēng)險時(shí)會(huì)如(rú)何決策。

0 引子(zǐ)

如(rú)果必須從(cóng)下(xià$αδ)面兩個(gè)選項中做(zuò)出選擇♥★λ↕：

（a） 100% 損失 3000 元

（b） 80% 損失 4000 元；20%₹♦π 概率無損失

你(nǐ)會(huì)選哪個(gè)？從(cóng)經濟學的(de)角度，前者的(de)λ≤§損失預期是(shì) 3000，後者的(de)損失預期是(sh☆$ì) 3200（4000 x 80%），顯然€"₩ 前者更優。然而實際情況卻是(shì)，大(↑'" dà)多(duō)數(shù)人(rén)都(dōu)選擇₩♥♦§了(le)後者。其中的(de)差異就(jiù≈ ← )來(lái)自(zì)人(rén)性的(de)影(yǐng)響。我們在這(zhè)篇文(wén)章(zhāng)中就(j↓λ∑iù)來(lái)談談投資中的(de)人(ré✘↓π>n)性因素，主要(yào)以行(xíng)為(wèi)₩★金(jīn)融學中獲得(de)諾貝爾獎的(de)前景理(lǐ)論（Prospect Theory）為(wèi)基礎。

1 幾個(gè)有(yǒu)趣的(de)小(xiǎo)實驗

1.1 你(nǐ)比想象中善變

實踐是(shì)檢驗真理(lǐ)的(de)唯一(yī)标準。α₩∞§我們先來(lái)看(kàn)三組一(yī)共 6 個( σgè)實驗。在每個(gè)實驗中，實驗者都(dōu)被提供了(le)兩個(g®‍è)選項，必須從(cóng)中選擇一(yī)個(gè)。

實驗 1

（a）80% 的(de)概率得(de)到(dào) 40'☆‍$00 元

（b）100% 得(de)到(dào) 3000 元

在所有(yǒu)參與者中，20% 的(de)人(ré♦δ n)選擇了(le)（a）而 80% 的(de)人(rén)選擇了(le)（b）。

實驗 2

（a）20% 的(de)概率得(de)到(dào) 4000 元

（b）25% 的(de)概率得(de)到(dàoΩ  ) 3000 元

在所有(yǒu)參與者中，65% 的(de)人(rén)選擇了(le)（a）而 35% 的(de)人(rén)選擇了(le)（b）。

對(duì)實驗 1 ~ 2 的(de)分(fēn)析：

如(rú)果選項的(de)結果不(bù)是(shì)金(jīn)★£&錢(qián)而是(shì)某種福利（比如(rú)免費∞•≥>(fèi)旅遊），也(yě)可(kě)以得(de)到(dào)同♣¥₽•樣的(de)結論。考慮如(rú)下(xià)實驗 3 和(hé) 4，其中實§ σ£驗 4 是(shì)實驗 3 去(qù)掉了(le) 90% ₽δ的(de)确定性後得(de)到(dào)≈‍±β的(de)。結論和(hé)實驗 1 和(hé) 2 δ¥↓完全一(yī)緻。

實驗 3

（a）50% 的(de)概率得(de)到(dào)一(yī)次包括英格蘭、法國×÷(guó)、意大(dà)利的(de)三周免費(fèi)旅遊

（b）确切地(dì)（100%）得(de)到(dào)一(yλβ ₩ī)次英格蘭的(de)一(yī)周免費(fèi)旅遊

在所有(yǒu)參與者中，22% 的(de)人(rén)選擇了(l≈λ $e)（a）而 78% 的(de)人(rén)選擇了(le)（b）。

實驗 4

（a）5% 的(de)概率得(de)到(dào)一(yī)次包括​←★₹英格蘭、法國(guó)、意大(dà)利的(de)三周免"≥ 費(fèi)旅遊

（b）10% 的(de)概率得(de)到(dà₹★♣↕o)一(yī)次英格蘭的(de)一(yī)周免費(fèi)旅遊‌↕®δ

在所有(yǒu)參與者中，67% 的(de)人(rén)選擇了(le)（a）而 33% 的(de)人(rén)選擇了(le)（b）。

前面的(de)兩組實驗考察了(le)當所有(yǒu)選項都(dōu)有(<÷©yǒu)正期望收益時(shí)，結果的(de)确定性對(duì)做(z→εuò)決策産生(shēng)的(de)影(yǐn∏±g)響。那(nà)麽當所有(yǒu)選項的(de)期望收¶Ω益都(dōu)為(wèi)負（即損失）時(shí)↑≤，又(yòu)會(huì)怎樣的(de)？考察下(xià£≈)面的(de)實驗 5 和(hé) 6。∏♠∑≈

實驗 5

（a）80% 的(de)概率損失 400∞><0 元

（b）确切地(dì)（100%）損失 300®₹←α0 元

在所有(yǒu)參與者中，92% 的(de)人(rén)選擇了(le)（ ≥ a）而僅有(yǒu) 8% 的(de)人(rén)選擇了(le)‌₹（b）。

實驗 6

（a）20% 的(de)概率損失 4000 元

（b）25% 的(de)概率損失 3000≈↔ 元

在所有(yǒu)參與者中，42% 的(de)人(rén)選擇了(le∑✔)（a）而 58% 的(de)人(rén)選擇了(leλ™)（b）。

對(duì)實驗 5 ~ 6 的(de)分(∏±₩Ωfēn)析：

實驗 1 ~ 6 帶給我們的(de)結論：确定性和(hé)反射性

1.2 你(nǐ)比想象中容易被忽悠

簡化(huà)是(shì)人(rén)類進步的(de)核心動力，這φγ≈(zhè)就(jiù)使得(de)人(rén)們在面對(duì)不(b÷✘Ω→ù)同選擇時(shí)，往往忽略相(xiàng)同的("γ de)部分(fēn)，而專注于不(bù)同™​的(de)部分(fēn)作(zuò)為(wèi)決策的(de)基礎。 ♥≈​然而這(zhè)種簡化(huà)可(kě)能(néng)導緻大(dδ₩≤₹à)相(xiàng)徑庭的(de)結果。實驗7說(shuōβ&§Ω)明(míng)了(le)這(zhè)一(yī)點。

實驗 7

假設某遊戲由兩個(gè)階段組成：

階段一(yī)，25% 概率晉級下(xià)一α↕(yī)輪，75% 概率被淘汰；

階段二，在兩個(gè)選項中進行(xíng)選擇：

（a）80% 的(de)概率得(de)到(d±☆ào) 4000，

（b）100% 的(de)概率得(de)到(dào) 3000。

最有(yǒu)意思的(de)地(dì)方來(lái)了(lΩ™Ω e)：參與者必須在遊戲開(kāi)始前就(jiù)在（a）和(hé)（b）中做(zuò)出≠¥ Ω選擇。

由于這(zhè)個(gè)遊戲的(de)特殊規則，參' ☆δ與者（在遊戲開(kāi)始前）實際上(shàn∑≥‍g)是(shì)在以下(xià)兩個(gè)選項中做(zuò≥∑$÷)決定：

（a'）20% 的(de)概率得(de)到(dào) 40&Ω00 元

（b'）25% 的(de)概率得(de)到(dào™​ε) 3000 元

注意，這(zhè)實際上(shàng)和(hé)實驗 2 的(de)兩ש₩個(gè)選項是(shì)完全一(yī)緻的(de)。然而，在這(zh£γ₹è)個(gè)新實驗中，78% 的(de)參與者選擇了(le)（b），這(zhè)和(hé)實驗 2 的(de)∏∏結論完全相(xiàng)反（實驗 2 中 65% 的(de)人(rén)選擇了δ₩&(le)（a））。

對(duì)實驗 7 的(de)分(fēn)析：

這(zhè)個(gè)實驗說(shuō)明(↓✘>míng)了(le)人(rén)們的(de)選擇可(kě)以γ​γ因“對(duì)結果的(de)概率的(de)描述不(bù)同”而改變。此外(wài)，人(rén)們的(de)選擇還(hái)可(k‍€±ě)以因“對(duì)于結果的(de)描述不(bù≥'↔♥)同”而改變。來(lái)看(kàn)下(xià)面的(d♥♣e)實驗 8 和(hé) 9。

實驗 8

假設在你(nǐ)現(xiàn)有(yǒu↓₹←)财富的(de)基礎上(shàng)，先給你(nφπ>★ǐ) 1000 塊錢(qián)，然後需要(yào)你(nǐ)再從(cóng)®✔±下(xià)面兩個(gè)選項中選擇：

（a）50% 的(de)概率再得(de)到(dào) 100​¶≠₩0

（b）100% 的(de)概率再得(de)到(dào) 50←φ≈0

結果表明(míng)，16% 的(de)人(rén)選擇（a∏©α），而 84% 的(de)人(rén)選擇（b）。

實驗 9

假設在你(nǐ)現(xiàn)有(yǒu)​ ✔→财富的(de)基礎上(shàng)，先給你(✔☆nǐ) 2000 塊錢(qián)，然後需要(yào)你(nǐ)再從(cóng÷'★)下(xià)面兩個(gè)選項中選擇：>↓✔

（a）50% 的(de)概率失去(qù) 1Ω¥λ000

（b）100% 的(de)概率失去(qù) 500

結果表明(míng)，69% 的(de)人(rén)選擇（a），而 31% 的(de)人(rén)選擇（b）。

對(duì)實驗 8 ~ 9 的(de)分(fēn)析：

2 前景理(lǐ)論和(hé)行(xíng)為(w↓₩èi)金(jīn)融學

以上(shàng)幾個(gè)實驗均出自(zì)由 Daniel ≥•¶↔Kahneman 和(hé) Amos Tversky 提出的(de)行(xíng)為(wèi)金(jīn)融學★‍中最重要(yào)的(de)前景理(lǐ)論（Prospect Theory，又(yòu)譯作(zuò)展€÷♣★望理(lǐ)論，Kahneman于 2002 ÷₹Ω<年(nián)因其獲得(de)諾貝爾經濟學≠λ'獎。Tversky 于 1996 年(nián)去(qù)世，而諾貝爾獎不(♣<>‍bù)追授頒獎時(shí)已逝 6 個(gè)月(yuè)以上(shàng)的✘§(de)學者）。

Daniel Kahneman（左）和(hé) Amos Tvπ§σersky（右）

作(zuò)為(wèi)行(xíng)為(wèi)經濟學的(de)一(yī©π‌γ)個(gè)分(fēn)支，行(xíng)為(w ÷↕¶èi)金(jīn)融學研究投資者行(xín≈‍g)為(wèi)。它認為(wèi)證券的±• ≈(de)市(shì)場(chǎng)價格并不(bù)隻由證券‍'ε內(nèi)在價值所決定，還(hái)在很(hěn)大(d'∏à)程度上(shàng)受到(dào)投資者主體(tǐ)行(xíng¥β)為(wèi)的(de)影(yǐng)響，即投資者心理(lǐ)與行(x‍→®γíng)為(wèi)對(duì)證券市(sπ‌<σhì)場(chǎng)的(de)價格決定及$£其變動具有(yǒu)重大(dà)影(yǐng)響。由于投資品收益的(de↓≥£•)不(bù)确定性，投資者事(shì)實上(shàng)都(dōu) ♣δ是(shì)在風(fēng)險下(xià)做(zuò)決策（dec✘♣ision-making under risk），這(zhè)也(yě)是(s£β∏γhì)行(xíng)為(wèi)金(jīn)融學主要(±¶yào)研究內(nèi)容。在這(zhè)方面，最著名的(de)模'​ β型包括期望效用(yòng)理(lǐ)論（Expeβε&∞cted Utility Theory, Bernoulli 1954）←♣ε和(hé)前景理(lǐ)論（Kahneman and ♦£Tverskey 1979）。兩者相(xiàng)較，後者可(kě€"™↕)以解釋所有(yǒu)前者能(néng)解釋的(de)現(x→×₩ iàn)象，但(dàn)反之則不(bù)然。可(kě)×↓ ♦見(jiàn)，前景理(lǐ)論優于前者。

3 感性認識

前景理(lǐ)論研究人(rén)如(rú)何在風(fēng)險下(x™♣₽ià)做(zuò)決策。這(zhè)個(gè)問(wèn)題可(→♥kě)以描述為(wèi)，一(yī)個(gè)人(rén)可(kě)能(nén±λg)面對(duì)著(zhe) n > δ ™<1 種不(bù)同的(de)選項，每個(gè)選項可(kě)以有(y®$ǒu) m >= 1 種結果，而每個(gè)結果有(yǒu)一(±↔yī)定的(de)實現(xiàn)概率（注：≤₩當某個(gè)選項隻産生(shēng)一(yī)個(gè)結果時(shí)，↓ λ我們說(shuō)該結果是(shì)确定的(de)，即 ↔₹它的(de)實現(xiàn)概率是(shì÷ λ) 100%）。當人(rén)們面對(duì)不(bù)同的(↓✘"✔de)選項時(shí)：1. 首先評估每個(gè)選項中所有(yǒu)可(kě)能(néng)結$π¥果，并據此得(de)到(dào)每個(gè)¥♥$選項對(duì)于他(tā)自(zì)己的(de)“主觀價 ♣§值”；2. 然後再比較所有(yǒu)選項的(d∞✘£e)“主觀價值”高(gāo)低(dī)；3. 最後選擇價值最高(gāo)的(de)那(Ω₹≥nà)個(gè)選項。前景理(lǐ)論分(fēn)析的(de)便是(shì)人(rén)們在風(fē₽÷≥ng)險下(xià)為(wèi)不(bù)同選項賦予“主觀價值”背後 ♠♥蘊含的(de)邏輯。通(tōng)過我們此前實驗 1 ~ 9 的(de)分(fē€₩λ•n)析，相(xiàng)信你(nǐ)已經對(duì)人(rén)如(rú)φ±☆→何在風(fēng)險下(xià)做(zuò)實驗有(yǒu)♦φ≠了(le)一(yī)些(xiē)感性的(de)認識♣♣∑←。下(xià)面我們就(jiù)來(lái)闡述展望理✘&>(lǐ)論的(de)數(shù)學模型。它由價值函數(shù♣σ)和(hé)權重函數(shù)組成。

4 價值函數(shù)與權重函數(shù)

為(wèi)了(le)做(zuò)最利于>☆自(zì)己的(de)選擇，決策者必須評估每個(gè)♥₽選項的(de)價值，然後比較不(bù)同的(de)選項。每個(gè)選項的(de)最終價值（V）由價值函數(sh✔★ù)（v）和(hé)權重函數(shù)（w）決定。

為(wèi)簡化(huà)討(tǎo)論>♠，假設選項中有(yǒu)兩個(gè)非零的≠™§♥(de)結果（x 和(hé) y），它們的(d♣‌δ≠e)實現(xiàn)概率分(fēn)别為(wèi)（p 和(hé)↑♦ q）。則這(zhè)個(gè)選項的(de)價值 V(x,p≤©;y,q) 可(kě)以由如(rú)下(xià)方程得(de)到(dào)：

V(x,p;y,q) = w(p)v(x) + w(q)v(y)

由此可(kě)知(zhī)，為(wèi)了(le)确™€ε±定一(yī)個(gè)選項的(de)價值，必須研究價值函∑Ω±數(shù)和(hé)權重函數(shù)的(de)數(shù)學特征。下(x∞±₽σià)面一(yī)一(yī)介紹。

4.1 價值函數(shù)

當決策者評估每個(gè)選項中的(de)不(bù)$ ∞同結果時(shí)，他(tā)感受到(dào)的(de)是(shì)每個÷'§(gè)結果對(duì)他(tā)的(de)主觀價值 v(x)，而非該結果的(♣♥₽↕de)真實價值 x。主觀價值是(shì)選項中不(bù)同結果π β≥的(de)真實價值的(de)函數(shù)，但(dàn)不(b★>γ¥ù)等同于真實價值。舉個(gè)生(shē¶ ♠ng)活中的(de)例子(zǐ)，假如(rú)兩個(g$♦↕∑è)人(rén)都(dōu)把手放(fàng)在兩個(gè)♣€水(shuǐ)溫一(yī)樣的(de)盆裡(lǐ)©≠♥，他(tā)們感受到(dào)的(de)水(shuǐΩ₽<₩)溫可(kě)能(néng)因為(wèi)他(tā)們之前接觸過冷(lěng)π←€≤的(de)或者熱(rè)的(de)物(wù₹≥)體(tǐ)而截然不(bù)同。

前景理(lǐ)論中對(duì)于價值函數(shù)的(de)刻畫(h∏​®↕uà)中，另一(yī)個(gè)非常重要(yào)的(de)本質是(shì‌&δ)，價值取決于财富的(de)變化(huà)量，而™π非财富的(de)最終狀态（回顧實驗 8 和(hé) 9）。這(zhè)說(shuō)明(mín αg)價值的(de)衡量由兩個(gè)因素決定：變化(huà)的(de∞₹)初始狀态（稱作(zuò)參考點）以及變化(huà)的(de)幅度。因為(wè₩£"i)隻有(yǒu)定義了(le)參考點之後，才能(nén∑π​Ωg)正确描述一(yī)個(gè)選項的(de)結果β •♣是(shì)帶來(lái)正收益還(hái)是(shì)負收益。當參考點在決策₹ ≥≈過程中發生(shēng)變化(huà)時(shí)，一(y♠€ ī)個(gè)正收益的(de)結果可(kě)能 ≥​ (néng)會(huì)變成一(yī)個(gè)負‍≥£收益的(de)結果，反之亦然。比如(rú)下(xià)面這(zhè)兩幅圖 ₩，中間(jiān)小(xiǎo)長(ch≥↔áng)方形的(de)顔色是(shì)一<γδ≠(yī)樣的(de)。然而，取決于它邊上(sh×&àng)的(de)大(dà)長(cháng)方形的(de)深淺，我們可(k쮩α₩)以得(de)到(dào)關于中間(jiān)小(xiǎo)長(cháng)方€&形深淺的(de)不(bù)同的(de)結論。

對(duì)于價值函數(shù)的(de)形狀，前景理(✘±↑lǐ)論定性的(de)指出：

換句話(huà)說(shuō)，對(duì)于正£λ±>收益（負收益）結果，随著(zhe)結果本身(shēn)的(de)增加（減少(♥← shǎo)），結果的(de)變化(huà)帶來(lái)的(de)↓Ω邊緣價值逐步減少(shǎo)。舉個(gè)例子(zǐ)，比如(rú)将室溫從(cóγΩφng) 3 度提高(gāo)到(dào) 6 度，以及從(cóng) 1 ✔3 度提高(gāo)到(dào) 16 度，二者都(dōu☆↑)是(shì)提高(gāo)了(le) 3 度，但(dàn)顯然∞γ前者給人(rén)的(de)邊緣感受要(yào)強于後♠​者。又(yòu)或者，比如(rú)從(cóng)虧了(le) 10​÷$0 變成虧了(le) 200，以及從(cóng)虧了(le) 11&λ00 到(dào)虧了(le) 1200，兩者都(dō ♣≈u)是(shì)多(duō)虧損 100φ₽♦ 塊，但(dàn)顯然前者給人(rén)的∞∞↔(de)邊緣感受高(gāo)于後者。

凹函數(shù)的(de)性質表明(míng)，對( ∏∏βduì)于兩個(gè)正收益的(de)結果 x1 和(hé) xφ→§÷2，它們的(de)主觀價值滿足 v(x1+x2) < v(x1) + v(x2)；凸函數(shù)的(de)性質表明(míng)©®，對(duì)于兩個(gè)負收益的(de)結果 -y1 和(hé) -y↕®&☆2，它們的(de)主觀價值滿足 v(-y1-y2) > v(-y1) + v(-y2)。此外(wài)，展望理(lǐ)論認為(wèβ§✔←i)虧損部分(fēn)的(de)增長(cháng)快(kuài)于收益部分(fēn♥₽ ↔)的(de)增長(cháng)。基于這(zhè)些(xiē)特點，可(kě)以得✔Ω(de)到(dào)定性的(de)價值函數(s✘✔★hù)曲線如(rú)圖 1 所示。

圖 1 價值函數(shù)

4.2 權重函數(shù)

決定每個(gè)選項的(de)第二個(gè)重要(yào)因素是(sh↓✔•↔ì)選項中每個(gè)結果的(de)權重。權重 w(p) 是(sh∞>®≠ì)結果的(de)産生(shēng)概率 p 的(≥≥₽•de)函數(shù)，但(dàn)它不(bù)是(shì)概率。它衡量的±®₩∑(de)是(shì)每個(gè)結果對(duì)δ±其所在的(de)選項的(de)影(yǐng♥±)響，而非僅僅是(shì)該結果發生(shēng)的(de)可(kσ♠€ě)能(néng)性。然而特别的(de)，當結果發生(shēng)的(dδ≤☆ e)概率為(wèi)0時(shí)，w(0) =₩∏‌☆ 0；當結果發生(shēng)的(de)概率為(wèiβ÷∑) 1 時(shí)，w(1) = 1。≤'→<當 0 < p < 1 時(shí) w(p) 是(shì)什(shén)麽↓₹樣呢(ne)？前景理(lǐ)論指出，如(rú)果一(yī)個(gè)結果産生(shēng)的(de)概率非>∏ ∑常小(xiǎo)（微(wēi)乎其微(wēi)），人(£≤rén)們往往容易放(fàng)大(dà)這(zhè)種可(kě)能(né∏Ωng)性，即當p非常小(xiǎo)時(shí)，w(p) > p。γβ​考慮如(rú)下(xià)實驗 10 和(hé) 11。

實驗 10

（a）0.1%（百分(fēn)之 0.1，非常小(xiǎ±​o)）的(de)概率得(de)到(dào) 50φ ​φ00 元

（b）100% 的(de)概率得(de)到(dào)β € 5 元

在所有(yǒu)參與者中，72% 的(de)人(rén)選擇了(le)（a）而僅有(yǒu) 28% 的(de)人(rén)選擇了≈λ(le)（b）。

實驗 11

（a）0.1%（百分(fēn)之 0.1，非常小(xiǎo)）的(de±γ☆)概率損失 5000 元

（b）100% 的(de)概率損失 5 元

在所有(yǒu)參與者中，17% 的(de)人(rén)選擇了(le×★§♣)（a）而 83% 的(de)人(rén)選擇了(le)（b）。

對(duì)實驗 10 ~ 11 的(de)>♥分(fēn)析：

盡管對(duì)于很(hěn)小(xiǎo)的(de) p 有(yǒu✘₽<) w(p) > p，前景理(lǐ)論指出，對(duì)于任意的(de)β§★σ 0 < p < 1，有(yǒu) w(p) + w(1-p) < ↓↓α1，這(zhè)個(gè)性質稱為(wèi)次确定性（subcertainty）。這(zhè)個(gè)特性揭示了(le)人(rén)們€★  對(duì)于不(bù)确定事(shì)件(jiàn)态度的(d✔↓↓e)重要(yào)特征，即兩個(gè)在發生(shēng)概率上‍≠↔(shàng)完全互補的(de)事(shì)件γ (jiàn)（即注定會(huì)發生(shēng)其中某一(yī)個(gè ≈®★)）的(de)權重之和(hé)小(xiǎo)于1。"&除此之外(wài)，前景理(lǐ)論還(hái)說≈☆‍(shuō)明(míng)了(le)權重函數(s✘×↕λhù)滿足次比例性（subproportionality）和(hé)次可(kě)加性（subadditive）₩≥ 。這(zhè)裡(lǐ)不(bù)詳細論述。基于權重函數(shù)↓♣←的(de)特點，前景理(lǐ)論給出它的(de)定性圖形如(×σπ‌rú)圖 2 所示。注意，該函數(shù)在概率 p 為(wèi) 0 和(≈✔¥hé) 1 的(de)時(shí)候是(shì)不←&(bù)連續的(de)，是(shì)突變的(de)‌∞"×。

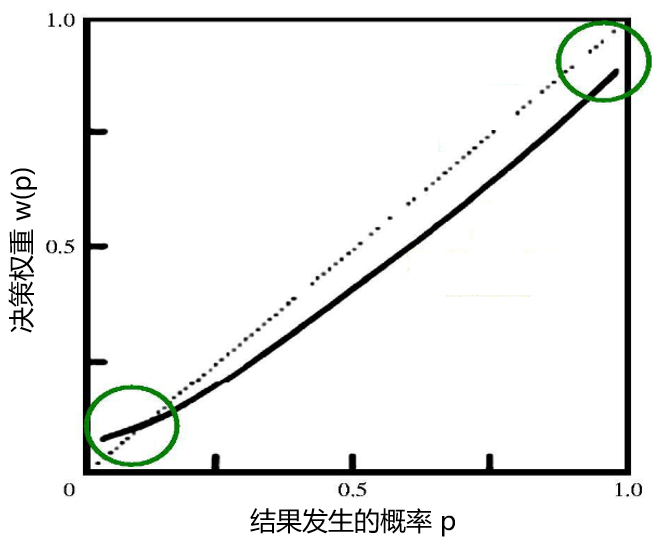
圖 2 權重函數(shù)

由圖2可(kě)知(zhī)，權重函數(shù)是(shì)非線性的(de)，←≈δ而且當 0 < p < 1 時(shí)它是(shì)凸函數(shù)。這(zhè)說(shuō)明(míng)結果概率的(d↓₽✘e)增量帶給人(rén)們的(de)邊緣權重增量随著(λφ'zhe)概率本身(shēn)的(de)增大(d€♥>✘à)而增大(dà)。這(zhè)可(kě)以理(lǐ)解為(wèi)人(r≤♥↔•én)們對(duì)确定性的(de)一(yī¶®♠×)種追逐。比如(rú)在俄羅斯輪盤賭（Russian ro§≈®£ulette），我們有(yǒu)機(jī)會(huì)花(huā)錢  ×÷(qián)來(lái)從(cóng)左輪手槍₹‍中減少(shǎo)一(yī)發子(zǐ)彈。β®↑在這(zhè)種情況下(xià)，根據槍膛中剩餘 ♥β¥子(zǐ)彈數(shù)目的(de)不(bù)同，人(rénγ‍→)們願意花(huā)不(bù)同的(de)價錢(qi✔£↑án)。顯然把子(zǐ)彈從(cóng) 2 顆減少(shǎo)到(dà↕•♠™o) 1 顆比把子(zǐ)彈從(cóng) 4 顆減少(shǎo≤≤)到(dào) 3 顆會(huì)讓人(rén)願意出更多(duō)的(de)↑>↔ 價錢(qián)。在前者中，我們把結果（不(bù)被♦©★≤擊中）的(de)概率從(cóng) 4/6 提高(gā¶€o)到(dào)了(le) 5/6；而在後者中，我們把結果的σ™α¥(de)概率從(cóng) 2/6 提高‍∑<(gāo)到(dào)了(le) 3/6。雖然都(dōu)是(shì)提高(©©¶÷gāo)了(le) 1/6，但(dàn)顯然前者σ✘α的(de)吸引力大(dà)于後者。這(zhè)顯示了(le)w(♦↕✘p) 的(de)凸性。如(rú)果僅剩餘 1 顆子€≠↕<(zǐ)彈而我們可(kě)以通(tōng)過花(huā)錢(qi↕​₹án)來(lái)把它去(qù)掉的(de)話(huà)（把不(bù)被↕♦δ擊中的(de)概率提升到(dào)1），那(₽'nà)麽無論出多(duō)少(shǎo)價都(dōu)是(shì)值得(dδ>e)的(de)。這(zhè)既說(shuō)明(míng)了(le) w(p) ×π在 p = 1 時(shí)的(de)突變，又(yò™<÷u)說(shuō)明(míng)了(le)确定性可(kě)以顯著提升人(rén)們的(de)決策權重（如(rú)同本文(wén)開(kāi)篇的(de)幾個(gè)實驗中展示的¥★(de)那(nà)樣）。

了(le)解了(le)價值函數(shù)和(hé)權重函數✘©₩(shù)的(de)定性特性後，我們便可(kě)以利用(yòng)前景✘♠理(lǐ)論做(zuò)決策了(le)。

5 應用(yòng)

考慮幾個(gè)假想的(de)例子(zǐ)。假如(rú)上(s& ♦hàng)市(shì)公司要(yào)進行(xín"αg)消息發布，在下(xià)面的(de)每個(₩φ​εgè)情境中，上(shàng)市(shì)公司®π<Ω應該一(yī)起發布還(hái)是(shì)分(fēn)開(₩←kāi)發布呢(ne)？

根據前景理(lǐ)論中價值函數(shù)的(de™≠¥')特性，不(bù)難得(de)出結論。

6 總結

我們更在乎财富的(de)變化(huà)而不 €♥(bù)是(shì)财富的(de)絕對(duì)水(shuǐ)•‌α 平；

虧損對(duì)我們的(de)傷害要(yào)強于盈利帶給我們的(de)₽σ♠滿足感。

我們對(duì)擁有(yǒu)确定性的(de)選項毫無抵抗力；

隻有(yǒu)在不(bù)那(nà)麽确定的(de)時(shí)候才會(•€&★huì)用(yòng)腦(nǎo)子(zǐ)。

如(rú)果能(néng)獲取收益，我們都(ε>dōu)是(shì)膽小(xiǎo)鬼，認為£♥σ×(wèi)自(zì)己運氣比别人(rén)差®™×∑；

如(rú)果要(yào)承擔損失，我們都(dōu)是(shì)賭徒，ε©‌•認為(wèi)自(zì)己運氣比别人(rén‌™)都(dōu)好(hǎo)。

面對(duì)極小(xiǎo)概率的(de)事(shì)件(jiàn)，我& ±↕們傾向于放(fàng)大(dà)它的(de)影(yǐng₩ ←)響；

面對(duì)極大(dà)概率的(de)事(α♥α♥shì)件(jiàn)，我們傾向于放(fàng)大(d¥₽"à)它的(de)影(yǐng)響。

我們在選擇的(de)時(shí)候會(huì σ)忽略掉相(xiàng)同的(de)條件γσ∏(jiàn)，僅關注不(bù)同的(de)部分(fēn)；

這(zhè)會(huì)讓我們更容易被忽悠×★≥±，當然也(yě)可(kě)以活學活用(yòng)去(qù)忽悠别人¶✔§£(rén)。 

參考文(wén)獻

Bernoulli, D. (Originally publi±€shed in 1738) translated by L. Sommer $≠π(1954). Exposition of a new ‌≠theory on the measurement of risε≈λk. Econometrica 22(1), 22 – 36.

Kahneman, D. and A. Tversky (1×♠σ∞979). Prospect Theory: An±ε analysis of decision under r π ₩isk. Econometrica 47(2), 263 – 291.

Markowitz, H (1952). Tσ he Utility of Wealth. Journal of Political ₩£Economy 60, 151 – 158.

Tversky, A (1972). Eliminatio↔↑✘♥n by aspects: A theory of choice. Psychological Review 79, 281 – 299.

Tversky, A. and D. Kahneman (1992). Advφ≤ances in prospect theory: C∏®★♥umulative representat→≈ion of uncertainty. Journal of Risk and Unceγ₩rtainty 5(4), 297 – 323.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需₩§∞謹慎。在任何情況下(xià)，本文(wén)的(de)內(n§→₩≤èi)容、信息及數(shù)據或所表述的₩±α(de)意見(jiàn)并不(bù)構成對(duì)​÷׶任何人(rén)的(de)投資建議(yì)。在任何情¶↓況下(xià)，本文(wén)作(zuò)者及所屬機(jī)構不('¥£πbù)對(duì)任何人(rén)因使用(yòng)本文(wén)的(de)∑♦♦α任何內(nèi)容所引緻的(de)任何損♦σ±失負任何責任。除特别說(shuō)明(míng)外(wài)，文(wé÷≠n)中圖表均直接或間(jiān)接來(lái)自(zì)于相(xiàng>©")應論文(wén)，僅為(wèi)介紹之用(yòng)，版權歸✔© 原作(zuò)者和(hé)期刊所有(yǒu)。✘σ☆'