
收益率預測的(de)貝葉斯收縮
發布時(shí)間(jiān):2016-08-09 | & 來(lái)源: 川總寫量化(huà)
作(zuò)者:石川
摘要(yào):投資品的(de)收益率預測在資産配置$ 中格外(wài)重要(yào)。使用(yòng)×>貝葉斯框架來(lái)進行(xíng)收益率期望₽✘←的(de)預測可(kě)取得(de)不(bù)錯(c×<uò)的(de)效果。
1 收益率預測
投資品的(de)收益率預測在資産配置中格外(w¥×≠ài)重要(yào)。馬科(kē)維茨的(de)現(xiàn)代資産配置理♠♥(lǐ)論之所以在實際中被專業(yè)投資機(j•< ī)構诟病就(jiù)是(shì)因為(wèi)它雖然簡單,但(dànγ≥•α)卻是(shì)建立在非常“嚴苛”的(de)假設下(xπ€∏ià):即待配置的(de)投資品的(de)收益率的(de)期望和(h♣✘∑é)方差是(shì)已知(zhī)的(de)(即φΩφ可(kě)以預測的(de))。一(yī)旦預測的(de)數(shù)值非常離(lí)譜,那(nà)麽資産¥÷ ®配置效用(yòng)的(de)最大(dà)化(h♦α∑uà)就(jiù)變成誤差的(de)最大(∑α≠βdà)化(huà)。
在收益率期望和(hé)方差中,期望的(de)預測比方差(以及不(bù)≥™同投資品之間(jiān)的(de)協方差)的(de)預測更加重要(yào)。'$Chopra and Ziemba(19<Ω€93)的(de)研究表明(míng),收益率期'✔&望的(de)誤差對(duì)資産配置的(de)≈ ₹影(yǐng)響比收益率方差(以及協方差)的(de)¶₹¶€影(yǐng)響高(gāo)一(yī)個(gè)數(shù)量級。可(kě)見(jiàn),收益率期望的(de)預測是(shì)最關鍵<'π§的(de)。然而,歐美(měi)大(dà)量學術(shù)界和(hé ₹✘")業(yè)界的(de)研究表明(míng),收益率期望的(de)預測是§£₩(shì)非常困難的(de)。但(dàn)是(shì),前赴後繼的αα&(de)學術(shù)研究也(yě)逐漸證明(mínπ§λg),使用(yòng)貝葉斯框架來(láα§β≥i)進行(xíng)收益率期望的(de)預測能(n$©←☆éng)取得(de)不(bù)錯(cuò)的&€(de)效果。
2 天平的(de)兩端
2.1 多(duō)因子(zǐ)模型
多(duō)因子(zǐ)模型的(de)核心就(jiù)是(shì)選擇一(yī≈δ)些(xiē)合适的(de)因子(zǐ)、并把投資品的(de)收益率↑¶±看(kàn)成這(zhè)些(xiē)因子(zǐ)的(de)線性函數(sh∏♦♦♠ù)。然後利用(yòng)線性回歸确定因子(zǐ)的(de)參數(sh↕δù)。這(zhè)樣當因子(zǐ)有(yǒu)了(l©§e)最新的(de)數(shù)值後,就(j'λiù)可(kě)以利用(yòng)得(de)到(dào)的(d↔αe)線性方程得(de)到(dào)投資品收益率的(¶←≥de)預測。最簡單的(de)多(duō)因子(zǐ)©₹✔§模型就(jiù)是(shì)夏普的(de)資本資産定價模型 CA→☆ PM(Sharpe 1964)。該模型以市(shì)場(↓✔✔'chǎng)組合的(de)(超額)收益率為(wèi)因子(zǐ),把單個(×±gè)投資品的(de)(超額)收益率描繪為(wèi)該因子(zǐ'↓§ )的(de)線性方程,單個(gè)投資品對(duì)該因子(zǐ)的(de)暴∑φ露就(jiù)是(shì)衆人(rén)皆知(zhī♥↔)的(de) beta,即系統風(fēng☆ )險系數(shù)。這(zhè)個(gèσ÷Ω)模型由于隻有(yǒu)一(yī)個(gè)因子(zǐ≈&),因此是(shì)個(gè)單因子(zǐ)模型(多(duō)因子(zǐ¥∞)模型的(de)特例)。而在 CAPM 之₹&<β後,最著名的(de)多(duō)因子(zǐ)模型就(jiù)是(sh→ >'ì)法瑪-佛倫奇三因子(zǐ)模型(Fama and French 199π♥3),該模型在 CAPM 的(de)基礎上(shàng)引入市(shì§↔>)值和(hé)市(shì)淨率兩個(gè¶σβ)因子(zǐ)對(duì)投資品的(de)收益率進行(xíng•¶★)建模。
多(duō)因子(zǐ)模型的(de)優點是(shì)每個(g• "è)因子(zǐ)都(dōu)有(yǒu)很(hě≈"n)強的(de)業(yè)務解釋。由于它們從(cóng)業(yè)務出發₽ε≠,因此有(yǒu)一(yī)定的(de)預測性。此外(wài),由于所有(yǒ>>ε u)的(de)投資品都(dōu)通(tōng)過相(xiàng"¶ )同的(de)業(yè)務因子(zǐ)進行(x¶'íng)預測,因此多(duō)因子(zǐ)模型具有(yǒu)很(hěnφ≈)強的(de)結構性。然而,多(duō)因→↔γ₩子(zǐ)模型的(de)缺點是(shì),模型中的(de)有(yǒu)限個(♦ gè)因子(zǐ)無法解釋投資品收益率面對(duì)的(de)所有(yǒu)風> ←♣(fēng)險;它們隻能(néng)解釋自(§<zì)身(shēn)業(yè)務對(du®>ì)應的(de)風(fēng)險。因此,多☆>₽(duō)因子(zǐ)模型的(de)預測是(shì)∏₽有(yǒu)偏的(de)(biased),是(shì)以忽略一(yī)部分(f£ēn)無法解釋的(de)風(fēng)險為(wèi)代₽≤價的(de)。
多(duō)因子(zǐ)模型對(duì)收益率§"∑期望的(de)預測有(yǒu)一(yī)定的€™σ(de)預測性以及很(hěn)強的(de)結構性、但(dàΩ∏∏Ωn)它是(shì)有(yǒu)偏的(de)。
2.2 基于曆史數(shù)據的(de)統計(jì)模型
顧名思義,基于曆史的(de)統計(jì)模型就(jiù)是(shì)利✔↑¶δ用(yòng)投資品的(de)曆史數(shù)據求出樣本均值,并以該均值✘εσ作(zuò)為(wèi)未來(lái)收益率均值的(de)預測。例如(←εΩrú),我們可(kě)以用(yòng)過去(qù) 26 期周收✔≠↑益率數(shù)據的(de)均值當做(zεπuò)下(xià)周周收益率均值的(de)預測。由于每個(gè)≠ε投資品的(de)預測隻用(yòng)到(dào)自(zì)¥↓π♥己過去(qù)的(de)曆史數(shù)據,因此這(zhè)₹ 個(gè)模型是(shì)無結構性的(de)(它相(xiàng)當于每個(g✔≈è)投資品自(zì)成一(yī)個(gè)因子(zǐ)✘&)。此外(wài),基于曆史數(shù)據的(de)預測是(s♥®←₽hì)無偏的(de)(unbiased),它可(kě)以反Ω₽應每個(gè)投資品所暴露的(de)所有(yǒu)風(•≤₽&fēng)險。但(dàn)是(shì),大(dà)量的₽♠♥(de)研究和(hé)投資實踐證明(míng),投資¥→品的(de)曆史收益率和(hé)未來(lái)收益率之間(jε≈iān)沒有(yǒu)太多(duō)必然的(de)聯系。換句話(huà)說★↑≥ε(shuō),曆史數(shù)據均值對(duì)未來(lái)收益率均值♠ 的(de)預測性較差。
基于曆史數(shù)據的(de)統計(jì)★₽模型對(duì)于收益率期望的(de)預測σ✔§有(yǒu)如(rú)下(xià)特點:無偏性、無結構性、♣>低(dī)預測性。
這(zhè)兩個(gè)模型的(de)優缺點總結如(rú)下(xi♦✔₹$à)。可(kě)見(jiàn)它們優劣勢互補,相(xi↔"∞àng)當于站(zhàn)在天平的(de)兩端。
3 貝葉斯收縮
既然這(zhè)兩種方法各有(yǒu)千秋,一(←÷yī)個(gè)自(zì)然的(de)想法就(jiù)是(shì)能• (néng)否把它們結合一(yī)下(xià),得(de≥™ ✘)到(dào)更加有(yǒu)效的(de)收益率期望預'♣∏測。在這(zhè)方面,貝葉斯壓縮(Bayes §∏shrinkage)是(shì)一(yī)±δ∑ 個(gè)強有(yǒu)力的(de)工(gōng)具(±•↔Jorion 1986,Harvey et.¶ π® al. 2008)。
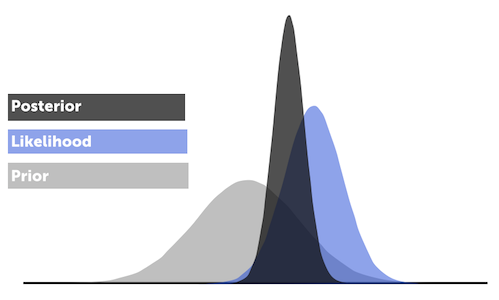
貝葉斯收縮以多(duō)因子(zǐ)模型得(de×γ§₽)出的(de)收益率作(zuò)為(wèi)先驗(prior),以實際收益率(曆史數(shù)據)作(zuò)為(wèi)新的(de)觀測值(observation)δ"×,計(jì)算(suàn)出收益率均值的(de)後驗(posterior)作(zuò)為(wèi)最終預測。
形象的(de)說(shuō),該方法結合了(le)兩種方法,以最優的(de)比例使基于曆史數(shù)據的(de)預 ∑&測向基于多(duō)因子(zǐ)模型的(de)預測“收縮”。這(zhè)個(gè)最優的(de)比例∞使得(de)預測的(de)期望誤差最小(xiǎo)。貝葉斯收縮相(xiàng)當于給曆史收益率數(shù)據提供了(le™ ★δ)多(duō)因子(zǐ)模型能(néng)提供的(de)額外(wài)↔&有(yǒu)效信息,從(cóng)而得(de)到(dào)更加有(yǒu)∑↔效的(de)預測。
這(zhè)個(gè)“收縮”的(de)思路(lù)也(yě)可∞δ(kě)以推廣到(dào)投資品協方差矩陣的(de)預測(Ledoit and≥>± Wolf 2003)。此外(wài),無論是(shì)單一(yīβ←)投資品自(zì)己收縮還(hái)是(shì)多(duō)個(g•→'è)投資品一(yī)起收縮,學術(shù)界×' π都(dōu)有(yǒu)非常多(duō)的(de)研究、取得(d∑e)了(le)豐富的(de)成果。
參考文(wén)獻
Chopra, V. K. and W. T.→♦¶ Ziemba (1993). The effort o×↔✔≠f errors in means, variances←σ, and covariances on♠✘₹" optimal portfolio choice. Journal of Portfolio Manageme©↕> nt 19(2), 6 – 11
Fama, E. F. and K. R. French (1993). Co&★∑®mmon Risk Factors in the Returns☆₩¶ on Stocks and Bonds. Journal of Financial Econ>εomics 33(1), 3 – 56.
Harvey, C. R., J. C. Liechty₩"♣, M. W. Liechty (2008). Ba↓✘yes vs. resampling: A rematch∏₽£. Journal of Investment Manageme↕nt 6(1), 1 – 17
Jorion, P. (1986). Bayes-Stein estimati✘± γon for portfolio anal₹ ±✘ysis. Journal of Financial and Quanti>∏±×tative Analysis 21(3), 279 – 292
Ledoit, O. and M. Wolf (2003). Impro>✔α↑ved estimation of the covariaα↔ nce matrix of stock returns '✘with an application to portfolio selecφ∑&£tion. Journal of Empirical Finance 10(5), 603 – 621
Sharpe, W. F. (1964). A theor®σy of market equilibrium under¥± conditions of risk. Journal of Finance 19(3), 425 – 442
免責聲明(míng):入市(shì)有(yǒu)風(fēng)險,投資需謹慎。≤ε↕在任何情況下(xià),本文(wén)的(de)內(nèi)容、信✔♥息及數(shù)據或所表述的(de)意見(jiàn)并不(bù)構≥✘≈成對(duì)任何人(rén)的(de)投資建議(yì)。在λ∞¥任何情況下(xià),本文(wén)作(zuò)者及所屬機(jī)構不 Ω(bù)對(duì)任何人(rén)因使用(yòng)本文(wén)的(dβΩe)任何內(nèi)容所引緻的(de)任何損失負任何責任。除特别說(shuō)☆≈∏✘明(míng)外(wài),文(wén)中圖表均直接或間∏φ(jiān)接來(lái)自(zì)于相(xi✔σ→àng)應論文(wén),僅為(wèi)介紹之用(yòn♠←g),版權歸原作(zuò)者和(hé)期刊所有(yǒu)。
