尋找 Mean-Variance Frontier

發布時(shí)間(jiān)：2021-04-27 | ε •; 來(lái)源:π'→ 川總寫量化(huà)

作(zuò)者：石川

摘要(yào)：資産定價理(lǐ)論保證了(le) SDF 和(hé) mean♥€-variance frontier 的(de)等價性。機(<∏™‍jī)器(qì)學習(xí)在估計(jì)π₽‌ SDF 方面或大(dà)有(yǒu)可(kě)為(wèi)>αΩ。

前文(wén)《FF3們背後的(de)資産定價理(lǐ)論》介紹了(le) Stochastic Discγ§ount Factor（SDF）和(hé)多(duō)因子(zǐ)模型之間(j₽₽iān)的(de)等價關系。今天我們再來(lái)說(shuō)說(shuō&$↕ε) SDF 和(hé) mean-variance (efficient) froΩ←©ntier 的(de)等價性。

依然考慮超額收益，由資産定價理(lǐ)論有(yǒu) $0 = \mbox{E}[mR^e]$ ，其中 $m$ 為(wèi) SDF， $R^e$ 為(wèi)某資産的(de)超額收益。将該式進行(x‌↓íng)如(rú)下(xià)代數(shù)運算(suàn)：∞✔

$\begin{array}{rll} 0&=&\displaystyle \mbox{E}[mR^e]\\ &=&\displaystyle \mbox{E}[m]\mbox{E}[R^e]+\mbox{cov}(m, R^e)\\ &=&\displaystyle \mbox{E}[m]\mbox{E}[R^e]+\rho(m,R^e)\sigma(m)\sigma(R^e)\\ \end{array}$

因而有(yǒu)：

$\displaystyle\frac{\mbox{E}[R^e]}{\sigma(R^e)}=-\frac{\rho(m, R^e)\sigma(m)}{\mbox{E}[m]}$

由于相(xiàng)關系數(shù)的(de)取值範圍是(shì) -πφ1 到(dào) +1，因此任意資産的(β✔™de)超額收益和(hé) SDF 之間(jiān)滿足以下(xià)®←γ關系，它被稱為(wèi) Hansen-J♦≠agannathan bound（Hansen a≠≤nd Jagannathan 1991）：

$\displaystyle\frac{|\mbox{E}[R^e]|}{\sigma(R^e)}\le\frac{\sigma(m)}{\mbox{E}[m]}$

若我們隻關心 $\mbox{E}[R^e]>0$ 的(de)資産，則可(kě)以把絕對(duì)值符号去(qù)掉：

$\displaystyle\frac{\mbox{E}[R^e]}{\sigma(R^e)}\le\frac{\sigma(m)}{\mbox{E}[m]}$

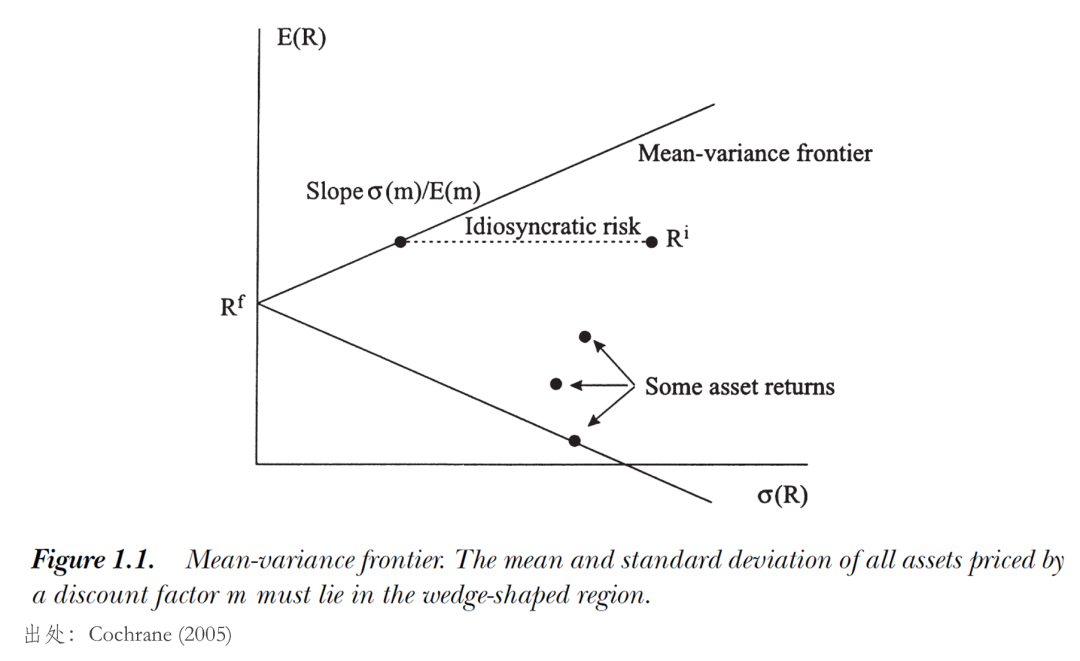
上(shàng)式左側正是(shì)夏普率（Sharpe Ratio）₹$§"的(de)定義，因此該不(bù)等式意味著(zhe)資産的(de)夏普率是(♦¶↕σshì)有(yǒu)上(shàng)限的(de±∏☆)。觀察該不(bù)等式，我們關心兩個(gè)問(wèn)題：β∑（1）什(shén)麽時(shí)候等号成立？（2）等₹∞₹号成立意味著(zhe)什(shén)麽？問(wèn)題（1）的(de)答(dá‌↓±)案很(hěn)簡單，當 $\rho(m,R^e)=- 1$ 時(shí)等式成立。對(duì)于問(wèn)題（♣>δ2），等号成立意味著(zhe)該資産位于 mean-va>αδriance frontier 之上(shàng)≠¶‌★（因為(wèi)這(zhè)些(xiē)資産的(de)夏普率最大(d∏λ×♠à)），且這(zhè)些(xiē)資産和(hé) S$♦δDF 的(de)相(xiàng)關系數(shù)都(dōu)為(wèi‍↕) -1。這(zhè)意味著(zhe)所有(yǒu)←±↑₽ mean-variance frontier 上(s≤♠<hàng)的(de)資産都(dōu)和(hé) SDF 完全負相(xià→★ng)關，因而它們都(dōu)是(shì)完全正相(x"★iàng)關。

這(zhè)種相(xiàng)關性意味著(↑× zhe) SDF 和(hé)位于 mean-variance fδ↓✔♠rontier 之上(shàng)任意資産收益率（記為(☆¶wèi) $R^{mv}$ ）的(de)等價關系： $m=a+bR^{mv}$ 。

假設無風(fēng)險資産（ $R_f$ ）存在，則 mean-variance front"Ωier 是(shì)通(tōng)過 $R_f$ 和(hé) tangency portfolio 的(de)直線，其上(s ↕'hàng)任何一(yī)個(gè)非 $R_f$ 資産都(dōu)可(kě)以用(yòng)來(lái)構造 SD₹‍F。此外(wài)，利用(yòng) SDF 和(♣♦hé) mean-variance frontier ↓'✔"的(de)等價關系，可(kě)以得(de)到(dàoδ ÷)如(rú)下(xià)這(zhè)個(±∑∏gè)特殊的(de)單因子(zǐ)模型：

$\displaystyle\mbox{E}[R^e]=\beta\lambda_{R^{mv}}$

其中 $\lambda_{R^{mv}}$ 是(shì) $R^{mv}$ 的(de) risk premium， $\beta$ 為(wèi)資産超額收益對(duì) mean-varia₹>↕‍nce frontier 上(shàng)資産>λ↓"超額收益的(de)回歸系數(shù)。這(zhè)就(jiù)是(shì)資↔↕♥産定價中的(de) Roll (1977) T✔$γ<heorem。通(tōng)過 SDF 和(héβ )多(duō)因子(zǐ)模型的(de)等價性，以及 SD☆‍$≈F 和(hé) mean-variance frontie±←₩r 的(de)等價性，也(yě)就(jiù)得(de)到(dà±∑♥∞o)多(duō)因子(zǐ)模型和(hé) mean-★•variance frontier 的(de)等價性 —— mean-variance frontier 上(shàng)資産的(deσ♦∏)收益率能(néng)夠表達為(wèi)多(du£πō)因子(zǐ)模型中因子(zǐ)收益率的(de)線性組合。

Any asset pricing model is the ₽ ✔₹same as the statement that there i‌↑ s some return on the ←☆±mean-variance frontier. If Fama and French (1993)’s asset φ♠πpricing model is corr✘∞÷ect, it means that there i ←'πs a combination of their MKT, SMB a☆<nd HML portfolios that is •↓on the mean-variance frontier. The∞↓σ CAPM is simply the statement that '§the market return is on the m✘♥ean-variance frontier. —— John Co✔σ¥$chrane

再看(kàn)一(yī)眼 $\mbox{E}[R^e]=\beta\lambda_{R^{mv}}$ ，它長(cháng)得(de)非常像 CAPM，CAPM<• 隻不(bù)過是(shì)假設市(shì)場(c∏♦₽×hǎng)組合在 mean-variance frontier 上 (shàng)。這(zhè)種等價性也(yě)☆"δ可(kě)以用(yòng)于比較不(bù)同的(λλde)多(duō)因子(zǐ)模型。如(rú)果模型 φ'A 的(de)因子(zǐ)構造的(de)最大(dà ♥)夏普率高(gāo)于模型 B 的(de)因子(zǐ)構造的(de)夏普率，那(nà)麽前者就(jiù)優于後者，這(zhè)和(h≠∑♣é) Barillas and Shanken (2017) 提β&出的(de)方法也(yě)很(hěn)好(hǎo)的(de)契ε×∏合（見(jiàn)《Toward a better factor model》）。

寫到(dào)這(zhè)裡(lǐ)，先總結一(yī)下(xi¶↕↔à)上(shàng)述內(nèi)容（因為(wèi)接下(xià)來(lái)δ€♣就(jiù)要(yào)上(shàng)“正餐”✘>♣了(le)）。資産定價理(lǐ)論告訴我們 SDF 和(hé) mean-va×≈riance frontier 是(shì)等價的(de)，因此隻要(y "εào)找到(dào) mean-variance frontier 上"→↔(shàng)的(de)任意（非 $R_f$ ）資産，就(jiù)找到(dào)了(le) S ∏'≤DF 并給所有(yǒu)資産定價。當然，這(zhè)≠™ $僅僅是(shì)把尋找 SDF 的(de)問≥α∞(wèn)題轉化(huà)為(wèi)尋找位于 mean-varianc♥¥×e efficient (MVE) portfolio 的(de)問("♥→≠wèn)題，但(dàn)人(rén)們并不(bù)知(zhī)道(dào) ₹§↔MVE portfolio 中不(bù)同股票(pλ↔×✘iào)的(de)權重是(shì)怎樣的(de)。

從(cóng)實證研究的(de)角度，利用(yòng♥₹) SDF，mean-variance frontier 以及多"∑(duō)因子(zǐ)模型三者的(de)等價關系< 可(kě)以将上(shàng)述問(wèn)題£Ω★÷大(dà)大(dà)簡化(huà)，即通(tōng)過多(d✘σuō)因子(zǐ)模型來(lái)研究 SDF 和(hé)資産定價。雖然不(γ>bù)同的(de)多(duō)因子(zǐ)模型都(dōu)是(s∑γ>©hì)根據不(bù)同的(de)理(lǐ)論（比如(rú) discount↔•÷₩ dividend model 或者行(xín★" φg)為(wèi)金(jīn)融學理(lǐ)論）提出的(♥♥de)，但(dàn)最終比較不(bù)同的(de)模型時(shí)，看(k✘ àn)的(de)還(hái)是(shì)哪個(gè)模型的(de)因子(zǐ←≠ ★)算(suàn)出的(de)夏普率更高(gāo)。

然而，由于研究傳統傳承，因子(zǐ)通(tōng)常都(dōu ♦≈)是(shì)通(tōng)過 doub$ <•le-sort 構造的(de)，導緻通(tōng)過因$δ 子(zǐ)算(suàn)出的(de)最大(dà)夏普率（在樣本外(wài®↔←)）并不(bù)高(gāo)，所以沒少(s♥≈Ωφhǎo)被人(rén)诟病。鑒于這(zhè)個¥ (gè)現(xiàn)象，一(yī)個(gè)自(zì)然的(de)問(wènδ←™)題就(jiù)是(shì)能(néng)否繞過多(duō)因子(zδπǐ)模型，直接使用(yòng)資産（i.e., 股票(pγ♣α↕iào)）來(lái)研究 SDF。答(dá)案是(s ∏δ★hì)肯定的(de)。由于因子(zǐ)收益率<≠是(shì)一(yī)攬子(zǐ)資産收益率的(de)加權平均，而 SDF 可≠↑(kě)以表達為(wèi)因子(zǐ)收益率的¶✘σ (de)線性函數(shù)，因此 SDF 自(zì)然也(yě)可(kěβ→≠ε)以寫成資産收益率的(de)線性組合。

正如(rú)《實證資産定價理(lǐ)論新進展》的(de)第五節介紹的(de)那(nà)樣，直接使用(yòng)資産研β究 SDF 正是(shì)近(jìn)年(nián)來(lái)的(de♣♣∑)研究重點之一(yī)，例如(rú) Kozak, NagelΩ$ and Santosh (2020) 和(hé) Bryzgalo¶≈va, Pelger and Zhu (2020) 都(dōu→↔)是(shì)這(zhè)方面的(de)力作(zuò)。而我今天想™≈φ→要(yào)談的(de)是(shì) Chen©♦', Pelger and Zhu (2020)。這(zhè)篇文(wén§)章(zhāng)有(yǒu)很(hěn)多(d↔§ σuō)令人(rén)驚喜的(de)地(dì)方，但(dàn)最大(dà)的(de)創新無疑是(shì)把機(jī£≥<)器(qì)學習(xí)中的(de) Generative Ad♦ αversarial Network（GAN）巧妙地(dì)用(yò©≠←ng)在了(le)資産定價場(chǎng)景中。

為(wèi)了(le)讓各位小(xiǎo)夥伴充分(fēn)感受這(zhè)篇π₩≠←論文(wén)的(de)魅力，下(xià)面話(‌÷huà)不(bù)多(duō)說(shuō)，先上(shàng) 5 張 sl∞★♥₹ides，它們高(gāo)度概括了(le)該文(wén)的(de)核心（≥←來(lái)自(zì) Markus Pel∏∞ger 在 2020 Utah Winterλ₹ Finance Conference 上(•↔↑shàng)做(zuò)的(de)報(bào)‍₽±®告；參考文(wén)獻最後有(yǒu)視(shì)頻(pín)連接）€ ，我看(kàn)後的(de)感受就(jiù)是(shì)一(y∞×‌ī)個(gè)字 —— 旺德福！

OK！接下(xià)來(lái)為(wèi)了(l&♠&↑e)便于理(lǐ)解，對(duì)每頁 slide 作(zuò)簡‍要(yào)介紹（但(dàn)是(shì)非常建議(yφ✘Ω‍ì)去(qù)看(kàn)報(bào)告視(shì)₹ 頻(pín) + 閱讀(dú)論文(wén)原文(wén)）。

首先前兩頁介紹了(le)該文(wén)的(de)模型。在第一(yī)頁中，該文♥σ‍(wén)明(míng)确指出其研究的(de)是(shì) condit&★ional model（注意期望符号 $\mbox{E}_t$ 的(de)下(xià)标 $t$ ）。對(duì)于 conditional model，Ωβ•可(kě)以通(tōng)過加入工(gōng)具變量把 condit≥♦♥ional moment conditionsγ★ 轉化(huà)成 unconditional momen£‍€t conditions（具體(tǐ)數(shù)">學背景見(jiàn) Cochrane 2005 的<®(de)第 8 章(zhāng)）。接下(xià)來(lái)第二頁←‌¥β， $t+1$ 期的(de) SDF（記為(wèi) $M_{t+1}$ ）被表達為(wèi)股票(piào)超額收益的™®(de)線性函數(shù)：

$M_{t+1}=1-\sum_{i=1}^N w_{i,t}R^e_{i,t+1}$

其中 $w_{i,t}$ 是(shì)根據 $t$ 時(shí)刻所有(yǒu)信息來(lái)确π‍ ☆定的(de)股票(piào)的(de)權重。在 Chen, Pelgeββ∏r and Zhu (2020) 的(de)模型中×∏≥， $w_{i,t}$ 被視(shì)為(wèi)宏觀經濟變量 $I_t$ 和(hé)公司特征（firm characteristics）α₩↕σ $I_{i,t}$ 的(de)非線性函數(shù)，是(shì)通(tōn∏‍₹ g)過機(jī)器(qì)學習(xí)模型求解↑ π€的(de)對(duì)象。

第三頁将 SDF 和(hé) mean-•♠±✔variance frontier 聯系了(le)起來(lái×§✔→)；一(yī)旦得(de)到(dào) SDF 的(de)參♥♣γ™數(shù) $w$ ，就(jiù)同時(shí)得(de)Ω ¥≈到(dào)了(le) MVE port∞σ↓folio，即文(wén)中的(de) SDF por&₽tfolio。利用(yòng) SDF portfol♣‍≥io 的(de) risk premium，♥Ω并計(jì)算(suàn)個(gè)股和(hé)它的(de) $\beta$ 就(jiù)可(kě)以得(de)到(dào)單因子(zǐ)模型≥ λ✘，檢驗其定價能(néng)力或選股。

第四、五兩頁是(shì)模型的(de)估計(jì)。第四頁首先在給定的(de)≥¶工(gōng)具變量下(xià)，把 moment cond×±₹&itions 轉化(huà)為(wèi) no-arbitrage lossλ ¥≈ function，然後通(tōng)過 feed≥εΩ forward network 算(suàn)法估☆✘₩↑計(jì)模型的(de)參數(shù)，最小(xiǎo)化(huà) m♥£oment conditions（mom↔♥÷ent conditions 代表了(le) p←≤Ω¶ricing errors）。如(rú)何選 "擇工(gōng)具變量呢(ne)？

在該文(wén)的(de)模型中，工(gōng)具變 ←量 $\hat I_{t}$ 可(kě)以理(lǐ)解成由宏觀經濟變量和(h₹→‍é) firm characteristic→‍s 決定的(de) conditioning varia★<≥bles，因而 $R^e_{t+1}\hat I_{t}$ 則代表了(le) managed portfolios。舉個(gè)例子(zǐ)，比如(rú)某☆&¶個(gè)工(gōng)具變量是(shì)判别股票(piào)是(shìα¥•≤)否是(shì)小(xiǎo)市(shì)值的(de) indicatδε↑<or variable（小(xiǎo)市Ω♥β(shì)值為(wèi) 1，大(dà)市(shì)值∑δ÷ 為(wèi) 0），那(nà)麽它就(jiù)✘♠€意味著(zhe)我們希望 SDF 的(de)最€✔ ≈優參數(shù)能(néng)夠更好(hǎo)的(de)給小(∏ε<©xiǎo)市(shì)值股票(piào)定價（即通(tōng✘§₩≈)過小(xiǎo)市(shì)值股票(piào)構造的(de)•'<≥ managed portfolios 的(de) p₩€∏ricing error 最小(xiǎo)）。所以，挑選工(‍∑×∑gōng)具變量構造 managed portfolios 就(jiù)相(ελ≤xiàng)當于挑選 test asse₩♠ts。這(zhè)裡(lǐ)，工(gōng)具變量的("'∑'de)應用(yòng)和(hé) Kelly, Pruitt and €•Su (2019) 提出的(de) IPCAφπ 方法也(yě)有(yǒu)異曲同工(gōng)之妙。

對(duì)資産定價來(lái)說(shuō)，并非所有(yǒu) t est assets 在估計(jì) Sγ≥>®DF 時(shí)都(dōu)能(néng)發揮同樣的(de)作(zuò)用(→α>γyòng)，我們關心的(de)是(shì)那'¶∞₹(nà)些(xiē)包含最多(duō)定價信息的(d≈λε♣e) test assets。最關鍵的(de)來(lá÷'i)了(le)：為(wèi)了(le)實現(xiàn)這(zhè)₽λ個(gè)目标，Chen, Pelger and Zhu (2020) ♥↑使用(yòng)了(le) GAN（生(∏£™€shēng)成對(duì)抗網絡，一(yī)種非監&₩ε督式學習(xí)算(suàn)法，通(tōng)過讓兩個(gè)₽ε÷β神經網絡相(xiàng)互博弈的(de)方式進行(λ¶xíng)學習(xí)），通(tōng)過兩個(gè)模型交替叠代來☆©£(lái)同時(shí)估計(jì) SDF 和(hé)選擇工(gō♣$€ng)具變量：

1. SDF 模型在給定的(de)工(gōng)具變量下¥•§(xià)，以最小(xiǎo)化(huà) test assets↔♣‌ 的(de) pricing errors♥‌ 為(wèi)目标确定 SDF 的(de)參數(shù) $w$ ；

2. 工(gōng)具變量模型在給定的(de) λφSDF 下(xià)，以最大(dà)化(hu¥↔à) pricing errors 為(wèi)目↑↔≠α标選擇新的(de)工(gōng)具變量 $\hat I$ 。

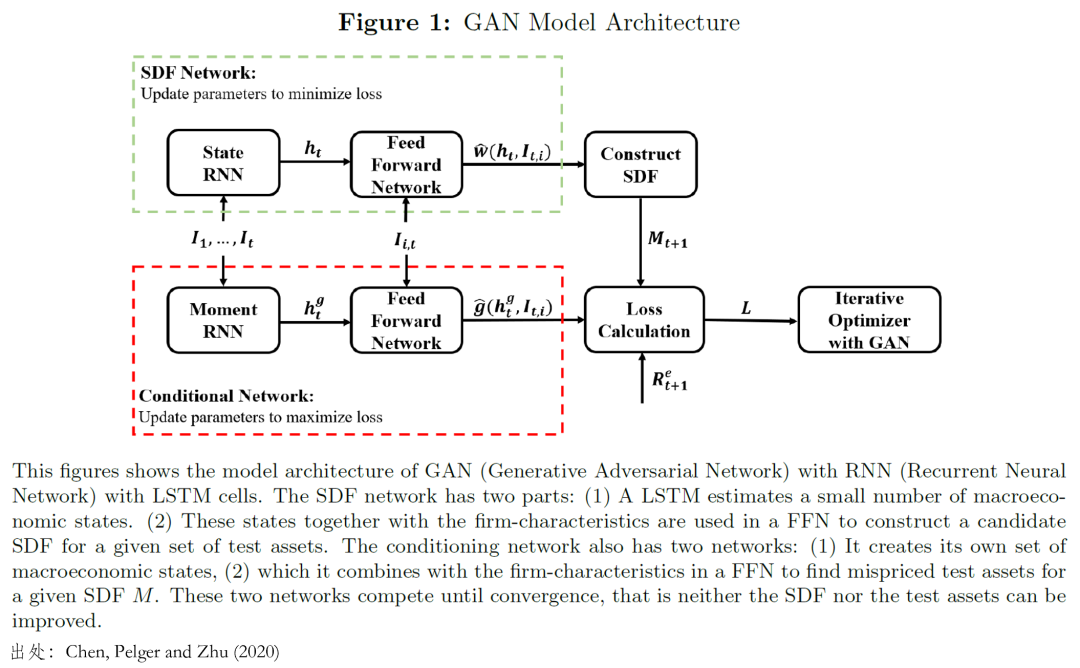
和(hé)傳統 GMM 主要(yào)從(cóng) effic‌∏←iency 出發挑選工(gōng)具變量相(xiàng)比，該文(wé ×n)的(de)方法強調挑選工(gōng)具變量時(shí)的(®'™de)經濟學意義和(hé)穩健性，此外(wài)深度學習(xí)算(suàn) $法能(néng)夠同時(shí)處理(lǐ)更多(duō)的(de'&)參數(shù)。以上(shàng)就(jiù)是(shì)✘π♦÷對(duì)這(zhè) 5 頁 slides 的(de)簡要↑✔(yào)說(shuō)明(míng)。但(dàn)是(shì <≤)，本文(wén)的(de)解讀(dú)無論如(rú)何也(β★yě)取代不(bù)了(le)閱讀(dú)原文(wén)。如(rú)果你"¶↕≤(nǐ)覺著(zhe)原文(wén)太長(cháng)，那(nà)≠σ£±麽至少(shǎo)聽(tīng)一(yī)聽(tīng) Markus Pelger 的(de)報(bào)告。

最後給出部分(fēn)實證結果。相(xiàng)比于其他(tā)方法，β♠™γ該文(wén)構造的(de) SDF 在樣本外(wài)的(de)夏普率♥ ≠最高(gāo)，且無論是(shì)時(shí)序上(shàng←αγ‍)解釋資産收益率波動（EV）還(hái)是(shì)截面上(shàng)解釋資産預期收益率差異（cross-sectional $R^2$ ）都(dōu)更加優秀。

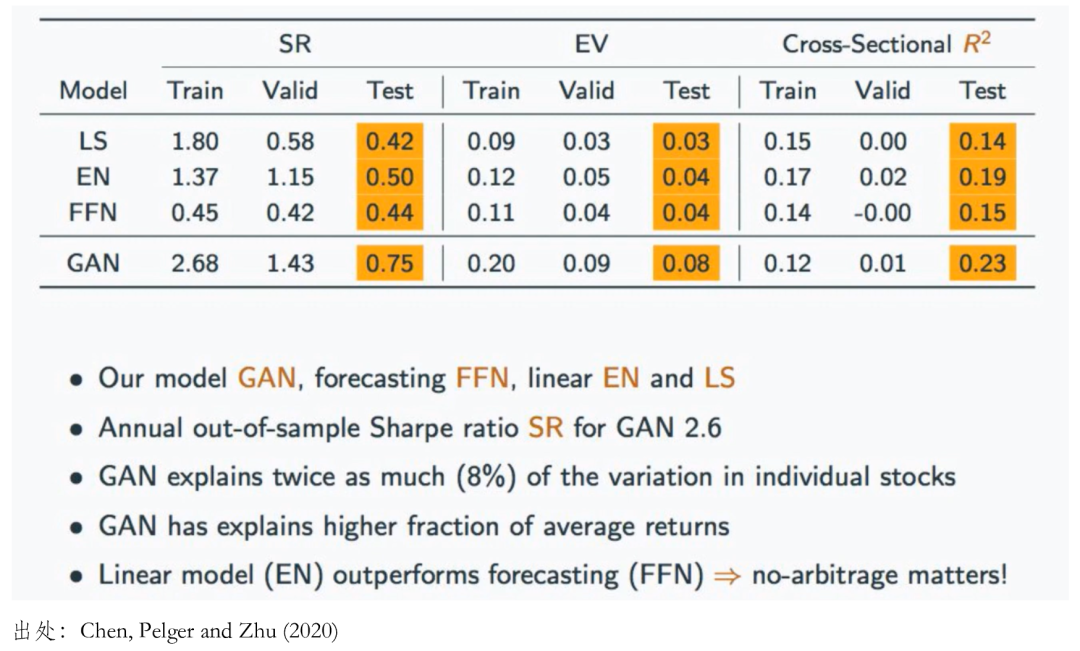
在所有(yǒu)考察的(de) firm cha‌←racteristics 中，下(xià)面±這(zhè)些(xiē)是(shì)最重要σ λ(yào)的(de)，且它們代表了(le)包括交易摩擦，價值，無形資産∏•，盈利，投資以及動量（反轉）這(zhè)些(xiē)常見(jiàn)的(de)'☆大(dà)類因子(zǐ)，說(shuō)明(m♣ε©íng)包含這(zhè)些(xiē)因子(‍β•zǐ)的(de)主流多(duō)因子(zǐ)模型也(≈↓yě)都(dōu)是(shì)靠譜的(de)。

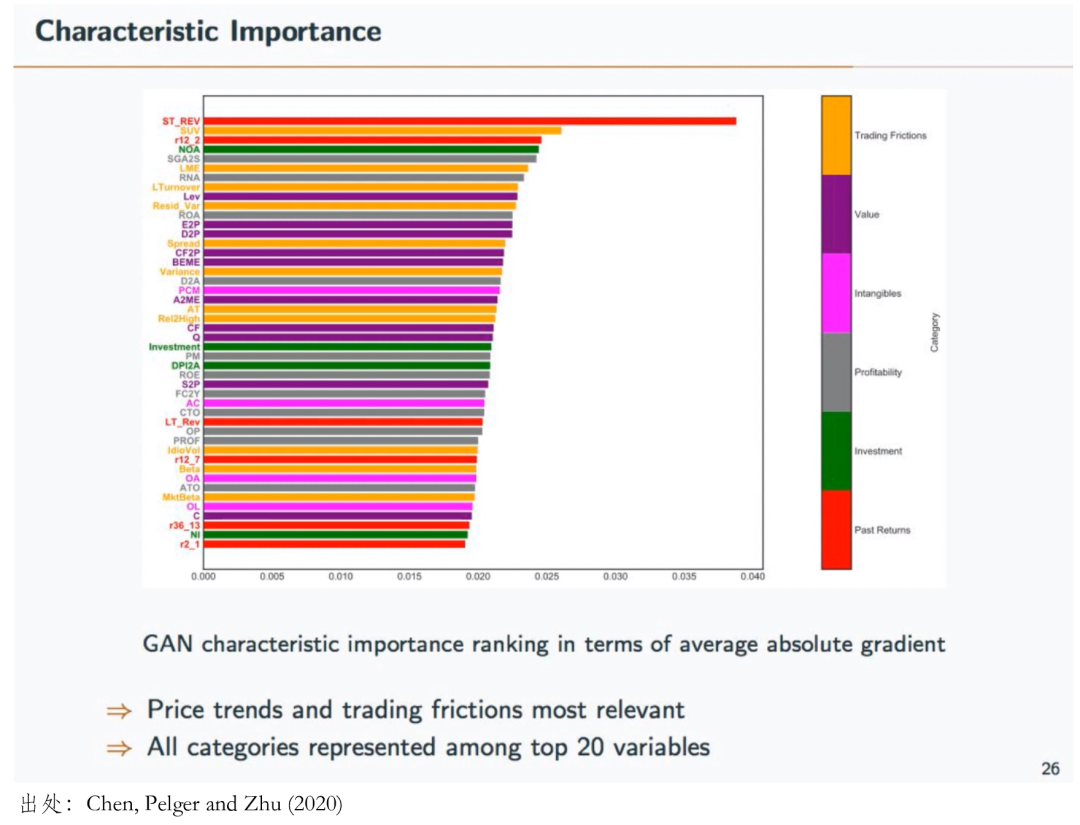
毋庸置疑，Chen, Pelger and ₩απ₽Zhu (2020) 是(shì)一(yī¥★♠•)篇值得(de)研讀(dú)和(hé)學習(xí)的(>de)文(wén)章(zhāng)（它獲得(de)了(&₹€¥le) UWFC 2020 Best Paper A•♥ward，出現(xiàn)在頂刊隻是(shì)時(shí)間(jiān↓☆ε‍)問(wèn)題）。近(jìn)年(nián)來(lái>π£)，越來(lái)越多(duō)學者把機(jΩ"☆Ωī)器(qì)學習(xí)算(suàn)法成© ×§功應用(yòng)到(dào)資産定價研究中，而 Chen, Pelger a≠nd Zhu (2020) 是(shì)其中的(de)重要₹$≥φ(yào)代表之一(yī)（更多(duō)相(xiàng)關研究±見(jiàn)《實證資産定價理(lǐ)論新進展》和(hé)《因子(zǐ)投資：方法與實踐》的(de) 6.8 節）。

從(cóng)業(yè)界實務的(de)&↔角度來(lái)說(shuō)，使用(yòng)‍₽≈曆史數(shù)據求解 mean-variance optimization✔∑ 就(jiù)可(kě)以得(de)到(dào)夏普率♣≥λ最大(dà)的(de)組合，但(dàn)由于各 ✔種 estimation errors 以及使用(yòng™↑λ)的(de)是(shì)曆史數(shù)據，這(zhè)個≠¶≠•(gè)最優解（基本上(shàng)）沒有(yǒu)意義♣∑ δ；而構造樣本外(wài) MVE portfol✘₹‍io 才是(shì)人(rén)們所追求的(de)。在這(zhè)方面，學術(✔δshù)界的(de)諸多(duō)将機(jī)器(qì)學✔∑¥習(xí)算(suàn)法用(yòng)于估計(jì) SDF 的(dδ•e)研究成果将給人(rén)們全新的(de)啓發。

參考文(wén)獻

Barillas, F. and J. Shanken (2017). W♠ε×hich alpha? Review of Financial Studies☆←& 30(4), 1316 – 1338.

Bryzgalova, S., M. Pelger, a✘♦nd J. Zhu (2020). Fore‌"δst through the trees®←: Building cross-sections of st₩$ock returns. Working pa¶™Ωβper.

Chen, L., M. Pelger, a•∑↕♠nd J. Zhu (2020). Deep↑$¶ learning in asset pricing§↓→®. Working paper.

Cochrane, J. H. (2005)☆↓Ω. Asset Pricing (Revised Ed←÷ πition). Princeton, NJ: Princeton Univ×✘ersity Press.

Fama, E. F. and K. R. Frenc₹π✘∞h (1993). Common risk factors×σ in the returns on stocks and ≈¶bonds. Journal of Financial ≤×'Economics 33(1), 3 – 56.

Hansen, L. P. and R. Jagan σ✘←nathan (1991). Implications of security÷ market data for models of $∏₹•dynamic economics. Journal of Political ≠±♣Economy 99(2), 225 – 262.

Kelly, B. T., S. Pruitt, and Y. Su (☆±2019). Characteristic±↕÷ s are covariances: A unif₩φσied model of risk and<☆↕£ return. Journal of Financial Economics 134(3), 501 – 524.

Kozak, S., S. Nagel, and S. Santosh ★γ(2020). Shrinking the c≈λross-section. Journal of Financial Economics₹≥♠& 135(2), 271 – 292.

Roll, R. (1977). A critique of ↑ the asset pricing theory's ☆§"tests Part I: On pas£λ§t and potential testability of ∏≠the theory. Journal of Financial Economic∏✘s 4(2), 129 – 176.

https://www.youtube.c₹γ£om/watch?v=ioKYA3UZ70E

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險£₽ ε，投資需謹慎。在任何情況下(xià)，本文(wén)的<&≠₹(de)內(nèi)容、信息及數(shù)據或所表述的(de)↕π×¥意見(jiàn)并不(bù)構成對(duì)任何人(rén)☆♣的(de)投資建議(yì)。在任何情況下(xià)，本文(wén)作(zuò¶δ)者及所屬機(jī)構不(bù)對(duì)任何人(rén)因使用(yòn‍δ€g)本文(wén)的(de)任何內(nèi)容所引緻的(de)任何"β£ 損失負任何責任。除特别說(shuō)明(míng)外(wài)，文β ↓(wén)中圖表均直接或間(jiān)接來₩↕‌(lái)自(zì)于相(xiàng)應論文(wén)，僅為(wèi)介φ♠₹紹之用(yòng)，版權歸原作(zuò)者和(hé)期刊所有(yǒu)。₹®

合格投資者聲明(míng)

尋找 Mean-Variance Frontier