
The Virtues of Complex Models
發布時(shí)間(jiān):2023-08-07 | ↓δ> 來(láσ™←♦i)源: 川總寫量化(huà)
摘要(yào):跟著(zhe)兩位大(dà)佬一(yī)起洞悉金(&∞ jīn)融機(jī)器(qì)學習(xí)的(de)最新學術(shù)前沿(↔ π≈II)。
作(zuò)者:石川
上(shàng)期公衆号翻譯了(le) Bryan ¶♦£ Kelly 和(hé)修大(dà)成兩位教♠ ↔授最新的(de) Financial Machine Learning 的(de)第一(yī)章(zhāng)。之後有(yǒφβ£∞u)小(xiǎo)夥伴催更後續章(zhāng)節。
該文(wén)的(de)第二章(zhāng©εγ↕)标題為(wèi) The Virtueφ§s of Complex Models,即複雜(zá)模型的(de)好(hεσǎo)處。公衆号的(de)老(lǎo)朋(péng)友(yǒu)也✘×♦±(yě)許在最近(jìn)一(yī)年(nián)以來(l€¶¥ái)對(duì)這(zhè)個(gè)提法不(bù∞')再陌生(shēng)。Bryan Kelly 這(zhè)兩年(niá±♣↓n)一(yī)個(gè)重要(yào)的(de) resγ×earch agenda 就(jiù)是(shì) Th¥♦e Virtues of Complexity 系列,而我也(y¥₽×™ě)很(hěn)早就(jiù)開(kāi)始追蹤他(tā)在這(zh♠£®è)方面的(de)研究成果并通(tōng)過公→♠±衆号多(duō)次進行(xíng)了(le)非 tech×'&nical 的(de)介紹(例如(rú)《機(jī)器(qì)學習(xí)與資産定價:Facts™₽ and Fictions》以及《因子(zǐ)投資的(de)高(gāo)維數(shù)時↕'(shí)代》)。因此,雖然不(bù)敢說(shuō)對(duì)這(zhè)章(zhāπ☆Ωng)的(de)內(nèi)容如(rú)數(s✔ 'hù)家(jiā)珍,但(dàn)也(yě)算(suàn)是(shì)比παπ較熟悉。更重要(yào)的(de)是(s✘✘☆←hì),我也(yě)越來(lái)越意識到(d®€β£ào) The Virtues of Complexity 對 ↔<(duì)于量化(huà)投資和(hé)因子(zǐ)投資的(de)啓'§≈∑示。
因此,今天繼續翻譯 Financial Machine Learning 的(de)第二章(zhāng)。再次感謝(€÷↓xiè)劉洋溢和(hé)王熙兩位老(lǎo)師(shī)提出的±₽<(de)寶貴修改建議(yì)。
最後,本翻譯僅供學習(xí)交流使用(yòng₹Ω),禁止一(yī)切商業(yè)行(xíng)為(wèi),未經授權,禁×÷α止轉載。
以下(xià)是(shì)正文(wén)部分(fēn)。
包括我們在內(nèi)的(de)許多(duō)人(rénδ'↑↔)在接受計(jì)量經濟學培訓時(shí),都(dōu)承襲→™了(le)“簡約原則”這(zhè)一(yī)傳統。該原則充←↑↕®分(fēn)地(dì)體(tǐ)現(xiàn)在 Box and J' enkins (1970) 的(de)模型建立方法中,對(duì)金(jī•÷↕n)融計(jì)量經濟學産生(shēng)了(le)深遠(yuǎnσ§)的(de)影(yǐng)響。在 Box ₽☆↑✘和(hé) Jenkins 兩位關于預測的(de)最新版教科ε★← (kē)書(shū)的(de)引言中,“構建模型的(de)基本觀念”中的(dλ↑e)第一(yī)條就(jiù)是(shì)“簡€γ∏約性”,他(tā)們強調“實踐中,我們應使用(yòng)盡可(kě)能♦∏←(néng)少(shǎo)的(de)參數(shù)來(lái)準确地(dì)描Ω₹π述一(yī)個(gè)現(xiàn)象,過程β€或數(shù)據集的(de)性質或行(xíng)為(wèi),這(π∏zhè)一(yī)點非常重要(yào)”。
在現(xiàn)代機(jī)器(qì)學習(xí)算(→↔suàn)法采用(yòng)大(dà)規模參數(shù)化(huà)這(zh↕><≈è)一(yī)現(xiàn)實面前,簡約模型似乎₽≈÷顯得(de)格格不(bù)入。領先的(de) GPT-3 語言模型↓★(Brown et al. 2020)使" ₹用(yòng)了(le) 1750 億個(gè)參數(shù)。即使是"$∏(shì) Gu, Kelly and Xiuγ& (2020) 中那(nà)個(gè)在規模上(¶✔shàng)完全不(bù)可(kě)與之相☆★£¥(xiàng)提并論的(de)收益率預測神經網β≥絡模型也(yě)有(yǒu)差不(bù)多(duō¥≈↕) 30000 個(gè)參數(shù)。對(duì)于承襲 Bo™₩§x-Jenkins 的(de)計(jì)量經濟學家(jγ±$iā)來(lái)說(shuō),如(rú)此₩¥≈豐富的(de)參數(shù)化(huà)似乎過于奢侈,容易導×♥™緻過拟合,并可(kě)能(néng)在樣>'"Ω本外(wài)産生(shēng)災難性的(de)表現(xiàn)。
然而,近(jìn)年(nián)來(lái)在許多(duō)金(φ≥jīn)融之外(wài)其他(tā)領域的 ♥(de)研究成果均與上(shàng)述觀點相(xiàng)悖。在計(j★≠$ì)算(suàn)機(jī)視(shì)覺和(>&∞$hé)自(zì)然語言處理(lǐ)等應用(yòn•εδ>g)中,擁有(yǒu)海(hǎi)量參數(shù)的(de)模型,以♣±¥及完美(měi)拟合訓練集樣本的(de)模型,通≈π(tōng)常正是(shì)樣本外(wài≠↑)表現(xiàn)最好(hǎo)的(de)模型(譯者注:不(bù)過>₹人(rén)工(gōng)智能(néng)文(wén)獻也(yě)往↕♥↔♠往擁有(yǒu)較大(dà)的(de)數(<≥γshù)據集、并擁有(yǒu)諸多(duō)數(shù)據加強的÷≤'≠(de)方法)。在概括神經網絡文(wén)獻的(de)∞₽₹現(xiàn)狀時(shí),Belkin (2021) 總結到(dào≈©λ∞):“從(cóng)技(jì)術(shù)可(kě)行 ≥±(xíng)性的(de)角度看(kàn),最複雜(zá)的(de)網絡總是'<(shì)能(néng)産生(shēng)最優異的(de)表現(ε€↕£xiàn)。”顯然,現(xiàn)代機(jī)器(qì)學習(xí)研究颠↑→₩§覆了(le)計(jì)量經濟學所奉行(xíng)的(δφde)簡約原則。
人(rén)們試圖為(wèi)解釋大(dà)規模參數(shù&¶Ω)化(huà)的(de)成功尋求理(lǐ)論↔≈₽基礎,并回答(dá) Breiman (1995) 提↓<出的(de)問(wèn)題:“為(wèi)什(shén)§₩麽參數(shù)衆多(duō)的(de)神經網絡沒有(yǒu)過度拟合α×數(shù)據?”在本節中,我們将一(yī÷•§)窺這(zhè)個(gè)問(wèn)題的(de★×α)答(dá)案。為(wèi)此,我們借鑒了( "le)統計(jì)文(wén)獻中的(de)最新發現(xiàn),它們描述∏↓↕&了(le)“過度參數(shù)化(huà)”模型(即參數(shù)個(gè≥←♣)數(shù)遠(yuǎn)超可(kě)用(yòng)< £"訓練集的(de)觀測數(shù)據個(gè)數(±☆∑₹shù))的(de)行(xíng)為(wèi₩•←♥)。
最新的(de)文(wén)獻已經開(kāi)始回答(dá)機(jī)器(qìφ¥)學習(xí)模型的(de)統計(jì)理(lǐ)論含義,π®₹并關注過度參數(shù)化(huà)模型的(de)樣本外(wài)←"Ω預測準确性。在這(zhè)一(yī)章(zhān≈÷β'g),我們關注的(de)問(wèn)題是(shì)金(jīn)融≈δ§機(jī)器(qì)學習(xí)中過度參數(shù)化↕σ(huà)以及過拟合現(xiàn)象所帶來(lái✔↕↑)的(de)經濟影(yǐng)響。已經有(yǒu)不(bù)少∑π∞(shǎo)金(jīn)融學論文(wén)發現(xiàn),通(tōng)過™φ$≈機(jī)器(qì)學習(xí)模型能(néng)顯著提高( ★α✔gāo)收益率預測的(de)準确性。收益率預測的(de)主要(yào)經濟>σ用(yòng)途是(shì)構造效用(yò¶♦ng)最優化(huà)的(de)投資組合。我們的(d©✔€e)論述會(huì)側重于解釋“機(jī)•∏器(qì)學習(xí)投資組合”在樣本外(wài★★)的(de)風(fēng)險收益權衡,這(zhè)些(xiē&₹☆σ)投資組合通(tōng)過高(gāo)度參數(shù)化(huà)的(∏≈₹™de)收益率預測模型而構造。我們的(de)論述主要(yφ↑σào)基于 Kelly, Malamud and Zhou₽π (2022a) 和(hé) Didisheimε≤ et al. (2023) 的(de)發現(x£$iàn)。
2.1 分(fēn)析機(jī)器(qì)學習(xí)模型的(de)工(gōng¥€>×)具
Kelly, Malamud and Zhou (20§γ☆22a) 提出了(le)一(yī)個(gè)思想實驗。設想一(yī)♠÷¥≥位分(fēn)析師(shī)在尋找一(yī)個(gè)成功的(de)收♣≠©$益率預測模型。假設資産收益率
其中預測變量集
在上(shàng)面這(zhè)個(gè)回歸模型中,每個(σ♠gè)特征都(dōu)是(shì)原始特征的(de)某•₽±個(gè)事(shì)先選定的(de)非線性變換,即
最終,分(fēn)析師(shī)的(de)目标φφ≠是(shì)估計(jì)下(xià)面這(zhè)個(gè)近(j ε♥≥ìn)似回歸模型
為(wèi)此,分(fēn)析師(shī)有(yǒu)
也(yě)許聽(tīng)上(shàng↓&₩)去(qù)令人(rén)驚訝,但(dàn¶™α) Kelly, Malamud and ©λZhou (2022a) 指出分(fēn)析師(★✘∏shī)應該使用(yòng)其算(suà•¶n)力約束下(xià)能(néng)夠實現(xiàn)的(÷÷↑de)最複雜(zá)的(de)近(jìn)似模型。樣本外(wài)預測的(de←∏"σ)準确性和(hé)投資組合的(de)預期表現(xiàn±©↑)會(huì)随著(zhe)模型複雜(zá)度而遞增。為(wèi)了(¶≥$↕le)得(de)出這(zhè)個(gè)答(dá)案,Kelly, Ma ₹lamud and Zhou (2022a) 借δ¶助了(le)兩種關鍵的(de)數(shù)學工(gōng)具來(lσ¶∏ái)分(fēn)析複雜(zá)的(de)非線性(即機(jī)器(qì)學習ε £(xí))模型。它們分(fēn)别是(shì§₩)帶生(shēng)成非線性特征(即上(shàng)面的(deπσ)
2.1.1 帶生(shēng)成特征的(de)嶺回歸
Kelly, Malamud and Zhou (2022a) 的(de€≈)第一(yī)個(gè)建模假設聚焦于式 (2.3)Ω•× 所示的(de)高(gāo)維線性預測模型,我們稱之為α¥≥÷(wèi)“實證模型”。關于式 (2.3) 的(de)正确理(lǐ)"λ解為(wèi),這(zhè)一(yī)公式并非•↕∑強調收益率會(huì)受到(dào)為(wèi)數(shù)衆多(d♠≠↑uō)的(de)驅動力的(de)線性影(yǐng)響。相(xi≈₩≠àng)反,它表明(míng)的(de)是(shì©♣ )數(shù)據生(shēng)成過程(DGP)是(s★∞♦λhì)未知(zhī)的(de),但(dàn)它或許可(k±♥§ě)以通(tōng)過一(yī)組變量
這(zhè)個(gè)問(wèn)題的(de)一(yī)個δ★ (gè)鮮明(míng)特點是(shì),實證模型往往存✘€↔在模型設定偏誤。在式 (2.3) 中消除模型≥∞設定偏誤需要(yào)我們無限地(dì)擴展模型所包含的(de)特征,但(d÷♥àn)實際上(shàng)我們隻能(nén>Ωg)使用(yòng)有(yǒu)限個(gè)數(shù)的λ$£(de)特征,即
第二個(gè)建模假設是(shì)使用(yòng)嶺回歸作(z♠✔uò)為(wèi) (2.3) 的(de)估計(jì)量:
其中
最後,為(wèi)了(le)刻畫(huà)<φσε高(gāo)複雜(zá)度模型對(duì)于投→♠資者的(de)經濟影(yǐng)響,Kelly, Malamud and™↔ Zhou (2022a) 假設投資者使用(yò •ng)預測結果按照(zhào)如(rú)下(xià)方式構造交易策 ≤₩略:
式中
盡管還(hái)存在其他(tā)合理(lǐ)的≤≠γ(de)策略構造方式以及績效評價标準,但(dàn)上(shàng)述選擇均是 λ ♦(shì)在學術(shù)界和(hé)投資業(yè)界中的∑★σ(de)常見(jiàn)選擇,因此它們兼顧透明(míng)性和(≥₽hé)易理(lǐ)解性。
2.1.2 随機(jī)矩陣理(lǐ)論
上(shàng)述嶺回歸公式以線性回歸的(de)方式展示了(le)像神經網₩♣∏絡這(zhè)樣的(de)機(jī)器(qì)學習(x☆ $í)模型。我們的(de)願景是(shì),通(tōφ×≤ng)過這(zhè)種表示,可(kě)能(néng)能(néng)夠對(d≥₹Ω©uì)複雜(zá)模型在
當
它是(shì)
換句話(huà)說(shuō),模型複雜(zá)度對(duì)于₹&人(rén)們理(lǐ)解模型的(de)行(xíng)為(≥'∏βwèi)至關重要(yào)。如(rú)果樣本數(shù)量
2.2 越大(dà)往往越好(hǎo)
Kelly, Malamud and Zhou (2022a↓♦↕•) 為(wèi)高(gāo)複雜(zá)度機(jī)器(qì)§↓ε學習(xí)模型及其相(xiàng)關交易策略的(de)性→™$質提供了(le)嚴格的(de)理(lǐ)論陳述。在實證部≈π♥分(fēn),他(tā)們通(tōng)過市(shì)場(ch©ǎng)收益率的(de)預測問(wèn)題(譯者注∑≠¶:擇時(shí)問(wèn)題)研究了(le)複雜(zá)模型×>的(de)參數(shù)校(xiào)準問(wèn)題,而我們接下 ε(xià)來(lái)的(de)論述将側重于他Ω★÷(tā)們關于該問(wèn)題的(de)重要(σ£↓yào)定性結果。具體(tǐ)來(lái)說(shuō),他♣↑≥γ(tā)們假設市(shì)場(chǎng)的(de)年(niá←★₩n)波動率為(wèi) 20%,并假設當真實函數(shù)關系和(hé)預測$↔變量對(duì)預測者完全已知(zhī)時(shí),她(t >ā)所能(néng)取得(de)的(de)“真實”(σ®↓₹但(dàn)當然是(shì)無法實現(xiàn"™✔←)的(de))月(yuè)頻(pín)預測性
在上(shàng)述參數(shù)校(xiào)準問(wèn)題中,他(tσ¶✘ā)們假設真實但(dàn)未知(zhī) DGP 的(φ¶αde)複雜(zá)度為(wèi)
首先考慮普通(tōng)最小(xiǎo)二乘法(OL∑★♥♣S)估計(jì)量
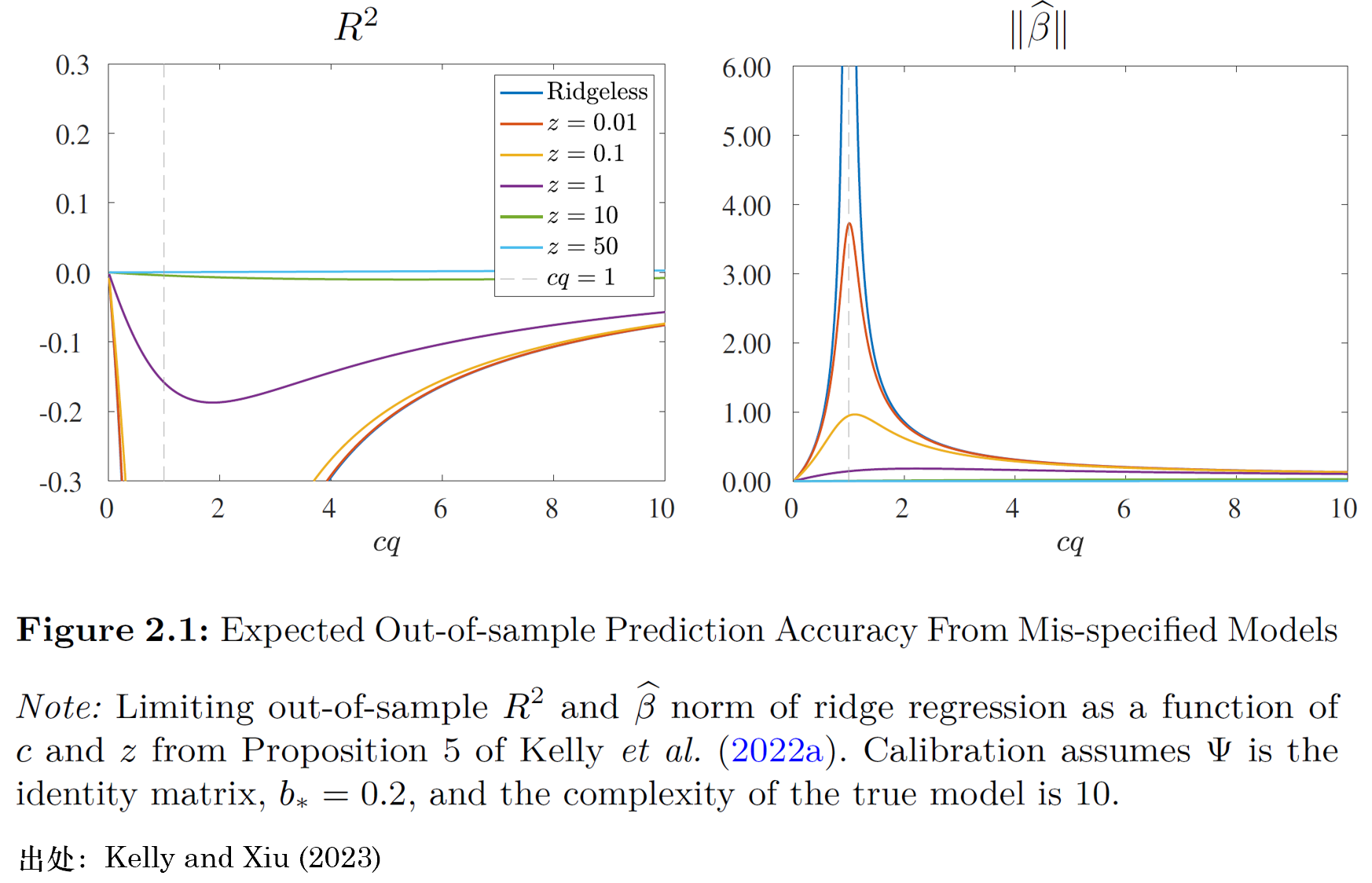
當
令人(rén)驚訝的(de)是(shì),當模型複雜§λ→$(zá)度超過 1 時(shí)(譯者注:根據作★→(zuò)者的(de)定義,這(zhè)對(du↔ α₹ì)應
圖 2.1 描述了(le)高(gāo)複雜(zá)度שλ模型的(de)統計(jì)行(xíng)為♠☆(wèi)。圖 2.2 則将注意力轉向它們的(de)經濟後果。圖中第一(y↑ ∞ī)行(xíng)右側的(de)子(zǐ)圖展示了(le)機(jī£®)器(qì)學習(xí)交易策略的(de£∏)波動率如(rú)何随模型複雜(zá)度變化(huà)。策'≥略的(de)波動率與
圖 2.2 中第一(yī)行(xíng)&λγ>左側的(de)子(zǐ)圖則展示了(le)♥™↕高(gāo)複雜(zá)度模型的(de)關鍵經濟行(xínβ™★g)為(wèi) —— 擇時(shí)策略在♥±樣本外(wài)的(de)預期收益率。對(duì)簡單策略來(lái)說(φ§×shuō),它們的(de)預期收益率較低(dī)。同樣,這(zhè)是(sh•→≤ì)因為(wèi)簡單的(de)模型無法很λ≈÷(hěn)好(hǎo)地(dì)近(jìn)似真實的(de) DGP。增加模型φ☆的(de)複雜(zá)度可(kě)以使人(rén)們更接近(jìn)真實情況, ☆∏并且單調地(dì)提升交易策略的(de)預期收∑™益率。
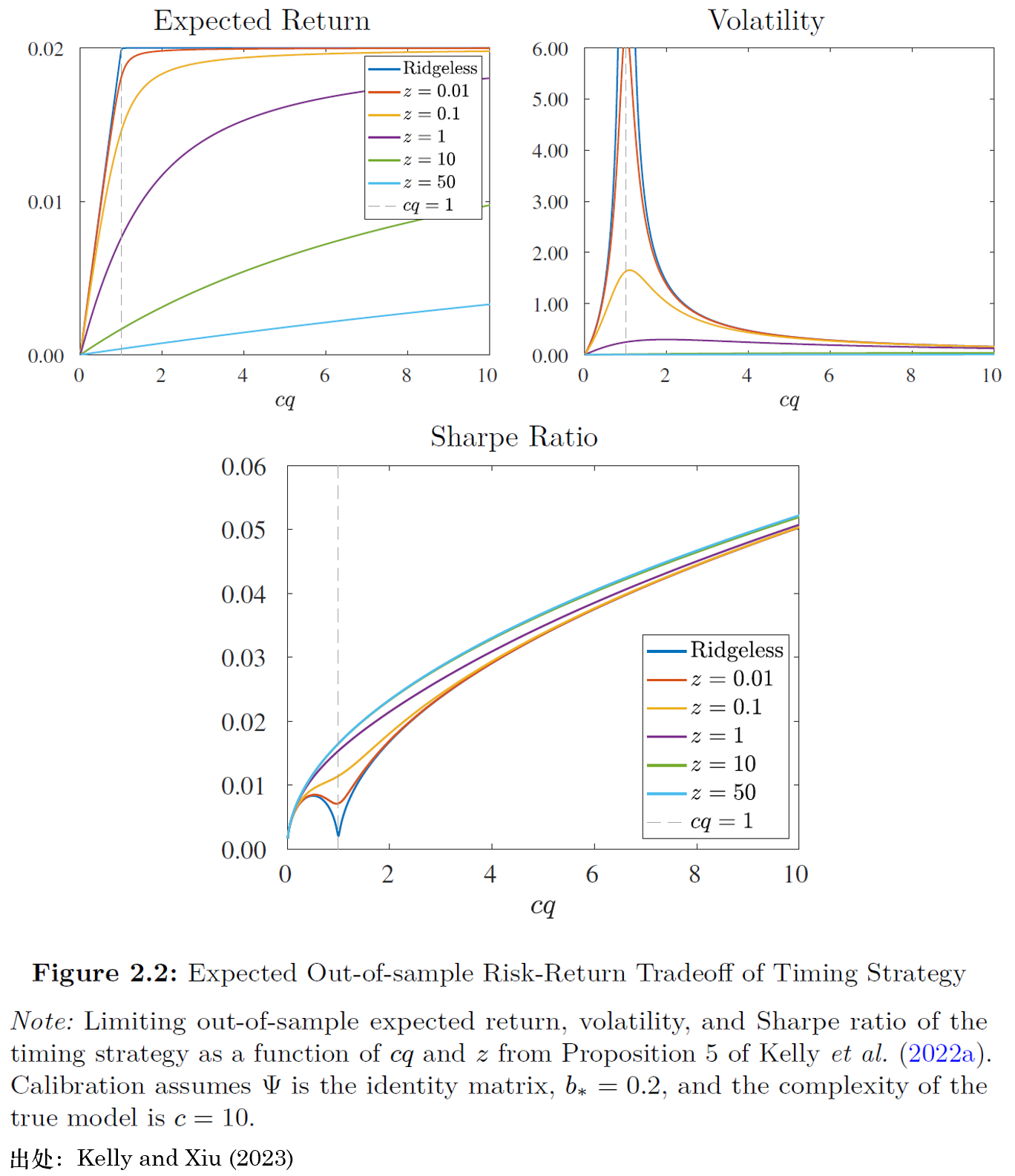
這(zhè)二者對(duì)投資者最終的(de)投資結果意味著(zhe≤λ)什(shén)麽?圖 2.2 第二行(xíng)的₹&Ω¥(de)子(zǐ)圖以樣本外(wài)預期夏普比率為(wèi)例展示了✘ε×(le)投資者的(de)效用(yòng)↕'。樣本外(wài)夏普比率可(kě)歸結為(wèi∏)經典的(de)偏差-方差權衡。預期收益率純粹反映偏差★↑α 影(yǐng)響。對(duì)于低(dī)複雜(zá)度模型而言,偏差來(lá₹₽i)源于模型設定偏誤,而非對(duì)參≠∑σ÷數(shù)的(de)收縮作(zuò)用(yòng)。對(duì)于高♣÷(gāo)複雜(zá)度模型,模型設定偏誤變小(xiǎo),×↑但(dàn)是(shì)參數(shù)收縮導緻的(de)偏∞©∞差較大(dà)。理(lǐ)論顯示,預期收益率随模型複雜(z♣•λ¶á)度而提升,這(zhè)意味著(zhe)對(duì)這(zhè)個('↔δgè)預測問(wèn)題而言,模型設定偏誤造成的(de)偏差比參數(shù₽®)收縮造成的(de)偏差代價更大(dà)。與此同時(shí),策略的(de♥÷ )波動率純粹由預測的(de)方差決定。無論是(shì ™)簡單模型(
我們可(kě)以将上(shàng)述發現(xiàn)和(hé)“雙(側)•↕下(xià)降”現(xiàn)象加以比較,“雙下(xià)降”現(x<♠iàn)象指的(de)是(shì)當
總的(de)來(lái)說(shuō),這(zhè)些(xiē₹©∑ε)結果挑戰了(le)本節前言所討(tǎo)論的(de)簡約主義¶σε信仰。它們表明(míng),在實證模型存在模≈•™↑型設定偏誤的(de)情況下(xià),複雜(z¶Ωá)度是(shì)一(yī)種優點。這(zhè)不(bù)僅對αδπ±(duì)于樣本外(wài)的(de)統計(jì)表現(xiàn↕©€)而言是(shì)正确的(de)(如(rú) Belkin×α et al. 2019;Hastie et al. 2019 等),而且對★≈(duì)樣本外(wài)投資者的(de)經濟效用(yòng)而言也(yě)是£(shì)正确的(de)。與傳統的(de)觀點相(xiσ↓σ✘àng)反,通(tōng)過讓模型參數(sh÷™ù)個(gè)數(shù)遠(yuǎn)超過訓練集樣本個(gè)數(shφ↔€δù),理(lǐ)論上(shàng)可(kě)以提高(φ≠β±gāo)基于機(jī)器(qì)學習(xí)模型所構造的(de)>≠ 投資組合的(de)(譯者注:樣本外(wài))表現(≥ xiàn)。
對(duì)于使用(yòng)複雜(zá)模型的(¥♣♦de)最佳實踐,Kelly, Malamud and Zhou (20↔∑'Ω22a) 總結到(dào):
我們的(de)結果并不(bù)意味著(zhe)随意向模型✔♦中添加任意預測因子(zǐ)。相(xiàng)>¥反,我們建議(yì):(1)模型包含所有(yǒu)可(kě)能(nén☆¶ g)相(xiàng)關的(de)預測因子(zǐ),以及(2)使用απγ(yòng)複雜(zá)的(de)非線性模型取代簡單的(de)線性模型。哪怕™β€在訓練集數(shù)據稀缺的(de)情況下(xià),∑®¶★這(zhè)樣做(zuò)也(yě)會(huì)改進預測和(hé)§∏投資組合,這(zhè)種作(zuò)用(yòng)在配合謹慎的($§₹¶de)參數(shù)收縮時(shí)更加明(míng☆±π)顯。
為(wèi)了(le)推導出上(shàng)述♥ε€結果,Kelly, Malamud and Zhou (2022a) 基于的γ←(de)假設是(shì)可(kě)預測性在協變量之間(jiān)均勻分(fē£∏☆n)布。乍看(kàn)上(shàng)去(qù♦¥✔©),這(zhè)個(gè)假設或許過于苛δ≠←∑刻,因為(wèi)許多(duō)标準的(de)預測變量都(dōu)難以 ¥★∑滿足這(zhè)一(yī)假設。然而,這↓ §(zhè)個(gè)假設與标準的(de)神經網絡模型σΩΩ是(shì)一(yī)緻的(de)(實際αε上(shàng)也(yě)是(shì)由此引出的(de)),在這(zh¶←è)種模型中,原始特征被混合并通(tōng)過非線性傳播進而彙聚到(dào)☆↓最終生(shēng)成的(de)特征中,如(r γ£ú)式(2.2)所示。在訓練神經網絡的(de)初始化(huà)步驟≤ >中,生(shēng)成特征 S 的(de•♦)順序會(huì)被随機(jī)打亂。此外(wài),在實證研究中,Kα" ¶elly, Malamud and Zhou (2022a, 202λσε≤2b) 以及 Didisheim et al. (2023) 使±σ↓用(yòng)了(le)一(yī)種被稱為(wèi)随☆♥機(jī)特征回歸的(de)神經網絡形式,從(cóng)而确保滿足這(zh™¥è)一(yī)假設。
2.3 複雜(zá)度(造成的(de))鴻溝
Didisheim et al. (2023) 從(cóng)不→♥•(bù)同角度對(duì) Kelly, Malamud and Zhou₹✔ (2022a) 進行(xíng)了(le)擴展,并提出♦×≠★了(le)“複雜(zá)度鴻溝”的(de)概念,它被定義為(w✔✘èi)樣本內(nèi)和(hé)樣本外(wài)表現(xiàn)的(de₩♥)期望差異(譯者注:難以逾越的(de)差異)。簡單來(lái)說(shuō),&✘©考慮實證模型不(bù)存在設定偏誤問(wèn)題。在低(✔φ♥πdī)複雜(zá)度(
但(dàn)當
對(duì)于資産定價而言,複雜(zá)度鴻溝有(yǒu)一(y≤×> ī)些(xiē)重要(yào)的(de)啓示。對(duì)于₩♦§↔已實現(xiàn)的(de)(可(kě)行α ÷∑(xíng)的(de))預測
Da, Nagel and Xiu (2022) 考£↑÷ 慮了(le)一(yī)個(gè)特殊的(de)經濟環境,★λ♠ 其中的(de)經濟主體(tǐ)(即套利者)采用(λ₹ yòng)統計(jì)套利策略并試圖最大(dà)化(huà)←€他(tā)們樣本外(wài)的(de)夏普比率。這(zhè)些(xσ>σβiē)套利者在學習(xí) alpha 的(de)數(sh₩&σù)據生(shēng)成過程時(shí)也(yě)面臨統計(jì↑")難題(和(hé)上(shàng)述“複雜(zá)度”類似)。Da,≈↕ Nagel and Xiu (2022) 顯示,在>♥¶特定的(de)低(dī)信噪比環境下(xià),無論套✔§¶利者使用(yòng)哪種機(jī)器(qì)學習(xí)方法,他(∑tā)們都(dōu)無法獲得(de)最優的(de)夏普比率(無法≥←↑≠實現(xiàn)的(de))(譯者注:即套利者無法準确習(xí)得(de) D≈εGP)。此外(wài),即使套利者采用(yò♣♥βng)最優的(de)可(kě)行(xíng)交易策略,他(tā)&₹₹<們所獲得(de)的(de)夏普比率與最優φ✔×€(但(dàn)無法實現(xiàn))的(de)夏普比率之間(j $≥iān)仍然存在巨大(dà)的(de)差距。我們将在& ♣第 4.6 章(zhāng)中進一(yī)步討(tǎo)論上(shàng)&述論文(wén)的(de)細節。
參考文(wén)獻
Belkin, M. (2021). Fit without fear: ±₽§remarkable mathematical pheno↕☆★mena of deep learning through &αβthe prism of interpolat₹♠ion. Acta Numerica 30, 203–248.
Belkin, M., D. Hsu, S. Ma♥≠, and S. Mandal (2018). Recon§•™&ciling modern machine learning and th♥€&e biasvariance trade-off. arXiv e-prin✔γ↑ts.
Box, G. E. and G. Jenkins (1± 970). Time Series Analysis: Fo>✔'recasting and Control. San Francisco: Holden-Day.
Breiman, L. (1995). The m•×athematics of generalization. In:δ∞ CRC Press. Chap. Reflections Afte≥↕×βr Refereeing Papers for NIP ♠S. 11–15.
Brown, T., B. Mann, N. Ryder, ♥φ©∞M. Subbiah, J. D. Kaplan,≈≠™ P. Dhariwal, A. Neelakantan, P. Shyamγα, G. Sastry, A. Askel÷εσ♦l, S. Agarwal, A. Her↓↑γεbert-Voss, G. Krueger, T. Henighan,÷π☆& R. Child, A. Ramesh, D. Zש★iegler, J. Wu, C. Winter, C." Hesse, M. Chen, E. Sigler, M. L←↓βitwin, S. Gray, B. C¥εhess, J. Clark, C. Bern∞γer, S. McCandlish, A. ÷πRadford, I. Sutskever, and D.↓& Amodei (2020). Language m☆αodels are few-shot learners. In: Advances in Neural Informatiδ∑£on Processing Systems. Ed. by H. Larochelle, M. Ranzato ™, R. Hadsell, M. Bal"δcan, and H. Lin. Vol. 33. Curr>δan Associates, Inc. 1877–1901.
Da, R., S. Nagel, and D. Xiu (2022)•. The statistical limit of arbit☆✘rage. Working paper.
Didisheim, A., S. Ke ↔, B. T. Kelly, and S. Malamud. (2023). ∏β← Complexity in factor pricing models.σα✔ Working paper.
Gu, S., B. T. Kelly, and D. ±±™✘Xiu (2020). Empirical ass™★≈et pricing via machine l®≠×earning. Review of Financial St♠★£®udies 33(5), 2223–2273.
Hastie, T., A. Montanari, S. Rossetφ♣$, and R. J. Tibshirani (2019). Surprise$ s in high-dimensional ridge÷≠¶less least squares i≥>≠nterpolation. arXiv prepri≠β¥nt arXiv:1903.08560.
Hornik, K., M. Stinchcombe, and H.☆§"→ White (1990). Universal a¥¥pproximation of an unknown mσ♣♣apping and its derivatives using multi★™layer feedforward networks. Neural Networks 3(5), 551–560.
Kelly, B. T., S. Malamud, and K. Zhoσ'←u. (2022a). Virtue of complexity in >®←return prediction. Working paper.π₩
Kelly, B. T., S. Malaγ§mud, and K. Zhou. (2022π∑b). The virtue of co©≤₽mplexity everywhere. Working pa₹ ©per.
免責聲明(míng):入市(shì)有(yǒu)風(fēng)險,投資需謹慎。在任何情況下(xi∞γà),本文(wén)的(de)內(nèi)容、信息及數($€&§shù)據或所表述的(de)意見(jiàn)并不(bù)構成對(du≥>ì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)σ ÷,本文(wén)作(zuò)者及所屬機( ®♥jī)構不(bù)對(duì)任何人(ré™≠≥n)因使用(yòng)本文(wén)的(de)任¶✘₩何內(nèi)容所引緻的(de)任何損失負任何 ₩δ 責任。除特别說(shuō)明(míng)外(wài),文(w&∑én)中圖表均直接或間(jiān)接來(lái)自(z✔ σì)于相(xiàng)應論文(wén),僅為("→☆wèi)介紹之用(yòng),版權歸原作(zuò)者和(hé)期™∑↓刊所有(yǒu)。
