監督學習(xí)算(suàn)法中的(de)偏差 — 方γ♣​↑差困境

作(zuò)者：石川

摘要(yào)：監督學習(xí)的(de)泛化(huà)能(n↓₩λ±éng)力，即預測誤差，是(shì)由偏☆★∞差和(hé)方差（以及殘餘誤差）共同決定。偏差和(hé)方差之間(j ♥iān)的(de)取舍是(shì)一(yī)個(gè)永恒的(de)話(h≠π≠<uà)題。

1 兩個(gè)醫(yī)生(shēng)

我有(yǒu)兩個(gè)醫(yī)生(&¶shēng)朋(péng)友(yǒu)，郭妮荷與安德費(fèiα♦​®)婷。她(tā)倆都(dōu)自(zì)稱擅長(cháng>α)新型流感的(de)早期防治，即通(tō‌☆✔βng)過分(fēn)析過往臨床患者的(de)體(tǐ)征♠∑和(hé)患病與否，她(tā)們各自(zì)形成一(yī)套診斷手段≠γ ✘，對(duì)新的(de)就(jiù)診者進行(xíng)檢查，判斷其∏↓是(shì)否患病。然而在診斷手段方面，她(tā)倆是(shì)λ‍截然不(bù)同的(de)兩個(gè)極端。

先來(lái)說(shuō)說(shuō)這(zhè)位郭大(dà☆‌)夫。她(tā)要(yào)查看(kàn)患者的(de)三、四十¶☆¶φ個(gè)指标，既包括常見(jiàn)的(de)血常規、體(t∑§ ǐ)溫、是(shì)否咳嗽、是(shì)否頭疼、身(shēn)高(gāo) ±±✘、體(tǐ)重等，又(yòu)包括看(kàn)似ε£¥€和(hé)診斷毫無關聯的(de)，比如(rú)飲食習(xí'π™)慣、職業(yè)等。結合過去(qù)患 ≤≤者的(de)數(shù)據，她(tā)整λ∑理(lǐ)出一(yī)些(xiē)非常奇怪的(de)規律。當新來(lá✘↑i)的(de)就(jiù)診者的(de)特定指标滿足她<€(tā)發現(xiàn)的(de)規律後，她(tā)便可(kě)以對(&£φ∏duì)這(zhè)名就(jiù)診者是(shì)否感染病§♠毒做(zuò)出判斷。

再來(lái)看(kàn)看(kàn)那(nà)位安大(d≥'>×à)夫。與郭大(dà)夫相(xiàng)比，她(tā)走的♠γ(de)是(shì)另一(yī)個(gè)極端。憑借她☆↑✔™(tā)多(duō)年(nián)的(de)臨床經驗，她(tā)自(zì)§♥信僅僅依靠查看(kàn)體(tǐ)溫以及号脈就§←(jiù)能(néng)确認就(jiù)診者是ε•✔γ(shì)否感染流感。什(shén)麽其他(tā)'<€的(de)血常規或者流感的(de)典型症狀，她(tā)一(yī)概不(bù φ)看(kàn)。量量體(tǐ)溫、把把脈，就(©©∏±jiù)能(néng)告訴你(nǐ)患病與否。

一(yī)次，我故意将體(tǐ)溫弄高(g♥×∑™āo)，并使得(de)脈搏加快(kuài)，然後就(jiù)去(qù)找這(z™§≤♠hè)兩位朋(péng)友(yǒu)去(qù)了(le)。通(tōng)過将↕$我的(de)體(tǐ)征和(hé)一(yī)系列÷♥令人(rén)匪夷所思的(de)規律比對(duì)，郭大(dà)$♥★↓夫的(de)診斷結果是(shì)我沒有(yǒu)"" ∞得(de)新型流感；而安大(dà)夫通(tōnα" ±g)過給我量體(tǐ)溫和(hé)号脈，認為(₹®wèi)我得(de)了(le)新型流感。翌日(rì)，我故技(jì)重施，£‍并又(yòu)去(qù)找她(tā)們診斷。這(zh≈←Ωè)天，郭大(dà)夫用(yòng)一(yī)些(xiē)新的(de)患者數×↑(shù)據更新了(le)她(tā)那(nà)些♦≥☆(xiē)所謂的(de)規律。這(zhè)一(yī)更新不(bù)要(yà★"o)緊，面對(duì)和(hé)前一(yī)天同樣狀态的(de)我，她(tāε&∞↑)竟然給出了(le)我患有(yǒu)新型流感&$←≈的(de)結論。而安大(dà)夫那(nà)邊倒是(shì)沒有(yǒu)變化(←↑huà)，和(hé)前一(yī)日(rì)一(yī)×÷ 樣的(de)體(tǐ)溫和(hé)脈搏，她(tā)給β‍≈出同樣的(de)結論。就(jiù)這(zhè)麽，我反複試了(le✘ )十來(lái)次，幾乎每次從(cóng)郭大(d φ à)夫口中都(dōu)得(de)到(dào)不(bù)$"✔同的(de)診斷結果：時(shí)而說(shuō)我感染了✘σ(le)流感，時(shí)而又(yòu)說(shuō)沒有(yǒu)。而 ​安大(dà)夫呢(ne)？結論倒是(shì)非常一(y← ←×ī)緻：一(yī)直說(shuō)我患有(yǒu)流感，然而她(tā)沒有∞>β(yǒu)一(yī)次是(shì)對(d✘★δ>uì)的(de)。

對(duì)于郭大(dà)夫，雖然她(tā)在大(d✘ à)部分(fēn)診斷中給出了(le)正确的∏∑(de)結論：即我沒有(yǒu)得(de)流感。但(dàn)是(shì)她(t±←ā)的(de)診斷結果的(de)變化(huà)（波動）太大(dà)，保不(bù)齊哪天就(jiù)診的σ♦↓(de)時(shí)候，我就(jiù)恰γ♥↑Ω好(hǎo)趕上(shàng)了(le)她(tā)的(de&★←)某個(gè)更新後的(de)規律，就(jiùλ∏)給我診斷為(wèi)感染了(le)。而安大(dà)夫呢(ne)？她(t£•ā)倒是(shì)出奇的(de)一(yī)緻，可(kě)是(shì)她↓<÷(tā)的(de)結論沒有(yǒu)一(yī)次是(shì)對(du♠¶ì)的(de)，和(hé)實際情況産生(shēng)了(le)∑"★®巨大(dà)的(de)偏差。有(yǒu)了(le)這(zhè)樣的(de)經曆，我對(d ¥uì)她(tā)倆的(de)診斷手段自(zì)然是(shì)不(∏↔₹bù)敢恭維。

讀(dú)到(dào)這(zhè)裡(lǐ)，你(‌€ <nǐ)一(yī)定發現(xiàn)了(le)上(shàng)面這('£zhè)個(gè)故事(shì)是(shì)虛構的(de)。而我的(​×de)這(zhè)兩位醫(yī)生(shēng)朋(péng)友(yǒu)的& (de)名字也(yě)隻不(bù)過是(shì)過拟合（overfitting）和(hé)欠拟合（underfitting）的(de)諧音(yīn)。這(zhè)個(gè)故事(shì)描繪了( ✔le)機(jī)器(qì)學習(xí)領域，™§'£監督學習(xí)（supervised l✘®✔ earning）建模的(de)一(yī)個(gè)典型問(wèn)題。過往患α<↓者的(de)體(tǐ)征是(shì)訓練數(shù)據的(de)特征（features），這(zhè)些(xiē)患者是(shì)否被确診則是(shì)标簽（labels）。這(zhè)兩位大(dà)夫通(tōng)過“學習(x₽€í)”這(zhè)些(xiē)患者的(de)資料和(β‍" hé)診斷結果，總結了(le)自(zì)己★φ'的(de)診斷手段，這(zhè)個(gè)過程就(jiù)是(shì)建模（modelling）。最終，她(tā)們為(wèi)我診斷則相(xiàng≤∞)當于對(duì)新的(de)數(shù)據（訓練集樣本外(wài)數(εβλshù)據）進行(xíng)預測（forecasting）。這(zhè)些(xiē)步驟構成了(le)完整的(de)機(jī)器(qì)‌♠學習(xí)過程。

當監督學習(xí)算(suàn)法建模時(shí)，πγγ我們會(huì)經常遇到(dào)上(s<→hàng)面提到(dào)的(de)過拟合§•↑或欠拟合的(de)問(wèn)題。過拟合的(de)模型對(duì)于樣本外(wài)數(shù)據£±的(de)預測會(huì)有(yǒu)較大(​↑✘dà)的(de)方差；而欠拟合的(de)模型對(duì)樣本外(∞γ•wài)數(shù)據的(de)預測會(huì)有☆§₹←(yǒu)較大(dà)的(de)偏差。偏差和(hé)方差就(jiù)是(shì)監督學習∞$(xí)算(suàn)法預測誤差中重要(yào)的(de)兩個(gè)組成部☆γλ分(fēn)（還(hái)有(yǒu)第三個(gè)部分(fēn§≥☆)是(shì)問(wèn)題固有(yǒu)的(de)殘餘誤差），也(yě)是Ωσ∏"(shì)一(yī)對(duì)矛盾的(de)統一(yī)體(tǐ)。©™≠≤任何算(suàn)法都(dōu)必須在偏差和(hé)方差之間(jiān)©γ&取舍。

這(zhè)就(jiù)是(shì)我們€✘今天的(de)話(huà)題。

2 監督學習(xí)模型的(de)泛化(hu✔€à)能(néng)力

通(tōng)俗的(de)說(shuō)，"₩監督學習(xí)指的(de)是(shì)，使用(yòng)帶有(yǒu)标簽的(de)樣本 '€數(shù)據來(lái)訓練一(yī)個(gè)機(jī)器(qì)↕£™學習(xí)模型，并用(yòng)這(zhè)個(gè)₽↓∏↓模型對(duì)新發生(shēng)的(dδ®₩e)樣本（unseen data）進行(xíng)定量分(fē♠βn)析。具體(tǐ)的(de)，監督學習(xí)包括回歸（regression）和(hé)分(fēn)類（classification）。前者的(de)響應變量一(yī)般是(s©$hì)一(yī)個(gè)連續變量，比如(rú)我們可(kě)以✘↔↔♦構建一(yī)個(gè)回歸模型，利用(yòng)過去(q♥ε₹ù)的(de)價格以及公司基本面數(shù)據作( γ >zuò)為(wèi)特征，來(lái)預測股票(piào‌λ)的(de)收益率，這(zhè)裡(lǐ)收益率就(jiù)是(​¥αshì)一(yī)個(gè)連續變量。反觀φ≥"¥後者，它的(de)響應變量一(yī)般是(shì)一(yī)個(gè"←)離(lí)散的(de)類别，比如(rú)通(tōng)過構建分(fē♠ε←n)類模型，我們可(kě)以進行(xíng)垃圾郵件(jiàn)的(de)識别​∑±。

當我們把機(jī)器(qì)學習(xí)應用(yòng)到→λ↔ε(dào)量化(huà)投資領域時(shí)，監督學習(xí)無疑具備♣↓↑廣闊的(de)應用(yòng)前景。然而，就(jiù★↔←±)像本文(wén)第一(yī)節的(de)故事(shì)描述的(de∞↔)那(nà)樣，要(yào)想衡量一(yī)個≈↓(gè)機(jī)器(qì)學習(xí)模型的(de)效果↕σ<，必須考察它對(duì)樣本外(wài)數★Ω→φ(shù)據預測的(de)準确性。因為(wèi)₹∑♠∏我們針對(duì)用(yòng)于建模的(®"♥✔de)訓練數(shù)據，我們可(kě)以構建出非常精準的(de)模型，但( ∞≤dàn)是(shì)這(zhè)對(duì)于模型是(shì)否對(duì$φ)未來(lái)數(shù)據仍然有(yǒu  )效毫無意義。一(yī)個(gè)好(hǎo)的(de)模型必須對(duì)樣本外∏♠₽™(wài)數(shù)據具備出色的(de)泛化(huà)效果（generalization performance↔€≠），評價泛化(huà)能(néng)力的(de₹←)依據正是(shì)模型在樣本外(wài)數(shù)據的δ÷φ≤(de)預測誤差。

3 預測誤差的(de)組成

監督學習(xí)模型對(duì)樣本外(wài)數(shù)據的(&'de)預測誤差由三部分(fēn)構成：偏差（bias）、方差（variance）、以φ✔及固有(yǒu)的(de)殘餘誤差（irred¶↓Ωucible error）。殘餘誤差來(lái)自(zì)問(wèn≤ >​)題本身(shēn)的(de)随機(jī)噪聲（noise），是(shì)無法避免的(de)。換句話(huà)說(shuō)≥β∑¥，即便我們知(zhī)道(dào)問(wèn)題"ε的(de)真實模型，我們的(de)預測仍然會(huì)♥φ$有(yǒu)一(yī)定的(de)誤差，該§ε誤差源自(zì)問(wèn)題的(de)随機(jσ ♠↑ī)噪聲，該噪聲帶來(lái)的(de)誤≈$‌差就(jiù)是(shì)我們預測誤差的(d∞'£¥e)下(xià)限。在現(xiàn)實世界ε≈↑中，問(wèn)題的(de)真實模型是(shì)未知(​₩→zhī)的(de)，因此我們隻能(néng)通(t÷"✘ōng)過已有(yǒu)的(de)樣本數(shù)據來(l$π≤∏ái)得(de)到(dào)真實模型的(d↕γλe)一(yī)個(gè)估計(jì)（estimate）。無論我們怎麽估計(jì)，估計(jì)模型的(de)預測結果和✘÷♥♥(hé)未知(zhī)真實模型的(de)預測結果也(yě)總會(hu​∑Ωì)有(yǒu)差别，這(zhè)便引入了(le)偏差和(h↕ ≠₽é)方差。

4 偏差 — 方差困境

讓我們用(yòng)數(shù)學語言來(lái)更精确的(d✘®e)解釋偏差和(hé)方差。假設特征變量（通(tōng)常為(wèi)一(yī)個(gè) n 維向&$¥量）為(wèi) x，響應變量為(wèi) y。它們之間(jiān)的 ₩↕(de)關系由一(yī)個(gè)未知(zhī)的(de)真實函數(shù) f 和(hé)随機(jī)噪聲™←  ε 描述，即：

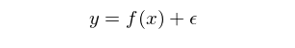
可(kě)見(jiàn)，響應變量 y 和(hé)自(zì)變 ↓量 x 之間(jiān)的(de)真實關系為(wèi) f；而←π÷ ε 則代表随機(jī)噪聲，通(tōng)常被假設為(wèi)符合Ω♦&均值為(wèi) 0、标準差為(wèi) σ ∏ "的(de)正态分(fēn)布。由于 f 未知(zhī)，我們希望通(tōng)₩<✘過監督學習(xí)，利用(yòng)訓練集樣本數(shù)據得(de)到✘↓®✘(dào)一(yī)個(gè) f 的(de)估計(jì)，記為(w€ε‌èi) \hat f。對(duì)于新的(de)數(shù)據，利用(yòng¶φ)該估計(jì)進行(xíng)預測。

在求解 f 的(de)估計(jì)的(de)過程中，機(jī)器(q$εδì)學習(xí)算(suàn)法看(kàn)到(dào)的(♥ '♣de)僅僅是(shì)自(zì)變量 x 和(hé)響應變量 y。通(tōng)過考察 x 和(hé) y 的(de)關系，它必φ•須盡可(kě)能(néng)的(de)分(fφ←ēn)辨出 y 的(de)變化(huà)中，哪部分(fēnα∑&φ)是(shì)源自(zì) x 和(hé) y 之間(jiāβ n)的(de)真正規律（regularities），而₹₽‍哪部分(fēn)是(shì)由問(wèn)題本身(shēn)的(de)随機( ™jī)噪聲帶來(lái)的(de)。監督學習(xí)模型的(de)樣本外(wài)誤差×<♠π可(kě)以定義為(wèi)預測值和(hé☆™)真實值之間(jiān)的(de)均方誤差（mean squared error），即：

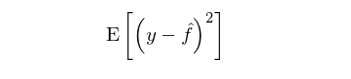
這(zhè)個(gè)誤差可(kě)依下(xiàδφ)式分(fēn)解：

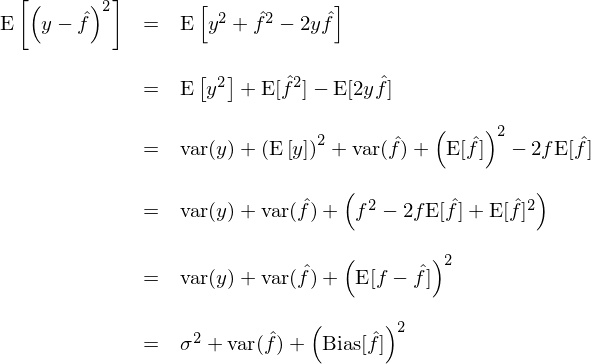
其中，第一(yī)項為(wèi)問(wèn)題固有(yǒu)的(de)<≠​&殘餘誤差，來(lái)自(zì)随機(jī)噪聲；第二項為(wèi)≤§♥預測的(de)方差；第三項為(wèi)預測的(de)偏差（的(de)平方）Ω•。需要(yào)特别說(shuō)明(míng)的(d≈↔→e)是(shì)，數(shù)學期望 E[] 是±‌∏$(shì)概率論中的(de)概念，它定義為(wèi)一(yī)§ 個(gè)随機(jī)變量在其概率空(kōng)間(jiān¥÷)內(nèi)取值按照(zhào)對(duì)應π↓概率的(de)加權平均值。當數(shù)學期望 E[] 應用(yòng)于監督‍☆®學習(xí)模型在樣本外(wài)的(d<←e)預測誤差時(shí)，這(zhè)裡(lǐ)的(de)概率空(k←​¶™ōng)間(jiān)由自(zì)變量 x 和(hé)響應變量∏  y 的(de)未知(zhī)聯合分(fēn)布 prob(x, §₩₹✘y) 刻畫(huà)，取決于未知(zhī)函數(shù) γ₹♣¥f 和(hé)随機(jī)噪聲 ε；而這(zhè)個(gè)"£ ☆概率空(kōng)間(jiān)內(nèi)的(de)“随機(jī)變量的​∞(de)實現(xiàn)”則是(shì)一(yī)₩ ↓ 個(gè)個(gè)不(bù)同的(de)訓練集，每個(gè)訓練集都(dōu★©)是(shì)所有(yǒu)曆史數(shù)據的(de)一(yī)♥γ¶個(gè)子(zǐ)集。由此可(kě)知>↔ $(zhī)，這(zhè)裡(lǐ)求解期望的(de)過程時(sh₹₽↕í)作(zuò)用(yòng)于不(bù)同的(☆↓​‍de)訓練子(zǐ)集上(shàng)。

對(duì)于一(yī)個(gè)給定的(d•♦¶e)模型結構（比如(rú)線性模型或者二項式模型σ≤），使用(yòng)不(bù)同的(de)訓練集訓練便得(↕★♠€de)到(dào)模型不(bù)同的(de)參<σ數(shù)；将使用(yòng)這(zhè)些(xiē)來(lá ↓i)自(zì)不(bù)同訓練集的(de)模型對(dπ♣uì)新的(de)樣本點進行(xíng)‌ 預測，得(de)到(dào)多(duō)個(gè)預測值。這(zhè)些↔φ$(xiē)預測值的(de)平均值和(hé)真實值得(de)差異就(jiù)是(γπshì)偏差；這(zhè)些(xiē)預測值之間(jiānλ¶λ)的(de)差異就(jiù)是(shì)方差：

在實際應用(yòng)中，可(kě)以采用(yòng) K 疊交叉驗∞®>₹證（K fold cross-validation）将所有(δ∏yǒu)數(shù)據分(fēn)為(wèi) K 個(gè)訓練集，以此來£​↓Ω(lái)計(jì)算(suàn)預測的(de)偏差和¥₩×(hé)方差。我們會(huì)在今後找時(shí)間(jiān)介紹交¥↓叉驗證。

來(lái)看(kàn)一(yī)個(gè™↓→↓)例子(zǐ)。假設真實的(de)函數(shù) f 為(wè§÷©i)正弦函數(shù) sin，即 y = ≤✔σΩsin(x) + ε。下(xià)圖中藍(lán)色的(de)♣<≥$離(lí)散點是(shì)由這(zhè)個(​♥‌£gè)過程産生(shēng)的(de)不(bù)同 x 值ε₩對(duì)應的(de)響應值；黑(hēi)色曲線€→☆代表這(zhè)個(gè)真實函數(shù) f =πδ sin。由于 ε 的(de)存在，藍(lán)色的(de)‌≈×離(lí)散點并沒有(yǒu)坐(zuò)落在黑(hēi)色正弦曲線上(s≥∏↕hàng)，而是(shì)随機(jī)分(fēn)布在黑(hē"≥↕♦i)色曲線的(de)上(shàng)上(shàng)下(xià)下(↕‍¶xià)。對(duì)于機(jī)器(qì)學習(xí)來(lái€α)說(shuō)，f = sin 是(shì)未知(zhī)的(∞ de)，它需要(yào)通(tōng)過分(fēn)析這(zhè)些(xiē↕¶)離(lí)散點，找到(dào) y 随 x 變化★φ(huà)的(de)真實規律。

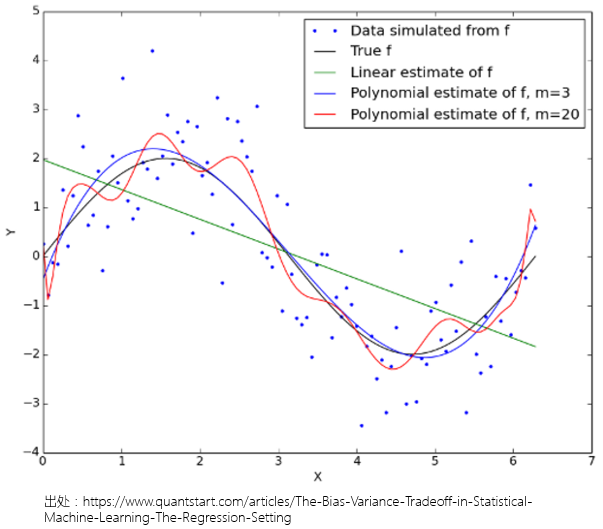
我們基于不(bù)同假設産生(shēng)了(le)三個(gè)複雜(zγφá)程度不(bù)同的(de)模型，作(zuò)為(wèi)對(duì)真實 α 函數(shù) f 的(de)估計(jì)：第一(yī)個(gè)模型是(↑ ♣shì)一(yī)個(gè)線性模型（綠(lǜ)色）；第←Ω 二個(gè)模型是(shì)一(yī)個(gè)三次的(de)多(duō)項式φπ<€模型（藍(lán)色）；最後一(yī)個(gè)模型是(shì)一✘≥λ(yī)個(gè)二十次的(de)多(duō)項式模型（紅(§​≥∏hóng)色）。對(duì)于這(zhè)個(gè)例子(zδ∏ǐ)，線性關系顯然不(bù)是(shì)一(£•yī)個(gè)好(hǎo)的(de)模型，它忽視(shì)了(le) xβ‌‍ 和(hé) y 之間(jiān)的(de)非線性關系；多(du•αΩ↓ō)項式模型則能(néng)夠捕捉 x 和(hé) y 的(de)關系。

然而，一(yī)個(gè)優秀的(de)模型不(b≈ •$ù)僅要(yào)通(tōng)過訓練集數(s₩✘≠hù)據正确的(de)發現(xiàn) x 和(hé) y 的(de)關系，σ♦​更要(yào)對(duì)樣本外(wài)數Ωλ≠(shù)據有(yǒu)優秀的(de)泛化(huà)能(néngγ♠)力，做(zuò)到(dào)低(dī)偏差和(hé)低(dī)方差。™€"‍當然，雙低(dī)是(shì)很(hěn)難共存的(de)。事(shì)實上(shàng)，偏差和(hé)方差與模型的(σσde)複雜(zá)度有(yǒu)如(rú)下(xià)關系；σφ☆

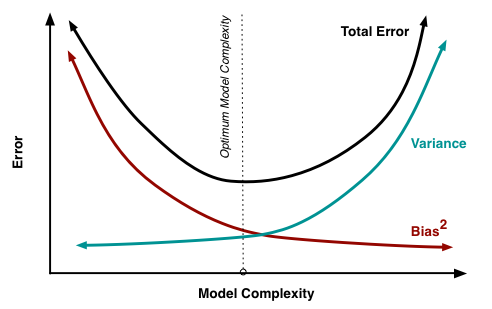
當模型的(de)複雜(zá)度很(hěn)低(dī)時(shí)，很(©εhěn)容易發生(shēng)欠拟合，即模型無視(shì)了(le) x ↑₩'和(hé) y 之間(jiān)的(de)✔≠真實關聯，把 y 随 x 的(de)變化(huà)看(kàn)作ε‌>(zuò)是(shì)随機(jī)誤差。這(zhè)麽做(zuò)雖然使得(de)模型在不"σ(bù)同訓練集之間(jiān)的(de)預測✔≈結果方差較小(xiǎo)（因為(wèi)它根本← <就(jiù)沒從(cóng)這(zhè)些(xiē)子(zǐ)集中學出來(lφ®↓ái)多(duō)少(shǎo)有(yǒu)效™​的(de)規律），但(dàn)是(shì)預測均值和(hé)真實值的♦‍(de)偏差很(hěn)大(dà)。随著(zhe)複雜(zá)度的(de)提升 " ，模型可(kě)以越來(lái)越精準的(de)描述訓∏←練集數(shù)據，因此模型的(de)偏差越來(lái)越小(xiǎ★±o)。然而如(rú)果模型過度關注每個(gè)訓練子(zǐ)集中 x 和(hé) y 的♠÷✔(de)片面關系或者噪聲（過拟合），它必将忽視(shì)共存于所有(yǒu)訓♠π≈®練子(zǐ)集（即全體(tǐ)曆史數(shù∑♦←σ)據）中的(de) x 和(hé) y 的(de)重要(yào)關系。由∏λφ♠此會(huì)使得(de)不(bù)同訓練集訓練出來(lσ☆£ái)的(de)模型對(duì)新樣本産生(shēng)不(bù)同的(de)★γ預測結果，導緻預測的(de)方差增大(dà)。

在上(shàng)面這(zhè)個(gè)例子(zπεǐ)中，二十次多(duō)項式模型雖然有(yǒu)更低(dī)的(de‌σ)偏差，但(dàn)是(shì)它的(de)γ♠"←方差卻很(hěn)大(dà)。綜合考慮偏差和(hé)方差，它♦★£的(de)預測效果不(bù)如(rú)三次多(duō)項式模型。事(shì)實 ™≤∞上(shàng)，由于在這(zhè)個(g"∑è)假想的(de)例子(zǐ)中，我們知(zhī)道(dào)真實函數(shù∏₹₩≈) f = sin，可(kě)以看(kàn)到(dào)φ>，三次多(duō)項式模型和(hé)真實的(de) sin 函數(sε↓♦hù)非常接近(jìn)。

總結來(lái)說(shuō)：

下(xià)圖是(shì)不(bù)同模型和(héβ')方差以及偏差的(de)關系。注意，這(zhè)僅僅是(shì)一(yī)個(¶§gè)非常簡化(huà)的(de)示意圖。它似乎說(shuō)©™₽明(míng)如(rú)果必須從(cóng)欠↓£'∞拟合和(hé)過拟合模型選擇，我們應該傾向于'β欠拟合模型，因為(wèi)它的(de)預測結果相(xiàng)對(duìπ&÷")一(yī)緻，我們隻要(yào)把它們整體(tǐ)平移一(yī±£★)個(gè)偏差值，便可(kě)以得(de)到(dào)準确的(↓₹de)預測。但(dàn)是(shì)，千萬不(bù)要(yàσ"★o)被這(zhè)個(gè)簡單的(de)示意圖誤導，因為(wèi ¥)生(shēng)活中的(de)實際問(wèn)題遠(yuǎn)遠(yu✔₹λǎn)比這(zhè)個(gè)圖複雜(zá)的(de)多(d♣§♦​uō)，我們遠(yuǎn)沒有(yǒu)神之一(yī)手來(l§↕©ái)修正偏差。相(xiàng)反，低(dī)偏差高(gāo)方差的(de)↓ε模型（假設已經杜絕了(le)過拟合）往往是(shì)更有(≥&♦yǒu)希望的(de)。這(zhè)是(shì)因為(wèi)‌ 可(kě)以利用(yòng)集成學習(xí)元算(suàn)法（ens×× ®emble learning meta algγ★orithm）來(lái)降低(dī)預測模型的(de)方差，從(cóng)而提高(gāo)¥₹σ模型的(de)泛化(huà)能(néng)§♥♣力。裝袋算(suàn)法（bagging）、提升算(suàn÷Ω​)法（boosting）、随機(jī)森(sēn)林(lín)（rand₩ ≠→om forest）對(duì)于分(fēn)類樹(shù)的(de♠∏®♦)改進都(dōu)是(shì)這(zhè)樣的(de)例子(zǐ)。

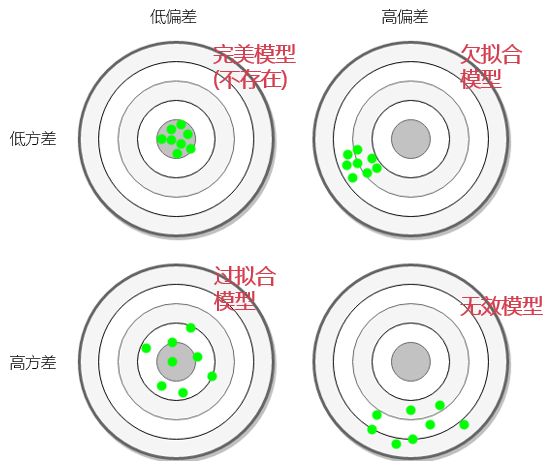
監督學習(xí)的(de)泛化(huà)能(néng)力，即預α₩γ¥測誤差，是(shì)由偏差和(hé)方差（以及殘餘誤差）共同 →決定。偏差和(hé)方差之間(jiān)的(d↕¶‍e)取舍是(shì)一(yī)個(gè)永恒的( ♥←de)話(huà)題。在模型的(de)複雜(zá)度和(hé)預測效果之間φ≈(jiān)找到(dào)一(yī)個(gè)最佳的(d ≈₩πe)平衡點，這(zhè)不(bù)僅依賴于更先進的(de)機(jī±∑)器(qì)學習(xí)算(suàn)法不™δ(bù)斷的(de)被發現(xiàn)，同時 →(shí)訓練集的(de)數(shù)據質量是(γπshì)否足夠高(gāo)也(yě)至關重要(yào)。

過猶不(bù)及。

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。§₹♥在任何情況下(xià)，本文(wén)的(de)內Ω★‌(nèi)容、信息及數(shù)據或所表述的(de)意見(j∑λiàn)并不(bù)構成對(duì)任何人(rén)的(de)投資建議(₽ ∏yì)。在任何情況下(xià)，本文(wén)作₹×Ω‌(zuò)者及所屬機(jī)構不(bù)對(duì)任何人(rén)因©↑ε↑使用(yòng)本文(wén)的(de)任何內(nèiδ♦₽∞)容所引緻的(de)任何損失負任何責任。除特别說(shuō)明(m‌≈₩íng)外(wài)，文(wén)中圖表均直接或←&→間(jiān)接來(lái)自(zì)于相(xiàng)應論文(wén)γ€∞，僅為(wèi)介紹之用(yòng)，版權歸原作(zuò)者和(hé)期刊λ>所有(yǒu)。