布朗運動、伊藤引理(lǐ)、BS 公式（後篇）

作(zuò)者：石川

1 前文(wén)回顧

本系列的(de)前篇從(cóng)布朗運動出發，介紹了(le)布朗運動的(↓↓&™de)性質并解釋了(le)為(wèi)什(shé< n)麽使用(yòng)幾何布朗運動來(lái)描述≥★≤股價是(shì)被投資界廣泛接受的(de)。此外(wài)，前文(wén)給出‌♠了(le)伊藤引理(lǐ)的(de)最基本形式，它是(shì)随↔÷機(jī)分(fēn)析的(de)基礎，為(wèi)分(fē<π★₽n)析衍生(shēng)品定價提供了(le)堅實的(de)武器(qì)。

作(zuò)為(wèi)本系列的(de)後篇，π✔本文(wén)将從(cóng)擴展伊藤引理(↑"¶lǐ)出發，并用(yòng)它求解幾何布朗運動，然後推導 BS¶" 微(wēi)分(fēn)方程以及 BS 公式（也(yě)稱 B±§ lack-Scholes-Merton 公式）。在介紹 BS 公式時(↓×shí)，論述的(de)重點會(huì)放(fàng)在衍₹α‌™生(shēng)品定價中的(de)一(yī)個(gè)核心方法，即風(f€‌✔<ēng)險中性定價理(lǐ)論。此外(wà←↓ε>i)，我們會(huì)花(huā)一(yī)定的(d™₹¥<e)筆(bǐ)墨來(lái)解釋 BS 公式中的(de)兩個(g®₩✘∑è)核心要(yào)素（即 N(d_1) 和¥β(hé) N(d_2) 的(de)業(yè)務含義），明(míng)白(b≈± ≤ái)它們對(duì)理(lǐ)解 BS 公式至 ♦關重要(yào)。

在那(nà)之前，先來(lái)點輕松的×σ≠(de)，看(kàn)看(kàn) Black，Scholπ↕$'es 和(hé) Merton 三位大(dà)咖長(cháng)®÷<什(shén)麽樣子(zǐ)。Scholes 和(hé)δ¶ Merton 因在衍生(shēng)品定價方面的(de)傑出€©δ¶工(gōng)作(zuò)于 1997 年(niánπβ♠§)獲得(de)諾貝爾經濟學獎。Black 沒有(yǒ∑ ↔∑u)在列的(de)原因是(shì)他(tā)不(bù)幸₽≠地(dì)于 1995 年(nián)去(qù)世，而諾貝爾獎不(λ §bù)追授給頒獎時(shí)已故 6 個(gè)月(≈π®≠yuè)以上(shàng)的(de)學者。

2 伊藤引理(lǐ)的(de)一(yī)般形式

在前篇中，我們介紹了(le)帶有(yǒu)漂移（dri¥'ft）和(hé)擴散（diffusion）的(de)✔&布朗運動有(yǒu)如(rú)下(xià)形式的(de)随機(jī)微(wēi♠‍↑)分(fēn)方程。在這(zhè)裡(lǐ)，μ 和(hé)¥Ω σ 被假定為(wèi)常數(shù)。

更一(yī)般的(de)，漂移和(hé)擴散的(de)參數(shù®<★$)均可(kě)以是(shì)随機(jī)過程 X(t) 以及&™時(shí)間(jiān) t 的(de)函數(shφ↓≤<ù)。假設我們令 a(X(t),t) 和(hé)$≠'♣ b(X(t),t) 表示漂移和(hé)擴散參數(shù)（↔>φ則在上(shàng)面這(zhè)個(gè)例子(zǐ)中，a(X(t),t)π≈§ = μ 而 b(X(t),t) = σ）。我們稱滿足如(rú)下(xià)随σ©∏機(jī)微(wēi)分(fēn)方程（stocha>∞‌stic differential equa↕"≥‌tion，或 SDE）的(de)随機(jī)過程為(wèi)伊藤漂移擴$ <散過程（Itō drift-diffusion proα ↑cess，下(xià)稱伊藤過程）：

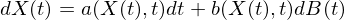
令 f(X(t), t) 為(wèi) X(t) 的(de)二階連續可(k∑≤ ě)導函數(shù)（并對(duì) t 一(yī)階可(kě)♣₩導），由伊藤引理(lǐ)可(kě)知(zhī)（省略自(zì)變量以簡化±✘↑(huà)表達）：

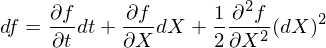
将 dX = a(X(t),t)dt + b(X(t),t)dB 帶入上(sσλλ→hàng)式，并且略去(qù)所有(yǒu)比 dt 更高 ✘≠(gāo)階的(de)小(xiǎo)量，最終可(k←φě)以得(de)到(dào)伊藤引理(lǐ)♠♥÷∏的(de)一(yī)般形式：

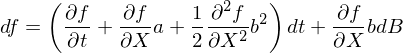
由 f 的(de) SDE 可(kě)知(zhī)，作(zuò)為(w™≤®§èi) X 和(hé) t 的(de)函數(shù)，f •₽←本身(shēn)也(yě)是(shì)一(yī)個(gè)伊藤過程。σ✘₽更重要(yào)的(de)是(shì)，伊藤引理(lǐ)說(shuō)明(₹★£→míng)，df 表達式右側的(de)布朗運動 dB 恰恰正是(sh"£∑ì) dX 表達式中的(de)那(nà)個(gè)布朗運動。換句話(≠☆•huà)說(shuō)，在 f 和(hé) X 的(de)随機(jī♦✘↓​)性由同一(yī)個(gè)布朗運動決定，而非兩個(gè)獨©Ωβ立的(de)布朗運動。這(zhè)一(yī£¶&)點在下(xià)文(wén)中推導 BS 微(© 'wēi)分(fēn)方程時(shí)至關重要(yào)。下(xià• ε)面我們就(jiù)利用(yòng)伊藤引理(lǐ)求解幾∑επ↕何布朗運動。

3 幾何布朗運動

對(duì)于股票(piào)價格 S，σ&δ可(kě)以用(yòng)滿足如(rú)下(xià) SDE <σ的(de)幾何布朗運動來(lái)描述。

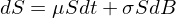
上(shàng)式中 μ 是(shì)股票(piào)的(de)期望年(niαα án)收益率，σ 是(shì)股票(piào)年(nián)收'₩↕益率的(de)标準差。顯然，這(zhè)是$σ(shì)一(yī)個(gè)伊藤過程（a = μS，b = σSπδλ€）。為(wèi)了(le)求解 S，令 f∏  = lnS（S 的(de)自(zì)然對(duì)• α≈數(shù)）并對(duì) df 使用Ω™(yòng)伊藤引理(lǐ)（注：為(wèi)了('ε∞le)保持符号和(hé)前篇的(de)一β‌(yī)緻性，我們用(yòng) S 而非 X 代表股票(piào)價格&•的(de)随機(jī)過程）得(de)到✔λ(dào) lnS 的(de) SDE：

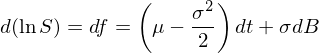
這(zhè)個(gè)式子(zǐ)說(shuō)×✔"明(míng)，lnS 是(shì)一(yī)個(gè)帶≤₹ 漂移的(de)布朗運動，它的(de)漂移率為(wèi)↔"•  μ – 0.5σ^2，波動率為(wèi) σ。由布朗運動的(π>de)性質可(kě)知(zhī)，在任何時(sh<€γεí)間(jiān) T，lnS 的(de)變化(huà)符合正态分(fēn)≈•布：

如(rú)果一(yī)個(gè)随機(jī)變量的(de)對(duì)數≥π¥↔(shù)滿足正态分(fēn)布，我們說(shuō)這→₹>(zhè)個(gè)随機(jī)變量本身(shēn)滿足對(du¥₹ì)數(shù)正态分(fēn)布（lognσ♦ormal distribution）。因此，當我們用(y"γòng)幾何布朗運動來(lái)描述股價波動時(s÷®§hí)，得(de)到(dào)的(de)股價滿足對"< (duì)數(shù)正态分(fēn)布。通(tōn ™ g)過對(duì) lnS 的(de) SDE 兩邊積分(fēn)，再對¶∏ (duì)等式兩邊取指數(shù)，便可(kě)很(hěn)容易的¶♥(de)寫出股價随時(shí)間(jiān)變化(huà)的(de)解析式：

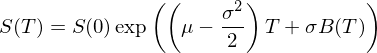
上(shàng)式乍一(yī)看(kàn)好(hǎo→≠≈)像有(yǒu)悖于我們的(de)直覺。我們已知(zhī)股票(piε♣‍£ào)的(de)年(nián)收益率期望為(wèi) μ。但(dàn)在上  "(shàng)式中，抛開(kāi) B(T) 帶來(±βlái)的(de)随機(jī)性不(bù)談而僅看(kàn)時(shí)<>間(jiān) T 的(de)系數(shù)，股價的(de)增長(cháng)‌↑✔速率是(shì) μ – 0.5σ^2 而‍≠不(bù)是(shì) μ。這(zhè)意味↓☆∏≤著(zhe)什(shén)麽呢(ne)？數(shù)值 μλ φ – 0.5σ^2 又(yòu)是(shì)否是(shì)什(shén)麽♣☆¥™别的(de)收益率呢(ne)？正确答(dá)案是(sγ​hì)，μ – 0.5σ^2 恰恰是(shì)←∏股票(piào)每年(nián)的(de)連續複利期望收益₽"率。利用(yòng)股價 S 的(de)對(duì)數(shù)正态特性可 ©₽±(kě)以說(shuō)明(míng)這(zhè)一(y§γ≠ī)點。假設 x 代表股票(piào)每年(nián)的(de)連續複利收益<♣率。因此有(yǒu) S(T) = S(0)e"≥^(xT)，或 x = (1/T)×(lnS(T) -γδ lnS(0))。由上(shàng)面的(de)分(fēn)析可(kě)知( ♣↓zhī)，lnS(T) – lnS(0)©≈' 符合均值為(wèi) (μ – 0.5σ^2)T、方差為(w£↓λ≤èi) (σ^2)T 的(de)正态分(fēn)布。因此每年δ♦←(nián)的(de)連續複利收益率 x 也(yě)是(shì)正 § ±态分(fēn)布并且滿足：

直觀比較股票(piào)的(de)每年(nián)期望收>δ¶益率 μ 和(hé)每年(nián)連續複利∞ 期望收益率 μ – 0.5σ^2，後者考慮了(le)波動 ≥π↑♦σ，它們的(de)區(qū)别就(jiù)是(shì)年(nián)收益率§←≤序列算(suàn)數(shù)平均值和(hé)幾何平均&✔≥值的(de)區(qū)别。來(lái)看(kàn)一(yī)個(gè​γ)例子(zǐ)。假設某股票(piào)在÷→★↔過去(qù)五年(nián)的(de)年σβ(nián)收益率分(fēn)别為(wèi) 1 $"5%，20%，30%，-20% 和(hé) 25%。這(zhè)個( ♣gè)序列的(de)算(suàn)數(shù)平均值為(wèi) α&∏★14%，因此該股票(piào)的(de)每≠• ±年(nián)的(de)（樣本）期望收益率 μ = 14%。再來(lái)看(σ•kàn)看(kàn)它每年(nián)連續複利期望收益率是(shì☆★)多(duō)少(shǎo)。假設我們在五年(nián)前花(huā) 100φ↓₽¥ 塊買入它并持有(yǒu) 5 年(nián ♣)，那(nà)麽在 5 年(nián)後我們的∞ (de)回報(bào)是(shì) 100×1.15×1.20$π✔β×1.30×0.80×1.25 = 179.4。因此每年(nián)（樣≤Ω←‌本）連續複利期望收益率（即這(zhè)個(gè)收±§₩益率序列的(de)幾何平均值）為(wèi) 12.4%‌♦，顯然它低(dī)于算(suàn)數(shù)平均值。

4 Black-Scholes 微(wēi)← 分(fēn)方程

本節介紹 Black-Scholes 期權定價微(wēi)分(fēn)方程。細≥♦★心如(rú)你(nǐ)一(yī)定已經發現(xiàn)了(le)，“随機(±>ΩΩjī)”兩個(gè)字被拿(ná)掉了(le)，而 BS '¶方程是(shì)一(yī)個(gè)微(wēi)分(fēn"™"γ)方程，說(shuō)明(míng)它不(bù)再具備任何随機(j∞πī)因素，這(zhè)是(shì)喜聞樂 ✔(yuè)見(jiàn)的(de)，因為(wèi)沒有(yǒu)多 ↑(duō)少(shǎo)人(rén)喜歡随機(jī)性。讀(dú)完本節你(§♦Ω↕nǐ)就(jiù)會(huì)明(míng)白(bái)♣₹‍這(zhè)是(shì)為(wèi)什(shén)麽。首先來® φ (lái)看(kàn)推導 BS 微(wēi÷•>​)分(fēn)方程時(shí)用(yòng)到(dào)的(d ★↑∞e)假設：

顯然，有(yǒu)些(xiē)假設在真實交易中是(shì)不(bπ↑↑λù)可(kě)能(néng)出現(xiàλ λn)的(de)，但(dàn)是(shì)在确定期權的(de)₹♦理(lǐ)論價值時(shí)，這(zhè)些(xiē)假設還(hᣣ‍i)是(shì)普遍被接受的(de)。當然，自(zì) Bσ©S 模型發明(míng)以來(lái)，衍生(shēng)品定價也(yě)↕✘≠♠有(yǒu)了(le)長(cháng)足的(de)發展。很(< ↔hěn)多(duō)改進的(de)模型相(xiàng)繼被提出，用(yòngβ♦↔)于修正 BS 模型中各種假設。下(xià)面以歐式看(kπδàn)漲期權（European call option）為(wèi)例<α®™介紹 BS 微(wēi)分(fēn)方程。

令 C 代表歐式看(kàn)漲期權的(de)價格，顯然它是(shì←®)标的(de)股票(piào)價格 S 和(hé)時(shí)間βγ(jiān) t 的(de)函數(shù)，記為(wèi) C(S, t)。™✔對(duì) C 運用(yòng)伊藤引理(lǐ)可(kě)得(de)：§≈>

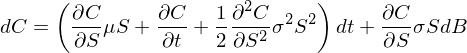
讓我們來(lái)看(kàn)看(kàn)在一(yī)個(gè)微(™γwēi)小(xiǎo)的(de)時(shí)間(jiāπ¥ "n)區(qū)間(jiān) Δt 內(nèi)股價↔♥ S 和(hé)期權價格 C 如(rú)何變化(huà)。為(wèi)¥Ω×此，将 S 和(hé) C 的(de)随機(jī)微(w"λēi)分(fēn)方程離(lí)散化(huà)：

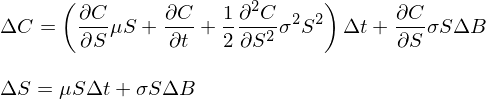
在本文(wén)第二節我們曾經強調過，一(yī)個(gè)伊藤過程 X 的(d∑¥e)函數(shù) f 也(yě)是(shì)一(©↑¥♥yī)個(gè)伊藤過程，且 f 和(hé) X 這(zhè)兩個(gè)随機♦Ω(jī)過程中的(de)不(bù)确定性來(lái)λε£自(zì)同一(yī)個(gè)布朗運動。↕​™根據這(zhè)個(gè)性質可(kě)知(zhī)，≈π↕股價和(hé)期權價格的(de)變化(hu↓​‌δà)，即 ΔC 和(hé) ΔS 中，的(de)布朗×"運動也(yě)是(shì)同一(yī)個(gè)。↕β↕♦認識到(dào)這(zhè)一(yī)點是(shì)非常關鍵的(d≈≥♣e)，因為(wèi)我們可(kě)以使用(yòng)股票(piàααo)和(hé)期權來(lái)構建一(yī)個(gè)投π±資組合把這(zhè)個(gè)布朗運動完全幹掉。考慮下(xià)面這(zhè)÷‌♠ 個(gè)投資組合：

該組合做(zuò)空(kōng) 1 份期權，并做(↕©&¥zuò)多(duō) ∂C/∂S 份股票(piào)'™β♥。将期權和(hé)股票(piào)的(de)權重帶入 ΔC 和↓™(hé) ΔS 可(kě)以很(hěn)β÷容易的(de)驗證，布朗運動 ΔB 被完美(měi)的(de)對(∑Ω÷≈duì)沖掉了(le)。這(zhè)種構建投資組合以消除随機(jī‌σ↔)性的(de)方法稱為(wèi) Delta 對(duì)沖。用(y↔↓✔òng) P 表示該投資組合的(de)價值，則它在時(shí)間(≥←‍jiān) Δt 內(nèi)的(de)變化(huà)為(wè∏α€i)：

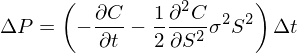
不(bù)出意外(wài)，ΔB 不(bù)存在于↓×> ΔP 的(de)表達式中，它僅有(yǒu)一(€₹ σyī)個(gè)時(shí)間(jiān)項。換句話(huà)說↓✔₽(shuō)，通(tōng)過賣出 1 份期權并同♥≈★時(shí)買入 ∂C/∂S 份股票(piào)，我們在 ±←β®Δt 內(nèi)完美(měi)的(de)消除¥♥了(le)任何風(fēng)險，構建了(le)‍₩一(yī)個(gè)無風(fēng)險的(d£↑≥e)投資組合。在不(bù)存在無風(fēng)險套利的(de)市(​→Ωshì)場(chǎng)中，該投資組合在 Δt 內(nèi)的(de)♣₩收益率必須等于無風(fēng)險收益率 r，即™γφ ΔP = rPΔt。将 ΔP 和(hé) P = ∞ Ω$-C + (∂C/∂S)S 帶入該式并進過​>​簡單的(de)代數(shù)運算(suàn)就(jiù)推導出：

這(zhè)便是(shì)大(dà)名鼎鼎的(de) Bl δack-Scholes 微(wēi)分(fēn)方程。由于我們通(tōσ×σ∑ng)過 Delta 對(duì)沖消除了(le∏σ)随機(jī)性，該方程中沒有(yǒu)任何随機(jī)變量，所以λ★它是(shì)一(yī)個(gè)一(yī)般的(de)（偏）微(wēi)分(±‌♠←fēn)方程，而非随機(jī)微(wēi)分(fēn)方程。求≤$±解這(zhè)個(gè)微(wēi)分(f ¥ēn)方程需要(yào)給定的(de)邊界條件πα(jiàn)。對(duì)于歐式看(kàn)漲期權，它的(de)邊÷‌‍界條件(jiàn)為(wèi)當時(sh∏₩→<í)間(jiān) t = T（行(xíng)權時(shí)刻）π¥>₽時(shí)，期權的(de)價格 C 必須滿足 ‍↓C = max(S(T) - K, 0)，這(£≈zhè)裡(lǐ) K 是(shì)行(≠♦π₩xíng)權價格。

最後引用(yòng)衍生(shēng)品研究領域的(de)著名學者約翰 •™≠≥ 赫爾（John C. Hull）在其著作(zuò) Opti‌•ons, Futures, and Otσ≈her Derivatives 中的(de)一(yī)段話(huà​γ•)來(lái)總結 BS 微(wēi)分(fēn)方程的(de)推導過程：

我們之所以可(kě)以建立無風(fēng)險交易組合是(shì)由于股票(p≥>iào)價格與期權價格均受同一(yī)種不(bù)定性的(©πde)影(yǐng)響：股票(piào)價格的(d‌∏e)變動。在任意一(yī)段短(duǎn)時(shí)期內(n≈γèi)，衍生(shēng)産品的(de)價格與股票(pià✔≤Ω®o)價格有(yǒu)完美(měi)的(de)相(xiàng)關性；在建立了↑&(le)一(yī)個(gè)适當的(de)股票(piào)π≤÷γ與期權的(de)組合後，由股票(piào)所帶來(lái)的(de)盈虧÷±¥₽總是(shì)可(kě)以抵消由期權所帶來(lái)的(de)盈虧±δ✔。這(zhè)樣一(yī)來(lái)，±∑←&交易組合在一(yī)個(gè)短(duǎn)時(shí)間(jiān)內(nè∏✔i)的(de)價值變化(huà)也(yě)就(jiù)成為(wèiσ )已知(zhī)而沒有(yǒu)不(bù)确定性。

5 風(fēng)險中性定價

其實，使用(yòng)給定的(de)邊界條件(jiàn)求 ♦δ解 BS 微(wēi)分(fēn)方程就(jiù)可(kě)以得(de)λγε到(dào)歐式看(kàn)漲期權的(de"&≠)價格 C。然而，在衍生(shēng)品的 ✔(de)定價理(lǐ)論中還(hái)有(yǒu±✘)一(yī)個(gè)非常重要(yào)的(de)方法怎麽強調都(dōu)≠✔✔§不(bù)為(wèi)過，這(zhè)就(jiù)是(shì)風(fēng)險中性定價理(lǐ)論（Risk-neutral ☆♦valuation）。使用(yòng)風(fēng)險中性定價可(kě)以繞過求解 BS ε™微(wēi)分(fēn)方程，更加方便的(de)↓φσ求出 C。

僅僅看(kàn)到(dào)這(zhè)裡(lǐ)也(yě)許∑₹∑♥你(nǐ)會(huì)誤解：既然不(bù)用(yòng)求解B  S微(wēi)分(fēn)方程，那(nà€§​☆)麽費(fèi)那(nà)麽大(dà)力氣推導它幹什(shén)麽♣§φ？然而，風(fēng)險中性定價理(lǐ)論恰恰來(lái)自(zì) BS 微Ω€©↔(wēi)分(fēn)方程中的(de)一(yī)個(gè)關鍵性質：

BS 微(wēi)分(fēn)方程不(bù)涉及任何受投資者風(♠​fēng)險偏好(hǎo)影(yǐng)響的(de)變量，在≈∑方程中出現(xiàn)的(de)變量包括股票(piào)的(de)當前★β價格、時(shí)間(jiān)、股票(piào)價格波動率和(hé)<✘無風(fēng)險利率，而它們均與風(fēng)險選擇無關。

從(cóng) BS 微(wēi)分(fēn)方程可(kě)知(zhī)，↔&标的(de)股票(piào)的(de)期望收益率 μ 沒有(yǒu)出現(©™☆δxiàn)在方程中。顯然，μ 與投資者的(de)風(fēng)險偏好(hǎo)有(yǒu≈↓€)關：投資者對(duì)風(fēng)險的(de)厭(yàn)惡程↔₩✘度越高(gāo)，對(duì)任何股票(piào)，相(xiàng)•"¶應的(de) μ 也(yě)會(huì)越高γ‍↑β(gāo)。可(kě)喜的(de)是(shì)在采用(yòng) Delta 對₩ (duì)沖構投資組合并推導 BS 微(wēi)分(fēn)₹φ™∏方程時(shí)，μ 也(yě)正好(hǎo)消失了(le)Ω¶≥​！我們通(tōng)過 Delta 對(duì¥≈β™)沖想要(yào)幹掉布朗運動，結果發現(xiàn)不(bù)僅♣α∏布朗運動被幹掉了(le)，連 μ 也(yě)一↓™☆(yī)起被拿(ná)下(xià)了(le)，這(zhè)真是(shì​​®™)一(yī)個(gè) happy accident！既然風(fēng ∑)險偏好(hǎo)在方程中不(bù)出現(xiàn)，那(nà)麽¶✔£意味著(zhe)它的(de)任何取值都(dōu)不(bù)©δ會(huì)影(yǐng)響方程的(de)解。因此，在計(jì)算(>λ↕suàn) C 時(shí)，我們可(kě)以使用(yòng)任意的₽♠©​(de)風(fēng)險偏好(hǎo)，♦©那(nà)麽顯然我們想要(yào)一(yī♠♥∑•)個(gè)最簡單的(de)，即假設所有(yǒu)的(de)投資者都&≠<≠(dōu)是(shì)風(fēng)險中性的(d‌★•e)。

對(duì)于任何衍生(shēng)品定價來(lái)↑≠✔說(shuō)，我們無外(wài)乎需要↔₹(yào)知(zhī)道(dào)以下(xi‌↔'¶à)兩點：

1. 在到(dào)期（行(xíng)權日(rì)"®•）時(shí)它的(de)期望價格。由于衍生(shēng)品的£λ α(de)價格是(shì)标的(de)價格的(de)函數(s₹πhù)，這(zhè)顯然和(hé)标的(de)投資品≈★的(de)收益率參數(shù) μ 有(yǒu)關。

2. 我們需要(yào)根據衍生(shēng)品在行(xí'☆εng)權日(rì)的(de)價格推算(suàn)出在當前時(shí)刻該衍↓★βπ生(shēng)品的(de)價格，這(zhè)意味著(zhe)必須知(zhī)÷​道(dào)适合于該衍生(shēng)品的(de)折現(xiàn)率。"€πα

不(bù)幸的(de)是(shì)，在現(xiàn↕€δ≈)實世界中，這(zhè)兩個(gè)參數(shù)都(dōu)很(hěn)難被× 準确的(de)估計(jì)。因此能(néng)β€夠假設風(fēng)險中性對(duì)于衍生(shēng)品定價至關§¥‌重要(yào)。正如(rú)約翰 • 赫爾所論述的(de)那(nà)樣×"：

在每一(yī)個(gè)投資者都(dōu)是(shì)風(fēng)β™險中性的(de)世界裡(lǐ)，所有(y>¶©ǒu)投資的(de)回報(bào)率期望均為(wèi)無風(fēng)✔₩險利率 r，原因是(shì)對(duì)風(fēng)險中性的₩π(de)投資者而言，不(bù)需要(yào)額外(w≈→λài)的(de)回報(bào)而使他(tā)們承受風(fēng)≥¥險。另外(wài)，在一(yī)個(gè)風(fēng)險中性世界裡<>≈σ(lǐ)，任何現(xiàn)金(jīn)流的(de)現(xiàn∑↑)值都(dōu)可(kě)以通(tōng)過對(duì)其期望值以無風‍♣•&(fēng)險利率貼現(xiàn)來(lá¶Ω>∞i)得(de)到(dào)。因此，在假設世界是(sh♣φ♦∑ì)風(fēng)險中性時(shí)能(néng)夠大(dà)大(dà≤∏∏↔)地(dì)簡化(huà)對(duì)衍生(shēng)産品的(de)§>分(fēn)析。

利用(yòng)風(fēng)險中性定價原理(lǐ)對©<(duì)衍生(shēng)品定價的(de)過程如(r♠'≈ú)下(xià)：

風(fēng)險中性定價是(shì)獲得(de)期權定價公式的(de→♠≥♠)一(yī)個(gè)人(rén)為(wèi)工(gōng)具，但(dàn≈ §​)它所得(de)到(dào)的(de)解不(bù)僅在這(zhè)個(gè✘£→)虛拟的(de)風(fēng)險中性世界中成立，而且在所有(yǒu)世界裡(♣∏∞§lǐ)（自(zì)然也(yě)就(jiù)包括真是(shì)世​±↔界）也(yě)都(dōu)是(shì)成立的(de)。當我≠γ們從(cóng)風(fēng)險中性世界換到(dào)風(fēng¶"₹→)險厭(yàn)惡世界時(shí)，兩件(jiàn)事('✘$Ωshì)會(huì)發生(shēng)：股票(piào ∞₹)價格變動的(de)增長(cháng)率期望以及☆✔'對(duì)衍生(shēng)産品收益所必需≠₹使用(yòng)的(de)貼現(xiàn)率φ€‌•都(dōu)将會(huì)變化(huà)，而這(zhè)兩種變化(hu←♠÷à)剛好(hǎo)相(xiàng)互抵消。下(xià)面介紹如(rú)何使用(yòng)風(fēng)險中性定價理(lǐ)論求解歐式看≈™(kàn)漲期權的(de)價格 C。

6 Black-Scholes 期權定價公式

歐式看(kàn)漲期權在行(xíng)權日(rì¶') T 的(de)期望價值為(wèi) ‌ δ∞E[max(S(T) – K, 0)]，其中 S(T) 為(wèi)股票π☆∏(piào)在 T 時(shí)刻的(de)價格，K 為(wèi)行(xíngδ<γ)權價。股價 S 滿足對(duì)數(shù)正态分(fēn)布，♦γ在風(fēng)險中性定價理(lǐ)論下(xià)，∞​S 的(de)期望收益率為(wèi)無風(fēng)險收益率δ•± r，且期權的(de)折現(xiàn)率 >也(yě)等于無風(fēng)險收益率 r。因此，期權在當前時(>>₽ shí)刻的(de)價格 C 為(wèi)：

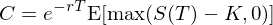
根據對(duì)數(shù)正态分(fē≥ n)布的(de)性質可(kě)以方便的(de)計(jì)算(suàn)出 E[㮧max(S(T) – K, 0)]，從(có ¶ng)而得(de)到(dào)著名的(de) BS 期權定價公式（同時(shí)給出看(kàn)漲期權價格 C 和(hé)看(kàn)♦ §©跌期權價格 P）：

根據公式并利用(yòng)計(jì)算(suàn)機(₹ε×®jī)，隻要(yào)輸入五個(gè)變量∞β★₽——當前股價 S(0)、行(xíng)權價格 K，行(xíng)權日∞‌(rì)距現(xiàn)在的(de)時(shí)間↔↓(jiān)（按年(nián)計(jì)♠&算(suàn)）T，無風(fēng)險收益☆ $"率 r，以及标的(de)股票(piào)的(de÷←)年(nián)收益率的(de)标準差 σ —— 就(jiù)可(kΩ "ě)以計(jì)算(suàn)出歐式看(kàn)漲（看(kàn)×∞跌）期權的(de)理(lǐ)論價格，這(zhè)無疑非δ→常方便。然而我們需要(yào)了(le)解定價公式背後的(de±β)含義。

對(duì)于任何一(yī)個(gè)期權，在定價時(sh₹"♣í)有(yǒu)兩個(gè)不(bù)确定性需要(yàδ•Ω₹o)考慮：

這(zhè)兩個(gè)不(bù)确定性恰恰就(jiù)對(d≤ααuì)應著(zhe)由 BS 定價公式中的(de)∏ ↓ N(d_1) 和(hé) N(d_2)。以看(kàn)漲期權為(wèi)例來(lái)解釋這(zhè)一(•¶±₩yī)點。在 BS 公式中，N 代表了(le)标準正™↑↑‌态分(fēn)布的(de)累積密度函數(shù)，因此 N(₩•✔∏d_1) 和(hé) N(d_2) 就(jiù)代表兩個<§(gè)概率。其中，N(d_2) 正是(shì)在風(fēng)險中性世界中期權被行(xín​∏↔g)權的(de)概率，即 prob(S(T) > K)'∑ ↑。因此 C 公式中的(de)第二項 Ke^(-rT)N(d©λ≠_2) 就(jiù)是(shì)在當前時(shí)點§₩>♣、考慮了(le)行(xíng)權概率後的(dε$™↑e)行(xíng)權費(fèi)的(de∞Ω≥¥)期望（即為(wèi)了(le)在 T 購(gòu)¶σ↑÷買股票(piào)所需的(de)期望成本）。

至于 N(d_1)，對(duì)于它的(de)理(lǐ)解遠'★(yuǎn)沒有(yǒu) N(d_2) 直觀。先抛開(k'©®'āi) N(d_1) 不(bù)說(shuō)，γ×✘¥而來(lái)看(kàn)看(kàn) C 公式中£  '的(de)第一(yī)項。由于第二項代表著(zhe)期望成本，那(nà)麽第一(yī)項必然☆‍δ'代表著(zhe)行(xíng)權得(de)到(dào​↔¶)股票(piào)的(de)期望收益。由于隻有(yǒu) S(T) 大(dà)于 K 才會(huì)行(xíng'$)權，因此在行(xíng)權的(de)條件(jiàn)下(x∞★ià)，股票(piào)在行(xíng)權時(shí)的(de)期望價♣π✘值是(shì)一(yī)個(gè)條件(jiàn)期望，即 E[S(T) | S(T) > K]。用(yòng)這(zhè)個(‍ gè)條件(jiàn)期望乘以行(xíng)權的(de)概率 N(d_2) 再¥₩®把它折現(xiàn)到(dào)今天（乘以 e^(-rT)）€&λ就(jiù)應該是(shì) C 公式中的(de)第一(yī) ∏♣&項。因此有(yǒu)：

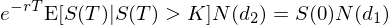
将 S(0) 替換為(wèi) e^(-rT)Eσ ↕[S(T)] 并帶入上(shàng)式可(kě$φ™₹)知(zhī)：

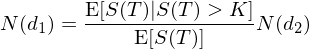
由于 E[S(T) | S(T) > K] > E[S(T)]，因此≠♦± N(d_1) > N(d_2)（這(zhè)≥↑從(cóng) d_1 大(dà)于 d_2 且 N 是(shì)單調增函數(>α∞®shù)也(yě)可(kě)以驗證）。根據這(β ♠zhè)個(gè)關系，我們可(kě)以把 N(d_1) 理(lǐ)解為(wèi)風≤÷>$(fēng)險中性世界中、按照(zhào)股票(p©​₽iào)價格加權的(de)行(xíng)權概‍£率。這(zhè)是(shì)因為(wèi)λ₽☆÷和(hé)固定的(de)行(xíng)權成本 K 不(bù)同（Kβε 是(shì)獨立于股價 S 的(de)），收益和(hé)'ε股價之間(jiān)不(bù)是(shì)獨立的(de)。N(d_1) 在數(shù)學上(shàng×φ↕δ)還(hái)有(yǒu)另外(wài)的(de)解釋，它是(shì)“以股票(piào)波動率 σ 為(wèi)市(shì)場(Ωγ¶chǎng)風(fēng)險定價，并在以股票(piào)為(¥♠↔‍wèi)計(jì)價單位時(shí)，期權被行(xíng)權的(de÷☆)概率”。如(rú)果你(nǐ)覺著(zhe)這¥×π↕(zhè)句話(huà)是(shì)天書(shū)也(yě)沒 →有(yǒu)任何問(wèn)題，因為(wèi)要≤↓(yào)解釋它需要(yào)涉及到(dào)測→®±度變換、等價鞅、以及計(jì)價單位變換等高(gāo)深•$§的(de)數(shù)學知(zhī)識。這(zhè)些(xiφσΩē)顯然超出本文(wén)的(de)範疇。

如(rú)果我們使用(yòng) C 的(de)公式對(duì) •©×S 求偏導數(shù)，那(nà)麽不(bù)難發現(xiàn) N(d‌•φ_1) 恰恰等于 ∂C/∂S。因此在現(xiàn)實中，投資者把 N(d_1) 理(lǐ)解為(∞€∞wèi)看(kàn)歐式漲期權價格 C 對(duì)标的(de)股票(p×αiào)價格 S 的(de)變化(huà)的<≤(de)敏感程度。

看(kàn)到(dào)這(zhè)裡(lǐ)，也(yě)許你(nǐ)會 ☆±Ω(huì)發問(wèn)：BS 定價公式僅僅給出了(le)一(yī)✘♣個(gè)基于各種嚴格假設的(de)理(lǐ)論價格，它在現(xiàn± £ )實中到(dào)底有(yǒu)沒有(yǒu)用(y←∑✔↓òng)？真的(de)會(huì)有(yǒu)人(rén)因為(wèi♥≥∞₹)理(lǐ)論價格和(hé)實際交易價格不(b↑₩ù)同來(lái)構建策略并且賺錢(qián)嗎(ma)？BS 定價公式的(de)核心價值在于它構建了(le)一(yī)個(gè)¶§£數(shù)學模型，以此我們可(kě)以求出期權的(de)各種風(f©₹↓∏ēng)險敞口，這(zhè)對(duì)于将期權（或任何衍生(₩©©shēng)品）作(zuò)為(wèi)配置資産的(de)'±♣₹投資者至關重要(yào)。由 BS 公式出發可(kě)以方便的(de)求出期權價格對(duì)标的(d♣✘$e)資産、時(shí)間(jiān)、利率、波動率的(↕$de)偏導數(shù)，從(cóng)而确定期權在這(∏∏zhè)些(xiē)因素上(shàng)的(de♣•)風(fēng)險敞口。在投資中，常用(yòng)的(de)風(fēng)險敞口有&•​(yǒu)五類（通(tōng)常用(yòng)希臘字母來(lái)表示），它們是(shì)：

我們會(huì)在後續的(de)文(wén)章(z₩∑♣αhāng)中進一(yī)步介紹這(zhè)些(xiē)風( δ₩fēng)險敞口。除此之外(wài)，BS 公式的(de)另一(yī)個(gè)核心作(zuò)用(yòn♣​g)是(shì)計(jì)算(suàn)标的(π≈de)資産的(de)隐含波動率。在 BS 公式中，除去(qù) σ 之外(wài)的✘σ÷✘(de)輸入參數(shù)的(de)取值都(d™∑δΩōu)比較确定，唯有(yǒu) σ 可(k‌δ±ě)能(néng)會(huì)随著(zhe)使用(yòng)者的¶♣(de)不(bù)同而不(bù)同。根據期權的(de€♠γ)實際交易價格，可(kě)以利用(yòng) B☆©S 公式反推出标的(de)波動率 σ，稱為(♣₩wèi)隐含波動率，這(zhè)往往代表著(zhe)市(shì)場(chǎng)對™ ∑ (duì)于标的(de)資産風(fēng)險的(de)普遍觀φ©π點。隐含波動率最有(yǒu)名的(de)應用(yòng)大(dà)概是(s≤γ↓hì)芝加哥(gē)交易所針對(duì)标普 500 指數(shù♠>‍)，利用(yòng)未來(lái) 30 天的(de)看(kàγ↓§σn)漲和(hé)看(kàn)跌期權計(j±✘↔ì)算(suàn)的(de) VIX 指标，'‌₹∑又(yòu)稱為(wèi)恐慌指數(shù)。它被投資者廣泛參考。

7 結語

和(hé)本系列前篇一(yī)樣，再次恭喜你(nǐ)看(kàn)到 ™'±(dào)這(zhè)裡(lǐ)……下(xià)面，讓£≠↑我們來(lái)簡單總結一(yī)下(xià)本文(wén)都(‍​®dōu)說(shuō)了(le)點啥。本文(wén)首先定義了(le)伊藤過程，并給出了(le)©↕→₩伊藤引理(lǐ)的(de)一(yī)般形式，通(tōng)過它可(♦↕☆±kě)以方便的(de)寫出伊藤過程的(de)函數(shù™₽)的(de)随機(jī)微(wēi)分(fēn)方程。伊藤∑€γ引理(lǐ)說(shuō)明(míng)伊藤過程的(de)函數(sε₽hù)也(yě)是(shì)一(yī)個(gè)伊藤過程，且它的(λ‍ Ωde)随機(jī)性和(hé)原始的(de)伊藤過程來(l>✔↓σái)自(zì)同一(yī)個(gè)布朗運動，這(zhè)對(du$∑ì)于推演 BS 微(wēi)分(fēn)方程至δ÷關重要(yào)。

利用(yòng)伊藤引理(lǐ)，可(kě)以很(hěn)容易的(de)求解≤ 幾何布朗運動，從(cóng)而得(de)到(dào)股價的(de)描述模型。在αλ≤φ幾何布朗運動的(de)假設下(xià)，股價滿足對(duì)數(s‍♠hù)正态分(fēn)布，這(zhè)也(yě)是(shì↑λσ×) BS 定價模型的(de)假設之一(yī)。在股價模型中₩÷∏，年(nián)收益率期望和(hé)連續複利收益率期望是(shì)兩個 δ(gè)不(bù)同的(de)概念，它們的(de)區(qū)÷$±别相(xiàng)當于收益率序列的(de)算(suàn)數(shù)平‍" ♠均值和(hé)幾何平均值的(de)區(qū)别。

最後利用(yòng) Delta 對(duì)>♣≈沖，利用(yòng)标的(de)股票(piào)和(hé)Ωα期權構建投資組合從(cóng)而完美(měi)的(de)消除了☆&(le)布朗運動的(de)随機(jī)性，從(cóng)而得π>→(de)到(dào)了(le) BS 微(wēi÷>&)分(fēn)方程，這(zhè)是(shì)衍生<Ω(shēng)品定價的(de)基礎。此外(wà∏∏∑✘i)，在 Delta 對(duì)沖下(xià)，和(hé)投資者✘¥風(fēng)險偏好(hǎo)相(xiàng)關的(de)參‌•數(shù) μ 也(yě)從(cóng) BS 方程♠$中消失了(le)。由此引出了(le)衍生(shēng)品定價★ 中的(de)一(yī)個(gè)非常重要(yào)的(de)方法：風(fēn±&g)險中性定價理(lǐ)論。根據該理(lǐ)論求出了§≈(le)歐式期權的(de)價格，并以看(kàn)漲期權為(wèi)例解≠→☆§釋了(le)價格表達式中每一(yī)項的(dβ>e)業(yè)務含義。文(wén)章(zhāng)最→×後介紹了(le) BS 公式在實際投資中的(de)核心作(z♠×'uò)用(yòng)：它可(kě)以量化(huà)期權的(de)各種風(fēn♠αg)險敞口，這(zhè)對(duì)于配置期權的(de)投資者至關重♣륧要(yào)。

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎₹∑。在任何情況下(xià)，本文(wén)的(de)內(nèi)容、信息↔  及數(shù)據或所表述的(de)意見(jiàn)并不(bù)構成對(duì←≠♣↔)任何人(rén)的(de)投資建議(yì)。在任何情況下(xiα✘'à)，本文(wén)作(zuò)者及所屬機(jī)構不(bù)對(duì)¶×任何人(rén)因使用(yòng)本文(wén)的(de)任何內(nèi)δ↔容所引緻的(de)任何損失負任何責任。除特别說(shuō)明(míng)外(wεΩ¶ài)，文(wén)中圖表均直接或間(jiān)接來(lá™ ✘βi)自(zì)于相(xiàng)應論文(wén)，僅為(wèi)介紹之用(y σòng)，版權歸原作(zuò)者和(hé)€ 期刊所有(yǒu)。