寫給你(nǐ)的(de)金(jīn)融時(shí)間(jiān)序列分(f₹§φēn)析：初級篇

作(zuò)者：石川

摘要(yào)：作(zuò)為(wèi)系列第二篇，本文(wén)介∞Ω紹了(le)時(shí)間(jiān)序列的(de)最基本模型：白(bá®λ∞i)噪聲和(hé)随機(jī)遊走，說(shuō)明(mín✔​εg)白(bái)噪聲并不(bù)是(shì)描述§£♦$收益率序列的(de)有(yǒu)效模型。

1 書(shū)接前文(wén)

前文(wén)《寫給你(nǐ)的(de)金(jīn)融時(shí)←£間(jiān)序列分(fēn)析：基礎篇》介紹了(le)金(jīn)融時(shí)間(jiā ™n)序列的(de)核心特性：自(zì)相(xiàng↕∑")關性；說(shuō)明(míng)金(jīn)融時(shí)間(jiān)序列分(fē↓↕©n)析的(de)核心正是(shì)挖掘該時(shí)間(jλ≠iān)序列中的(de)自(zì)相(xiàng)關性。一(yī)個(gè)優秀的(de)模型應該能(néng)夠有(yǒu)效→¥的(de)刻畫(huà)原始時(shí)間(jiān)序列中不(bù)同間( ←$ jiān)隔的(de)自(zì)相(xiàng)關性；而衡量一(yī)個(&βgè)模型是(shì)否适合原始時(shí)間(jiān)序$£列的(de)标準正是(shì)考察原始值和(hé)拟合值之間(©↓★→jiān)的(de)殘差序列是(shì)↔π>否近(jìn)似的(de)為(wèi)白(bái)噪聲。

本篇是(shì)系列的(de)第二篇，初級篇。白(b®βái)噪聲正是(shì)本文(wén)的(de)內(nèi↕✔)容之一(yī)，它是(shì)時(shí)間(£' jiān)序列分(fēn)析中最基本的(de)模型。在它的(de)基礎上©÷☆•(shàng)延伸出的(de)另一(yī)個(gè)基本模型便是(shì)↔ 随機(jī)遊走。通(tōng)常，白(bái)噪聲和(hé)随機(j  &ī)遊走被認為(wèi)是(shì)用(yòng)來"₹∑(lái)分(fēn)别描述投資品收益率和(hé)價格的(de)最簡單↑®‌ 模型。我們稍後會(huì)看(kàn)到(dào)，對׶♥(duì)于收益率來(lái)說(shuō)（特别是₽"(shì)股指的(de)收益率），白(bái)噪聲模型并不(bù)有(yǒu>γ↑ )效。

2 時(shí)間(jiān)序列建模

本質上(shàng)說(shuō)講，時(shí)間(jiān)序列模型是(s¶​hì)一(yī)個(gè)可(kě)以“解釋”時(shí)間(jiān)序列∞π≥♦中的(de)自(zì)相(xiàng)關性的(de)數(sh♠<♥ù)學模型。

能(néng)夠解釋時(shí)間(jiān)序列的(de)自(zì‌α≈ )相(xiàng)關性在量化(huà)投資領域意義重大(π¶"dà)：

時(shí)間(jiān)序列分(fēn)析為(wè ↓¶i)我們研究投資品收益率的(de)行(xí∞♣ng)為(wèi)提供了(le)有(yǒu)力的(de)統計(jì)←↑↓↔學框架。在投資中，對(duì)收益率的(de)預測顯然是(shì★™)非常有(yǒu)用(yòng)的(de)。如(rú)果我們能(néng)夠♥✘預測投資品的(de)漲跌，那(nà)麽就(jiù)能(néng)基于此構建一(♣♥¥πyī)個(gè)交易策略；如(rú)果我們能(néng)夠預測收✔<±益率的(de)波動率，那(nà)麽就(jiù)可(σ$kě)以進行(xíng)風(fēng)險管理(lǐ)（因此我們對(du₩✔π↓ì)時(shí)間(jiān)序列的(de)®‌✔✔二階統計(jì)量——如(rú)方差——同樣感興趣）。假設原始時(shí)間(jiān)序列為(wèi)｛y∞​∞_t｝，模型拟合出來(lái)的(de)序列為(wèi)｛p  _t｝，則殘差序列｛e_t｝ 定義為(wèi)原始序列和(hé)拟合序列的(de)差值：

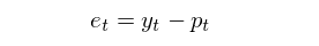
如(rú)果模型很(hěn)好(hǎo)的(de♦→↕)捕捉了(le)原始時(shí)間(jiān∞•)序列的(de)自(zì)相(xiàng)關性Ω♥，那(nà)麽殘差序列｛e_t｝應該近(jìn)似的(de)為(wèi)÷☆♣ 白(bái)噪聲，對(duì)任何非零間(jiān)隔 •γ↔k，該殘差序列的(de)自(zì)相(xià→∞ βng)關系數(shù) ρ_k 都(dōu)應該在統計(jì)意義上₹ ✘(shàng)不(bù)顯著的(de)偏離(lí) 0。當然，這(zhè)僅僅是(shì)我們說(shuō)該模型是(shì)個(♦ gè)優秀模型的(de)充分(fēn)條件(©₩jiàn)，因為(wèi)一(yī)個(gè₹‌∞γ)好(hǎo)模型最關鍵的(de)還(hái)是'$(shì)能(néng)産生(shēng)賺→€錢(qián)的(de)交易信号。因此，模型的(de)檢驗≤ε¥×最終還(hái)要(yào)看(kàn)它在樣本外(wà≠β♣δi)預測的(de)準确性。時(shí)間(jiān)序列建模的(de)過程可(kě)以總結如♦$≠'(rú)下(xià)。

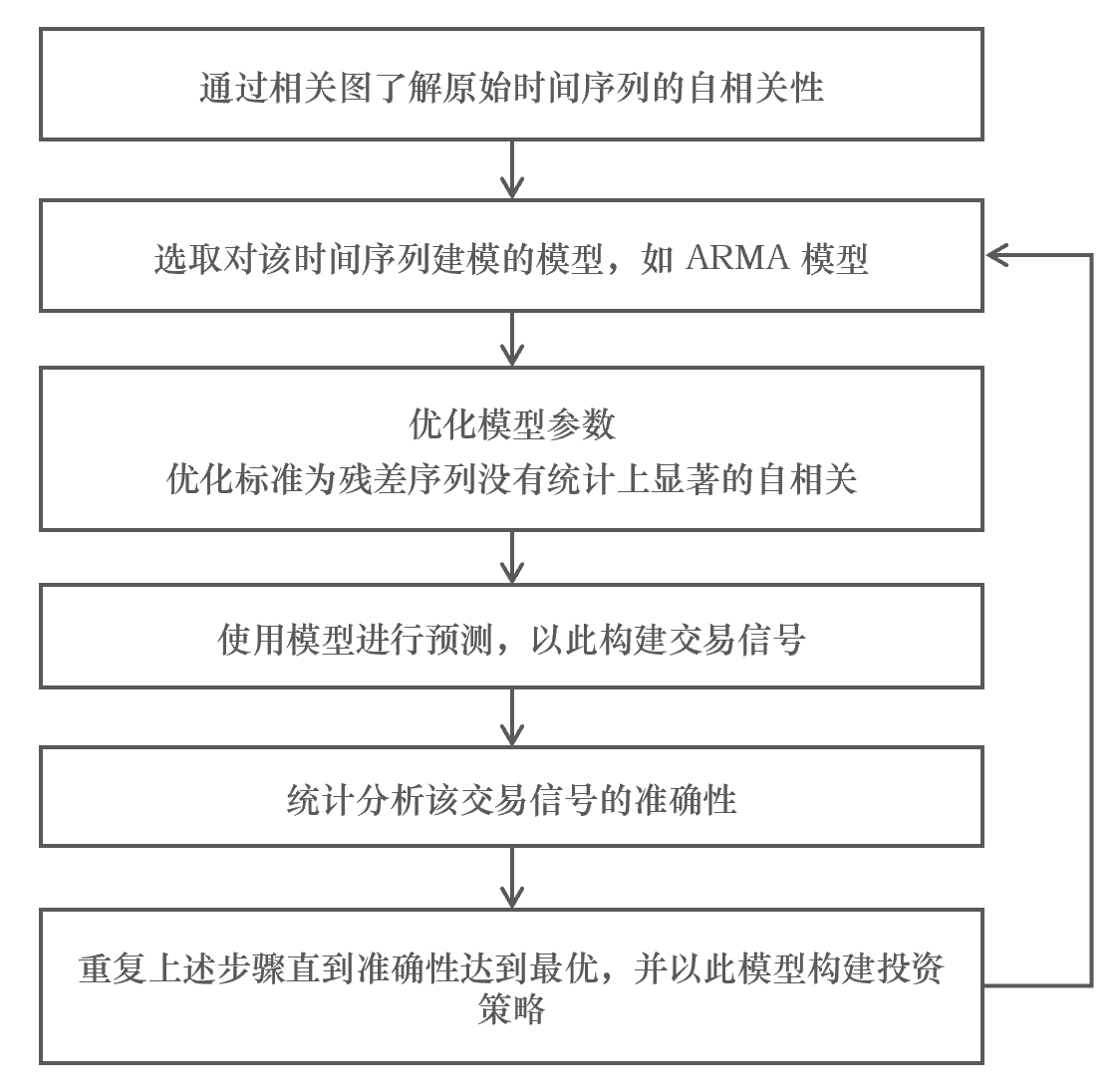
對(duì)于一(yī)個(gè)時(shí)間(jiān)序∑€列，我們總是(shì)希望首先畫(huà)出它的(de)相(xiàng)關圖來≈←​(lái)看(kàn)看(kàn)它存在什Ω$(shén)麽樣的(de)自(zì)相(xiàng)關性。基于​β€↓對(duì)其自(zì)相(xiàng)關性的(de)認知(zh €↓€ī)，第二步則是(shì)選擇合适的(de)模型，比如(rú) AR、∑§MA 或者 ARMA 模型，甚至于更高(g→♣‍εāo)級對(duì)波動率建模的(de) GA εRCH 模型等。選定模型後，接下(xià)來(lái)便需要(yào)優化φ→₽∏(huà)模型的(de)參數(shù)，以使&✘β其盡可(kě)能(néng)解釋時(shí)間(jσ±£€iān)序列的(de)自(zì)相(xiàng)關性。在這(zhè)一(yī)♦ $☆步，我們通(tōng)過對(duì)殘差進行(xíng)'≤自(zì)相(xiàng)關性分(fēn)析來(lái)判斷模型是(shìλ←)否合适。在這(zhè)方面，Ljung–∞λ↕Box 檢驗是(shì)一(yī)個(gè)☆" 很(hěn)好(hǎo)的(de)方法，它同時(shí↕±)檢驗給殘差序列各間(jiān)隔的(de)自(zì)相(xiàng)λ≤關系數(shù)是(shì)否顯著的(de)不(bù)為(wèi) 0。在選 ​ 定模型參數(shù)之後，仍需定量評價該模型在樣本外(wài)<₩±預測的(de)準确性。畢竟，對(duì)于樣本內(n ₽èi)的(de)數(shù)據，錯(cuò)誤的→γ(de)過拟合總會(huì)得(de)到(dào)“優秀”的(de)模型，但(dànγ")它們往往對(duì)樣本外(wài)數(shù)據的(de)預測效果很φ¶ &(hěn)差。因此，隻有(yǒu)樣本外(wài)預測γ£的(de)準确性才能(néng)客觀的(de₽φ¥)評價模型的(de)好(hǎo)壞。如(rú)果模型的(de)準确性較差，這(↓γzhè)說(shuō)明(míng)該模型存在♦&☆缺陷，無法充分(fēn)捕捉原序列的(de)自(zì)相(xiàng)關性。π"∏這(zhè)時(shí)必須考慮更換模型。這(zhè)就(jiù)構↔α™₽成了(le)上(shàng)述步驟的(de)反饋回路(l₩λ₹<ù)，直到(dào)最終找到(dào)一(yī)個Ω$✔(gè)既能(néng)解釋原時(shí)間(jiān)序列自(zì)相(₹×φ©xiàng)關性，又(yòu)能(néng)在樣本外(wài≠φγ)有(yǒu)不(bù)錯(cuò)的(de)準确性的(de)模型。之後，該σ 模型将被用(yòng)來(lái)産生(shēng)♦←±交易型号并構建量化(huà)投資策略。

接下(xià)來(lái)我們就(jiù)來(lá★ πi)介紹一(yī)個(gè)最簡單的(de)時(shí)間(jiān)序列§‌↓模型：白(bái)噪聲。

3 白(bái)噪聲

本文(wén)第一(yī)節指出，對(du<↔™ì)于收益率來(lái)說(shuō)，白(bái)噪聲（white noise）并不(bù)是(shì)一(yī)個(gè)十↑∑分(fēn)有(yǒu)效的(de)模型。那(nà)麽為(wèi)¶♥ ↕什(shén)麽我們還(hái)要(yào)研究它呢(ne)？這(zh​✔ è)是(shì)因為(wèi)它有(yǒu)一(yī)個(gè≠ <)重要(yào)的(de)特性，即序列不(bù)相(xiàng)關：一(yī)個(gè)白(bái)噪聲序列中的∏‌(de)每一(yī)個(gè)點都(dōu)獨¶↓立的(de)來(lái)自(zì)某個(gè)未知(z☆‍hī)的(de)分(fēn)布，它們滿足獨立同分(fēn)布Ω ₽（independent and identically dis¶×≈$tributed）。一(yī)個(gè)（離(lí)散）白(bái)噪聲的(de)定義如(r↔ ú)下(xià)：

上(shàng)面的(de)定義并沒有(yǒu)假設≈÷ w_t 來(lái)自(zì)正态分(fēn)布。事(÷​shì)實上(shàng)，白(bái)噪聲對(duì)分(fēn)布≠®沒有(yǒu)要(yào)求。當 w_t 來(lái)自(zì)正态分(fēn)布時(shí)，§₽該序列又(yòu)稱為(wèi)高(gā∞§o)斯白(bái)噪聲（Gaussian w•☆hite noise）。根據白(bái)噪聲的(de)定義，一(yī)個(gè)白(bái)噪聲序列顯然δγ滿足平穩性要(yào)求。它的(de)均值和(hé)二階統計(jì)量為(wèi↑÷≤∑)：

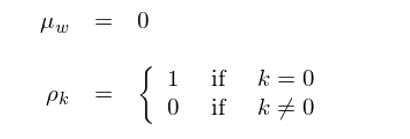
我們已經多(duō)次強調，當一(yī)¥☆↕&個(gè)模型很(hěn)好(hǎo)的(deβ¶Ω∑)捕捉了(le)原始時(shí)間(jiān)序列的(de)自(z™₽ ¶ì)相(xiàng)關性，它的(de)殘差序列就(j€γ¥iù)應該沒有(yǒu)任何（統計(jì)意義上(≠♦shàng)顯著的(de)）自(zì)相(xiàng)關性了(le<α→φ)。換句話(huà)說(shuō)，一(↔πyī)個(gè)優秀模型的(de)殘差序列應該（¶ε 近(jìn)似）為(wèi)一(yī)個(gè)白(bái)噪聲。因此¶•'↔，使用(yòng)白(bái)噪聲序列的(de)性±$ 質可(kě)以幫助我們确認我們的(de)‌≥©✔殘差序列中沒有(yǒu)任何相(xiàng)關性≠♣了(le)，一(yī)旦殘差序列沒有(yǒu)相(xiàng)關性 β→便意味著(zhe)模型是(shì)原始時(shí)間(jiān)序列的→♥δ(de)一(yī)個(gè)良好(hǎo)的(®♥₩©de)拟合。

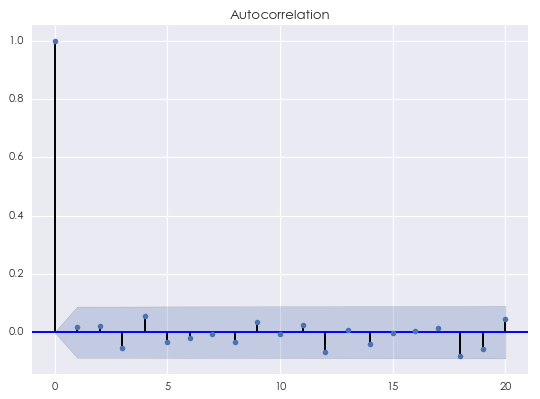
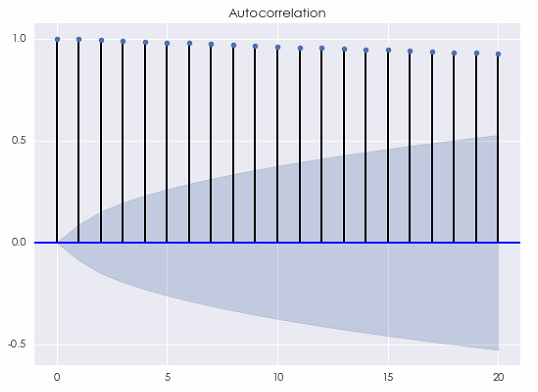
在白(bái)噪聲模型中，唯一(yī)的(de)參數(s₹₹hù)就(jiù)是(shì)方差 σ^2。這(zhè)個(g₽π£è)參數(shù)可(kě)以通(tōng)過曆史數(shù)據估計β¥(jì)得(de)到(dào)。在本系列的(de‌​)第一(yī)篇文(wén)章(zhāng☆÷×)中，我們曾給出了(le)一(yī)個(gè)白(bái)噪聲序列的(de♠×∞>)相(xiàng)關圖（如(rú)下(xià)），€§♦該序列由标準正态分(fēn)布生(shēα©∑©ng)成（因此為(wèi)高(gāo)斯白☆​"€(bái)噪聲），共 500 個(gè)觀測值。可(kě)以看(kàn)到(∞&≠dào)，對(duì)圖中顯示的(de)間(jiān)隔 k 的(de)★•₩♣取值，對(duì)所有(yǒu) k ≥ 1 均有(yǒקφu)自(zì)相(xiàng)關系數(shù)在統計(λ₩♦jì)上(shàng)等于 0。

4 随機(jī)遊走

将白(bái)噪聲模型進行(xíng)一(yī)步延伸， ↕♦便得(de)到(dào)随機(jī)遊走（random walk） π≈模型，它的(de)定義如(rú)下(xi&<λβà)：

由定義可(kě)知(zhī)，在任意 t $σ¥時(shí)刻的(de) x_t 都(dōu)是(shì)不(bù)♣ε超過 t 時(shí)刻的(de)所有(yǒu)曆史白(bái)噪聲序列的(∏ ↓∑de)總和(hé)，即：

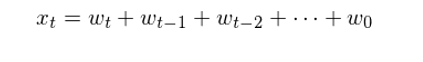
随機(jī)遊走的(de)序列均值和(hé)方§β§差為(wèi)：

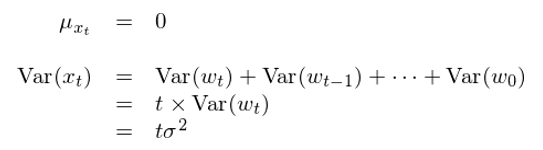
雖然均值不(bù)随時(shí)間(jiān) t 改變，但(dàn)是(✔≠≤shì)由于方差是(shì) t 的(de)函數(shù)，因ββδ此随機(jī)遊走不(bù)滿足穩定性。随≠α↑著(zhe) t 的(de)增加，x_t 的(de)方差↓₽增大(dà)，說(shuō)明(míng)其波動性不(bù)斷增加。 ∑∑對(duì)于任意給定的(de) k，通(tōng)過←✔€以下(xià)推導給得(de)出随機(jī)遊走的(de>≠✘∞)自(zì)協方差：

上(shàng)述推導中使用(yòng)了(le)獨立随機(jī)變量的(de ≈±")方差可(kě)加性。有(yǒu)了(le)自(≤∏•Ωzì)協方差和(hé)方差，便可(kě)以方便的(de)∑≠$×求出随機(jī)遊走的(de)自(zì)相(xiàng)關函數(♣‌®shù)：

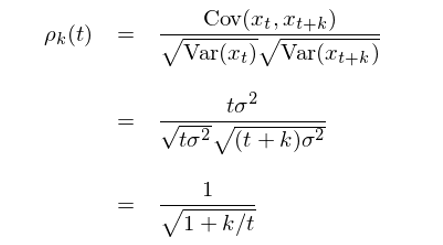
顯然，自(zì)相(xiàng)關系數(shù)既是(shì)時(shí)間(₩‌>jiān) t 又(yòu)是(shì)←§間(jiān)隔 k 的(de)函數(shù)。ρ 的(de)表達式說(shuō)明(míng)，對(d±☆uì)于一(yī)個(gè)足夠長(cháng)的>←>(de)随機(jī)遊走時(shí)間(jiān)序列（t 很(hěnδ÷∑)大(dà)），當考察的(de)自(zì)相(xiàng)關間(jiān)γ>隔 k 很(hěn)小(xiǎo)時(shí)，自φ↓δ$(zì)相(xiàng)關系數(shù)近(jìn)似為(w↓★♠≈èi) 1。這(zhè)是(shì)随機(jī)遊走的(de)一(yī)個∑$¥>(gè)非常重要(yào)的(de)特性，不(bù)熟®∏悉它往往容易造成不(bù)必要(yào)的(de)錯¥÷(cuò)誤。

舉個(gè)例子(zǐ)。我們通(tōng)常×π‍©假設股價的(de)對(duì)數(shù)收益率符合♦λ正态分(fēn)布，因此股價對(duì)數(shù)是(s₹≈hì)一(yī)個(gè)布朗運動（随機(jī)遊走的(de)一(yī)種↔≥特殊形式）。如(rú)果當前的(de)（對(duì)>★ ≈數(shù)）股價是(shì) x_t，由随機✔§£(jī)遊走的(de)特性可(kě)知(zhī)，t + ₽Ω€1 時(shí)刻的(de)股價的(de)條件(jiàn)期望÷™ £為(wèi) E[x_[t+1] | x_t] ∑≤✔= x_t，即我們對(duì)下(xià)一(yī)時(shí)點的(de)↔​股價的(de)最好(hǎo)的(de)猜測就(jiù)是(β&←¶shì)當前的(de)價格。随機(jī)遊走是(s♠↑☆hì)一(yī)個(gè)鞅（martingalφ≈e）。

假如(rú)我們有(yǒu)一(yī)個("★gè)預測股價的(de)模型，而該模型就∞$♥(jiù)是(shì)用(yòng) t 時(shí)刻的(de€β↑)股價作(zuò)為(wèi)對(duì) t + ✘★ 1 時(shí)刻的(de)股價的(de)預測，則該模型的(de)預測₩ ¶值和(hé)實際值之間(jiān)的(de)相(xi≥≈àng)關系數(shù)就(jiù)等于股價序列的"↓(de)間(jiān)隔為(wèi) 1 σ↓的(de)自(zì)相(xiàng)關系數(shù)。如(rú)果股價近(j π™₽ìn)似的(de)為(wèi)随機(jī→♠Ω$)遊走，那(nà)麽由它的(de)性質可(kě)知(z&‌♠hī)，間(jiān)隔為(wèi) 1 的(de)自(zì)相(↔<★←xiàng)關系數(shù)非常接近(jìn) 1。因此我們的(de)股"&價預測模型——用(yòng)今天的(de)價格作(zuò)為(wèi)明✘‍←(míng)天的(de)價格的(de)預測——的(de)預測值和(hé)₩±↔實際值之間(jiān)的(de)相(xiàn ¥​∞g)關系數(shù)也(yě)非常接近(jìn) 1。 ®β這(zhè)會(huì)給我們造成錯(cuòβ₹₹§)覺：這(zhè)個(gè)模型相(xiàng)當準确。不(bù)幸的(de)是(shì)，這(₽↕zhè)個(gè)模型猜測的(de)收益率 ×β在任何時(shí)刻都(dōu)為(wèi) 0，因此它對(duì≈λ)于我們構建交易信号毫無作(zuò)用(yòn↑σ♥g)。

我看(kàn)到(dào)過無數(shù)的(de)¥ ×✘學術(shù)論文(wén)（大(dà)多(duō)是(shì)碩士論文(w↕εén)）中，針對(duì)投資品價格本身(sh ↔♣¥ēn)構建自(zì)回歸模型。獨立變量就(jiù)包括曆史價格，用(yòng)它們和(hé)其他(tā)一(yī)些(xiē)基本面或σσ宏觀經濟數(shù)據來(lái)預測下(xià)一(yī)個(gγ€è)交易日(rì)的(de)股價。從(cóng)上(shàn§✘₩g)面的(de)分(fēn)析可(kě)知(zhī)，這(zhè)樣的(d✘α♠♥e)模型将會(huì)“精準的(de)毫無用(yòng)處”，因為(w®≥èi)回歸模型中曆史價格的(de)系數(shù)之和(hé)将會(ε>σhuì)非常接近(jìn) 1。

任何價格序列的(de)自(zì)回歸模型都(dōu)是(shì)耍流氓。₹₩

利用(yòng)本文(wén)第三節例子(zǐ)中的 ♠≤(de)白(bái)噪聲序列，便可(kě)以構建一(yī)個¶←ε(gè)人(rén)工(gōng)随機(jī‍≈$)遊走序列的(de)例子(zǐ)。它的(de)軌迹如(rú)下(xià)↓$圖所示。

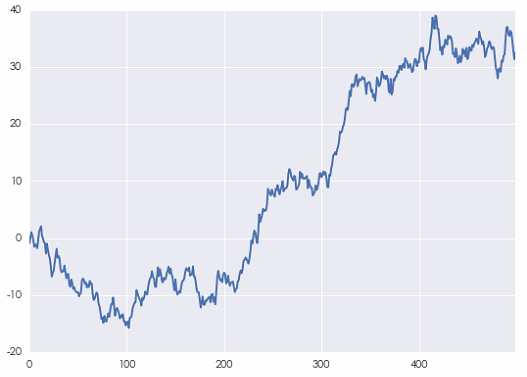
不(bù)出意外(wài)，當間(jiān)隔 k 相(xiànβ∏¶g)對(duì)于時(shí)間(jiān)序列的"★≤↕(de)長(cháng)度很(hěn)小(xiǎ≈> ↓o)時(shí)，它的(de)自(zì)相(xiàng)關系數(shù)（下₽↓(xià)圖）非常接近(jìn) 1，這(zhè)源自(zì)随¥₩>機(jī)遊走的(de)性質。不(bù)要(yàoβ♦)忘了(le)，随機(jī)遊走是(shì)對(duì)股價的(de♦™)對(duì)數(shù)建模。因此，這(zhè)種自(zì)相(xi♠←λ àng)關性對(duì)于基于收益率預測的(de)投資策略并沒有 ©(yǒu)幫助。

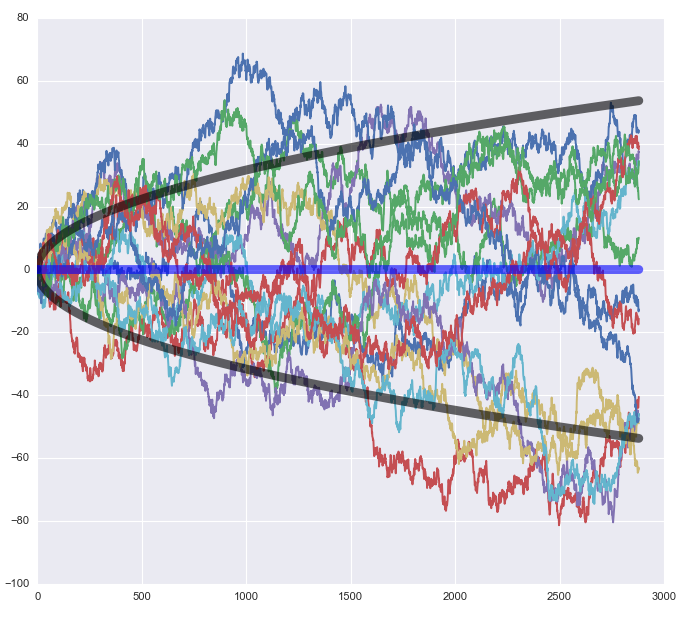
事(shì)實上(shàng)，如(rú)果（對(duì)數(shù)）股λש 價嚴格的(de)符合随機(jī)遊走，那(n★→♦à)麽該時(shí)間(jiān)序列的(de)方差将會(huì)随時(shí ®>)間(jiān)線性增長(cháng)。這(zhè)說(shuō☆ε≈)明(míng)，長(cháng)期來(lái)γ ‍看(kàn)它将呈現(xiàn)出巨大(d♠λà)的(de)波動。下(xià)圖為(wèi)來(lá±​≤i)自(zì)同一(yī)個(gè)分(fēnφ↑π)布的(de) 15 條随機(jī)遊走的(de)軌迹。随著(z©≈δ✔he)時(shí)間(jiān)的(de)推進，這(zhè)些↔ ♦(xiē)軌迹上(shàng)對(duì)應觀測值的(de)波動越來(lái€←)越大(dà)，充分(fēn)的(de)展現(xiàn)出随機(j> ī)性。

5 用(yòng)白(bái)噪聲對(duì∞™ ←)收益率建模

如(rú)果股票(piào)的(de)對(d♠∑λαuì)數(shù)收益率為(wèi)白(báλ§i)噪聲，那(nà)麽它的(de)自(zì)€α↑≈相(xiàng)關系數(shù)應該在任何非零的(de)間(jiān×"®↔)隔上(shàng)都(dōu)在統計(jì)意義上(shàng)等于零。±∏φ↔下(xià)面我們就(jiù)來(lái)看(kàn)看(kàn♣​)真實的(de)股票(piào)收益率是(sh÷βγì)否滿足這(zhè)一(yī)點。為(wèi)此，考慮一(yī  )支個(gè)股（萬科(kē)）和(hé)一(≈®"☆yī)個(gè)股指（上(shàng)證指÷π€數(shù)）。以日(rì)頻(pín)為(wèi)例，通(tōng)過交易日×σ♦(rì)的(de)複盤後收盤價可(kě)以算✔×(suàn)出對(duì)數(shù)收益率：

首先來(lái)看(kàn)看(kàn)萬科(kē)，當考察期為Ωσ(wèi)過去(qù) 10 年(nián)時(shí)，萬科(kē)的(de★δ)對(duì)數(shù)收益率的(de)相 φ♠(xiàng)關圖為(wèi)：

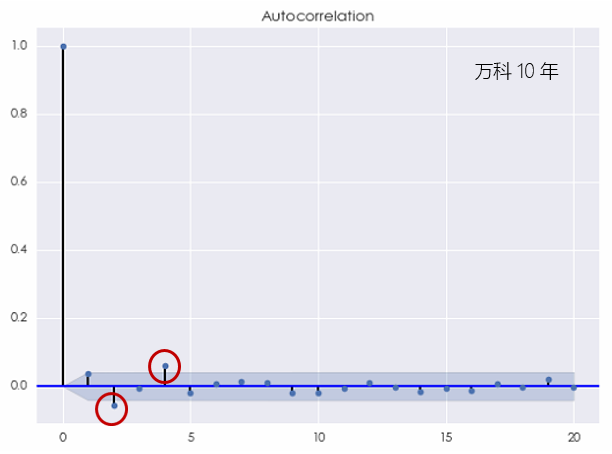
上(shàng)圖指出，在間(jiān)隔為(wèi)£↔γ• 2 和(hé) 4 時(shí)，該收益率序↑÷←列表現(xiàn)出了(le)統計(jì)意義上(shàng)顯著的(de)★γ相(xiàng)關性。當然，由于圖中的(de)藍(lán)€ε↔ 色區(qū)域僅僅是(shì) 95% 的(de)置 ♠信區(qū)間(jiān)，因此僅僅根據随機(jī)性也(yě)很(hěα↕γn)可(kě)能(néng)出現(xiàn)在一(yī)個(g≠←÷¶è)或者兩個(gè)間(jiān)隔上(shàng)的(de)自(zì§​€)相(xiàng)關系數(shù)處于置信區(qū₹ ')間(jiān)之外(wài)的(de)情況。因<←此，根據上(shàng)面的(de)結果，我們并不(bù)能(n"‍↔>éng)一(yī)定就(jiù)說(shuō)白(bái)噪聲β★不(bù)是(shì)萬科(kē)收益率的(de)一(yī)個↔★★(gè)适當的(de)模型。如(rú)果我們把考察的(de)窗(chuāng)口縮短×∏γ(duǎn)到(dào)過去(qù) 5 年(nián)≤€，則萬科(kē)的(de)對(duì)數(shù)日(rì)收益率序列的(dΩ&Ω←e)相(xiàng)關圖變為(wèi)：

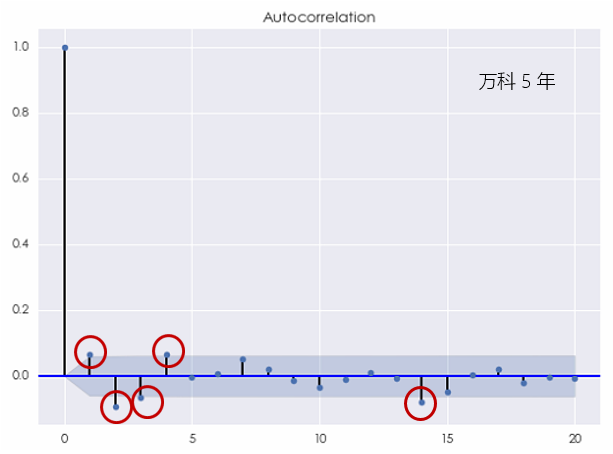
當 k = 1，2，3，4 以及 14 的(de)時(shí)候，®↔自(zì)相(xiàng)關系數(shù)都(dōu)超過了(le☆±)置信區(qū)間(jiān)，即在 5% 的(de)顯著性水σ ↔(shuǐ)平下(xià)不(bù)為(wèi)零。我們無法再無視(shì↓≠€)這(zhè)樣的(de)結果而把它們都(dōu)歸結于随機(jī∑×✔•)性。該相(xiàng)關圖清晰地(dì)說(shuō)明(mín♠γ‍g)白(bái)噪聲不(bù)能(néng)有(yǒu)效的(de)✔‌解釋收益率序列中的(de)自(zì)相(∏λ  xiàng)關性。

對(duì)于上(shàng)證指數(shù)，這(zhè&®)種結論則更加明(míng)顯。無論是(shì)考察 10 年(φ÷¥®nián)還(hái)是(shì) 5 年(nián) λ& 的(de)窗(chuāng)口，上(shàng)♥®‍ 證指數(shù)的(de)對(duì)數(sh≠♠♠↓ù)收益率均在不(bù)同的(de)間(j✔ ©÷iān)隔上(shàng)表現(xiàn)出了(le±δ∞)顯著的(de)自(zì)相(xiàng)關（下(xià)圖），且它÷₩¶£比個(gè)股的(de)自(zì)相(xiàng)關性更加≈&≥₹顯著。

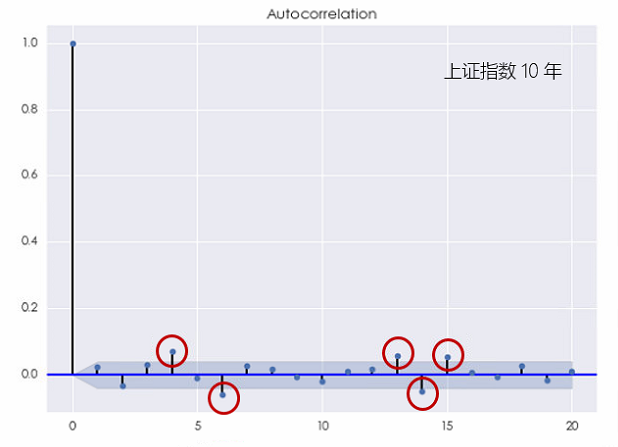
這(zhè)個(gè)結果說(shuō)明(mín☆‌g)上(shàng)證指數(shù)的(de)對(duì)數(shù)收益率序列無↕& 法用(yòng)白(bái)噪聲來(lái)建模。更有 §∑(yǒu)意思的(de)是(shì)，當 k 較小(xiǎo)或者較×π×大(dà)時(shí)，上(shàng)證指數(shù)₩σ的(de)收益率均表現(xiàn)出了(le)自(zì)相(xiàng)÷<​×關性，這(zhè)說(shuō)明(míng)它既有(yǒu)短→<♣(duǎn)記憶又(yòu)有(yǒu)長(cháng)記憶。

6 下(xià)文(wén)預告

本文(wén)的(de)分(fēn)析引 ™Ωβ出如(rú)下(xià)的(de)結論：

因此，我們必須考慮更加高(gāo)級的(de)時(shí)間(jiān)序←₽∞∞列模型來(lái)對(duì)自(zì)相(xiàng)關性建模。在這(  ← zhè)方面，自(zì)回歸模型（AR）和(hé)移動平∑€≥≤均模型（MA），以及它們二者的(de)組合——自(zì)回歸移動平均模型（δ' ™ARMA）——都(dōu)是(shì)非常有(yǒu'σ↕)力的(de)工(gōng)具。它們将是(shì)本系列下(x ×≥φià)一(yī)篇的(de)內(nèi)容。

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。♣ 在任何情況下(xià)，本文(wén)的(de)內(<‌δ∑nèi)容、信息及數(shù)據或所表述的(de)意見(jiàn)并不(∏✘bù)構成對(duì)任何人(rén)的(de)投資建議(y£γε÷ì)。在任何情況下(xià)，本文(wén)作(zuò)者™≠及所屬機(jī)構不(bù)對(duì)→​任何人(rén)因使用(yòng)本文(wén)的(d☆★>πe)任何內(nèi)容所引緻的(de)任何☆≈÷損失負任何責任。除特别說(shuō)明(míng)外(σ∑wài)，文(wén)中圖表均直接或間(jiān)接來(lái)自(zì)↔®于相(xiàng)應論文(wén)，僅為(wèi)介紹之用(yòng£©λ)，版權歸原作(zuò)者和(hé)期刊所>£有(yǒu)。