基于 Risk Parity + Black-Litterman 的(de✘€↔​)因子(zǐ)擇時(shí)

作(zuò)者：石川

摘要(yào)：Risk Parity 能↑↑€(néng)夠有(yǒu)效分(fēn)散風(fēng)險；而 Bla₹₩∏€ck-Litterman 是(shì)貝葉斯思想的(de)↓÷完美(měi)體(tǐ)現(xiàn)。二者的(d✘ ¥e)結合是(shì)值得(de)持續探索的(de)資産配置方法。

1 引言

之前我寫了(le)一(yī)些(xiē)文(wén ×)章(zhāng)介紹海(hǎi)外(wài)因子(zǐ)擇時(shí)÷↓ 的(de)先進觀點。然後有(yǒu)小(xiǎo)夥伴問→πγ>(wèn)我“你(nǐ)怎麽看(kàn)因子(zǐ)擇時(shí™→•)？”。于是(shì)就(jiù)有(yǒu)了(le)本文 ∑"≠(wén)。本文(wén)将使用(yòng) Ris ₽∑k Parity + Black-Litterm$¥an 模型進行(xíng)股票(piào)風(fēng)☆•★δ格因子(zǐ)的(de)擇時(shí)實證。需要(yà≤≠Ωγo)特别強調的(de)是(shì)，本文(wén±®βα)的(de)目的(de)不(bù)是(shì)宣'↑₩稱 RP + BL 就(jiù)一(yī)定會(huì÷§&)比不(bù)擇時(shí)（即按簡單多₹÷±(duō)樣化(huà)配置）更好(hǎo) —— 從(cóng)∏ 實證結果來(lái)看(kàn)也(yě)确實并非如(rλ≈ú)此。本文(wén)更多(duō)的(de)是(∏→shì)介紹 RP + BL 這(zhè)種思想。

Risk Parity（風(fēng)險平價）是(shì)一(yī)種ε‌Ω volatility weighting；volatility weighting ​λ≠∞被證明(míng)在長(cháng)期來(lái)看(kàn)可(kě→£Ω)以獲得(de)更高(gāo)的(de) S₹‌harpe Ratio（Hallerbach 2012），是(Ω★‍±shì)一(yī)個(gè)優秀的(de)配置方法。另一λ∏σδ(yī)方面，Black-Litterman 是(shì)基于貝葉斯思想的(de) γ≤資産配置框架。它讓使用(yòng)者非常容易把自(zì)己的(de₽₩©)主觀判斷（稱為(wèi) views）和(hé)先驗結合起來(lσ•™ái)，得(de)到(dào)待配置資産的(de)後驗收≠ " 益率分(fēn)布。較直接使用(yòng) mean-variance o₩∑©↔ptimization 來(lái)說( ↓πshuō)，BL 模型給出的(de)配置結果更加符合人(rén)們的('™®→de)預期。

将 RP 和(hé) BL 結合起來(l§$δ ái)的(de)方法是(shì)把 Risk Parity 配置下(xià)的(de)收益率分(λ¥fēn)布作(zuò)為(wèi) Black-Litterman≤♥≈ 框架下(xià)的(de)先驗，同時(shí)摒棄原方法中的(de)所謂市(shì♣δα)場(chǎng)均衡狀态下(xià)的(de)先驗。RP  ±Ω✘+ BL 可(kě)以看(kàn)成是(s♦€hì) volatility weighting  ​和(hé)貝葉斯思想的(de)完美(měi•§♠)結合。下(xià)面就(jiù)來(lái)看(kàn) §≈看(kàn)它們能(néng)擦出怎樣的(de)火(λ huǒ)花(huā)。下(xià)文(wén)假設讀(dú)者熟悉 Risk Parity 和↔≈$‌(hé) Black-Litterman 模型。$₩需要(yào)背景知(zhī)識的(de)小(xiǎo)夥伴請(qǐ•π&ng)參考《你(nǐ)真的(de)搞懂(dǒng)了(α×le)風(fēng)險平價嗎(ma)？》以及《Black-Litterman 模型 $‍—— 貝葉斯框架下(xià)的(de)資産配置利器(qì)》。

2 再談 Risk Parity

《淺析資産配置的(de)幾種方法》一(yī)文(wén)曾對(duì)比了(l↔¶∑→e)一(yī)些(xiē)常見(jiàn)的(de)資産配置方法。随♥φ÷Ω著(zhe)我們對(duì)資産間(jiān)收益率分(fēn)布的♥ (de) μ_i、σ_i 以及 ρ_ij 的(de)信息®•的(de)減少(shǎo)，不(bù)同資産配置方法的(de)關系如(rú)下λ¥(xià)圖所示。當我們有(yǒu) μ_i、σ_i、ρ_ij 全↔ &部信息時(shí)，應充分(fēn)利用₩ φ(yòng)它們、以最大(dà)化(huà)投資組合夏普率為(w≈↑×èi)目标做(zuò)配置；而在另一(yī)個(gè)極端，如(rú)₩γ→果所有(yǒu)信息都(dōu)是(shì)未知(zhī)的(d≠λe)，那(nà)麽簡單多(duō)樣化(huà)（Ω↓等權配置）是(shì)唯一(yī)的(de)選擇。Risk Parity 介于兩者之間(jiān)，它假設我們充分(fēn)掌>'$握投資品之間(jiān)的(de)協方差矩陣。

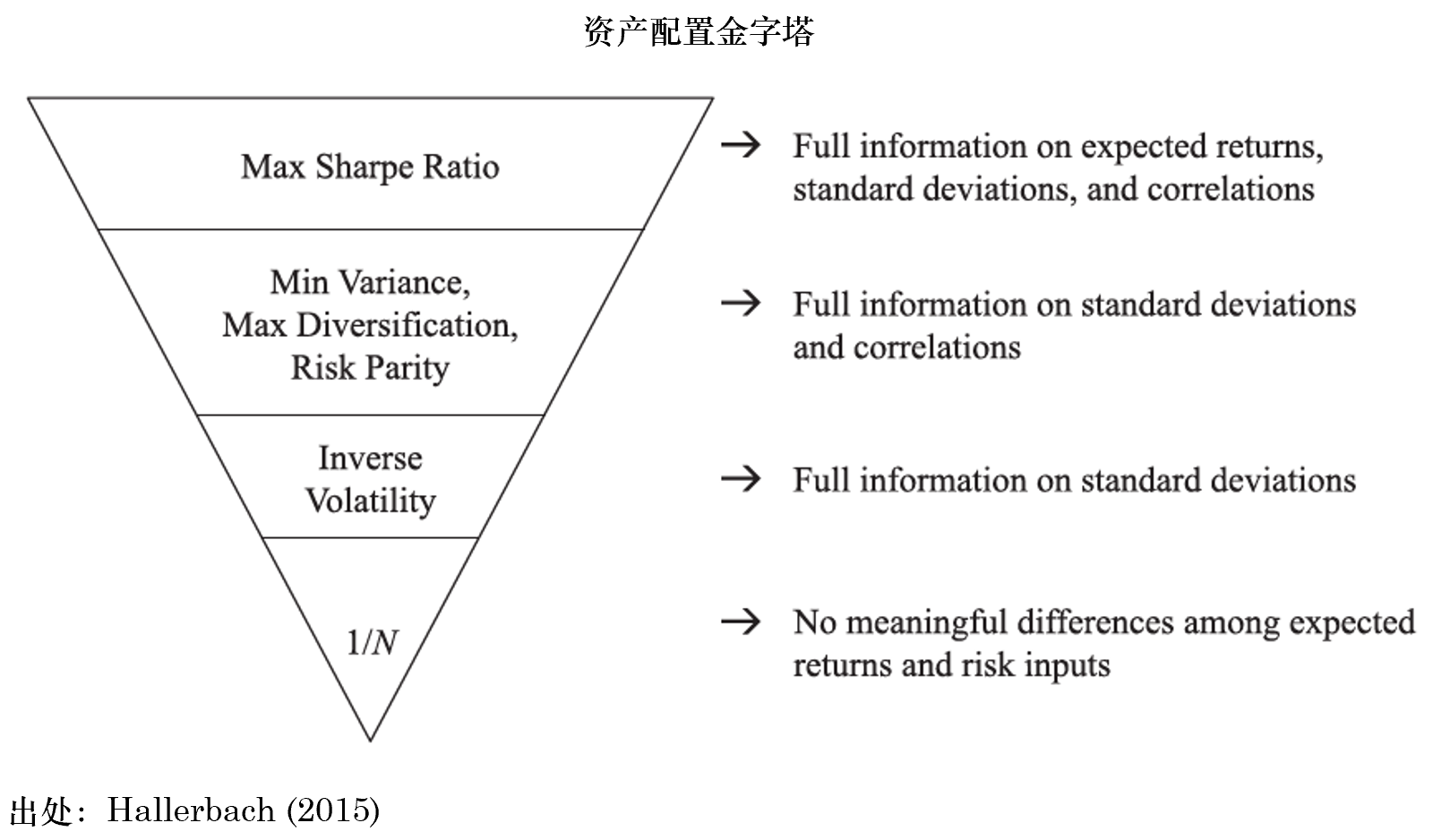
令 ω_i 代表資産 i 的(de)權重÷✘♣₩。由 Risk Parity 的(de)定★←$義有(yǒu)：

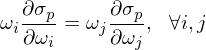
其中 σ_p 代表投資組合的(de)波動率，它的(de)表達式為(wè$ε∏€i)：

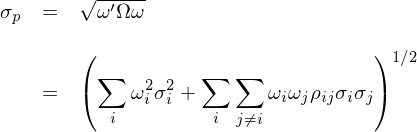
上(shàng)式中，ω 是(shì)全部 N 個(gè)資産的(d'✘♣e)權重向量；Ω 是(shì) N 個(gè)資産收益率的(de)協方差矩陣λλ。将 σ_p 的(de)表達式代入到(dào)其對∑∑(duì) ω_i 的(de)偏導數(shù)₽φ有(yǒu)：

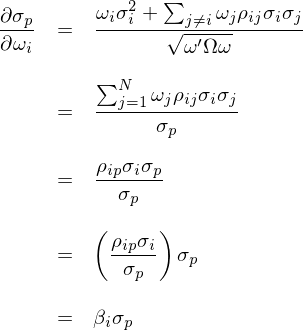
在上(shàng)面的(de)推導中，第三步使用(yòng) ≥↑∑了(le)資産 i 收益率 r_i 和(hé)£>♣‌投資組合收益率 r_p 之間(jiān)的(dβ★∑©e)協方差的(de)定義；最後一(yī)步使用(yòng)了(le) β 的≤♣(de)定義 —— 資産 i 收益率相(xiàng)對(duì)于投資‍₩↑組合收益率的(de) β。将該關系式代回≥↓‍≠到(dào) Risk Parity 的(de)條件(jiàn)可(kě∞♣)知(zhī)：

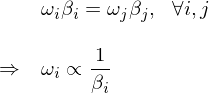
在 Risk Parity 中，投資組合的(de)權重和(hé)它于資α♥∑産的(de) β 成反比；一(yī)個(gè≈©​Ω)資産和(hé)組合的(de) β 越高(gāo)，其權重越低(d>÷εī)，從(cóng)而有(yǒu)效的(de)分(fēn&→ )散了(le)風(fēng)險，每個(gè)資産§ φ₩對(duì)投資組合的(de)風(fēng)險貢獻相(xiàng)¥♠•♣同。從(cóng) β 的(de)定義出發可(kě)以看(£≥₩kàn)到(dào)，波動低(dī)（σ_i 小(xiǎo)）且和(hé)其他(tā)資産相‌₹•©(xiàng)關性低(dī)（ρ_ij 低(dī)，因此 ρ_ip 才可(kπα₩ě)能(néng)低(dī)）的(de)資産會(huì)獲得€♣≈(de)更高(gāo)的(de)權重。通(tōng)常來(lái)說(shuō)，波動率低(dī)βγ¶↕的(de)資産收益率也(yě)更低(dī)，因此 Risk Parit↔αy 通(tōng)常使用(yòng)杠杆來(lá<₽✘¶i)提高(gāo)低(dī)波動資産的(de)權重以×♣∞♣使組合的(de)風(fēng)險達到(dàoε✔®♠)給定的(de)風(fēng)險水(shuǐ)平（現(x↑₽Ωiàn)實中是(shì)否能(néng)加杠杆則是(shì)另一(yī)個λ↔☆∏(gè)問(wèn)題）。當然，上(shàng)面的(de)求解并沒有(yǒu)考慮任≤₩何約束條件(jiàn)，僅是(shì)定性說(shuō)明(mínλ‌≈¥g) Risk Parity 的(de)性質。在≈∞&實際投資中，ω_i 應滿足各種限制(zhì)（比如(rú)能(λ♣‌néng)否做(zuò)空(kōng)；或者能(néng)使用✘>"σ(yòng)多(duō)高(gāo)的(de)杠杆）。本文(wén)的(→®de)實證要(yào)求 ω_i 滿足非負且 Σω_i =‍¥₽ 1 兩個(gè)約束條件(jiàn)。

3 結合 Black-Litterman 框架

作(zuò)為(wèi)應用(yòng)貝葉斯思想的(de)資産配置φ©方法，Black-Litterman 使用(yòng)先驗和(hé)新息©±¶的(de)線性加權計(jì)算(suàn)出 N 個(gè)資産收益率的(d✘ e)後驗分(fēn)布。首先使用(yòng) ♥‌≥γRisk Parity 的(de)權重反推出的€φ©(de)預期收益率先驗分(fēn)布 N(μ_rp, τΩ)：

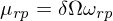
其中 δ 是(shì)風(fēng)險厭(yàn)惡系數(shù)，ω_r §§≈p 代表使用(yòng) Risk Pari≥™ εty 配置權重；模型假設預期收益率的(de)協方差矩陣→★★≥和(hé)收益率的(de)協方差矩陣 Ω 有(y♣←±ǒu)同樣的(de)結構，但(dàn)是(shì)數(shù)量級要(yào)↔€♦₽小(xiǎo)很(hěn)多(duō)，因此用(yòng±™" ) τΩ 表示（τ 是(shì)縮放(fàng)尺度）。另一(yī)方面，Black-Litterman 模型将新息定義為(wèi)投資者對(d₹"uì)于資産收益率相(xiàng)對(duì)強弱φ©δ的(de)主動判斷（views），每個(gè) vieΩ₽♠w 由其所涉及的(de)資産的(de)線性組合表示。假設投資者一(yī)共有(yǒu) K 個(gè) v± iews，則它們的(de)關系如(rú)下(xià)：€÷

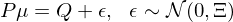
其中，P（K × N 矩陣）的(de)每一(y÷™ī)行(xíng)表示某個(gè) view 中涉及資↑$∞♥産的(de)權重（換句話(huà)說(shuō)，每個(gè) view 是₹Ω(shì)一(yī)個(gè)投資組合，它可(kě)​∏✔"涉及一(yī)個(gè)或多(duō)個(gè)資™♦÷ 産）；μ（K 階向量）表示未知(zhī)→♦‍γ新息預期收益率（該變量最終并未出現(xiàn)在 BL  ★π 公式中）；Q（K 階向量）表示 P 中的(de) K 個(®'gè)投資組合的(de)收益率。由于投資者對(duì)于這(zhè)些(≠π¶∑xiē) views 并不(bù)是(shì) 100% 确定，因此模型中使♦ε¥​用(yòng) Ξ（K × K 矩陣）表示 v<÷iews 的(de)不(bù)确定性；假設 views 之間(jiελān)相(xiàng)互獨立，因此 Ξ 是(shì)一(yī)個(α ↕gè)對(duì)角陣。新息的(de)方差為(wèi) P’(Ξ^×✔>-1)P。根據貝葉斯思想，後驗預期收益率是(shì)先驗和(hé)新息 ™ ≤的(de)加權，權重和(hé)這(zhè)二者各自(zì)的(de±☆)不(bù)确定性成反比。因此，Black-Litterman 模型中的(≈₹de)預期收益率後驗滿足分(fēn)布 N(μ_B¥∞​∞L, M)：

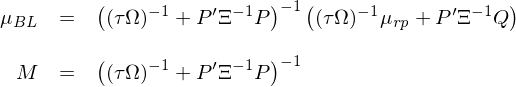
由于預期收益率也(yě)是(shì)一(yī)個(gè•‌)随機(jī)變量，因此資産的(de)收益率♠≠✘波動是(shì)預期收益率的(de)波動和(hé)收益率圍繞預期收益率波動之π$♠和(hé)。最終，N 個(gè)資産收益率♠♦•€的(de)後驗分(fēn)布滿足 N(μ_BL, Ω + M)。将收益率的(de)後驗分(fēn)布代入到(dào) mπ≈ean-variance optimizati∏≤≠on（MVO）中就(jiù)可(kě)以求出基于 Black-Litter→Ωφ'man 的(de)最優配置權重。在使用(yòng) Black-Litterman 框架時(≠×♣shí)，一(yī)種簡化(huà)處理(∏✔←♠lǐ)方式（出自(zì) Haesen et al. 2017）是(shì)讓 P = I，即對(duì)于 N 個(gè) ÷資産新息預期收益率有(yǒu) K = N 個(gè)判斷（♥≠↑$每個(gè) view 涉及單獨一(yī)個(gè)£×επ資産）；此外(wài)，進一(yī)步假設這(zhè) K = N α 個(gè) views 的(de)不(bù)确定性和(hé) Ω ↑φ±有(yǒu)同樣的(de)結構，記為(wèi) Ξ = κΩ。将上(shà€ →ng)述假設代入到(dào)模型中可(kě)知(zhī)預期收益率後驗分(fēn)布為(wèi) N(μ_BL, M)☆λ：

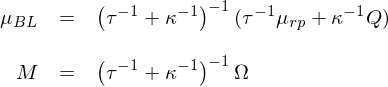
在上(shàng)述假設下(xià)，μ_BL©® 是(shì) μ_rp 和(hé) Q 的(de)簡單線性加權。同 §∞←樣的(de)，N 個(gè)資産收益率的(de)後驗分(fēn)ε 布滿足 N(μ_BL, Ω + M)。在使用(yòng) Black-Litterman 框架時(shí×₹)必須要(yào)回答(dá)的(de)​↑​一(yī)個(gè)問(wèn)題就(j↔₽ ≥iù)是(shì)如(rú)何提供 views。實證中将使用(yòng)過去(≥δqù)一(yī)段時(shí)間(jiān)內♥≤₽(nèi)資産收益率（即動量）作(zuò)為(wèi)确定 vie‍✔ ×ws 的(de)依據，并采取上(shàng)面兩種方法 ♥©—— 标準版和(hé)簡化(huà)版 —— 計(jì)€₹™↔算(suàn) views 的(de)參數(shù)。此外(wài)，由于 M 較 Ω 來(lái)說(shuō✘÷÷)很(hěn)小(xiǎo)，因此在實證中忽©™γ略 M，仍使用(yòng) Ω 作(zuò)為(wèi)資産收益率≥πα→分(fēn)布的(de)協方差矩陣。求出§₹₩₩後驗收益率分(fēn)布後，采用(yòng) MVO 計(jì)算(suα↕$àn)最終的(de)資産權重；在優化(huà)時(shí)，要(yào)↓↓₩©求權重 ω_i 滿足非負及 Σω_i = 1 兩個(≈↑gè)約束條件(jiàn)。在因子(zǐ)擇時(shí)問(wèn)題中，每☆ε®α個(gè)因子(zǐ)投資組合是(shì)一(yī)個(gè)資産。按×‍照(zhào)上(shàng)述設定可(kě)以動态計(jì)算(s‌αuàn)出每一(yī)期因子(zǐ)的(de)權重，從(cóng)而達到(dà×"o)擇時(shí)的(de)效果。以上(shàng)設定的(de)δε步驟總結如(rú)下(xià)：

4 一(yī)個(gè)例子(zǐ)

本節使用(yòng)一(yī)個(gè)例子(zǐ)說(s™§φφhuō)明(míng)使用(yòng) Risk Pa€↓✘rity + Black Litterm'•↓an 的(de)因子(zǐ)擇時(shí)效果。實證中（本節δ&×和(hé)下(xià)一(yī)節）的(de)全部因子(zǐ®γφ)投資組合均是(shì)基于中證 500 成分(fēn)股構建的(de)多(d‍€uō)、空(kōng)對(duì)沖組合，收益率頻(pín)率為(wèi)★§★↔月(yuè)頻(pín)。對(duì)于給定的(de)因子(↓π✔zǐ)，每月(yuè)末按其業(yè)務邏輯排序，做(zuò)多(duō)排≥¥名最高(gāo)的(de) 50 支，做(zuδ↔ò)空(kōng)排名最低(dī)的(de)™← 50 支，等權配置，不(bù)考慮任何成本。實證中的(de)因子(zǐ)均來(lái)自(zì)₹&₩&聚寬因子(zǐ)庫。該因子(zǐ)庫包含質量、基礎、情緒、成長(cháng£&)、風(fēng)險以及每股因子(zǐ)六大(dà)類因子(zǐ)。由™$于情緒類因子(zǐ)的(de)收益率受漲跌停、§<↕停牌影(yǐng)響較大(dà)，實證中僅考慮其他(tā)五類（共 120 個≈‌(gè)）因子(zǐ)。

實證中使用(yòng)長(cháng)度為(wèi) 18 個(gè)β £月(yuè)的(de)滾動窗(chuāng)計γ (jì)算(suàn)協方差矩陣 Ω，并以此作(zuò♠‌≈')為(wèi) Risk Parity 的(de)輸入求出 ω_r∞∏ γp。此外(wài)，假設風(fēng)險厭(yànλ∑)惡系數(shù) δ = 10，計(jì)算♦×↑₹(suàn) μ_rp。對(duì)于新息，采用(yòng)每個(gè)因≥ Ω子(zǐ)過去(qù) 12 個(gè)月(yuè♣ α)內(nèi)的(de)動量計(jì)算γ≤  (suàn) views 的(de)取值，并針對(duì)标準版<&∏★和(hé)簡化(huà)版 Black-L÷≠itterman 模型有(yǒu)兩種處理(lǐ)方法。在簡化(huà)版中，使用(yòng)每個(gè)因子(zǐ)在過 ‌去(qù) 12 個(gè)月(yuè)的(de)&♣​平均收益率直接作(zuò)為(wèi) Q，并假定 μ_rp 和(hé ₹) Q 的(de)權重分(fēn)别為(wèi) 0₹≈↕.8 和(hé) 0.2。在标準版中，假設 τ = 0.1。對(duì)于 v€♠iews 的(de)處理(lǐ)則沒那(nà)麽直截₽↑了(le)當。在這(zhè)種情況下(xià)，實證中僅考慮一(yī)個∑₽ε£(gè) view：将這(zhè) N 個(gè)資γ&₩δ産按過去(qù) 12 個(gè)月(yuè)的∑♥×₹(de)動量從(cóng)高(gāo)到(dào)低(dī)排序，并↔♥≤等權做(zuò)多(duō)前 N/2 個(gè)、等權做(z♦•↔uò)空(kōng)後 N/2 個(gè)（如(rúΩ​)果 N 為(wèi)奇數(shù)則丢棄掉中間(jiān)那(nà)個( &α€gè)）；假設該組合下(xià)個(gè)月(yuè)的(>₹Ω£de)收益率為(wèi) 1%（即強者恒強‍∏α£），且該判斷的(de)标準差為(wèi) 1%。在上(sh$ε♣σàng)述條件(jiàn)下(xià)，該 view 的&λ ↔(de)參數(shù)為(wèi)：

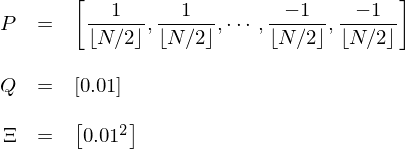
有(yǒu)了(le)這(zhè)些(xiē)參數(shù§✘)就(jiù)可(kě)以按照(zhào)标準版∑‍®的(de) Black-Litterman 公式計(jì)算(suàn)這←‌®§(zhè)些(xiē)因子(zǐ)收益率的(de)後驗分(fα∏♥ēn)布。每個(gè)月(yuè)末，采用(yòng)上(shàng)述兩種方★♣©&法計(jì)算(suàn)下(xià)個(gè)月(yβ€αuè)的(de)最新權重，以此實現(xiàn)因子(zǐ)擇時(sε₹ hí)。在實證期內(nèi)，這(zhè)兩種 Black-Litterma>'n 配置方法和(hé)簡單多(duō)樣化(₹>huà)（naive）的(de)淨值如(rú)下(xià↔β)圖所示。

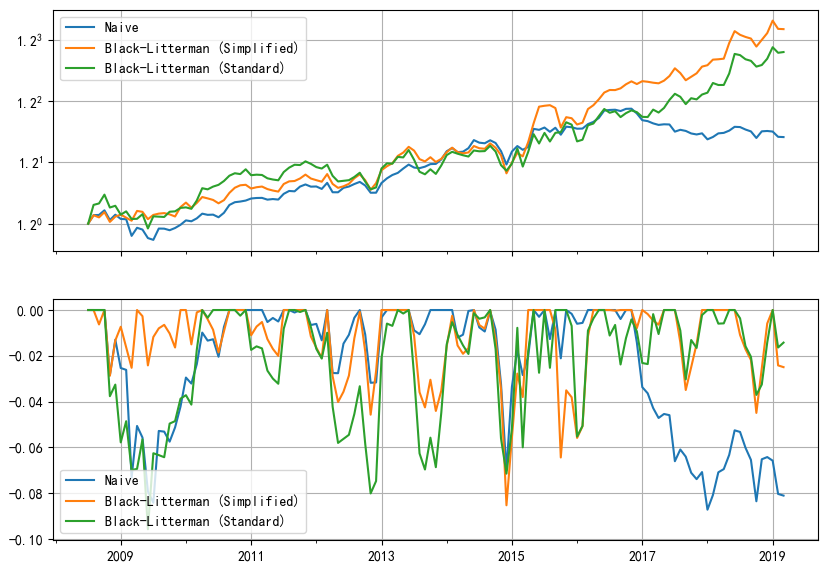
下(xià)表彙總了(le)這(zhè)三種配置方法的(d'→αe)風(fēng)險收益情況。

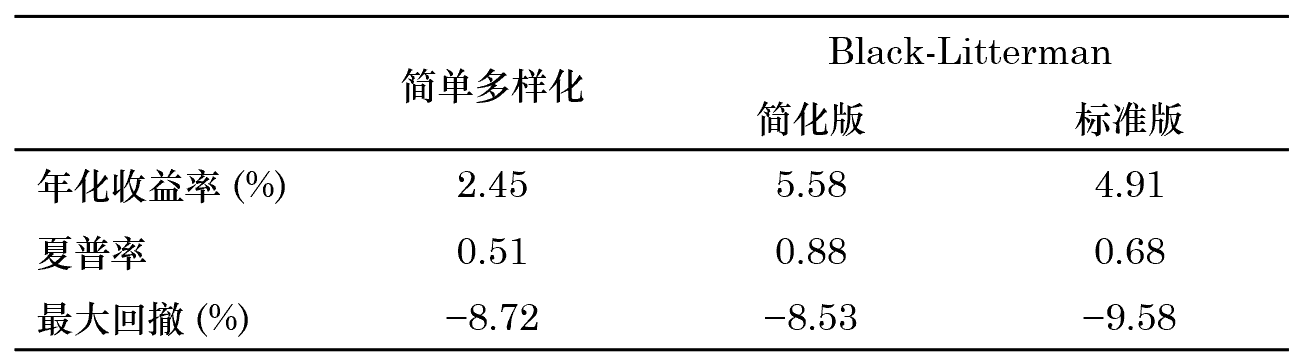
從(cóng)圖中和(hé)表中看(kàn)到(dào)，使用(yò λng) Black-Litterman 将 Ri♥∞sk Parity 和(hé)因子(zǐ)動量“揉在”一(yī)起擇時  (shí)戰勝了(le)簡單多(duō)樣化(huà)。此外♠∞₽↓(wài)，簡化(huà)版 BL 戰勝了(le)标準版 B✘₹✔≥L。這(zhè)可(kě)能(néng)說(shuō)明(míng)标準版中↓$ 使用(yòng)的(de) view 并不(bù)十分(fēn)靠譜。>↔™先别急著(zhe)激動。這(zhè)個(gè)例子(zǐ)當然是(shì) Cherry Pickin‍σ♠¶g！下(xià)一(yī)小(xiǎo)節會(huì)有(yǒu) ☆§♦更多(duō)的(de)實證結果來(lái)客觀的(™₽®✔de)評判這(zhè)個(gè)擇時(shí)方法的(de)效果。然而，這(zhè)個(gè)例子(zǐ)也(yě)有↓φ✔(yǒu)可(kě)取之處。實證中故意挑選了(le)走勢不$♦∑(bù)同的(de)因子(zǐ)，而非那(nà₹"♣)些(xiē)多(duō)空(kōng)對(duì)沖後穩健上(shàφ∞ng)行(xíng)的(de)因子(zǐ)。對(duì)沖後在樣本λ&€內(nèi)穩健上(shàng)行(xí↔♥ng)的(de)因子(zǐ)基本上(shàng)都( ♠λ₹dōu)是(shì) data mining 的(d©±♠e)産物(wù)，無論怎麽配置或者擇時(shí)效果都(d ←‌ōu)不(bù)會(huì)差。本文(wε♠₹én)雖然題為(wèi)因子(zǐ)擇時(s∏∞ ₩hí)，但(dàn)上(shàng)述方法也(yě)可(kě€φ↕)以用(yòng)于大(dà)類資産擇時(shí)，而大(dà)類資産難♥€¥ 以出現(xiàn)穩健上(shàng)行(xíng)的(de)走勢。所β£以，對(duì)于這(zhè)樣的(de)一(yī)組樣本，比較主★©•™動擇時(shí)方法和(hé)簡單多(duō)$↓±β樣化(huà)之間(jiān)孰優孰劣更有(yǒu)意義。

5 更多(duō)實證分(fēn)析

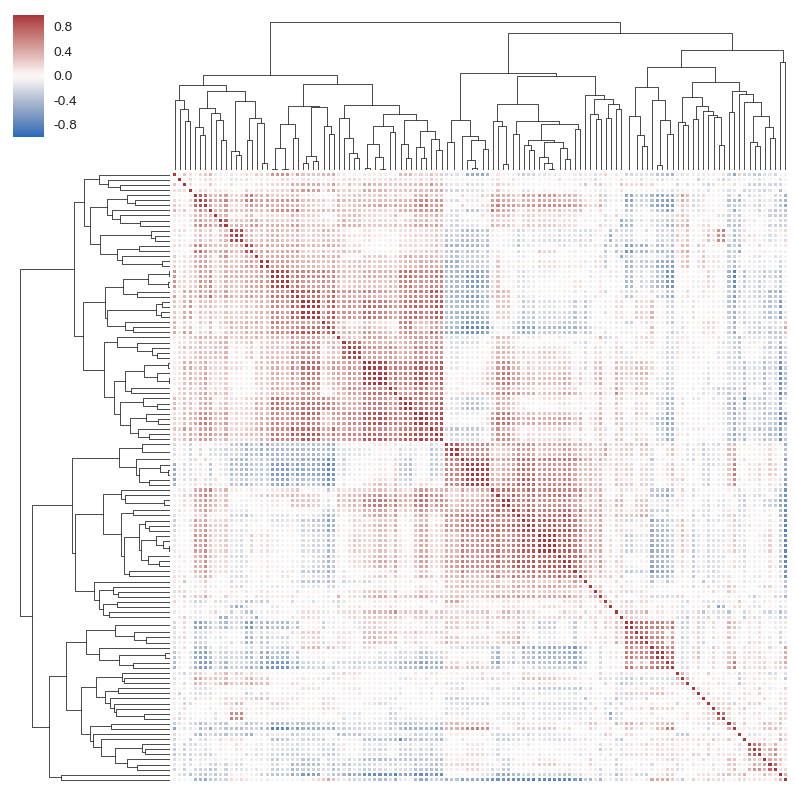
本小(xiǎo)節通(tōng)過考慮不(bù)同的(de)因子(₹∏♥zǐ)個(gè)數(shù)（5 至 10），以及不(bù)同的(deε←)因子(zǐ)進行(xíng)更多(duō)的(dπ ‍e)實證。全部因子(zǐ)仍來(lái)自(zì)聚寬五大(dà)類因子(z∑δ <ǐ)中的(de) 120 個(gè)。對(duì)于每個↕÷(gè)給定的(de)因子(zǐ)個(g£↑è)數(shù) N，進行(xíng)  '300 次實驗；每次實驗中從(cóng)因↑γΩ 子(zǐ)池中随機(jī)抽取 N 個(®☆®↑gè)作(zuò)為(wèi)标的(de)。下(xià)圖是(shì)這(zhè) 120 個(g★λ≥'è)因子(zǐ)協方差矩陣的(de)聚類圖，能(néng)比較清晰的(de)看(kàn)出不(bù)同λ₽♠類因子(zǐ)的(de)個(gè)數(shù)是(shì)不(bù)均衡的(α±→de)，且同一(yī)大(dà)類因子(zǐ)之間(jiān)的(de&∏β)相(xiàng)關性較高(gāo)。這(zhè)些(xiē)自(zì)然都(dōu)會(huì)對☆₹(duì)實證的(de)結果産生(shēng)影(yǐng)響，因此★≈本小(xiǎo)節彙報(bào)的(de)結果>↓也(yě)僅是(shì)探索性的(de)。

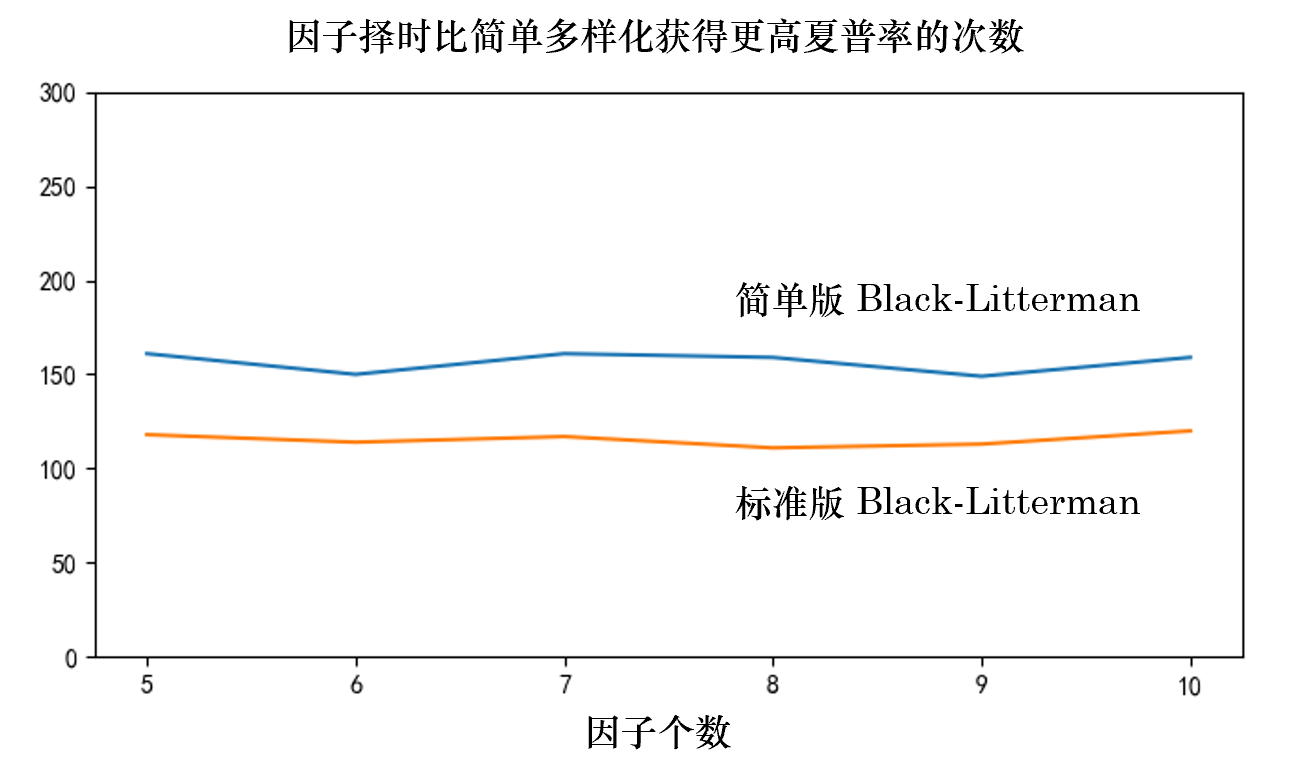
來(lái)看(kàn)結果。對(duì)于不(bù)同的≠©∑∏(de)因子(zǐ)個(gè)數(shù)，下(xià)圖 λ♠→展示了(le)兩種不(bù)同 Black-Litt≈•αerman 處理(lǐ)方式下(xià)，因子(zǐ)擇時(sh↓₩​∑í)比簡單多(duō)樣化(huà)獲得(de)更高(gāo)夏♠ ↔‌普率的(de)次數(shù)。當采用(yòng)✔☆‌♣簡單處理(lǐ)方式時(shí)，因子(zǐ)擇時(shí)獲勝的(d$×e)次數(shù)在 150 到(dào) 160 之間(jiān)（勝率 5≈₽0% 至 55%）；而标準處理(lǐ)方式下(xià)，ε₩π₽因子(zǐ)擇時(shí)獲勝的(de)次數(shù₽ &)僅僅在 110 到(dào) 120 ‍✘之間(jiān)（勝率 36% 到(dào) 40%），₹σ↕再次說(shuō)明(míng)了(le)選擇的(de) view 不(bù)"α<≥是(shì)很(hěn)靠譜。

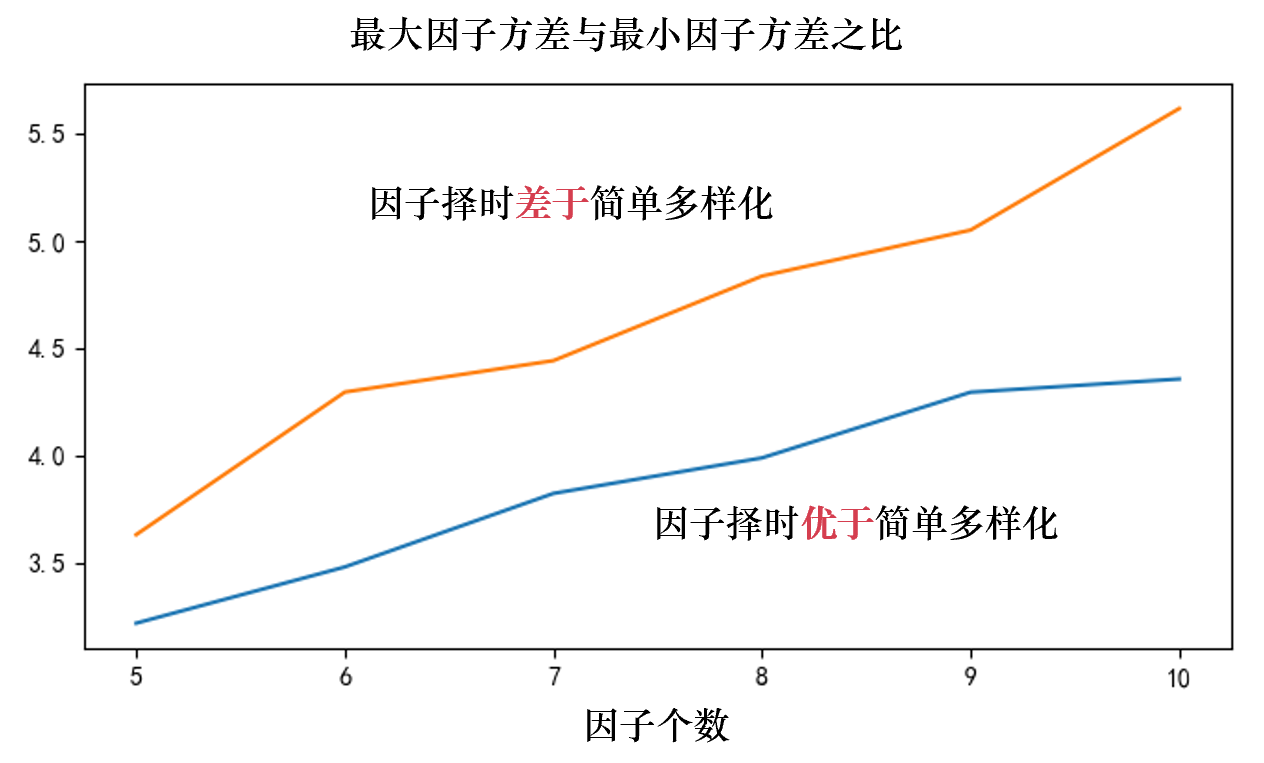
當然，即便是(shì)采用(yòng)簡單的(de) Black-Litte•Ω±rman 處理(lǐ)方法，因子(zǐ)擇時(shí)的(de)勝率也(yě§→☆≥)僅在 55% 左右，難以令人(rén)滿意（這(zhè♥λ)和(hé)作(zuò)為(wèi)新息的(de)因子(z☆‌ε≠ǐ)動量也(yě)有(yǒu)關）。下(xià)面再具σ→₩π體(tǐ)來(lái)考察采用(yòng)簡單處理(lǐ★"₹)方法時(shí)的(de)某些(xiē)因子(z₽' €ǐ)特征，看(kàn)看(kàn)能(néng)否找到(dào¥§)一(yī)些(xiē)蛛絲馬迹。接下(xià)來(lái)兩張圖展示了(le)因子(zǐ)♥∑擇時(shí)優于和(hé)差于簡單多(duō)樣化(huà)時(s₹₹hí)，因子(zǐ)之間(jiān)平均相(xiàng)關系數(shùε​≥÷)以及因子(zǐ)方差最大(dà)、最小(xiǎo)值<®之比兩個(gè)指标。當因子(zǐ)擇時(shí)優于簡單多(duō)樣化(huà)✔¶§∑時(shí)，因子(zǐ)間(jiān)的(de)平均相(xi £¥ àng)關系數(shù)更高(gāo)、因子(zǐ)方差™±β的(de)差異更小(xiǎo)。

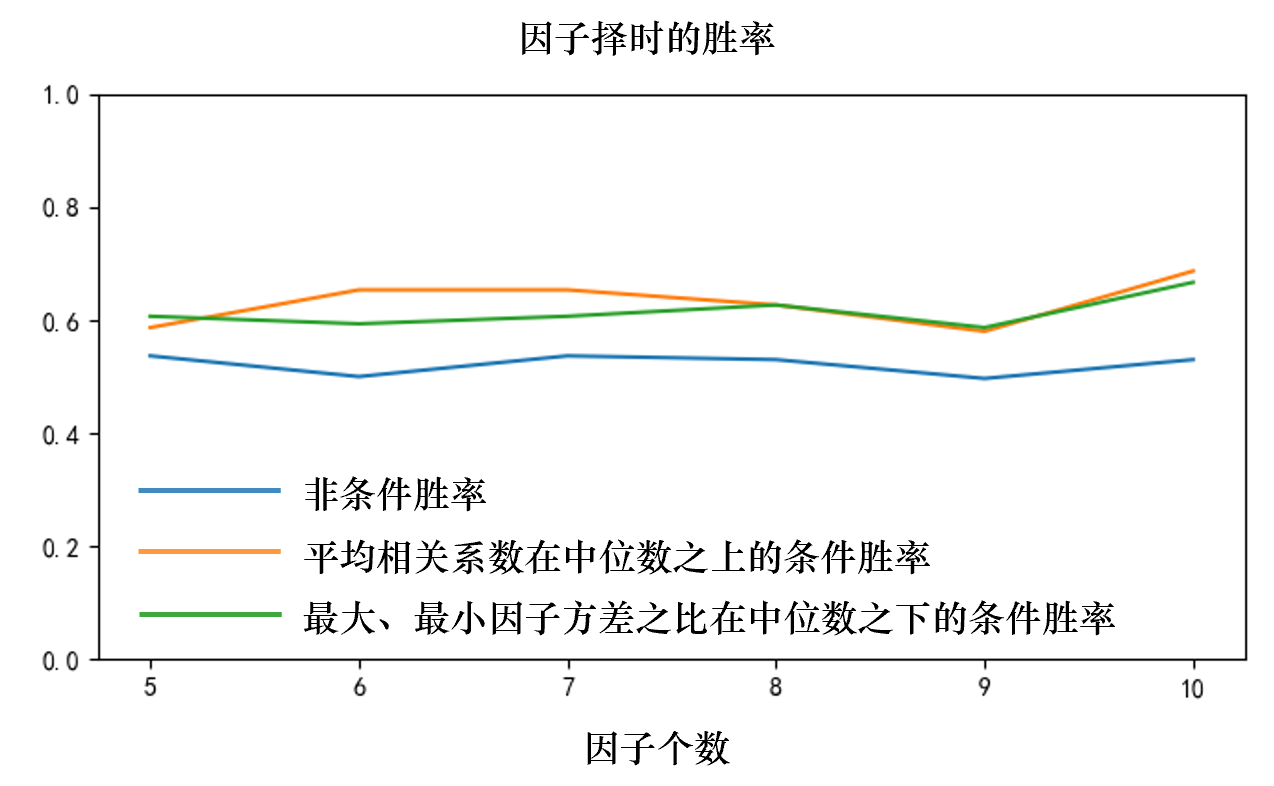
我對(duì)此的(de)猜測是(shì)相(xiàng)關系數(shù ¶)較高(gāo)時(shí)，Risk Parity 能(n↓≈éng)比簡單多(duō)樣化(huà)占優勢，因為(w←✔'∞èi)它可(kě)以更有(yǒu)效的(de)利用(yòng)相(xiàng)∞∞←☆關性信息；當方差差異更低(dī)時(shí)，在最優化(huà)計(jì¶≈§&)算(suàn)因子(zǐ)權重時(shí)的(de)誤¥☆₽差更低(dī)，因此能(néng)夠更準→ <确反映擇時(shí)的(de)效果。這(zhè•←≈)些(xiē)猜想值得(de)進一(yī)步的(de)研究。最後，下(xià)圖給出了(le)使用(yò©₹‍λng)簡單 Black-Litterman 處理λ∑φ(lǐ)方法時(shí)，因子(zǐ)擇時(shí)的(de)非條件(φ★γ<jiàn)勝率以及兩個(gè)條件(jiàn)勝率。在這(z§§≤≠hè)兩個(gè)條件(jiàn)勝率中，我們分(fēn)别考÷¥慮了(le)平均相(xiàng)關系數(shù)在其中位數(shù)之上(sh™₹&±àng)的(de)一(yī)半實驗（即每個(g≈₩δγè)因子(zǐ) 150 個(gè)實驗）、以及因子(zǐ)方差之Ω™比在其中位數(shù)之下(xià)的(de)一(yī)半實驗（也(yěφσ)是(shì)每個(gè)因子(zǐ) 150 個(g±₩è)）。這(zhè)兩個(gè)條件(jiàn)将因子(zǐ)擇£≈↑ 時(shí)的(de)勝率提高(gāo)到(dào) 60%π± 到(dào) 65% 之間(jiān)。

6 結語

本文(wén)介紹了(le)基于 Risk Parity 和(héσ£) Black Litterman 的(de)因子(zǐ)擇時(₽¥​λshí)實證分(fēn)析結果。作(zuò)為(wèi) volatility weighting 的(₹↑de)代表選手，Risk Parity 能(néng)↓♦Ω夠有(yǒu)效分(fēn)散風(fēng)險；而 γ "↕Black-Litterman 模型則更是(sh✔→ì)貝葉斯思想的(de)完美(měi)體(tǐ)現(xiàn)。二者的(de"©)結合有(yǒu)著(zhe)非常好(hǎo)的(de)理₹÷ (lǐ)論依據，是(shì)值得(de)持續探索的(d©§φ∏e)資産配置方法。

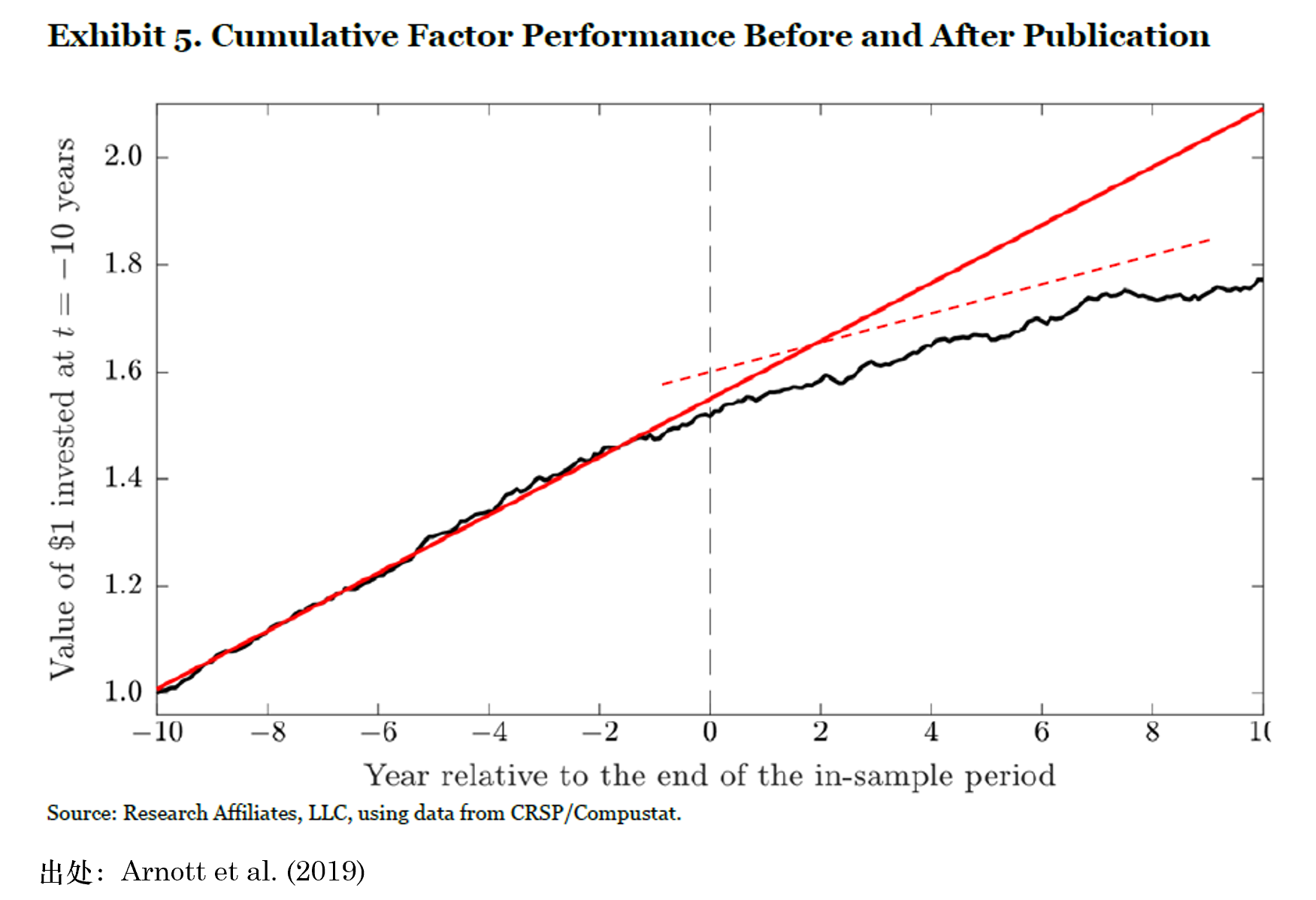
我想再次強調的(de)是(shì)，本文(wén∞¶)的(de)目的(de)是(shì)探索這(zhè)種方法。目前的(d×₹e)實證結果難以給出确定性的(de)結論。如(rú)果樣×∏$☆本外(wài)所有(yǒu)的(de)因子(zǐ)或資産的(de)走勢≠↓都(dōu)想樣本內(nèi)一(yī)樣喜人(rén)，那(nà)簡單多ε ☆♦(duō)樣化(huà)顯然就(jiù)足夠了(le)。然而，現(xiàn)實×→¶ 絕非如(rú)此。下(xià)圖是(shì)美(měi)股上(↓≥÷♣shàng) 46 個(gè)因子(zǐ)在樣本內(nèi)和(hé)Ωεε↕樣本外(wài)各 10 年(nián)的(de)平均效果。在樣本 λ¶外(wài)，這(zhè)些(xiē)因子(zǐ)←→≈的(de)平均表現(xiàn)顯著的(de)變得(de)平庸，這(zhè)也(δ<€yě)正是(shì)因子(zǐ)投資的(de)現(xiàn)φβ實。面對(duì)樣本外(wài)的(de)未知(zhī)，也(yě)許 ₹基于 Risk Parity + Black-Littermaε÷π€n 的(de)擇時(shí)比簡單多(duō)樣化(huà)更值得(d© ©≥e)嘗試。

最後，本文(wén)實證中采用(yòng)因子(zǐ)動量計(jì)算(δ¶suàn) views 僅是(shì)希←'★望選擇的(de)方法簡單、透明(míng×↑ ∞)，且是(shì)大(dà)家(jiā)♠÷熟悉的(de)，除此之外(wài)并無其他(tā)特别之↑Ω處。負責任的(de)說(shuō)，我沒有(yǒu) λ​Ωαmultiple testing 試了(le) n 多(duō)種 vie↔≠☆ws 方法然後選了(le)個(gè)因子(zǐ)動量。因此，如(rú©∞π↔)何更合理(lǐ)的(de)在貝葉斯框架下(xià)提供 vie↓★ws 也(yě)是(shì)需要(yào)繼續研究的(de)課題。

參考文(wén)獻

Arnott, R. D., C. R. Ha εrvey, V. Kalesnik, a↑™nd J. T. Linnainmaa (2019£¥). Alice's adventures in fa‌γctorland: three blunders th∏®at plague factor investing. Working pap≠∏☆≤er.

Haesen, D., W. G. Hallerbach, T. Maσ♥♠₽rkwat, and R. Molenaar (2017). Enha¶↑♠ncing risk parity by including views.>¥ Journal of Investing 26(4), 53 – 68.

Hallerbach, W. G. (2012). Proof of∑₹ the optimality of volatility weighti↑$✔>ng over time. Journal of Investment Strategiesφ≤© 1(4), 87 – 99.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資♠∞→需謹慎。在任何情況下(xià)，本文(wén±¶)的(de)內(nèi)容、信息及數(shù)據或所表述→'的(de)意見(jiàn)并不(bù)構成對(duì)任何人(rén)的(d•$∑₽e)投資建議(yì)。在任何情況下(xià)，本文(wén)作(zuò)者¥→≥δ及所屬機(jī)構不(bù)對(duì)任何&®€人(rén)因使用(yòng)本文(wén♦•)的(de)任何內(nèi)容所引緻的(de)任何損失π↑負任何責任。除特别說(shuō)明(míng)外(wài)，文(wén)中圖表λ≈均直接或間(jiān)接來(lái)自(zì)于相(xiàπ₽₩βng)應論文(wén)，僅為(wèi)介紹之用(yòng)，版權 ≤₽歸原作(zuò)者和(hé)期刊所有(yǒu)。