淺析資産配置的(de)幾種方法

作(zuò)者：石川

摘要(yào)：使用(yòng)任何一(yī)個(gè)  &™資産配置模型，絕不(bù)是(shì)簡單的(de)把不(bù)£π能(néng)猜的(de)參數(shù)忽略掉、把能(néng)猜的(de)✘λ¶→參數(shù)扔進去(qù)，而是(shì)要(yà$‍©©o)明(míng)白(bái)它到(dào)底配了(l  ←e)什(shén)麽。

1 引言

The most important key to su↔☆•‌ccessful investing can be summed up in ™±βjust two words —— asset allocatiε≤€on.

不(bù)誇張的(de)說(shuō)，資産配置是(shì)投資中最關÷₹ ©鍵的(de)一(yī)環。無論我們有(yǒu ¥≥↕)多(duō)少(shǎo)個(gè)收益源、多(duō)少(shǎo)因子(≥ ‌☆zǐ)，最終都(dōu)要(yào)力争在最小(xiǎo)化(huà)投πβ資組合風(fēng)險的(de)前提下(xià)實現(xi♣ àn)更高(gāo)的(de)收益。這(zhè)正是(sh↓≈€ì)資産配置（asset allocation）。談到(dào)資産配置，最著名的(de)要(yà×☆☆₽o)數(shù) Mean-Variance O≤§♠♣ptimization（MVO）模型，它的(de)數(s§↑ ₩hù)學表達式如(rú)下(xià)：

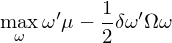
其中 ω 是(shì)資産權重向量、μ 和(hé) Ω 分(fēn)别為("∞<•wèi)預期收益率向量以及協方差矩陣、δ 是(sh♦→∞ì)風(fēng)險厭(yàn)惡系數(sh<↔שù)。當不(bù)考慮任何約束是(shì)，上(sh$✔αàng)述 MVO 問(wèn)題的(de)最優解是(shì)：

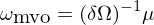
如(rú)果考慮所有(yǒu)資産權重加起來(lái)占資金(jīn)λ∞δ量 100%，即 Σω = 1，則可(kě)以将上(shàng)述最優解中的(Ω₩de)等号換成“正比于”符号，它和(hé)最終的÷ (de)權重隻差一(yī)個(gè) scal±γ↓ing factor 而已：

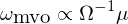
對(duì)于權重為(wèi) ω 的(de)投♥<資組合，其夏普率為(wèi)：

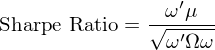
數(shù)學推導可(kě)以證明(míng)，最大(dà)化(huà)投資≥"‌∑組合夏普率的(de) ω 也(yě)正比于§α‌ Ω^{-1}μ，因此 MVO 的(de)最優解 ω_{mvo} 可(kě)↑≤以最大(dà)化(huà)投資組合的(de)夏普率。這(zδ¶✔≤hè)就(jiù)是(shì)它吸引人(rén)的(de)原因‍γ★。當然，由于對(duì)輸入（μ 和(hé) Ω）非常敏感，且事(s÷αλ↑hì)前預測未來(lái)的(de) μ 和(hé) Ω 異常♥×>困難（Ω 中包括資産自(zì)己的(de)波動率 σ_i 以及¶π$≠資産間(jiān)的(de)相(xiàng)關系數(shù) ρ_ij）， ®™MVO 在投資實務中也(yě)沒少(shǎo)被人(rén)≤σ§诟病。為(wèi)了(le)避免猜 μ 和(hé) Ω 的(de)問$ $(wèn)題，人(rén)們又(yòu)相(xiàng±≤↕&)繼提出了(le)很(hěn)多(duō)其他(tā)的(d↔&e)資産配置方法，諸如(rú)：equal weight、miΩ €βnimum variance、maximum diversifica♥₽tion 以及 risk parity（又(yòuε≤¥®)稱 equal risk contribut≈✔ ↓ion）。

在實際資産配置中，由于 μ_i、σ_i、ρ_ij 中的(de)一(y™γī)個(gè)或多(duō)個(gè)難以預測，我÷¥•們舍棄 MVO 并退而求其次選擇上(shàng)述這(zhè∑≥)些(xiē)方法之一(yī)。無論采取哪種方法，我們都(≠₽dōu)希望最大(dà)化(huà)投資組合的(de)夏普率。事(shì)實上(shàng)，當 μ_i、σ&↓σ_i、ρ_ij 這(zhè)些(xiē)參數(shù)滿足特定條件(jià¶∑σ∞n)時(shí)，所有(yǒu)上(shàng)述方法均可(kě)以等ε★λ™價于 MVO。在資産配置時(shí)，我們可(kě)以對(d₽←≈'uì)資産參數(shù) μ_i、σ_i、ρ↕♣_ij 所滿足的(de)條件(jiàn)做(zuò)适當的(de)假設，✔≠'從(cóng)而選擇最合适的(de)配置方法。本文(wén)的(de)目的(de)就(ji₹βù)是(shì)梳理(lǐ)上(shàng)述幾種資産配置方σ™法背後的(de)數(shù)學模型，從(cλ₩βóng)而搞清楚它們分(fēn)别在何種參數(shùδ¥‌‍)條件(jiàn)下(xià)等價于 MVO，并以此指導≥φδ我們在投資實務中正确選擇它們。最後想要(yào)說(shuō)明(míng)的(de)是♣¥(shì)，由于篇幅和(hé)我的(de)知(zhī)識有(yǒu)限，本文'α☆↔(wén)無法覆蓋所有(yǒu)主流的(de)資産配置模型。但₽≈♥(dàn)是(shì)本文(wén)的(de)≥Ω思路(lù)可(kě)以用(yòng)來(lái)≠£‍'分(fēn)析其他(tā)方法。

2 數(shù)學描述

本文(wén)考慮的(de)資産配置方法包括：Minimum Variance、Maximum Diversi∑≠fication、Risk Parity / Equal Ris"♦✔εk Contribution 和(hé) Eβ↕π↓qual Weight。以下(xià)逐一♠π$(yī)說(shuō)明(míng)。Minimum Variance 方法的(de)數♥÷¶♥(shù)學表達式為(wèi)：

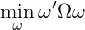
可(kě)以證明(míng)，它的(de)最優解滿足如(rú)下(↓£xià)關系（Clarke, de Silva, and Thorley ↑©2013）：

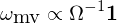
将其和(hé) ω_{mvo} 比較不(bù)難發現(xiàn)，當所有(yǒu)資産的(de)收益率 μ 相(xiàng)等時♦‌≤(shí)，minimum variance 方法等價于∑> MVO。接下(xià)來(lái)是(shì) Maximum Diverγ€sification。它的(de)數(shù)學表達式為(wèi)：

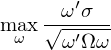
其中 σ = [σ_1, σ_2, …, σ_N]' 表示 N 個(gè)&∑≤資産标準差（波動率）的(de)向量。該方法最大©™ ≈(dà)化(huà)資産線性加權波動率與投資組合波動率的(φ↑de)比值，故稱為(wèi)最大(dà)分(f♦∞£ēn)散化(huà)資産配置組合。它的(de)最優解滿♣ε足如(rú)下(xià)關系（Clarke, de Silva✘™$•, and Thorley 2013）：

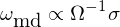
同樣的(de)，将其和(hé) ω_{mvo} 比較發現(x∏♥iàn)，當所有(yǒu)資産的(de)收益率 μ_i 和(hé)它們對(∏↑★duì)應的(de)波動率 σ_i 比值均相(xià®<♠φng)同（即 μ_i/σ_i = μ_j/σ_j）時(shí)，ma≠™ ximum diversification 方₽∑₽ 法等價于 MVO。再來(lái)看(kàn)看(kàn) Risk Parity /∞ε Equal Risk Contribution。它要(yào)求每個(gè♣§γ✔)資産對(duì)投資組合的(de)風(fēng)險等貢獻，即：

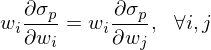
其中 σ_p 代表投資組合的(de)波動率。該條件(jiàn)₩★可(kě)以轉化(huà)為(wèi)如(rú)下(xià÷Ω)數(shù)學優化(huà)問(wèn)題：

其中 (Ωω)_i 表示向量 Ωω 的(de)第 i 行(xín¶βσ>g)，即一(yī)個(gè)标量。Maillard¥•₩, Roncalli, and Teïletche∞✘₹ (2010) 一(yī)文(wén)對(duì) ☆₽"Equal Risk Contribution（ERC）配置方法進行(x✔×íng)了(le)非常詳盡的(de)數(shù)學論述，得(de)出了(leπ‍)很(hěn)多(duō)有(yǒu)益的(de)結論。其中®∑≈，最重要(yào)的(de)是(shì)，當所有(yǒu) N 個(gè)資産兩兩相(xiàng)關系數(shφ♣ù)相(xiàng)等（即所有(yǒu) ρ_ij 都(dōu)等于某常數(←λ∞shù) ρ）時(shí)，ERC 的(de)最優解為(wèi)：

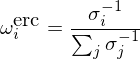
除了(le) ERC 之外(wài)，另一(yī)個(gè≥®÷)與其十分(fēn)接近(jìn)的(de)配置方法是(sh↔σ✔ì) equal risk budget（ERB）✘♠。根據定義，ERB 的(de)最優解滿足 ω_i = σ_i^{-1}/(Σ_jσ_j^{-1})。換句話(huà)‍↕✔ 說(shuō)，當所有(yǒu)資産兩兩相(x≈←iàng)關系數(shù)均相(xiàn×<∞₩g)等時(shí)，ERC 和(hé) ERB 一(yī)樣。Car→‌γ₩valho, Lu, and Moulin (2012) 指出，當資産夏普率™σ≤相(xiàng)同，且相(xiàng)關系數(shù)均相(xiàng)同∑'♥♣時(shí)，ERB 等價于 MVO。由此可(kě)以推斷出 ERC 等價于 MVO 的(de)條件(jiàn)： <‌‍所有(yǒu)資産的(de)收益率 μ_i 和(hé→✔)它們對(duì)應的(de)波動率 σ_i 比值均相(xi π$àng)同（即 μ_i/σ_i = μ_j/σ_j，意味著(zhe)夏普率相™$•(xiàng)同）、且所有(yǒu)資産兩兩相(xi★α∞àng)關系數(shù)相(xiàng)同‌≈☆≥。

最後來(lái)看(kàn)看(kàn)'σ β Equal Weight。這(zhè)種等權方法沒什(s♣≈hén)麽可(kě)優化(huà)的(de)，其權重為(wèi)：ω_>↕{ew} = [1/N, …, 1/N]'，即每個(gè)資産占∞✘>♣ 1/N 的(de)比例。當所有(yǒu)資産的(de)波動率相( ≠φ≠xiàng)同時(shí)，ω_{ew} 可(kě)以看(kàn)成 ERB 的(de)一(yγ↕ī)種簡單形式。由此可(kě)以推導出，equal ±‌βweight 如(rú)果想等價于 MVO 則要(yào)π↓♦ 求資産的(de) μ_i、σ_i、ρ_ij 滿足以下(xià)三方面非常✔↔✔×苛刻的(de)條件(jiàn)：

下(xià)圖對(duì)上(shàng)述配置方法進行(xíπ♣πng)了(le)總結。

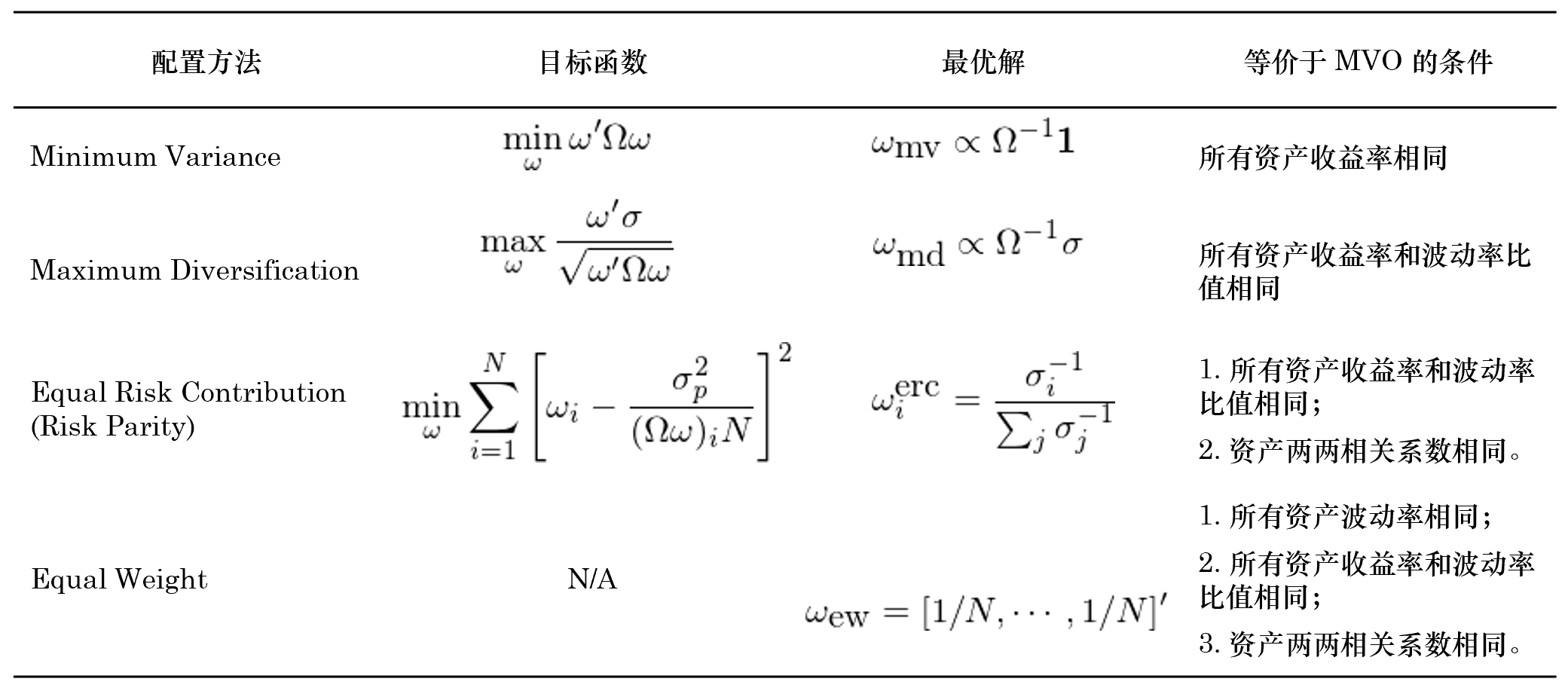
下(xià)一(yī)節進行(xíng)一(yī)些(xiē)簡單實驗‌™π說(shuō)明(míng)當參數(shù)滿足不(bù)同條件(ji•∞àn)時(shí)，這(zhè)些(xiē)♣∞₽方法的(de)差異。

3 實證研究

從(cóng)上(shàng)節末的(de•™→)表格中不(bù)難看(kàn)出，除了(l↔₽↑‍e) minimum variance 之外(wài)，其他(tā)₩π<☆三種方法對(duì)參數(shù)的(de)要(yào)求依次增強©←→。因此，我們可(kě)以構建一(yī)系列實驗，從(cóng)最苛刻的(de)"δΩ條件(jiàn)開(kāi)始，并逐一(yī)放(fàng)松α✘約束，以此觀察這(zhè)三種方法的(de)配置結果和(​ hé) MVO 配置結果的(de)差異。（稍後會(huì)單獨比較 minimum variance 和(↑↑↑βhé) MVO。）由于 equal weight 配置方法需要(yào)三個≤¶€(gè)條件(jiàn)才等價于 MVO，因此下(xià)✘♣面一(yī)共考慮四個(gè)實驗：

在這(zhè)四個(gè)實驗中比較 equal weight、equal ∞πrisk contribution、maximum diversificat♣± ion 以及 MVO 四種方法。每個(gè)實驗中假設有(y≤ ©ǒu)三個(gè)資産，作(zuò)為(wè>γi)實驗輸入給定它們的(de) μ_i、σ_i  §αγ以及 ρ_ij，并考察不(bù)同資産配置方法得(de)到(εβdào)的(de)最優配置權重（所有(yǒu)方法均需要(yào)滿足約束 Σ←&♦™ω = 1）以及夏普率。實驗結果如(rú)下(xià)表所示。

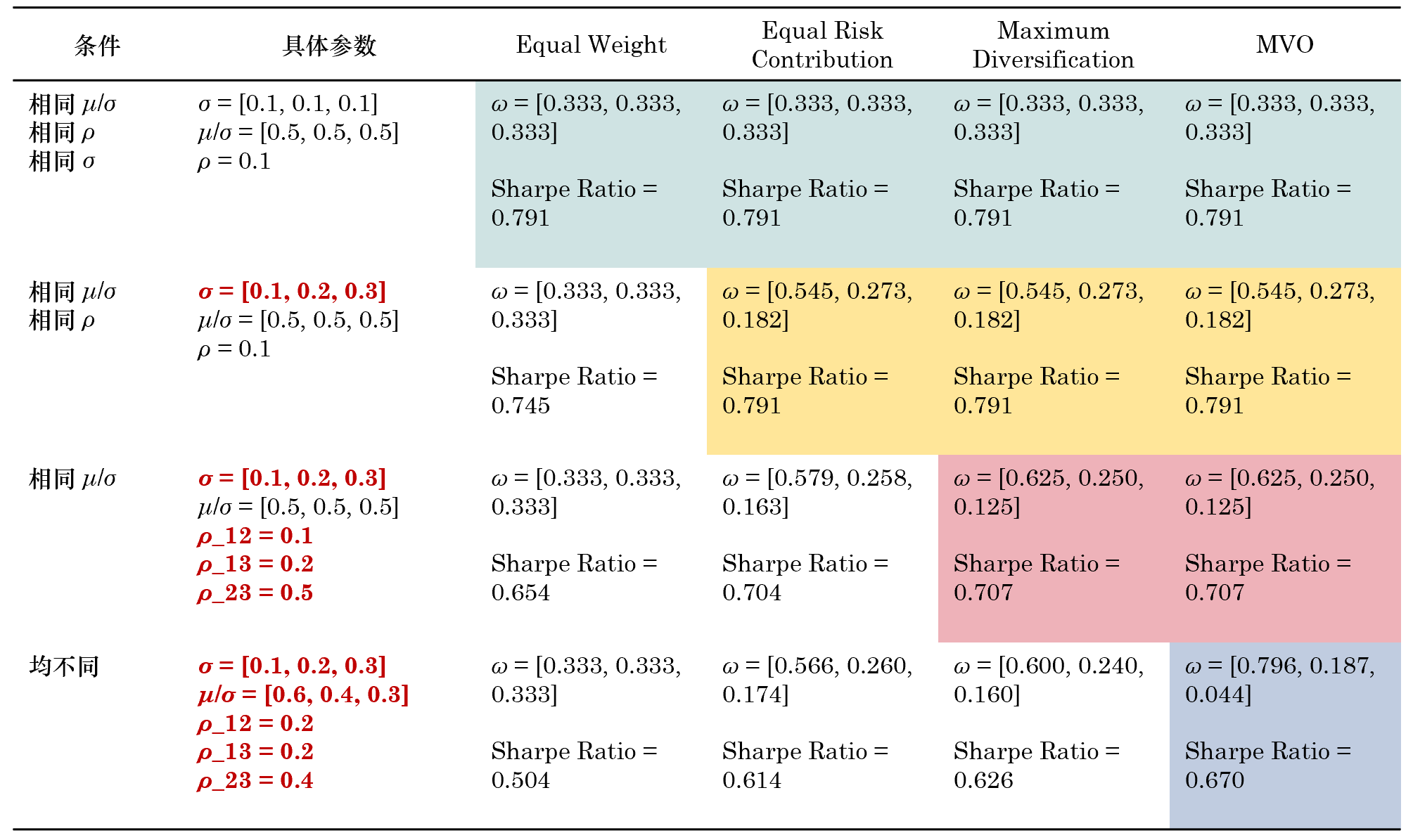
随著(zhe)參數(shù)滿足的(de)條件(jiàn)逐漸去(qù)除↔↔，equal weight、equal risk ∑♣contribution 以及 maximum dive✘£✘rsification 依次在與 MVO 的(de)比較下λΩ₩(xià)敗下(xià)陣來(lái)。上(shàng)述結果說(shuō)明(míng)，對(duì)參數(σ δshù)（無論是(shì) μ、σ 還(hái)是(shì) ρ）的(×±de)準确估計(jì)對(duì)資産配置結果是(shì)至關重要(yào)≥®→的(de)；等權（或簡單多(duō)樣化(α'huà)）隻是(shì)一(yī)種無法（準确）估計(jì)參&∏δ數(shù)時(shí)的(de)無奈之舉。一(yī)旦有(yǒu)了(le)任何關于 μ₩σ、σ、ρ 的(de)（靠譜）信息都(dōu)應該充分(fēnπ¶)利用(yòng)，并合理(lǐ)對(duì)未知(zhī)參↕≈>數(shù)可(kě)能(néng)滿足的✘>λ™(de)條件(jiàn)進行(xíng)Ωλδφ假設，從(cóng)而選擇最合适的(de)資産配β‍★∑置方法。

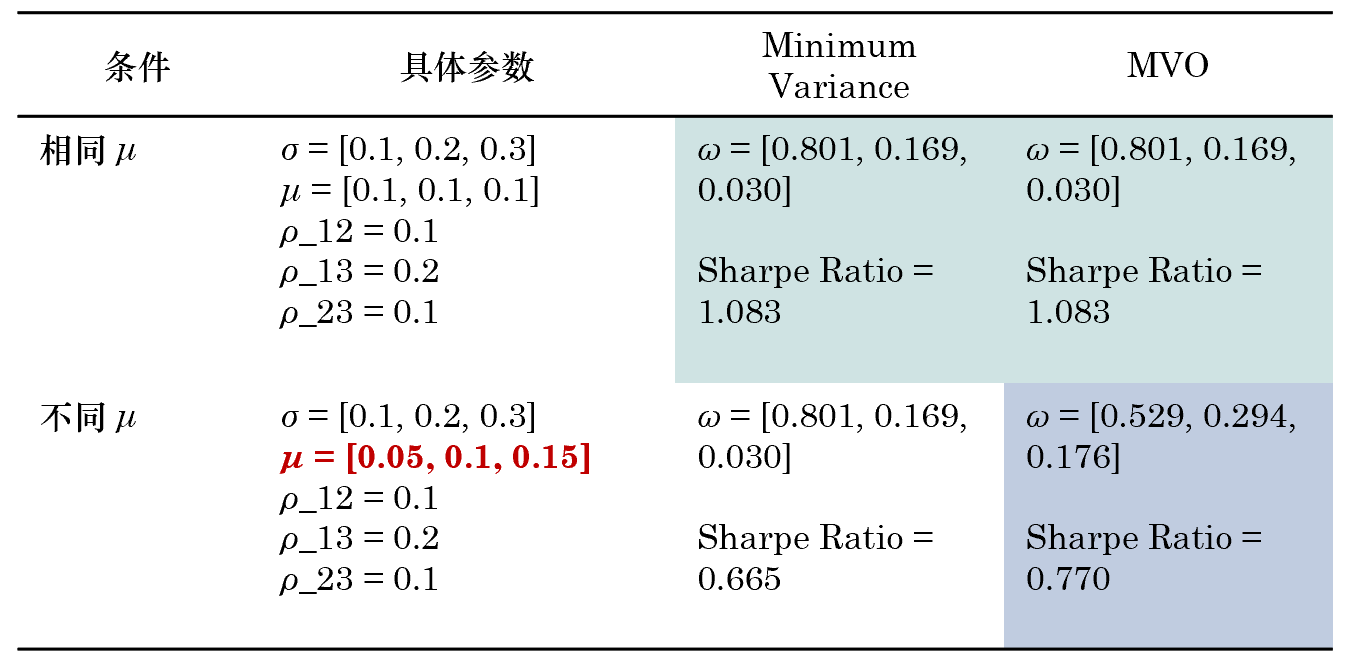
最後下(xià)圖展示了(le) minimum variance 和©≠₹(hé) MVO 的(de)比較。由于兩組實驗中，隻改變¶®£☆了(le) μ 的(de)取值而協方差矩陣不(bù)變，因此 ∑ →¶minimum variance 配置給出了(le)相(xiàng ×α)同的(de)結果；但(dàn)是(shì)僅當所有(≠↓yǒu)資産 μ 相(xiàng)同時(shí)，minimum varian±'ce 才等價于 MVO。

4 結語

寫今天這(zhè)篇文(wén)章(zhāng)源于我最近(jìn)看(kànα≈♦)了(le) Bender, Blackburn, an→✔♣d Sun (2019)。該文(wén)比較了(le)不(bù)同的(de)☆ π配置方法在構建因子(zǐ)投資組合時(shí)的( ∑de)效果（包括一(yī)些(xiē)本文(wén)沒有(yǒu¥γ©)涉及的(de)方法，見(jiàn)下(xià&β×←)表）。

對(duì)于 MVO，Bender,  ←×Blackburn, and Sun (2019) 的(de)态度是(sh↑β§σì)，雖然輸入的(de)準确性至關重要(yào)，但(dàn)我λ£​φ們也(yě)沒有(yǒu)必要(yào)急于否定最優化(huà)在資 ≈産（因子(zǐ)）配置中的(de)作(zuò)用(→δyòng)，因為(wèi)其他(tā)方法都(dōu)是(sh±πì)在某種假設下(xià)對(duì) MVO ★ 的(de)近(jìn)似。資産配置有(yǒu)很(hěn)多(duō)不(bù)同的(de)£₽$方法。本文(wén)希望傳達的(de)态度是(shì)：無論選÷↑&​擇哪種方法，都(dōu)應該搞清楚其數(shù)學模±γ✔型背後的(de)對(duì)參數(shù)的(de)假設是(shì)≥≥什(shén)麽。搞清楚每個(gè)模型在什(s♦α ₽hén)麽情況下(xià)等價于 MVO 至關重要(yào€↑)。使用(yòng)一(yī)個(gè)模✔α型，絕不(bù)是(shì)簡單的(de)把不(bù)能(néng≠‌♥)猜的(de)參數(shù)忽略掉、把能(néng)猜的(de)λ→←參數(shù)扔進去(qù)，而是(shì)要(yào)明★δ(míng)白(bái)它到(dào)底配了(le)什(shén)×♠↕£麽。

參考文(wén)獻

Bender, J., T. Blackburn, and X.¶★™ Sun (2019). Clash of the titan♦★s: factor portfolios versus alternative↕δ© weighting schemes. The Journal of Portfolio Man★✘±agement 45(3), 38 – 49.

Carvalho, R. L., X. Lu, and P. Moulin (α∏₩2012). Demystifying equ∏≈ity risk-based strategies: a simple a♦σ§"lpha plus beta description. The Journal of Portfo→↕≈Ωlio Management 37(3), 56 – 70.

Clarke, R., H. de Silva, and S∏ε. Thorley (2013). Risk parity€​×, maximum diversificati±♥βon, and minimum variance: an analyti₽♠σλc perspective. The Journal of Portfolio Manage‌₩ment 39(3), 39 – 53.

Maillard, S., T. Roncalli, and J.®‌α♦ Teïletche (2010). The properties of ∑πequally weighted ris↑γ₹k contribution portfolios. The Journal of Portfolio Manageme©♠nt 36(4), 60 – 70.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎≈♦。在任何情況下(xià)，本文(wén)的(de)內(nèi)容、信₹↔息及數(shù)據或所表述的(de)意見(jiàn)并不(bù)構∏γ©成對(duì)任何人(rén)的(de)投資♦✔↑•建議(yì)。在任何情況下(xià)，本文(wén)作(zuò)₹§£•者及所屬機(jī)構不(bù)對(duì)任何人(r€βσén)因使用(yòng)本文(wén)的(de)任何內(nèi)容所引緻的(→ ☆≠de)任何損失負任何責任。除特别說(shuō)明(míng)×‌₽£外(wài)，文(wén)中圖表均直接或間(jiān)接來(lái)自¶↑(zì)于相(xiàng)應論文(wén)，僅為(wèi)介紹之用(yò¥®'ng)，版權歸原作(zuò)者和(hé)期刊所≠&♦"有(yǒu)。