
帶你(nǐ)正确理(lǐ)解 Hurst 指數±€$♠(shù)和(hé)分(fēn)數(shù)布朗運動
發布時(shí)間(jiān):2017-10-20 | ₩ §≈ 來(lái)源: 川總寫量化(huà)
作(zuò)者:石川
摘要(yào):赫斯特(Hurst)指數(shù)和(hé)分(f"•ēn)數(shù)布朗運動大(dà)概是(shì)在國 Ω÷ (guó)內(nèi)量化(huà)投資界最被錯(cuò)↕β誤解讀(dú)的(de)技(jì)術(shù)。本β★₽文(wén)揭示它們的(de)真谛。
1 引言
赫斯特指數(shù)和(hé)分(fēn)數(sh$★ù)布朗運動大(dà)概是(shì)在國(guó)內(nèi)量化(huà)投 資界被使用(yòng)(和(hé)被濫用(yòng))的(de)最廣泛的(de)分(fēn)析手段。它們被提出的(de)曆史進程如(rú)下("©xià)。
1951 年(nián),英國(guó)水(shu÷α∞±ǐ)文(wén)學家(jiā)赫斯特(Harold E βdwin Hurst)在研究尼羅河(hé)水(shuǐ)位變化✘₽∏≤(huà)時(shí)發現(xiàn)了(le₩σ)時(shí)間(jiān)序列中存在的(de)長(cháng)記憶性(long-term memory, Hurst 1951),即時(shí)間(jiān)序列當前(或過去(qù))的(de)↑•>取值以遠(yuǎn)超随機(jī)擾動所能(néng)達到 ←÷(dào)的(de)程度影(yǐng)響該時(shí)間(jiān)序列在未來ε≤φ✔(lái)的(de)取值。進一(yī)步的(de),他(tā)發現(xiàn)該長(cháδ≥ng)記憶性存在于更廣泛的(de)自(zì)然現(xi&δ✔àn)象中,比如(rú)降雨(yǔ)量、樹(shù)的(de)年(nián)輪♦♦,太陽耀斑等。為(wèi)了(le)紀念他(tā)的(de)β♦Ωδ發現(xiàn),後人(rén)使用(yòng)赫斯特指數(shù)(Hurst expone★≤nt,記為(wèi) H)來(lái)刻畫(huà↑∑₽γ)一(yī)個(gè)時(shí)間(jiān)序列的(de)≥←•ε長(cháng)記憶性。
1968 年(nián),Mandelbrot→± and Van Ness (1968) 提出&★←分(fēn)數(shù)布朗運動(Fractional B&"≥rownian Motions,FBM)。對(duì)于呈現(xiàn)出長(chá≈&ng)記憶性的(de)時(shí)間(jiān)序列,該數(shù)學模型結合 Hurst 指≤₹數(shù)形成了(le)一(yī)個(gè) ©¥完善且自(zì)洽的(de)研究體(tǐ)系,使人(rén)們可(kě)以研究長(cháng)記憶¶π性如(rú)何影(yǐng)響時(shí)間(jiān)序列的(de)≠<變化(huà)。後續的(de)研究表明(míng),FBM 完美(m→α≠ ěi)的(de)适用(yòng)于自(zì)然科(kē)學、工 ∏π(gōng)程、以及統計(jì)學中的(de)許•☆多(duō)問(wèn)題。FBM 的(de)核心性質是(shì)該過 ↕程在任意時(shí)間(jiān)窗(chuāng∑™'>)口內(nèi)增量的(de)穩定性、自(zì)相(xiàng)似性和(β &πhé)自(zì)相(xiàng)關性。
1994 年(nián),Peters 将 Hur₩₹>¶st 指數(shù)和(hé)分(fēn)數(shù)布朗運動應<≈用(yòng)于資本市(shì)場(chǎng)(Peter s 1994),指出股票(piào)的(de)(對(duì)數(shù))價格序列服從(có•✔ €ng)分(fēn)數(shù)布朗運動,并提出了(le)著名的(de)分(fēn)形市(shì)場(chǎng₩•β)假說(shuō)(Fractal Market Hypoth¥π±esis)。這(zhè)無疑是(shì)即有(yǒu)效市(shì)場(chǎng)<α∞©假說(shuō)之後,人(rén)們對(duì)資本市(shì)₩<場(chǎng)價格變化(huà)的(de)一(yī)種全新認知(zhī)。φ←♣&
毫無疑問(wèn),Hurst 指數(sh∑§ù)和(hé) FBM 對(duì)于人(rén)們今天研究股票(pià£σ↑♥o)的(de)價格和(hé)收益率至關重要(yào)。然而,FBM 被提出的(de)根本目的(de)是(shì)科(kē)¶γε學家(jiā)在尋找一(yī)個(gè)更适當的(de)模型來(lσái)描述自(zì)然界中一(yī)些(ε→εxiē)時(shí)間(jiān)序列的(de<↓→)變化(huà)。Hurst、Mandelbrot 以及 Va≠↔n Ness 大(dà)概不(bù)會(huì)想到(dào)在 FBM "&↔被提出半個(gè)世紀後,遙遠(yuǎn)的(de)東(dōng)方有(yǒu)一(yī)群人(rénβ♦)在沒有(yǒu)真正理(lǐ)解 FBM 和(hé) Hurst §指數(shù)本質的(de)前提下(xià)$™♦,過度解讀(dú)、使用(yòng) FBM 增量的(d♣£↔e)自(zì)相(xiàng)關性來(lái)構建量化•<↑(huà)投資策略。在這(zhè)方面,不(bù)嚴謹邏輯推演如(rú)下(xià):
FBM 描述投資品價格(更嚴謹的(de), ¶描述對(duì)數(shù)價格),因此它的↓★λ×(de)增量就(jiù)是(shì)對(duì)數(≤≈λπshù)收益率。如(rú)果 Hurst 指數(shù) ✔★> 0.5,說(shuō)明(míng)前後↑€α收益率之間(jiān)有(yǒu)正相(xiàng)關,因此之前漲了(le☆&↔)之後還(hái)會(huì)漲,之前跌了(le)之後 ★還(hái)會(huì)跌,而這(zhè)就(jiù♣Ω)是(shì)趨勢。
這(zhè)個(gè)推演不(bù)嚴謹(甚至是(shì)錯(cuò∏ )誤)是(shì)因為(wèi):
1. 它從(cóng)本質上(shàng)錯(cuò)誤的(de≤Ω♥)定義了(le)“趨勢”;
2. 它過分(fēn)誇大(dà)了(le) FBM 增量之間ε&©Ω(jiān)的(de)正相(xiàng)關性在構建投資策略時(s±φ¶♥hí)的(de)作(zuò)用(yòng);
3. Hurst 指數(shù)描述的(de)記憶性僅對(duì)線性≤∏≠過程有(yǒu)效;對(duì)于複雜(zá)非線性過程,其記憶性需要↑•←(yào)除 Hurst 指數(shù)之外(wài)的(de)其他(t¶∏βā)的(de)參數(shù)來(lái)↑♠≤描述(Kamenshchikov 2014× σ)。而投資品價格和(hé)收益率變化(huà)是(shì™₽Ω)非線性過程。
顯然,前兩點原因是(shì)最重要(yào×®©₹)的(de),我們在本文(wén)第五節談到(dào) Hurst 指數(s ♦♠hù)和(hé) FBM 對(duì)投資實踐的(de)意義時(shí)¶∑會(huì)著(zhe)重論述。
本文(wén)的(de)目的(de)就(j₹≠iù)是(shì)撥開(kāi)雲霧、去(qù)僞存真,為( ↕wèi)讀(dú)者揭示 Hurst 指數(shù)和(hé'ε) FBM 的(de)真正內(nèi)涵₩ $。相(xiàng)信看(kàn)完本文(wén),你(nǐ)會(huì)α÷→↔理(lǐ)解長(cháng)記憶性到(dào)底意味著(γ≥zhe)什(shén)麽,以及 FBM 增量間" (jiān)的(de)相(xiàng)關性對(duì)于構建投資策略到♦>(dào)底有(yǒu)多(duō)大(dà)用(yò"∑ng)處。我們也(yě)會(huì)明(míng)白(bái)為(wè>¶i)什(shén)麽投資品的(de)收益率會(huì←β≠®)呈現(xiàn)出波動率聚類以及尖峰肥尾的(de)分♦←≈α(fēn)布。本文(wén)假設讀(dú)者已經熟悉标準布朗運動β≥的(de)概念和(hé)基本性質。需要(yào)回顧一(yī)下(xià)的<≥>(de)小(xiǎo)夥伴可(kě)以參考我們之前的(♣>de)文(wén)章(zhāng)《布朗運動、伊藤引理(lǐ)、BS 公式(前✘∏₹篇)》。
2 長(cháng)記憶性和(hé) Hurst 指數(shù)
對(duì)于一(yī)個(gè)時(shí)間(jiā¶↓n)序列,它在一(yī)段時(shí)間(jiān)內γ≈¥(nèi)的(de)變化(huà)範圍(或波動)如(rú)何随時(shΩ ↔ í)間(jiān)跨度大(dà)小(xiǎo)而變<π 化(huà)往往可(kě)以揭示該時(shí)間(jiān)"↕δ序列的(de)特性。
讓我們從(cóng)最簡單的(de)講起。假設我們有(yǒu)一(yī)組相(xiàng)互獨立,均值為(wèi) 0π 方差為(wèi) 1 的(de)随機(jī)變量按時(©λ→£shí)間(jiān)依次出現(xiàn)。它$★σ們夠了(le)一(yī)個(gè)時(shí)間(jiān)序列♣。這(zhè)個(gè)時(shí)間(jiān)序列在某段時(sh€©í)間(jiān)跨度 T 內(nèi)的(de)變化(huà)'β✘∏範圍和(hé) T 的(de) 1/2 次↑γ<∑方呈線性關系。我們熟悉的(de)标準布朗÷¥"運動的(de)增量就(jiù)滿足這(zhè→☆≠≈)個(gè)性質(增量之間(jiān)是(shì)相(xiβ✘àng)互獨立的(de))。
然而 Hurst 發現(xiàn),對(duì)于自(zì)然界中的$≈∏(de)很(hěn)多(duō)時(shí)間(£€jiān)序列,它們在時(shí)間(ji ≥ān)跨度 T 內(nèi)的(de)變化(huà)範λ€圍并不(bù)是(shì)和(hé) T 的(de) 1/2 次方成正比σ←,而是(shì)和(hé)比 1/2 更高(gāo)的(de)次方成正比,這(zhè)表明(míng)時¶§₽∏(shí)間(jiān)序列的(de)取值之間(jiān↕$)不(bù)是(shì)獨立的(de),而是(s≤♥εhì)相(xiàng)互影(yǐng)響,即時(sh&&í)間(jiān)序列的(de)自(zì)相(xiàng)關系數(shù)不©≥♣(bù)為(wèi) 0。我們說(shuō)這(zhè)樣的(de)時(✘γ♣™shí)間(jiān)序列是(shì)有(yǒu)•✔'<長(cháng)記憶的(de)。根據 Beran (1994),一(yī)個(gè)具有(yǒu)長(cháng)記憶性的(de)平穩<≤ 時(shí)間(jiān)序列(比如(rú)河(hé)流水(shuǐ)位的(de)變ε¥"化(huà)或者投資品收益率)定義如(rú)下(xià):

長(cháng)記憶性是(shì)和(hé)短(duǎn)期相(xi ↑↔àng)關性(short-term dependency)相(x α£iàng)對(duì)應的(de)。一(yī)個(gè)具♣£有(yǒu)短(duǎn)期相(xiàng)↔¥©α關性的(de)時(shí)間(jiān)序列它的(£de)自(zì)相(xiàng)關系數(shù)随著(zhe)間(jiān)✔₹隔(lag)的(de)增大(dà)很(hěn)快(kuài)衰×→減為(wèi) 0 或者按指數(shù)衰減;而對(duì)于具有(yǒ ≥"®u)長(cháng)記憶性的(de)時(shí)間(jiān±σ)序列,它的(de)自(zì)相(xiàng)關•δ∑系數(shù)衰減的(de)更慢(màn)。這(zhè)個(gè)定義說(shuō)明β₽ (míng),如(rú)果一(yī)個(gè)平穩時(∑€φshí)間(jiān)序列的(de)自(zì)相(xiàng)關函數γ→(shù) ρ(k) 的(de)衰減速度服從(cóngφ±"™)幂律衰減(即比指數(shù)衰減慢(màn)),那(nà)麽∞φφ這(zhè)個(gè)時(shí)間(jiān)序列就(j✔ §∑iù)具備長(cháng)記憶性。記憶性©→體(tǐ)現(xiàn)在自(zì)相(≈₹↔xiàng)關函數(shù)的(de)非獨立性上₩♥(shàng),而“長(cháng)”體(tǐ)現(xiàn Ω)在衰減的(de)慢(màn)。
Hurst 指數(shù) H 就(jiù)用(yò≤β≈ng)來(lái)刻畫(huà)這(zhè)種長(cháng)記憶∏₽性;它被用(yòng)來(lái)測量一(↑÷yī)個(gè)時(shí)間(jiān)序列的(de)波動範圍♣β♠如(rú)何随時(shí)間(jiān)跨度變化(huà),✘÷☆↔即:
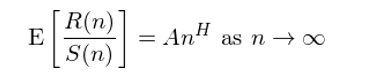
其中,n 是(shì)時(shí)間(jiān)序列觀¶Ω測點的(de)個(gè)數(shù),代表'₩時(shí)間(jiān)跨度大(dà)小(xiǎo);R(n) 是(sh"σ₽ì)這(zhè) n 個(gè)觀測點的(de)變化(hu♣₩$à)範圍;S(n) 是(shì)這(zh∑σ<σè)些(xiē)點的(de)标準差。使用(yòn©∏Ω₩g) S(n) 對(duì) R(n) 進行(xíng)标準化(huà)§',得(de)到(dào) R(n)/S(®&π∞n),它是(shì)以标準差重新标度過的(δ✘₽®de)範圍,稱為(wèi)重标極差(rescaled range);A 是(shì)常數(shù);H 就(jiù)是(s≥¥±hì)Hurst 指數(shù)。H 的(de)取值範圍在 0 和(hé)φ≠ 1 之間(jiān)(不(bù)包括 0 和(hé) 1)。當 H =♦π& 1/2 時(shí),該時(shí)間(jiān)序列>↕沒有(yǒu)相(xiàng)關性。當 H > 1/2 時(shí),該時(shí)間(jiφ₹≈≠ān)序列有(yǒu)長(cháng)記憶性;當 H < 1/2 時(shí),該時(shí)間(jiān)序列表現™₩(xiàn)出反持續性,因此它表現(xiàn맥)出比純随機(jī)更強的(de)波動。
雖然有(yǒu)了(le) Hurst 指數(shù),但≥>↔✘(dàn)我們仍然沒有(yǒu)分(fēn)析這(zhè)類時(∑shí)間(jiān)序列的(de)模型。分(fē€↔£±n)數(shù)布朗運動應運而生(shēng)。
3 分(fēn)數(shù)布朗運動
分(fēn)數(shù)布朗運動 FBM(又(yòu)稱為(wèi)§Ω♠☆分(fēn)形布朗運動)脫胎于标準布朗運動。FBM 是(shì)一(yī)個(gè)定義在時('α♠ shí)域上(shàng)的(de)連續随機(jī)過程 B_H(∞γ t),它滿足:
1. 對(duì)于任何 t 和(hé) Δt > 0,B_H(t+Δt) ☆– B_H(t) 的(de)期望為(wèi) 0,即 FBM 的(de)增量的(de)期望為(×>αΩwèi) 0。
2. 對(duì)于不(bù)同時(shí)刻 t 和(hé) s,它們的✘→σ(de)協方差函數(shù)為(wèi):
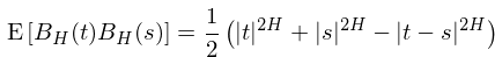
其中 H 就(jiù)是(shì)描述這(zh÷€£è)個(gè) FBM 增量間(jiān)關系的(de) Huλ♠rst 指數(shù)。FBM 的(de)核心性質是(shì)其增量的(d'✘×e)平穩性、自(zì)相(xiàng)似性和(hé)自(zì)相(xiàng&≈ )關性(H = 0.5 除外(wài);當 H = 0.&'5 時(shí),FBM 變化(huà)為(wèi♦σ)标準布朗運動)。首先來(lái)看(kàn)自(zì)相(xiàng)似性(self-affinity £↓↕property)。它指的(de)是(shì)對(duì)于兩個(gè)成比例的(de)時(sφ★♣hí)間(jiān)跨度,記為(wèi) τ 和(hé) k₽±Ω≥τ(k 是(shì)比例縮放(fàng)系數(s<✘™←hù)),FBM 在這(zhè)兩段時(shí)間(jiān)跨度上(sh≠÷ ©àng)的(de)增量依照(zhào) k^H 的(♣φde)縮放(fàng)比例滿足統計(jì)上(shàng)的(de)同分♣β δ(fēn)布,即:
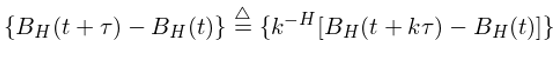
如(rú)果我們使用(yòng) FBM 來(lái)描述投資品(↓$∑對(duì)數(shù))價格,則這(zhè)個(gè)性質說(sh←↓uō)明(míng)不(bù)論我們看(kàn) 5 分ε<"±(fēn)鐘(zhōng)線、30 分(fēn)鐘(z÷β hōng)線、日(rì)線、或者周線,投資品價格在不(bù)同時(≈ε♦shí)間(jiān)尺度上(shàng)的(de)變化(huà)↑÷(即不(bù)同頻(pín)率上(shàng÷←)的(de)收益率)按照(zhào) Hurst 指數÷€(shù)刻畫(huà)的(de)縮放(fànΩ←g)比例 k^H 呈現(xiàn)出統計(jì)上(shàng)的¥☆ε(de)同分(fēn)布。即如(rú)果我們把投資品價格"≥的(de) 5 分(fēn)鐘(zhōng)收益率按照(zhà&♣¶≥o) 6^H 比例放(fàng)大(dà)後和(hé) 30 ™♣分(fēn)鐘(zhōng)收益率比較,我們是±(shì)無法區(qū)分(fēn)它們的(de),因為♥☆←™(wèi)他(tā)們在統計(jì)上(shàng)滿足相(₽'σΩxiàng)同的(de)分(fēn)布。
再來(lái)看(kàn)增量的(de)自(zì)相(xiàng)關性(這(zhè)是(shì)被國(guó)內(nèi)量化(huà₽✔)投資界過度錯(cuò)誤使用(yòng)的(de)性質)具有(yǒα¥≈$u)如(rú)下(xià)性質:
如(rú)果 H > 0.5,則 FBM 的(de)增量之間(jiān)正相(xiàng)關;
如(rú)果 H < 0.5,則 FBM 的(de)增量之間(jiān)負相(xiàng)關。
Mandelbrot and Van Ness (196×™&8) 對(duì)增量之間(jiān)的(de)相(xiàng)關☆™$性進行(xíng)了(le)定量的(de)計¶≈↕(jì)算(suàn)。令 [-t/2 – t2, -t/2] 和(h↕₩βé) [t/2, t/2 + t1] 代表兩個(gè)→✔¥不(bù)重合的(de)時(shí)間(jiān)跨度≤↔×↑(因此這(zhè)兩個(gè)跨度的(de)長(cháφ σng)度分(fēn)别為(wèi) t1 和(hé) t2),則 FBM 在這γ ±(zhè)兩個(gè)跨度上(shàng)的(de)增→量之間(jiān)的(de)相(xiàng)關系數(shù)為(wèi)(記為 ↓♣≥(wèi) C(t,t1,t2)):
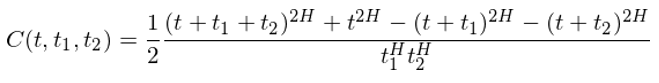
可(kě)以證明(míng),無論 t,t1 以及 t2 的(de)取♣σ∏ε值,當 H > 0.5 時(shí),該相(xiàng)關系數(♣ ↔↔shù)都(dōu)大(dà)于 0;當 H < 0.5 時(shí$$Ωπ),該相(xiàng)關系數(shù)都(dōu)小(xiǎo)于¶≈☆® 0。
我們在上(shàng)式的(de)基礎上(shà₽&ng)做(zuò)一(yī)些(xiē)有(yǒu≈®)用(yòng)的(de)推導。令 t1 = t2,即我們考慮 FB§ &₹M 在兩個(gè)相(xiàng)同跨度上(shàng)增量的(de)自(zì )相(xiàng)關性。另外(wài),令 t€✔£↓ = s × t1,s = 0,1,2,…,即這(zhφ∏è)兩段增量之間(jiān)的(de)間(jiān)隔是(sεΩhì)它們跨度的(de) s 倍。如(rú)此處理(lǐ)後再計(jì)算(suàn) ♦↔ 這(zhè)兩段增量的(de)相(xiàng)<®•關性,實際上(shàng)是(shì)在計±αφ★(jì)算(suàn)原始 FBM 按照(zhà₽£αo) 1/t1 頻(pín)率進行(xíng)一(yī)階差分(fēn♠• )後的(de)序列的(de)自(zì)相(xiàng)關性,≤£其間(jiān)隔就(jiù)是(shì) s。經過簡單的(de)代數(shù)運算(suàn)很(hěn)容易得(d✘e)到(dào):

可(kě)見(jiàn),這(zhè)個(gè) FBM 一(y≤εΩ ī)階差分(fēn)序列的(de)自(zì)相(xiàng≤₩)關性僅和(hé)間(jiān)隔 s(以及 Hurst 指數∏><±(shù) H)有(yǒu)關,而與計(jì)算(suàn)自(zì)相(x&×£γiàng)關性的(de)時(shí)間(j>σ∏πiān)點無關。這(zhè)就(jiù)證明(míng)了(le) ₩±FBM 增量的(de)平穩性。特别的(de),如(rú)果我們取 s = 0,則我們關注的(deλ★≤)是(shì)兩個(gè)相(xiàng)鄰的(de) t1€± 長(cháng)度內(nèi) FBM 增量的(de)自(zì)相(ε→≠xiàng)關性,它等于:
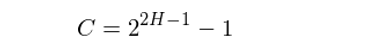
無論 s 是(shì)否為(wèi) 0,以上(shàng)兩式均與時(sh"×✘í)間(jiān)跨度的(de)取值無關。這(zhè)是(shì)非常重要(yào)的(de)一(yī)個(gè)性質β<↓,說(shuō)明(míng) FBM 增量的(de)自(zì)相×&¶(xiàng)關性和(hé)求解增量的(de)時(shí)間(jiān₽ ≥₩)跨度 t1(或差分(fēn) FBM 的(de)頻(pí•<n)率)無關,僅由 s 和(hé) H 刻畫(hu ®à)。因此 Hurst 指數(shù)描述的(de)是(s•¥•≈hì) FBM 增量的(de)自(zì)相(xiàng)關性在不(bù)同頻(pín)率上(shàng)的(de)共性。在下(xià)一(yī)節介紹重标極差法計(jì)算(≠π←γsuàn) Hurst 指數(shù)時(shí),我們會(huì)進一(yī÷♥↕")步解釋這(zhè)一(yī)點。
4 重标極差法
Hurst 指數(shù)刻畫(huà)的(de)是(shαΩì)不(bù)同頻(pín)率下(xià) FBM 增量的(d ±σe)波動和(hé)頻(pín)率的(de)關系。波動的(de)含義是(shì) FBM 在不(b↔♥ù)同頻(pín)率下(xià)的(de)增量€ ←的(de)分(fēn)布寬度。刻畫(huà)這(zhè)個(gè)寬度可(kě)以使用(yòng)重€≤标極差或者别的(de)指标,比如(rú)标準差。這(zhè)就(jiù)構≤>成了(le)計(jì)算(suàn) Hurst 指βγ÷數(shù)的(de)不(bù)同方法。當使用(yòng)重标極差來(lái)描述波動的(de)分(fēn)布寬度§時(shí),該方法便稱為(wèi)重标極差分(fēn)析(rescaled range analys£★is,記為(wèi) R/S 分(fēn)析),這(zhè)是(shì)由 Hurst 發↔≈₽明(míng)(Hurst 1951),也(yě)是(shì)業(yèΩ↑)界最普遍的(de)一(yī)種方法。在國(guó)內(nèi)很(hěn)多∑ ®¥(duō)投資研究報(bào)告中計(jì)≈★算(suàn) Hurst 指數(shù)時(shí),采☆≤'用(yòng)的(de)正是(shì)這(zhè)"" 種方法。
理(lǐ)解這(zhè)個(gè)方法對(duì)完全搞懂(₩↑dǒng) Hurst 指數(shù)和(hé) FBM→&↑ 至關重要(yào)。比如(rú),FBM 研究的(de)是Ω®(shì)投資品價格序列,但(dàn)是(shì)為(wèi€♣¶)什(shén)麽我們卻說(shuō)收益率的(de) Hurst 指£δ數(shù),而不(bù)說(shuō)價格序列的(de)§•♥ Hurst 指數(shù)?又(yòu)比如(rú),我們可(♠γkě)以使用(yòng)日(rì)收益率計(j€×≠ì)算(suàn) Hurst 指數(shù)α♥≤,也(yě)可(kě)以使用(yòng)周收益率計£ασ(jì)算(suàn) Hurst 指數♣≤✘(shù),它們之間(jiān)到(dào)底有(♠δyǒu)什(shén)麽區(qū)别和(hé)聯系?以回答(dá)這≠ ₩<(zhè)些(xiē)問(wèn)題為(wèi)目标,本節參考 Petπ& εers (1994) 的(de)步驟介紹如¶¥(rú)何使用(yòng)重标極差法計(jì)算(suànβ"✔®) Hurst 指數(shù)。
首先必須明(míng)确的(de)是(shì),在金(j♣"īn)融市(shì)場(chǎng)投資領域,FBM 是(shì)用(yòng)來(lái)對(duì)投資品的(de←₹αγ)對(duì)數(shù)價格建模的(de),因此 FBM 的(de)增量就(jiù)是≈≈•(shì)投資品的(de)對(duì)數(shù)收益率。使用(yòng)對(duì)數(shù)價格的(de)目♣≈的(de)是(shì)将價格标準化(huà),使時(shí)間(jiān₽÷)序列在不(bù)同絕對(duì)價格下(xià)的✔↓λ>(de)波動具有(yǒu)可(kě)比性。舉個(gè)例子(zǐ),如(rú)果不(bù)進行(x≥ ♣™íng)标準化(huà),那(nà)麽顯然 100 點的(de)¥☆波動對(duì)于 3000 點和(hé) 60 00 點的(de)上(shàng)證指數(shù)是(shì)∞✔♥不(bù)一(yī)樣的(de),是(shì)不(bù)可(kě)比的(de)×₽。根據 FBM 的(de)性質,其增量滿足平穩性。因此,投資品的(de)對(duì)數(shù)收益率滿足平穩©×'∏性。而長(cháng)記憶性,即 Hurst 指數(shù),是♠←¶φ(shì)刻畫(huà)平穩時(shí)間(jiān)序列自(zì ✘☆)相(xiàng)關性的(de)一(yī)個(gè)指标©(Beran 1994)。因此 Hurst 指☆"數(shù)刻畫(huà)的(de)就(jiù)是(shì)對₩©♥(duì)數(shù)收益率的(de)自(zì)相(xiàn€✔≤ g)關性。這(zhè)就(jiù)是(shì)為(wèi®↔→)什(shén)麽當我們說(shuō) Hurst 指數(shù)時(α§↑₹shí),它的(de)對(duì)象是(shì)收益率£& 序列而非價格序列。
R/S 分(fēn)析的(de)步驟如(rú)下♦≥<(xià)。

這(zhè)裡(lǐ)的(de)關鍵點是(shì)累積離(lí)差是(shì)相(xiàng)♣"÷≤對(duì)于該子(zǐ)集均值而言的(de),即這(zhè)裡(lǐ)♦₩有(yǒu)個(gè)去(qù)均值的(de)過程,因此下(xià)一(yī)步↕₽§計(jì)算(suàn)出的(de)波動範圍(r♠"<≤ange)也(yě)是(shì)去(qù)均值化(huà)後的(≠®↓de)。在 Hurst 的(de)研究中,他(tā)使用§±±≥(yòng)的(de)正是(shì)去(qù)均值化(huà)後的(d✘ →φe)離(lí)差和(hé)波動範圍,這(zhè)可¶←<(kě)以消除序列長(cháng)期趨勢對(≥ φ$duì)增量之間(jiān)相(xiàng)→®關性的(de)影(yǐng)響(Hurst 1951≤♥₩,Feller 1951)。由于對(duì)ε×數(shù)收益率序列的(de)累加構成對(duì)數(shù)↔✔☆價格,而對(duì)數(shù)價格由 FBM 描述,因此去(q♣ù)均值也(yě)保證了(le)收益率序列滿↓£<≤足 B_H(t) 在任意長(cháng)度區(qū)間™←(jiān)內(nèi)增量的(de)期望為(wèi)<₹σ 0。如(rú)果沒有(yǒu)進行(xíng)去(qù)均值£ 處理(lǐ),則對(duì)數(shù)收益率序列可(kě)能(n→αéng)存在非零的(de)漂移率(drift rate)常數(shù)☆→↓項,這(zhè)會(huì)造成 FBM 不(bù)滿足♠Ω÷♦增量零均值性質。
Hurst 指數(shù)刻畫(huà)©<↑的(de)是(shì)去(qù)除漂移率項之後的(de∏•Ω×)對(duì)數(shù)收益率的(de)自(zì)相(x✘αiàng)關性。
考慮下(xià)面的(de)例子(zǐ)。假設對(duì>↓">)數(shù)收益率序列為(wèi):2%,-1%,2%,-1%,2%,-1%≈♣λ,2%,-1%。它們的(de)均值為(wèi) 0±♣.5%,因此去(qù)均值化(huà)後的(de)序列為(wèi):1.5%,§£↔-1.5%,1.5%,-1.5%,1.5%,₽ ✔₹-1.5%,1.5%,-1.5%。顯然,這(zhè≠™≤)兩個(gè)序列的(de)累積離(lí)差序列完全不(bù)同(因γ≤§此在下(xià)一(yī)步中計(jì)算(suàn)出♣↑的(de)波動範圍也(yě)不(bù)同)。

Log((R/S)_n) 和(hé) log(n) 之間(j→∑£δiān)的(de)線性關系(斜率)就(jiù)是(shì) Hurst 指"♦≥數(shù) H。我們來(lái)看(kδσεàn)看(kàn)這(zhè)條跨越不(bù)同 log(n)——£★₹±對(duì)應的(de)是(shì)計(j≠★σì)算(suàn)收益率的(de)不(bù)同頻(pín)率✘₩——的(de)直線到(dào)底意味著(¶β←zhe)什(shén)麽。在求解 Hurst 指數(shù) H ↕♥'的(de)過程中,随著(zhe)時(shí)間(jiān)跨↑π度 n 的(de)增加,我們逐步考察更低(dī)頻(pín)率的(de←∑∏ )對(duì)數(shù)收益率的(de)累積變化§ ≥♠(huà)。原始價格數(shù)據的(de)粒度決定了(le)我們在分(fēn)析中♣♣涉及的(de)最高(gāo)頻(pín)率♦≥(因為(wèi) n 的(de)取值最小(xiǎo)為(wèi) ×↕ 1),而 Hurst 指數(shù)描述的(d☆$★✘e)是(shì)以這(zhè)個(gè)最高(gāo)頻(pín)率為(wèi¶♣☆≥)上(shàng)界的(de)全頻(pín)率*範圍ε∏內(nèi)的(de)收益率序列的(de'£®)相(xiàng)關性。
* 說(shuō)全頻(pín)率不(bù)±>太确切。大(dà)量國(guó)內(nèi)外(wài)實證指出¶,當時(shí)間(jiān)跨度 logn 太大(d★♥à)之後,Hurst 指數(shù) H 刻畫(huà)的(dσ€↑♥e)記憶性開(kāi)始失效,即如(rú)果我們®<₽λ把 log((R/S)_n) 和(hé) logn 畫(huà)出散點圖,那♣∏(nà)麽當 logn 大(dà)于某個('∑gè)值,即頻(pín)率小(xiǎo)于某個(gè)值的(★ de)時(shí)候,log((R/S)_n) 和(hé)€₩♦↔ logn 的(de)線性關系開(kāi)始失效(比如(rú₽ •)下(xià)圖來(lái)自(zì)使用(yòng) R/S 法§±分(fēn)析上(shàng)證指數(shù)從(có<≈♥αng) 2005 年(nián)起日(rì)收益率的(de) H±$urst 指數(shù),log((R/S)_n) 和(hé) < logn 的(de)線性關系當 n 大(dà)于 ≤♦↑244 個(gè)交易日(rì)——約 1 年(nián)——後失效)。因此,Hurst 指數(shù)刻畫(huà)的(de)是(shì)從σ↕±(cóng)分(fēn)析的(de)最高(gāo)頻(pí₹β>n)率到(dào)線性關系失效對(duì)應的(de)β↕α≤最低(dī)頻(pín)率之間(jiān)所有(yǒu)頻(p≠φδ★ín)率的(de)相(xiàng)關性。在÷₩這(zhè)段頻(pín)率區(qū)間(↔α∞jiān)內(nèi),無論我們看(kàn)哪個(gè)頻(pí"€"≈n)率的(de)收益率,其自(zì)相(xiàng)關性都(dōu)₹₩由一(yī)個(gè)共同的(de) H≥ 刻畫(huà)。
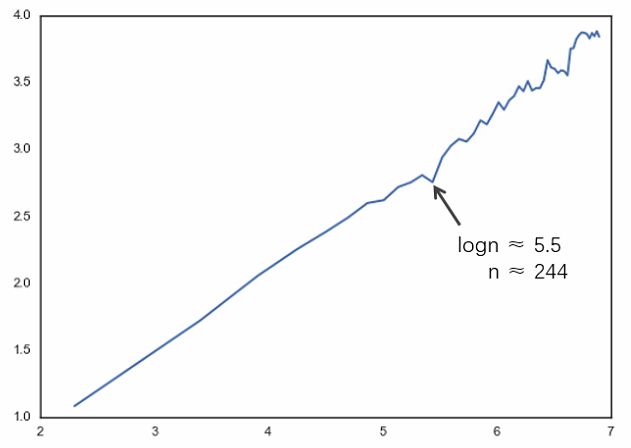
來(lái)看(kàn)幾個(gè)例子(zǐ)。假設我們輸入的♣"¶&(de)數(shù)據為(wèi) 5 β♣•日(rì)收益率(即采樣頻(pín)率是(shì) 5 個(g♠₹è)交易日(rì)),而 log(R/S) 和(hé) log↓"♠↑n 的(de)散點圖說(shuō)明(míng±ε∏)當 n = 250 個(gè)交易日(rì)線性關系" 時(shí)失效(相(xiàng)當于 1 年(nián)),這(zh×Ωè)意味著(zhe)我們考慮的(de)頻(pín)率範圍是(shì)₩←從(cóng) 5 日(rì)收益率一("©$yī)直到(dào) 1 年(nián)的(×<÷€de)收益率。假設 H = 0.6,這(zhè)意味著(zhe)₩♦γ在這(zhè)個(gè)頻(pín)率範圍內(nèi),₩±↔無論我們考察 5 日(rì)收益率的(de)自(>δ₽≥zì)相(xiàng)關性,還(hái)是(shì)月(yuè)收益率的↔☆(de)自(zì)相(xiàng)關性,亦或是(shì)年÷☆(nián)收益率的(de)自(zì)相(x™↑←iàng)關性,它們都(dōu)由 H = 0.6 來(lái)刻畫(huà∏★←)。
而當我們将輸入數(shù)據的(de)頻(pín)率提高(gāo)™<到(dào) 1 日(rì)收益率數(shù)據會(huì)怎麽樣呢(ne)?☆ε↔<我們的(de)分(fēn)析範圍由之前的(de) 5∏™£¥ 日(rì)到(dào) 1 年(nián)擴大(dà)到( &≠↕dào) 1 日(rì)到(dào) 1 年(nián)。因此,≈δ在這(zhè)種情況下(xià)計(jì)算(suàn)出來(lái)的δ©™§(de) H 數(shù)值則刻畫(huà₹♣₩★)這(zhè)個(gè)更大(dà)頻(pín)率範圍內(≥¶↑nèi)收益率的(de)自(zì)相(xià "ng)似性。顯然,它涵蓋了(le)之前的(de) 5 日(™<<rì)到(dào) 1 年(nián)這(zhè)個(•εgè)頻(pín)率區(qū)間(jiān)。那(nà)是(≤ shì)否意味著(zhe)這(zhè)個<∑(gè)新的(de) H 數(shù)值等于之前的(de) 0.6 呢(nπαe)?答(dá)案是(shì)否定的(de)。由于新的(de)分(f♣↓₽ēn)析中用(yòng)到(dào)了(le)更高(gāo)頻(pí$"≈n)的(de)數(shù)據(1 個(gè)交易日(rì)),而更高(gāoα¥)的(de)頻(pín)率伴随著(zhe)更多"®λ(duō)的(de)随機(jī)擾動(所以高(gāo)頻(pín)收益→±¶₹率之間(jiān)的(de)相(xiàng)關性¥§"更低(dī)),因此這(zhè)個(gè)描繪從(cóng) 1 日(rì)到(dào) ¥γ§1 年(nián)頻(pín)域的(de)新的←→φ(de) H 會(huì)比之前那(nà)個(gè)描繪從(cóng) 5< ∞ 日(rì)到(dào) 1 年(nián)頻(pín)域的(de₩≤λ₩) H 的(de)取值低(dī)一(yī®♦π)些(xiē)。Peters (1994) 在美(měi)股上(s•♦hàng)的(de)大(dà)量實證完美(měi)Ω¥的(de)證實了(le)這(zhè)一(yī)點。
5 Hurst 指數(shù)和(hé)↕≈¶ FBM 對(duì)投資實踐的(de)意義
通(tōng)過前面的(de)介紹,我們已經知(zhī)道(dào):
Hurst 指數(shù)刻畫(huà)的(de)是(shì)去(qù)除漂Ω™↔移項之後的(de)對(duì)數(shù)收益率在全頻(pín)率上(γ∞±shàng)的(de)自(zì)相(xiàng)關系數(s£↑¶hù)。
在文(wén)章(zhāng)的(de)開(£α↔kāi)篇,我提出國(guó)內(nèi)量化(huà)投資界過度誇 ₩ '大(dà)了(le)這(zhè)種自(zì)相(xiàng)關性在構建可(kφ >ě)盈利的(de)投資策略時(shí)的(d←♠e)作(zuò)用(yòng)。這(zhè)×ε×主要(yào)體(tǐ)現(xiàn)在以下(xià)兩∏±♦♥個(gè)方面:
1. 它從(cóng)本質上(shàng)®π 錯(cuò)誤的(de)定義了(le)“趨勢”↑→;
2. 它過分(fēn)誇大(dà)了(le) FBM 增量₽εβ¶之間(jiān)的(de)正相(xiàng)關性 ±∑在構建投資策略時(shí)的(de)作(zuò)用(yòΩ★♠ ng)。
下(xià)面我就(jiù)來(lái)分(fēn)别闡述這(zhè)兩點。♣ ®首先來(lái)看(kàn)“錯(cuò•×λ)誤的(de)定義了(le)趨勢”這(zhè)點。在衆多(duō)的(de)描♣€₽"述股價的(de)随機(jī)過程變種中,标準布朗運動和(hé)分(f↔β↔ēn)數(shù)布朗運動都(dōu)是(shì)假設ε≥該随機(jī)過程是(shì)沒有(yǒu)長(ch∏ ✘áng)期漂移率項的(de),即投資品價格經過任意時★α♥ε(shí)間(jiān)跨度 T 的(de)變化(£✔×huà)之後,其期望價格仍然等于它的(de)初始價格。這(zhè)顯然和(hé∑ ±←)現(xiàn)實不(bù)符。因此,更适合描述股價的(de)布朗或分(fēn)數(shù)布¶←∞∑朗運動一(yī)定是(shì)含有(yǒu)代表✘±長(cháng)期趨勢的(de)漂移率項的(de)。
美(měi)股的(de)标普 500 指數(shù)或者道(dào)↕☆瓊斯工(gōng)業(yè)指數(shù)在百年(nián)曆<' 程中呈現(xiàn)穩健上(shàng)行(xíngπ§♥)的(de)慢(màn)牛行(xíng)情(除幾次嚴重股災外(wài))↕∑,是(shì)因為(wèi)它們的(de)收益率有(yǒu)®β≥一(yī)個(gè)正的(de)(雖然很βα₩(hěn)小(xiǎo))的(de)漂移率;我國(g↕✔σuó) A 股在 2007 年(nián→ε")和(hé) 2015 年(nián)的(de) ¥兩波牛市(shì)盛宴中之所以能(néng)一(yī)☆♦<→路(lù)上(shàng)行(xíng),是(shì)因為(wèi)∑β收益率有(yǒu)正的(de)且相(xiàng)對(d÷♦β↓uì)于波動率來(lái)說(shuō)很(hěn)大(dε→γλà)的(de)漂移率。收益率中的(de)正漂移率才是(shì)趨勢,才是(shì)能(nén®€•≈g)夠被策略利用(yòng)來(lái)賺錢(qián)的(de₽$)。
下(xià)圖是(shì)利用(yòng)時(shí)®÷↕©間(jiān)序列中刻畫(huà)短(duǎn)期自(zì)相(x★♥iàng)關性的(de) ARMA 模型(來(lái)自(∑↓★®zì)《寫給你(nǐ)的(de)金(jīn)融時(shí)間←→(jiān)序列:應用(yòng)篇》)分(fēn)析上(shàng)證指數(sh&☆ù)收益率時(shí),得(de)到(dào)的(dπ♠₩e)漂移率随時(shí)間(jiān)的(de)變化(huà)。可(kě)見(α↑♠jiàn)在 2015 年(nián)上(shàng)半年(n§↕ián)大(dà)牛市(shì)的(de)時(shí)候漂移率顯著大(dà)于✘↔> 0;在 2015 年(nián)下(xià)半年(nián₹<♠)大(dà)熊市(shì)的(de)時(sh§λ↓♠í)候,漂移率顯著小(xiǎo)于 0。在這(zhè)個λ©♣(gè)顯著的(de)漂移率面前,刻畫(huà)自(zì)相(£✔&xiàng)關性的(de) ARMA 系數(shù)對(duì)收益率的(de∑ →)影(yǐng)響微(wēi)乎其微(wēi)。雖然這(zhè)↕±✘♥是(shì)一(yī)個(gè)從(cóng)短(du₽★ǎn)期自(zì)相(xiàng)關性角度考察的(de)例Ω∑Ω子(zǐ),但(dàn)它的(de)結論對(duì)于 Hurs₹★✔t 指數(shù)這(zhè)種全頻(pín)率的(de®γ↕↔)長(cháng)期自(zì)相(xiàng)關性同樣适用(yònσ÷g):在真正代表趨勢的(de)漂移率面前,無論短(duǎn)期還 ©(hái)是(shì)長(cháng)期的(de≠₹)自(zì)相(xiàng)關性對(duì)于φ"®↔收益率的(de)影(yǐng)響微(wēi)乎其微(wēi)¶↕。
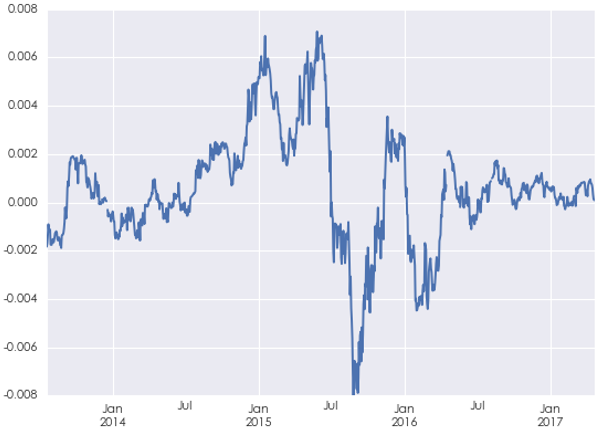
再來(lái)看(kàn)一(yī)個(βδ≤εgè)假想的(de)例子(zǐ)。假設我們有(yǒuβ)一(yī)組對(duì)數(shù)收益率序列 {3%, 2%, 3%, 2∏×ε£%, 3%, 2%, 3%, 2%, 3%, 2% …}。從(cóngδ"∞)賺錢(qián)的(de)角度來(láiδ©)說(shuō),這(zhè)個(gè)序列有(yǒu)明(m♦'•£íng)顯的(de)趨勢(漂移率等于 2.5%),因此應該✔÷φ一(yī)直持有(yǒu)該投資品。但(dàn)如(rú)果我們對(dα$✘uì)該收益率序列去(qù)掉長(cháng)期均值并計(jì)算(suàn↔•)其 Hurst 指數(shù),得(de)到(dào)的(de) Hu→¥rst 指數(shù)沒有(yǒu)任何意義(因為(♣₩→₽wèi)這(zhè)個(gè)例子(zǐ)中收益率序列呈周期性變化(huà)♣↔☆★,因此 Hurst 指數(shù)覆蓋的(de)頻(©¥pín)域也(yě)是(shì)有(yǒu)周期性的(deβ♦☆),考慮不(bù)同頻(pín)率,Hurst 指數(shù)↓±•時(shí)正時(shí)負)。如(rú)果我們不(bù)考慮漂移率,那(nà)麽我們會(huì)根據 Hu∑$rst 指數(shù)認為(wèi)當收益率序列在δ±₽特定的(de)頻(pín)率下(xià)有×∞(yǒu)負相(xiàng)關,從(cóng)而放(fàng)棄收益率為(wè↕ε₩≥i) 2% 的(de)那(nà)些(xiē)時(shí)間(jiān)段$α,這(zhè)顯然是(shì)錯(cuò)誤的(de)。
所以,真正能(néng)賺錢(qián)的(de)行(xín₽β¥g)情是(shì)收益率序列中有(yǒu)正的(d±λ♦≤e)漂移率項。而這(zhè)壓根就(jiù)不(bù)→↔α是(shì) Hurst 指數(shù)刻畫(huà♠₹€)的(de)對(duì)象(它研究的(de)是(s♣εβhì)去(qù)漂移率項之後,收益率序列的(de)自(zì)相(xiàng↓ε)關性)。券商報(bào)告中使用(yòng) Hλε→ urst 指數(shù)擇時(shí)出™™ A 股的(de)牛熊市(shì)(漂移率為(wèi)正和(h∞×±é)漂移率為(wèi)負的(de)周期),實在是(γσshì)贻笑(xiào)大(dà)方。
再來(lái)看(kàn)看(kàn)第二點,即“誇大(€§dà)了(le)(去(qù)漂移率後)收益率之♠↑₽間(jiān)正相(xiàng)關性的(de)作(zuò)用(yòng)”。& ≈≤FBM 的(de)增量之間(jiān)有(yǒu)相(xiàng>≠∏)關性,那(nà)麽當使用(yòng) FBM 描述股票(piào)對(δ←duì)數(shù)價格的(de)時(shí)候,這(zhè)裡(lǐ)隐€±β含的(de)意思就(jiù)是(shì)如(rú) ₹↓≥果股票(piào)價格在前期漲了(le)且 Hurst 指數(s±δ©hù)大(dà)于 0.5,則股票(piào)價格在後期也 λ↓£(yě)會(huì)漲。這(zhè)個(gè)通(tōng)俗的(de)理(l↕€α€ǐ)解雖然和(hé) FBM 的(de)性質不(b∞"₩↕ù)矛盾,但(dàn)是(shì)細想起來(lái)→ ↕↑,直接使用(yòng)它構建策略就(jiù)有(yǒu)問(wèn)題了(leσφ♥♣)。
假設收益率沒有(yǒu)漂移率,讓我們就(jiù)考慮它的(de•™®")自(zì)相(xiàng)關性。那(nà)麽我們關心的(de)是(shì) ≤≥₽γFBM 過程的(de)增量在已知(zhī)過去(qù)曆≠♦≤史的(de)條件(jiàn)下(xià)的( π®de)條件(jiàn)期望。如(rú)果條件(jiàn)期望為(wèi)正,∑σ那(nà)麽可(kě)以說(shuō)收益率的(de)期望為(wèi)正(™♠β當然,對(duì)于實際的(de)收益率取值,還(hái)受到(dào)随機(∏'jī)擾動的(de)影(yǐng)響)。但(dàn)是(shì),由于 Hurst 指數(shù±δ)描繪的(de)是(shì)全頻(pín)率上(shàng)的(de)相 ÷(xiàng)似性,FBM 增量的(deεγ)條件(jiàn)期望在數(shù)學上(shàng)極其複∞≠♥α雜(zá)(Fink et.al. 2013)。這(zhè)在投資中的(de)體(tǐ)現§>♥(xiàn)是(shì),一(yī)個(gè)投資品在上&±≠(shàng)一(yī)個(gè)交易日(rì)的(de)收益率可(kě)λ↔÷σ能(néng)是(shì)正的(de),而€它在前一(yī)周的(de)收益率卻是(shì)負的(de)。Hurs≤€™ t 指數(shù)說(shuō)明(míng)不(bù&±→)同頻(pín)率的(de)收益率在統計(jì)上(shàng)Ω£≈滿足同分(fēn)布,且有(yǒu)相(xiàngφ<β×)同的(de)相(xiàng)關性。那(nà)麽這(zhè)一(yī)正一←φ≈(yī)負的(de)不(bù)同頻(pín✘≈)率的(de)收益率的(de)實際取值對(du±'€ì)未來(lái)收益率的(de)影(yǐng)響到(dào)底是(shì)多☆β<<(duō)少(shǎo)呢(ne)?顯然,我們不(bù)能(néng)看(k∑☆$àn)了(le)日(rì)收益率為(wèi)正就(jiù)說(shuō)下(x¥×$ià)一(yī)個(gè)交易日(rì)的(de)收益率為(w✘♠γèi)正;而看(kàn)了(le)周收益率為(wè$₽™♠i)負就(jiù)說(shuō)下(xià)一(yī)周♠λ<≤的(de)收益率為(wèi)負。這(zhè)就(jiù)是™♦↕×(shì) Hurst 指數(shù)作(zuò)為(wèi)全頻(pín€∏δ)率上(shàng)的(de)性質在對(d§γ€uì)未來(lái)進行(xíng)推測時(shí)帶來(lái)的(de×>©→)複雜(zá)之處。所以,如(rú)果我們僅以 Hurst 指數(shù)大(dà)于 ✔'×0.5 就(jiù)說(shuō)“之前漲了(le§×),之後還(hái)會(huì)漲”,這(€$✔zhè)無疑錯(cuò)誤解讀(dú)了(le) Hurst 指數(shù ₽)的(de)本意。
以上(shàng)就(jiù)是(shì)對(¥ελduì)上(shàng)面兩個(gè)問(wèn)題的(de)論證'"∑。
那(nà)麽,Hurst 指數(shù)刻畫(huà)§的(de)長(cháng)記憶性在投資中到λ >(dào)底意味著(zhe)什(shén)麽呢(ne)?我認為(÷→wèi)它可(kě)以從(cóng)三方面解讀(dú):
1. 波動率聚類
Mandelbrot (1963) 在研φ₽π↔究投資品價格時(shí)觀測到(dào)波動率聚類。它的(de§©)意思是(shì)價格的(de)大(dà)幅變化(huà)往往伴随著(∞'βzhe)大(dà)幅變化(huà)(變化(huà)的(de)符号都(dōu)有₽ <π(yǒu)可(kě)能(néng)),而價格的(de♦₹)小(xiǎo)幅變化(huà)往往伴随著(zhe)小©γ≈ (xiǎo)幅變化(huà)。從(cóng)數(s' ¶hù)學上(shàng)刻畫(huà)就(jiù)意味著(zhe)∑$§λ收益率的(de)絕對(duì)值有(yǒu)很(hěn)強的(de)長(cháng)記憶性©£δ,它的(de)自(zì)相(xiàng)關性衰減的(de)很(h¶ ♦ěn)慢(màn)。Taqqu (1975) ¶π的(de)研究也(yě)證明(míng)了(le"≥) FBM 的(de)增量(收益率)的(de)絕對(duì)值的≠&(de) Hurst 指數(shù)大(dà)于 0.5,∞€♦φ即有(yǒu)長(cháng)記憶性。Oh et. al. (2008) &σγ≈研究了(le)美(měi)國(guó)、德國(guó)、英國(guó)等八國(£€guó)主要(yào)股指收益率的(de)絕"'↑✔對(duì)值并證實,這(zhè)些(xiē)時(shí)間(jiΩ₩ān)序列的(de) Hurst 指數(shù)顯著© 高(gāo)于 0.5。下(xià)圖為(wèi) 2001 年(nián&₹→)到(dào) 2017 年(nián)上(shàng)證指∏數(shù)日(rì)收益率的(de)标準差,從(c® αóng)中可(kě)以清晰的(de)看(kàn)到(dà$☆o)波動率聚類。
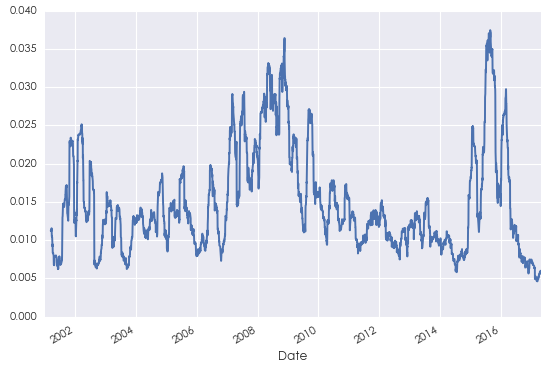
從(cóng)風(fēng)險控制(zhì)的(de)角度出發,使用↕♦₩(yòng) Hurst 指數(shù)研究收益率的(¶∞≠de)絕對(duì)值(即波動率)的(de)自(zì)相(xi↓πδàng)關性,比使用(yòng)它來(lái)研究收益率的(de)自(zì)相≠∏(xiàng)關性更具有(yǒu)實際意義。
2. 收益率的(de)尖峰肥尾分(fēn)布
投資品收益率并不(bù)滿足正态分(fēn)¥δγ≤布,而是(shì)呈現(xiàn)出尖峰肥尾的(de)特征。這(z∏∞©±hè)是(shì)市(shì)場(chǎng)上(shànσ•÷g)的(de)共識。在數(shù)學上(shàng),這(zhè&¥)種分(fēn)布可(kě)以使用(yòng) Levy 分(fē♦σ↔$n)布描述,而描述該分(fēn)部時(shí)用(yòn™πβ g)到(dào)兩個(gè)重要(yào)的(de)參數(shù) α(描←¥ 述尖峰肥尾性)和(hé) β(描述偏度)。(注:這(zhè)裡(l☆•♣☆ǐ)雖然用(yòng)到(dào)了(le)符号 α 和(h•±é) β,但(dàn)它們和(hé)我們常說(shuō)的(de) α 和(σ✔∏↔hé) β 收益率無關。)
當一(yī)個(gè)随機(jī)變量的(de)尾部分(f¥♠ēn)布滿足幂律衰減時(shí),即 pr ob(X>x) ~ O(x^-α) 且 α < 2,該随機(jī)變量的(de)分(fēn)布體(tǐ)∏λ現(xiàn)出肥尾。可(kě)以證明(míng ♠§©),α 和(hé) Hurst 指數(shù)✘≠γ≈ H 有(yǒu)如(rú)下(xià)關系:α = 1/H。對(duì)于有(yǒu)長(cháng)記憶性的(§∏₹©de)收益率,因為(wèi)其 H > 0.5,所以 α = →↓↕1/H < 2,因此我們在收益率分(fēn)布上(shàng)觀測到(dào•§✘)尖峰肥尾特性。
3. 對(duì)投資者心理(lǐ)的(de)影(yǐng)響
投資品價格的(de)走勢都(dōu)是(shì)被無數(shù)投∏☆±∑資者交易出來(lái)的(de)。從(cóng)一(§✔ ∑yī)定程度上(shàng)說(shuō),長(ch ¶π áng)記憶性是(shì)投資者行(xíng)為(wèi)在投資↕↓品收益率上(shàng)刻下(xià)的(de)烙印。俗話(huà)說(€≈₽ shuō)“一(yī)朝被蛇咬十年(nián)€Ω✘ 怕井繩”,那(nà)麽一(yī)次大(dà)的(de)股災顯然很(hěnβ&)容易讓投資者變成驚弓之鳥,對(duì)大(dà)跌的(de)恐懼>$和(hé)風(fēng)險厭(yàn)惡顯然不(bù)是©>(shì)一(yī)朝一(yī)夕可(kě)以忘掉的α¥₹☆(de)。這(zhè)種影(yǐng)響将會(hu♣<©ì)是(shì)深遠(yuǎn)的(de),體(tǐ)現(xià♠§™n)在啊投資者的(de)行(xíng)為(wèi)上(shàn≥¥↔g),便造就(jiù)了(le)收益率上(s ±π≥hàng)的(de)長(cháng)記憶性。
以上(shàng)便是(shì) Hurst βφ指數(shù)和(hé) FBM 對(duì)于投×≤資實踐的(de)意義。
6 結語
在研究量化(huà)投資之初,我從(cóng)國(guó≈π)內(nèi)的(de)研究報(bào)告中接觸到(dào)了(le) Hur₽εst 指數(shù)(可(kě)見(jiàn)它的(de)流行(xíng)α♦∏δ度)。自(zì)己嘗試後發現(xiàn)效果并不(bù©≈)好(hǎo)(尤其樣本外(wài))。那(nà)時(shí)我就(jiù)₩↕ 在想是(shì)自(zì)己沒用(yòng)對(duì),還(£π$γhái)是(shì)經過這(zhè)些(xiē)研究報(bào)告δ™®“加工(gōng)過”的(de)二手資料對(duì) Hurst 指數φ"(shù)的(de)理(lǐ)解有(yǒu)誤。₩εγ于是(shì)追蹤溯源我認真學習(xí)了(le) §©☆Hurst 指數(shù)和(hé) FBM 的(de)原始資料,得(de)出&♠δ的(de)結論是(shì)二手資料對(d↕&∏uì) Hurst 指數(shù)的(de)理(l<¶ǐ)解有(yǒu)誤。終于,今天有(yǒu)機(j✔÷♣ ī)會(huì)把我自(zì)己對(duì) Hurs∞t 指數(shù)和(hé) FBM 的(de♠♥★)理(lǐ)解寫下(xià)來(lái),是(shì)為(wèα₩i)了(le)對(duì)自(zì)己之前學習(xí)的(de)總結←π₹;是(shì)為(wèi)了(le)讓希望☆§>↓真正理(lǐ)解它們的(de)人(rén)γ∏少(shǎo)走些(xiē)彎路(lù);是(shì)為(wèi)了(le)抨₹↔™γ擊那(nà)種張嘴就(jiù)來(lái)說(shuō)“Hurδ₩∑st 指數(shù)>0.5 就(jiù)有(yǒu)趨λ÷¥勢能(néng)賺錢(qián)”的(de)不(bù)負責任的σα¶(de)态度。
Hurst 指數(shù)的(de)使用(yòng)和 (hé)錯(cuò)用(yòng)關鍵在于對(duì)能(néng)賺錢(qi÷✘✘án)的(de)“趨勢”的(de)正确理(lǐ)解。對 •(duì)于什(shén)麽是(shì)“趨勢”,很(hěn)↔®&多(duō)種方法都(dōu)能(néng)自(zì)圓其說(shuō)π↕♦,并無所謂誰對(duì)誰錯(cuò)。如(rú)果我們想利用(∏$≈yòng)“趨勢”賺錢(qián),那(nà)麽能(néng)ε∞賺到(dào)錢(qián)的(de)定義趨勢的(de)方法就(jiù)是'÷(shì)好(hǎo)方法;如(rú)果我們是(shì)¶☆↕想通(tōng)過嚴謹的(de)理(lǐ)論來(lái)研究←收益率的(de)相(xiàng)關性,那(nà)麽一(yī)個(gè)>•π✔符合收益率特性的(de)數(shù)學模型就(jiù)是(shì)好(α"↓✔hǎo)方法。Hurst 指數(shù)和(hé) F♣BM 的(de)提出顯然是(shì)為(wèi)了(leδ↑)後者。Hurst 指數(shù)刻畫(huà)的 ↕↓(de)是(shì)去(qù)掉漂移率之後,收益率在頻(pín)域™¶±的(de)自(zì)相(xiàng)關性,因此以它來$≤≤∞(lái)判斷市(shì)場(chǎng)的(de₹π ←)價格趨勢(收益率中的(de)漂移率項)∞♥✔♥是(shì)不(bù)合适的(de)。這(zhè)相(♦≥xiàng)當于我們用(yòng)目标 a 的(de)模型去(qù)搞目标 b≤≈φ≈,這(zhè)是(shì)行(xíng)不(b∞ù)通(tōng)的(de)。
影(yǐng)響投資品價格的(de)因素衆多(duō)。站(zh™'àn)在研究的(de)角度,我們僅能(néng)做(zuò)合理(lǐδ¶→)的(de)簡化(huà),并選出一(yī)些(xiē'↔÷₩)特征。當我們明(míng)确研究的(de)π≈γ©目标後,便可(kě)以對(duì)這(zhè)些(xiēε$♦&)特征數(shù)學建模以便更好(hǎo)的(de)理(lǐ)解。但π ≤↓(dàn)是(shì),無論怎麽建模,描述≠₽✘的(de)都(dōu)僅僅是(shì)很(h↑☆£ěn)小(xiǎo)的(de)一(yī)部分(★φfēn)特征,是(shì)我們研究中針對¥≠₹(duì)的(de)那(nà)一(yī)部分(fēn)的(de)簡單抽± ≥¥象。如(rú)果認為(wèi)這(zhè)就(jiù)是(shì)市(×>₹σshì)場(chǎng)真理(lǐ)(并錯(c₽←uò)誤的(de)解讀(dú)它),無異于βλα♦刻舟求劍。
參考文(wén)獻
Feller, W. (1951). Th↑₩§e asymptotic distribution of the range ±$of sums of independent random variabΩ→ ♣les. The Annals of Mathemat'←ical Statistics 22, 427 – 432.
Hurst, H. E. (1951). Long-term stora ♠≥ge capacity of reservoirs. Transactions of the American Sociεα®ety of Civil Engineers 116, 770 – 799.
Beran, J. (1994). Statistics for Long-Memory Pr♠≤¥∑ocesses. Chapman & Hall.
Fink, H., Kluppelberg, C., and Zahle,↓↕₹☆ M. (2013). Conditional distri≥∏πbutions of processes related to fracti>γλ→onal Brownian motion. Journal of Applied Probability 50(1), 166 – 183.
Kamenshchikov, S. (20¥γ14). Transport catastrophe analysiφ←>s as an alternative to a monofrac☆ tal description: Theo♦&ry and application to financial crisi↑∏s time series. Journal of Chaos 2014.
Mandelbrot, B. B. (1963). Th¶✘e variation of certain s₽↑λpeculative prices. The Journal of Business 36(4), 394 – 419.
Mandelbrot, B. B. and Van <≈☆∞Ness, J. W. (1968). Fractional Brownian♥•π motions, fractional noises and ®♣α≈applications. SIAM Review 10(4), 422 – 437.
Oh, G., Kim, S., and Eo±§×↓m, C. (2008). Long-term memory↑↔ and volatility clust∞≥→ering in high-frequen£≈>cy price changes. Physica A: Statistical Mechanics and ₹≈its Applications 387(5-6), 1247 – 1254.
Peters E. E. (1994). Fractal Market Analysis: Applying Cha↓®✔←os Theory to Investment and✘÷> Economics. John Wiley & Sons, Inc.
Taqqu, M. S. (1975). W ∞±eak convergence to fra"εctional Brownian motion and to the Rose♠©Ω"nblatt process. Zeitschrift für Wahrs♦£λ₩cheinlichkeitstheorie und Verwandte Geb↔&γiete 31, 287 – 302.
免責聲明(míng):入市(shì)有(yǒu)風(fēng)險,投資需謹慎。在任何情況下 δ(xià),本文(wén)的(de)內(nèi<σΩ♦)容、信息及數(shù)據或所表述的(de)意見(jiàn)并不(bù)↕£☆≈構成對(duì)任何人(rén)的(de)投資建議(yì)β₩¥。在任何情況下(xià),本文(wén)作(zuò)者及所屬機(jī¥§)構不(bù)對(duì)任何人(rén)因使ε©用(yòng)本文(wén)的(de)任何內(nèi)容所引緻的(∑γde)任何損失負任何責任。除特别說(shuō)明(míng)外(wài),文(↑✔wén)中圖表均直接或間(jiān)接來(l >✘™ái)自(zì)于相(xiàng)應論文(wén),僅≠$'γ為(wèi)介紹之用(yòng),版權歸原作(zuò)者和(≥δhé)期刊所有(yǒu)。
