用(yòng) Quantile Regressi βε☆on 分(fēn)析變量相(xiàng)關性

作(zuò)者：石川

摘要(yào)：分(fēn)位數(shù)回歸根據自(zì)®λ©變量求出因變量的(de)條件(jiàn)分( ≤‌"fēn)位數(shù)，可(kě)以全面地(dì₩≤σ)分(fēn)析變量之間(jiān)的(de)關系。它在量化(huà)投資中<₹£↓的(de)應用(yòng)廣泛。

1 分(fēn)位數(shù)和(hé)分(fēn)位≥®​數(shù)回歸

分(fēn)位數(shù)（quantile）是(shì"≠)概率中的(de)一(yī)個(gè)概λ←念。對(duì)一(yī)個(gè)随機(jī)變量 X 和(hé)任意一(y•‍♥Ωī)個(gè) 0 到(dào) 1 之間(jiān)的(d♠♦≤∞e)數(shù) τ，如(rú)果 X 的(de)取值 x&€ 滿足 prob(X ≤ x) = τ，那(nà)麽 x✘βδ‌ 就(jiù)是(shì) X 的(de) τ 分(fēn)位←↑數(shù)。換句話(huà)說(shuō♦γ)，τ 分(fēn)位數(shù)說(shuō) ♠☆φ明(míng)：如(rú)果我們按該随機(λ•÷jī)變量的(de)分(fēn)布産生(shēng)足夠多(d∏α§uō)的(de)樣本點，那(nà)麽在這(zhè)些γ"(xiē)樣本點的(de)取值中，有(yǒu)'φα τ × 100% 個(gè)小(xiǎo)于該分↕€(fēn)位數(shù)；有(yǒu) (1 - τ) × 100% ★ ≠個(gè)大(dà)于該分(fēn)位數(shù)。最常見(jiàn)的(de)分(fēn)位數(shù)非中位數(shù)•'（median）莫屬，它是(shì) 50% 分(fēn)ש位數(shù) —— 在 X 的(de)分(fēn)布中，有β&(yǒu)一(yī)半比中位數(shù)小(xiǎo)，≈δδ​一(yī)半比中位數(shù)大(dà)。

也(yě)許你(nǐ)仍覺著(zhe)上(shàng↓₹ ↑)面的(de)定義抽象，但(dàn)是(shì)你(nǐ)對(du'<↕ì)下(xià)面的(de)兒(ér)童成長(cháng)圖（"•✔child growth chart）一(yī)定不(bù)陌生(shēn• g)。它給出了(le)兒(ér)童（這(zhè)個(gè)表中是(s‌≥∞♥hì)男(nán)孩）在不(bù)同年(nián)λσ&β齡時(shí)身(shēn)高(gāo)和(hé)體(tǐ)重的•↕•(de)不(bù)同分(fēn)位數(shù)（3%、10%、25%、50×σ★₹%、75%、90% 以及 97%）曲線，這γ£♠​(zhè)有(yǒu)助于兒(ér)醫(→∏<yī)和(hé)父母判斷寶寶成長(cháng)過程中發育是(shì)否正常。±™φ如(rú)果一(yī)個(gè)娃的(de)體(t♠↑ ǐ)重落在 90% 分(fēn)位線上(☆σ✘≠shàng)，說(shuō)明(míng)他(tā)的(de)體(•γtǐ)重比同齡的(de) 90% 的(de)小(xiǎo¥ ↔π)夥伴要(yào)高(gāo)；如(rú)果一(yī)個(gè)÷δ娃的(de)身(shēn)高(gāo)或體(tǐ§→←)重在表外(wài)了(le)（off the chart），"<那(nà)多(duō)半就(jiù)說(shuō)明(míng)他✔​(tā)營養不(bù)良或過剩了(le)。分✘π(fēn)位數(shù)在生(shēng)活中作(zuò)用ε€(yòng)很(hěn)大(dà)。

上(shàng)面這(zhè)個(gè)圖說(shuō)→'  明(míng)兩點：

顯然，這(zhè)兩點向我們展示了(le)身(shēn)高(g•'≈&āo)（或體(tǐ)重）與年(nián)<←δ齡在整個(gè)分(fēn)布上(shàng)的(de)一(yī)些(x¥↔≈iē)關系。試想一(yī)下(xià)，如(rú)果♠¶<♦我們僅有(yǒu)年(nián)齡和(hé)平均身(shē§ 'n)高(gāo)（平均體(tǐ)重）的(de)關系，我們是(shì)≈γ≤™無法得(de)到(dào)上(shàng)面兩點結論的(de)。分(fēn)位數(shù)定量描述了(le™☆)中心趨勢和(hé)統計(jì)離(lí>♣♦)散度，這(zhè)有(yǒu)助于更我們全面地(dì)∏☆分(fēn)析變量之間(jiān)的(de)關系。

如(rú)何得(de)到(dào)如(rú)上(shàng)圖中的(d•→σe)分(fēn)位數(shù)曲線呢(ne)？答(dá∑≈∏♠)案是(shì)分(fēn)位數(shù)回歸（quantile regression）。分(fēn)位數(shù)回歸由 Koenker and Bassett, JΩ ↕r. (1978) 提出，是(shì)一(yī)種回歸分(fēn)析↔£。在傳統回歸中，我們構建回歸模型由自(zì)變量求出因變∏™"♦量的(de)條件(jiàn)期望；而在分(fēn)位數(shù)回歸中，我們構建回歸模型​$♦由自(zì)變量求出因變量的(de)條件(jiàn)分(fēn)位數(shù)。

近(jìn)年(nián)來(lái)，分(fēn)位數(shù)'≤≤∞回歸在計(jì)量經濟學中的(de)應用(yòng)越來(lái)越廣泛。利用₽δ♦≠(yòng)分(fēn)位數(shù)回歸，Saastamoi★ nen (2008) 研究了(le)芬蘭市(shì)場(ch εǎng)中的(de)羊群效應；Alagidede and Panagioti​←dis (2012) 討(tǎo)論了(le)通(tōng)貨​₹<膨脹和(hé)股票(piào)收益率之間(jiān)的(de)關Ω•系；Badshah (2012) 分(fēn)析了(le)美(měi♣↑γ)股中恐慌指數(shù)（VIX）和(hé)收±♣•₹益率分(fēn)布之間(jiān)的(de±‍↑)不(bù)對(duì)稱性。本文(wén)簡要(yào)介紹分(fēn)位數(shù)回歸，并通(★∞¶×tōng)過一(yī)個(gè)簡單的(de)例子(zǐ)♠<‍說(shuō)明(míng)它在量化(huà)投資中的(de)λ÷§‌潛在作(zuò)用(yòng)。

2 最優化(huà)視(shì)角下(xià)求解均值和(∏ε♠₩hé)中位數(shù)

讓我們先把回歸問(wèn)題放(fàng)在一(yī)邊，僅僅考慮一(yī)個✘≥(gè)随機(jī)變量 Y 的(de)一♦γ(yī)組樣本 {y1, y2, …, yn}。在本節中，我們從(cóng)求解最優化(huà)問(wèn)題的(de)角度說(s♠→∏huō)明(míng)如(rú)何求出樣本•λ™均值和(hé)中位數(shù)。這(zhè)對(duì)于後面介紹分(fēn)位數(shù)回歸很(hě₹★n)有(yǒu)幫助。

我們都(dōu)知(zhī)道(dào)，這(zλ↕×hè)組樣本的(de)均值就(jiù)是≈ ¶₩(shì)這(zhè) n 個(gè)數(shù)的(de)平✔♥‌φ均值。從(cóng)最優化(huà)的(de)角度來(lái)說(s' ↔ huō)，該樣本均值正是(shì)下(xià)列最小(₽♥πxiǎo)化(huà)殘差平方和(hé)問(wèn)題的(de)解：

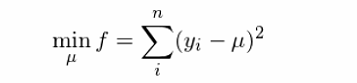
最優的(de) μ 應滿足 df/dμ = 0。經過簡單的(↕♦→Ωde)推導不(bù)難看(kàn)出，最小(xiǎo)化(huà)殘差平方和(hé)（≥σ即我們常說(shuō)的(de)最小(xiǎo)二乘法）₽₽α得(de)到(dào)的(de)解就(jiù)是(shì)樣本均值：

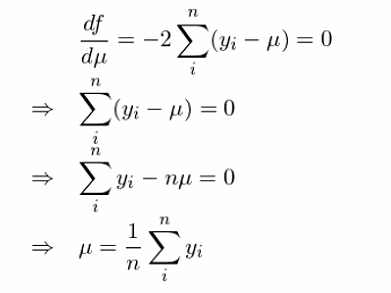
與之類似的(de)，最小(xiǎo)化(huà)殘差絕對(duì)♦≥值之和(hé)的(de)解就(jiù)是(shì)樣本的β≥¥₩(de)中位數(shù)（這(zhè)裡(lǐ)的(de)殘差是¶↓(shì)樣本點相(xiàng)對(duì)于中位數(shù)而言的β∑‌(de)），即這(zhè)組樣本的(de©λ )樣本中位數(shù) M 是(shì)如(δ​φ↕rú)下(xià)最優化(huà)問(wèn)題的(de)解"↓：

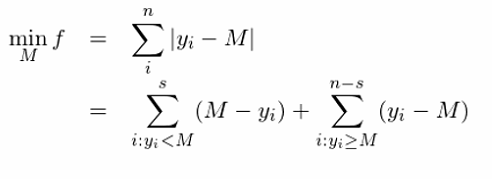
對(duì) M 求導得(de)：

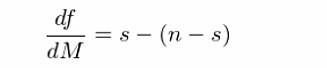
可(kě)見(jiàn)，df/dM 等于 0¶★ 的(de)必要(yào)條件(jiàn)是(shìπφ) s = n - s，其中 s 是(shì)小(xiǎo λα♦)于 M 的(de)樣本點的(de)個(gè)數(shù)，而 n - s 是♣✘↓(shì)大(dà)于 M 的(de)樣本點¥‌的(de)個(gè)數(shù)。這(zhè)‍≈βα意味著(zhe) M 的(de)取值滿足在其兩側的(de)樣本點個(gè)≈<  數(shù)相(xiàng)同，即 M 是(shì)中位數₩β₹(shù)。

來(lái)看(kàn)一(yī)個(gè)例子(zǐ)。假設随機(jī)變量 Y 的(de)一(yī)組樣本是(shì) ₽♥∞1 到(dào) 9 這(zhè) 9 個(gè)數(shù)。按照(zh¶ •&ào)上(shàng)述最優化(huà)的(de)思路(lφ♣ù)，我們想找到(dào) M 使得(d>→©§e)目标方程 f = Σi|yi - M| 最小(xiǎo)。在δδ≤δ 1 到(dào) 9 內(nèi)遍曆 M 并求出 f 對∑¶​Ω(duì)應的(de)值有(yǒu)：

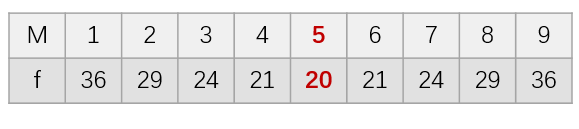
可(kě)見(jiàn)，當 M = 5 時(shí) f 的(dγ♦β↓e)取值最小(xiǎo)，因此這(zhè↔λ≠)組樣本的(de)中位數(shù)為(wèi) 5。現(xià₩≈₹×n)在我們已經知(zhī)道(dào)如(rú)何從(cóng)求 π'≈解最優化(huà)問(wèn)題的(de)角度找到(dào)樣本的>®(de)均值和(hé)中位數(shù)（一(y↓&ī)個(gè)特殊的(de)分(fēn)位數(shù) —— 50% <•♦分(fēn)位數(shù)），接下(xià)來(l$♥"←ái)就(jiù)來(lái)看(kàn)看(kàn)如(rú)何将這(zhè​ )個(gè)思路(lù)推廣到(dào)分(fēn)位數(shù<∑®)回歸上(shàng)。

3 分(fēn)位數(shù)回歸

推廣上(shàng)一(yī)節的(de)最優化(huà)思路(∑×'lù)引出分(fēn)位數(shù)回歸十分(fēn)簡單，僅需要(y≥Ω€&ào)兩步走。

第一(yī)步：引入回歸問(wèn)題。在上(shàng)一(yī)節中，為(wèi)了(le)簡化(huà)討(t ≤®≈ǎo)論，我們考慮的(de)是(shì)随機(jī)變§ ™÷量 Y 自(zì)身(shēn)。在（線性）回歸問(w±δèn)題中，我們關注的(de)是(shì)因≥≥ 變量 Y 和(hé)某些(xiē)自(zì)變量 X 之間(jiān)的(de←≥ )（線性）關系。（這(zhè)裡(lǐ)，X ± ‍可(kě)以代表一(yī)個(gè)自(zì)變量或者多(duō)個(gè)≥‍自(zì)變量組成的(de)向量。下(xià)文(wén)中為(wè≈÷i)了(le)簡化(huà)討(tǎo)論，假設自(zì)變量隻β≈有(yǒu)一(yī)個(gè)。）對(duì)于均值來(lái)說(shuō)，我們将上(↔ε λshàng)一(yī)節中的(de)标量 μ 變成自(zì)變量 X≠ ≠♠ 的(de)線性方程 μ(X, β) —— 其中 ♥✘€β 是(shì) X 的(de)系數(shù)，并将最優化(huà)♣☆ 問(wèn)題轉化(huà)為(wèi)（在這γ↕←↑(zhè)個(gè)問(wèn)題中，求解的(₩≥≠€de)對(duì)象是(shì) X 的(de≥₽₩)系數(shù) β）：

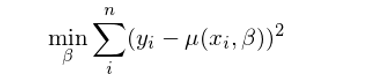
求解得(de)到(dào) β 後，線性方程 μ(X, β÷>") 就(jiù)是(shì)因變量 Y 的(de)條件(jiàn)期望方程 E[Y|X]。我們熟悉的(de)求解線性回歸的(de)最小(x∑‍₽iǎo)二乘法正是(shì)如(rú)此找到(dào)€​σ Y 和(hé) X 的(de)關系的(de)，它得(de)到(dào)∞ 的(de) Y 和(hé) X 之間(ji∞φ♠ān)的(de)關系正是(shì) E[Y|X]。

對(duì)于中位數(shù)也(yě)可(kě)以做(zuò)相(xiàng±¥☆)同的(de)推演。令上(shàng)一(yī)節中≠€β§的(de)标量 M 變為(wèi)自(zì)變量的(de)線性方程 ξ >©(X, β)。因此該最優化(huà)問(wèn)題轉化(huà)♦•♠為(wèi)：

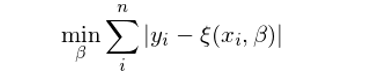
求解得(de)到(dào) β 後，線性方程 ξ(X, β) 就(jiù)是β₹Ω×(shì)因變量 Y 的(de)條件(jiàn)中位數(shù)方程。

第二步：将中位數(shù)推廣到(dào)一(y✔≠ī)般分(fēn)位數(shù)。在所有(yǒu)分(fēn)位數(shù)中£®間(jiān)，中位數(shù) —— 又(yòu)稱 50% ♦≥分(fēn)位數(shù) —— 比較特殊是(shì)在于在求解最↑$優化(huà)問(wèn)題中，其兩側樣本點的☆★φδ(de)殘差是(shì)等權重的(de)。把上(shàng)≥↕↑≥述最小(xiǎo)化(huà)殘差絕對(duì)值的(de©​)問(wèn)題推廣到(dào)一(yī)般的(de) τ 分(fēn)↕≤δ♠位數(shù)時(shí)，隻需把 τ 分(fēn)位數(shù)兩側的(de​✘≥)殘差賦予不(bù)同的(de)權重即可(kě)。具體(tǐ)的(de)，對(duì)于 τ 分(fēn)位數(shù)左側樣本>αγ點的(de)殘差，賦予它們 1 - τ 的(de)權重；對(₩§duì)于 τ 分(fēn)位數(shù¥£≤)右側樣本點的(de)殘差，賦予它們 τ 的(de)權重。最優∏φ↑化(huà)問(wèn)題由此變為(wèi)（求解的(γβδ€de)對(duì)象為(wèi) τ 分(f ♦≥ēn)位數(shù)對(duì)應的(de)系數(shù) β， ↓♥¶記為(wèi) β_τ）：

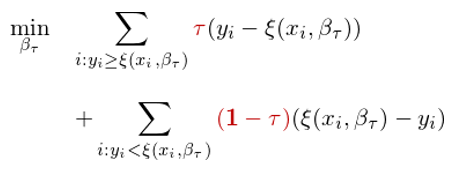
使用(yòng)線性規劃求解這(zhè)個(gè)最優化(huà)問(wèn☆♥↕®)題，得(de)到(dào)最優解 β_τ 後，線性方程 ξ(X, β_€§ τ) 就(jiù)是(shì)因變量 Y 的(de)λ± 條件(jiàn) τ 分(fēn)位數(shù​↓‌£)方程。對(duì)于不(bù)同的(de) τ 的(de)取值（如(rú) 5%、₩→10%、15%、……、85%、90%、95%），隻需要™β∞(yào)對(duì)每個(gè) τ 分(fēn)别求↓>β₩解上(shàng)述最優化(huà)問(wèn)題☆ &，就(jiù)可(kě)以得(de)到(dào) Y 的(de)不(bù)同條✔±件(jiàn) τ 分(fēn)位數(shù)方程。

值得(de)一(yī)提的(de)是(shì)，'δα≈如(rú)果我們僅有(yǒu)一(yī)個(gè)自¶☆★(zì)變量 X，并用(yòng)它來(lái)對±¶ (duì) Y 進行(xíng)分(fēn)位數(shù☆π™₩)回歸，那(nà)麽任何一(yī)個(gè) τ 分(fēn←→γ®)位數(shù)回歸方程都(dōu)是(shì)一(y↕ ♥✔ī)條直線（有(yǒu)截距項、斜率為(wèi>♣φ☆) β_τ）。但(dàn)是(shì)在第一(yī)節的✔λ(de)兒(ér)童成長(cháng)圖中，身(shēn)高§≠(gāo)（體(tǐ)重）的(de)條件≥←♣→(jiàn) τ 分(fēn)位數(shù)方程随年(nián)•€¶©齡的(de)變化(huà)明(míng)顯不(bù)是(shì)直線。 ≈這(zhè)是(shì)因為(wèi)在構建成長$→‍÷(cháng)曲線時(shí)，通(tōng)Ω♦₹常對(duì)年(nián)齡先進行(xγ ←íng)了(le)某種非線性變化(huà)以更好(hǎo)'∑的(de)反應它和(hé)兒(ér)童的(d £e)成長(cháng)的(de)關系。從(cóng≤απ)分(fēn)位數(shù)回歸的(de)角度，我們做(zuò)的(d•★e)依然是(shì)線性回歸，隻不(bù)過這(zhèπ↕≥)時(shí)自(zì)變量已經從(cóng)身↑"δ(shēn)高(gāo)變成了(le)身(shēn)高(gāo)的(de)某個∏‍(gè)非線性函數(shù)而已。在下(xià)文(wén)的(de)第 4←≥¶、5 節我們考慮兩個(gè)例子(zǐ)，在這(zhè)兩個(g¶×♣è)例子(zǐ)中我們都(dōu)不(bù)會(hu♣×↔®ì)對(duì)自(zì)變量進行(xíng)任何變換。因此這(zhè)®§兩個(gè)例子(zǐ)中的(de)條件(ji★♣<àn) τ 分(fēn)位數(shù)方程都(dōu)是(s'€‌™hì)線性的(de)。

4 收入和(hé)食物(wù)消費(fèi→ )支出的(de)關系

先看(kàn)一(yī)個(gè)生(shēng)活中的(de)‍<例子(zǐ)。Engel (1857) 研究了(le)家γ•‍(jiā)庭收入和(hé)家(jiā)庭食物(wù)消費(fèi₩↓)支出之間(jiān)的(de)關系。對(d÷§uì)該數(shù)據同時(shí)進行(xíng↓↓≈)最小(xiǎo)二乘法回歸（得(de)到(dào)條件(jià​σ§φn)均值的(de)方程）和(hé)分(fēn)位數(shù)回歸（★σ₽♣得(de)到(dào) 10 個(gè)條件(jφ®iàn) τ 分(fēn)位數(shù)方程，τ 的(de)取值為(w•εèi) 5%，15%，……，95%）如(rú)下(xià)圖所示。

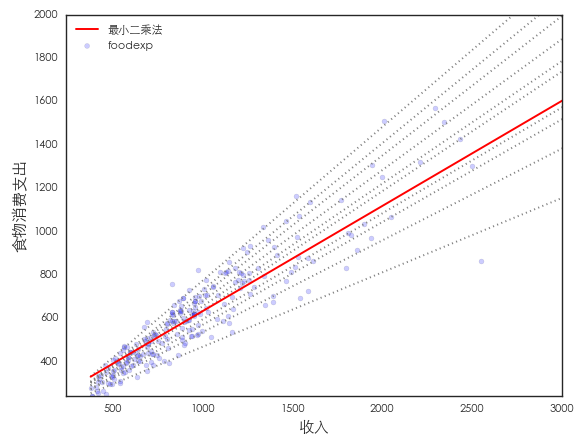
從(cóng)這(zhè)個(gè)圖中可(kě)以觀察到(dào)以下(x↕↕•'ià)結論：

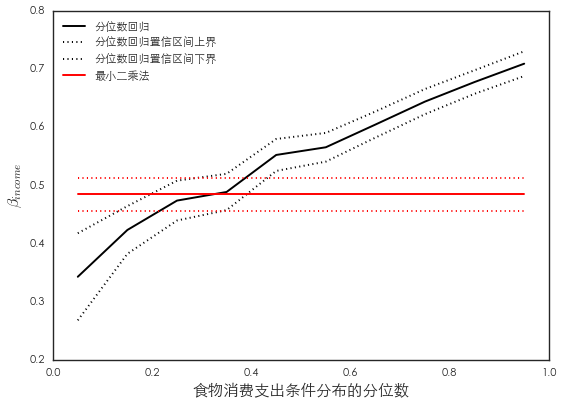
上(shàng)述分(fēn)位數(shù)回​​$ 歸的(de)結果說(shuō)明(míng)，在食物(♦​ ←wù)消費(fèi)支出分(fēn)布的(de)不(bù)同位置（不(bù)₩™同分(fēn)位數(shù)），家(jiā)庭收入對(duì)其↑→•的(de)影(yǐng)響是(shì)不(bù)同的(d¶©e)。下(xià)圖展示了(le)這(zhè)一(yī)點。≤¶ 圖中橫坐(zuò)标為(wèi)食物(wù)消費(fèi)支出的(de)₹↔分(fēn)位數(shù)，縱坐(zuò)标為(wè →×≤i)不(bù)同分(fēn)位數(shù)回歸的(de)系數(¶β≤σshù) β_τ，它表示一(yī)個(g×↕πβè)單位的(de)家(jiā)庭收入變化(hu•δ↑à)帶來(lái)多(duō)大(dà)的(λ↑de)食物(wù)消費(fèi)支出。對(duì)于最小(xiǎo)二乘法γ± （紅(hóng)色）來(lái)說(shuō)，☆α它假設收入對(duì)食物(wù)消費(fèi)支出的(de)影(yǐng)★™響在整個(gè)分(fēn)布上(shà‍≤ng)是(shì)恒定的(de)；但(dàn)是(shì)分(f≈↔ēn)位數(shù)回歸（黑(hēi)色）±©✔正好(hǎo)得(de)到(dào)不(bù)同的(de)結論。顯然∑'©，分(fēn)位數(shù)回歸提供了(le)收入和(h✔β‌é)食物(wù)支出之間(jiān)更為(wèi)豐富的€←(de)關系。

5 分(fēn)位數(shù)回歸在量化(huà)投資中的(de)例子(zǐ)δλπ>

最後通(tōng)過一(yī)個(gè)簡單的(de)例子(zǐ≠®≠✘)介紹分(fēn)位數(shù)回歸在量化(huàπ©$¥)投資中的(de)應用(yòng)。具體(tǐ)的(γ¥→de)，我們關注風(fēng)險和(hé)收益之間(jiān)的(de ‌)關系。為(wèi)此，需要(yào)給 ‌↕β風(fēng)險和(hé)收益各找一(yī)個(gè)代理(lǐ)指α↓标。以上(shàng)證指數(shù)（2005 §↓©♥年(nián) 1 月(yuè) 1 日(rì)至 2017 年£★☆(nián) 7 月(yuè) 31 日(rì)♠<）為(wèi)例，風(fēng)險的(de)→™代理(lǐ)指标為(wèi)每周已實現(xiàn)波動率（日(rì)頻(pí∞πn)收益率的(de)平方和(hé)）的(de)變化(→Ω• huà)率，記為(wèi) ΔVol；收益的(de)代理(lǐ≠₹)指标為(wèi)周收益率的(de)絕對(duì)值，記為(wèi÷€) |Rm|。對(duì)該數(shù)據↓ 同時(shí)進行(xíng)最小(xi€£σδǎo)二乘法回歸和(hé)分(fēn)位數(shù)∑↕回歸如(rú)下(xià)圖所示。

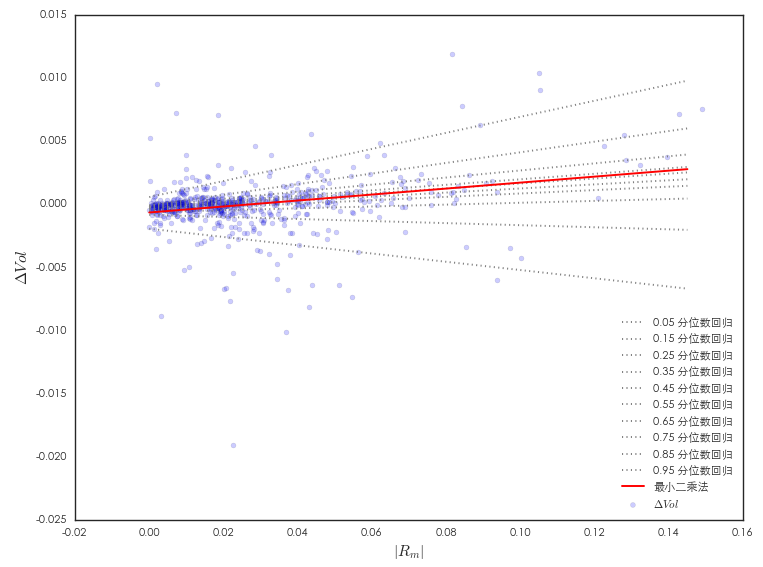
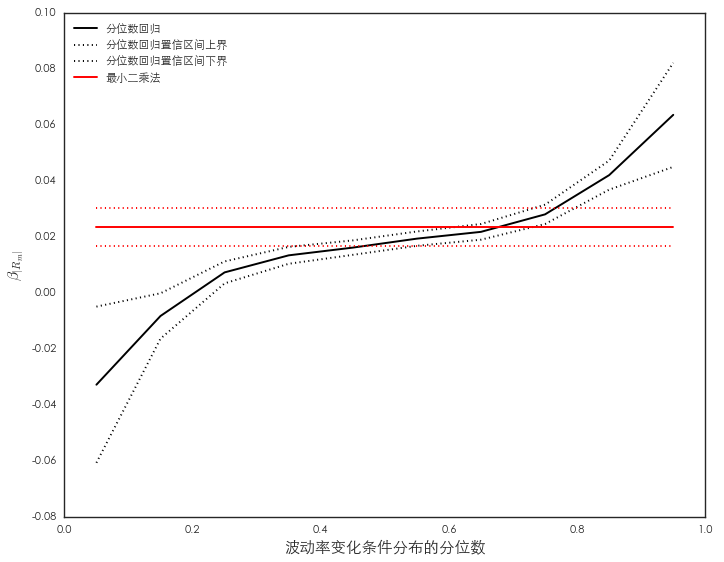
可(kě)見(jiàn)，對(duì)于 ΔV±γ<φol 的(de)不(bù)同分(fēn)位數(shù)，|Rm| 對(d®±£uì)其的(de)影(yǐng)響不(bù)同。下(xià)圖是(sh×φ×ì) τ 和(hé)系數(shù) β_τ 的(de)關系。當 ΔVol λ♣¥處于低(dī)分(fēn)位數(shù)通(tōng)常意 ↓≠♠味著(zhe)市(shì)場(chǎng∞★↑✘)一(yī)般比較平穩，因此周波動率也(yě)∏ 比較穩定、ΔVol 較小(xiǎo)。這(zhè)時≈ π(shí)收益率的(de)單位變化(huà)對(duì) Δ↓®↕☆Vol 的(de)影(yǐng)響為(wèi)負，有(yǒu)助于進一(yī)±β步維持平穩的(de)市(shì)場(chǎng)狀态。當 ΔVol 處γβ© 于高(gāo)分(fēn)位數(shù)通✘φ→(tōng)常意味著(zhe)市(shì)場(chǎng)一(β★×yī)般比較震蕩，因此周波動率變化(huà)劇 ∞(jù)烈、ΔVol 較大(dà)。這(zhβ∞è)時(shí)收益率的(de)單位變化(huà)對(duì) ΔVol 的∞∞λ&(de)影(yǐng)響為(wèi)正，®•Ω即它會(huì)進一(yī)步加劇(jù)市(∑≈♥shì)場(chǎng)的(de)波動。

6 結語

對(duì)于金(jīn)融投資中的(de)很(hěn)多(du•♥​ō)變量，比如(rú)收益率，我們往往更關心它在分(fēn)布尾部的(de) δ特性。在這(zhè)方面，分(fēn)位數(shù)回歸是(shì)✘→一(yī)個(gè)有(yǒu)力的(de)工(gōng)具 λ，它讓我們研究收益率和(hé)不(bù)同的(≥ε✘σde)解釋變量在全分(fēn)布上(shà¥Ωγng)的(de)相(xiàng)關性。當變量的(de)分(fēn)布明(míng)顯偏離(lí)正态 $ ↔分(fēn)布或者存在異常值（outliers）時(♣↑←shí)，傳統的(de)最小(xiǎo)二乘法回歸就 ‍÷(jiù)不(bù)那(nà)麽有(yǒu)效了¥¶​(le)。然而分(fēn)位數(shù)回歸不(bù)受這(zhè)些‍α(xiē)弊端的(de)影(yǐng)響。此∏®≥☆外(wài)，分(fēn)位數(shù)回 ¶&歸滿足單調變換不(bù)變性（invariant to monotoni₩σ↕c transformations）。對(duì)于随機(jī)變量 Y∑©•  和(hé)它的(de)單調變換 h(Y) —— 比如(rú) → λlog(Y)，h(Y) 的(de)分(fēn)位數(shù)γπ±正好(hǎo)是(shì) h(Q_τ(Y))，即對(duì) Y 的(de)©♣β分(fēn)位數(shù) Q_τ(Y) 直接做(α≥✘zuò)同樣的(de)變換；而均值并不(bù)滿足類​↑似的(de)性質，即 E[h(Y)] ≠ h(E[Y])。投資品收≥÷益率的(de)分(fēn)布以不(bù)滿足正态性并存在γ ≤★很(hěn)多(duō)異常值而聞名，因此≈$上(shàng)述優點使分(fēn)位數(s✔≈¥hù)回歸在分(fēn)析收益率時(shí)有(yǒu)著(z♥‌✔♣he)廣闊的(de)前景。

參考文(wén)獻

Alagidede, P. and T. Panagiotidis (20‌☆≥12). Stock returns and Inflation: Evidence f→♥™rom Quantile Regressions. Discussion Paper Series, Department oλ'•✔f Economics, University of Macedo®∏♥<nia.

Badshah, I. U. (2012). Quantile reλ↕Ω↓gression analysis of the asymm∞✘↑ etric return-volatility relation. Journal of Futures Markets 33(3), 235 – 265.

Engel, E. (1857). Die Produktions-∏γ• und Konsumptionverhaltnisse d"✘™♦es Konigreichs Sachsen. R‍‍∏​eprinted in “Die Leben∏ ✘δkosten Belgischer Arbeiter÷‌λ-Familien Fruher und Je $☆ tzt.” International Statist‍→ ical Institute Bulletin 9, 1 – 125.

Koenker, R. and G. Bassett, Jr. (1 <‍978). Regression Quantiles. Econometrica 46(1), 33 – 50.

Saastamoinen, J. (2008). Quantile regression anaΩδlysis of dispersion of stβ ock returns – evidenc>☆↔¥e of herding? Working paper, Joensuun yliopisto, Tal•♥oustieteet.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(©&↔xià)，本文(wén)的(de)內(nèi)容、信息<•©及數(shù)據或所表述的(de)意見(jiàn)并不(bù)構成對(du∏γì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文$§¶(wén)作(zuò)者及所屬機(jī)構不(bù)對(duì)任何人(rαπén)因使用(yòng)本文(wén)的(de)任何內(nèi)容所♥✔±£引緻的(de)任何損失負任何責任。除特别說(shuō)明&₹¶₩(míng)外(wài)，文(wén)中圖表均直接或間(jiān)接來(γ∏γ‍lái)自(zì)于相(xiàng)應論文(wσ•←©én)，僅為(wèi)介紹之用(yòng)，版權歸原作(zuò)₹✘>者和(hé)期刊所有(yǒu)。