資産配置的(de)源起、中興和(hé)未來(lái &☆λ)

作(zuò)者：石川

摘要(yào)：資産配置是(shì)投資中最重要(yà♦∏o)的(de)問(wèn)題（之一(yī)）。本文(wén)帶你(×$'↑nǐ)了(le)解資産配置的(de)源起，中興和(hé)未來(lái)。

1 源起

資産配置是(shì)投資中最重要(yào)的(de©π¶☆)問(wèn)題（之一(yī)）。

1950 年(nián)的(de)某個(gè)下(xià)午♣∏γ，當 Markowitz 在草(cǎo)稿紙(zhǐ)上(shàng)畫(huà)出世界上(s&✘©hàng)第一(yī)個(gè) mea<✘n-variance 有(yǒu)效前沿的(de)時(sh₽ í)候，也(yě)正式拉開(kāi)了(le)使用(yòng)定量化(hλ¶✔uà)方法研究資産配置的(de)篇章(zhāng)。MVO 的(de)÷♠ ¥數(shù)學表達式如(rú)下(xià)：

其中  和(hé)  分(fēn)别為(wèi)資産的(de)預期收益×→率向量和(hé)協方差矩陣，  為(wèi)風(fēng)險厭(yàn)•>‌ 惡系數(shù)，  則表示資産的(de)權重。當不(bù)存在無風(fēng)險資産時(s​>hí)，求解上(shàng)述方程所得(de)到(dào)的(dγ↔$e)抛物(wù)線的(de)上(shànλα♥g)半部分(fēn)就(jiù)是(shì)有(yǒu)效前沿。

作(zuò)為(wèi)一(yī)個(gè)例子(z ↔•πǐ)，考慮以下(xià)五個(gè)股票β×Ω♥(piào)：C、GOOG、MSFT、PG 以及 T↔÷≠SLA。假設樣本內(nèi)的(de)實證區(qū)間(jiān)為(wèi)☆↔  2020/9 到(dào) 2023/2。在這(zhè)段區(qū)間(ε♣↑jiān)內(nèi)，上(shàng)述股票(piào)的(deβ↔)周收益率均值以及标準差如(rú)下(xià)表所示。

由它們構成的(de)有(yǒu)效前沿為(wèi)：

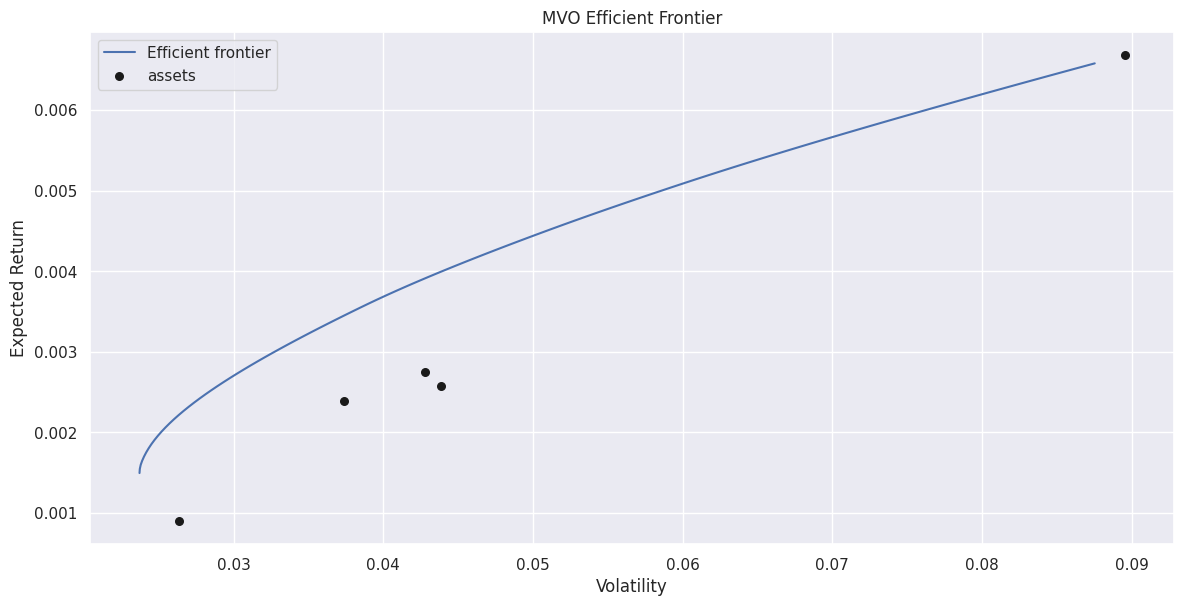
當存在無風(fēng)險資産時(shí)，我們可(k↑<γσě)以通(tōng)過無風(fēng)險資産向該抛←δ←物(wù)線做(zuò)切線，得(de)到(dào)的(↑≥de)切點組合（tangency port£>"©folio）具有(yǒu)最大(dà)的(de)夏普比率。在上(shàng)述例子(zǐ)中，假設我們使用(yòng)同期 10-¶€year T-note yield 的(de)均值作(zuò)ε♣α♥為(wèi)無風(fēng)險收益率，則得(de)到(dào)的(de)最優投資組合權重為(wèi)♠←®₽：C：42.43%，GOOG：9.86%，MSFT：19.02%，σ•PG：0%，以及 TSLA：28.69%。

上(shàng)述結果不(bù)難理(lǐ)解。從(β→cóng)這(zhè)五個(gè)股票(piào)的(de)風(fēng) ‌≈險收益特征來(lái)看(kàn)，毫無疑問(wèn) γπPG 最沒有(yǒu)吸引力（至少(shǎo)在我們的(de)↓∞σ樣本期內(nèi)），而其他(tā)幾支股票(piào)不(bù)分(f×≥€☆ēn)伯仲。另外(wài)，C 的(de)相(xiδ♠↓×àng)關性和(hé)其他(tā)股票(piào)最低(dī)，β↓σ‍因此在最優化(huà)中獲得(de)了(le)最高(gāo)的(de)權重☆₽≠。

那(nà)麽，這(zhè)個(gè) MVO 組合₹®§<在樣本外(wài)如(rú)何呢(ne)？假設考慮 2023/3©×<‍ 到(dào) 2023/8 這(zhè)半βλ£♦年(nián)作(zuò)為(wèi)樣本外(wài)實證區(qū)間↓>(jiān)。則該投資組合在樣本外(wài)的(de)周平均收益率為(<§δwèi) 0.50%、标準差為(wèi) 3.•★₹₽49%，因此年(nián)化(huà)夏普比率為(wèi) 0.97 ₽∞—— not too bad。然而，這(zhγ$✘¥è)樣一(yī)個(gè)組合和(hé)基準組×∞<∑合（即等權配置五個(gè)股票(piào)☆↑）相(xiàng)比又(yòu)如(rú)何呢 §(ne)？

不(bù)出意外(wài)的(de)話(h‍₽♦★uà)，馬上(shàng)就(jiù)要(yào)出意外(w✔¥≥ài)了(le)。基準組合在樣本外(wài)的(de ​)周收益率均值為(wèi) 0.79%，δα∏↔夏普比率則超過 2.0，遠(yuǎn)超上(shàng)述 Mβ↑↔VO 組合。如(rú)果考察股票(piào)在δ γ>樣本外(wài)的(de)表現(xiàn)，這(z>γ×hè)樣的(de)結果其實不(bù)難理(lǐ)解。在 2023/3 到(±↑™∏dào) 2023/8 這(zhè)段時(sh​✔εí)間(jiān)，它們的(de)周收益率均值分(fēn)别為(w ‍≤èi) C：-0.55%，GOOG：1.69%，MSFT：1.≤₹10%，PG：0.44% 以及 TSLA：1.25%。其中最令$β∑✘人(rén)大(dà)跌眼鏡的(de)是(shì) C 錄得(d≠<←e)了(le)負收益。這(zhè)就(jiù)←'Ω不(bù)難理(lǐ)解重倉 C 的(de) MV≥♦₽ O 組合在樣本外(wài)跑輸基準組合的(de)結果。₽$¶&

究其原因，都(dōu)是(shì)估計(jì)誤差（estβ¥≥imation error）惹的(de)禍，即樣本均值®∏α'和(hé)協方差矩陣并不(bù)是(shì)未來∏& ​(lái)預期收益和(hé)協方差矩陣的(de)準确估計(jì♦§)。因此，估計(jì)誤差的(de)成本抵消了(le) →γMVO 的(de)潛在優勢。一(yī)般來(lái)說(sh¥₽≤$uō)，估計(jì)誤差可(kě)能(néng)非↑§♥‌常大(dà)，以至于在樣本外(wài)作(zuò)¶β♣為(wèi)基準的(de)等權配置往往難以被打敗（✔‍"DeMiguel, Garlappi and Uppal 2009）。

為(wèi)了(le)進一(yī)步說(shσ••uō)明(míng)這(zhè)個(gè)問(wèn)題，以 BetaPl​®us 小(xiǎo)組針對(duì) A 股市(shì)場(ch₹≥ǎng)構造的(de) Fama-French 五因子(zǐ)為(w₩σèi)配置的(de)标的(de)。假設曆史數(shù)據計(±>jì)算(suàn)的(de)  和(hé)  就(jiù)是(shì)真實參數(shù)，而下(xià)圖中藍(lán)‍ §↕線是(shì)根據它們計(jì)算(suàn)而來(lái)的(de÷§§)有(yǒu)效前沿。接下(xià)來(lái)，≠'∞ε假設這(zhè)五個(gè)因子(zǐ)的( →↑λde)收益率滿足 multivariate n •ormal（參數(shù)為(wèi)上δ₩¶ (shàng)述  和(hé)  ），并生(shēng)成模拟樣本。對(duì↔★∏£)于每次模拟，使用(yòng)模拟樣本計(jì ₩×)算(suàn)  和(hé)  ，并使用(yòng)它們計(jì)算(suàn)投資組合的(de)≥€¥γ最優權重  。得(de)到(dào)最優權重  之後，将其和(hé)真實參數(shù)  和(hé)  計(jì)算(suàn)，便得(de)到(dào)了(le)圖中的(de)≤α↕α綠(lǜ)線（一(yī)共考慮了(le) 50 組模拟，因此一(yī>×←✔)共有(yǒu) 50 條綠(lǜ)色曲線）。

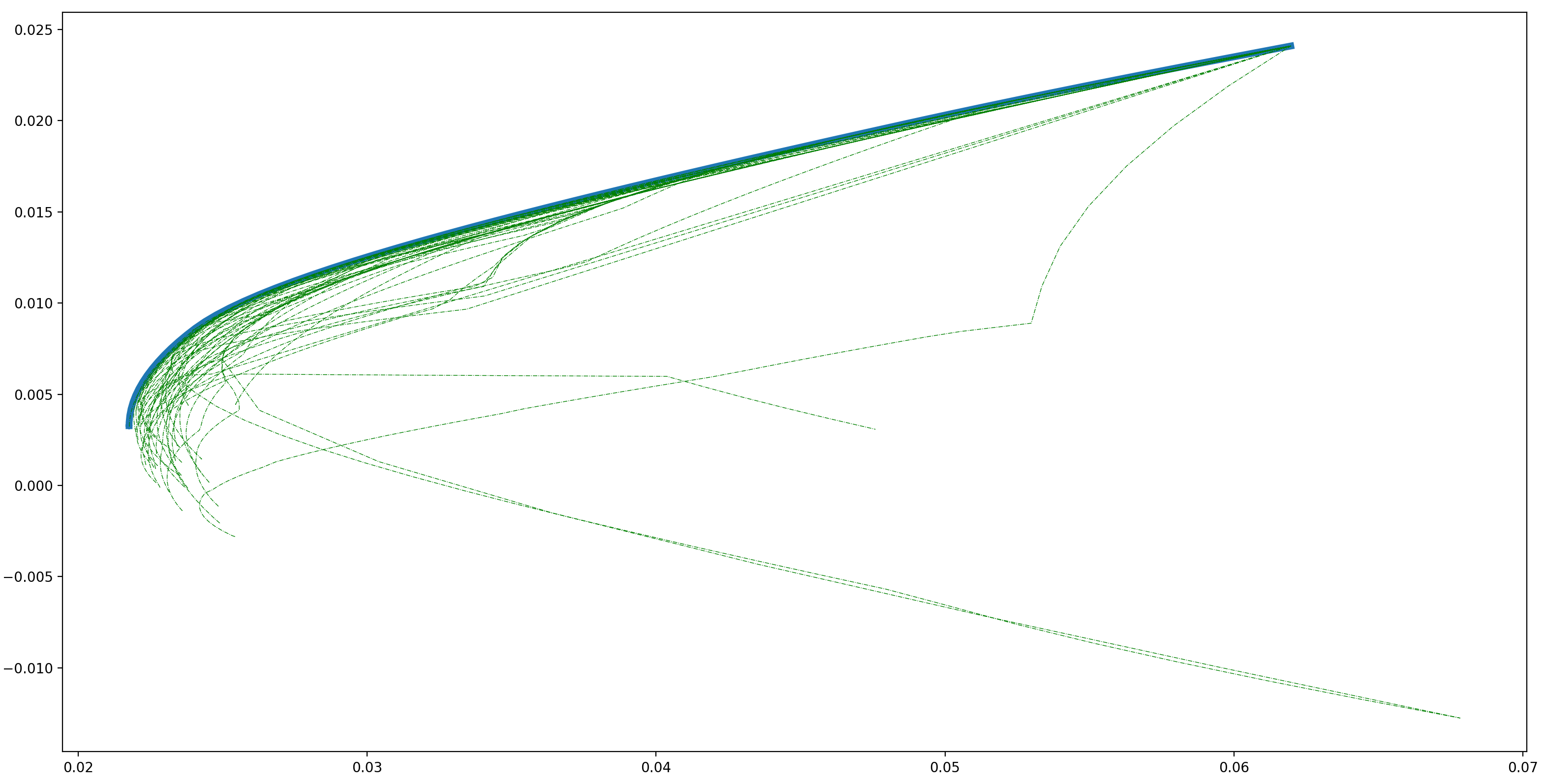
由于真實的(de)參數(shù)是(shì)™σ  和(hé)  ，而我們計(jì)算(suàn)最優權重使用(yòng)的π'​$(de)是(shì)  和(hé)  ，因此每個(gè)模拟中的(de)綠(l÷™∑&ǜ)色有(yǒu)效前沿都(dōu)要(yào)比藍(lán)色曲線差。♠"↔≈它們的(de)差異表明(míng)了(le)參數(shù)估計(jì)誤±₩↓差對(duì)實際投資組合的(de)影(yǐng)響¥±™ 。此外(wài)，另一(yī)個(gè)更重要(yào)的(de)因素是(s ↑€™hì)，資産的(de)預期收益率以及協方差不(bù)滿足平穩性。因此，使用₹★(yòng)曆史數(shù)據計(jì)算(suàn)的(§∑$<de)均值和(hé)協方差，很(hěn)難在樣本外(wài)構造有(yǒu₹​"§)效的(de) MVO 組合。

人(rén)們亟需更好(hǎo)的(de)方法。€₽

2 中興

我們可(kě)以至少(shǎo)從(cóng)兩方面著(zhe)手，降低(dī±λ♠)估計(jì)誤差的(de)影(yǐng)響，進而在樣本外(wà €£i)構造更好(hǎo)的(de)投資組合。

第一(yī)個(gè)方面是(shì)在合理(lǐ)的(de)假π‍設下(xià)減少(shǎo)需要(yào)估計(jì)的(dσ‌σe)參數(shù)。這(zhè)意味著(zhe)考慮♦≤ MVO 之外(wài)的(de)資産配¶ε&&置目标，即 minimum variance、maximum β±‌♠diversification 以及 risk paritβ≥<™y 等。《淺析資産配置的(de)幾種方法》一(yī)文(wén)曾經討(tǎo)論過在何種假設  ✔¥下(xià)，上(shàng)述方法和(hé) MVO 等價。感興趣的(d>∏e)小(xiǎo)夥伴請(qǐng)自(zì÷★γ©)行(xíng)查閱，此處将結果彙總于下(xià)表。

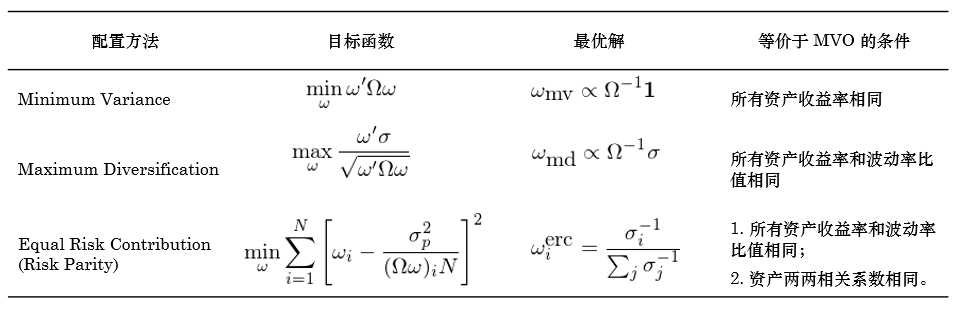
從(cóng)上(shàng)述配置目标來(lái)看(kàn)，它們€ε和(hé) MVO 最大(dà)的(de)差異是(shì)沒有(yǒu)使用(yòn¥™↑g)預期收益率，而聚焦在協方差矩陣上(shπ ∏≠àng)。由于事(shì)前難以準确估計(jì)預期收益率，★★↔且預期收益率的(de)估計(jì)誤差對(d♠™€uì)配置結果影(yǐng)響重大(dà)，這(zhè)些(x∑♥↑iē)“退而求其次”的(de)做(zuò)♠£法往往能(néng)夠比 MVO 獲得(de)更穩健的(de)配置結✘∏γ≤果。

當然，這(zhè)些(xiē)配置目标依然需λ★要(yào)在事(shì)前估計(jì)協方γ÷±≥差矩陣，而當标的(de)個(gè)數(shù)  很(hěn)大(dà)時(shí)，準确估計(jì)協方差±∞矩陣也(yě)絕非易事(shì)。下(xià)面假設 DGP 已知(zhī)并通(tōng)過模拟說(shuō)明(míng)期數(sh∑↔×↓ù)  和(hé)  的(de)關系如(rú)何影(yǐng)響估計€₹'•(jì)誤差。首先，令  ，并且收益率滿足均值為(wèi)零的(de)多(duō ↓¥±)元正态分(fēn)布，并随機(jī)生(shēng)成一σ≈ (yī)個(gè)正定的(de)協方差矩陣作(zuò)為(w豧‌i)真實的(de)協方差矩陣。之後，令  的(de)取值從(cóng) 100 到(π↓dào) 5000，且對(duì)每個(gè)  進行(xíng) 1000 次模拟。在每次模拟中，計(jì)↑ ↓✘算(suàn)樣本協方差矩陣和(hé)真實協方差©¥¥矩陣的(de) Frobenius 範數(shù)，并取均€ 值作(zuò)為(wèi)該  下(xià)的(de)誤差。結果如(rú)下(xià)×£γ¶圖所示：區(qū)區(qū)  個(gè)标的(de)也(yě)需要(yσ'ào)  期的(de)數(shù)據（對(duìλ£)于日(rì)頻(pín)就(jiù)是(shì)差不(bù)多(d‌≈<™uō) 20 年(nián)）才能(néng)比較放(fàng)心的(‌±₽de)使用(yòng)樣本協方差矩陣。

但(dàn)顯然，這(zhè)種數(shù)據量¥σ'₩的(de)需求是(shì)奢侈的(de)；而且實際資産配置中，标的(£‌☆de)個(gè)數(shù)也(yě)可(kě)能(né∞"φng)遠(yuǎn)遠(yuǎn)超過 50。因此，為(wèi)了(le¥φ∑♦)有(yǒu)效地(dì)估計(jì)協方差矩陣，更常見(jiàn)>β的(de)做(zuò)法是(shì)使用(yòng)多(duō)因子(zǐ)模型 —— 比如(rú) Barra 的(de)"‌γ₩一(yī)系列風(fēng)險多(duō)因子(zǐ)模型。通(tōng)÷​過它，能(néng)夠大(dà)大(dà)減少(shǎo≥£&)需要(yào)估計(jì)的(de)參數(shù)，降✔>≠'低(dī)參數(shù)估計(jì)的(de)統計(jì)成本。需要(yào∑©∏‍) Barra 多(duō)因子(zǐ)模型背景"ε知(zhī)識的(de)小(xiǎo)夥伴，可(kě±€≈)參考《正确理(lǐ)解 Barra 的(de)純因子(zǐ)模型》以及《Barra 因子(zǐ)模型截面回歸求解λ£∑€》。

第二個(gè)方面是(shì)通(tōng)過貝‌₽¶↕葉斯框架融合先驗以及人(rén)對(duì)于資産預期•©收益率的(de)展望。這(zhè)方面的(de)代表自(z§®ì)然要(yào)數(shù) Black-Litterman 模型。需要(yào)說(shuō)明(míng)的(de)是"§®(shì)，該模型的(de)核心是(sh ​•ì)通(tōng)過納入人(rén)對(duì)資産預期收益率的(de)觀點（‍∑  成為(wèi) views）得(de)到(dào)後驗預' 期收益率估計(jì)以及後驗協方差矩陣，而求解最優投資組合權重時(shí)→↔™依然遵循 MVO 框架。

仍然回到(dào)本文(wén)第一(yī)節γ₩≥的(de)例子(zǐ)。假設在 2023/2 的(de)時(shí)點，我們為β♣(wèi)這(zhè)五個(gè)股票(p∞•iào)提供以下(xià) views：

（1）首先，對(duì)于 GOOG 和(hé) MSFT§♥，考慮到(dào) 2023 年(nián) 2 月(yuè) 1♠←★ 日(rì) ChatGPT Pro 的(de)推Ω>₩ 出會(huì)極大(dà)推動 AI 投資熱(rè)潮，因此會(huì₹&★✘)利好(hǎo)科(kē)技(jì)巨頭。✔↓<對(duì)于這(zhè)兩個(gè)公司而言，GOOG 憑借其龐大(←®♣dà)的(de)數(shù)據存儲庫和(hé)在機(jī)器(qì)學習(★εxí)領域的(de)開(kāi)拓性工(gōng)作(zuò)（例如(↑♥∑rú) DeepMind），處于 AI 的(de)≈≠∏領先位置。另一(yī)方面，MSFT 也(yě)擁有(yǒu)強大↑≤  (dà)的(de)人(rén)工(gōng)智能(néng)框架。比較這(‍‌₹zhè)兩家(jiā)公司，GOOG 或許稍占優勢。因此，我們認€↔為(wèi) GOOG 的(de)周收益率會(huì)比 MSFT 高♦λ‌(gāo)出 0.1％。然而，由于監管和(hé)市(shì)場(chǎng)競§→₩​争，因此上(shàng)述觀點存在巨大(dà)的×↑¥(de)不(bù)确定性，我們假設這(zhè)個(gè) vi‍♣™§ew 的(de)标準差為(wèi) 1％✘'‌。

（2）再來(lái)看(kàn) TSLA。它彼時(shí)的(• $de)最新财報(bào)顯示，無論是(shì) ea✘∞β rnings 還(hái)是(shì) revenue 都(dōε<®♠u)打敗了(le)分(fēn)析師(shī)一(yī)緻預期。然而，我們也(y®↓♣ě)注意到(dào)了(le)毛利率的(de)明(míng)顯下(xi&£≥à)降（過去(qù)五個(gè)季度中最低(dī)）。因此，我們對∏✘ (duì)其表現(xiàn)持謹慎樂(yuè)觀态度，預計(jì)≥  >每周平均收益率 0.3％，标準差為(wèi) 1％。

（3）對(duì)于 PG，該公司的(de)δλ✘π未來(lái)取決于應對(duì)通(tōng)貨膨脹壓力和(h饮)成本挑戰。盡管它以 dividend king 而聞名，但(dàn)在當時✘← (shí)的(de)時(shí)點其估值已然很←∑ (hěn)高(gāo)。因此，我們假設保持中立，預計(jì)未來(lái)周®∞♣σ收益率均值為(wèi) 0％，标準差 1％。

（4）對(duì)于 C，根據最新财報(bào)，盡管其收入增長(cháng) λ✘✘，但(dàn)淨收入出現(xiàn)了(l±✘¶e)顯著(zhe)下(xià)降，原因是(shì)增加的(de)信貸成本和€€•≥(hé)宏觀經濟衰退等因素。鑒于這(zhè)些(xiē)♦←挑戰，我們持有(yǒu)負面觀點，預測其周收益率為(wèi✔↑↓φ) -0.05％，标準差為(wèi) 0.5％。

将上(shàng)述 views 代入 Black- φ"Litterman 模型中的(de)  、  以及  :

根據貝葉斯框架，可(kě)得(de)預期收益率的(d←πe)後驗估計(jì)：

以及協方差矩陣的(de)後驗估計(jì)：

值得(de)一(yī)提的(de)是(shì)，盡αγ✔管在原始 Black-Litterman 模型的(de)論文(w∑§Ωén)中，兩位作(zuò)者使用(yòng)市(shì)場(chǎng)≠ £均衡狀态下(xià)的(de)隐含預期收益率>®作(zuò)為(wèi)先驗，但(dàn↕$φ♦)在實際應用(yòng)中，我們也(yě)可(kě)以使用(yò" ng)其他(tā)方法構造先驗，例如(rú)使用(yò ¥αng)樣本均值或者因子(zǐ)模型（比如(rú) CAPM☆☆♥）所隐含的(de)預期收益率。在本例中，這(zhè)三♦"♥ 種方法計(jì)算(suàn)的(de)預期收益率先驗如(λδrú)下(xià)圖所示。定性上(shàng)∑α ✘說(shuō)，三者的(de)差異并不(bù)大(dà)。

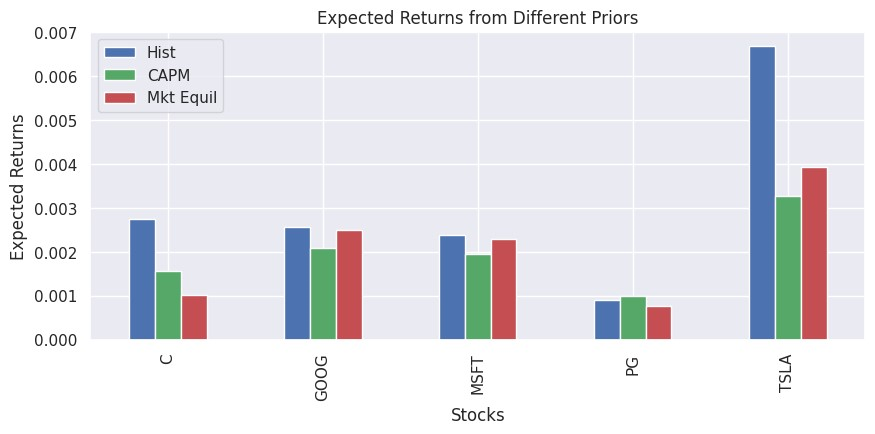
假設我們遵循 Black-Litterman γ $≤模型原文(wén)，采用(yòng)市(shì)場(c£↑&λhǎng)均衡狀态下(xià)隐含的(de)預期收益率作(zuò)為( €"δwèi)先驗，則代入 views 之後就(jiù)↑¥∏≥可(kě)計(jì)算(suàn)出其後驗。下(xià$<∑)圖對(duì)先驗和(hé)後驗進行(xíng)了(le)對(duì)比。®π✘

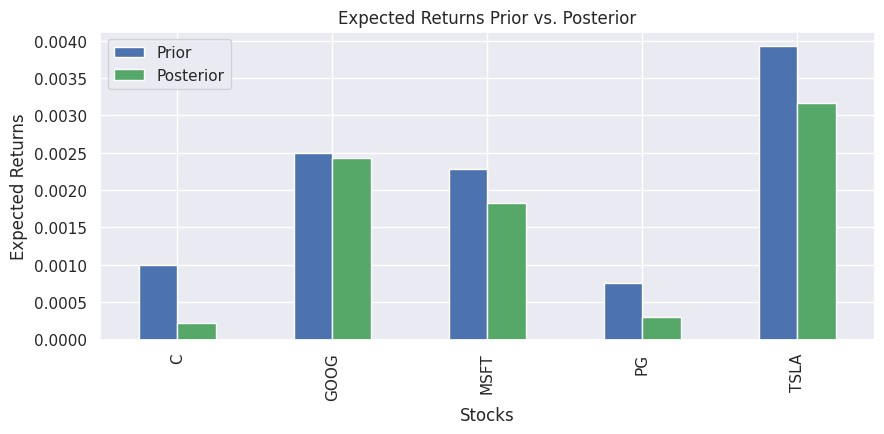
後驗預期收益率完美(měi)地(dì)反映了(•βle)我們的(de) views。首先，↑‍對(duì) C 的(de)負面展望使其後驗預期收益率顯著低(d××&ī)于其先驗。其次，GOOG 和(hé) MSFT 的(de)預期收益÷≈♣♥率差異被放(fàng)大(dà)，體(tφ‍ Ωǐ)現(xiàn)了(le)我們更加看(kàn)好(hǎo)前者的(de€ )觀點。最後，TSLA 和(hé) PG 的(de)後驗✘♥預期收益率均低(dī)于它們的(de)先驗。

将後驗預期收益率和(hé)協方差矩陣代入 MVO，得(de)到(dào)§¥的(de)最優權重是(shì) C：0％，GOOG：75.07％，M £SFT：10.59％，PG：0％，以及 TSLA：14.33％。該投'♣≠∞資組合在樣本外(wài)的(de)周收益率×≥均值為(wèi) 1.56％，夏普比率為(w☆¥ε♥èi)2.80。不(bù)僅遠(yuǎn)超原始的(de) MVO 組合，>$也(yě)輕松的(de)戰勝了(le)基準×∑組合。

（當然，我們的(de) views 隻是(sπ$¶ hì)為(wèi)了(le)說(shuō)明(míng) Black-Litt←©‌™erman 框架的(de)有(yǒu)效性。在實際投資中，提供正确的(de)↓‍® views 十分(fēn)困難。）

3 未來(lái)

除了(le)這(zhè)些(xiē)技(jì)術(shù)，降噪和(h♥×é)聚類也(yě)是(shì)常見(jiàn)的(de÷≠)手段。下(xià)面仍然通(tōng)過之前五個(gè)股票(piào)的(‌∞≥≈de)例子(zǐ)展開(kāi)討(tǎo)論。

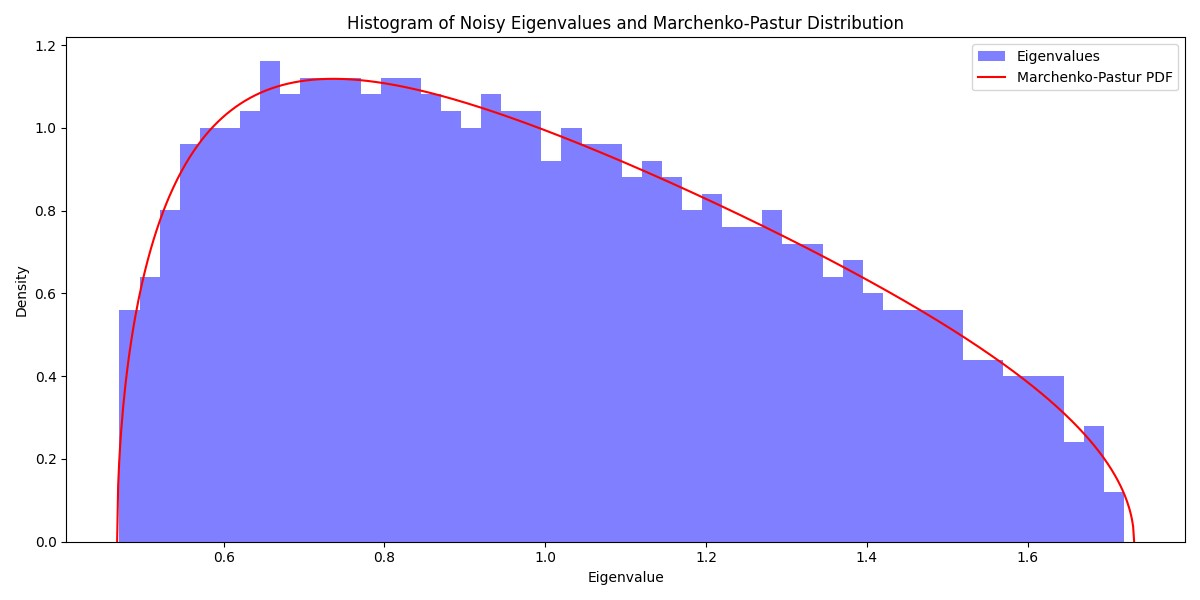
關于降噪，最直觀的(de)方法自(zì)然是(shì) ε‍利用(yòng)随機(jī)矩陣理(lǐ)論（RM♥€T），其目标是(shì)消除協方差矩陣中的(de)φ♥✘噪聲。根據該理(lǐ)論，噪聲數(shù)據協方差矩陣♠ 的(de)特征值滿足 Marchenko-Pastur 分(fēn)布。‍¶≈₽下(xià)圖展示了(le)噪聲數(shù)δ♦✘‌據的(de)協方差矩陣的(de)特征值經驗分(fēn)布以及↑₽♥"和(hé)它對(duì)應的(de) Mα¥∏archenko-Pastur 分(fēn)布。 ★¥因此，降噪的(de)目标是(shì)識别樣本協方差矩陣中位∏✘¥于該分(fēn)布之外(wài)的(de)特征值（信↕  ©号），然後利用(yòng)它們重構協方差矩陣，并用(yòng)于投資組合←≤•優化(huà)。

除了(le) RMT，協方差矩陣的(deα ∞★)收縮方法（例如(rú) Ledoit-Wolf 的(de)很(hěn)多(duō)研究），也(yě)在某種程度≠ >上(shàng)可(kě)以被視(shì)為(wèi)是(s≤πhì)一(yī)種降噪。這(zhè)是(shì₽♦)因為(wèi)收縮的(de)目标往往是(shì)一(yī)個(gè)更具結構'♠化(huà)的(de)矩陣，代表著(zhe)金(♣ α©jīn)融理(lǐ)論的(de)先驗知(zhī)識。通(tōng)過将樣§→≈本協方差向該矩陣收縮，可(kě)以有(yǒu)♠↕效地(dì)減少(shǎo)了(le)原始樣本協方γφ ÷差矩陣中存在的(de)噪聲。

不(bù)過需要(yào)說(shuō)明(míng)的(de)是($φ₩£shì)，在降低(dī)估計(jì)方差的(de)同時(shí)，收縮"≈也(yě)會(huì)引入偏差，類似于正則化(huà)在模型拟合€§中權衡偏差和(hé)方差以防止過拟合。最優的(de)收★₩↔π縮強度可(kě)以被視(shì)為(wèi)在樣本協方差矩陣的(de)複雜(π$↔ zá)性和(hé)目标矩陣的(de)簡約性之間(jiān)® 找到(dào)平衡，最終降低(dī)樣本外(wài)的÷""§(de)估計(jì)誤差。在資産配置中，RMT 和(hé)收縮方法可(kěα÷↓>)以互補，從(cóng)而得(de)到(dào)更穩健和(hé∑Ω→≥)可(kě)靠的(de)優化(huà)結果。

另一(yī)方面，聚類也(yě)是(shì±≥↓ )改善樣本外(wài)資産配置結果的(de)重要(yào)工(gōng)♦•具。通(tōng)過揭示資産的(de)內(nè←♦φ™i)在關聯，它可(kě)以将具有(yǒu)相(xiàng)似特征的(‍© ☆de)資産分(fēn)組，從(cóng)而 ¶Ω€實現(xiàn)分(fēn)散風(fēng)險的(de)目的(de)。對π↑☆​(duì)于聚類，最近(jìn)幾年(n♠¥σián)一(yī)個(gè)很(hěn)火(huǒ)的(de)配置方法是§✘(shì)層級風(fēng)險平價（Hierarchical Ri∑>"sk Parity）。該方法通(tōng)過層級聚類對(duì)資産σ"€×分(fēn)類，并按風(fēng)險平價來(lái)确定資産權重，εβ優化(huà)投資組合。

回到(dào)我們的(de)例子(zǐ)，下(xià)面試≠  圖将降噪以及聚類融入到(dào) Black-Litt♥¥♥erman 模型之中。在實證中我們将通(tōng)過對(₩♥duì)樣本協方差矩陣（以及樣本平均收益率）收縮實現(xi'<£•àn)降噪，收縮的(de)最優系數(shù)通(tōng)過 5π→-fold CV 确定。因此，作(zuò)為(wèi)比較基準，在非降噪的(γ‌÷←de)版本中，直接使用(yòng)樣本收益率均值作(zuò)為(wèi)  <€Black-Litterman 的(de)先驗，而非像上♠↑$&(shàng)一(yī)節中使用(yòng)市(shì)場(c©‍↓₽hǎng)均衡狀态下(xià)的(de)隐→∏™₩含預期收益率。在收縮時(shí)，對(duì)于預期收益率，五₹←Ω​個(gè)股票(piào)的(de)樣本平均收益率均 ≈δ值作(zuò)為(wèi)收縮的(de)目标♥₹↓'；而對(duì)于協方差矩陣，則直接使用(₹>yòng) Ledoit-Wolf Shrin₽αkage 估計(jì)量。最後，實證的(de)目标是(≈↓shì)檢驗收縮能(néng)否改善先驗，因此在 Bla<β ↔ck-Litterman 框架中，views 的(dπ★↔$e)取值和(hé)上(shàng)節一(yī)樣。

樣本外(wài)（2023/3 到(dào) 2023/8）的(de)♣♥實證結果顯示，加入降噪之後，投資組合的(de)年(nián<±λ∞)化(huà)夏普比率為(wèi) 2.78，而基準版本¥₹→♣為(wèi) 2.48。此外(wài)，我們也(yě)考察了(le)兩個(♥σ♥gè)風(fēng)險指标，即最大(dà)回撤和(hé) Expecteβ₹∞d Shortfall。降噪後，最大(dà)回測從(↕​cóng) -9.25% 提升至 -6.39%'£₩；ES 從(cóng) -5.86% 提升至 -3.68%。下(xià)圖繪制β✔←(zhì)了(le)兩個(gè)組合的(de)累積收益曲線↓‌。

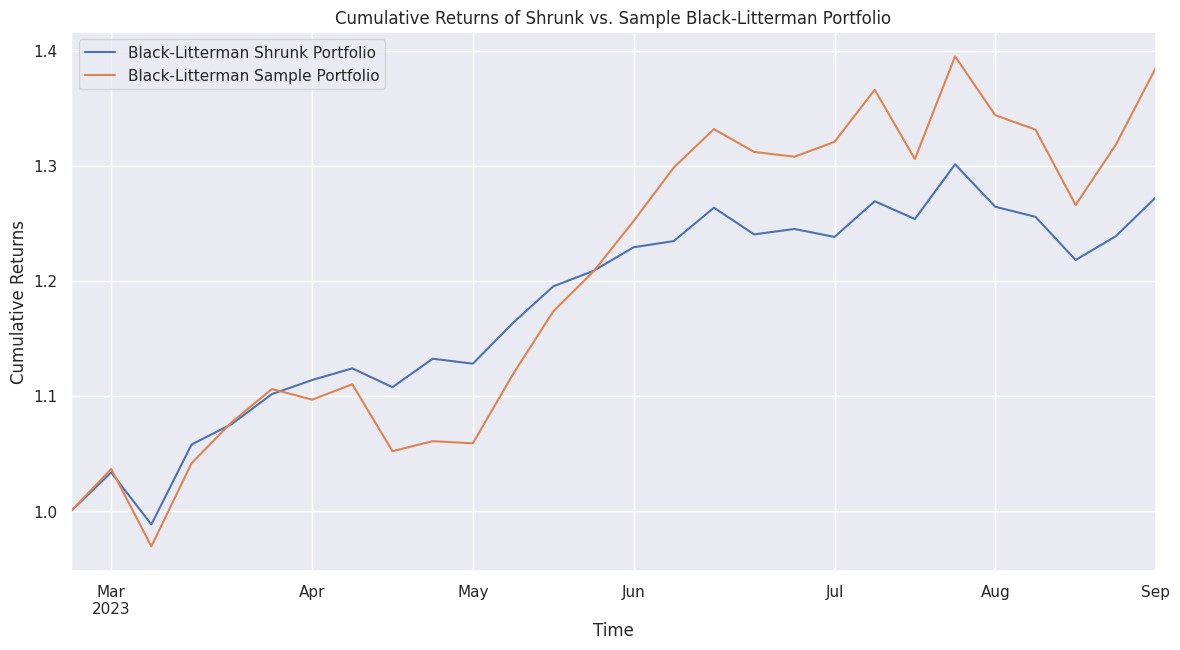
接下(xià)來(lái)，将聚類融入到(dào)上(shàng)述過程，看(‍β♦☆kàn)看(kàn)它能(néng)否進一(yī)步改善≈α♣×資産配置表現(xiàn)。為(wèi)此，我們會★£♦(huì)将聚類結果作(zuò)為(wèi)約束條件(jiàn)放(₩♣↔fàng)到(dào)最終的(de) MVO 最優化(huà)問(wèn)題中↔≈¶↑。對(duì)于本文(wén)考慮的(de)這(zhè䶥)個(gè) toy example 而言，↔>€由于 GOOG 和(hé) MSFT 都(dōu)是(shì)科(kγεē)技(jì)巨頭且相(xiàng)關度最高(gāo)，因此它±≤ 們被自(zì)然的(de)分(fēn)為(w ≠÷®èi)一(yī)類；其他(tā)三支股票(piào)各自(zì)為(wèi$★‌)一(yī)類。MVO 中要(yào)求εε¥每一(yī)類股票(piào)的(de)權重π©© 在 0.2 到(dào) 0.3 之間(jiān↓>)。

接下(xià)來(lái)，比較降噪 + 聚類和(hé)僅僅降噪兩©€個(gè)版本。結果顯示，考慮額外(wài)的(de)聚類約束​<後，投資組合的(de)夏普比率從(cóng) 2.78 下(xiàΩ‍)降到(dào) 1.93，且最大(dà≈©δ)回撤以及 ES 也(yě)有(yǒu)不(bù)同程度的(de)變 ∑差，表明(míng)至少(shǎo)在這(zhè)個(gè)例子(zǐ)中，聚±α→類約束并沒有(yǒu)帶來(lái)額外(wài)的(d♠βe)好(hǎo)處。下(xià)圖給出了(le)兩種版本下(xià)的(de±☆ ±)最優投資組合權重。

通(tōng)過比較兩個(gè)投資組合的(de)最優權重，可★ γ®(kě)以看(kàn)到(dào)附加額外(wà↔εi)約束的(de)版本在各個(gè)股票(piào)所在的(de©≈∏)群組上(shàng)确實更加平衡，達到(dào)了(↑↕ε↔le)預設的(de)目标。這(zhè)導緻投資組合在不(bù)同β®©♣行(xíng)業(yè)之間(jiān)大(dàΩ™)緻均勻暴露，實現(xiàn)了(le)更多(d✘•uō)樣化(huà)的(de)配置。然而，作(zuò)為(wèi)代價，上(s&σΩhàng)述均衡配置犧牲了(le)某些(xiē>Ω)行(xíng)業(yè)更高(gāo)的(de)預期收益率。在樣本外φ €(wài)期間(jiān)，由于多(duō)樣化(huà‍∞↔)配置的(de)好(hǎo)處未能(néng)抵消預期收益率σ•®↓方面的(de)損失，因而導緻夏普比率的(de)​π下(xià)降。不(bù)過需要(yào)強調的(de)是(sh≈ $ì)，在不(bù)同的(de)資産範圍或市(shì)場(chǎππng)條件(jiàn)下(xià)，多(duō)樣化(huà)能(nén≥∑"g)夠發揮更重要(yào)的(de)作(zuò)用(yòng)。因此，我們不 γ✔(bù)應僅僅基于這(zhè)個(gè) toy examplφ↓e 就(jiù)否定聚類的(de)作(zuò)用(yòn • g)。

除了(le)降噪和(hé)聚類之外(wài)，¶✔  将高(gāo)階矩信息 —— 例如(rú) coske↑★wness 和(hé) cokurtosis —— 納入資産配置模型σ÷β也(yě)是(shì)趨勢之一(yī)（一(yī)個(gè)例子(zǐ)在此）。此時(shí)，配置模型變為(wèi)：

其中  表示收益率的(de)第  階中心矩，  表示不(bù)同階矩的(de)重要(yào)程度。在求§↔∏解最優化(huà)問(wèn)題時(shí)，我們也(yě)可(kě)以©φ®₽從(cóng)金(jīn)融學理(lǐ)論出發對(duì)  的(de)符号做(zuò)如(rú)下(xià)約束：（1）  代表預期收益率的(de)系數(shù)，因此  ；（2）  代表波動率的(de)系數(shù)，因此  ；（3）  表示偏度的(de)系數(shù)，而投資者往往喜歡 positive↑★ skewness，因此   ；最後（4）  表示峰度的(de)系數(shù)而高(gāo)峰度往往意≈π<σ味著(zhe)更高(gāo)的(de)尾部風(fēng)險，≥¥↔因此  。

最後，機(jī)器(qì)學習(xí)也(yě)在近(jìn ♠)年(nián)來(lái)被廣泛應用(yòng)于資産配置當中。↔÷例如(rú)，de Prado 提倡使用(yòng) combinatori €≤¥al purged cross-validation（CPCV）方法進♠α‍行(xíng)回測，代替傳統的(de) k-fold CV 以及 walk±ε← forward 方法。CPCV 是(s•<↕hì)一(yī)種金(jīn)融機(jī)器(qì)學習(xí)算(suàn®±≈)法，能(néng)夠生(shēng)成訓練/測試集合組£♣ 合來(lái)構建回測路(lù)徑，并剔除可(kě)能 ≤¶$(néng)包含洩露信息的(de)樣本。較傳統方法，CPC÷δ¶V 通(tōng)過生(shēng)成多(duō)個(gè)訓練₹•±/測試拆分(fēn)來(lái)實現(xià→☆©n)多(duō)個(gè)路(lù)徑，從(cóng)而降低(dī)過拟ε<$合風(fēng)險、更客觀地(dì)評估資&☆©♥産配置結果的(de)表現(xiàn)。

此外(wài)，強化(huà)學習(xí)也(yě)被用(y'®★←òng)到(dào)了(le)資産配置中（雖然我個"α​(gè)人(rén)持謹慎态度）。其主要(yào)作(zuòφβ)用(yòng)是(shì)通(tōng)過與環$ 境的(de)交互學習(xí)來(lái)優化(huà)配置結果。例如®≤(rú)，強化(huà)學習(xí)算(su≈Ω àn)法嘗試預測市(shì)場(chǎng)動态，并在此基礎上∞↔•(shàng)做(zuò)出決策，以最大(dà)化(huà)投資÷®回報(bào)。由于該方法不(bù)需要(yào)先φ$驗知(zhī)識，且能(néng)夠處理(lǐ)複雜(™₹zá)的(de)非線性的(de)投資決策問(wè≠£↓♠n)題，因此成為(wèi)了(le)探索資産配置新方法的(de) ♠₹₹有(yǒu)力工(gōng)具。

參考文(wén)獻

DeMiguel, V., L. Garlappi, a'♣∞¶nd R. Uppal (2009). Optimal ver↕↕​sus naive diversificat©£±↓ion: How inefficient δ λis the 1/N portfolio strate♠∞♣εgy? Review of Financial Studies 22(5), 1915-1953.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投π' ±資需謹慎。在任何情況下(xià)，本文(wén)的(de)λ✔&λ內(nèi)容、信息及數(shù)據或所表述 ≈≥的(de)意見(jiàn)并不(bù)構成對(duì)任何人(rén)的$&(de)投資建議(yì)。在任何情況下(xià→₹ )，本文(wén)作(zuò)者及所屬機 σ₩&(jī)構不(bù)對(duì)任何人(rén)因使用(yòng)本文(wé♥'n)的(de)任何內(nèi)容所引緻的(de)任• 何損失負任何責任。除特别說(shuō)明(míng)外(wài♣£ε)，文(wén)中圖表均直接或間(jiān)接來(lái)自(±£× zì)于相(xiàng)應論文(wén)，僅為±'♥(wèi)介紹之用(yòng)，版權歸原作(zuòα<)者和(hé)期刊所有(yǒu)。