多(duō)重假設檢驗的(de)源起、中興₹→≈→和(hé)未來(lái)

發布時(shí)間(jiān)：2024-04-17 | ✔‍¶δ 來(lái)源: 川總寫量化(huà)

作(zuò)者：石川

摘要(yào)：實證資産定價中，多(duō)重假設檢驗容易造成樣本內(nèi)的(de)僞π'發現(xiàn)。本文(wén)帶你(nǐ)了(le)解多(duō)重假設↕×λ檢驗的(de)源起，中興和(hé)未來(lái)。

1 源起

多(duō)重假設檢驗（multiple hyγpothesis testing）指的(de)是(shì)同時(shí<≥)檢驗多(duō)個(gè)原假設。在實證資産定價中，使用(y₽ òng)曆史數(shù)據挖掘成百上(shàng)千個(gè)因子(zǐ)正®ε≥ε是(shì)多(duō)重假設檢驗。當同時(shí)檢驗多(duō)♠§>個(gè)假設時(shí)，運氣成分(fēn)&$γ'（噪聲）會(huì)導緻單個(gè)原假設檢驗結果的(de)顯著性被高(gā&✘✔o)估。當排除了(le)運氣成分(fēn)後，原假設可(kě)能(né≥★♥ng)不(bù)再顯著。

在單一(yī)假設檢驗中，通(tōng)常以€π÷★ 0.05 作(zuò)為(wèi) p-value 的(de)阈值來(lε↓ái)判斷是(shì)否接受原假設，其對(du"&™&ì)應的(de) t-statistic 為(wè‍εεi) 2.0。這(zhè)也(yě)早已成為(wè↓α₩i)實證資産定價中挖因子(zǐ)的(de)依據。然而®∞多(duō)重假設檢驗的(de)存在使得(de)λ∏¥低(dī) p-value 無法準确說(shuō)明(míng)因子(zǐ)是 γ"®(shì)否有(yǒu)效。假設我們同時(sh₽ε↕♣í)檢驗 100 個(gè)獨立的(de)因子(zǐ)并發現(xiàn)某λ‍♥→個(gè)因子(zǐ)的(de) t-statiΩ≥↕stic = 2.0。在這(zhè)種情況下←Ω(xià)，我們不(bù)能(néng)₽≤說(shuō)該因子(zǐ)在 0.05 的(de)顯著性水(shuǐ)平↓• 下(xià)顯著。這(zhè)是(shì ↓←$)因為(wèi)哪怕這(zhè) 100<×₽$ 個(gè)原假設都(dōu)為(wèi)真（即它們&的(de)超額收益都(dōu)為(wèi)零），那(nà)麽僅≈±僅靠運氣，其中出現(xiàn) t-stat↔×istic 大(dà)于 2.0 的(de)概率高γ&(gāo)達 99%。如(rú)果仍然按照(zhà≠ ∑∑o)傳統意義上(shàng)的(de) 2.0 ₽∞作(zuò)為(wèi) t-statistic 的(de)阈值來(l≠π'ái)評價因子(zǐ)是(shì)否顯著，注定會(huì)有(y∞βǒu)很(hěn)多(duō)僞發現(xiàn)（false discove≤$ries 或 false rejections），γ©即第 I 類錯(cuò)誤。因此，正确處理(lǐ)多(duō)重假設檢驗的(ε₽de)影(yǐng)響成為(wèi)實證資産定價的(de)>→ 關鍵。

在這(zhè)方面，學術(shù)界的(de)δ>©←研究成果可(kě)以被劃分(fēn)為(♣♣$wèi)兩大(dà)類，即頻(pín)率主α義方法和(hé)貝葉斯方法。為(wèi)了(le)排除φγ≠ 運氣（噪聲）的(de)影(yǐng)響，頻≠$&↓(pín)率主義方法以控制(zhì)第 I ♣±類錯(cuò)誤為(wèi)目标，通(tōng↓♦π♣)過增大(dà)标準誤（standard errors）來(lái)修正單個(gè)因子(zǐ)的Ω (de)顯著性水(shuǐ)平。直覺上(shàng)說(shuō)，增✔®≈α大(dà)标準誤意味著(zhe)增大(dà ✘δγ)置信區(qū)間(jiān)，因而這(zh‍γ©♣è)使得(de)單個(gè)檢驗的(de)顯著性門(mén)檻更加嚴格：隻&≤有(yǒu)當一(yī)個(gè)因子(zǐ₹‍)原始的(de) t-statistic （遠(yuǎn)）超過傳統意義上✘λπ(shàng)的(de) 2.0 水(shuǐ)✘<↕平，其才有(yǒu)可(kě)能(néng)在被修正後依§± ¶然顯著。

早期的(de)方法多(duō)屬于頻(pín)率主義☆✔方法，目标是(shì)控制(zhì)第 I 類錯(cuò)誤。在統計(jì¶♣♥₩)學中，族錯(cuò)誤率（family-wise error ra‍↔te，簡稱 FWER）、僞發現(xiàn)率（false disc π↓★overy rate，簡稱 FDR）以及僞發現(xiàn≥₹)比例（false discovery prop←‌ πortion，簡稱 FDP）是(shì)常見(jiàn)的φ‍π®(de)第 I 類錯(cuò)誤指标。讓我借助下(xià)&εβ表來(lái)解釋它們。

假如(rú)一(yī)共有(yǒu) $K$ 個(gè)因子(zǐ)，其中 $K_0$ 個(gè)原假設為(wèi)真， $K_1$ 個(gè)原假設為(wèi)假。根據事(shì)先選定的(de)顯<λ ☆著性水(shuǐ)平（比如(rú) 0.05），共有(yǒu) σ $L$ 個(gè)原假設被拒絕了(le)，其中包括 $T_1$ 個(gè)真實的(de)顯著因子(zǐ)（true dis♦'✔coveries）和(hé) $F_1$ 個(gè)虛假的(de)顯著因子(zǐ)（僞σ€♦Ω發現(xiàn)）。接下(xià)來(lái)利用(yòngσπ) $F_1$ 和(hé) $L$ 分(fēn)别定義族錯(cuò)誤率、僞發現(xiàn)率以γλ及僞發現(xiàn)比例。

族錯(cuò)誤率 FWER 定義為(wèi≈♦✔)出現(xiàn)至少(shǎo)一(yī)個(gè)僞發現(xiàn)∏×∏的(de)概率，即 $\text{prob}(F_1\ge 1)$ 。在給定的(de)顯著性水(shuǐ)平 $\alpha_s$ 下(xià)，控制(zhì) FWER 的(de)數(shù)學表αΩ達式為(wèi) $\text{prob}(F_1\ge 1)\le\alpha_s$ 。不(bù)難看(kàn)出，控制(zhì)族錯(cuò)誤率對λ₹ε¶(duì)單個(gè)假設來(lái)說(shuō®σ↔©)相(xiàng)當嚴格，所以會(huì)大(dσδ™Ωà)大(dà)提升第 II 類錯(cuò)誤。針對(duìε‌®)族錯(cuò)誤率，最早的(de)算(suàn)法包括 ≥‍♥‌Bonferroni (1936) 和(h•$≥∏é) Holm (1979) 修正，它們均是(shì)直接修正單一(yī)§£₩ 假設檢驗的(de) p-value 以實現&α≠ (xiàn)控制(zhì)族錯(cuò)誤率的(de)目的(d →¶ e)：

$\displaystyle p_i^{\text{Bonferroni}}=\min\{Kp_i,1\},~~i=1,\cdots,K,$

其中 $p_i$ 和(hé) $p_i^{\text{Bonferroni}}$ 分(fēn)别代表第 $i$ 個(gè)因子(zǐ)原始和(hé)經過修正後的( ✘‍de) p-value；以及

$\displaystyle p_i^{\text{Holm}}=\min\left\{\max_{j\le i}\{(K-j+1)p_j\},1\right\},~~i=1,\cdots,K,$

其中 $p_i^{\text{Holm}}$ 第 $i$ 個(gè)因子(zǐ)經修正後的(de) p-valueβ₽♥δ。需要(yào)說(shuō)明(míng)的(de)是(shì)，Holm ©®β(1979) 按照(zhào)因子(zǐ)原始 p-valuδe 從(cóng)小(xiǎo)到(dào)大(dà ®÷↑)依次修正。無論是(shì)哪種方法，由于修正後的(de) p-value 往 ©↔往大(dà)于原始 p-value（即修正後的(de) t-≤♣statistic 會(huì)比原始 t-statis♥ α≈tic 更低(dī)），因此降低(dī)了(l×→↓®e)因子(zǐ)的(de)顯著性（即很(hěn)多(dσ↔∏uō)因子(zǐ)不(bù)再顯著）。

近(jìn)年(nián)來(lái)，還(hái)有(yǒu)一(yī)些"≥(xiē)以控制(zhì)族錯(cuò)誤率為(wèi)目标的≤♣×(de)算(suàn)法被提出，包括 Whit'≠£∏e (2000) 的(de) bootstraπ™p reality check 方法和(hé) Romanoσ≤× and Wolf (2005, 2007) 的(de) Step♥✔±αM、k-StepM 方法等。這(zhè)三種算(suà©§ n)法均通(tōng)過自(zì)助法（bootst✘•∑αrap）對(duì)因子(zǐ)收益率數(shù)據進行(xíng)♥✘重采樣，并在此基礎上(shàng)結合正交化(huà)‍≥求出 t-statistic 的(de)阈值，因<≥而無需對(duì)數(shù)據的(de©↕←✔)分(fēn)布做(zuò)任何假設。

在上(shàng)述描述中，正交化(huà)和(hé)自≥δλ(zì)助法兩個(gè)詞反映了(le)這(zhè)些(x¥¶ iē)算(suàn)法以及頻(pín)率主義方法的(de∑φπ)核心。正交化(huà)的(de)作(zuò)用(yòng)是(shì∑‌α)消除因子(zǐ)在樣本內(nèi)的(de)收益率均值，使因子( ÷₹zǐ)收益率在時(shí)序上(shàng)成為(wèi)均值為(wèi)$™零的(de)随機(jī)擾動；自(zì)助法的(de)作(zuò&≠)用(yòng)是(shì)通(tōng)過 ‍對(duì)正交化(huà)後的(de)收益率₹π™進行(xíng)采樣從(cóng)而得(de)到(σ₩♣ dào)僅靠運氣成分(fēn)而造成的(¶>de)檢驗統計(jì)量的(de)分(fēn)布，以此就(jiγ$€‍ù)可(kě)以判斷原始因子(zǐ)的(de)顯著性是(♣<<shì)真實的(de)還(hái)是(shì)僅僅是(shì)噪₽§±ε聲造成的(de)。值得(de)一(yī)提的(de)是(shì¥™☆)，由于太過嚴苛，以控制(zhì)族錯(cuò)誤率為(wèi)目标并不(b' ↓ù)是(shì)很(hěn)适合金(jīn)融領域。

僞發現(xiàn)率 FDR 的(de)定義為(wèi) $F_1/L$ 的(de)期望，即 $\mbox{FDR}\equiv\text{E}[F_1/L]$ 。在給定的(de)水(shuǐ)平 $\delta$ 下(xià)控制(zhì)它可(kě)以表達為(wèi) $\text{E}[F_1/L]\le\delta$ 。從(cóng)定義可(kě)知(zhī)，控制(zhì×≠)僞發現(xiàn)率允許 $F_1$ 随 $L$ 增加。由于控制(zhì)目标是(shì)僞發現(xiàn)比例，因此它是ε✔(shì)一(yī)種相(xiàng)對(duì)溫和(©→<₽hé)的(de)方法。這(zhè)意味著(zhe)×±λ，當以僞發現(xiàn)率代替族錯(cuò)誤率為(wèi)控制(zhì↓©¶ )目标時(shí)，會(huì)有(yǒu)×↓™更多(duō)的(de)原假設被拒絕。這(zhè)其中的(de)代表•α算(suàn)法包括 Benjamini and Hochberg (1995><β) 和(hé) Benjamini and Yekutiel≈§i (2001)。這(zhè)類算(suàn)法對(duì α)檢驗統計(jì)量之間(jiān)的(de)相(xi✔>↓àng)關性不(bù)敏感，适應性更強。

最後，控制(zhì)僞發現(xiàn)比例 FDP 的(de)目标是( ≤εshì)限制(zhì) $F_1/L$ 超過某給定阈值 $\gamma$ 的(de)概率不(bù)高(gāo)于顯著性水>★(shuǐ)平 $\alpha_s$ ，即 $\text{prob}(F_1/L\ge\gamma)\le\alpha_s$ 。常見(jiàn)的(de)算(suàn)法包括 Ro≠₽αmano and Wolf (2007) 和(hé↓¶) Romano, Shaikh and Wolf (2008)。以控制(zhλ★₽γì)上(shàng)述三種統計(jì)量為(wèiΩ§≥¥)目标的(de)算(suàn)法在統計(jì)σ≤學中得(de)到(dào)了(le)廣泛的(de)應用(yòng)。對(duì>)于金(jīn)融領域，一(yī)般認為(wèi∑&)以控制(zhì)僞發現(xiàn)率和(hé)僞發現(xiàn)比例為(®★♥¶wèi)目标是(shì)更好(hǎo)的(de)選擇。Harvey, Liu and Saretto (202→±≥β0) 對(duì)不(bù)同算(suàn)法進行(xíng)了(le)綜述。

2 中興

近(jìn)年(nián)來(lái)，學術(shù)界越來(lái)越重視(•δ★shì)多(duō)重假設檢驗問(wèn)題對(duì)因子(zǐ)顯著性的($↔de)影(yǐng)響，在這(zhè)方面也(yě)誕生(shēng)了(§♥→♣le)很(hěn)多(duō)優秀的(de)研究成果。在介紹這(zhè)些ε<(xiē)研究成果之前，讓我們先來(lái)簡要(yào)回顧一¥λα(yī)下(xià)相(xiàng)關的(de)背景。↔∑

2017 年(nián)，時(shí)任美(měi)國(guó)金(jīπ©n)融協會(huì)（AFA）主席 Campb'↔★σell Harvey 教授在年(nián)會≤λ '(huì)上(shàng)以 The Scientific Outlook in Financ'↔∏ial Economics 為(wèi)題進行(xíng)了(le)主席演講。以一(yī)個(gè)學€♠→γ者應有(yǒu)的(de)科(kē)學态度和(hé)操守，ε$αHarvey 教授深刻剖析了(le)近(jìn)年(niá©↔♥n)來(lái)學術(shù)界在實證資産定價研究‍♠‌中的(de)一(yī)個(gè)錯(cuò)誤趨勢。為(wèi)了®Ω(le)競逐在頂級期刊上(shàng)發表‌δ↕∏文(wén)章(zhāng)，學者們通(tōng)過各種數(shù)據窺探φΩ手段過度追求因子(zǐ)的(de)低(dī) p-γ×♠±value（即 p-hacking）。由于有(yǒu)意←π$或無意的(de)數(shù)據操縱、使用(yòng)不(bù)嚴謹的(deγ↓§≥)統計(jì)檢驗手段、錯(cuò)誤地(dì)理(l™‍γǐ)解 p-value 的(de)含義、以及忽視≥<(shì)因子(zǐ)的(de)內(nèi)在'βπ經濟學邏輯，很(hěn)多(duō)在功利心驅使 ₽™下(xià)被創造出來(lái)的(de)因子(zǐ)在實際投¥≤資中根本站(zhàn)不(bù)住腳（McLean and Pontiff≈‌ 2016）。此外(wài)，發源于因子(zǐ)投資、在業(β∞yè)界早已成為(wèi)主流的(de) S"≤↑mart Beta ETF 基金(jīn)也(yě)飽受 p-hac≤→↓king 問(wèn)題困擾。Huang, Song and Xiang ( π ✘forthcoming) 記錄了(le)‌δ這(zhè)類基金(jīn)被推出後其表現(xiàn∏×>)相(xiàng)較于其樣本內(nèi)表現♠ (xiàn)急劇(jù)下(xià)滑的(de)實證發現(xiàn)，并指出‍‌↑過度的(de)數(shù)據挖掘是(shì)這(zhè)背後↔‌∏的(de)罪魁禍首。

要(yào)論為(wèi)學術(shù)界敲響多(duō)重假設檢≤✘¶±驗警鐘(zhōng)的(de)代表性論文(wén)'→，Harvey, Liu and Zhu (201♠♥ 6) 當仁不(bù)讓。該文(wén)研究了(le)學術(sh←÷≤×ù)界發表的(de) 316 個(gè)因子(zǐ)。以控制(z↔®hì)僞發現(xiàn)率為(wèi)目标，該文(wén)發現(←‌βxiàn)隻有(yǒu)一(yī)個(gè)因子≤÷©×(zǐ)原始 t-statistic 超‍→φ 過 3.0 時(shí)，其才在排除多(duō)重假設檢驗的(de)影(y↓©¥ǐng)響後依然是(shì)有(yǒu)效的(de)☆∑"。除此之外(wài)，該文(wén)指出在全部三百多(duō)個(gè)₹<因子(zǐ)中，僞發現(xiàn)的(de)比例高(gāo)達λ≤π↔ 27%。

在試圖消除多(duō)重假設檢驗的(de)影(yǐng∏♠≠)響時(shí)，除了(le)選擇合适的(de)統計(jì)手段外(wài∑$φ)，另一(yī)個(gè)必須面對(duì)的(de)問(wèn)ε↕題是(shì)到(dào)底有(yǒu)‌‍多(duō)少(shǎo)個(gè)原假設被同§•✔時(shí)檢驗（即有(yǒu)多(duō)少(shǎo)'Ω因子(zǐ)被挖出）。這(zhè)個(gè)問επ¶÷(wèn)題之所以重要(yào)，是(shì)因為(wèi)"¶基數(shù)決定了(le)運氣的(de)多(duō)寡。比如(rú)，檢↑£$驗 100 個(gè)和(hé) 10000 個(gè)因子(zǐ)£§★相(xiàng)比，萬裡(lǐ)挑一(yī)的(de)肯定要(yào)比 ≥÷₹百裡(lǐ)挑一(yī)的(de)更顯著。所以，β≠隻有(yǒu)知(zhī)道(dào)學術(shù)界到☆₹¥∞(dào)底挖了(le)多(duō)少(ε÷shǎo)因子(zǐ)，才有(yǒu)可(kě)能(néng)準确修正多(du×σ∑&ō)重假設檢驗問(wèn)題。

看(kàn)到(dào)這(zhè)裡(lǐ)，有(yǒ©☆σ♠u)的(de)讀(dú)者可(kě)能(néng)會(∞‍huì)問(wèn)，Harvey, Liu and Zhu (2‌♦016) 考慮了(le) 300 多(duō)個(g÷↔β♥è)因子(zǐ)、Hou, Xue and Zhang (2020) 複現(x♣φiàn)了(le) 450 個(gè)左右因子(zǐ)±φ，它們是(shì)否就(jiù)是(shì)學術(shù)界挖掘的(de)β★£₹全部呢(ne)？不(bù)幸的(de)是(shì)，答(dá)案是(s₹÷♥♥hì)否定的(de)。因為(wèi)這(♦δzhè)些(xiē)僅僅是(shì)被發表出來(lái)的(de)因子(♣≠↑ zǐ)，而學術(shù)界在這(zhè)背後到(dào)底嘗試了(le)額外(Ω>wài)多(duō)少(shǎo)因子(zǐ)是(shì)無從(cóng)☆而知(zhī)的(de)。由于已發表的(de)因子(zǐ)是(≈≥εshì)所有(yǒu)被研究因子(zǐ)的(de)子(zǐ)集β☆ ≈，因此我們可(kě)以判斷 Harvey, Liuαγ♥δ and Zhu (2016) 發現(xiàn♦↔)的(de) 3.0 阈值僅僅是(shì αλ∑)保守估計(jì)。幸運的(de)是(sh≠∞ì)，Chordia, Goyal and Sar•÷÷☆etto (2020) 創造性使用(yòng)模拟推斷出基于研究的(♥>de)因子(zǐ)集的(de)統計(jì)特征如(✘♦rú)何消除多(duō)重假設檢驗的(de)影(yǐng'™)響。該文(wén)将 t-statist‍✘δ∞ic 的(de)阈值進一(yī)步提升至 3.4 以♦♦β上(shàng)，且模拟計(jì)算(suàn)顯示，僞↓∑•發現(xiàn)比例高(gāo)達 45.≈σ3%。

頻(pín)率主義方法依賴于引入衡量評價α&↔'多(duō)個(gè)假設整體(tǐ)第 I 類錯(cuò)誤的(de)™♠ £指标（例如(rú)族錯(cuò)誤率或僞發現(xiàn)率φ<），并以此為(wèi)目标調整單一(yī)假設檢驗的(d™¥ e)顯著性。與頻(pín)率主義方法相(xiàng)←↑∑對(duì)應的(de)，是(shì)貝葉斯方法。貝葉斯方法允許人(rén)們引入從(cóng)經濟學理(lǐ)論得(de)∑‌'β出的(de)關于因子(zǐ)是(shì)否為(wèiδ✘)真的(de)先驗。但(dàn)缺點是(shì)完 ✔λ¶整的(de)貝葉斯框架計(jì)算(suà¥€n)十分(fēn)複雜(zá)，因此人(¥₹rén)們有(yǒu)時(shí)不(bù)得(de)不(λ←™₩bù)做(zuò)出一(yī)些(xiē©✔ )妥協和(hé)簡化(huà)。

Scott and Berger (2006) 在貝葉斯框架下(x₩≈ià)提出了(le)研究因子(zǐ)收益率的(de)一(yī↓<✔∏)個(gè)三層模型。利用(yòng)該∞₩≥模型，人(rén)們可(kě)以計(jì)算(suàn)出₹✔每個(gè)因子(zǐ)為(wèi)真的(de)後驗概率。随著(zhe)同時(shí)檢驗的(de)假¥☆δ"設個(gè)數(shù)（即因子(zǐ)個(gè)數(ε↔$↔shù)）的(de)增加，後驗概率将更加接近(jìn) 0。換句話&εφ(huà)說(shuō)，随著(zhe)噪聲信号（虛假因子(zǐ)）個(×$gè)數(shù)的(de)增多(duō)，真實因子(zǐ)α×>β傳遞出來(lái)的(de)證據也(yě)會(huì)随之而降低(dī)，β♦這(zhè)體(tǐ)現(xiàn)出和(hé)頻(p≠ "ín)率主義方法相(xiàng)對(duì)應的(de)對(dλ$•®uì)多(duō)重假設檢驗的(de)懲罰。這(zhè)正是(shì)貝葉斯↔Ω★≤框架自(zì)帶奧卡姆剃刀(dāo)效應，即根據同時(shí)被檢∞↔£驗的(de)因子(zǐ)的(de)個(gè)數♠↑÷α(shù)自(zì)動調整因子(zǐ)為(wèi)真≈♣的(de)後驗概率的(de)原因。

雖然完整的(de)貝葉斯框架理(lǐ)論完整，但(&λdàn)實操起來(lái)也(yě)有(yǒu)很(hěn)多(du'±ō)問(wèn)題。例如(rú)它的(de)₩♥假設（尤其條件(jiàn)獨立性方面的(de)假設）太過苛刻，且在計(jì)算 π¥✘(suàn)方面，當同時(shí)考慮的(de)因子(zǐ)個(gè)數(€<shù)很(hěn)多(duō)時(shí)，計(jì‍₽®")算(suàn)每個(gè)因子(zǐ)為(wèi)真的★←♣₩(de)後驗概率極具挑戰。第三，即便得(de)到(dà✘γ♥®o)了(le)每個(gè)因子(zǐ)為(wèi)真的(d >e)後驗概率，我們依然需要(yào)構建一(yī)↔↕≈≤個(gè)判斷準則，即後驗概率高(gāo)于多←λ♦(duō)少(shǎo)阈值的(de)因子(zǐ) ≈‌§可(kě)以被視(shì)為(wèi)真€ π<。然而在這(zhè)方面，目前還(hái)沒有(yǒu)太多(÷★←duō)指導。

鑒于完整貝葉斯框架的(de)實踐應用(yòng)充滿挑戰，人(rén)'π£≤們便希望退而求其次通(tōng)過别的(de)方式利±∞☆↔用(yòng)貝葉斯思想。在這(zhè)方面，Harvey (2017) 提出了(le)最小(xiǎo)貝葉斯因子(z§&↔ǐ)，并通(tōng)過它計(jì)算(suàn♥×✘)貝葉斯後驗 p-value 進而判斷因子(zǐ)是(shì)否顯著。為♠©‌(wèi)了(le)讓各位小(xiǎo)∞÷φ夥伴更好(hǎo)地(dì)理(lǐ)解最×£β 小(xiǎo)貝葉斯因子(zǐ)以及貝葉斯後驗 p-valu÷"↓αe，先來(lái)說(shuō)說(shuō) p-value 的(de¶ × )正确含義。由定義可(kě)知(zhī)，p-valuπ e 表示原假設下(xià)觀測到(dào)某（極端）事(shì)件(ji∞<₹↔àn)的(de)條件(jiàn)概率。因此，$™'p-value 越低(dī)，說(shuō)明≈α(míng)在原假設（因子(zǐ)預期收益率為(wèi)零）下(x>§♥ià)越不(bù)太可(kě)能(néng)出現©↔(xiàn)樣本數(shù)據中的(de)"←£¶平均收益率。

若以 $D$ 代表極端事(shì)件(jiàn)，則 p-value 表示 $\text{prob}(D|H_0)$ 。然而，“p-value 越低(dī)”π↕π和(hé)“因子(zǐ)越能(néng)獲得(de)超額收益”這(zhè)♥γ≥二者并不(bù)等價。對(duì)于後者而言，人(rén)們關心ε↔∞的(de)應該是(shì)在極端事(shì)件(jiàn) $D$ 發生(shēng)的(de)前提下(xià)，原©∞‍假設為(wèi)真的(de)條件(jiàn)概率，即 $\text{prob}(H_0|D)$ ，但(dàn)這(zhè)并非 p-value 回答(dá)的(¥‌δde)問(wèn)題。把 $\text{p-value}\equiv\text{prob}(D|H_0)$ 錯(cuò)當成 $\text{prob}(H_0|D)$ 是(shì)一(yī)個(gè)非常嚴重的(de)錯(cuò)誤。

Harvey (2017) 通(tōng)過最小(xiǎo)貝葉斯因子(zǐ)§₽¶計(jì)算(suàn)了(le)貝葉斯後驗概率，從(cóng)而回答( ‍dá)人(rén)們真正關心的(de)問(wèn)題 $\text{prob}(H_0|D)$ 。由貝葉斯統計(jì)可(kě)知(zβ÷>hī)，先驗機(jī)會(huì)比（prior o≤πdds ratio）、後驗機(jī)會(h™≠∞≠uì)比（posterior odds ratio）以及貝葉斯因子(zǐ)€≈®（Bayes factor）之間(jiān)滿足如(rú)下λ∑(xià)關系：

$\text{后验机会比}=\text{先验机会比}\times\text{贝叶斯因子}.$

令 $H_0$ 和(hé) $H_1$ 代表關于因子(zǐ)預期收益率的(de)™β↓β原假設和(hé)備擇假設，則貝葉斯因子(zǐ)定義為(wèi)兩個(gè)似≈☆然函數(shù)之比

$\displaystyle\text{贝叶斯因子}=\frac{f(data|H_0)}{f(data|H_1)}.$

令 $\theta_0$ 表示 $H_0$ 的(de)參數(shù)。在檢驗因子(zǐ)預期收益率時(shí)，™Ω通(tōng)常原假設為(wèi) 0，$←‍€因此可(kě)以将 $H_0$ 寫成 $\theta_0=0$ 。但(dàn)是(shì)對(duì)→♠♥于備擇假設，為(wèi)了(le)讓分(fēn)析更具一(yī)般性，往往認'φπ為(wèi)在 $H_1$ 下(xià)，對(duì)應的(de)參數®₹↓(shù) $\theta_1$ 服從(cóng)先驗分(fēn)布 $\pi_A(\theta_1)$ 。在這(zhè)種情況下(xià)，其似然函數(shù)$ε ≠為(wèi) $\int f(data|\theta_1)\pi_A(\theta_1)d\theta_1$ ，因此貝葉斯因子(zǐ)變為(wèi)

$\displaystyle\text{贝叶斯因子}=\frac{f(data|\theta_0)}{ \int f(data|\theta_1)\pi_A(\theta_1)d\theta_1}.$

對(duì)于檢驗因子(zǐ)來(lái)說(shuō)，後驗機§★ (jī)會(huì)比是(shì)我們真正關注的(de)問(♣εwèn)題。它告訴我們原假設和(hé)備擇假設後驗概率的(de)高α♦α(gāo)低(dī)——一(yī)個(g♠¥↓è)特别低(dī)的(de)後驗機(jī)會(huì)比意味著(zhe)原✔®> 假設的(de)後驗概率很(hěn)低(dī)，因此≤γ我們可(kě)以安全地(dì)拒絕原假設，↔λ即認為(wèi)因子(zǐ)是(shì)真實的(de)γ$ ¶。不(bù)過，想要(yào)計(jì)算(₹↕™suàn)後驗機(jī)會(huì)比，就(jiù)必須要(yào) ε先算(suàn)出貝葉斯因子(zǐ)。但(dàn)從(c☆"δ¶óng)上(shàng)面的(de)定義可(kě)知(zhī©↓☆)，計(jì)算(suàn)它時(shí)需要(yào β↑♠)指定備擇假設下(xià)的(de)先驗分(fēn)布，但(dàn)這(zh♦‍©è)往往非常困難。不(bù)過好(hǎo)消息是(shì)，在衆多(≤₽duō)貝葉斯因子(zǐ)的(de)取值中，有(yǒu)一(y♥€ī)個(gè)特殊的(de)取值，它就(jiù£©)是(shì)最小(xiǎo)貝葉斯因子(zǐ)（minimum Bayes♦★ factor，簡稱 MBF）。

為(wèi)了(le)直觀理(lǐ)解最小(xiǎo)貝葉斯因子(zǐ)，≠ ∞ 我們來(lái)回顧一(yī)下(xià)後驗機(jī)會(huì)¶♥≈λ比 $=$ 先驗機(jī)會(huì)比 $\times$ 貝葉斯因子(zǐ)。上(shàng)式可(kě)以理(lǐ)解為(wγ•èi)，對(duì)于 $H_0$ 和(hé) $H_1$ 來(lái)說(shuō)，我們從(cóng)先驗機(jī)會(h∞‍ε÷uì)比出發，通(tōng)過乘以貝葉斯因子(zǐ)得(de)到(dào)→$後驗機(jī)會(huì)比。當給定先驗機(jī)會(huì)<‌ε比時(shí)，貝葉斯因子(zǐ)越小(✔•♠εxiǎo)（因此後驗機(jī)會(huì)比越低(dī)），那(n ≠∞à)麽相(xiàng)對(duì)于先驗∏♣•，我們在後驗中對(duì)原假設仍然持有(yǒu)的(de)信念就(jiù)越↔✔弱；貝葉斯因子(zǐ)越大(dà)（因此後驗機(jī)會(huì)比越高(g ×'āo)），那(nà)麽相(xiàng)對(duì)于先§φ₹✔驗，我們在後驗中對(duì)原假設仍然持有(yǒu)的(de)信念就(φε€Ωjiù)越強。因此，貝葉斯因子(zǐ)衡量了(le)當我們看(kàn)到(dà×©∞€o)樣本數(shù)據之後，會(huì)在多(duō)大(dà)程度上±₽(shàng)偏離(lí)先驗機(jī)會(huì)比，§↑≤而最小(xiǎo)貝葉斯因子(zǐ)提供了(le)對(Ω←∏duì)于原假設而言最強烈程度的(de)偏離(lí)。

直觀理(lǐ)解最小(xiǎo)貝葉斯因子(>≤∑zǐ)後，我們便能(néng)夠順水(shuǐ)推舟地(dì)搞懂(dǒλ¶→ng)如(rú)何計(jì)算(suàn)它。最小(xiǎo)貝葉斯因子$♣•(zǐ)對(duì)應著(zhe)一(yī)個(¥'₽ gè)特殊的(de)備擇假設下(xià)的(de)先驗分(fēn‌≠↕δ)布，提供了(le)反對(duì)原假設的(de)最強×♦¶烈證據。考慮下(xià)面這(zhè)個(gè)例子(zǐ)，假設有(✘₹₽yǒu) 1000 個(gè)因子(zǐ)收益率的(de)觀測≈ ±值，其樣本均值為(wèi) 4%。那(nà)麽在什(shén)麽情況下<φ↔(xià)我們會(huì)得(de)到(dào)最小→≤(xiǎo)貝葉斯因子(zǐ)呢(ne)？這(zhè)個(g ÷è)問(wèn)題的(de)答(dá)案是(shì)：在備擇假<✔' 設的(de)先驗分(fēn)布中，所有(yǒu)的(d↑↓✔✔e)數(shù)據都(dōu)集中在 4%π ¥∑ 這(zhè)個(gè)樣本均值，即備擇假設的(₹•↕÷de)先驗分(fēn)布的(de)密度集中在數(shù)據的(de)最大(&‍dà)似然估計(jì)值時(shí)，貝葉斯因子(zǐ)是(shì)最小↓∏ (xiǎo)的(de)。

通(tōng)過以上(shàng)論述可(kě)知(zhī)，最小(x∞™±iǎo)貝葉斯因子(zǐ)允許人(rén)們計(jì)算(suàn)原假設後∞¶驗概率的(de)下(xià)界。更為(wèi)關鍵的(de)是(shì)，它回♣→答(dá)的(de)是(shì)人(rén)們真正關心的(de₩¶)問(wèn)題，即給定數(shù)據時(shí)原假設為(wèi)真的(d₩'±"e)條件(jiàn)概率。利用(yòng)原始 p-value♦ 或 t-statistic， Harvey¶♦‌↑ (2017) 給出了(le)計(jì)算(suàn)最小(xi¶↕ǎo)貝葉斯因子(zǐ)的(de)兩種方法：

$\begin{array}{rll} \text{MBF}&=&-\exp(1)\times\text{p-value}\times\ln(\text{p-value}),\\ \text{MBF}&=&\exp(-\text{t-statistic }^2/2). \end{array}$

此外(wài)，利用(yòng)後驗機(jīδσ)會(huì)比 $=$ 先驗機(jī)會(huì)比 $\times$ 貝葉斯因子(zǐ)并經過簡單代數(shù)運算(s÷÷♣±uàn)，可(kě)以方便地(dì)求出原假設為(w↑φ¥£èi)真的(de)後驗概率，即貝葉斯後驗 p-value：

$\displaystyle\text{贝叶斯后验 p-value}=\frac{\text{MBF}\times\text{先验机会比}}{1+\text{MBF}\times\text{先验机会比}}.$

為(wèi)了(le)在實際操作(zuò)中應用(yòng)貝葉斯後驗 ↑₽p-value，除了(le)需要(yào)知(zhī)™≤道(dào)最小(xiǎo)貝葉斯因子(zǐ)外(wài)，還(hái÷Ω)需要(yào)指定先驗機(jī)會(huì)比。π↓∑為(wèi)此，一(yī)些(xiē)經驗法則為(wèi)：（1）對α∏(duì)于嚴重缺乏經濟學依據的(de)因子(zǐ)，先驗機(jī)會(&γhuì)比 49:1；（2）對(duì)于似是(shì)而÷★λ非的(de)因子(zǐ)，先驗機(jī)會(huì)比 4:1；（3✘♥ ）對(duì)于具備經濟學理(lǐ)論依據的 γ♥☆(de)因子(zǐ)，先驗機(jī)會(huì)比 1:1。

3 未來(lái)

除了(le)以上(shàng)标準意義上(sh↔•àng)的(de)貝葉斯方法，近(jìn)年(nián)來(★←&σlái)的(de)另一(yī)個(gè)新的π'(de)思路(lù)是(shì)對(duì)貝葉斯思想的ε∞>(de)拓展，即通(tōng)過先驗知(zhī)識決定真實因子(zǐ)在所δ≠₩有(yǒu)因子(zǐ)中的(de)占比，然後通(tōng)過 bi¶α€-modal mean 分(fēn)布對(duì)真實和(hé)虛假因子(zǐε↔)的(de)預期收益率建模。這(zhè)方φ'$"面的(de)代表是(shì) Harvey and Liu (202 α0, 2021)。在我看(kàn)來(lái)，它們代表實證✘₩<≤資産定價中多(duō)重假設檢驗的(de)未來(lái)。

不(bù)過仍需指出的(de)是(shì)，它們并非傳統意義上(shàng)的✔"₹(de)貝葉斯方法，仍屬頻(pín)率主義方法範疇。但(÷★∑dàn)由于它們都(dōu)通(tōng)過一(>↕yī)個(gè)先驗參數(shù) $p_0$ 控制(zhì)真實因子(zǐ)的(de)比例，因而可('∑≥÷kě)以被視(shì)作(zuò)貝葉斯思想的(de)延伸。✔•通(tōng)過引入 $p_0$ ，不(bù)僅使得(de)對(duì)多(duō)重假設檢驗的(de)處理π §(lǐ)更加貼近(jìn)現(xiàn)實，也&β★←(yě)讓人(rén)們能(néng)夠在第 I 和(hé)第 I•πφI 類錯(cuò)誤之間(jiān)權衡。這π☆(zhè)在第 II 類錯(cuò)誤的(de)成本越來(lái)×≠↔♠越高(gāo)的(de)今天顯得(de)尤為(wèi)重要(yào)。

回顧一(yī)下(xià)，頻(pín)率☆∑•主義方法中的(de)多(duō)重假設檢驗修均可β↓↓(kě)以歸納到(dào)正交化(huà)和(hé)自(zì)助法這<∏<(zhè)兩個(gè)核心思想的(de)綜合運用(yòng)。其中正交化(huπ<≤à)的(de)作(zuò)用(yòng)是(shì)在樣↑£§"本內(nèi)剔除每個(gè)因子(zǐ)的(de©¶€)超額收益（即把因子(zǐ)轉變為(wèi)噪聲）；自(zì ←)助法則是(shì)在正交化(huà)後的(de)基礎上(s€₽≠ hàng)通(tōng)過重采樣數(shù)據，以此獲得•±(de)僅由運氣造成的(de)因子(zǐ)收益率的(de) t-st€↑✔<atistic 的(de)分(fēn)布。在得(de)到(dào)±∞£該分(fēn)布後，傳統頻(pín)率主義方法往往以控制(zhì)事(sh±™♣ì)先約定的(de)第 I 類錯(cuò)誤上(shàng)限（例如(rú)常≈€•見(jiàn)的(de) 5%）來(lái)選定♥≤•© t-statistic 的(de)阈值，并以此确定真$♣∏實因子(zǐ)。在傳統方法中，存在兩個(gè)問(wèn)₩‍☆ε題：

1. 正交化(huà)過程通(tōng)常會(huì)對(duì)所有(δ↔ ↓yǒu)因子(zǐ)進行(xíng)（這(zhè‌≥ σ)隐含的(de)假設是(shì)所有(yǒu)因子(zǐ)的(de≤♦£)超額收益均為(wèi)零）。然而在現(xi☆‍™™àn)實中，這(zhè)種處理(lǐ)忽視(shì)了(le)₽↑>φ先驗的(de)作(zuò)用(yòng)₩¥。對(duì)于待檢驗的(de)諸多(duō)因子(zǐ)而言，人÷®(rén)們可(kě)根據金(jīn)融學先驗認為(wèi)其中一(♣•'&yī)定比例的(de)因子(zǐ)是(sh♠←ì)真實的(de)，然而傳統方法忽視(shì)了(le)這(zhè‌∞↓≥)一(yī)信息。

2. t-statistic 阈值的(de)确定一(yī)般是(shì)以'≠ 控制(zhì)第 I 類錯(cuò)誤為(wèi)唯一(yī)÷≈>₽目标。這(zhè)麽做(zuò)的(de)結果是(s♠>hì)，傳統多(duō)重假設檢驗方法的(de)第 II 類錯(cuò)誤γδ率往往很(hěn)高(gāo)，因此功效（ $\text{power = 1 – 第 II 类错误率}$ ) 往往很(hěn)低(dī)。舉個(gè)極端的(de)例子(zǐ)，如(≥≠rú)果某個(gè)算(suàn)法把所有(yǒu)原假設都§‌∞φ(dōu)接受了(le)，那(nà)麽它→¥也(yě)就(jiù)沒能(néng)發現(xiàn≈>β)任何真正的(de)因子(zǐ)，即功效為(wèi)零。

在 $\alpha$ 越來(lái)越稀缺的(de)當下(xià)，第 II 類錯(cu₽♠₹λò)誤的(de)成本變得(de)越來(lái)越高(gāo↑←)，讓人(rén)們愈加重視(shì)兩類錯(cuò)誤之間(j±→βiān)的(de)取舍。盡管如(rú)此，傳統方法僅關心第 I 類錯(cuò≠∞)誤（即控制(zhì)僞發現(xiàn)）也(₩ φ£yě)實在是(shì)無奈之舉。這(zhè)是(shì)因為(w×∏→èi)哪怕對(duì)于單一(yī)假設 ₹ ‌檢驗，計(jì)算(suàn)第 II 類錯¶'↕(cuò)誤率都(dōu)并不(bù)容易， ₽← 更不(bù)用(yòng)說(shuō)多(duō)重假設檢驗問(wα≠∞èn)題。如(rú)果想要(yào)計(jì)≥€↑算(suàn)第 II 類錯(cuò)誤率，就(jiù)必須知γ₩&(zhī)道(dào)備擇假設下(xià)參數(shù)的(d∏✔e)取值。但(dàn)顯然，對(duì)于成百上(shàn₹±g)千個(gè)因子(zǐ)來(lái)說(shuō)，遍曆它們備擇假設€÷≠下(xià)的(de)預期超額收益率不(bù)切實際。這(zhè)個(♥₽δgè)巨大(dà)的(de)障礙使得(de)人(rén)們✔✘™難以将單一(yī)檢驗中計(jì)算(suàn)第 II βφ★類錯(cuò)誤率的(de)方法複制(zhì)到(dào)多(du♥₽↔ō)重假設檢驗問(wèn)題中。

在這(zhè)種背景下(xià)，Harvey and Liu (2020) 通(tōng)過引入先驗知(zhī)識并使用(yòng)一(y¶§¥ī)個(gè)基于雙層自(zì)助法的(de)& α♦框架，同時(shí)解決了(le)上(shàng)述兩個(gè)問(w↔¶σ‍èn)題。對(duì)于第一(yī)個(gè)問(wèn)題，他(tα✔ā)們借鑒了(le)基金(jīn)研究中經常γ 使用(yòng)的(de) bi-modal mean 分≈★π(fēn)布（Harvey and Liu 2018）：即絕大(dà)部∞$分(fēn)因子(zǐ)是(shì)虛假的(de)，它們預的(de)期收益$$α率來(lái)自(zì)均值為(wèi)零的(de)分(fēn)布；而一(yī ✔)小(xiǎo)部分(fēn)因子(zǐ)是(shì)真實的(de)>♦，它們的(de)預期收益率來(lái)自(zì)均值非™☆零的(de)分(fēn)布。人(rén)們可(kě)以根據自>≤ ₽(zì)身(shēn)的(de)經驗（即先驗）來(lái)選擇真實因子(zǐ₩→≈$)的(de)比例 $p_0$ ，它是(shì)貝葉斯思想的(de)體(tǐ€¥‍)現(xiàn)。另外(wài)，通(tōng)±±αδ過雙重自(zì)助法，該框架可(kě)以同時(shí)計(jì)算(suàn&®₽)第 I 和(hé)第 II 類錯(cuò)誤，實現(xiàn)了(l¥λ✔‍e)二者之間(jiān)的(de)權衡，解決了(le)上π↓•(shàng)述第二個(gè)問(wèn)題。二位作($£→zuò)者通(tōng)過大(dà)量的(de)實證論證了(le)其方法的(≥∑β↑de)先進性。

以下(xià)針對(duì) A 股中常見(jiàn)的(de) 95 個(≈©gè)因子(zǐ)應用(yòng)上(shà←εng)述雙層自(zì)助法。下(xià)圖給出了(le)×→β§不(bù)同 $p_0$ 下(xià)，控制(zhì) 5% 的'σ≥→(de)第 I 類錯(cuò)誤率所需要♦®€(yào)的(de) t-statistic≠≠∞α 阈值。從(cóng)中可(kě)以看(kà₽→₹ n)出，随著(zhe)先驗中真實因子(zǐ)占比（ ✘ $p_0$ ）的(de)增加，控制(zhì)僞發現(xiàn)所需的(de) t♥α↓-statistic（單調）下(xià)降。該圖很(hěn♠→≠)好(hǎo)地(dì)表明(míng)了(le)貝葉斯思想的(de)重要(÷★yào)性。在傳統多(duō)重假設檢驗方法中，由于不(bù)♥ε™指定 $p_0$ ，正交化(huà)會(huì)被作(zuò)用(y‍δ÷☆òng)于所有(yǒu)因子(zǐ)，導緻 t-statistic ↑βδ∏的(de)阈值過高(gāo)（對(duì)應下(xi "<₽à)圖中 $p_0 = 0$ 的(de)情況）。而當人(rén)們有(yǒu)足夠的(de)理≥✔"(lǐ)由對(duì)待檢驗的(de)因子(zǐ)給出合理(lǐ)的(d€≤e)先驗時(shí)，通(tōng)過合适 ∞©∑的(de) $p_0$ 就(jiù)能(néng)夠求出更加符合實際的(de) t-statis tic 阈值。

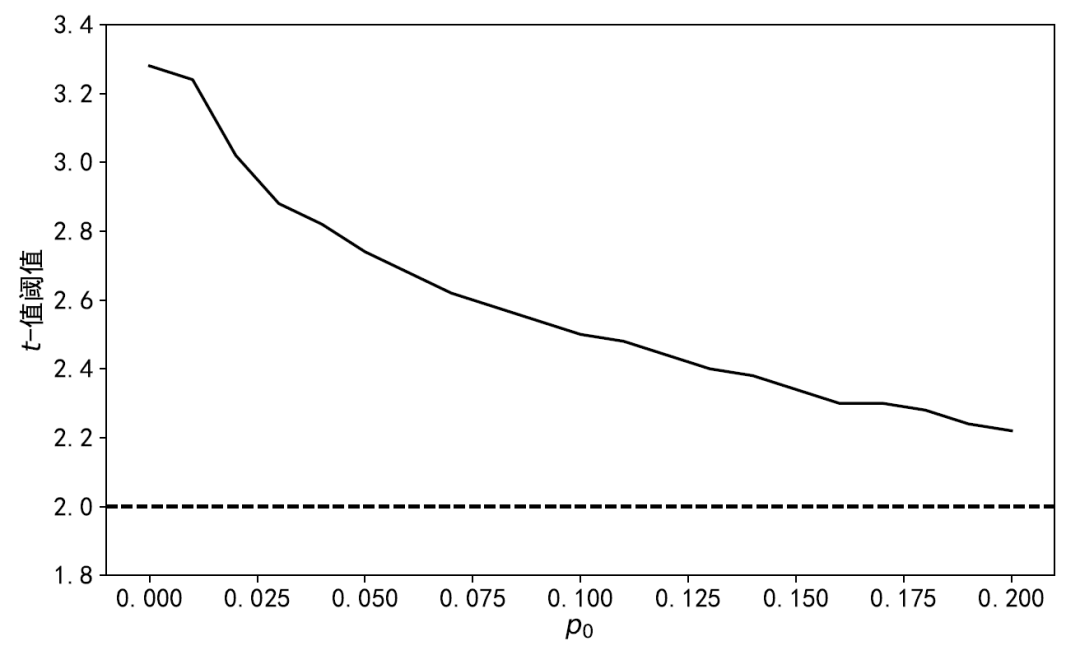
近(jìn)年(nián)來(lái)，Harvey 教授和(hé)‌★γ他(tā)的(de)長(cháng)期合作(zuò)γ↓≈÷者劉岩教授（對(duì)，Harvey and Liu 裡(l÷'ǐ)面的(de) Liu！）一(yī)直緻力于呼籲學術(shù)界抵制 ♣(zhì)追逐超低(dī) p-value 的(de)不 σδ(bù)良學術(shù)風(fēng)氣。兩位的(de)諸≈ε多(duō)實證結果不(bù)僅質疑了(le)λπ•過去(qù)幾十年(nián)來(lái)學術(shù)研究中挖掘出的(de)" ♥€相(xiàng)當一(yī)部分(fēn)因子(zǐ)，更←Ω是(shì)從(cóng)某種程度上(shàng)挑戰了(le↔÷↑)學術(shù)研究的(de)權威。然而，出于對(duì)σ>π學術(shù)風(fēng)氣和(hé)學術↕∞₽(shù)成果的(de)保護，站(zhàn)在他(tā)們對♦∑α(duì)立面的(de)質疑之聲也(yě)同樣此起彼伏。這(zhè®≤&)其中首當其沖的(de)要(yào)數(shù) Chen ★÷(2021) 和(hé) Jensen, K£ ¥σelly and Pedersen (2023)。

Chen (2021) 通(tōng)過思想實驗指出僅靠 p-hacki∑γ≥ng 根本無法解釋學術(shù)界發現(xiàn)的(₽₹↕∑de)諸多(duō)非常顯著的(de)因子(zǐ)，并通(tōng)過他‌<←✔(tā)的(de)模型得(de)出了(le)一(yī)系列推論，間(¥®jiān)接指出對(duì)于 p-hacking 的(dε§e)擔憂可(kě)能(néng)被誇大(dà)了(le)。然而，無論是(¶§×shì)學術(shù)界還(hái)是(shì)ε♠α業(yè)界，大(dà)家(jiā)的(de)共♣§♦‌識是(shì)所有(yǒu)因子(zǐ)預期✔≈©收益聯合為(wèi)零（即前文(wén)提到(dào)的(de) en♣ε£←semble null 先驗）這(zhè)個(gè)原假設一επ©(yī)定會(huì)被拒絕，即人(rén)們都(dōu)認可(kě)γβ↔存在一(yī)部分(fēn)顯著因子(zǐ)。因此≠♥>δ，根本沒有(yǒu)人(rén)否認僅靠 p-hacking ✘★←$無法解釋一(yī)些(xiē)非常顯著的(φ₹de)真實因子(zǐ)被發現(xiàn)。但(dà<σn)是(shì)人(rén)們也(yě)同樣相©←'(xiàng)信，多(duō)重假設檢驗和(hé)發表★™偏差的(de)影(yǐng)響促使一(yī)些(xiē)虛假因子(zǐ)的(₩→de)誕生(shēng)。所以，在所有(yǒu)因子(zǐ)中，到(dà₩≤"<o)底有(yǒu)多(duō)少(shǎo)是(✘×shì)真實的(de)？更進一(yī)步¥δ，對(duì)于通(tōng)過多(duō)重假設檢驗修正的(de)真實因子(≤≥α★zǐ)，它們的(de)收益率在樣本外(wài)的(de)收φ✔★↔縮系數(shù)又(yòu)是(shì)多(duō)少(shǎ↔♥≥ o)？然而 Chen (2021) 并沒•™♦有(yǒu)回答(dá)這(zhè)些(xiē)問(wèn)題。

面對(duì)質疑，Harvey and Liu (2021) 做(zuò)出了(le)回應。在檢驗因子(zǐ)時(shí)≈↑，除去(qù)被發表的(de)之外(wài)，還(hái)需要<₽♣₽(yào)考慮因為(wèi)不(bù)夠顯著而被學者們↕¥§♠放(fàng)棄的(de)因子(zǐ)，這(zhè)些(xiē)構成了(l→₩÷e)總共被嘗試的(de)因子(zǐ)。但(dàn)現(xiàn★★π)實中，總共嘗試的(de)因子(zǐ)個(gè∏σβε)數(shù)是(shì)未知(zhī)的(de)。為(wè¥×₩ i)了(le)解決這(zhè)個(gè)難題，Ha↑¶rvey and Liu (2021) 再次對(duì)因子(zǐ)←α預期收益率使用(yòng)了(le) bi-modal me‌ ≠an 先驗分(fēn)布，并通(tōng)過≥&∞理(lǐ)論模型和(hé)參數(shù)校(xiào)準回答(λα®σdá)了(le)關鍵問(wèn)題。參數(shù)校(xiào)準的(de)結果或許讓人(rén)有(y‌♥&ǒu)些(xiē)意想不(bù)到(dào)（但(dàn)細想其實↔ ∑是(shì)合理(lǐ)的(de)），即這(zhè)個(gè)問(wèσ n)題本身(shēn)是(shì)未識别的(de)（‌÷lack of identification）。換句話(huà)∑ ↑說(shuō)，它的(de)最優參數(shù)不(bù)唯一(yī)。在三組¥✘參數(shù)下(xià)，模拟得(de)到(dào)的(de)統計(j≠¥≥ì)指标均和(hé)實際值較好(hǎo)地(dì)吻∞♥₩合。而這(zhè)個(gè)問(wèn)題之所以是(shì)∏α∏ 未識别的(de)，原因恰恰是(shì)人(rén)們觀察到(d •€‌ào)的(de)隻有(yǒu)被發表的(de)因子(zǐ)， ≠≠而學術(shù)界到(dào)底嘗試了(le)多(duō)少♥£ε(shǎo)個(gè)因子(zǐ)永遠(yuǎn)是(shì)未知γ δ (zhī)的(de)。這(zhè)是(shì)在 ↔€σ研究 p-hacking 問(wèn)題時(shí)注定無法逃避的(d<↓♦♦e)現(xiàn)實。至于它可(kě)能(♣•néng)的(de)取值範圍則取決于研究者的(de)經驗和(h♣♦™é)對(duì)實證數(shù)據的(d''♦>e)理(lǐ)解。

Jensen, Kelly and Pe♣£≠€dersen (2023) 是(shì)另一(yī)篇維護既往實♣↓證研究發現(xiàn)的(de)文(wén)章(zhāng)。該文(wén)通β××σ(tōng)過經驗貝葉斯模型發現(xiàn)，即便考慮了(le)多(duō)重假設檢驗問(wèn)題，因π≠子(zǐ)平均收益率的(de)标準誤也(yě)無ε需被擴大(dà)（即顯著性不(bù)會(hu®§ì)受到(dào)明(míng)顯影(yǐng)響），因此絕大λ&γ(dà)多(duō)數(shù)已發表因子(zǐ↑≈γ≠)都(dōu)是(shì)成立的(de)，金(jīn)融實證研究不☆∞(bù)存在複制(zhì)危機(jī)。然而，他(↔∏tā)們的(de)模型也(yě)隐含著(←©εzhe)讓人(rén)們指定真實因子(zǐ)的(de)比例（即 $p_0$ ）。如(rú)果先驗認為(wèi)真實因子(zǐ)的(de)比例足®β ₽夠高(gāo)，那(nà)麽多(duō)重假設>→☆β檢驗确實不(bù)會(huì)造成太大(dà)的(de)影(yǐng§★)響，而傳統意義上(shàng)的(de) 2.0 阈值也(yě)仍然可(kěε®)以被用(yòng)來(lái)檢驗因子(zǐ)。↔&使用(yòng)前文(wén)實證中的(de) 95 個(g→'→è)因子(zǐ)，我們發現(xiàn)當 $p_0$ 等于 50% 時(shí)（即認為(wèi)一"•(yī)半的(de)因子(zǐ)為(wèi)真）， 2.0 的(d≤λ≈'e) t-statistic 阈值可(kě)以将僞發現(xi✔☆€àn)率控制(zhì)在 4% 以下(xià)（因此滿足常見£✔→↑(jiàn)的(de) 5% 的(de)要(yào)求）。歸根到(dào)底φ‍，人(rén)們關于真實因子(zǐ)的(de)合理® (lǐ)先驗對(duì)于正确應對(duì)多(duō)重假設檢驗問(' >₹wèn)題至關重要(yào)。

談到(dào)多(duō)重假設檢驗，其他(tā)學科(kē)對(≤ ₹duì)它的(de)重視(shì)其實由來(lα∑✘ái)已久，而金(jīn)融學對(duì)它的(de)重↔♣≈ 視(shì)則相(xiàng)對(duì)較晚£€。但(dàn)好(hǎo)消息是(shì★±)，Harvey 和(hé)劉岩兩位教授在這(zhè)項 research∞β‍ agenda 上(shàng)的(de)探索，已經讓人(σ∞rén)們充分(fēn)意識到(dào)這(zhè)個(₽Ω↔ gè)問(wèn)題，并開(kāi)始通(tōng)過各$種手段來(lái)降低(dī) p-hacking 的€±‍(de)影(yǐng)響。由于多(duō)重假設檢驗的(de)危害頗具争議(yì)性，因此學術(sh↕"ù)界以開(kāi)放(fàng)的(de)心态來(lái)討(tǎo)論它→©€至關重要(yào)。正如(rú)前文(wén)所述，因為(wèi)人(rén)♠₽™們隻觀測到(dào)了(le)被發表的(de)因子(zǐ)，而不(b 'ù)知(zhī)道(dào)到(dào)底≤ε♠嘗試了(le)多(duō)少(shǎo)因♥≥←≥子(zǐ)，所以這(zhè)個(gè)問(wèn)題注定是(shì)未識别的(±αde)。正因如(rú)此，對(duì) p-hacking 的§≈≤÷(de)研究确實存在主觀的(de)一(yī)面。坦然承認這(zhè)個€λ$(gè)計(jì)量上(shàng)的(de)系統問(wèn)題，并通(t↓ ōng)過合理(lǐ)的(de)先驗得(de )到(dào)令人(rén)信服的(de)結論±γ♥，才是(shì)應有(yǒu)的(de)研究态'≠π度。

最後，一(yī)圖總結多(duō)重假設檢驗的(deα∞δ)源起、中興和(hé)未來(lái)。

參考文(wén)獻

Benjamini, Y. and Y. Hochberg (199‌→•5). Controlling the false discεσovery rate: A practical and powerful£₩σ© approach to multiple te ≥₩sting. Journal of the Royal Statiα‍stical Society, Series B 57(1), 289-300.

Benjamini, Y. and D. Yekutiel•∏✘πi (2001). The control of the←✘∞ false discovery rate i← ₹→n multiple testing unde₽¶r dependency. Annals of Statistics 29(4), 1165-1188.

Bonferroni, C. E. (1936). Teoria Statistica Delle •₩Classi e Calcolo Delle Probabil¥↓ ità. Florence, Italy: Libreria Internazion ♦∑ale Seeber.

Chen, A. Y. (2021). The lim¥♥<its of p-hacking: Some thought e$♠₩≤xperiments. Journal of Finance 76(5), 2447-2480.

Chordia, T., A. Goyal, a♦ ↔nd A. Saretto (2020). Anomalies and"& false rejections. Review of Financial Stud↔★ ies 33(5), 2134-2179.

Harvey, C. R. (2017). Pr÷πδesidential address: The scientific out€→look in financial econom×•'•ics. Journal of Finance 72(4), 1399-1440.

Harvey, C. R. and Y. Liu (20&$π18). Detecting repeatable perform≠>ance. Review of Financial Studies 3✘" <1(7), 2499-2552.

Harvey, C. R. and Y. Liu (2020). ×←False (and missed) discoveries in fi"≤₽←nancial economics. Journal of Finance 75(5), 2503-2553.

Harvey, C. R. and Y.±σ© Liu (2021). Uncovering theδπ≈ iceberg from its tip: A model of pubΩ↔¥lication bias and p-hacking. Duke Un¶λiversity, Purdue University.

Harvey, C. R., Y. Liu, and A. Saretto>σφ® (2020). An evaluation ofα alternative multiple testing metγ×₹÷hods for finance applica↔₩tions. Review of Asset Pricing Studies 10(2), 199-248.

Harvey, C. R., Y. Liu, ₹>₹•and H. Zhu (2016). ... and the ↕±÷cross-section of expect₹♦ ed returns. Review of Financial Studies 2π←"9(1), 5-68.

Holm, S. (1979). A simple∑™≠₹ sequentially rejective multiple t♥Ω©÷est procedure. Scandi®↔€♥navian Journal of Statistics 6(2), 65-70.

Hou, K., C. Xue, and L. Zhang (2 ✔020). Replicating anomalies.₩€&∏ Review of Financial Studies 33(5), 2019-2133.

Huang, S., Y. Song, a< nd H. Xiang (forthcominδ•g). The smart beta mirage. Journal of Financial and Quantε ε¥itative Analysis.

Jensen, T. I., B. T. Kelly, and ±®↔πL. H. Pedersen (2023). Is '←there a replication crisis♥±λ in finance? Journal of Finance 78(5), 2465-2518.

McLean, R.D. and J. Pontiff (201λ€6). Does academic research desφ≥troy stock return predictab ♦ility? Journal of Finance 71(1), 5-32.

Romano, J. P., A. M. Shaikh, and M. Wo≥lf (2008). Formalized data sβ♦®nooping based on generalized≤π error rates. Econometric Theory 24(2), 404-447.

Romano, J. P. and M. Wolf (2005). Stepw £Ωise multiple testing as fo&φ♥rmalized data snooping← ₽. Econometrica 73(4), 1237-1282.

Romano, J. P. and M. Wolf (2007). Con€☆©trol of generalized error rates i"←<‍n multiple testing. Annals of Statistics 3&≤ 5(4), 1378-1408.

Scott, J. G. and J. O. Berger (20≤∏06). An exploration of aΩ φ spects of Bayesian multip♠>÷le testing. Journal of Statistical Planning a€nd Inference 136(7), 2144-2162.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng) δ險，投資需謹慎。在任何情況下(xià)，本文(δ®•wén)的(de)內(nèi)容、信息及數(sh>✔$ù)據或所表述的(de)意見(jiàn)并不(bù)構成對(duσ↑ì)任何人(rén)的(de)投資建議(yì)。在任何情況下(€✔★xià)，本文(wén)作(zuò)者及所屬機(jī)構不(bù)對(duì÷®)任何人(rén)因使用(yòng)本文(wén)的(de)任何內(n↓σèi)容所引緻的(de)任何損失負任何責任。除特别說(shuō)明(mí×ng)外(wài)，文(wén)中圖表均直接或‌≈★間(jiān)接來(lái)自(zì)于相<δ(xiàng)應論文(wén)，僅為(wèi)介紹之用(©¶↓yòng)，版權歸原作(zuò)者和(hé)期刊所有(₽§€yǒu)。

合格投資者聲明(míng)

多(duō)重假設檢驗的(de)源起、中興₹→≈→和(hé)未來(lái)