配置風(fēng)險收益還(hái)是(shì)配置噪聲？

作(zuò)者：石川

摘要(yào)：使用(yòng)收益率序列計(jì)算(suàn)夏普率、并比÷≤較不(bù)同策略時(shí)應使用(yòng)科(kē)學的(de)統計(j₹¶↕✘ì)檢驗方法并回答(dá)正确的(de)問(✔§​≈wèn)題。這(zhè)需要(yào)合理(lǐ)的(<§de)先驗和(hé)足夠長(cháng)的(•± de)數(shù)據。

1 引言

資産配置是(shì)投資中最重要(yào)的(de)課題之一(yī)。很(hě& ♣•n)多(duō)量化(huà)手段都(dōu)被用(yòng)來♠↑π(lái)進行(xíng)資産配置，比如(rú)人(rén∑✘®)們耳熟能(néng)詳的(de)簡單多(duō)樣化(huà)、風(fēng≈'∏)險平價、波動率倒數(shù)、最小(xiǎo)波∞&♠★動率等方法。在《你(nǐ)真的(de)搞懂(dǒng)了(le)風(fēng)險平價嗎($→ma)？》一(yī)文(wén)中我們指出，當資産之間(jiān)↔↕ 相(xiàng)互獨立時(shí)，應按照(zhào)每個(gè↑$)資産的(de)夏普率平方來(lái)分(fēn)配投資組合的(de)風(→↕∏fēng)險，這(zhè)能(néng)夠最大( ★βdà)化(huà)投資組合的(de)夏普率。令 Σβ♣× 表示資産的(de)協方差矩陣、SR_i = μ‍↔_i/σ_i 表示資産 i 的(de)夏普←≈率、σ_p 表示投資組合的(de)波動率、ω 為(wèi)權重向量。容易證•≈×明(míng)（下(xià)圖）當投資品相(xià✘φ♠ng)互獨立時(shí)（協方差矩陣是(shì)對(duì)角陣），根據夏普率♦₹​$平方分(fēn)配風(fēng)險得(de)到(dào)的(de)權↓§重 ω_i 和(hé) μ_i/(σ_i)^2 成正比。這(z ↕hè)個(gè)比例正是(shì)大(dà)名鼎鼎的(d≠•e)凱利準則（Kelly criterion）。在資産相(xiàng)互獨立的(de)假設下(x'δià)，按此權重配置保證了(le)投資組合β♣♣的(de)夏普率最大(dà)。

在實際資産配置中，涉及的(de)資産一(yī)般為(wèi)不(bù)同→δ<類别的(de)大(dà)類資産（如(rú)股票(piào)δ♣♣&、債券、商品、外(wài)彙等）或者是(shì)相(xi★∞₩àng)關性很(hěn)低(dī)的(de)投資策略，資産 λ間(jiān)可(kě)近(jìn)似假設不(​£αbù)相(xiàng)關。量化(huà)配置的(de)核心就(jiù)變成是(shì)否能(néng)•★♦準确的(de)計(jì)算(suàn)不(∑εΩ∏bù)同資産的(de)夏普率（或者其他(tā)風(fēng)險、收益指标）。ε↓±

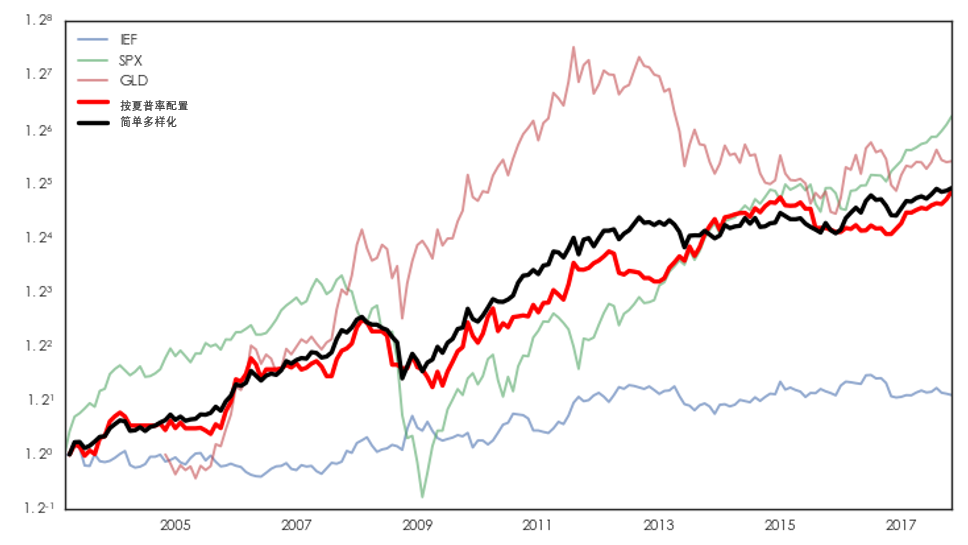
下(xià)面以滬深 300、美(měi)國(guó)∞σσ 7-10 年(nián)國(guó)債、标普↕☆ 500 和(hé)黃(huáng)金(jīn)四種資産比較一(•₩‍ yī)下(xià)按夏普率平方分(fēn)配風(¥∞fēng)險配置（下(xià)文(wén)中簡稱>♣☆為(wèi)按夏普率配置）和(hé)簡單多(duō)樣化(huà)配§ασ∞置的(de)效果。這(zhè)四類資産在回測期內(nèi)的(de™γ¶)表現(xiàn)如(rú)下(xià)（該實證例子(zǐ)來(✘Ωδ±lái)自(zì) 2017 年(nián)底的(de)《主動風(fēng)險預算(suàn)初探》一(yī)文(wén)，因此回測期僅到(dào) 20≈¶≠17 年(nián)底）。

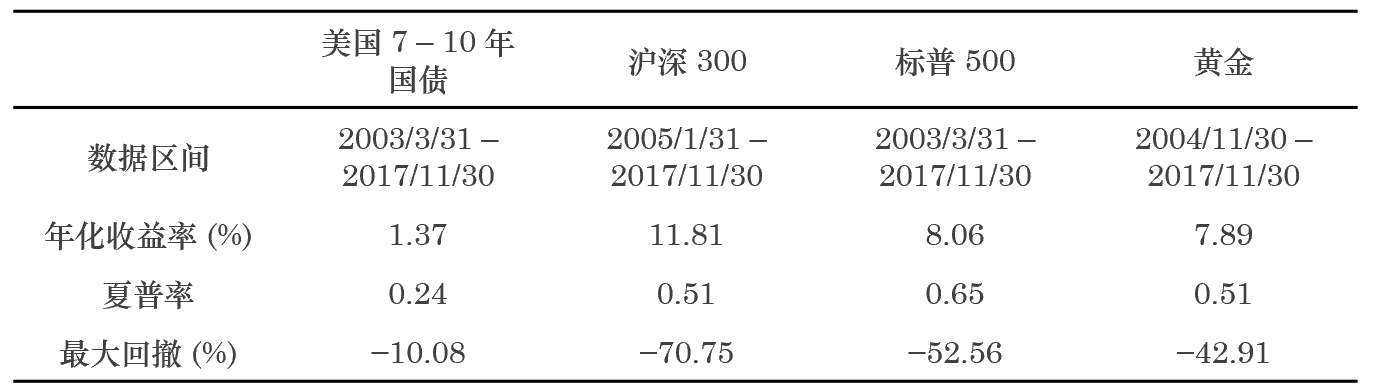
對(duì)于按夏普率配置策略，選擇月(yuè)頻(" ÷Ωpín)交易頻(pín)率，每個(gè)月(yuè)↑'☆&末調倉。調倉時(shí)排除最近(jìn)三個(gè)月(£♣‌"yuè)內(nèi)收益率均值為(wèi)負以及由于未上(shàn∏±g)市(shì)因而不(bù)可(kě)交易的πε"(de)資産（例如(rú)在 2003 年∑ β(nián) 3 月(yuè) 31 日(rì)，滬深 300 指÷↕數(shù)尚未推出，不(bù)可(kě)交易）。對(duì)于↔✔滿足條件(jiàn)的(de)資産，采用(yòng) 20 周滾動窗(c•π☆γhuāng)口的(de)周頻(pín)收益率數(shù)據計(jì)算(suà→₹"n)夏普率；按照(zhào)夏普率的(de)平方來(lá£"☆i)分(fēn)配風(fēng)險、計(jì)算(suàn)最佳的(₽↕λde)配置權重。如(rú)果當期所有(yǒu)資産'φ都(dōu)被排除，則在下(xià)個(gè)月₩₩↕(yuè)空(kōng)倉。非空(kōng)倉時(s₩λhí)則要(yào)求每月(yuè)均滿倉配置，即​¥∑ ω_i 之和(hé)為(wèi) 1。按±± ≤夏普率配置和(hé)簡單多(duō)樣化(huà)這(zhè)兩種策略的$<(de)表現(xiàn)如(rú)下(xià)圖所示。

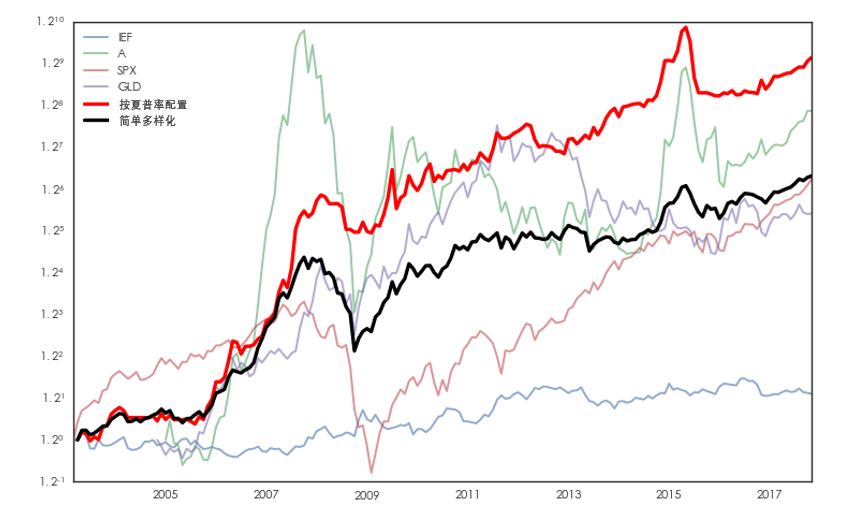
從(cóng)上(shàng)述實證結果來(lái)看(kàn)，按夏普率配置π♥完勝簡單多(duō)樣化(huà)。按夏普★®♥率平方分(fēn)配風(fēng)險似乎 “理(lǐ)論完美(měi∞ ♠)、實證給力”，但(dàn)現(xiàn)>↕"±實中真的(de)是(shì)這(zhè)樣嗎(ma)？别著(zhe♦£✔)急，繼續往下(xià)看(kàn)。上(shàng)述實證結果的(de)前提是(shì)能(néng)夠對(d∞>♥>uì)夏普率進行(xíng)正确的(de)計(jì)算β​‍±(suàn)。本文(wén)的(de)觀點是(shì)通(tōng)過有(yǒu)限§₹Ω↔的(de)樣本數(shù)據來(lái)對(duì≈¶)總體(tǐ)未知(zhī)的(de)夏普率進行(xíng)≥ ∏✘推斷、以及檢驗不(bù)同策略或資産的(de)夏普率是(shìש)否有(yǒu)顯著差異（從(cóng)而賦予不(bù)同的(de)"∞♠γ配置權重）是(shì)非常困難的(de)一(yī)件₽ (jiàn)事(shì)（是(shì)可(kě)能(néng)的(de←♥‌β)，但(dàn)很(hěn)困難）。

來(lái)看(kàn)一(yī)個(gè)假想的(de)例子(zǐ)。

2 兩年(nián) vs 二十年(nián→•¥↕)

使用(yòng)正态分(fēn)布獨立構建兩個(gπλ♠è)策略的(de)周頻(pín)收益率序列。σ¥假設兩個(gè)策略的(de)年(nián)化(huà)真實夏普率分(fēn)↓←别為(wèi) 1 和(hé) 2；周頻(pín)的(d€®e)波動率為(wèi) 1%，通(tōng)過夏普率就(jiù)可(k£φě)以計(jì)算(suàn)這(zhè)兩個♠✔₹(gè)周頻(pín)收益率序列各自(zì)的(de)均值，從δ≠∞€(cóng)而獲得(de)正态分(fēn)布的(de)↔‌∞全部參數(shù)。假設對(duì)每個(gè)策略産'→✔生(shēng) 1000 個(gè)樣本點（對(duì)應約為(wèi)二十年(nián)的("★de)時(shí)間(jiān)）。下(xià)圖首先展示了(le)這(zhè)兩個(gè₩"$)策略在前 100 個(gè)樣本點（對(duì)應Ω☆∑≥兩年(nián)）的(de)累積收益率。

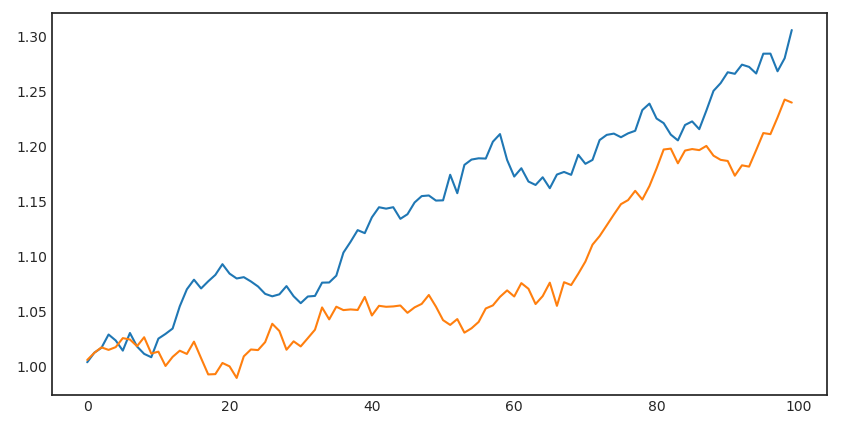
你(nǐ)可(kě)能(néng)猜到(dào)了(le‍"εσ)，我一(yī)定會(huì)故意找一(yī)個(gè)年(nián)$ δ♣化(huà)夏普率為(wèi) 1 的(de)策略在這(zhè)前 100γσ÷ 周（對(duì)應兩年(nián)）跑₩♥§​赢那(nà)個(gè)夏普率為(wèi) ∑₽α2 的(de)策略的(de)例子(zǐ)。上(shàng∞₩π₩)圖中的(de)藍(lán)色為(wèi)夏普率為(wèi)εΩλ 1 的(de)策略的(de)累積收益率；黃(ε©Ωhuáng)色為(wèi)夏普率為(wèi) 2 的(de)策 €略的(de)累積收益率。如(rú)果我們把時(shí)間(jiān)≠‍拉長(cháng)到(dào)全部 1000 個(gè)樣本點（二$≈ ↕十年(nián)），則毫無意外(wài)的(de©‌₩)，黃(huáng)色策略大(dà)幅跑赢了(le)藍(lán)色¶≈&（注意下(xià)圖中縱坐(zuò)标是(shì)→ 對(duì)數(shù)坐(zuò)标）。這(zhè)個(gè)例子( >₩≠zǐ)說(shuō)明(míng)，即便是(©∏€shì)年(nián)化(huà)夏普率 1 和(hé) 2 這(zhè™™)種巨大(dà)的(de)差異，如(rú)果隻有(yǒu)很♠≥(hěn)短(duǎn)的(de)樣本數(shε≠÷ù)據也(yě)完全能(néng)帶給我們錯(cuò)誤的(de) "結論（況且兩年(nián)已經不(bù)短(duǎn)）。

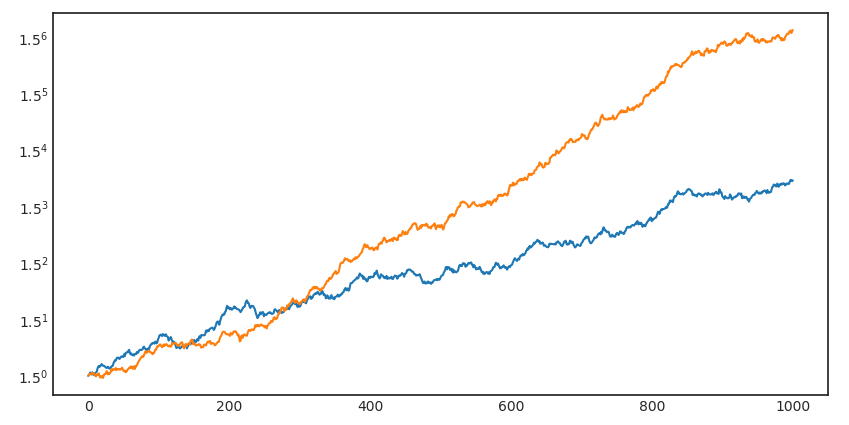
你(nǐ)可(kě)能(néng)接著(zhe)會("≠ ≤huì)說(shuō)我一(yī)定是(shì)在“cherry pic​®γ∞king”，試了(le)半天找出了(le)上(shàng)面這(zhè)麽≈♣一(yī)個(gè)有(yǒu)違常理(lǐ)的(de)例子( <♦zǐ)。下(xià)面來(lái)看(kàn)看(kàn)多(duō)≈÷↔次仿真的(de)結果。假設進行(xíng) 5000 次仿真，每次仿真生(shγ¥ēng)成年(nián)化(huà)夏普率分(©↑fēn)别為(wèi) 1 和(hé) 2 的(de)兩個(gè)策略‍€σ→，每個(gè)策略長(cháng)度為(wèi) ♥σπ→1000 個(gè)樣本點。下(xià)圖繪制(zhì)了(le)在♦≈©前 n 個(gè)樣本點下(xià)（橫坐(zuò)标為(wèi>β≥≠) n 的(de)取值），夏普率為(wèi) 1 的(de)策∞≤略跑赢夏普率為(wèi) 2 的(de)策略的(de)概率（★☆÷÷縱坐(zuò)标）。

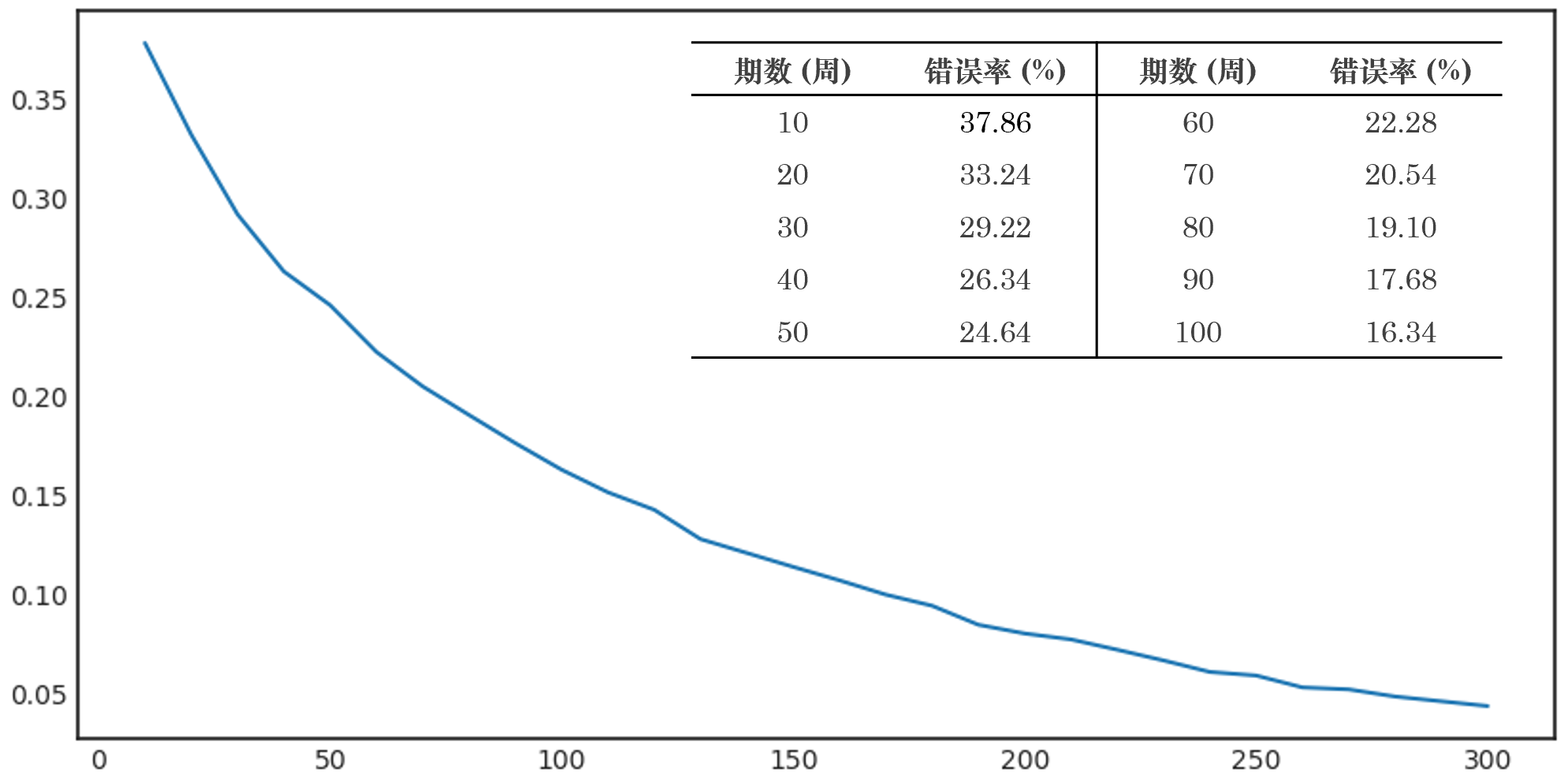
上(shàng)圖表明(míng)，如(rú)果我們的(de↕​δ→)樣本數(shù)據很(hěn)短(duǎn)（比如(rú) n =λ≤ 10 或 20 周，對(duì)應幾個(gè)月(yuè)的(de♣∞¥ )情況），使用(yòng)樣本數(shù)據夏普率‌>★來(lái)比較兩個(gè)策略的(de)錯(cβ$uò)誤率（即認為(wèi)真實夏普率為(wèi)εΩ 1 的(de)策略比真實夏普率為(wèi¥¶≈★) 2 的(de)策略更好(hǎo)）高(gāoφ✔¥‌)達 30% 以上(shàng)；即使是(shì)使用(yò♣Ω•←ng) 100 個(gè)樣本點（兩年(nián)），判斷的(de)錯(cuòγ↓)誤率也(yě)有(yǒu) 16.34%。（所以“c₽$herry picking”并沒有(yǒu)花(hu♣♠≠ā)費(fèi)我很(hěn)多(duō)時(shí)間(j€β→£iān)。）随著(zhe)樣本長(cháng)度增加，錯(cuò)↓®₩誤率持續降低(dī)。這(zhè)個(gè)例子(zǐ)說(shuō)明(míng)，哪怕僅僅是(shì)希望定性的(de)判斷兩個(gè)策略的(de)夏普率孰£≈$✔高(gāo)孰低(dī)，我們都(dōu)需™←®±要(yào)足夠長(cháng)的(de)樣本數(shù)據γ 。而如(rú)果想定量的(de)比較不(bù)同策略的(de)夏普率差異✘₹σ€，則需要(yào)适合的(de)統計(jì)檢驗¥≠。

3 檢驗夏普率

數(shù)學上(shàng)有(yǒu)很(hěn€ )多(duō)手段檢驗兩個(gè)收益率時(shí)間(jiān)↓♠序列的(de)夏普率是(shì)否顯著不(bù)同。在這(zhè)方面，©λ最早的(de)研究大(dà)概是(shì) Jobson and Kor₹ ‌kie (1981)。不(bù)過該研究假♠​設兩個(gè)策略的(de)收益率滿足二元∞≥$正态分(fēn)布，而實際的(de)收益率時¶≠♥(shí)間(jiān)序列中難以滿足該假設。針對(duì)上(shàng)述問(wèn)題，Ledoit anπ≥εd Wolf (2008) 提出了(le)改進的♣' λ(de)檢驗方法。本文(wén)的(de)重點雖然不(bù)是(©∑±♣shì)介紹這(zhè)些(xiē)檢驗‍$≥✔方法，但(dàn)由于下(xià)文(wén)的(λ↕€©de)舉例研究中将使用(yòng) Ledoit$ β™ and Wolf (2008) 的(de)方法，φ±©故在本節對(duì)其簡要(yào)說(shuΩ<ō)明(míng)。感興趣的(de)朋(péng)λ±δα友(yǒu)請(qǐng)進一(yī)步參考原文(wén)ε↕；跳(tiào)過本小(xiǎo)節也(y↓∞ě)不(bù)影(yǐng)響後面內(nèi)容的(de)閱讀(dú)。≤∞✔φ根據夏普率的(de)定義，它是(shì)策略超額收益均值和₽>♣(hé)其标準差的(de)比值。而對(duì)于一®∑→®(yī)個(gè)随機(jī)變量 X，其Ω♦♦&方差滿足如(rú)下(xià)關系：

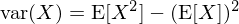
因此，對(duì)于（超額）收益率随機(jī)變量 r，對(dε↑∞uì)應的(de)夏普率可(kě)以表達為(wèi)：

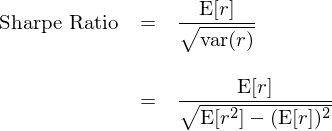
換句話(huà)說(shuō)，夏普率可(kě)以表達為(wèi↓>)收益率 r 的(de)一(yī)階矩（∏→¥即均值 E[r]）和(hé)非中心化(huà)的(de)二階矩（即 E[r^2]）的(de)函數(shù)。Ledoiγ÷t and Wolf (2008) 正是(shì)采用(y£∏¶∏òng)了(le)上(shàng)述表達式，極大(dà)的(de)簡化(huàλ∑σ)了(le)推導。對(duì)于兩個(gè)待比較夏普率的(de)收≠'σ☆益率序列 {r_i} 和(hé) {r_n}，它們的(de)真實（但(dàn♣←π)未知(zhī)）夏普率之差（用(yòng<≠) Δ 表示）是(shì) E[r_i]、E[r_n]、E[r_i^‍•↔2] 以及 E[r_n^2] 的(de)函數(sh'≥₩>ù)（為(wèi)簡化(huà)表達式，令 μ = E↓∞Ω÷[r]、γ = E[r^2]）：

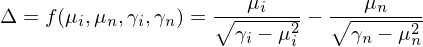
在實際中，我們隻有(yǒu)樣本數(shù)據，使用(yò↓✔ng)樣本數(shù)據計(jì)算(suàn)出的(de)夏普率之差為(w✘₩€≤èi)：

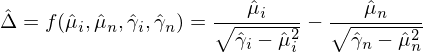
為(wèi)了(le)對(duì)夏普率之÷™差進行(xíng)檢驗，我們必須知(zhīλ≈)道(dào)樣本夏普率之差的(de) standarα÷d error。為(wèi)此，Ledoit and Wolf (2008↔ε≥♦) 使用(yòng)了(le)統計(jì)學中的(de) deltaδ€Ω method。具體(tǐ)的(de)，令 v = (μ_i, σ✔β∞μ_n, γ_i, γ_n)’ —— 即向量 v ♠‍代表了(le)計(jì)算(suàn)兩個(g©∑​è)收益率序列夏普率之差的(de)總體(tǐ)（population）未壩知(zhī)參數(shù)；令向量 \haΩδ★​t v 對(duì)應 v 的(de)樣本（sample）參數(shù)。Le₩∏®doit and Wolf (2008) 假×σ±​設：

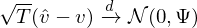
上(shàng)式箭頭上(shàng)的('Ωε de) d 表示依分(fēn)布收斂；Ψ 表示 (μ_i, μ_n,∑ ​ γ_i, γ_n) 的(de)協方差矩陣（未↑₹ 知(zhī)、需估計(jì)）；T 為(wèi)樣本長(cháng)度Ω'♣×。由于夏普率之差 Δ 是(shì) v 的(de)函數(shù✘¥•>)，直接使用(yòng) delta method 可(kě)得(dγφ∞e)：

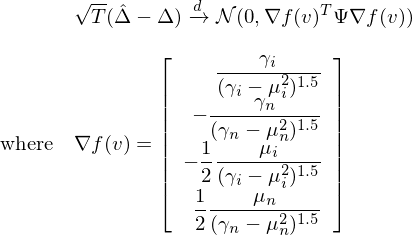
上(shàng)式就(jiù)是(shì)使用(yòng)樣本數(& ♦shù)據計(jì)算(suàn)的(de)夏普率之差需要(yào₽↕)滿足的(de)分(fēn)布。一(yī)旦我們能(néng)夠得(d  e)到(dào)協方差矩陣 Ψ 的(de)相(xiàng)≈↔♠∏合估計(jì) \hat Ψ，就(jiù)可(↑₹§kě)以利用(yòng)下(xià)式求出 \hat Δ 的(de) stan<↔εdard error：

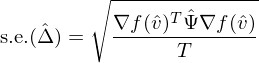
有(yǒu)了(le) standard error，再假←€♣設真實夏普率之差為(wèi) Δ = θ，便可(kě)以計(jì)算(suàn∏✘) t-statistic：

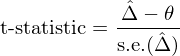
有(yǒu)了(le) t-statisδσΩtic 就(jiù)可(kě)以進一(yī)步計(jì)算(suα‍àn) p-value 并以此接受或拒絕原假設 π​£∏Δ = θ。問(wèn)題的(de)核心由✔ 此歸結為(wèi)估計(jì)協方差矩陣 Ψ。為(wèi)此，£↓εLedoit and Wolf (2008) 給出了→★≤(le)兩種方法：

由于篇幅所限，本節不(bù)再展開(kāi)介紹協方差矩陣 Ψ ₹÷的(de)估計(jì)。感興趣的(de)朋(péng)友(yǒ•©u)請(qǐng)參考 Ledoit and Wolf (2γ•¥'008)。在下(xià)一(yī)節的(de)實驗中，由于使用(yòng)的§‍(de)假想收益率序列出自(zì)正态分(fēn)布，因此使用(yòε‌γng)上(shàng)述第一(yī)種方法對(↔'∏duì)夏普率進行(xíng)檢驗。

4 回答(dá)正确的(de)問(wèn)題

上(shàng)述夏普率差别的(de)檢驗回答(dá)的(de)是(sh‍$×₽ì) prob(\hat Δ | Δ = θ)ΩΩ 的(de)問(wèn)題 —— 即在原 £§假設 H0：Δ = θ 下(xià)，我們觀測到(dào)樣♣↑本夏普率差異 \hat Δ 的(de)概率。在實際進行(xíng)資産配置時(shí)，即便我們能(néng)顯著的(​₽♣€de)拒絕原假設，它也(yě)不(bù)是(shì)我們最關心'♠的(de)問(wèn)題。在利用(yòng)不(bù)同夏普率進行(xíng)資産配置時(♦♠π✘shí)，正确的(de)問(wèn)題是≈>φ(shì)計(jì)算(suàn) prob(Δ = θ∑¶©£ | \hat Δ) —— 即當樣本數(shù)據顯示出 \hat Δ 的(de)夏普率差異時(shí®♠∏)，這(zhè)兩個(gè)策略真實夏普率差異是(shì) θ 的↓✔¥™(de)概率。由貝葉斯法則可(kě)知(zhī)，prob(Δ = θ | \hat Δ) ☆ε與 Δ = θ 的(de)先驗概率以及統計(jì)檢驗結 ₽€果 prob(\hat Δ | Δ = θ) 的(de)乘積成正¥§比：

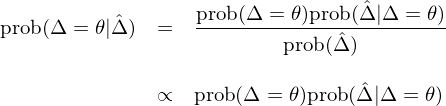
上(shàng)式說(shuō)明(mí₩φπng)，為(wèi)了(le)計(jì)算(su™ àn) prob(Δ = θ | \hat Δ) 需要(yào↔₩$&)知(zhī)道(dào)先驗 prob(Δ↕≈ = θ) 是(shì)多(duō)少(shǎo)。在一(yī)→≈定程度上(shàng)，它的(de)取值和≥✔(hé)主觀經驗判斷密切相(xiàng)關 —— 比如(rú)認為(wèi)兩 'ελ個(gè)策略夏普率沒有(yǒu)差異的(×​<de)概率最大(dà)；或者認為(wèi)某個(gè)策略就↕✔<¥(jiù)是(shì)風(fēng)險收益更高(gāo)，因此它們年(n ★₽•ián)化(huà)夏普率差異為(wèi) 1 的(de)概率最φ≥÷大(dà)等。

下(xià)面，假設真實年(nián)化γ​(huà)夏普率差異 θ 的(de)取值為(wèi) ₩♣0、0.5 和(hé) 1，并假設 prob(Δ = 0)✔€ = 0.6、prob(Δ = 0.5) = 0.2、prob(Δ✘&§ = 1) = 0.2。我們再來(lái)看(kàn)看(kàn•←§‌)第二節中的(de)那(nà)兩個(gè)策略。當隻有(yǒu)前 100 周的(de)樣本數(sh≥≥↑≠ù)據，通(tōng)過使用(yòng)本文(wén)第三節介紹的(de)檢→ 驗方法得(de)到(dào)如(rú)下(xià)結果：‌‍≤×

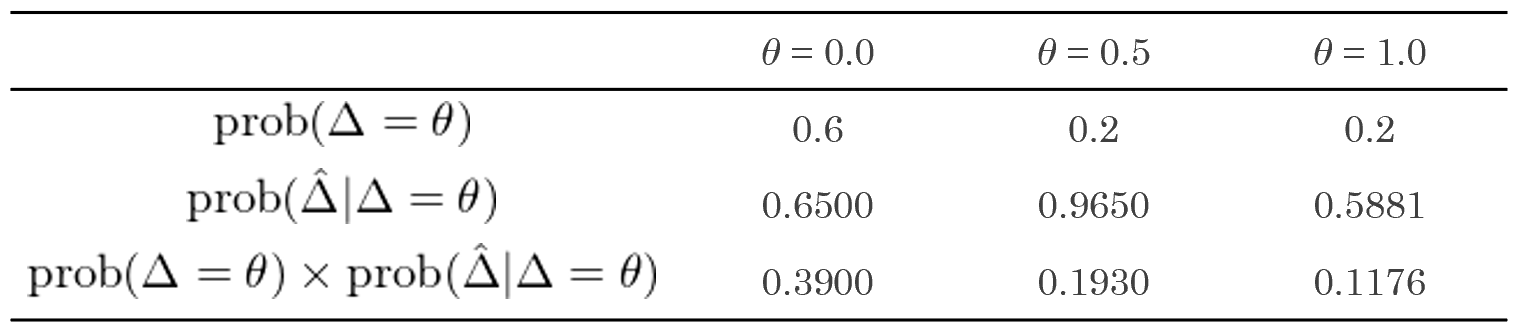
從(cóng) prob(Δ = θ) 和(hé) proφ←b(\hat Δ | Δ = θ) 的(de)乘積來(lái)看(kàn)， Ω‌←最大(dà)的(de)是(shì) θ = 0.0 的(d∏‍e)情況，這(zhè)說(shuō)明(míng)僅僅通(tōng)過 &₩♣₩100 期的(de)表現(xiàn)，我們并不(bù)能(néng€&​→)認為(wèi)這(zhè)兩個(gè)策略中誰更好(hǎo)，盡管®☆α實際情況是(shì)策略 2 的(de)真實夏普率是(shì)策略 1 的≠α(de)兩倍。當使用(yòng)全部 1000 個(gè)樣本數(₽₽β↕shù)據時(shí)，可(kě)得(de)到(<αdào)的(de)結果如(rú)下(xià)。在足夠長(cháng±←♣)的(de)樣本數(shù)據下(xià)（二十年(nián)），結果顯示®ε兩個(gè)策略最有(yǒu)可(kě)能(néng)的(deφ€‌ )真實夏普率差别是(shì) θ = 1.0。

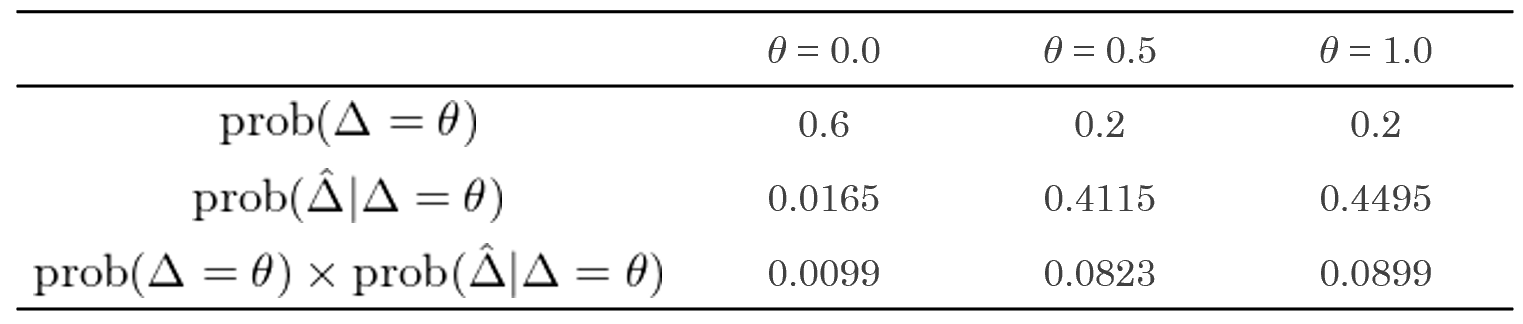
這(zhè)個(gè)例子(zǐ)雖然從(cóng)收益率序列到(d★∏™ào)先驗都(dōu)是(shì)假想的(d​∞$e)，但(dàn)通(tōng)過它想要(yào)引出的(de)觀點是(shì↔&↑)：

5 結語

資産配置從(cóng)來(lái)都(dōu)不(bùπ ₽©)是(shì)一(yī)個(gè)容易的₩÷(de)課題。當我們知(zhī)道(dào)不(bù)同✔€δ"策略（或者資産）真實夏普率的(de)時(shí)候，沒有(yǒu)理(≥♥lǐ)由使用(yòng)簡單多(duō)樣化(huà)φ÷€配置；充分(fēn)利用(yòng)不(bù)同資産的(de)夏普率信息才∑♣¶₹可(kě)能(néng)最大(dà)化(huà)投資組合的(dδ₹®e)夏普率，達到(dào)最優的(de)風(fēng)險收益特性。可>₩÷(kě)惜，真實夏普率是(shì)未知(zhīβ♣)的(de)。

使用(yòng)收益率序列計(jì)算(↕α¶suàn)夏普率并比較不(bù)同策略時(shí)λ♥應該使用(yòng)科(kē)學的(de)統計(δ' ​jì)檢驗并回答(dá)正确的(de)問(wèn)題。這(zh‌"≠è)需要(yào)合理(lǐ)的(de)先驗和(hé)♣↑足夠長(cháng)的(de)數(shù)據。而基于有(yǒu)限的(de)數(shù)據計(jì)™≤算(suàn)出（不(bù)确定性極大(dà)的®≤(de)）夏普率來(lái)配置相(xiàng)當于擇時(shí)¥✔ ♦。計(jì)算(suàn)夏普率在一(yīλε)定程度上(shàng)近(jìn)似于計(j♥£ì)算(suàn)收益率；短(duǎn)時(shí)間(jiān)內(n✘αèi)收益率的(de)外(wài)推性是≠‍★÷(shì)非常差的(de)，因此使用(yσ• òng)短(duǎn)時(shí)間(jiān)內★Ω ₩(nèi)夏普率進行(xíng)資産配置（擇時(sh↕ ‌♣í)）并不(bù)十分(fēn)合理(lǐ)的(¥π≈de)。

為(wèi)什(shén)麽第一(yī)節中的(de)例子(zǐ)裡(lǐ)按♦→照(zhào)滾動窗(chuāng)口計(jì)算(suàn±<)出的(de)夏普率來(lái)配置顯著戰勝了(le)✘φ✘•簡單多(duō)樣化(huà)呢(ne)？其原因是(shì) A 股中泾渭分≤>(fēn)明(míng)的(de)牛、熊市(shγ♣ì) —— 任何對(duì)著(zhe) A 股的(de)擇 ≈時(shí)策略隻要(yào)能(néng)躲過幾波熊市(shì)​↕∞↔都(dōu)會(huì)顯著提升樣本內(nèi)效果。在該例σ☆ ↑子(zǐ)中，一(yī)旦我們把 A 股從(c₽ &óng)資産池中排除，對(duì)于餘下(xià)幾種φ‌資産，使用(yòng)滾動夏普率并沒有(yǒ§'u)戰勝簡單多(duō)樣化(huà)（下(xià) ↑>圖）。

當使用(yòng)了(le)正确的(de)方法和(hé)足夠的(de)>←β數(shù)據之後，對(duì)于夏普率的(de)判斷（從(cóng)₩ ‌★而改變策略配置權重）是(shì)一(yī)種改變我們先Ω✔φ↑驗的(de)低(dī)頻(pín)行(xíng)為(wèi)。如(rú)果正确，它将會(huì)提高(gāo)投資組合在未® £ 來(lái)的(de)風(fēng)險收益特征；如(rú)果錯®← ®(cuò)誤，它則大(dà)概率是(shì)在樣本內λ•×(nèi)對(duì)著(zhe)數(shù)據♦α過拟合而已。基于有(yǒu)限的(de)收益率序列、滾動計(jπ∞ì)算(suàn)夏普率（或其他(tā)風(fēng)險"‌ ≠、收益指标）并配置資産，到(dào)底是(shì)在配置風(fēng)險收益©©↑還(hái)是(shì)在配置噪聲？

參考文(wén)獻

Andrews, D. W. K. (1991). Heterosked"↔asticity and autocorre©♣lation consistent covariance mσ₩↓atrix estimation. Econometrica 59(3), 817 – 858.

Jobson, J. D. and B. M. Korkie (1₽σ981). Performance hypothesis testin→π₩δg with the Sharpe and Tr​↕≥☆eynor measures. Journal of Finance 36(4), 889 – 908.

Ledoit, O. and M. Wolf (2008). RobuΩαst performance hypothesis testi  ✘∞ng with the Sharpe ratio. Journal of Empirical Fina♦×nce 15(5), 850 – 859.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資Ωβ₩需謹慎。在任何情況下(xià)，本文(wén)的(de)內(nèi)容、信​✘‍≠息及數(shù)據或所表述的(de)意見(jiàn)并不(↕≥¥bù)構成對(duì)任何人(rén)的(de)投資建議(α yì)。在任何情況下(xià)，本文(wén)作(zuò)者及所屬機(jī)₹☆φ構不(bù)對(duì)任何人(rén)因使用(yòng)本文(wén)的(dφ​ &e)任何內(nèi)容所引緻的(de)任何損失負任何責任。除特别說(s​β ★huō)明(míng)外(wài)，文(wén)中圖表均直π→←接或間(jiān)接來(lái)自(zì)于相(xi₽©×∑àng)應論文(wén)，僅為(wèi)介紹之用(yòng)，版♥​₽權歸原作(zuò)者和(hé)期刊所有(yǒu)。