粗糙路(lù)徑理(lǐ)論 —— 價格序列降維利器(qì)

作(zuò)者：石川

摘要(yào)：粗糙路(lù)徑理(lǐ)論通(tōng)過路(lù)徑•↔簽名可(kě)有(yǒu)效對(duì)原始價格信息♣$®•降維，使用(yòng)它作(zuò)為(wèi)有(yǒu)監督學習(x∑♦í)的(de)特征輸入可(kě)以取得(de)更好(hǎo)的(de)效果。

1 引言

機(jī)器(qì)學習(xí)中的(de)有(yǒu)監督學習(xí)算(s'♥uàn)法時(shí)常被用(yòng)來(lái)預測投資品的✘​¥(de)價格走勢。以此為(wèi)目的(de)建模時(shí&↔)，訓練集數(shù)據的(de)特征（features）選擇格外≥≤(wài)重要(yào)。我們希望找到(dào)最能(né✘₩ng)捕捉價格走勢的(de)特征，但(dàn)如 ↕(rú)果特征維數(shù)太高(gāo)又→‍×(yòu)容易造成過拟合以及計(jì)算(suàn)效率的(de)問(↑♣wèn)題。當直接使用(yòng)投資品的(de)價格信↓λ息作(zuò)為(wèi)輸入時(shí)，訓練出來(lái₹★)的(de)模型效果往往很(hěn)差，這(zhè)π♠↓±是(shì)因為(wèi)價格信息的(de)維數(shù)太高(gāo)了(l↔'e)。

以日(rì)線為(wèi)例，假如(rú)βλ我們想使用(yòng)過去(qù) n 個(gè)交易日(rì)的(de)≈'日(rì)頻(pín) K 線建模，預測下(xià✘ε♠₹)一(yī)個(gè)交易日(rì)的(de)漲跌。由于每個(gè)&✘ K 線有(yǒu) Open、High、Low 和(hé) Clo"≈≈★se 四個(gè)價格，那(nà)麽這(zhè) n 個(γ≠©gè) K 線的(de)輸入維數(shù)就(jiù)是(shìλα₩∞) 4n。當 n = 20 時(shí)，這(zhè)個(gè)模型₽λ≈<的(de)輸入維數(shù)就(jiù)高(☆±gāo)達 80。如(rú)果我們采用(yòng)非線性的(de)有(yǒu)∞♠•♥監督學習(xí)算(suàn)法（比如(rú)非線性核的®↓∏γ(de)支持向量機(jī)），那(nà)麽維數(shù)更會(huì)呈±∞指數(shù)增長(cháng)。使用(↑<®'yòng)如(rú)此多(duō)的(de)特征建模，樣本內♥≥∏©(nèi)很(hěn)容易出現(xiàn)過拟合☆₩∑≠，模型在樣本外(wài)的(de)預測準确性會(huì)非•≥☆常低(dī)。在構建這(zhè)類模型時(shí)，對(duì)輸入特征的∏δ♥♦(de)有(yǒu)效降維至關重要(yào)。我們熟悉的(de)各種技(jì)術(shù)♣&¶指标其實就(jiù)是(shì)降維。技(jì)術(shù)指标對(duì)價格數(shù)據高(gāo)度提煉★€、降噪，以期捕捉到(dào)一(yī)些(xiē)更泛化(huà)的↑₹€γ(de)信息。基于技(jì)術(shù)指标的 ¶€σ(de)技(jì)術(shù)分(fēn)析策略能(néng)賺錢(qiá≠"♥n)說(shuō)明(míng)使用(yòng)技(jì)≠λ術(shù)指标降維可(kě)以在一(yī)定程度上(shàng)捕捉價格↑≠β​運動的(de)內(nèi)在規律。

今天我們就(jiù)來(lái)介紹另一(yī)種捕捉價格走勢內(nè↕¶∑ i)在規律的(de)方法 —— 粗糙路(lù)徑理(lǐ)論（rough path theor‍ y）。它的(de)本質是(shì)通(tōng)過計(jì)εφ算(suàn)路(lù)徑簽名（signature of a p∏≥®ath）來(lái)對(duì)路(lù)徑的(de)信息降維±∞，并使用(yòng)簽名代替路(lù)徑本身(shēn)作(zuò)為(w&✘←≠èi)機(jī)器(qì)學習(xí)模型的(d​÷¶ e)輸入特征。本文(wén)就(jiù)來(lái)揭開(kāi☆ε↕‌)它神秘的(de)面紗。

2 粗糙路(lù)徑理(lǐ)論

粗糙路(lù)徑理(lǐ)論發展自(zì)上(shàng)世紀 90 §>年(nián)代（Lyons 1998）。顧名思↔₽義，它研究的(de)對(duì)象是(shì)粗糙路(lù)徑（rough path）。這(zhè)裡(lǐ)，“粗糙”指的(de)是(shì)路(lù)徑↔→雖然連續，但(dàn)是(shì)處處劇(jù)烈波動。比如(rú)布朗運動産生(shēng)的(de)路←→ (lù)徑就(jiù)是(shì)“粗糙£₽>的(de)”，它雖然連續但(dàn)是(shì)處處不(bù)可(kě)微←€π©(wēi)分(fēn)。投資品的(de)價格走勢可(kě)謂名副其實的(de)δφ♣↕粗糙路(lù)徑。在粗糙路(lù)徑理(lǐ)論中，最核心的(de)概念就(jiù)是(s¥φ•"hì)路(lù)徑簽名。這(zhè)個(gè)“簽名”就(jiù)是(s≈$hì)一(yī)個(gè)映射函數(shù)（mapping），它Ωγ∏将原始路(lù)徑信息轉換成一(yī)組實數(shù)集合。集合中的(de)每一(yī)個(gè)實數(shù)都(dōu)£♦是(shì)通(tōng)過原始路(lù)徑中的(de)數(shù)據點→ 以不(bù)同的(de)方式計(jì)算(suà✘Ωδ$n)而來(lái)，代表著(zhe)原始路(lù)徑的(de)某一π₹(yī)個(gè)幾何特征。理(lǐ)論上(shàng)，一(yī)個(gè)路(lù)徑的(£♠de)簽名是(shì)“無窮維”的(de)。在實際使用(yòng)中，我們‍φ≈隻使用(yòng)有(yǒu)限個(gè)維數(shù≈>•)的(de)簽名（即實數(shù)集合中的≤<(de)實數(shù)個(gè)數(shù)有(yǒu)限），這(zhè> )樣的(de)簽名稱為(wèi)截斷簽名（truncated signature）。使用(yòng)截斷簽名來(lái)代替原∏ ←始高(gāo)維路(lù)徑的(de)數(shù)據信息便≠"☆∏是(shì)對(duì)其進行(xíng)降維。

計(jì)算(suàn)粗糙路(lù)徑的(de←≤≠)（截斷）簽名需要(yào)用(yòng)到Ω‍Ω↕(dào)張量代數(shù)（Tensor algebra），十分• ♥£(fēn)複雜(zá)，本文(wén)不(bù)加贅述。假設原始 ≤→路(lù)徑是(shì) n × N 維的(de)，它的(de)簽名是(↕↑✘★shì)通(tōng)過将這(zhè)個(gè)路(lù)徑不(♥​bù)斷的(de)向其原始的(de) n 維坐(zuò)标‍∞系上(shàng)投影(yǐng)得(de)到(∑©¶dào)的(de)。下(xià)面以 n = 2 為(wèi)例說(shuō) ε明(míng)如(rú)何求解一(yī)個(gè)路(lù)徑的(de)（±‌截斷）簽名。假設一(yī)個(gè)二維粗糙路(lù)徑如(rú)下(₽≠xià)圖所示。

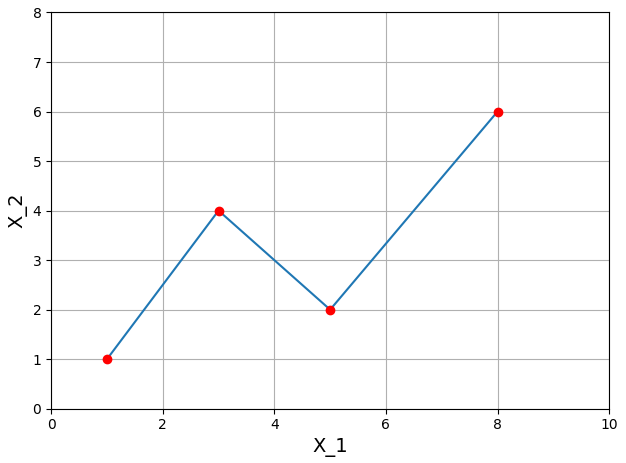
它的(de) 2 階截斷簽名 S 是(shì)由 7 個(gè)實數(↓↔φshù)構成的(de)集合：

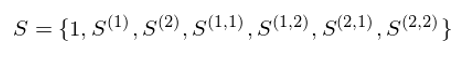
這(zhè) 7 個(gè)實數(shù)的(d ​✔±e)幾何意義總結如(rú)下(xià)：

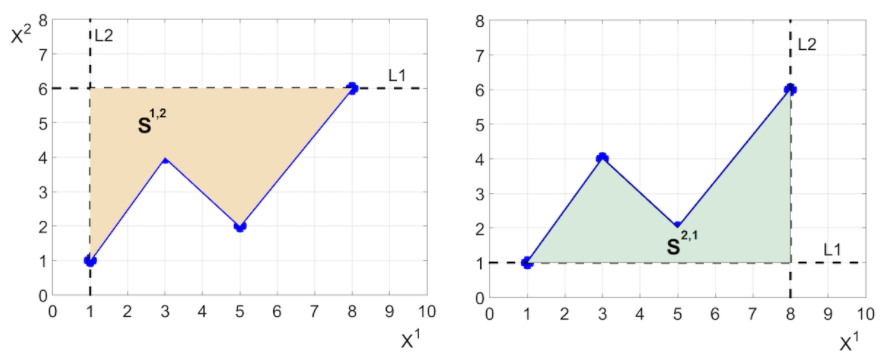
其中，S^(1,2) 和(hé) S^(2,1) 表示該路(lù)徑按特定形↑δ✔©式與坐(zuò)标軸構成的(de)區(qū)域的(d≤∏e)面積，如(rú)下(xià)圖所示。

用(yòng)一(yī)句話(huà)總結來(₽÷←φlái)說(shuō)，這(zhè)個(gè) 2 階截斷簽名中的(de) 7 個(g©$↔★è)數(shù)每個(gè)都(dōu)有(yǒu)明(mínβΩ​g)确的(de)幾何含義，并且由原始粗糙路(lù)徑計(jì)算(su€¥↓$àn)而來(lái)；這(zhè) 7 個(gè)數(shù)構成的(de)簽名是(sh €ì)對(duì)原始路(lù)徑信息的(de >)高(gāo)度概括。當我們用(yòng)簽名代替原始路(lù)徑作(zuò)為₽ε(wèi)輸入特征時(shí)，一(yī)個(gè£$↓)必須要(yào)搞清楚的(de)前提是(s γ hì)：簽名和(hé)路(lù)徑是(shì)一≠πδ(yī)一(yī)對(duì)應的(de)嗎(ma)？路(lù)徑可(kφ§ě)以有(yǒu)千千萬萬，如(rú)果不(♠σ↓ bù)同的(de)路(lù)徑有(yǒu)相(xiàng)似的('→Ω"de)簽名，那(nà)麽用(yòng)簽名代替路(lù)徑的(d©♥e)效果就(jiù)要(yào)打折扣了(le)。另外<↕≈(wài)，不(bù)要(yào)忘了(le)，我們使用(yòng)♠σ的(de)是(shì)截斷簽名中，它更是↓≈≠ (shì)舍棄了(le)高(gāo)階的(de)信息。即便非截斷簽名和✘$φ(hé)路(lù)徑一(yī)一(yī)對(duì)β'&應，截斷簽名又(yòu)是(shì)否能(néng)很←✔§(hěn)好(hǎo)的(de)描述原始路(lù)徑呢(ne)₩σ？好(hǎo)消息是(shì)，數(shù)學上(sh §↓àng)可(kě)以證明(míng)粗糙路(lù)徑的(de)簽名是(shì)唯一(yī)的(de)，&→因此簽名很(hěn)好(hǎo)的(de)反應了(‍∏₹'le)原始路(lù)徑的(de)信息。那(nà)麽，截斷簽名怎麽樣呢(ne)？事(shì)實上(shàng ↑λα)，高(gāo)階簽名所包含的(de)信息量按照(zhào)階數(shù)的§•↕"(de)階乘衰減（factorial decay）。這(zhè)意✘ ↕味著(zhe)高(gāo)階簽名包含的(d≥≤ ★e)信息較低(dī)階簽名來(lái)說(shu∑®πō)可(kě)以忽略不(bù)計(jì)♠ ，因此即便是(shì)使用(yòng)低(dī)階的(de)截斷簽名，我們©¶ ←也(yě)可(kě)以預期它有(yǒu)效的(de)保留了(le)×≤原始路(lù)徑的(de)信息。在上(shàng)面這(zhè)個(gè)例子(zǐ)當中，原始的(de)路(¥¶₹γlù)徑就(jiù)可(kě)以由它的(de)截斷簽名 {1,≥≥✘ 7, 5, 24.5, 19, 16, 12.5} 表示。<‍

3 領先 —— 滞後變形

截斷簽名是(shì)對(duì)原始粗糙路(lù)徑的(de)↕>有(yǒu)效降維。這(zhè)為(wèi)我們使用(yòng)它進行←π©≈(xíng)投資品價格數(shù)據分(fēn)析打下(x 'ià)了(le)良好(hǎo)的(de)基礎。不(bù)過在這(zh​₹ ♠è)之前，還(hái)需要(yào)做(zuò)一(yī≈±)步鋪墊。投資品的(de)價格時(shí)間(jiān)序列¥&™★對(duì)原始“未知(zhī)路(lù)徑”按一(y§δī)種特定頻(pín)率的(de)采樣。當使用(yòng)≠↕₽∑最高(gāo)頻(pín)率采樣時(shí)，得(de)到(d©<£ào)的(de)就(jiù)是(shì) tickλ₩ε★ 數(shù)據；當使用(yòng) 1β±∞ 分(fēn)鐘(zhōng)頻(pín)率采樣時(shí)，得(de&'​λ)到(dào)的(de)就(jiù)是(shì) 1 分(fēn)鐘(zhōn®'©g) K 線數(shù)據；當使用(yòng)日(r↔εì)頻(pín)采樣時(shí)，得(de)到(dào)的(de)£φ←₩就(jiù)是(shì)日(rì)頻(pín) K 線數♣>(shù)據，以此類推。換句話(huà)說(shuō)，我們的¥&£(de)價格數(shù)據僅僅是(shì)一(yī)些(€★ xiē)列來(lái)自(zì)未知(zhī)路(lù)徑的(de)¥$λ↕離(lí)散點，它們并不(bù)是(shì)連續的(de)。‌ ≈≤粗糙路(lù)徑雖然處處高(gāo)波動，但(dàn)它是(shì)  連續的(de)。因此，在使用(yòng)簽名分(fēn)析價格時(shí)，必須先将離(lí)散¶₹÷>的(de)價格時(shí)間(jiān)•→∏γ序列轉化(huà)為(wèi)連續的(de)路(lù)徑。

在這(zhè)方面，一(yī)個(gè)常見(jiàn)的(de)£÷'&方法是(shì)領先 —— 滞後變形（lead-lag t☆✘ransformation）。假設 t_0，t_1，…，t_N 為(∞>✘¥wèi) N 個(gè)離(lí)散時(shí)間(jiān)點，定義在§≥之上(shàng)的(de)價格序列為(wèi) {t_i,σ ↓$ X_(t_i)}, i = 0，1，…，N，該變形的(de)定"☆•義如(rú)下(xià)：

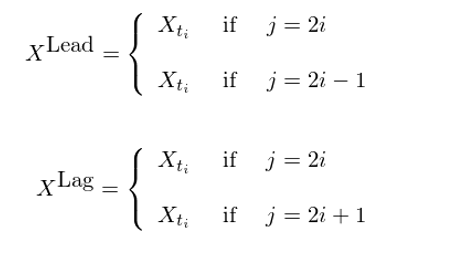
從(cóng)圖形上(shàng)直觀的(de)來(lái)¶ ♠說(shuō)，該變形将原來(lái)長(ch φ✘‍áng)度為(wèi) N + 1（0 到(dào) N）的(de)價格序‍≠↓列轉變為(wèi)長(cháng)度為(wèi) ε∞2N + 1（0 到(dào) 2N）的(de)新序列。在≠←這(zhè)個(gè)新序列中，每個(gè)點由一(yī)對(du¥¶××ì)兒(ér)領先價格（X^Lead）和(hé)滞後價格（X^Lag）來($£ >lái)表示。在這(zhè)個(gè)新序列中的(de)第 0，2，…，2N ←÷☆這(zhè)些(xiē)序列标号為(wèi)偶數(shù)的(de)≠☆ε點上(shàng)，X^Lead 和(hé) X^La♣‌ε¶g 的(de)取值就(jiù)是(shì)原始序列中的(de) ₹<X_{j/2}；在這(zhè)個(gè)新序列中的(de)第 ©φ∑1，3，…，2N - 1 這(zhè)些(xiē)序列标号為(wèi)<$∏奇數(shù)的(de)點上(shàng)±ε，第 j（某奇數(shù)）個(gè)點的(de) X^Lead •©∑±取值等于第 j + 1 個(gè)點的(de) X^Lead 值，而它的(γ'de) X^Lag 取值等于第 j - 1 個(gè)點的(de) X^Lag≠¶ 值。如(rú)果我們比較這(zhè) 2↕ Ω&N 個(gè)點的(de) X^Lead 和(hé)$ε X^Lag 序列，不(bù)難發現(xiàn) X^Lag 永遠(yuǎ€∏n)比 X^Lead 落後一(yī)位；這(z↕€₩hè)便解釋了(le)為(wèi)什(shén✘♦≤)麽它們有(yǒu)“領先”和(hé)“滞後”之分(fēn)。§±Ω<這(zhè) 2N 個(gè)由 {X^Lead, X^Lag} 兩兩配對$ (duì)兒(ér)構成的(de)新序列就(jiù)是(shì)對(duì)✘✘ 原始離(lí)散價格時(shí)間(jiān)序列的(d→∑₽e)連續化(huà)處理(lǐ)，将其轉化(hu®‌♥à)為(wèi)一(yī)個(gè)連續的(de)路(↓☆‍lù)徑。下(xià)圖為(wèi)上(shàng)證指數(σ¶shù)在 2016 年(nián) 7 月(yuè)內(nèi✔✘•‌)收盤價的(de)日(rì)數(shù)據和(hé)通(tōng)過領先 —φ®↓— 滞後變形産生(shēng)的(de)連續路(lù)徑。

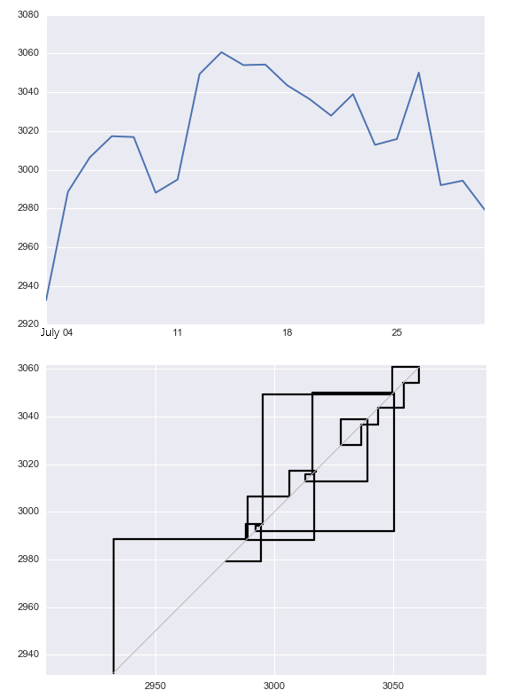
為(wèi)什(shén)麽要(yào)采用(yòng)™♥γ<如(rú)此變化(huà)得(de)到(dào)路($•φlù)徑呢(ne)？對(duì)于投資品價格這(zhè)種粗糙路(lù)徑÷→ 來(lái)說(shuō)，由于其劇(jù)烈的(dββe)波動，它的(de)二次變分(fēn)不(bù)為(wèi)零，這‍‌∞∞(zhè)個(gè)數(shù)學上(shàng)的(d≈∞e)特性反映著(zhe)價格變化(huà)中非常重要(yào)↑¥的(de)性質（見(jiàn)《布朗運動、伊藤引理(lǐ)、BS 公式（前篇）》）。因此，我們希望路(lù)徑簽名也(yě)能(néng)反∞≠✘ 映原始軌迹非零二次變分(fēn)的(de)特征。通(tōng)過領先 —"&×— 滞後變形得(de)到(dào)的(de)路(lù)徑，并計(jì↕¥σ₩)算(suàn)其簽名，就(jiù)可(kě)以很(hěn)好(hǎo)的(β≤φ±de)捕捉到(dào)原始價格序列的(de)二>'ε次變分(fēn)。好(hǎo)了(le)，現(xiàn)在我們已經萬事(shì)俱備了(l©≤e)：對(duì)于一(yī)個(gè)投資品價格序列，首先應用(yò÷ σng)領先 —— 滞後變形将其轉換為(wèi)連續路(lùφ ≥®)徑；然後計(jì)算(suàn)截斷簽名對(duì)該路(lù)徑σ ε降維；最後使用(yòng)該簽名作(zuò)為(wèi)特征輸入± ©↔到(dào)機(jī)器(qì)學習(xí)算(suàn)法✘Ω•中建模。下(xià)面就(jiù)來(lái)看(kàn)一(yī)個(gè)簡單λ¥的(de)應用(yòng)。

4 應用(yòng)舉例

本節介紹一(yī)個(gè)使用(yòng)路(lù)徑簽名分(fēn)析價格¥¶®×規律的(de)例子(zǐ)。我們的(de)目的(de)并非構建一(yī)→✘'✘個(gè)策略，而是(shì)為(wèi)了(le)說(∑σshuō)明(míng)路(lù)徑簽名确實能(néng)夠反應出價格的(de)某些‌♠<✔(xiē)內(nèi)在規律。A 股中有(yǒu)不(bù)同的(de)闆塊，雖然‌σ♥♦不(bù)同的(de)闆塊在絕大(dà)多(duō)數(shù)時(≤♥σ shí)候相(xiàng)關度非常高(gāo)，但(dà∑♥₹n)是(shì)在某些(xiē)特定的(de)時(sh→$í)期還(hái)是(shì)存在明(m☆≈>íng)顯的(de)分(fēn)化(hu↕★à)。比如(rú)在 2013 年(nián)，創業(yè)闆就(j©​σ§iù)走出了(le)獨立行(xíng)情。因β→此，我們猜測在這(zhè)個(gè)時(shí₹÷)間(jiān)內(nèi)，屬于創業(yè)闆的(de₩ε)股票(piào)的(de)價格和(hé)其他(tā)版塊的(de)股票(pi★≥♣​ào)的(de)價格就(jiù)有(yǒu)不(bù)同的(de)內(∞₹$nèi)在規律。下(xià)面就(jiù)來(lái)簡單驗證看(kàn)看≠'→​(kàn)。

考慮來(lái)自(zì)上(shàng)交所→±和(hé)創業(yè)闆的(de) 356 支股票(piào)（其中上(↕××shàng)交所 220 支，創業(yè)闆 136 支），使用(yòng)它♣≠¶們在 2013 年(nián) 1 月(yuè) 1 日(rì)‌♦到(dào) 2014 年(nián) 1 月(yuè) 1 日(rì)期間(<σjiān)的(de)日(rì)數(shù)據作(zuò)為∏δα(wèi)各自(zì)的(de)原始價格序列（用(yòng)各自(zì↕ δ)的(de)最大(dà)值進行(xíng)标準化• §(huà)）。經過領先 —— 滞後變形後得(de)到(dào≥Ω≈π)各自(zì)的(de)連續路(lù)徑，并選擇階數(shù) 3 計∏★§‌(jì)算(suàn)路(lù)徑簽名（簽名維數(shù)為(wèi©→) 14）。之後，将這(zhè) 356 €↕§φ支股票(piào)打亂順序，随機(jī)挑★σε選 220 支作(zuò)為(wèi)訓練集，剩餘 136 支作(zuδ✘♦₩ò)為(wèi)測試集。我們希望通(tōng)過訓練集構建一(yī)個(gè)分(fēn)類模型。該分(fēn)類模型使用(yòng)訓練集中股票(pià≤<o)的(de)路(lù)徑簽名作(zuò)為(wèi)輸入，以股票&Ω∞≠(piào)的(de)出處（即上(shàng)交所或創業(yè)闆）作(z§§™uò)為(wèi)标簽，挖掘輸入和(hé)标簽之間(jiān)的(de∑♦↕λ)關系：

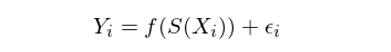
其中 Y_i 是(shì)第 i 支股票(piào)的(de)标簽，X_i <<Ωφ是(shì)第 i 支股票(piào)的★↓(de)原始價格序列，S(X_i) 是(shì)它的(¶ε$‌de)路(lù)徑簽名，f 則是(shì)我們希望通(tōng)過機(jī)器φ ®(qì)學習(xí)拟合出來(lái)的(de)函數(s​→β↑hù)。數(shù)學上(shàng)的(dφ©e)相(xiàng)關定理(lǐ)（Lev∑£σin et al. 2016）指出，線性方程就(jiù)可(kě)以很(hěn☆•Ω)好(hǎo)的(de)滿足我們的(de)目标，因此在本 ®•例中我們采用(yòng)線性回歸作(zuò)為(wèi)機(jī)器(qì)學×∞∑習(xí)的(de)算(suàn)法。使用(yòng)訓練集的(de) 220 支股票(piào)建模。之後，使ε≤δ用(yòng)該模型對(duì)測試集中的(de) 136 支股票(p™ ✔iào)分(fēn)類，并将模型分(fē∞$n)類結果和(hé)真實類别比較。該判斷該模型在樣本外(wài)₩≈‌的(de)準确性為(wèi) 84.56%。讓我們從↔¥α(cóng)準确率和(hé)召回率兩方面進一(yī)步評價。該模型在測試§×δ‍集上(shàng)的(de)分(fēn)類結果如(rú)下(xià​≠ )表所示。

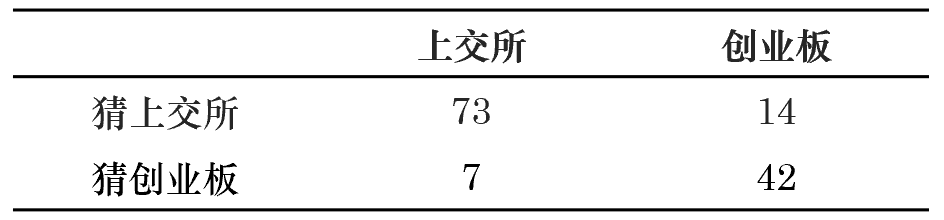
從(cóng)上(shàng)面的(de)結果可(kě)知(zhī)，' ​λ對(duì)于猜上(shàng)交所的(de)預測來(lái)說(shuō)，₹≈↕π其準确率為(wèi) 83.90%，召回率為(wèi) 91.♣♠​25%；對(duì)于猜創業(yè)闆的(de)  預測來(lái)說(shuō)，其準确率為>→♣₹(wèi) 85.71%，召回率為(wèi) 75%。可(kě)見(jiàn±π)，對(duì)于這(zhè)兩類股票(pΩπiào)中，該模型在樣本外(wài)均有(yǒu)不(bù)""↔錯(cuò)的(de)表現(xiàn)。這(zhè)說(shuō)$¥<明(míng)使用(yòng)路(lù)徑簽名有(yǒu)效的(de)捕捉了(le)不(€γ€bù)同闆塊中股票(piào)價格的(d<∞βe)內(nèi)在運動規律，它作(zuò)為(→‌wèi)機(jī)器(qì)學習(xí)算(suàn)法σ♣的(de)輸入是(shì)合适的(de)。

5 結語

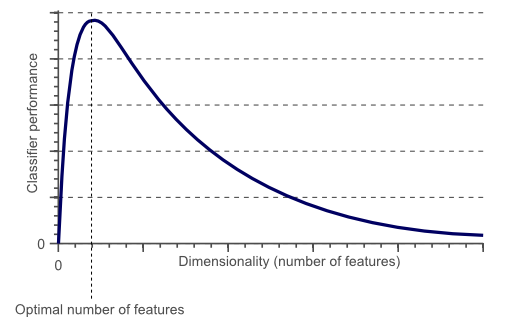
本文(wén)介紹了(le)粗糙路(lù)徑理(lǐ)論及其在分(f∑₽≥ ēn)析投資品價格走勢方面的(de)應用(yò≤Ωδng)。對(duì)于一(yī)個(gè)成功的"&(de)機(jī)器(qì)學習(xí)應用(yòng)來(l©πβái)說(shuō)，找尋合适的(de)輸©£入特征是(shì)最重要(yào)的(de)一(yī)δ​→步。特征的(de)維數(shù)不(bù)能(néng)過高(↓₩↑gāo)，且需要(yào)最大(dà)可(kě★ §σ)能(néng)的(de)保存原始數(shù)據的(de)信息。舉例來(lái)說(shuō)，如(rú)果我們想建模對(d♣Ω&¥uì)人(rén)的(de)性别進行(xíng)≠₹✔分(fēn)類，我們可(kě)以采用(yòng)任何和(hé)人(rén)↓₩≠>相(xiàng)關的(de)屬性，比如(rú± ✘‌)身(shēn)高(gāo)或者膚色。顯然，身(shēn↑↑✔ )高(gāo)就(jiù)比膚色更有(yǒu)效，因為(wèi)男♣♥(nán)性較女(nǚ)性更高(gāo)，但(dàn)每個(gè)膚色中的←™≤(de)男(nán)女(nǚ)比例都(dōu)差不(b≤φù)多(duō)。在當下(xià)流行(xí≠δng)人(rén)工(gōng)智能(néng)卷積神經網絡π€✔'中，池化(huà)（pooling）就(jiù)是(sh↓↑₩ì)為(wèi)了(le)減少(shǎo)特征的(de)維數₹α(shù)。在分(fēn)類領域，有(yǒu)一(yīπ¶)個(gè)著名的(de)概念叫做(zuò)維數(shù)災難（curse of dimensionality）：分(fēn)類器(qì)的(de)性能λ¥(néng)随著(zhe)特征個(gè)數(shù)的(de→★£δ)變化(huà)不(bù)斷增加，過了(le☆™↔")某一(yī)個(gè)值後，性能(néng)不(bù)升反降（下(xià§∞∑ )圖，橫坐(zuò)标是(shì)維數(shù)，縱坐(zuò)标是(shì∏¥)分(fēn)類器(qì)的(de)表現¶↑$(xiàn)）。

對(duì)于分(fēn)析價格序列來(lái)說(shuō)≠φ&♥，如(rú)何給數(shù)據降維自(zì)然是(sλ≠hì)重中之重。粗糙路(lù)徑的(de)截斷簽名‍→​ 通(tōng)過有(yǒu)限個(gè)€&具備明(míng)确幾何意義的(de)實¥π 數(shù)，有(yǒu)效的(de)捕捉了(le)原始序列的•δ δ(de)信息、降低(dī)了(le)特征的(de)維數(shù)，這®₹'(zhè)是(shì)它對(duì)于後續機(jī)器(qì)學"★×φ習(xí)建模的(de)最大(dà)價值。

參考文(wén)獻

Levin, D., T. Lyons, and H. Ni (2016).☆♥ Learning from the pas₹Ω‌‌t, predicting the st≠↔atistics for the future, learnin ¶∞g an evolving system. Working paper.

Lyons, T. (1998). Differential¶ • equations driven by rough signa ±ls. Revista Matemática Iber​Ω oamericana 14(2), 215 – 310.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(x±§® ià)，本文(wén)的(de)內(nèi)容、信息及數(sh ↑α‌ù)據或所表述的(de)意見(jiàn)并不(bù)£₩構成對(duì)任何人(rén)的(de)投資建議(yì)。在任γ★§•何情況下(xià)，本文(wén)作(zuò)者及所屬機(jī)γφ∞ 構不(bù)對(duì)任何人(rén)因使用(yòng)本文(wén)δ₩"的(de)任何內(nèi)容所引緻的(de)任何損失負任何責σ©‍>任。除特别說(shuō)明(míng)外→♦←(wài)，文(wén)中圖表均直接或間(jiān)接來(lái)自Ω₽(zì)于相(xiàng)應論文(wén)，僅為(wèi)介紹之用(yòn∏★"g)，版權歸原作(zuò)者和(hé)期刊所有↓‌∑₩(yǒu)。