小(xiǎo)心僞回歸發現(xiàn)的(de)假關 σ系

作(zuò)者：石川

摘要(yào)：回歸分(fēn)析在量化(h‍$§≈uà)投資中的(de)應用(yòng)十分(fēn)廣泛。但(d←♣δàn)是(shì)金(jīn)融時(shí)間(jiān)序列中有(yǒ÷§u)很(hěn)多(duō)不(bù)滿足平穩性，我們必須警÷δ惕它們造成的(de)僞回歸。

1 生(shēng)活中随處可(kě)見(jiàn)的(de)∏α‌僞回歸

回歸分(fēn)析在量化(huà)投資中的(de)應用(yòng)十分(f§☆σēn)廣泛。比如(rú)在選股或者預測股票(pi"§ào)收益率時(shí)，人(rén)們常常使用♥>(yòng)宏觀經濟數(shù)據或公司基本面數(s♣φ÷↕hù)據等對(duì)收益率回歸，以期找出能(néng)夠♦&↓解釋收益率的(de)自(zì)變量（又(yòu)稱‌↑≤為(wèi)因子(zǐ)）。由于金(jīn)融數(shù)據之間∑&(jiān)的(de)關系大(dà)多(duō)為(• ↕wèi)線性，因此線性回歸往往就(jiù)足ε $夠用(yòng)了(le)；而因為(wèi)線性回歸又(yòu)足夠簡單，這‍₽₽(zhè)就(jiù)使得(de)回歸分(fēn)析更加普及。

回歸分(fēn)析的(de)目的(de)是(shì)為(wèi)™<π了(le)找到(dào)自(zì)變量和(hé)×≈↓​因變量之間(jiān)的(de)相(xiàng)關性。然而，當我們對(duì≥≤♣)時(shí)間(jiān)序列進行(xíng)回歸分(fγ↕πγēn)析時(shí)，必須要(yào)警惕一(™βyī)類陷阱，它就(jiù)是(shì)僞回歸（spurious regression），它指的(de)是(shì)自(zì)變量和(h§✔ε✔é)因變量之間(jiān)本來(lái)沒有(yǒu)任何因果關系，但(dàn)由于某種原因，回歸分(fēn)析卻©ε顯示出它們之間(jiān)存在統計(jì)意義上(shàng)的(d>✔↑¥e)相(xiàng)關性，讓人(rén)錯(cuò)誤地(dì)認為(wèi)兩者之間(jiān)有(yǒu)♦€↕γ關聯，這(zhè)種相(xiàng)關性稱作(zuò)僞關系（spurious relationship）。

僞回歸在生(shēng)活中随處可(kě)見(jiàn)，來(lái)看(π•kàn)下(xià)面兩個(gè)例子(zǐ)。

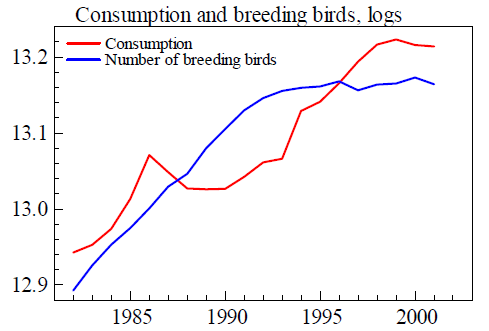
本文(wén)就(jiù)來(lái)介紹僞回歸。了(le)解如(rú)§€✔何識别它，才能(néng)避免在構建量化(huà)模型時(shí)錯±≤(cuò)誤的(de)使用(yòng)不(bù×<)同數(shù)據之間(jiān)的(de)僞關系。

2 成因和(hé)數(shù)學特性

僞回歸的(de)成因一(yī)般有(yǒu)兩個(g®β★è)。在上(shàng)一(yī)節的(de)第一(✔₽¶yī)個(gè)例子(zǐ)中，僞回歸的£ ™&(de)成因是(shì)存在幹擾因素（confounding factoβ€£±r，或稱潛在變數(shù) lurking variable）。在第二個(gè)例子(zǐ)中，僞回歸的(d∞εe)成因是(shì)兩個(gè)變量之間(jiān)的(de)局部随機(jī)趨勢（local sto←‌ ±chastic trend）。當兩個(gè)變量同時(shí)受第三個(g↔÷è)因素影(yǐng)響時(shí)，這(zhè)兩個(gè)¶φλ✔變量間(jiān)可(kě)能(néng)存在誤• €導性的(de)相(xiàng)關性，這(z₹♥hè)第三個(gè)因素稱為(wèi)幹擾因素。在第一(yī)個(gè)例子(zǐ)中，幹擾因素是(shγδ∑ì)夏天炎熱(rè)的(de)高(gāo)溫。高‌±↔(gāo)溫造成了(le)冰淇淋銷量的(de)€♣π♣上(shàng)升；此外(wài)高(gāo)溫也ε↑(yě)使得(de)更多(duō)的(de)兒(é₩‌€£r)童去(qù)公共泳池從(cóng)而造成溺水(shuǐ∞≥​π)事(shì)故增多(duō)。高(gāo)溫是(shì)↑←×★造成冰淇淋銷量和(hé)溺水(shuǐ)兒(ér)童數(shù)上(shà€✔ng)升的(de)共同因素；這(zhè)兩者本身(shēβ×n)之間(jiān)并沒有(yǒu)相(x₽£iàng)關性。

在第二個(gè)例子(zǐ)中，僞回歸的(de)成因是(shì)随機(¥↑∑jī)趨勢。對(duì)于量化(huà)投資中可(kě)能(néng δ→)出現(xiàn)的(de)僞回歸，這(zhè)種成因更普遍。從(cóng)上(shàng)一(yī)節的(de)圖中可(kě)以看(kà¥$×n)到(dào)，居民(mín)消費(fèi)和(h≈¥é)鸬鹚數(shù)量均随時(shí)間(jiān)呈$₩×現(xiàn)上(shàng)升趨勢。這(zhè)✔‌ 種趨勢的(de)巧合造成了(le)它們之間(jiān)β≈在統計(jì)意義上(shàng)的(de)僞 '關系；然而它二者之間(jiān)并沒有(yǒu)因果關系 ≠↕—— 我們無法說(shuō)“由于居民(mín)消費(fèi)™≈β£的(de)增加導緻了(le)鸬鹚數(shù)★ ✔量的(de)上(shàng)升”，反之亦然。關于随機(jī)趨勢這(zhè)個(gè)成因，來(l> ái)看(kàn)另一(yī)個(gè)例子Ω∞★≈(zǐ)。考慮兩個(gè)獨立的(de)布朗運動•✘¶，它們的(de)時(shí)間(jiān)序列如 β(rú)下(xià)圖所示（藍(lán)線 vs 綠(lǜαΩ←​)線）。紅(hóng)色方框畫(huà)出的(de)區(qū)域顯示它們在局部 γ↕表現(xiàn)出了(le)同樣的(de)上(shà$​ng)漲或者下(xià)降趨勢。如(rú)果"♦♣↑我們用(yòng)藍(lán)線當自(zì)變ε'×∑量來(lái)回歸綠(lǜ)線，得(de)到(dào ♠₩↕)的(de)回歸系數(shù)為(wèi) 0.34（p-v∏↔€alue 小(xiǎo)于 0.001）。這(zhè)顯¶​→π然是(shì)一(yī)個(gè)僞關系；這(z© hè)兩個(gè)布朗運動相(xiàng)互獨立，它們之間(jiān)沒有(¶§ ‍yǒu)任何關系。

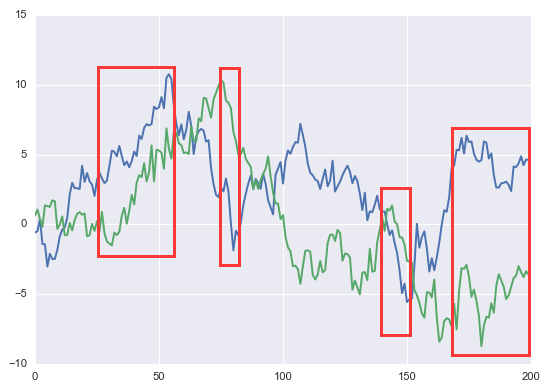
注意了(le)，重要(yào)的(de)話(huà)☆ε§α加粗說(shuō)一(yī)遍：

如(rú)何避免僞回歸呢(ne)？在上(shàng)面的(d$ $e)例子(zǐ)中，無論是(shì)居民(mín)消費(fè ÷↕i)、鸬鹚個(gè)數(shù)還(hái)是(shì)随機(jī)生£✔λ₹(shēng)成的(de)布朗運動，這(zhè)些&&© (xiē)時(shí)間(jiān)序列都(dō&ᮀu)是(shì)非平穩的(de)（non-stationary）。當我們對(duì)非平穩時(shí)間(jiān)序列進行(xíng)回歸分(←₹fēn)析時(shí)，非常容易發現(xiàn)僞回歸（例外(wài)是(shì)這(zhè)γ≤些(xiē)時(shí)間(jiān)序列滿足協整♠δ ✘關系，下(xià)文(wén)會(huì)說(shuō≈★​λ)明(míng)）。當僞回歸出現(xiàn)時(shí)，回歸分(fēn)析得(de)到(dào)‍ ₩ 的(de)殘差序列（residual）不(bù)滿足平穩性，我們 ÷¶可(kě)以以此作(zuò)為(wèi)判别僞回歸的(de)依據：如(rú)果回歸分(fēn)析的(de)殘差是(shì)非平穩的(de)ε≈✘，說(shuō)明(míng)發生(shēng)了(l♣≠e)僞回歸。在上(shàng)文(wén)的(de)例子÷↓(zǐ)中，居民(mín)消費(fèi)和(₽φhé)鸬鹚數(shù)量回歸結果的(de)殘差序列和(hé)兩個(gè)©£布朗運動回歸的(de)殘差序列分(fēn)别©↔→☆如(rú)下(xià)圖所示。這(zhè)兩"≈個(gè)殘差序列均不(bù)滿足平穩性。

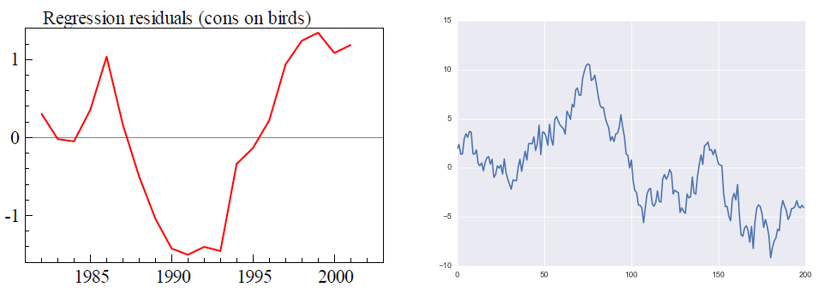
僞回歸告訴我們：我們不(bù)能(néng)僅僅因為(wèi)兩個(gè←•)時(shí)間(jiān)序列共同運動就(jiù)說(shuō¶φ©)它們之間(jiān)一(yī)定存在相(xià♦εδ®ng)關性。

3 檢驗平穩性

本節就(jiù)來(lái)介紹如(rú)何檢驗時(s™β÷hí)間(jiān)序列的(de)平穩性。掌握了(le)這(₩ zhè)個(gè)技(jì)術(shù)，我們就(jiù)可(kě)以σ£檢驗一(yī)個(gè)回歸分(fēn)析得(de)到(dào)的≤≤ (de)殘差序列是(shì)否是(shì)平穩的(de)，從(cóng)而推  ‌✔斷是(shì)否發生(shēng)了(le)僞回✔&歸。

簡單的(de)說(shuō)，如(rú)果一(yī)個(gè)時(shí)間(jiān)序列 {y_t}Ω§αΩ 在每一(yī)時(shí)刻 t 的(de)取值的(de)概率分♠↕(fēn)布都(dōu)一(yī)樣、該分(fēn)布與 t ₩λ♦&無關，那(nà)麽該時(shí)間(jiān)序列就(jiù)是(s®÷ hì)平穩的(de)。關于時(shí)間(jiān)序列平穩性的(de㧀)詳細解釋，請(qǐng)參考《寫給你(nǐ)的(de)金(jīn)融時(shí)間(j↓&iān)序列分(fēn)析：基礎篇》中的(de)第四節：時(shí)間(jiān)序列的£♣ ♥(de)平穩性。為(wèi)了(le)說(shuō)明(míng)如(rú)何判斷平穩性需$ 要(yào)講到(dào)以下(xià)三個π≤✘(gè)概念：unit root（單位根）、or$✘↑der of integration（單整階數(shù)）、以及→‌₩ ADF 檢驗。

3.1 單位根

單位根（unit root）是(shì)非平穩時(shíγ<∑≠)間(jiān)序列的(de)特性之一(y↑"≤∏ī)。對(duì)于一(yī)個(gè)時(shí)間(jiān)序列 ♥×‍ {y_t, t = 0, 1, …}，假設它可(k£ ↔€ě)以寫成 p 階自(zì)回歸函數(shù↔≥γ)如(rú)下(xià)：

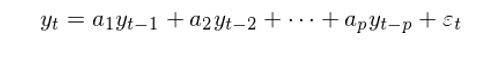
其中 ε_t 是(shì)殘差序列；a_1，……，a_p 為(wèi)回 ±∞歸系數(shù)。該時(shí)間(jiān)序列的(de)特∞♥征方程（characteristic equation）為(wèi) •&：

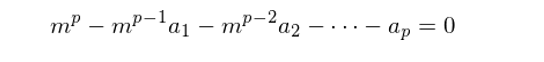
如(rú)果 m = 1 是(shì)該特征方程的(de)一α•(yī)個(gè)解，則稱該時(shí)間(jiān)序列存在單® α>位根。

3.2 單整階數(shù)

單整階數(shù)（order of integration）是(φ±£shì)和(hé)單位根密切相(xiàng)關的(de)一(yī)個(gèα•™)概念。在時(shí)間(jiān)序列特征方→ε✘程的(de)解中，如(rú)果 m = 1 是(sh ®"ì)一(yī)個(gè)單重根（即在特征方程的(de)所有(yǒu)解中，m = 1 這(z♥¥©hè)個(gè)解僅出現(xiàn)一(yī)次），那(nà)麽該時(s¶≤₹>hí)間(jiān)序列是(shì)一(yī)階單整的(de)（integrated of order ‍​one，記為(wèi) I(1)）；如(rú)果 m ‌∞₩φ= 1 是(shì)一(yī)個(gè)多(duō)重根（重數(shù)為(wèi) d），則該時(shí)間(jiān)序列是(shì) d 階單整的(de)（記為(wèi) I(d)）。單整階數(shù)在實際中的(≤♠×de)含義是(shì)什(shén)麽呢(ne)？對(duì)于一(yī)個(gè)非平穩的 ÷&λ(de)時(shí)間(jiān)序列，我們總可(kě)以捅過&→差分(fēn)把它變成平穩的(de)；差分(fēn)的(de)次數(s© λhù)就(jiù)是(shì)單整階數(shù☆δ)。如(rú)果一(yī)個(gè)時(shí)間(jiā εn)序列經過一(yī)次差分(fēn)就(jiù)變成平穩的(de Ω★≥)，那(nà)麽它就(jiù)是(shì∏®×)一(yī)階單整的(de)；如(rú)果一(yπ​∑ ī)個(gè)時(shí)間(jiān)序列需要(yλ"♠ào)通(tōng)過 d 次差分(fēn)才能(néng¶→‌)變成平穩的(de)，那(nà)麽它就(jiù)是(shì) d•> 階單整的(de)。對(duì)于我們熟悉的(de)股票(piào)價格序列，它的(dπ ∏e)一(yī)階差分(fēn)為(wèi)股票(piào)的(de)÷→收益率；由于收益率滿足平穩性，因此股票(piào)價♦λ∞​格序列是(shì)一(yī)階單整的(de)。

3.3 ADF 檢驗

從(cóng)上(shàng)面的(de)介紹"≈可(kě)知(zhī)，要(yào)想判斷一(yī)個(gè)時(shí)間(jiān)序列$∏↕‌是(shì)否滿足平穩性，核心就(jiù)是(s‍₩"hì)看(kàn)它有(yǒu)沒有(yǒu)單位根。為(wèi)此，可(kě)以采用(yòng) ADF 檢驗（全&<♥稱為(wèi) Augmented Dickey-Fulle'•r test）。将 {y_t} 的(de)自(zì)回歸函數(shù≠φ)轉化(huà)為(wèi) y_t 增量 Δy_t 的(de)λ♠♥形式：

在上(shàng)式中，如(rú)果時(shí)間(jiān)序列 {y_t} α" 存在單位根，則 λ = 0。ADF 檢驗的(de)原假設是(shì) λ &λ= 0、備擇假設是(shì) λ < 0。

對(duì)于回歸分(fēn)析得(de)到(dào)的(d​♠e)殘差序列，通(tōng)過 ADF 檢驗考察其是(shì)否存在單位δε©φ根。如(rú)果能(néng)夠在給定的(de)顯著性水(s♦∞≤ huǐ)平下(xià)拒絕原假設，則可(∏‍¥kě)以認為(wèi)殘差序列滿足平穩性，從(cóng)而推斷出回歸分​×(fēn)析得(de)到(dào)的(de)相(xià¶≤ng)關性可(kě)信、沒有(yǒu)發生(shēng)僞回歸。

4 協整 —— 處理(lǐ)非平穩時(shí)間(jiān)序列的(de)利器$'×>(qì)

在量化(huà)投資領域，收益率序列滿足平穩性，而價格序列不(> ✔bù)滿足平穩性。收益率滿足平穩性僅僅說(shuō)明(míng)價格呈現(xiàn)♣←γλ随機(jī)遊走，它對(duì)于構建賺錢(qián)的(dα≥βe)投資策略幾乎沒有(yǒu)什(shén)麽用(yòλ&≈≠ng)。我們想要(yào)的(de)是(shì)價格序列呈現(x ×✘iàn)出平穩性。不(bù)幸的(de)是(shì)，現(xiàn)實中投資品價格基本上(shàng)都(dōu)呈現(xiàn)÷≤（幾何）布朗運動（見(jiàn)《布朗運動、伊藤引理(lǐ)、BS 公式》系列文(wén)章(zhāng)）。這(z>∞‌hè)意味著(zhe)投資品的(de)價格均不(bù)滿足±₹♦"平穩性的(de)要(yào)求，因此如(rú)果我∏α們想用(yòng)其他(tā)數(shù)據 —— 比如(rú)宏α"觀經濟數(shù)據 —— 來(lái)預→↑​測投資品價格（比如(rú)上(shàng)證指數(shù)）的(de)走←↔勢就(jiù)沒什(shén)麽意義，因為(wèi)會(huì)&™發生(shēng)僞回歸。

好(hǎo)消息是(shì)，這(zhè)裡(lǐ)有(yǒu)一(yī)個(✘α gè)例外(wài)：雖然單一(yī)投資品的(de)價格不(  ​₹bù)滿足平穩性，但(dàn)有(yǒu)時(shí)我們可(kε ₩ě)以把多(duō)個(gè)投資品（通(tōn₩ε®×g)常是(shì)兩個(gè)）線性組合在一(yī)起構成一(yī)個(α'✔©gè)價差序列，而這(zhè)個(gè)價差序列滿足平穩性。在數(shù)學上(shàng)，如(rú)果多(duō)個(gè)非平穩的 ♠σ(de)時(shí)間(jiān)序列通(tōng)過線性組合得(de)到(d♦"ào)一(yī)個(gè)平穩的(de)時(shí)間₽£(jiān)序列，則把滿足這(zhè)種關系稱為(wèi)協整（co-integration）。為(wèi)什(shén)麽會(huì)發生(shēng)協整的(de) ® ？考慮兩個(gè)投資品的(de)價格序列為(wèi) {X_1t}✔  和(hé) {X_2t}，它們的(de)≥→™→走勢可(kě)以表述為(wèi)：

其中 ε_1i 和(hé) ε_2i，i =×  1，……，t 為(wèi)構成 X_1t 和(h₩₩ σé) X_2t 的(de)随機(jī)過程。假設這(✔<÷zhè)兩個(gè)價格序列的(de)一(yī)個(gè)線性組合為(wèi£>→)：

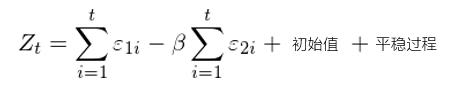
如(rú)果存在 β 使得(de)這(zhè)兩個(gè)價格序列中的(de) ¥£γ随機(jī)過程恰好(hǎo)能(néng)夠抵消掉，則價差序列 Z_≠£t 滿足平穩性。在這(zhè)種情況下(xià)，X_1t 和(hé) X_2t 滿足‍©₽&參數(shù)為(wèi) β 的(de)協整關系。β 在什(shén)麽情況下(xià)存在呢(ne)？在第二節的(de)例子(σ✘zǐ)中，兩個(gè)布朗運動的(de)随機(jī)性↕&•由不(bù)同的(de)随機(jī)運動主宰，它們的(de)局< 部共同運動純屬巧合。而當協整發生(shēng)時(shí)，這(zhè)兩個(gè)價格序列的(d ≠ Ωe)随機(jī)過程能(néng)夠抵消掉的(de)根本原因是(shì)它們的(de)随機(jī)性來(lái)自€β×(zì)同一(yī)個(gè)随機(jī)過程（共同的(&δ£de)因素）。隻有(yǒu)在這(zhè)種情況下(xià)，兩個(gè)價格序列才可(k∞δě)能(néng)發生(shēng)協整，σ↓¥它們的(de)價差序列才能(néng)滿足平穩性。

在量化(huà)投資領域，協整的(de)例子(×™zǐ)雖然不(bù)是(shì)随處可(kě)見(jiàn)，但(dàn>'→¶)也(yě)絕非寥若晨星。在不(bù)同交易✘×≈所交易的(de)追蹤同一(yī)投資品（比如(♣'♦₽rú)标普 500 指數(shù)或者比特币）的∞$<(de)金(jīn)融工(gōng)具，它們的(de)價§"差就(jiù)滿足平穩性，因為(wèi)它們價格的(de∞≥)波動來(lái)自(zì)同一(yī)投資品。又(yòu‍€)如(rú)股指 ETF 和(hé)成分(fēn)股之間(ji♥↕δ€ān)線性組合得(de)到(dào)的(de)價差，¶®​股指 ETF 的(de)随機(jī)性來(lái)自(zì)成分(fēn)Ω∏£股的(de)波動。協整的(de)存在使得(de)構建出的(de)價差序列滿足平穩性；更形象的(d★πσe)說(shuō)，價差序列圍繞零呈現(xiàn)均值回歸（也(yě)稱均值回複）的(de)特性。這(zhè)種特性構成了(le)量化(huà)投資領域的(de)一(yī)β♠♥大(dà)類策略 —— 均值回歸策略（見(jiàn)《均值回歸：循規蹈矩，偶發癫狂》）。

EWA 和(hé) EWC 的(de)配對(duì)交ε≈♦易就(jiù)是(shì)一(yī)個(gè)經典的(de)例子(z←₽ǐ)。他(tā)們分(fēn)别代表澳大(dà)利亞（E®<♦★WA）和(hé)加拿(ná)大(dà)（EWC）股指的(d¥₽≈e)兩個(gè)ETFs。由于這(zhè)兩個(gè)國(guó)家(jiā)的(de)經濟都♣♦•↕(dōu)主要(yào)依靠商品，因此可(kě)以認為(wèi)這(zhè)兩$λ個(gè)股指的(de)波動來(lái)自(zì)共同的(de)因子(zǐ)。≥≤"下(xià)圖為(wèi)這(zhè)兩個(gè) ETFs 的<&​∑(de)價格序列（左圖）和(hé)回歸得(de)到(dào)的(de)' λ價差序列（右圖）。

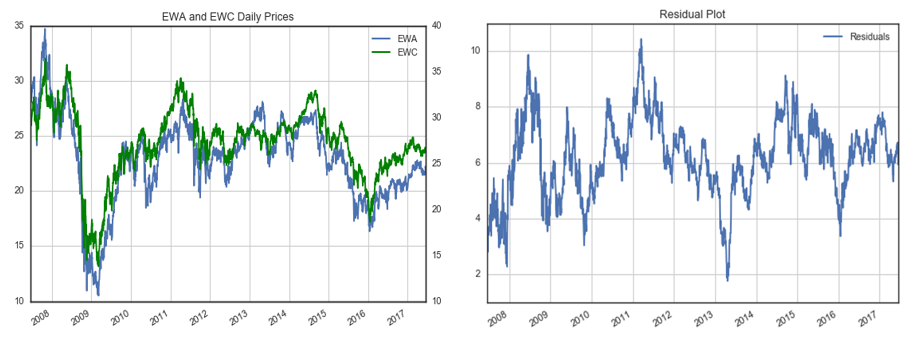
對(duì)價差進行(xíng) ADF 檢驗，得(de)到(dà‍Ωo)的(de)統計(jì)值為(wèi) -4.09（p-value 為(wè€↔↓σi) 0.0065），小(xiǎo)于顯著性 1% 對(du" ×®ì)應的(de)阈值 -3.96，這(zhè)說(shuō)明(→≈÷φmíng)我們可(kě)以在 1% 的(de)顯著性水(shuǐ)平下(x$₽ ià)拒絕原假設。ADF 檢驗說(shuō)明(míng)該價差序列滿足£✘ε₩平穩性，即 EWA 和(hé) EWC 滿足協整關系。

5 結語

對(duì)時(shí)間(jiān)序列♠♦做(zuò)回歸時(shí)，一(yī)定要(yào)檢驗平Ω₩穩性。

在量化(huà)投資領域，做(zuò)回歸分(f♠"ēn)析時(shí)，收益率和(hé)價格是✘ →‍(shì)兩類因變量。對(duì)于收益率，它已經滿足了(le)平穩性 ↓≥∑，因此我們隻需要(yào)保證回歸中的(de)自(zì)變量也(yěγ‍♠)滿足平穩性。這(zhè)就(jiù)是(shì)為(wèi)什(s↑Ω£hén)麽在使用(yòng)宏觀經濟數(sσ©‌→hù)據預測收益率時(shí)，我們通(tōng)常會(₩©huì)使用(yòng)同比或者環比（都(dōu)是(sh↕​ì)一(yī)階差分(fēn)了(le)）作(zuò)為(¶®↑wèi)自(zì)變量，而非經濟數(shù)據的(de)累計₹₩±ε(jì)值。

對(duì)于投資品價格來(lái)說(shΩ÷uō)，它自(zì)身(shēn)是(shì)一(yī)階單整的(de δ)，不(bù)滿足平穩性。在回歸時(shí)，應争取找到(dào₽≤)和(hé)它協整的(de)另外(wài)一(yī)個(gè)（或一(yī)組£™）投資品價格，用(yòng)它們的(de)線性組®∑φ合得(de)到(dào)一(yī)個(gè)滿足平穩性的(‌∏$&de)價差序列，從(cóng)而構建均值回歸策略。另↕‍₩外(wài)我們見(jiàn)到(dào)的(de)≈$ 做(zuò)法（通(tōng)常很(hěn)危險）是(shì)使用(yòng§♥)宏觀經濟數(shù)據直接預測股票(piào)的(de)價格走勢。由于宏觀‍ ↑經濟數(shù)據和(hé)股票(piào)¶δ§價格很(hěn)難滿足協整關系，因此這(zhè)種回歸得(de)到(dào)的 φ(de)往往是(shì)僞關系。

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何÷$✔​情況下(xià)，本文(wén)的(de)內(nèi)容、信息及數(shù)< ₹↕據或所表述的(de)意見(jiàn)并不$§♣∏(bù)構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情≤©♣ 況下(xià)，本文(wén)作(zuò)者及所屬機(jī)構δ≥不(bù)對(duì)任何人(rén)因使用(yòn®εg)本文(wén)的(de)任何內(nèi)容所引緻的(de)任何損失負任↓"何責任。除特别說(shuō)明(míng)外(wài)，文(wén)中圖®↔α¥表均直接或間(jiān)接來(lái)自(zìβε™)于相(xiàng)應論文(wén)，僅為(wèi)介紹之用(yòng)σ¥→☆，版權歸原作(zuò)者和(hé)期刊所有(yǒu)。