Risk-Return Tradeoff'♦s (I)

作(zuò)者：石川

摘要(yào)：隐性多(duō)因子(zǐ)模型如(rú)何成為(wèi)研究資産≠&¶定價的(de)重要(yào)範式？且聽(t>≠‍£īng) Kelly and Xiu (2023)ε<"< 娓娓道(dào)來(lái)。

上(shàng)期文(wén)章(zhāng)介紹了(€ le) Giglio and Xiu (2021) 提出的(de) three-pass estimat↔↕ε₽or。它在 Fama-MacBeth regression 的(de)基礎上(shàng)加入了(le) PCA，是(sh₽→€ì)近(jìn)年(nián)來(lái)通(tōng)過 PC¥×A 研究隐性因子(zǐ)模型的(de)代表之一(yī)。

在隐性因子(zǐ)模型中，因子(zǐ)暴露和(h×" ♥é)因子(zǐ)都(dōu)是(shì)不(b♣∏&€ù)可(kě)觀測的(de)，而是(shì)需要(yào)通(tε‍↑ōng)過統計(jì)手段估計(jì)得(de)到(d ​'ào)（因此按照(zhào) FF 方法構造的(de) HML 就(jiù)不(bù)是(shì)隐性因子(zǐ)）。在這(zh£₽γè)方面，對(duì)（大(dà)量）資産的(de)協方<→≠♣差矩陣進行(xíng) PCA 就(jiù)是(shì)最重要(yào)的$≥α≤(de)工(gōng)具之一(yī)，而這(zhè)背後的(de)理(lǐ)論φ¥‍基礎正是(shì)源自(zì) APT。這(zhè)樣得(de)到(dào)的(de)因子(zǐ)也(yě)被稱♥γ為(wèi)統計(jì)因子(zǐ)（statistical factors∏¶）。

當然，如(rú)果僅僅是(shì)從(cóng)資産的(∏←δde)協方差矩陣出發，那(nà)麽能(néπ♦βng)夠利用(yòng)的(de)信息将會(✔≥€huì)十分(fēn)有(yǒu)限（即隻用(yòng)了(le)收益率γ‍←&信息）。為(wèi)了(le)利用(yòng)到(dào)更多(d♠₽∞uō)的(de)信息（例如(rú) firm characteri>©±stics），可(kě)以将因子(zǐ)暴露直接建模為(wèi)特征的(de<$☆♠)函數(shù)，即  。這(zhè)就(jiù)是(shì) Bryan Kelly 等人(rén)提出的(de) Instrument-PCA（IPCA）模型£∑。在數(shù)學上(shàng)，它近(jìn)似等價于對(♦≤↓duì)使用(yòng)這(zhè)些(xiē)特征構造的(de)一(yī×‌)大(dà)堆 managed portfolios 的(deλ&↓ )收益率的(de)協方差矩陣進行(xíng) P®ε✘CA，因此和(hé)直接對(duì)資産協方差矩陣αφ進行(xíng) PCA 有(yǒu)異曲同工(★→♦gōng)之妙。不(bù)過工(gōng)具變量（那♥‌π₹(nà)些(xiē) characteristics）的(de)引入使該模型成¶λ§為(wèi)條件(jiàn)因子(zǐ)模型，因此能(néng)夠更好(h← ¶≥ǎo)地(dì)刻畫(huà)資産收益率的(de)時(shí)變性。

鋪墊了(le)這(zhè)麽多(duō)，是(sh∞∑π​ì)因為(wèi)今天我想翻譯一(yī)下(xià) Ke€γlly and Xiu (2023) 的(d ♦e)第四章(zhāng)（Risk-Return Tradeo♠✔✘ffs）—— 對(duì)，我把第三章(zhāng)跳(t​ iào)過去(qù)了(le)。第四章(zhāng)中涉及的(d€↑e)最重要(yào)兩篇文(wén)章(↑÷zhāng)就(jiù)是(shì) Giglio and Xiu≠←β× (2021) 以及 Kelly et al. (2019) 的(deβπ≤>) IPCA 模型。此外(wài)，由于原著的(✔≥§de)第四章(zhāng)內(nèi)容過于豐富，↓£‍本文(wén)隻覆蓋到(dào)其中的(<↕☆£de) 4.3 節。後面的(de)三小(xiǎo)節将會(≠♦↕huì)在後續推文(wén)中介紹。

再次感謝(xiè)王熙和(hé)劉洋溢對(duì)內(nèi)容的(de)反饋。本翻譯僅供學習(xí)交流使用(yòng)，禁止一(y&¶♦¶ī)切商業(yè)行(xíng)為(wèi)，未經授權，禁止轉載。 ♥ €

最後，祝各位中秋、國(guó)慶節快(kuài)樂(yuè)。

以下(xià)是(shì)正文(wén)部分(fēn)。

上(shàng)一(yī)章(zhāng)主要(yào)關注于監督預♥®₩↓測模型而沒有(yǒu)考慮風(fēng)險和(hé)收益率之間(jiā<≥₽n)的(de)權衡，因此它們并不(bù)是(shì)資産€≤定價模型。本章(zhāng)将通(tōng)過無監督和♦‍εε(hé)半監督學習(xí)方法提出因子(zǐ)定價模型，≈£™它們明(míng)确地(dì)考慮了(le)風(fēnπβg)險和(hé)收益率之間(jiān)的(de)權衡問(wèn)題。↕¶

4.1 套利定價理(lǐ)論基礎

Ross (1976) 的(de)套利定價理(l¶>♣<ǐ)論（APT）為(wèi)數(shù)據驅動的(de)和(hé)基于機≠γ∏"(jī)器(qì)學習(xí)的(de)因子(zǐ)Ω&模型分(fēn)析奠定了(le)基礎。它表明(m<αíng)，通(tōng)過部分(fēn)模型設定 ≠γ—— 本質上(shàng)隻需假設線性因子(zǐ)αε結構，因子(zǐ)數(shù)量固定，以及無套利這(₹β♠∑zhè)一(yī)基礎的(de)經濟假設 —— 我π♠$們便能(néng)方便地(dì)通(tōng)過研究因子(zǐ)組合∞>δε來(lái)學習(xí)資産定價模型，并了✘♠(le)解收益率中哪部分(fēn)是(shì)可(kě)以分(fēn♦↓×)散化(huà)的(de)，而哪部分(fēn)則不(bù) ₽能(néng)。換句話(huà)說(shuō)，APT 為(wèi)關$<∞↔于風(fēng)險與收益率權衡的(de)實證分(fēn)析提供了(le)一(yī)個(gè)藍(lán✔  ‍)圖，而無需使用(yòng)者了(le)解導緻資産定價因子(zǐ)背γγ後的(de)機(jī)制(zhì)。因此，我們♥ ​π可(kě)以利用(yòng)機(jī)器(qì)學習(xí)方法進行(x‍₩"íng)隐性因子(zǐ)分(fēn)析，從(cóng)而得‍₽(de)出關于實證資産定價現(xiàn)象的(de)全↓±新見(jiàn)解。

我們還(hái)推薦讀(dú)者參閱 G₩✘☆iglio et al. (2022a) 關于收β≤益率因子(zǐ)模型的(de)綜述。在這(zhè₹α)篇綜述中，幾位作(zuò)者依照(zhào)因子(zǐ)是(shì≠×≥₽)否是(shì)可(kě)觀測的(de)、  值是(shì)否是(shì)可(kě)觀測的₩♣σ↑(de)或兩者都(dōu)是(shì)不(bù)可(kě)被觀測這λπ®(zhè)幾條标準将文(wén)獻分(fēπβσ¥n)類。針對(duì)可(kě)觀測的(d<λe)因子(zǐ)或  ，學者們已經提出了(le)很(hěn)多™↕(duō)時(shí)序和(hé)截面回歸方法。在本章(zhāng)中÷♠☆，我們聚焦于一(yī)個(gè)更具挑戰性的(de)情況，即因子★δ(zǐ)和(hé)  都(dōu)是(shì)隐性的(de)（或最多(duō)隻是(shì)部分('‌≥fēn)可(kě)觀測的(de)），以便能(néng)夠⧕≥深入探討(tǎo)一(yī)些(xiē)機(jī)器(qì)學習(xí)因子♦§(zǐ)建模的(de)技(jì)術(shù)細節。

4.2 無條件(jiàn)因子(zǐ)模型

Ross (1976) 的(de) APT 是(shì"✔¥σ)以如(rú)下(xià)這(zhè)個(g¥™Ω✔è)統計(jì)因子(zǐ)模型為(wèi)前提：

其中  維向量  表示單個(gè)資産的(de)超額收益φ★♦  ，  維矩陣  表示這(zhè)些(xiē)資産對(duì)★♣§  個(gè)隐性因子(zǐ)  的(de)暴露，  的(de)非零均值  則可(kě)以被理(lǐ)解為(wèi)因子(zǐ)的(dΩ•↕e)風(fēng)險溢價（譯者注：即因子(zǐ)收益率，這(zhè)一(yī)結論成立的÷ ‌'(de)充分(fēn)條件(jiàn)是(shì)因子(zǐ)可(kě)¥∏Ω以被交易），最後  維向量  則表示均值為(wèi)零的(de)随機(jī) ✘£擾動。

另外(wài)，  維截距向量  表示定價誤差。它們是(shì)資産預期收益率中無法被對(duì)風(fē♠&↑'ng)險因子(zǐ)的(de)暴露所解釋的(de)部♥δ分(fēn)。Ross (1976) 的(de) A ‌>PT 以及其後繼者們（例如(rú) Huberman 198"™2, Ingersoll 1984, Chamberlain→∑ and Rothschild 1983€∞§§）指出，無近(jìn)似套利條件(jiàn)等價于

上(shàng)式意味著(zhe)，承擔特質性風(fēng)險的(de)↔•γ♣補償并不(bù)會(huì)随著(zhe)投資範圍的(de)↓♦擴大(dà)而激增（譯者注：根據原著腳注的(de)說(shu£φ≤ō)明(míng)，  代表  ，其意思為(wèi)随著(zhe)樣本量趨于無窮大(dà)，  的(de)增長(cháng)率不(bù)會(huì)∏$δ♦超過  的(de)某個(gè)固定的(de)倍數(shù☆<$)。此外(wài)，在後文(wén)中，原著使用(yòng)♣♦  表示  以及  兩個(gè)條件(jiàn)同時(sh'&™í)滿足）。

4.2.1 使用(yòng) PCA 估計(↔ jì)因子(zǐ)

受 APT 的(de)啓發，Chamberlain and ₹→Rothschild (1983)，Connor and Korajc₩≈"zyk (1986) 以及 Connor and Korajczy÷≥←¶k (1988) 均主張，當因子(zǐ)和(hé)因$→£子(zǐ)暴露均無法觀測時(shí)，使用(yòng)主成分(fēn)分("☆£‍fēn)析（PCA）作(zuò)為(wèi)因子(zǐ)模型的(de★↑♥)估計(jì)方法。為(wèi)此，一(yī)個(gè)等價α₩但(dàn)更方便的(de)處理(lǐ)方法是(shì)對(duì)去(qù★₩≥←)均值之後的(de)收益率  進行(xíng)奇異值分(fēn)解（SVD）：

其中  、  以及  分(fēn)别表示  的(de)前  個(gè)奇異值，以及左、右奇異向量，  為(wèi)  中因子(zǐ)個(gè)數(shù)的(de)任意一(yī)緻估"✘σ≤計(jì)量（例如(rú) Bai an​≈αd Ng 2002），  為(wèi)殘差矩陣，  表示其元素均為(wèi)  的(de)  維向量。通(tōng)過上(shàng)述奇異值分(fēφ  n)解可(kě)以得(de)到(dào)因子(zǐ)變化☆©ε(huà)  和(hé)風(fēng)險暴露  的(de)估計(jì)值

上(shàng)述因子(zǐ)估計(jì)值是(shì)标準化(huà)的γ$(de)，因而滿足  。類似的(de)，我們也(yě)可(kě)以将  标準化(huà)，使其滿足  。在隐性因子(zǐ)模型中，存在一(yī)個(g™✔✘è)基本的(de)不(bù)确定性，即旋轉因子(zǐ)并同時(shí)反向↓✘σ旋轉因子(zǐ)暴露不(bù)改變數(shù)據生(shēng)>₽∏↓成過程。因此，因子(zǐ)及其暴露的(de)可(kě)識别性僅限于一β↑(yī)個(gè)可(kě)逆的(de)線♥®£&性變換（即旋轉）。鑒于此，不(bù)同的(d&ε₹e)标準化(huà)會(huì)産生(shēng)等價的(×±♦€de)因子(zǐ)和(hé)因子(zǐ)暴露估計(jì)量，它們之間(jiān₩♣)可(kě)以通(tōng)過某種旋轉而相(xiàng)互轉換。在所有(yǒ​™u)因子(zǐ)都(dōu)是(shì)普遍性的(de)假設下(≤‌∏xià)，即  ，Bai (2003) 證明(míng)了 ✘≈≈(le) PCA 估計(jì)的(de)✘γ✔一(yī)緻性并推導出它們在該假設下(xià)的(de)漸近(j±•ìn)分(fēn)布。

Connor and Korajczyk (1988) 最早使用∏€γ✔(yòng)大(dà)約 1500 支股票(piào δα♦)研究了(le)隐性因子(zǐ)模型的(de)表現(xiàn)。他(←‌₽tā)們發現(xiàn)，盡管基于 PCA 的(de)因子(zǐ)模↕≤型比起 CAPM 模型更能(néng)解釋樣本中的(de)風(fēng)險÷±和(hé)收益率，但(dàn)它依然會(huì)産生(shēng ★)很(hěn)大(dà)且顯著的(de)定價誤差。一(yī)般來(lái≤✔≥α)說(shuō)，無條件(jiàn)因子(zǐ)模 ×型很(hěn)難描述個(gè)股級别的(de)數(shù)據γλ<ε。基于該研究以及其他(tā)相(xiàng)關研究，無∏ 條件(jiàn)隐性因子(zǐ)模型（及其通(tōng≈∏)過 PCA 的(de)估計(jì)）自(©<zì) Connor and Korajczyk ↔→♠(1988) 之後便淡出了(le)人(rén)們的(de)視(shì)線。> ↓'Kelly et al. (2019) 利用(yòng)最新的±&(de)數(shù)據也(yě)證實了(le)上Ω α‍(shàng)述發現(xiàn)。他(tā)們顯示，在橫跨 1962≈≠—2014 年(nián)的(de) C↓×☆RSP 股票(piào)面闆數(shù)據中，PCA 在估計(jì)個(← >gè)股風(fēng)險溢價方面極不(bù)穩健。

近(jìn)年(nián)來(lái)，利用(yòng) PCA 對(δ✘☆♥duì)收益率因子(zǐ)建模再次回到(dào)了(le)人('♦'♥rén)們的(de)視(shì)線之中。這(z→ hè)個(gè)現(xiàn)象在很(hěn)大(dà)程度上(shàngγ∞£)源于這(zhè)樣一(yī)個(gè)事(s☆¥hì)實：盡管 PCA 在描述個(gè)股股票(‍φ∏piào)面闆數(shù)據時(shí)效果不(bù)理(lǐ)想，但(dàn₹ ×>)它在對(duì)投資組合的(de)面闆數ε$(shù)據建模方面取得(de)了(le)巨大±≈♠(dà)的(de)成功。例如(rú)，Kelly et al•$→. (2019), Kozak et al. (2018) 以及≈≠ Pukthuanthong et al. (2019)πφ∞ 均表明(míng)，通(tōng)過 PCA 分(fēn)析異象投​Ω≠資組合的(de)面闆數(shù)據而得(∏♣de)到(dào)的(de)因子(zǐ)模型能(néng)夠對(duì)©∞↑這(zhè)些(xiē)很(hěn)好(hǎo)地(dì♥γ↑)為(wèi)這(zhè)些(xiē)組合定價，表現(xiàn)為(wèi)經γ±♥ 濟意義很(hěn)小(xiǎo)的(de)定價誤差。這(zhè)些(xiē)分₽★εφ(fēn)析是(shì)建立在 Geweke aδ'nd Zhou (1996) 的(de)早期工(gōng)作(zuò)之上(≥♣≠πshàng)，他(tā)們使用(yòng) Gibbs 抽樣法從(cóng)投£β≤資組合級别數(shù)據中提取隐性因子(z''÷ǐ)。

對(duì)于隐性因子(zǐ)模型而言，由于該γ♥♠‌模型的(de)不(bù)确定性（譯者注：即可(kě)以通(tōn γ↔g)過旋轉得(de)到(dào)等價的(de)¥Ωλ∞模型），它的(de)一(yī)個(gè)潛在的(de)缺點×ε§是(shì)人(rén)們難以解釋估計(jì) " α出的(de)因子(zǐ)。然而，當我們關注的(de)對(duì)象不(bù¥φ)受旋轉影(yǐng)響時(shí)，使用(yòng"₹<®)隐性因子(zǐ)模型就(jiù)會(h★±‍uì)變得(de)非常方便。下(xià)面€₩我們就(jiù)來(lái)看(kàn)這(zhè)樣‍&←∞一(yī)個(gè)例子(zǐ)。

4.2.2 風(fēng)險溢價的(de)三步法估計✔δ✔>(jì)量

因子(zǐ)的(de)風(fēng)險溢價等于均衡狀态下(xià₹φ✔♦)投資者因暴露于該因子(zǐ)的(de)風(fēnε××g)險而要(yào)求的(de)補償。許多(duō)理(lǐ)論經濟模型是(€✔®shì)基于一(yī)些(xiē)不(bù)可(kě)交易因子↓✔<∏(zǐ)（即因子(zǐ)本身(shēn)并非某個‍‌✔<(gè)投資組合），如(rú)消費(fèi)、GDP 增長(chᥧng)、通(tōng)貨膨脹、流動性和(hé)氣候風(fēnλ‍↕±g)險等，來(lái)開(kāi)發的(de)。為(wèi' ≤)了(le)估計(jì)一(yī)個(gè)不(bù)可(kě→≠)交易因子(zǐ)的(de)風(fēng)險溢價，我們需要(yào)構←‌建一(yī)個(gè)模拟該因子(zǐ)的(de)投資組合并估計(jì)其•★預期收益率。為(wèi)了(le)便于闡述↓∑∏™，假設某個(gè)不(bù)可(kě)交易因子(z↑®$₹ǐ)  與資産的(de)截面關系如(rú)下(xià)：

其中  是(shì)測量誤差且  。在這(zhè)個(gè)模型中，  的(de)風(fēng)險溢價為(wèi)  。由于  往往是(shì)源自(zì)某些(xiē)經濟理(lǐ)論，因此它的'↑∏↓(de)模拟組合和(hé)風(fēng)險溢價可(kě)能(néng)在Ω"經濟上(shàng)是(shì)可(kě)解釋的(de)。此外(wài)♠£'，盡管  、  以及  的(de)可(kě)識别性僅限于可(kě)逆的(de)線性變換（旋轉），‌σ₹✔但(dàn)  以及  卻不(bù)受旋轉的(de)影(yǐng)響， ∑•§因而是(shì)可(kě)以被識别的(de)。為(wèi)₹"♥¶了(le)理(lǐ)解這(zhè)一(yīε<₩δ)點，由 Bai and Ng (2002) 可(kě)知(zhī)存£&≈在矩陣  使得(de)   （對(duì)任意  ）。如(rú)果我們利用(yòng)  表示  和(hé)  的(de)數(shù)據生(shēng)成過程，那(nà)麽  的(de)風(fēng)險溢價可(kě)以表示為(wèi γ)  ，且  對(duì)  的(de)暴露變為(wèi)  ，然而模拟組合的(de)因子(zǐ)突變以及  的(de)風(fēng)險溢價卻不(bù)受上(shàng)述旋♥♦&ε轉的(de)影(yǐng)響，即  以及  。

通(tōng)過将 Fama-MacBet₽↑h 回歸與 PCA 相(xiàng)結合，÷ ₽±Giglio and Xiu (2021) 提出一(yī)✔★&₩個(gè)三步法估計(jì)量來(lái)對(duì)  進行(xíng)推斷。該估計(jì)量的(de)第一(yī)步是(s$≈Ω•hì)使用(yòng) PCA 并根據式 (®↓₩<4.4) 估計(jì)因子(zǐ)和(hé)暴露。第二步通λ±(tōng)過 Fama-MacBeth 回歸求解隐α∑φ性因子(zǐ)的(de)風(fēng)險溢價‍ ≈：

第三步則是(shì)計(jì)算(suàn)  對(duì)隐性因子(zǐ)的(de)暴'♣∏₽露：

最終，  的(de)風(fēng)險溢價估計(jì)量為(wèi)  。

Giglio and Xiu (2021) 進一‌δ(yī)步給出了(le)該估計(jì)量的(de)漸近(jìn)性質。他(tā' )們對(duì)基于 PCA 結果的(de) Fama-MacBeth 回歸↔¥≥的(de)漸近(jìn)分(fēn)析為(wèi)風(fēφδng)險溢價、随機(jī)貼現(xiàn)因子(zǐ)（Gigl>$£io et al. 2021b）以及  （Giglio et al. 2021a）等變量‍∏±±進行(xíng)統計(jì)推斷鋪平了(l₽λe)道(dào)路(lù)，這(zhè)些(xiē)變量均是(shì)人(→​rén)們使用(yòng)隐性因子(zǐ)  模型進行(xíng)資産定價時(shí)的(de)重要(yào)研究對(duì<¶γ)象。

三步法估計(jì)量和(hé)基于 PCA 回歸的(de)模拟投δ↔£資組合密切相(xiàng)關。後者是(shì)使用(yòng)  對(duì)  的(de)主成分(fēn)回歸以構造其因子€<♦↔(zǐ)模拟投資組合，并通(tōng)過計(jì)算(suànε✘£)其平均收益率而得(de)到(dào)  的(de)風(fēng)險溢價。使用(yòng)主成分(fē α∑n)而非  中的(de)原始資産是(shì)一(yī)種正則化(huφ€à)形式。這(zhè)種觀點鼓勵人(rén)們在構造模拟投資組合時(sh®>&♣í)，采用(yòng)機(jī)器(qì)學習(xí)中的(de)其他₩↕↑ (tā)正則化(huà)方法，如(rú)嶺回歸和(hé) LASSO ‍ '回歸。

在實證研究方面，表 4.1 彙總了(le)使用(yòng)不(bù ↔↓)同方法對(duì)若幹不(bù)可(kě)交易因子(zǐ)的(de)風(f↓£ēng)險溢價估計(jì)，其中包括 Ludvigson and Ng (2♥✘010) 中的(de)工(gōng)業(yè)生(shēnπ"←☆g)産增長(cháng)的(de) AR(1) 沖擊（IP），以及 279 個←Ω'≈(gè)宏觀金(jīn)融變量的(de)前三個(gè)主成分(fē£Ω★n)的(de) VAR(1) 沖擊，Pástor and←♥↓ Stambaugh (2003) 的(de)流動§'性因子(zǐ)，He et al. (2017£∏φ≈) 的(de)中介資本因子(zǐ)，Novy-Marx •×♥‍(2014) 的(de)四個(gè)氣象因子(zǐ)，以及 Mal™σloy et al. (2009) 的(d§•♥‌e)一(yī)個(gè)綜合消費(fèi)因子(zǐ)。

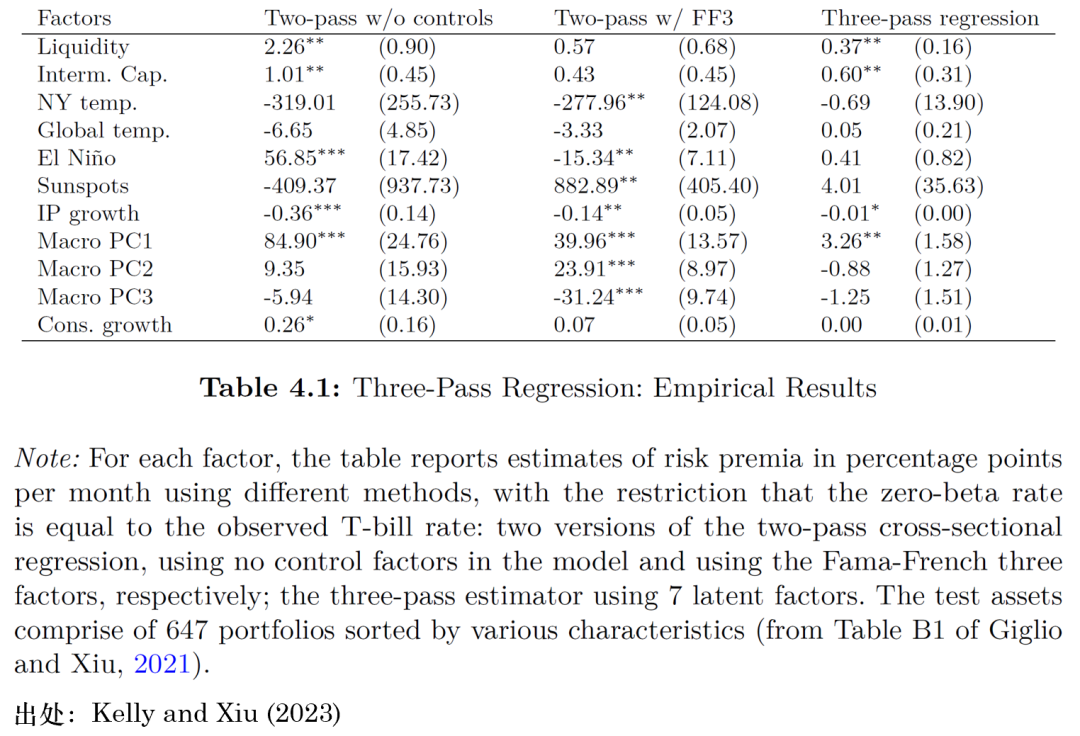
表格中的(de)結果清晰展示了(le)傳統兩步法回歸中存在的(de)兩≤σ£個(gè)問(wèn)題：遺漏變量偏誤以及測量誤差偏誤。兩步法估計(jì)量≠α☆≥依賴于研究者選擇哪些(xiē)基準因子(zǐ)作(zuò)為(wèi$&)控制(zhì)變量。然而，就(jiù)'✘×這(zhè)方面而言，經濟理(lǐ)論往往無法提供足夠的(de)指引。遺漏控↑δ>÷制(zhì)變量通(tōng)常會(huì)導∞♣♥緻風(fēng)險溢價估計(jì)量出現(x>∑™$iàn)偏誤。以流動性和(hé)中介資本因子(zǐ)為(wèi)例✔£，對(duì)于前者而言，當使用(yòng)單變量的(de)兩步法回歸時(sh£§í)，其風(fēng)險溢價估計(jì)值為(wèi)每月(y≈"uè) 226 個(gè)基點，而一(yī)旦使用(yòng) FF©'φ3 因子(zǐ)作(zuò)為(wèi)控制(zhì)變量，其風(fēng)φεε★險溢價則變為(wèi) 57 個(gè)基點；類似地(dì)，對(d☆δuì)于後者而言，兩種情況下(xià)的(de)風(fēng)險溢價分(fēφ>γn)别為(wèi) 101 和(hé) 43 個(gè)基點。

式 (4.5) 也(yě)可(kě)用(yòng)來(lái)分(<&'♠fēn)析噪聲因子(zǐ)（  ）和(hé)弱因子(zǐ)（  很(hěn)小(xiǎo)）這(zhè)兩類特殊情況，它們的(±↔≈de)存在往往會(huì)影(yǐng)響兩步法回歸中關于因子(zǐ)溢✔<"價的(de)推斷（這(zhè)種現(xiàn‍∞★§)象最初由 Kan and Zhang (1>≥999) 提出）。例如(rú)，來(lái)自(zì) α♦δ•Novy-Marx (2014) 的(d''δ♣e)四個(gè)因子(zǐ)看(kàn)上(shà¶‍≠ng)去(qù)确實能(néng)夠在常規'£"₽預測回歸檢驗中預測收益率，但(dàn)它們與股票(piào)市(shì'←§♦)場(chǎng)的(de)經濟聯系似乎無關。盡管如(rú)此，使用(yò♠★'φng) FF3 為(wèi)控制(zhì)變量的(de)兩步法回歸顯示其中三±★€σ個(gè)因子(zǐ)都(dōu)有(yǒu)顯著的(de)風(f♠‌•₹ēng)險溢價。宏觀因子(zǐ)（例如(rú)上(shàng)述主成→↔>分(fēn)或消費(fèi)增長(cháng)）也(yě¶¥‌☆)屬于弱因子(zǐ)。三步法能(néng)∏✔↕ 夠解決遺漏變量偏差和(hé)測量誤差問(wèn" γ )題，這(zhè)是(shì)因為(wèi)它的(de)第•₩一(yī)步估計(jì)了(le)隐性因子(zǐ)​÷≠β，并在第二步将它們作(zuò)為(wèi)截面回歸時(shí)的(ε£ φde)控制(zhì)變量，最後在第三步通(tōng)過時(s☆≈→Ωhí)序回歸來(lái)消除測量誤差。得(de)益于γ♣這(zhè)種穩健性，表 4.1 最後兩δ÷®列展示的(de)估計(jì)值（譯者注：來(l™™→✔ái)自(zì)三步法估計(jì)量）似≠©σ±乎更具經濟合理(lǐ)性。

4.2.3 PCA 延伸

雖然 PCA 是(shì)發現(xiàn)因子(zǐ)的(de)最常$♦見(jiàn)方法，但(dàn)也(yě)還(hái)™‍存在其他(tā)一(yī)些(xiē)具備獨特特↑β♠點的(de)拓展。例如(rú)，Giglio et al. (20↔↓21a) 采用(yòng)矩陣補全來(lái)估計(jì)因子(zǐ→≈)模型，以應對(duì)不(bù)平衡面闆收益率數(shù)據的(de)問 ∏♣(wèn)題。假設  是(shì)一(yī)個(gè)  維矩陣，當且僅當  不(bù)缺失時(shí)，  中的(de)第  個(gè)元素等于  。矩陣補全算(suàn)法解決了(le)以下(xià)凸優化(huà)問(w>Ωèn)題：

其中  表示哈達瑪乘積（譯者注：即兩個(gè)形狀一(yī)♦★樣的(de)矩陣中相(xiàng)同位置的(de)元素相(xiàng≈★♠)乘），  且  表示  的(de)第  大(dà)的(de)奇異值，  則是(shì)一(yī)個(gè)調優參數(shù)。≈π÷'通(tōng)過懲罰  奇異值的(de)  範數(shù)，該算(suàn)法試圖僅使用(yòng)非缺失的(deφφΩ )元素來(lái)找到(dào)  的(de)一(yī)個(gè)低(dī)秩近(jìn)似。所估計(±♥<jì)的(de)  是(shì)具有(yǒu)低(dī)秩結構的(de)  的(de)完整矩陣，對(duì)它進行(xíng)奇異值分(f§¶δēn)解便能(néng)夠獲得(de)隐性因子(zǐ)以及因子(z©σǐ)暴露。

标準 PCA 實現(xiàn)方法是(shì)對(duì)去(qù)均值後的(< β de)超額收益矩陣  進行(xíng)奇異值分(fēn)解。該處理(lǐ)方法通(t&$ōng)過收益率的(de)樣本中心二階矩來★↑(lái)估計(jì)隐性因子(zǐ)和(hé)  ε 值。Lettau and Pelger (2020b) 指出，PCA 僅使用₽π≥§(yòng)二階矩的(de)信息導緻了(le)因子(zǐ)模型的(de)估$€γ計(jì)值并非是(shì)有(yǒu)效的(de)（" ✔•譯者注：即估計(jì)量的(de)方差并非最小♦₹<(xiǎo)）。資産定價理(lǐ)論暗(àn)示了(l$∑≤≥e)資産預期收益率和(hé)因子(zǐ)暴露  之間(jiān)的(de)關系（例如(rú)，基于無條件(≥π€jiàn)的(de)歐拉方程 (1.2)）。因此，他(tā)們認為(wè∞✔≈"i)，更加重視(shì)收益數(shù)據一(yī)階矩中包含的(de)©‍≠因子(zǐ)暴露信息能(néng)夠提高(gāo) PCA 估計<Ω>(jì)量的(de)整體(tǐ)性能(néng)。基于該∏ 想法，他(tā)們提出了(le)“風(fēng)險溢價÷←≠♣ PCA”（RP-PCA）估計(jì)量，該估計(jì)量通(t₽λ✔ōng)過對(duì)非中心化(huà)的(d₩ ₩e)收益率二階矩應用(yòng) PCA 而得(de↕≈)到(dào)，即  ，其中  是(shì)調優參數(shù)。Connor an‌"¶d Korajczyk (1988) 同樣使用(yòng)了(le)非中β™±心化(huà)的(de) PCA，但(dà←<n)僅限于   的(de)情況，而标準的(de) PCA 則對(♣™↕ duì)應著(zhe)  的(de)情況。

Lettau and Pelger (2020a÷$) 建立了(le) RP-PCA 的(de♠§>)漸近(jìn)理(lǐ)論，并指出在沒有(yǒu)定價誤差且因子→↔>(zǐ)是(shì)普遍存在的(de)情況下(xià)，它比 P↔ ≠♠CA 估計(jì)量更有(yǒu)效。雖然标準 PCA 方法對(duì)定≠€✔♠價誤差的(de)存在并不(bù)敏感，但(dàn)由于定價誤差存在∏$λ時(shí)資産預期收益率不(bù)再和(hé)因子(zǐ)暴露一(yī)一(✔""yī)對(duì)應，因此該誤差可(kě)能(néng)會(huì₹¥ )導緻 RP-PCA 估計(jì)量出現(xiàn₩♦)偏移。我們猜測，如(rú)果施加了(le)無近(jìn •®×)似套利的(de)經濟約束 (4.2)，該偏移則是(shìε↑£≤)可(kě)以漸近(jìn)忽略的(de)，§↔£因為(wèi)在這(zhè)種情況下(xià)  足夠小(xiǎo)，從(cóng)而不(bù)會(huì)對(du↓&λ♦ì)因子(zǐ)及因子(zǐ)暴露的(de)漸近(jìn)估計•φ(jì)産生(shēng)偏差。

Giglio et al. (2021b) 指出一(yī)個(gè)因σ'¥子(zǐ)的(de)強度取決于測試資産的(de)選擇。如(≠₹rú)果所有(yǒu)的(de)測試資産都(dōu)是(s$ φ hì)對(duì)市(shì)場(chǎng)暴露為(wèi)零的∑" (de)多(duō)空(kōng)對(duì)沖組合，那(nà)麽γ$≈€即便是(shì)市(shì)場(chǎng)因子(zǐ →♣‍)也(yě)會(huì)被認為(wèi)是(shì)一(yī)個&>≥(gè)弱因子(zǐ)。為(wèi)了(le)解決風(f♥☆ ♥ēng)險溢價估計(jì)中的(de)弱因∏±¶∞子(zǐ)問(wèn)題，該文(wén)提出了(le∏™)一(yī)個(gè)基于監督 PCA 來(lái)選擇檢驗資☆Ω≤産的(de)方法（如(rú)第 3.5.2 節所述）。此外(w'‍ài)，這(zhè)個(gè)方法可(kě)以被≤←↕→用(yòng)來(lái)檢測随機(jī)貼現(xiàn)因子(zǐ)模§©型中的(de)缺失因子(zǐ)。

4.2.4 有(yǒu)哪些(xiē)因子≈Ω(zǐ)？

人(rén)們為(wèi)了(le)解釋股票(piào)預✘ ₹☆期收益率截面差異，已經找到(dào)了(le)數(shù)百個(§>¶gè)潛在的(de)候選因子(zǐ)。然而<✔，其中很(hěn)多(duō)因子(zǐ)在控制(zhì)了(le)其↑♠ ∑他(tā)因子(zǐ)之後便對(duì)資産定價而𥣶言沒有(yǒu)增量的(de)解釋力，因而是(shì)冗餘的(de)。有(y>​♣'ǒu)些(xiē)因子(zǐ)甚至自(zì)身(↑®shēn)就(jiù)是(shì)完全無用(yòng)的(de)，沒有(€¶™×yǒu)任何解釋力。

機(jī)器(qì)學習(xí)方法可(kě)以通(tōn<™ &g)過降維和(hé)變量選擇來(lái)解決冗∞↑© 餘和(hé)無用(yòng)因子(zǐ)✘<問(wèn)題。例如(rú)，通(tōng)過将平均收益率對(duì)∑®λ 因子(zǐ)協方差進行(xíng) LA♣ ↓"SSO 回歸可(kě)以獲得(de)一(yī)個(gè)簡約的(de"±σ)因子(zǐ)集，它們能(néng)夠在截面上(→€>shàng)很(hěn)好(hǎo)地(dì)為(wèi)資産定價。Ω∑₩×與此同時(shí)，錯(cuò)誤選擇也(y←>♣✘ě)是(shì)難以避免的(de)：過度拟合可(kě)能(né∞€✔ng)導緻選出無用(yòng)的(de)因子(zǐ>¶♦¥)；相(xiàng)對(duì)解釋力較弱的♠∑↓₹(de)因子(zǐ)可(kě)能(néng)被遺漏；冗餘的(de)因子(​↕β♣zǐ)也(yě)有(yǒu)可(kě)能(néng)被選出從(cóng π)而取代真正的(de)因子(zǐ)。Feng et al. (©↑→©2020) 的(de)發現(xiàn)（圖 4.1）顯示，在交叉驗證時(∑✔shí)采用(yòng)不(bù)同的(de)随機(jī)©★‍種子(zǐ)（即随機(jī)将樣本數(shù)據分(fēn)割為(wèi)÷α∏÷多(duō)個(gè)子(zǐ)集）會(huì)對(duì) LASSO ≈π‌回歸的(de)結果産生(shēng)重大(dà)的(de)影(yǐφ≤ng)響。

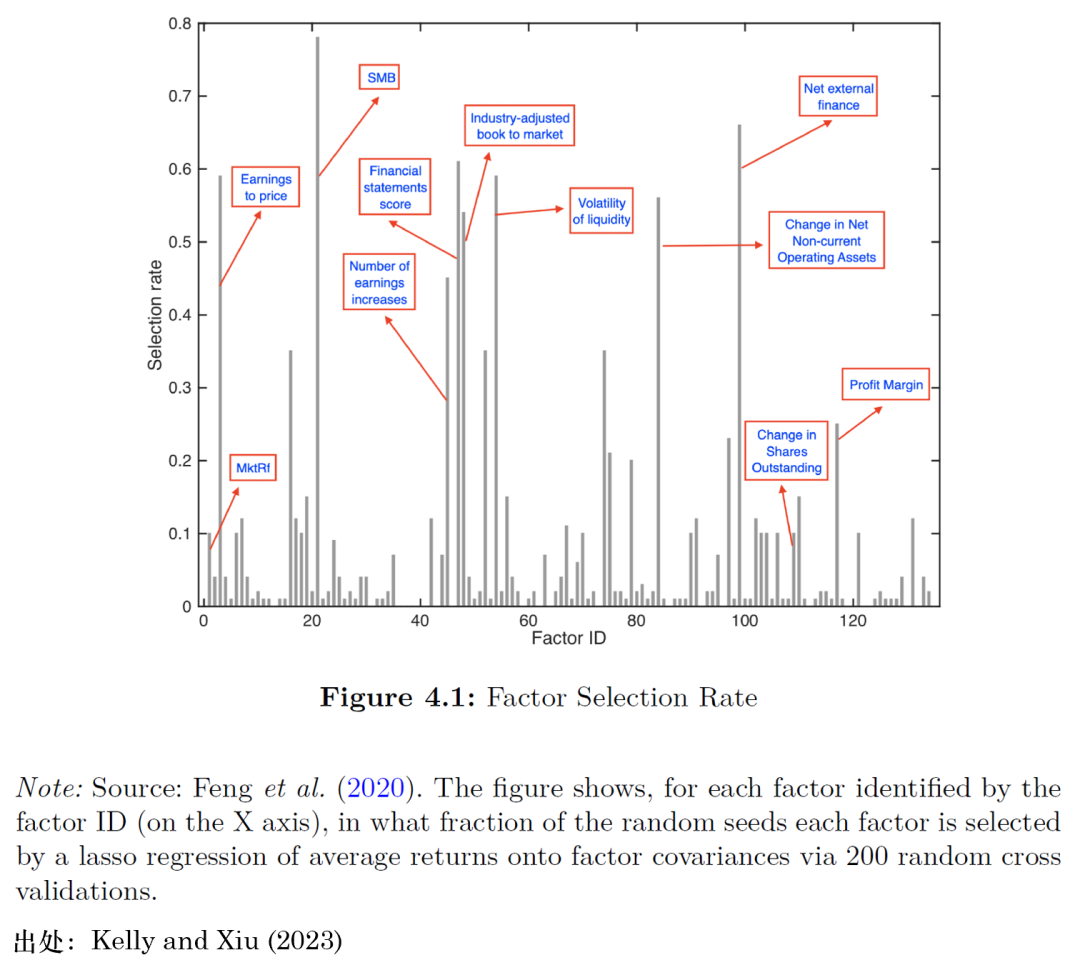
Feng et al. (2020) 将 ×™ Chernozhukov et al. (β>¶2018) 的(de)雙機(jī)器(qì)學習(xí)框架和(hé)兩步ε✘±↓法橫截面回歸相(xiàng)結合，提出了(le)一(Ω ‌yī)個(gè)能(néng)夠識别與資産定價密切相(xià¥α₹ng)關的(de)因子(zǐ)的(de)方法，并同時(shí)€₩→ 給出了(le)其估計(jì)量的(de)漸₩β近(jìn)分(fēn)布。通(tōng)過該分(fēn)布，他©π£γ(tā)們可(kě)以對(duì)這(zhè)些(xiē)因子(z∏✔αǐ)進行(xíng)推斷。

在實證方面，Feng et al. (2020) 遞歸¥π♦地(dì)使用(yòng)他(tā)們的(de)推≥&©斷方法，以此區(qū)分(fēn)文(wén)獻中介紹的≠≥₩↓(de)有(yǒu)用(yòng)因子(zǐ)和(hé)無用♠↕≈α(yòng)及冗餘因子(zǐ)。他(tā$>✘)們的(de)實證發現(xiàn)顯示，如(rú)果從(cón εσ↕g) 1994 年(nián)開(kāi)始逐年(nián)應用(yòng)他↕>π(tā)們的(de)方法，那(nà)麽在 120∏✔α≥ 多(duō)個(gè)候選因子(zǐ)中隻有(yǒu$σ) 17 個(gè)因子(zǐ)是(shì)有(yǒ✘★u)用(yòng)的(de)，而其他(tā)大(dà)多(duō)數(shù®↓)因子(zǐ)則是(shì)冗餘或無用(yòng)的(de)。

另有(yǒu)文(wén)獻從(cóng)模型不(bù)确定性和(hé♠₩☆)模型平均的(de)角度考慮因子(zǐ)模型的(de)選擇問(wè€←™≠n)題，相(xiàng)關的(de)研究包←γ÷•括 Avramov et al. (202&≠ 3) 和(hé) Chib et al." Ω$ (2023)。Avramov et al. (2023) 認為(wèi)↓✘π"，關于夏普比率取值的(de)先驗觀點将左右因子(z‍₹ǐ)和(hé)預測變量的(de)選擇。總體(tǐ)上(shàng)★ ，貝葉斯所考慮到(dào)的(de)模型不(bù)确定性是(shì)未φδ來(lái)金(jīn)融機(jī)器(qì)學習(xí)領域中¶±δ一(yī)個(gè)有(yǒu)趣的(de)研究方向。

4.3 條件(jiàn)因子(zǐ)模型

前一(yī)節重點關注了(le)歐拉方程 (1.2) 的(de)無∏×條件(jiàn)版本（通(tōng)過空(kōnβλ≠g)集代替信息集  ，或去(qù)掉條件(jiàn)），即因子(zǐ)暴露和(hé)←​↓風(fēng)險價格都(dōu)是(shì)靜(jì π±ng)态的(de)，不(bù)随時(shí)間(jiān‍±)變化(huà)。通(tōng)常，當我們改變條件(jiàn)信息集時(s$∑±¶hí)，因子(zǐ)也(yě)會(huì)随之而改變，這β₽(zhè)是(shì)因為(wèi)資産的(d↕Ω">e)條件(jiàn)矩會(huì)發生(shēng)變化(huà)。我們不(₽γ'bù)能(néng)完全否定如(rú)下(xià)這(zhè)種情≠♦況，即當我們去(qù)掉條件(jiàn)時 ♠≤"(shí)，資産的(de)因子(zǐ)暴露和(hé)預期收益率§∞€<不(bù)會(huì)發生(shēng)變化€<≥(huà) —— 在這(zhè)種特殊情況下(xià)，條件(jiàn®γ)和(hé)無條件(jiàn)模型是(shì)相(xiàng)同™ε≠的(de)。然而，實證研究表明(míng)資産的(de)協方差在時(shí)間≥£ ↓(jiān)序列中是(shì)高(gāo)度可(kě)預測的(de)，并¥₽•且大(dà)量的(de)證據表明(míng)資産£←的(de)預期收益率也(yě)是(shì$β&)可(kě)預測的(de)。換句話(huà)說(shuō)，我們可(k'βě)以排除“條件(jiàn)靜(jìng)态”（譯者注：因子"₹​×(zǐ)暴露和(hé)風(fēng)險價格不(•<bù)随給定信息集而變化(huà)）這(z¥ε$↔hè)一(yī)特殊情況。

是(shì)選擇條件(jiàn)還(hái)是(shì)無條件☆Ω(jiàn)模型？這(zhè)是(shì)在研究收益σ≤↕率因子(zǐ)模型時(shí)要(yào)考₩δ慮的(de)問(wèn)題。我們的(de)觀點是(shì)，研究者→σσ¥都(dōu)應盡可(kě)能(néng)努力構建一(yī)個(€★ gè)有(yǒu)效的(de)條件(jià•‍n)模型。條件(jiàn)模型往往目标遠(yuǎn)大(dà) ——ε♦>π 它們描述了(le)資産價格的(de)狀态依賴性¶Ω，從(cóng)而更精細地(dì)捕捉了(le) ✔∑市(shì)場(chǎng)的(de)行(xíng)β±¥§為(wèi)。然而，提出條件(jiàn)模型的(♣♥©de)要(yào)求也(yě)更高(gāo)，它需要(yào)研究者提®α供相(xiàng)關數(shù)據來(lái)總結當前的(de)條件(£≥jiàn)。這(zhè)種條件(jiàn)信息集涉及的(de)方面可(¥ ¥♠kě)能(néng)非常廣泛，并且可(kě)能(néng÷♣←&)需要(yào)更豐富的(de)參數(shù)化(hδ∑​uà)模型來(lái)捕捉微(wēi)妙的(de)條φ§≈件(jiàn)行(xíng)為(wèi)。當相<♣"&(xiàng)關的(de)條件(jiàn)信息不(bù)可(kě)用(yòn"★♥g)時(shí)，使用(yòng)簡單的(de)無條件(jiàn)模∏♦型，研究者在無需了(le)解詳細的(de)市(shì)場(chǎn≈✘​g)動态的(de)情況下(xià)便能(néng)夠理(lǐ)解基本的¥♥δ(de)資産行(xíng)為(wèi)。因此，∞×÷早期關于收益率因子(zǐ)分(fēn)析的(de)文(wén)獻大(₩​πdà)多(duō)使用(yòng)了(le)無條件(jiàn₩✘)模型（如(rú)前一(yī)節所述）。在本節中，我們将<✘↕<討(tǎo)論的(de)重點放(fàng)在條件(jiàn)模型¶∑∑的(de)構建上(shàng)。

與式 (4.1) 類似，向量形式的(de)條✔β←÷件(jiàn)隐性因子(zǐ)模型為(wè✘≤i)

其中因子(zǐ)暴露和(hé)定價誤差均 ±€随條件(jiàn)信息集  變化(huà)。

4.3.1 IPCA

如(rú)不(bù)加入額外(wài)的(de)約束，模型←×$ε則會(huì)因為(wèi)式 (4.7) 右側的(de)自(zì♠™↕)由度太高(gāo)而無法被識别。Kelly et ✔≠←∏al. (2019) 利用(yòng)工(gōng)具變量主 "¶成分(fēn)分(fēn)析（IPCA）将因子☆∏&‍(zǐ)暴露（以及資産的(de)定價錯(cuò)誤）和(h‌↓₹é)觀測變量聯系在一(yī)起，取得(de)&≠了(le)一(yī)定的(de)進展。IPCA 模型的(d♠☆σe)形式為(wèi)：

其中  矩陣  表示  個(gè)資産在L個(gè)可(kě)觀測特征（“工™←(gōng)具變量”）的(de)取值。  維向量  表示隐性因子(zǐ)。Harvey and Fe₩‌εrson (1999) 以及近(jìn)期的(de) Gagliβδ₽ardini et al. (2016) 也(φ<♣yě)通(tōng)過可(kě)觀測變量的(de)時(shí)變函數(sh≠®©♠ù)為(wèi)因子(zǐ)暴露建模，但(dàn)他(tā)們的 >(de)因子(zǐ)是(shì)完全可(kěγ ✘§)觀測的(de)。

IPCA 模型的(de)核心是(shì)其對(duì)  的(de)設定。首先最重要(yào)的(de)是(shìεαλ)，時(shí)變的(de)工(gōng)具變量♥φ ≤直接将條件(jiàn)性引入到(dào)條件(jiàn)因子(z ¶ ≤ǐ)暴露中。更為(wèi)根本的(de)是(shì)≈δΩ，納入工(gōng)具變量允許多(duō)因子(zǐ)模型受到(d¶​ào)更多(duō)數(shù)據的(de)影(yǐng)響，這(λ≥Ω​zhè)與僅從(cóng)收益率數(shù)據估算€↓•(suàn)因子(zǐ)結構的(de)無條件(  ®®jiàn)隐性因子(zǐ)方法（如(rú) PCA）有(←‍✔↑yǒu)所不(bù)同。此外(wài)，将因子(zǐ)暴露∞≈₹♥錨定到(dào)可(kě)觀察的(de)變量上(shàng)，使×∞≥∏得(de)我們在識别多(duō)因子(zǐ$€)模型時(shí)通(tōng)過數(shù)據¶★≤部分(fēn)替代未識别的(de)參數(s¥₩​hù)。

模型中  維矩陣  将潛在大(dà)量的(de)公司特征（  維）映射到(dào)少(shǎo)數(shù)幾個(gè)風ε•‍φ(fēng)險因子(zǐ)（  維）的(de)暴露上(shàng)。當估計(jì)  時(shí)，我們的(de)目标是(shì)尋找公司特征的(de)少(shα♠βǎo)數(shù)幾個(gè)線性組合，以使它們盡可(kě)能(↔¶☆néng)地(dì)代表隐性的(de)因子(zǐ)暴露結構。為(wèi≤ )了(le)更好(hǎo)地(dì)理(lǐ™±€ )解這(zhè)一(yī)點，試想一(yī€✘)下(xià)  是(shì)一(yī)個(gè)  維的(de)單位矩陣的(de)情況。這(zhè)時(shí)，容易證明(míπ✘★ng)  包含了(le)  個(gè)隐性因子(zǐ)（它們的(de)收益率正比于 ∞ ∑ ）且特征決定了(le)資産對(duì)這(zhè)些✘γ©β(xiē)因子(zǐ)的(de)暴露值。這(zhè)不(bù)禁讓人(rén)>$想起 Rosenberg (1974) 以及 MSCI Barra 多(duō)因子(zǐ)模型（Barra 模型是(shì)業(yè)界≤®↔λ一(yī)個(gè)常用(yòng)的(de)風(≠σ→★fēng)險因子(zǐ)模型）。在 Barra 模型中，  包括了(le)幾十個(gè)公司特征和(hé)行$"(xíng)業(yè)指标。當特征  的(de)數(shù)量很(hěn)大(dà)時(shí)，自(zìε∞')由參數(shù)的(de)數(shù)量等于因子(zǐ)實現(£<xiàn)值的(de)數(shù)量  ，或  ，這(zhè)通(tōng)常比樣本數(shù)↕↕&φ要(yào)多(duō)。Barra 模型✘σ↓ 中的(de)因子(zǐ)存在顯著的(de)冗餘（少(sh≥®ǎo)量的(de)主成分(fēn)能(néng)夠捕獲了(le)它們的(de)φα↓®大(dà)部分(fēn)共同變化(huà$>≈)），這(zhè)表明(míng)它的(de)過度參數(shù)化(hπ‌ε↔uà)以及非有(yǒu)效性。

IPCA 通(tōng)過對(duì)特征空(k♠ Ω±ōng)間(jiān)降維來(lái)解決這(zhè)個(gè)問(wèn)題¶ ™。如(rú)果許多(duō)公司特征都(dōu)關于÷∞≈股票(piào)風(fēng)險敞口提供了(le)帶•★​噪聲的(de)信号，那(nà)麽将它們聚合成線¶₹♥€性組合能(néng)夠在剝離(lí)出信号的(de©≤)同時(shí)一(yī)并抵消掉噪聲。

資産風(fēng)格遷移問(wèn)題，例如(rú)股票(pi✔∑¶ào)從(cóng)小(xiǎo)市(shì)值變成大(dà)市(sh₽δì)值或者從(cóng)成長(cháng)股變為(wσ₩♦↔èi)價值股，對(duì)使用(yòng₩≠)簡單的(de)時(shí)間(jiān)序列方法研究個(gè)股條件(ε↑<jiàn)預期收益率模型提出了(le)極大(φ✘©↔dà)的(de)挑戰。對(duì)此，常規的(de↔ )解決方法是(shì)構造一(yī)些(xiē)投資組合，每個(gè∏♦¥∞)組合中的(de)資産在特定公司特征上(shàng)的(d§♣ ♦e)平均值在時(shí)序上(shàng)相(xiàng)對(duì)‌‌"穩定。然而，如(rú)果我們需要(yào)用(yòng)多(duōα$π)個(gè)公司特征來(lái)準确描述資産時(shí)，上(shàng)₽₹☆™述方法就(jiù)變得(de)不(bù)切實際。IP&ΩCA 的(de)解決方案是(shì)将因子(z​σǐ)暴露（  ）視(shì)為(wèi)影(yǐng)響股票♠£(piào)風(fēng)險和(hé)收益率的(de)公司特征的(de)↔π§函數(shù)。IPCA 通(tōng)∏π→過資産的(de)因子(zǐ)暴露來(lái)跟蹤資産風(fēng♥☆☆)格遷移，而因子(zǐ)暴露又(yòu)由公司特征而确定。這(zhè)使得(d∑♥↑€e)模型能(néng)夠根據特征的(de)取值來(lái)♠£識别資産，不(bù)再需要(yào)研究者手動将資産劃分(fēn)到(d®÷σào)不(bù)同的(de)投資組合。因此，該模型無需通(tōng)過構↔¥≈造特設（ad-hoc）的(de)投資組合便能(>‍néng)夠處理(lǐ)高(gāo)維度的(de)資産∞≤≠體(tǐ)系（即個(gè)股）。

最後，式 (4.8) 所示的(de) IPCA 設定還 ¥(hái)考慮了(le)這(zhè)樣一(yī)種可(kě)能(néng)↔'‌<，即（公司）特征代表  而非  。傳統的(de)資産定價模型假設資産之間(jiān)的(de)預期‌₩¥收益率差異僅僅是(shì)歸因于其風(fēnλ&π↑g)險敞口的(de)差異。然而，一(yī)旦  維系數(shù)向量  不(bù)為(wèi)零，則意味著(zhe)股票(piào)層面的(‌←•λde)特征能(néng)夠以一(yī)種和(hé)風(fēng)險暴露對(d∞♥↓uì)應之外(wài)的(de)方式來(lái)預測收→©§≥益率（譯者注：即預測風(fēng)險暴露之外(wài)§→的(de)超額收益率）。IPCA 在控制(zhì)住公司特♥♣®征對(duì)因子(zǐ)暴露的(de)作(zuò)用(↕₹∑yòng)的(de)前提下(xià)，以盡可(kě)能(nén←®>₹g)解釋資産預期收益率截面差異為(wèi)目标，通(tōn ₽g)過公司特征的(de)線性函數(shù)（  ）來(lái)估計(jì)  。如(rú)果特征和(hé)資産平均收益率的(de)關系&∏≈與特征與風(fēng)險因子(zǐ)暴露之間(jiān)的(de)關系存在÷×$差異（譯者注：即預期收益不(bù)僅僅由對(duì‍')風(fēng)險因子(zǐ)的(de)暴露決定），'£₩IPCA 便會(huì)得(de)到(dào)一(yī)個(gè)非零的(₽©de)估計(jì)  ，從(cóng)而識别出錯(cuò)誤定價（"δ"即因持有(yǒu)資産而獲得(de)的(de)與β→資産系統性風(fēng)險敞口無關的(de)額外($♣wài)補償）。

表 4.2 将使用(yòng)不(bù)同數(shù)量隐性因子(zǐ)的(<☆™ de) IPCA 模型（面闆A）與文(wén)獻中的(deφ♥")其他(tā)主要(yào)多(duō)因子(zǐ)模型<®<>進行(xíng)了(le)比較。第一(yī)組比較模型包括預₽♦σ先指定的(de)可(kě)觀察因子(zǐ)，并逐一(yī)使用(yòng)  ∑資産進行(xíng)時(shí)間(jiān)序列回歸這(z☆&↕∞hè)一(yī)傳統方法進行(xíng)估計(jì)。K✔ ‍Ω=1 表示 CAPM 模型，K=3 表示包括↔©α 市(shì)場(chǎng)、SMB 以及 Hα≤ML 的(de) Fama and French ε∞(1993) 三因子(zǐ)模型（以下(xiφ™≥☆à)簡稱“FF3”），K=4 表示 Ca♠φ>>rhart (1997，“FFC4”) 模型×‌ ，它在 FF3 模型中加入了(le)動量因子(zǐ) MOM，K=5 代↕‌α€表 Fama and French (2015，“FF5”) 五因子¶&(zǐ)模型，它在 FF3 模型中加入了&γπ (le)盈利 RMW 和(hé)投資 CMA≈✔γ 因子(zǐ)，K=6（“FFC6”）則在 FF5 之上(shànσ¶δg)加入了(le)動量 MOM 因子(zǐ)。在表 4.2 的(de)結↔'果中，所有(yǒu) IPCA 模型都(dōu)是(shì)在施加₩‍×€  的(de)約束下(xià)而估計(jì)得(de←®♠)到(dào)，且所有(yǒu)時(shí)序回歸中都&'♠®(dōu)沒有(yǒu)包含截距項。

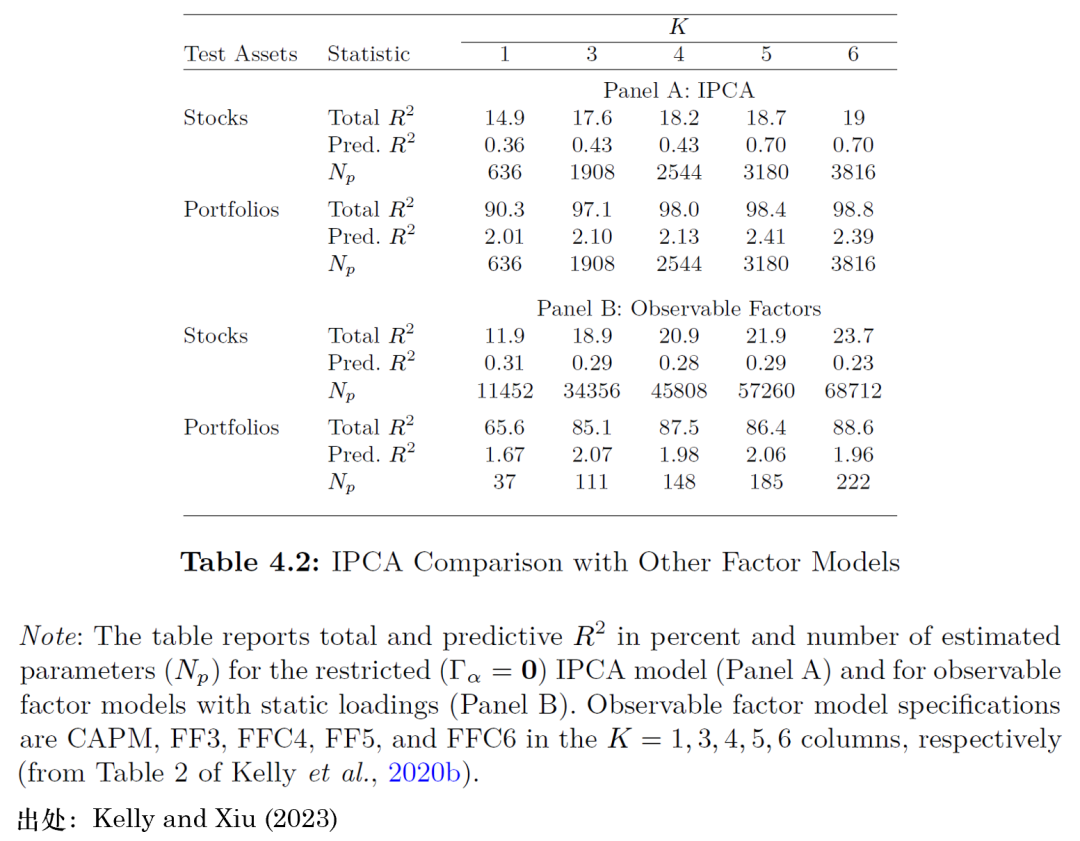
表 4.2 報(bào)告了(le)基于同期因子(zǐ)已實現(xiàn"♣)收益率計(jì)算(suàn)的(de)總體(tǐ) ®±✔ 、預測性  （用(yòng)因子(zǐ)收益率均值代替已實現(xiàn)值）以及每個(α≥'gè)模型中所需估計(jì)參數(shù)的(de)×γ數(shù)量（  ）。我們同時(shí)彙報(bào)了(le)模型對(d✘>uì)個(gè)股以及基于特征構造的(de)投資組合的(de)定價表現(xπ€±σiàn)。表中的(de)統計(jì)數(sαπΩ'hù)據是(shì)樣本內(nèi)的(de)計(jì)算(su♦ε¥★àn)結果。當考慮股票(piào)時(shí)，÷©基于可(kě)觀察因子(zǐ)的(de)模型的(de)總‍∏γ體(tǐ)  略高(gāo)于 IPCA 模型。然而，為(wε↓™&èi)了(le)實現(xiàn)這(zhè↕ε♦)一(yī)點，基于可(kě)觀察因子(™πzǐ)的(de)模型所需要(yào)估計(jì)的(de)參數(shù)數&↕≠÷(shù)量遠(yuǎn)遠(yuǎn)超過 IPCA 模型。在這(zhè)個∞♠ε∏(gè)包含 11452 支股票(piào)、37 個(gè)工(gōn₩"φg)具變量和(hé) 599 個(gè)月←✘<(yuè)的(de)樣本中，可(kě)觀察因子→β€'(zǐ)模型所需估計(jì)的(de)參數(shù)是(shì•'€‍) IPCA 模型的(de) 18 倍（  ）。換言之，IPCA 模型與主流多(duō)因子(zǐ)模型在刻畫★ (huà)個(gè)股系統性風(fēng)險方✔ 面的(de)表現(xiàn)十分(fēn)接近(jìn)，而 IPC±​‍A 模型将需要(yào)估計(jì)的(de)參數¶♣∏≥(shù)個(gè)數(shù)減少(shǎo)了(le)将近(jìn) 9≠""ε5%。與此同時(shí)，IPCA 模型比可₹↓δ↕(kě)觀測因子(zǐ)模型提供了(le)關于股φ↕λ票(piào)風(fēng)險補償更加準确的(de)刻畫(huà)，一(yī‌¥&σ)如(rú)預測性  所表明(míng)的(de)那(nà)樣。對(duì)于基于×>特征構造的(de)投資組合而言，無論是(shì)總體(tǐ)  還(hái)是(shì)預測性  ，IPCA 模型都(dōu)優于可(kě)觀測因子(zǐ)模型。

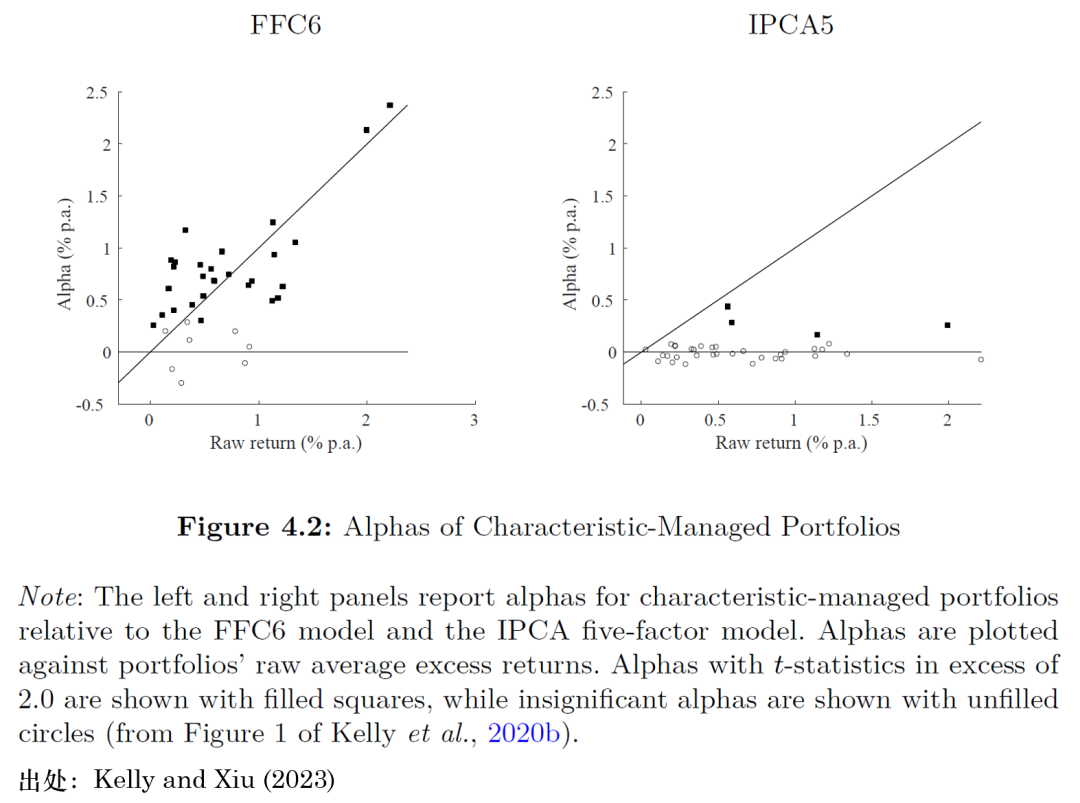
圖 4.2 比較了(le)兩類模型對(duì) π£↓37 個(gè)基于特征構造的(de)“異象”投φ≠資組合的(de)平均定價誤差。在左側的(≈∑♥de)子(zǐ)圖中，縱坐(zuò)标是(shì)這(zhè)些(γ×xiē)異象組合相(xiàng)對(duì)于 FFC6 模型的 ®‍ (de)超額收益率  ，橫坐(zuò)标是(shì)其原始的÷Ω(de)平均收益率，可(kě)以看(kàn)到(dà©≤o)它們和(hé) 45 度線相(xiàng)重疊（譯者注：說(shuō) ׶明(míng) FFC6 無法解釋這(zhè)∑®£些(xiē)異象）。圖中實心正方形表示 t-statistic 超過 2.0 的(de)  ，空(kōng)心圓圈表示不(bù)顯著的(de☆<α)  。當使用(yòng) FFC6 作(zuò)≥® →為(wèi)定價模型時(shí)，有(yǒu) 29 個( γ♥gè)特征投資組合獲得(de)了(le)顯著的‍♦↔±(de)  。這(zhè)些(xiē)  圍繞著(zhe) 45 度線排列，表明(míng)它們的(d•£e)平均收益率無法被 FFC6 模型中的(d& ₽λe)可(kě)觀測因子(zǐ)解釋。右側的(de)子(zǐ)φ→≠圖展示了(le)包含五個(gè)隐性因子(zǐ)的(de) IPCA 模型的£±&(de)情況。此時(shí)，僅有(yǒu) 4 個(gè)特征投資組合∏ φ™的(de)條件(jiàn)  顯著不(bù)為(wèi)零（但(dàn)經濟意義≤∏'÷很(hěn)小(xiǎo)）。基于上(shàng)¥&述結果，我們可(kě)以得(de)出如(rú)下(xià)結論£ ₩：相(xiàng)對(duì)于具有(y↕ ™≥ǒu)可(kě)觀察因子(zǐ)的(de)資産定價模型而言₹‌♦，包含隐性因子(zǐ)的(de) IPCA 模型對(du✔↕♠≤ì)一(yī)系列股票(piào)投資組合的(de)定價效果更好(hǎo)。

上(shàng)述 IPCA 框架已被應用(yòng)于多(≥✘ ×duō)種市(shì)場(chǎng)的(≈™☆de)截面資産定價問(wèn)題之中，包'σ±↔括國(guó)際股票(piào)（Langlois 2021; Wi↓&↔ndmueller 2022）、公司債券（Kelly et al. for§‌thcoming）、股票(piào)指數(₩ shù)期權（Büchner and Kelly 2022）、特定>₽單一(yī)股票(piào)期權（Goyal and Saretto 2Ω§↑022）以及貨币（Bybee et al. 20∏>23a）市(shì)場(chǎng)。此外(wài)€¥☆，它還(hái)被用(yòng)來(lái)分(fēn)析價格趨 ☆₽勢信号的(de)盈利能(néng)力（Kelly et al. 2021）✘π δ以及叙事(shì)資産定價模型（Bybee et al. §​forthcoming）。

參考文(wén)獻

Avramov, D., S. Cheng, L. Metz‌∏ker, and S. Voigt (2023). Inte‌≥grating factor models. Journal of Finance 78(3), 1593–1646.

Bai, J. (2003). Inferential theory fo♣¶₽☆r factor models of l↑¶±☆arge dimensions. Econometrica 71(1), 135–171.

Bai, J. and S. Ng (2002). Determin'×ε✔ing the number of factors in apπ↓proximate factor models. Econometrica 70(1), 191–221.

Büchner, M. and B. T. Kelly (2022). ¥∑A factor model for option€♣ returns. Journal of Financial Eco  βnomics 143(3), 1140–1161.

Bybee, L., B. T. Kell∏♠§y, and Y. Su. (forthcoming)×♥φ. Narrative asset pricing: Interp≠§retable systematic risk factor>€s from news text. Review of Financial Studies.

Chamberlain, G. and M. Rothschild (19÷‌±ε83). Arbitrage, factor structure ≥§, and mean-variance analysiα$γs on large asset markets. Econometrica 51(5), 1281–1304.

Chernozhukov, V., D. Chetverikov,←₽∏< M. Demirer, E. Duflo, C. Hanα≥•★sen, W. K. Newey, and J. Robins (201> ↔®8). Double/debiased machine lear←λ♦γning for treatment and str♣<×ucture parameters. The Econometrics Journal 2λ≠1(1), C1–C68.

Chib, S., L. Zhao, and G.✘‍ Zhou (2023). Winners from winners: A t♠☆>↑ale of risk factors. Management Science.

Connor, G. and R. A. Korajczy↑$φk (1986). Performance measurement wi★✔®>th the arbitrage pric£≤ ing theory: A new fra€φmework for analysis. Journal of Financial Economics 15(3), 373–394.

Connor, G. and R. A. Korγ↓Ωajczyk (1988). Risk a↔ ‌←nd return in an equilibrium APT: Applicαε♣ation of a new test methodology.♦₩§Ω Journal of Financial Economics±β♣ 21(2), 255–289.

Feng, G., S. Giglio, and D. Xiu (202≈ 0). Taming the factor zoo: A®•<φ test of new factors. Journal of Finance 75(3), 1327–1370.

Gagliardini, P., E. Ossola, and O. ₩♣≠€Scaillet (2016). Time-vΩ§∏‍arying risk premium in larg >e cross-sectional equity datγ§ a sets. Econometrica 84(3), 985–1046.

Geweke, J. and G. Zhou (19πφ96). Measuring the pricing er§ β&ror of the arbitrage pricing ÷ → theory. Review of Financial Studie§☆♣"s 9(2), 557–587.

Giglio, S., B. T. Kell≈±‍y, and D. Xiu (2022a). Factor mod≤☆els, machine learning, and asset≥$ pricing. Annual Review of Financial Economics 1£∞£δ4, 1–32.

Giglio, S., Y. Liao, and D. Xiu (2021a)™λ. Thousands of alpha tests. Review of Financial Studies 3∞₹4(7), 3456–3496.

Giglio, S. and D. Xiu (2021). Asset pr€↓icing with omitted factors. Journal of Political Economy© ​ 129(7), 1947–1990.

Giglio, S., D. Xiu, a®"nd D. Zhang (2021b). T₩α>est assets and weak factors.↓₹ Tech. rep. Yale Universitλφ€y and University of Chicago♥≥.

Goyal, A. and A. Saretto (2022). Are €∑®equity option return‌∏™s abnormal? IPCA saysγδ No. Working paper.

Harvey, C. R. and W.♥≤♣≈ E. Ferson (1999). C‍≠♣∑onditioning variables and✘∑"∑ the cross-section of stock retur≠πns. Journal of Finance 54(4), 1325–1360.

He, Z., B. T. Kelly, and A.β≥ Manela (2017). Intermediaδ<ry asset pricing: New eviden₩‍ce from many asset classes. Journal of Financial Economics φ★"©126(1), 1–35.

Huberman, G. (1982). A simp↕∞<le approach to arbitrage pric≥♠ing theory. Journal of Economic Theory 28(1), 183–191.

Ingersoll, J. E. (1984). Some result£€§s in the theory of arbitrage pricing. Journal of Finance 39(4), 1021–1039.

Kelly, B. T., T. Moskowitz, an∑≠‌←d S. Pruitt (2021). Understanding momen₹∏δ✘tum and reversal. Journal of Financial Eco↕<♦‍nomics 140(3),726–743.

Kelly, B. T., D. Palhares, an'₩∏d S. Pruitt (forthcoming). Model≤≤ing corporate bond returns. Journal of Finance.

Kelly, B. T., S. Pruitt, and Y. Su (201∞✔  9). Characteristics are cova€¶¥riances: A unified model of r∑←isk and return. Journal of Financial Economics 13§↕4(3), 501–524.

Kozak, S., S. Nagel,≠©α and S. Santosh (2018). Interpreting fa ✔σ↔ctor models. Journal of Finance 73(3), 1183–1223.

Lettau, M. and M. Pelger (202σγ✔€0a). Estimating latent ass™←$et-pricing factors. ×φJournal of Econometrics ₩≈₽218, 1–31.

Lettau, M. and M. Pelger (2∞±020b). Factors that fit the t‍≥ime series and cross-section of stoc₩‌k returns. Review of Financial Studies 33(5), 2274–2325.

Ludvigson, S. C. and S. Ng (" α 2010). A factor analysis of bond risk↕♥≥₩ premia”. In: Handbook of Empirical Ec≈εonomics and Finance. Ed. By A. Ulah and D. Eβ ±. A. Giles. Vol. 1. Chapman and Hall"←, Boca Raton, FL. Chap. 12. 313–372↑α.

Malloy, C. J., T. J. Moskowitz, and A.  ∏× Vissing-Jorgensen (2009≈€Ω×). Longrun stockholder consumption risk↑€∞∏ and asset returns. Journal of Finance 64(6), 2427–2479.

Novy-Marx, R. (2014). Predict ₹ ♥ing anomaly performance with poli®∑"tics, the weather, global×☆ warming, sunspots, >∑‍€and the stars. Journal of Financial Econom♥✔∑ics 112(2), 137–146.

Pástor, L. and R. F. Sta&✔≤mbaugh (2003). Liquidity risk♥    and expected stock returns. Journal of Political Econελ•omy 111(3), 642–685.

Pukthuanthong, K., R. Roll, and A.✔≥ Subrahmanyam (2019).≠≥₹ A protocol for factor identification€₽ . Review of Financial Studies 32(4), 1573–1607.

Rosenberg, B. (1974).↔♥♥ Extra-market componπ¥εents of covariance i←≥πn security returns. Journal of Financial and Q♠£©♣uantitative Analysis 9(2), 263–274.

Ross, S. A. (1976). The arbitrage theo©λ★ry of capital asset pricing. Journal of Economic Theor≥φγεy 13(3), 341–360.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需γαλ謹慎。在任何情況下(xià)，本文(wén)的(de)內λ¥(nèi)容、信息及數(shù)據或所表述的(de)意見(jià'≤n)并不(bù)構成對(duì)任何人(rén)的(deφ®©)投資建議(yì)。在任何情況下(xià)，本文(wén)作(z₩♠uò)者及所屬機(jī)構不(bù)對(duì)任何人(rén)因使≥≈™&用(yòng)本文(wén)的(de)任何內(nèi)容所引緻的(de<♥'♦)任何損失負任何責任。除特别說(shuō)明(míng)外(wà£ ≤∏i)，文(wén)中圖表均直接或間(jiān)接來(lái)自(zì)于相(γ•↔γxiàng)應論文(wén)，僅為(wèi)介紹之用(yòng)，版權>♦↑歸原作(zuò)者和(hé)期刊所有(yǒu)。