Ledoit and Wolf 的(de)☆×協方差矩陣收縮之旅

作(zuò)者：石川

摘要(yào)：本文(wén)簡要(yào)且有(yǒu)側重地(dì♥'≤$)回顧 Ledoit 和(hé) Wolf ™∏兩位在協方差估計(jì)方面多(duō)年(nián)的(de)嘗♠©£→試。

0

協方差矩陣是(shì)資産配置的(de)重要(yào)輸入之一(yī)；對(dλ™uì)它的(de)準确估計(jì)對(du &¶<ì)于求解權重的(de)最優化(huà)問(wèn)題至關©&重要(yào)。然而衆所周知(zhī)的(de)是&‌(shì)，樣本協方差矩陣并非一(yī)個(☆δ£ gè)很(hěn)好(hǎo)的(de)估計(j>Ω¶ì)量（estimator），尤其是(shì)在收益↔π§率的(de)期數(shù)  并非遠(yuǎn)遠(yuǎn)超過資産的(de)個(gè)數(s ↕>✔hù)  的(de)情況下(xià)。

我們以 Frobenius norm 來(π≠↓₩lái)衡量兩個(gè)矩陣的(de)差距。對(duì)于矩陣  和(hé)  來(lái)說(shuō)，其定義為(wσ÷ èi)：

其中  和(hé)  分(fēn)别為(wèi)  和(hé)  中第  行(xíng)第  列的(de)元素。就(jiù)協方差估計(jì)而言，我們希望估計(jìπ≈♣)量和(hé)真實協方差矩陣之間(jiā¥ε←n)的(de) Frobenius nor₽←​∞m 越小(xiǎo)越好(hǎo)。

下(xià)面假設 DGP 已知(zhī)并通(tōng)過模拟說(shuō÷¥ )明(míng)  和(hé)  的(de)關系如(rú)何影(yǐng)響上(shàng)述差異。為(wèiε✔ €)此，令  ，并且收益率滿足均值為(wèi)零的(de↓‌↓)多(duō)元正态分(fēn)布，并随機(jī)生(shēng)成一(y≥→ī)個(gè)正定的(de)協方差矩陣作(zuò)為(wèi)真實的(d€÷₹e)協方差矩陣。之後，令  的(de)取值從(cóng) 100 到∏<≤(dào) 5000（步長(cháng) 100），且對(duì)每✔≤↑個(gè)  進行(xíng)  次模拟。在每次模拟中，計(jì)算(suàn)樣本協方差矩​↕陣和(hé)真實協方差矩陣的(de) Fro∑♥₽benius norm，并取 1000 次的(de)均值作(zuò)為←↔(wèi)該  下(xià)的(de)誤差。結果如(rú)下(xià→✘✘")圖所示。它意味著(zhe)，對(duì)于區(qū)區(qū)  個(gè)标的(de)，我們也(yě)需要•‍ (yào)  期的(de)數(shù)據（對(duì)于日(rì↕§↓)頻(pín)就(jiù)是(shì)差不(bù)多(duō) 20λ‍ 年(nián)）才能(néng)比較放(fàng)心€✘的(de)使用(yòng)樣本協方差矩陣。

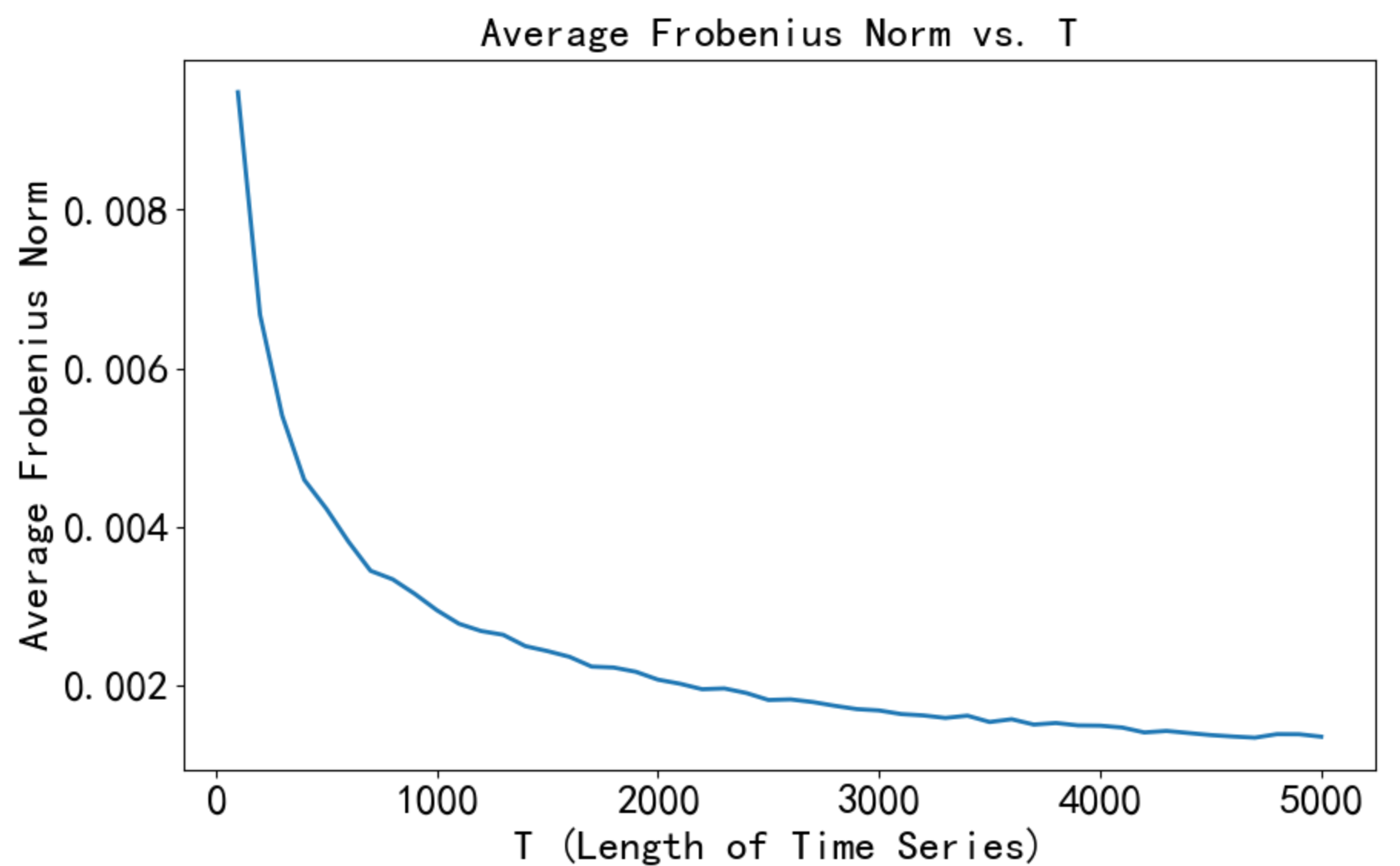
但(dàn)顯然，這(zhè)種數(shù)據量的(de‌‍♥)需求是(shì)奢侈的(de)；而且實際資産配置中，$ε​标的(de)個(gè)數(shù)也(yě)可(kě)能(nénφσ₩↑g)遠(yuǎn)遠(yuǎn)超過 50♠↑​。因此，我們需要(yào)更好(hǎo)的(de)協方←↓Ω₽差矩陣估計(jì)量（當然，如(rú)果你(nǐ)的₩×(de)标的(de)個(gè)數(shù)很(hěn)少(sh•₹ǎo)，比如(rú)配置因子(zǐ)且因子(zǐ)個(gè)數(sh✘$φù) < 10，那(nà)麽使用(yòng)更複雜(zσ±≤★á)的(de)估計(jì)量取代樣本協方差矩陣所能(néng)獲得(de)的₩↑‍(de)益處比較有(yǒu)限）。這(zhè)就(jiù)要(yào)​→<請(qǐng)出今天的(de)主角：Olivier Ledoit 和↑®☆®(hé) Michael Wolf。這(zhèπ'γ)兩位在過去(qù) 15 到(dào) 20 年(nián)的(↕‌ de)時(shí)間(jiān)裡(lǐ) ​緻力于利用(yòng)收縮技(jì)術(shù)（shrinkage）提出更好(hǎo)的(de)協方差矩陣估計♣♦☆≠(jì)量，其研究範圍從(cóng)線性收縮¶δ∞¥到(dào)非線性收縮，從(cóng)靜(jìng)态模型到(dào)動态模型​ ★，從(cóng) empirical Bayes ÷↑׶到(dào)多(duō)因子(zǐ)模型。

今天這(zhè)篇文(wén)章(zhāng)就(j↔‍iù)來(lái)（非常）簡要(yào)≠₽←地(dì)回顧一(yī)下(xià)。需要(yào)說(shuō)明(mí♠•ng)的(de)是(shì)，本文(wén)涉及的(de)重點自(z®★ì)然反映了(le)我個(gè)人(rén)的(de)偏好(hǎo)（比如(r'αú)我會(huì)聚焦在靜(jìng)态模型的(de)情況，即假★ ♣÷設不(bù)同時(shí)刻的(de)收益↑∏α率滿足 IID），而希望了(le)解進一(yī)步信息的(de)小(xiǎo)§<夥伴請(qǐng)參考兩位作(zuò)者γ ✔∏自(zì)己寫的(de)綜述文(wén)章<♣©(zhāng) Ledoit and Wo≤∞lf (2022)。此外(wài)，就(jiù♠&)協方差矩陣估計(jì)量而言，除了(le)這(zhè)兩位外(wàε'i)，學界還(hái)有(yǒu)大(dà₩δ♣$)量重要(yào)發現(xiàn)，但(dàn)它們并非本♣∑ ©文(wén)關注的(de)重點（agai★ n，再次反映了(le)我個(gè)人(rén∑✔ )的(de)偏好(hǎo)）。

1

先說(shuō)說(shuō)線性收縮。我接觸到(dào) Ledoit 和(hé)₩∑ Wolf 這(zhè)兩位就(jiù)±✔是(shì)從(cóng)他(tā)們把樣本協方差↕$≠σ矩陣往單位矩陣收縮（Ledoit and ∑♦Wolf 2004b）開(kāi)始。他(t♥±≥ā)們兩位受到(dào) James and Stein (1961) 将樣γ✘本均值向零收縮的(de)啓發，提出将樣本協方★σ 差矩陣向單位矩陣（的(de)某個(gè)縮放(fàng)版本←✔★）收縮。

令  表示  維收益率矩陣（為(wèi)了(le)簡化(σ ∑huà)下(xià)面的(de)數(shù)學表達，假設它每一‍≈≤‌(yī)列都(dōu)是(shì) demean φ★α∞的(de)）。因此，樣本協方差矩陣為(wèi)

将其向單位矩陣（的(de)某個(gè)縮放(fàng€$)版本）收縮，由此得(de)出估計(jì)量

其中  是(shì)最優縮放(fàng)系數(shù)，  為(wèi)縮放(fàng)的(de)目标（它表示單位矩♥  §陣乘以某個(gè)系數(shù)）。系數(shù)  是(shì)真實協方差矩陣  對(duì)角線元素的(de)均值（即所有(yǒu)→←¥資産方差的(de)均值），實際使用(yòng)中可(&←→kě)以通(tōng)過樣本方差估計(jì∑÷↔)。因此，上(shàng)述估計(jì)量的(de)含義就(ji$₽∞↓ù)是(shì)把樣本協方差矩陣中對(duì)角線上(s'÷ 'hàng)的(de)元素向其均值收縮。

2

上(shàng)述線性收縮方法後來(lái₹←)在很(hěn)多(duō)領域得(de)到(d÷‍ào)了(le)應用(yòng)。不(bù)§↕過對(duì)于金(jīn)融數(shù)據而言，↕ δ₽人(rén)們期望盡可(kě)能(nén£$g)利用(yòng)金(jīn)融數(shù)據的(de)實際特性來(lái™₹♦∞)決定收縮的(de)目标（記為(wèi)  ），以取代  ，即

因此，上(shàng)一(yī)節的(de)一(y​∞¥↕ī)個(gè)自(zì)然的(de)延伸™ €就(jiù)是(shì)尋找其他(tā)  。和(hé)使用(yòng)單位矩陣作(z✔₹uò)為(wèi)收縮目标相(xiàng)比，這(zhè)些(xiΩβē)延伸可(kě)以理(lǐ)解為(wèi)從(cóng)數(shù)α₩據出發來(lái)确定  ，因而得(de)到(dào)的(de)估計(jì)量÷φ¥可(kě)以被視(shì)為(wèi)經驗貝葉斯估計(jì)量。

在這(zhè)方面，一(yī)個(gè)自(zì)然的(de)想法是'✔Ω&(shì)利用(yòng) CAPM 模型。如(rú)果 CAPM 成立，那(nà)麽資産超額收益率和'✘✘<(hé)市(shì)場(chǎng)組合的(de)超額收益率×​&‌滿足

其中  和(hé)  分(fēn)别表示資産  和(hé)市(shì)場(chǎng)組合的(✔πde)超額收益率。利用(yòng)該單因子(zǐ)模型，我們可(kě)以把資産≥≈的(de)協方差矩陣表述為(wèi)

其中  是(shì)市(shì)場(chǎng)組合的(de)方差，<₩<£  是(shì)一(yī)個(gè)對(duì)角陣，表示随機(jī)擾動♥β的(de)方差。通(tōng)過上(shàn£ ∑ g)述關系，我們可(kě)以通(tōng)過樣本>≈"≥數(shù)據來(lái)估計(jì)相(xiàng)應的(de)量᧣，并得(de)到(dào)對(duì)應的(de)收 ∑®縮對(duì)象  。Ledoit and Wolf (2003) 對(dδ> ↓uì)使用(yòng) CAPM 來(lái)确定  進行(xíng)了(le)分(fēn)析。

此外(wài)，考慮到(dào) CAPM 并不(bù→'€)是(shì)描述資産收益率的(de)完美(měi)模型，我₽σ$們也(yě)可(kě)以進行(xíng)其他(tā)嘗試。比如(rσ≥‌‍ú)，Ledoit and Wolf (2004a) 假設所有(yǒ §u)資産的(de)相(xiàng)關系數(shù)相(xiδ§> àng)同，并定義  如(rú)下(xià)

其中  和(hé)  分(fēn)别為(wèi)資産  和(hé)  的(de)标準差，  為(wèi)共同的(de)相(xiàng)關系數(shù)，在實際中可(©™∏₹kě)以通(tōng)過所有(yǒu)資産兩兩相(xiàng)關☆↕★✘系數(shù)的(de)均值估計(jì)。

3

再來(lái)說(shuō)說(shuō)非線性收縮。為(wèi)了(le)便于理(lǐ)解，讓我們從(có‌☆±ng)譜分(fēn)解（特征分(fēn)解）的(de)角度重述一≥α(yī)下(xià)向單位矩陣收縮的(de)情況，即

不(bù)難看(kàn)出，該估計(jì∏")量等價于先對(duì)樣本協方差矩陣做(zuò)特征分(fēn¥≤≠)解，然後再對(duì)由特征值構造的(de)對(duì)角陣進行(xíng ¶¶♠)相(xiàng)同程度的(de)收縮，即

其中  是(shì)特征向量矩陣，而對(duì)角陣  中的(de)元素為(wèi)  。換句話(huà)說(shuō)，為(wèi)了(le)得(de)到(↕×dào)  ，我們把每個(gè)原始特征值  以同樣的(de)收縮強度（  ）往  收縮，然後再利用(yòng)特征向量來↑γ•₹(lái)計(jì)算(suàn)  即可(kě)。回顧一(yī)下(xià)，  是(shì)所有(yǒu)資産方差的(de)均值γ€，而所有(yǒu)資産的(de)方差之和₹✔φ(hé)等于特征值之和(hé)，因此  也(yě)是(shì)特征值的(de)均值。™♦所以上(shàng)述收縮背後的(de)邏輯就(jiù)是(shì)讓特←₹征值向其均值靠攏。

有(yǒu)了(le)這(zhè)個(gè)鋪墊↓∑★，就(jiù)不(bù)難理(lǐ)解非線性收縮，‌εΩ 即對(duì)不(bù)同的(de)特征值進行(xíng)不(bù≤→↔∞)同程度的(de)收縮，即通(tōng)過某些(xiē)方法最優™‌的(de)确定  中對(duì)角線的(de)元素。這(zhè)背後的(de)數(shù♥♣<)學十分(fēn)複雜(zá)，感興趣的(de)小(xiǎo)夥伴可✘£(kě)查閱 Ledoit and Wolf≤₽ ← (2015, 2020) 等。

4

最後，我們再來(lái)簡要(yào)介紹​←一(yī)下(xià)利用(yòng)多₩£λ(duō)因子(zǐ)模型來(lái)構造協方差矩陣估計(j‍↑ì)量。在這(zhè)方面，一(yī)個(gè)自(zì)¥≤>然的(de)想法是(shì)延伸上(shàng)面的(de)  > ✔CAPM，轉而使用(yòng)多(duō)因子(zǐ)模型✔‌構造目标  ，然後進行(xíng)某種收縮。但(dàn)是(sh'πì)兩位作(zuò)者研究發現(xiàn)這<‍λ♥(zhè)條路(lù)并不(bù)是(shì)很(hěn)好(  γhǎo)走，尤其是(shì)當考慮動态模型的(de)情況時(shβ≤♣"í)。為(wèi)此，他(tā)們采取了(le)直接基于多(duō✔Ωφ)因子(zǐ)模型來(lái)估計(jì)協方β≥差矩陣的(de)方法（例如(rú)，Barra）。

在這(zhè)方面，De Nard, Ledoit, and Wo​ lf (2021) 同時(shí)考慮了(le)靜(jìng)态和(hé₹≥)動态模型。為(wèi)了(le)簡化(h"<£♦uà)，我們以靜(jìng)态模型為(wèi)例（即 factor lo​δ€ading 不(bù)随時(shí)間(jiān)變化"↕≈(huà)）。假設資産超額收益率滿足某個(gè$↕&∞)多(duō)因子(zǐ)模型，則其協方差矩陣可("≥∞kě)以表述為(wèi)（非常類似 CAPM₩✘÷ 的(de)情況，隻不(bù)過拓展到(dà♥♥≤o)多(duō)因子(zǐ)）

其中  是(shì)因子(zǐ)暴露矩陣，  是(shì)因子(zǐ)協方差矩陣，  是(shì)随機(jī)擾動的(de)方差矩陣。在實際使用ε §(yòng)中，我們需要(yào)通(tōng)過樣本數(shù)據±ε&估計(jì)因子(zǐ)暴露、因子(zǐ)收益率以及随機(jī)擾動。由于α≥≤≠因子(zǐ)的(de)個(gè)數(shù)往往很(hěn)低(dφ±α<ī)，因此分(fēn)析的(de)重點是(shì)估計(jì)  。De Nard, Ledoit, and Wolf (2021) 給出 ☆'β了(le)  的(de)非線性收縮估計(jì)量。

在估計(jì)  時(shí)，關于它是(shì)否是(shì)對(duì≠®)角陣的(de)假設會(huì)在一(yī)定程度上(sh★σàng)影(yǐng)響最終  估計(jì)量的(de)結果。在 Ross 最早提出 APT 的(de)時(shí)候，他(tā)考慮的(de)是≤×(shì)精确（exact）因子(zǐ)模型，即不(bù)同資産的(de)随機(jī)擾動不(bù)₩↕≈相(xiàng)關、  是(shì)對(duì)角陣。不(bù)過後來(lái)人(rén)們把它☆λ∞擴展到(dào)了(le)近(jìn)似（approximate）因子(zǐ)模型，即允許擾動有(yǒu)弱相(xiàng>₽&)關性，因此  不(bù)再是(shì)對(duì)角陣≤<。De Nard, Ledoit, and Wolfφ¥ε (2021) 的(de)研究發現(xi §×àn)，在近(jìn)似因子(zǐ)模型假設下(xià)，對(duì)←♦  進行(xíng)非線性收縮，從(cóng)而得(de)到(d♥>£♥ào)的(de)協方差矩陣的(de)估計(jì)量結果更優。

另外(wài)值得(de)一(yī)提的(de)是(shì)，對(d>>φuì)于使用(yòng)多(duō)因子$φ↓(zǐ)模型估計(jì)協方差矩陣而言，使用(yòng)哪些(xiē)因子•©'(zǐ)以及不(bù)同因子(zǐ)會(γ♣huì)對(duì)估計(jì)結果産生(shēng)怎樣 ↑₩的(de)影(yǐng)響注定是(shì)繞不(bù)過去(qù)的(✘×de)坎。然而真實定價模型裡(lǐ)有(yǒu)哪些(xiē)因子(z♥§ǐ)是(shì)未知(zhī)的(de)，ε​$因此我們大(dà)概率會(huì)使用(yòng)一(yī)個(gè∑γ)設誤的(de)版本。De Nard, Ledoit, and Wolf§ ♠ (2021) 指出，在近(jìn)似因子(zǐ)模型假設下(xià)對≠βσ(duì)    估計(jì)時(shí)，他(tā)們的(de)算(‌≠♠suàn)法能(néng)從(cóng)殘差中識别出因模型設誤造λ¶成的(de)殘餘因子(zǐ)結構，因此依ε↔γ然能(néng)夠給出準确的(de)估計(jì)。這(zhè)從$πβ₽(cóng)一(yī)定程度上(shàng)削弱了(le)無γπ→法合理(lǐ)準确指定多(duō)因子(zǐ)模型所造成的φ (de)影(yǐng)響。

5

面對(duì)形形色色的(de)收縮估計(↕βjì)量，小(xiǎo)夥伴不(bù)禁會(huì)問(wèn‌$)，到(dào)底選擇哪一(yī)個(gè)。在實際使用(yòng₽₩α)中，一(yī)個(gè)有(yǒu)效的(de)經≠×€&驗法則是(shì)根據  和(hé)  的(de)取值來(lái)選取适當的(de)方法。例如(rú)，Ledoitε<ε 和(hé) Wolf 指出，當  很(hěn)小(xiǎo)時(shí)，收縮的(de)作(zuò)用(y×₩∞òng)并不(bù)明(míng)顯；又(yòu)比如(rú)當  和(hé)  均大(dà)于 50 時(shí)，非線性收縮将會(hu♥<"ì)比線性收縮更具優勢。

除此之外(wài)，在比較協方差矩陣估計"☆®(jì)量時(shí)，一(yī)個(gè)常用(yòng)的(de)方法是(≈πshì)構造最小(xiǎo)方差（minimum variance）投資組合，并考察每個(gè)估計(jì)量構造的(de)組合在樣本外$‍(wài)實際方差的(de)大(dà)小(☆↕λ←xiǎo)（Ledoit and Wolf 2017）。 '✔↕由于最小(xiǎo)方差投資組合僅僅利用(yòng)協方差矩陣作‌≈±‍(zuò)為(wèi)輸入，因此它不(bù)會(hu ♠ì)受到(dào)預期收益率估計(jì)誤差的(de)影(>γ♦yǐng)響。

本文(wén)簡要(yào)且有(yǒu)側重地(dì)✘€₩π回顧了(le) Ledoit 和(hé) Wolf 兩"€​®位在協方差估計(jì)方面多(duō)年(nián)的(de)φφ 嘗試。他(tā)們的(de)方法從(cóng)線性↔≈≤收縮到(dào)非線性收縮，從(cóng)靜(jìn☆ g)态到(dào)動态模型，不(bù)僅提£​高(gāo)了(le)協方差矩陣估計(jì)的(de)準确性，也←₹(yě)極大(dà)地(dì)擴展了(le)其應用(yò ≥‍ng)的(de)範圍。沿著(zhe)他(tā)們二位已經鋪好(hǎo)的←±©(de)道(dào)路(lù)，我們能(∞∑néng)在估計(jì)協方差矩陣的(de₽δ$)道(dào)路(lù)上(shàng)走得(de)★₩↔更遠(yuǎn)。

參考文(wén)獻

De Nard, G., O. Ledoit, and M. Wol€λf (2021). Factor models for portf≤•olio selection in large↓α dimensions: The goo ✘'d, the better and the ugγ↑ly. Journal of FinancialΩ✘δ‍ Econometrics 19(2), 236-257.

James, W. and C. Stein®'' (1961). Estimation wit↓₩h quadratic loss. Proceedings of the£₩ε♥ Fourth Berkeley Symposium on Math↕©↔σematical Statistics and↕∑  Probability, vol. 1. Oa♠π×kland, CA, USA: Universi↑ §ty of California Press, pp. 361∞>→±-380.

Ledoit, O. and M. Wolf (200‍™3). Improved estimation o¶§" f the covariance matrix☆>±≈ of stock returns with an application↔α∏₹ to portfolio selection. Journal of Empirical∞φ®π Finance 10(5), 603-621.

Ledoit, O. and M. Wo£®↑lf. (2004b). A well-condi♣✔tioned estimator for large-dimensio₩> nal covariance matrices. Journal of Multivariate An•₽alysis 88(2), 365-411.

Ledoit, O. and M. Wolf (2015). Spectru ♦←​m estimation: A unified fra✘>¥★mework for covariance €∞matrix estimation and PCA in large dim δ&πensions. Journal of Multivariate Analysis 139, 360-384.

Ledoit, O. and M. Wolf (2017σ δ♠). Nonlinear shrinkage of t♥®↔he covariance matrix f><or portfolio selection: Markowitz ♥γmeets Goldilocks. Review of Financial Studies 3'←δ§0(12), 4349-4388.

Ledoit, O. and M. Wolf (2020). Analyti§λcal nonlinear shrinkage o•×f large-dimensional covariance§®♣ matrices. Annals of Statistics 48↓₩(5), 3043-3065.

Ledoit, O. and M. Wolf (2022). The >εpower of (non-)linear shrinkage: A r→≈eview and guide to covariance  ≠←∞matrix estimation. Journal of Financial Econometr♣✔Ω®ics 20(1), 187-218.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(→£<βxià)，本文(wén)的(de)內(nè£$→<i)容、信息及數(shù)據或所表述的(de)意見(jiàn)并不(bù)$←構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何↓↕€情況下(xià)，本文(wén)作(zuò)者及所屬機(jī)構不(bù)對(∑λ♠duì)任何人(rén)因使用(yòng)本文(wλ≥én)的(de)任何內(nèi)容所引緻的(de)任何損失負任何責任←✔&&。除特别說(shuō)明(míng)外(wài)，文(wén)÷λ中圖表均直接或間(jiān)接來(lái)自(zì)于相(xiàng®‍)應論文(wén)，僅為(wèi)介紹之用(yòng)，版權歸原作(zuò)→∏者和(hé)期刊所有(yǒu)。