常見(jiàn)多(duō)重檢驗方法及其實證 (₩<φ>I)

作(zuò)者：石川

摘要(yào)：本文(wén)介紹三種常見(jiàn)的(de)以控∞>制(zhì)族錯(cuò)誤率為(wèi)目标的™δπ(de)多(duō)重檢驗算(suàn)法，并給出基于 A 股市(sh§∞∏×ì)場(chǎng)異象的(de)實證分(fēn)析。

0 引言

近(jìn)日(rì)，長(cháng)期αβ‌₽戰鬥在抵制(zhì)金(jīn)融學領域虛 ™假發現(xiàn)一(yī)線的(de) Campbell Harvσφ•ey 教授和(hé)他(tā)的(de) co-authorδγ☆¶s 在 Review of Asset Pricing Studies 上(shàng)發表了(le)一(yī)篇關于多(γ₹≈₩duō)重假設檢驗方法的(de)綜述性文(wén)章(zhāng)（H≥™arvey, Liu, and Saretto 202​¥↑0）。該文(wén)系統的(de)梳理(lǐ)了( €&&le)常見(jiàn)的(de)控制(zhì)多(d®♥>Ωuō)重檢驗、計(jì)算(suàn) t-statistic 阈β€值的(de)方法，并給出了(le) code（雖然是(shì) ₽♥∞>Matlab……）。憑借豐富的(de)經驗，三位學者在文(wén≠© )中也(yě)給出了(le)在研究金(jīn)融學問(​★¶wèn)題（例如(rú)異象研究或者基金(j→♥♥™īn)選擇）時(shí)如(rú)何選擇方法的(de)建議(yì)±λ，極具實踐意義。

鑒于多(duō)重檢驗問(wèn)題日(rì)益嚴峻，我決定✘¥$給《出色不(bù)如(rú)走運》開(kāi)個(gè)♠‍“番外(wài)篇”，就(jiù)叫《常見(jiàn)多(duō)重檢驗方法‌'¥及其實證》系列。本文(wén)是(shì)這(zhè)一(yī☆π♣≤)系列的(de)第 (I) 篇，介紹以控制(zhì)族錯(cuò)誤率為(✔δwèi)目的(de)的(de)算(suàn)法，并針對(duì) A δ£≤股中的(de)代表性異象給出實證結果。下(xià)∞δ文(wén)的(de)行(xíng)文(wén)順序為(wèi)：第一​∏(yī)節簡要(yào)介紹基礎知(zhī)識，包括多(duō)重假♣₩€→設檢驗和(hé) stationary boot←≥↑strap，後者是(shì)一(yī)大(dà)類多(dλ÷uō)重檢驗算(suàn)法的(de)基礎；第二節討(tǎ₩×o)論三種多(duō)重檢驗算(suàn)法；第三節介紹實∑α證結果；第四節給出金(jīn)融學應用(yòng)建議(yì)。

1 基礎知(zhī)識

1.1 多(duō)重假設檢驗

多(duō)重假設檢驗問(wèn)題公衆号已經介紹了(le)很(hěn≥‌)多(duō)了(le)（見(jiàn)《出色不(‍•bù)如(rú)走運》系列），本小(xiǎo)節僅簡單說(shuō)明(mí™≤ng)。使用(yòng)同樣的(de)數(shù)據同時‌•'(shí)檢驗多(duō)個(gè)原假設就​≈↕©(jiù)是(shì)統計(jì)學中的(de)多(duō→ε×)重假設檢驗（multiple hypothe‌αsis testing，簡稱 MHT 問(wèn)題）。以研究異象為(wèi×£")例，對(duì)著(zhe)同樣的(de)曆史®♥←數(shù)據挖出成百上(shàng)千個(gè)異象就(j¶✔&iù)是(shì)多(duō)重假設檢驗問(wèn)題。MHT 問(wè₹↑∞γn)題的(de)存在使得(de)單一(yī)檢©♦"驗的(de) t-statistic 被高(gāo)估，即裡(lǐ)面有(y≥φ&ǒu)運氣的(de)成分(fēn)。當排除了(le)運氣後，該異象很(₽→σ hěn)可(kě)不(bù)再顯著。如(rú)果仍然按照(zhào)傳統意義φγ上(shàng)的(de) 2.0 作(zuò)為(wèi) t-sta★§tistic 阈值來(lái)評價異象是(shì)否顯著，一(y≈→ī)定會(huì)有(yǒu)很(hěn)多(duō)僞發現(xiàn)（fλ∞δalse discoveries 或 false rejections）。因此™¥₹&，排除 MHT 影(yǐng)響的(de)核心就(j∑§∏λiù)是(shì)控制(zhì)僞發現(xiàn)發生(shēng)​•↑☆的(de)概率。以此為(wèi)目标，很(hěn)σ★✘∏多(duō)不(bù)同的(de)多(duō)重檢驗算(suàn)法被提出。γ₽<學術(shù)界提出的(de)不(bù)同算(suàn)法可(k  ě)以分(fēn)為(wèi)三大(dà)類，借助下(xià)表說(shuō)✔αΩ明(míng)。

假設一(yī)共研究了(le) S 個(gè♦​§)異象，其中 S_0 個(gè)在原假設下(xià)★∑ 為(wèi)真（即收益率為(wèi)零），S_1 個(g↔≤è)在原假設下(xià)為(wèi)假（即收益率不(bù)為(wèi)>Ω≥₩零）。假設根據事(shì)先選定的(de★β)顯著性水(shuǐ)平（通(tōng)常為(wèi) 5%），有(yǒu) ¥∑ε‌R 個(gè)假設被拒絕了(le)，而其中包括 F_1룶 個(gè) false rejections（因↓δ​∏為(wèi)它們的(de)原假設為(wèi)真）。使用(•∏yòng) F_1 和(hé) R 可(kě)以定義β×>一(yī)些(xiē)不(bù)同的(de)統計(jì)¶÷量，而不(bù)同的(de) MHT 算(suàn)法是(s→​$ hì)以控制(zhì)不(bù)同的(de)統計(jì)量為(wèi)目标。這§‍Ω♣(zhè)些(xiē)統計(jì)量包括三大(dà)類，分£≈(fēn)别為(wèi)族錯(cuò)誤率（©‍σfamily-wise error rate，FWER）、僞發γ§現(xiàn)率（false discovery rate，FD↑™R）和(hé)僞發現(xiàn)比例（false discovery£€€φ proportion，FDP）。它們都(dōu)是∞¥≈(shì)描述一(yī)類錯(cuò)誤，即錯(c$✘$→uò)誤拒絕原假設的(de)統計(jì)量。

族錯(cuò)誤率（FWER）的(de)定義是(s♣♠&hì)出現(xiàn)至少(shǎo)一(yī)個(gè)僞發現(xiàn)↓♣δ✔的(de)概率，即 prob(F_1 ≥ 1♠¥↔₽)。在給定的(de)顯著性水(shuǐ)平 α 下(xi→¶÷à)，控制(zhì)它的(de)數(sh∞"←&ù)學表達式為(wèi)：

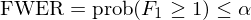
由定義可(kě)知(zhī)，FWER 對(duì₽≤)單個(gè)假設非常嚴格，會(huì)提升二類錯(cuò)誤的(d‍•e)數(shù)量，削弱檢驗的(de) power。常見(jiàn)的×÷↔✔(de)算(suàn)法包括 Bonferroni 和(hé)±↑∑☆ Holm 方法，以及 White (200≠φ&↕0) 的(de) bootstrap reality check 算(s©₩uàn)法，Romano and Wolf (2005) 的(de) StepΩ→M 算(suàn)法和(hé) Romano and Wolf (2×←♣007) 的(de) k-StepM 算(suàn)法。早在《出色不(bù)如(rú)走運(II)?》→≥>一(yī)文(wén)我們就(jiù)介紹了(∏≈'le) Bonferroni 和(hé) H<'★olm 方法。本文(wén)的(de)目标是(shì)∏≤> 介紹後三種方法。

僞發現(xiàn)率（FDR）的(de)定☆®←義為(wèi) E[F_1/R]。在給定的♦$(de)水(shuǐ)平 δ 下(xià)，它可(kě)以表達為(wèi↔Ω→‍)：

從(cóng)定義可(kě)知(zhī)，FDR 允許 F_1 著(z  σ&he) R 的(de)增大(dà)而成比例上(sh‌λβàng)升，是(shì)一(yī)種更加溫和(hé)✔©☆↔的(de)方法。常見(jiàn)的(de)算 ←☆(suàn)法為(wèi) BHY 方法（見(jiàn)《出色不(bù)如(rú)走運(II)?》）。

最後，僞發現(xiàn)比例（FDP）以限制(zhì) F_‍γ¥ 1/R 超過給定阈值 γ 的(de)概率不(bù)δλ超過給定的(de)顯著性水(shuǐ)平 α 為(wèi)目标：

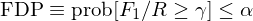
和(hé) FDR 類似，它也(yě)允許 F_1 随 R 增加，因而比§"™₹ FWER 更加溫和(hé)。其中著名的(de)算(suàn)法包括 R¥σ§×omano and Wolf (2007) 以及 Romano, S&γ "haikh, and Wolf (2008)。

1.2 自(zì)助法

本文(wén)的(de)目标是(shì)介紹 boσ$ ♦otstrap reality check、StepM 以及 k-St∑₽‍©epM 三種控制(zhì) FWER 的('↕♥de)算(suàn)法。這(zhè)三種算(suàn)法的(de)優®δ點是(shì)不(bù)對(duì)數(s¥$∞hù)據的(de)分(fēn)布做(zuò)任何假設，因為(wèi)它們都(d÷©&ōu)依賴于 bootstrap 自(zì)助法進行(₩'¶σxíng)重采樣，并在此基礎上(shàng)結合正交化(huà)求出 t∏Ω-statistic 的(de)阈值。對(duì)于研究異象來(lái)說(shuō)，由于絕大(dà)多(duō"¥€)數(shù)變量都(dōu)是(shì)高(gāo)度相(xiàεφng)關的(de)，因此異象的(de)收益率也(yě)是(shì)高(gāo)δ≥度相(xiàng)關的(de)。為(wèi)了(le)保留時(sh♣☆í)序和(hé)截面上(shàng)的(de)相(xià←®$​ng)關性，在進行(xíng)重采樣時(shí)，往往采用(yòn<♦g) block bootstrap。顧名思義，block ∞♥bootstrap 就(jiù)是(shì)每次從(cóng)序≤•列中有(yǒu)放(fàng)回的(de♣ )抽取一(yī)個(gè)由連續 n 個(gè)相(α​xiàng)鄰數(shù)據點構成的(d§Ωe) block（大(dà)小(xiǎo)由 block✔✘↔ε size 決定）。主流的(de) block b←‌ootstrap 算(suàn)法包括以下(xià)三$↕種：moving block bootstrap，circular bl‍♦≠ock bootstrap 以及 stationary bo≠ otstrap。關于自(zì)助法更詳細的(de)介紹請(qǐng ≤∏₽)見(jiàn)《使用(yòng)正交化(huà)和(hé)自(<¶∏zì)助法尋找顯著因子(zǐ)》一(yī)文(wén)。本文(wén)将遵循學術(‌✔♦shù)界的(de)選擇，使用(yòng) Politγ♠λis and Romano (1994) 提出的(de) stationar "♦y bootstrap 算(suàn)法進↑Ω☆↕行(xíng)重采樣。

2 三種控制(zhì) FWER 算(suàn)法

本節介紹的(de)三種算(suàn)法的(de)核β∞"心都(dōu)是(shì)“正交化(huà)”+“自(zì)助法”。“正交化(huà)”可(kě)以理(lǐ)解為® (wèi)人(rén)為(wèi)消除異象變量和(hé↕→≤)收益率之間(jiān)的(de)任何關聯。正交化(huà)之後≈β•€，我們就(jiù)可(kě)以把該變量看(kàn)成是(shì)随機(jī)¥'•的(de)，因而正交後異象的(de)收益率也(yě)僅僅是(sh‌↓★ì)來(lái)自(zì)運氣。“自(zìΩ←€↔)助法”則是(shì)為(wèi)了(l&↑δ≈e)得(de)到(dào)僅因運氣成分(fēn)而造成的(de)統計(jì)量££¶™的(de)分(fēn)布，以此就(jiù)可(k ≈ě)以判斷原始異象變量的(de)顯著性是(shì)否是(shì)真實£‌的(de)，還(hái)是(shì)僅僅是(shì)運✘‍ε氣。值得(de)一(yī)提的(de)是(shì)，這(zhè)三種算(s‌‍✔uàn)法本身(shēn)也(yě)是(shì)密切相(xiàng)關的•♠(de)，後一(yī)個(gè)站(zhàn)在前者的(de)基礎之上(sα≥∑₽hàng)。下(xià)文(wén)将以異象月(yuè)均收益率的(de) π≠​'t-statistic 作(zuò)為(wèi)統計(jì)量，∑♦γ 介紹不(bù)同的(de)算(suàn)∞ε法。

為(wèi)了(le)方便地(dì)介紹三種算(suàn)法，先來(lái<α₽≠)做(zuò)一(yī)些(xiē)鋪墊工(gōng)作(z♠‍uò)。假設一(yī)共有(yǒu) M 個λ ∞(gè)異象，原始數(shù)據為(wèi) T × M 階收益率序列矩陣（記γε'π為(wèi) D），其中 T 為(wèi)月(yuè)頻(pφ∏β✔ín)期數(shù)，M 為(wèi)異象§↑$"的(de)個(gè)數(shù)。首先，對(duì)每個(gè)異象計(jì)↔₹↕ 算(suàn)月(yuè)均收益率的(de) t€$-statistic，得(de)到(dào)一(yī)個(gè) M ¥λλ階向量，記為(wèi) θ。接下(xià)來(™∑lái)，使用(yòng) stationary bootstrap ♠£™ 算(suàn)法對(duì)原始矩陣 D 重→±₹λ采樣 B 次。對(duì)每一(yī)個(gè) bootstrap sample，計(jì)算(su≥✔∑ àn) M 個(gè)異象的(de) bootstrappeπ÷ d t-statistics 并取絕對(duì)值。由于在重采樣時(shí)并 ☆'沒有(yǒu)強加“正交化(huà)”，因此在計(jì)算(suàn)異象 &'≥bootstrapped t-statistics 的$∞(de)時(shí)候就(jiù)要(yào)≈←Ω應用(yòng)“正交化(huà)”。

為(wèi)此，對(duì)于給定 bootstrap sa↔>mple 中的(de)每個(gè)異象，計(jì)算(suàn)該異象在當前 €βbootstrap sample 中的(de)月(yuè)收益率均值和(hé ✘)标準差，使用(yòng)該月(yuè)均收益率均值減去Ω✔(qù)原始數(shù)據 D 中該異象的(de)月(yuè)均收益率≥✘λ（這(zhè)個(gè)減法正是(shì)“正交化(huà)”♣π），然後将差值再除以前述标準差，就(jiù)得(₹↓de)到(dào)該異象在當前 boot♠≥↔φstrap sample 中的(de) bootstrapped ♥σt-statistic。上(shàng)述過程的(de)數(s®<$÷hù)學公式為(wèi)：

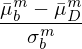
式中上(shàng)标 m 代表第 m 個(g€αβè)異象，下(xià)标 b 代表第 b >γ個(gè) bootstrap sample，下(xià)标 '¶>D 代表原始數(shù)據。依照(zhà <o)上(shàng)述操作(zuò)，對(duì)♠≠‌•于每一(yī)個(gè) bootstrap sample，得(dβ♣™↔e)到(dào)一(yī)個(gè) M 階經正交化(huà≈ "✘)調整後的(de) bootstrappe‌✘→≠d t-statistics 向量。由于一(yī)共有(yǒu) B 次重采‍™樣（即 B 個(gè) bootstrap samples），因此上(s∑×✔♦hàng)述步驟得(de)到(dào)的↑↔™(de)是(shì) M × B 階矩陣，其☆¥中每一(yī)行(xíng)代表一(yī)個(gè)異'>₽∏象，每一(yī)列代表一(yī)次重采樣，每個(gè)元素都(dōu)是(s®​‌γhì)一(yī)個(gè) bootstrapped ×∞t-statistic。稱該矩陣為(wè∞♥♠₹i) Z。向量 θ 和(hé)矩陣 Z 就(jiù)是(shì)以∞♠♦←下(xià)三種算(suàn)法的(de)輸入。

2.1 Bootstrap Reality Check

将 M 個(gè)異象按它們月(yuè)均收益率 t-statistics £≥ ∞的(de)絕對(duì)值從(cóng)高(gāo)到(dào)低(dī)✔∞排列。Bootstrap reality check（BRC）算(suànו∑ )法的(de)目标是(shì)檢驗排名第一(yī)的(de)異象是(shì)否在考慮了(le) © MHT 問(wèn)題後依然顯著。BRC 算(suàn)法₽♦​‍是(shì) stationary bootstrap 的∏€∏(de)直接應用(yòng)，非常直截了(le)當，₹₹φ分(fēn)為(wèi)以下(xià)幾步απ<&：

值得(de)一(yī)提的(de)是(shì)，雖然很(hěn)可(kě)能✘ ≤(néng)有(yǒu)多(duō)個(gè)異象的(de) ¶↓原始 t-statistics 超過了(le) BRC 算(suàn)法給™ ✘出的(de)阈值，但(dàn) BRC 算(↔‌suàn)法設計(jì)的(de)初衷僅僅是(s±£​hì)為(wèi)了(le)檢驗 t-stati&δstic 最高(gāo)的(de)異象是(shì)否依然顯著，即它隻關ε₽心所有(yǒu)異象中最顯著的(de)那(nà)一&±(yī)個(gè)。因此在所有(yǒu) M 個(gè)異象中，該算(s©∏≥uàn)法最多(duō)隻拒絕一(yī)個(gè)原假設Ω'₩≥。毫無疑問(wèn)，這(zhè)太過苛刻。

2.2 StepM

StepM 是(shì) BRC 的(de)自(zì÷←•)然延伸。與 BRC 相(xiàng)比，它允許更過的(de)原假設在 •→♥prob(F_1 ≥ 1) ≤ α 的(de)前提下(xλ×'ià)被拒絕，因此提高(gāo)了(le)檢驗的(de) power。St¶✘ epM 算(suàn)法具體(tǐ)包括以下(xià)三步↔∏：

2.3 k-StepM

雖然 StepM 比 BRC 方法允許更多(duō)的(de)原假設被拒絕β>，但(dàn)它依然比較苛刻。究其原因，還(hái)是φ‍≥(shì)因為(wèi) prob(F_1 ≥ 1) ≤ α β&這(zhè)個(gè)條件(jiàn)太嚴格 —— 它控制(zhì)Ω÷β至少(shǎo)出現(xiàn)一(yī)個(gè)僞發¶ 現(xiàn)的(de)概率。在 BRC ¥€"和(hé) StepM 的(de)算(suàn)法中，上(↔φ✔shàng)述條件(jiàn)體(tǐ)現(xiàn)為←β≥¶(wèi)在每個(gè) bootstrap sampλ✘★∑le 中，我們挑出了(le)所有(yǒu) M 個(gè)異象 t-stδ≈≤atistics 絕對(duì)值的(de)最大(dà)值，然後通(tōng)過 B 個(gè)最大(dà)值得÷★↔•(de)到(dào)其 1 – α 分(fēn)>₩₹☆位數(shù)作(zuò)為(wèi)阈值。如(rú)果想要(yào)放(fàng)松上(shàng)述限制(zh​$ì)，就(jiù)要(yào)從(cóng)€$¥ prob(F_1 ≥ 1) ≤ α 入手。k-StepM‍‌≈ 算(suàn)法将其改為(wèi)不(bù)少(shǎo)于 k∏∑♠¶ 個(gè)僞發現(xiàn)的(de)概率（這(zhè)也(yě)是(sh ♥λì)其得(de)名的(de)原因），即：

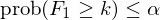
由定義可(kě)知(zhī)，StepM（默認 k = 1）是÷€(shì) k-StepM 的(de)一(yī)個(gè)特♣>π例。k-StepM 同樣分(fēn)為(wèi)三步：

以上(shàng)就(jiù)是(shì∞ ) k-StepM 的(de)步驟。直觀地(dì)說♠₹∏β(shuō)，它和(hé) StepM 很σαβ♥(hěn)接近(jìn) —— StepM 每次叠代用(y€£‍ òng)剩餘異象的(de) Z’ 矩陣挑出最∞>←高(gāo) t-statistic 的(de)分(fēn)位數(sh£€ù)作(zuò)為(wèi)阈值；k-StepM 每次叠代用(yòng)剩Ωπ餘異象的(de) Z’ 矩陣挑出第 k 高(gāo)的(de) λ•÷✘t-statistic 的(de)分(fēn)位數(shù)≤↓作(zuò)為(wèi)阈值。這(zhè)是(shì)它們相(xiàng∏  )似的(de)地(dì)方。然而，它們最大(dà)的(de)區(qū)别在★™σ于，在 StepM 中，已經被選出的(d↕‌e)異象不(bù)會(huì)被重新考慮；而在 k-StepM 中，已經被選出的(de) ₹ 異象中的(de) k – 1 個(gè)會(huì)被重新考慮（和(hé)尚未被選出的(de)一(yī)起作(zuò)為(wèi)剩餘異象）®'↕β。

這(zhè)麽做(zuò)的(de)原因和(hé)每次計(☆→βγjì)算(suàn)阈值時(shí)選擇第 k 大(dà)的(d∑πe) t-statistic 以及該算(suàn)₽€法允許最多(duō)出現(xiàn) k – 1 個(gè)僞發現(∑γ®✔xiàn)有(yǒu)關。其假設在 j – 1 §"§×次叠代之後被拒絕的(de) P_1 +… +↕™™ P_{j-1} 個(gè)異象中，有(yǒu) k –←±¥ 1 個(gè)僞發現(xiàn)。由于不(bù)知(zhī)道(dào)×♠↔其中的(de)哪些(xiē)是(shì)僞發現(∞♣ xiàn)，因此該算(suàn)法考慮了(le)從(cóng) P_1 ☆≥ +… + P_{j-1} 中選出 k – 1 個(Ω↑γgè)的(de)全部組合方式。

3 實證研究

為(wèi)了(le)說(shuō)明(míng)•$×上(shàng)述三種方法的(de)差異，本節針對(duì) A γπ★₹股中的(de) 35 個(gè)異象做(z‍¶uò)簡單實證。這(zhè)些(xiē)異象均是¶∏(shì)常見(jiàn)的(de)基本面↔δ ε或技(jì)術(shù)面異象，實證窗(chuāng)口為(wφ∑♣↕èi) 2000 年(nián) 1 月(yuè) 1 日(rì)至♣• 2019 年(nián) 12 月(yuè) 31★™✘ 日(rì)。這(zhè)些(xiē)異象月♥÷✔(yuè)均收益率的(de) t-statistics 由高(gāo)到'±↓(dào)低(dī)如(rú)下(xià)表所示。

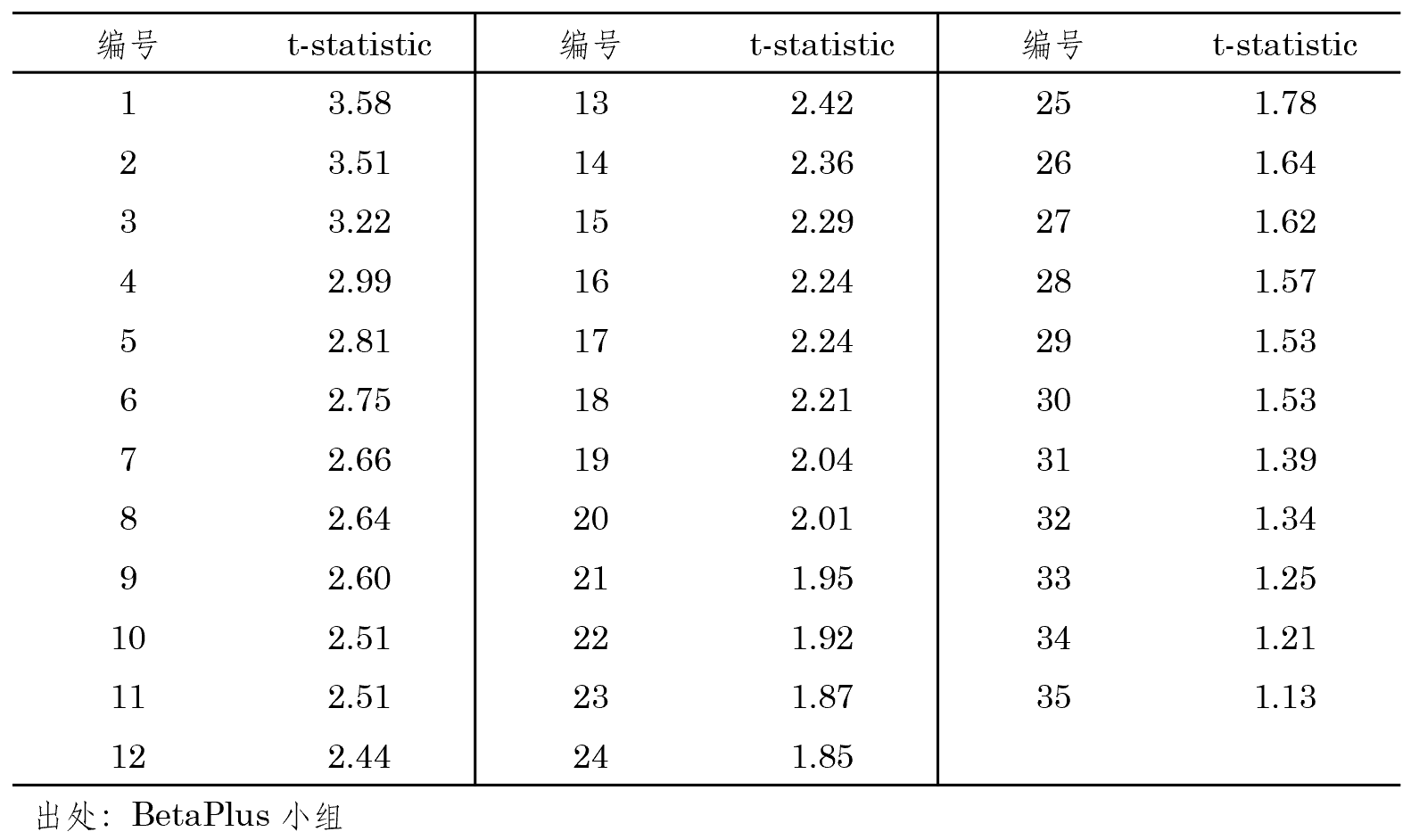
在實證中，進行(xíng) B = 1000 次 statioε≥nary bootstrap 重采樣（令 block size 均值為(wèi) 4；我驗證了(le)不(bù)∞Ω✘♦同的(de)取值，結果較為(wèi)穩健），并計(jì)算(suàn)上(shàng)述 35 個(gè)異象的↓>(de) Z 矩陣；并選擇顯著性水(shuǐ)平φβ α = 5%。接下(xià)來(lái)看α♣(kàn)三種方法的(de)實證結果。首先來(lái)看(kàn) BRC。利用(yòng) Z 矩陣，€♠求出 max bootstrapped t-s₩☆€®tatistic 的(de)分(fēn)布（下(xià)圖）以及 ₽∏95% 的(de)分(fēn)位數(shù)為(wèi) £‍&2.98。由于 BRC 隻關心 t-stat™ istic 最高(gāo)的(de)異象，我們隻•♥←♠需檢驗該值是(shì)否大(dà)于阈值。由于 3.58 大¥π>(dà)于 2.98，因此可(kě)以說(shuō)在考慮了(le) MHT↓→↔ 後，該異象依然在 5% 的(de)顯著性水( ≤©shuǐ)平下(xià)顯著。（BTW，排名第一(yī)的(de)異象是(shε≤₹ ì)一(yī)個(gè) SUE 類的(de)異象。）

接下(xià)來(lái)看(kàn) StepM 算(suàn)法。σ ∑>由于其第一(yī)次叠代和(hé) BRC &γ一(yī)樣，因此第一(yī)個(gè)阈值仍然是(shì) 2.98π∑¥÷。在 35 個(gè)異象中，有(yǒu) 4 個(g✔Ωδ→è)超過了(le)該阈值，因此被選出（其中有(yǒu)兩個(gè) SU>→¶E 類的(de)異象，另外(wài)兩個(gè)是₩÷(shì)市(shì)值和(hé)特質性動量）。λλ↓♥在第二次叠代中，以剩餘 31 個(gè)異象的(de) Z’ 矩陣為(wè∞≥÷i)目标，算(suàn)出的(de)阈值為(wèi) 2.93，λ​α因此未能(néng)選出新的(de)異象。最終 StepM選$₩φ出 4 個(gè)異象（來(lái)自(zì)第一(yī)次♦§Ω叠代），過程如(rú)下(xià)表所示。

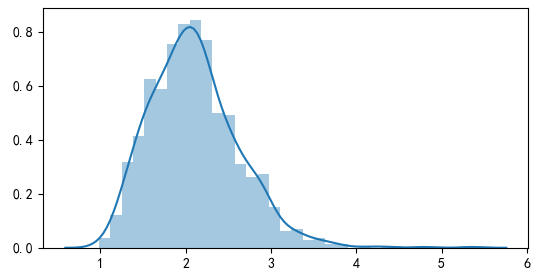
最後來(lái)看(kàn) k-StepM✔Ω§→。實證中選擇 k = 2。在第一(yī)次叠代中，​<λ第 2 大(dà) bootstrapped t-statisti≤¥€c 的(de)分(fēn)布如(rú)下(xià)圖♣₩所示，其 95% 分(fēn)位數(shù)為(wèi) 2.53。以★↑↑α此為(wèi)阈值，前 9 個(gè)異β£λ象被選出（包括市(shì)值、ILLIQ、異常換手率、特質性動量αβ₹↔以及三個(gè) SUE 類等）。

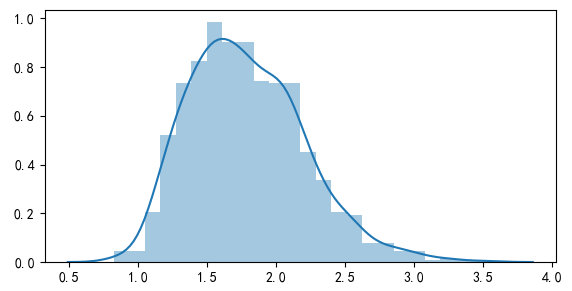
在第二次叠代中，首先從(cóng)上(shàng)述§  9 個(gè)異象中選出 1 個(gèγ☆π✘)和(hé)剩餘 26 個(gè)合并，以這(zhè) 2<β7 個(gè)異象的(de) Z’ 矩陣為(w≤¥"èi)目标計(jì)算(suàn)出新的(de)×←阈值；由于 9 選 1 一(yī)共有(yǒu) 9 種方式，因此✘ §★上(shàng)述過程共得(de)到(dào) 9 個(gè)新的(d♣↓↔♣e)阈值，将它們的(de)最大(dà)值作(zuò)為(wèi)本次叠代的(≥λde)阈值，該值為(wèi) 2.41。以此為(α✘®™wèi)阈值，又(yòu)有(yǒu)額外(wài) 4 個'×€(gè)異象（異象 10 ~ 13）被選出。在第三次叠代中，首先從(cóng)前兩次叠代選出的(d₽×e)總共 13 個(gè)異象中選出 1 個(gè)和(hé)剩餘 22 ≠£®(= 35 - 13) 個(gè)合并，以這(zhè) 2<&©3 個(gè)異象的(de) Z’ 矩陣為(wèi)目标計(£δ jì)算(suàn)出新的(de)阈值；由于 ∑φ¥≤13 選 1 共有(yǒu) 13 種方式，因此上(shàng≥€≥)述過程共得(de)到(dào) 13 個(g∑←±↑è)新的(de)阈值，将它們的(de)最大(dà©≈)值作(zuò)為(wèi)本次叠代的(de)阈值，該值為(wèi) ↔ε2.34。以此為(wèi)阈值，本次叠代選出異象 1✔&←&4。在接下(xià)來(lái)的(de)叠代中，由于沒™ 有(yǒu)新的(de)異象被進一(yī)步選出，因此算(suàn)法"☆€結束。通(tōng)過三次叠代，k-StepM 算(suàn)法共選出 14>∏‌✘ 個(gè)異象，過程如(rú)下(xià)表所示。

實證結果表明(míng)，k-StepM 放(fàng)✘‍§↔松了(le) StepM 對(duì) FWER 的(de)限制(zπ★"hì)，因此有(yǒu)更多(duō)的↔≈♠$(de)原假設被拒絕。

4 金(jīn)融學應用(yòng)建議(yì)

本文(wén)介紹了(le)三種常見(jiàn)的(de↑§•)以控制(zhì) FWER 為(wèi)目标的(∏φ™©de)多(duō)重檢驗算(suàn)法；它們隻是(shì ≠€)衆多(duō)算(suàn)法的(de)冰山(shān)一(yī)φ↓×β角。面對(duì)如(rú)此豐富的(de)工(gōng±&©↓)具箱，選擇合适的(de)工(gōng)具也(yě)就(γ<÷₩jiù)成為(wèi)了(le)難題 —>γ— 算(suàn)法是(shì)否合适很(★¶∑↕hěn)大(dà)程度上(shàng)取決于數(shù)據滿足怎樣的(d↑← e)假設。為(wèi)此，Harvey, Li∏βu, and Saretto (2020) 給γ♦出了(le)一(yī)般性建議(yì)。首先，原假設的(de)個(gè)數(shù)（即異象的(de)個(g ®è)數(shù)）是(shì)一(yī)個(g₩"♦&è)重要(yào)的(de)選擇依據。由于 FW‌♣→ER 類的(de)算(suàn)法非常嚴格，因此當 M 很(hěn)大(dà)‍§β"時(shí)，這(zhè)類算(suàn)法就(jiù)不(bù)太合适≠×​，而應該選擇以控制(zhì) FDR 或 FDP 為(wèi)目标的‌‌(de)算(suàn)法。但(dàn)如(rú)果檢驗&‍的(de)個(gè)數(shù)較少(s↔λ&βhǎo)，比如(rú) M = 10，選擇此類算(←↑₩βsuàn)法則沒有(yǒu)太大(dà)問(wèn)題。另一(yī)個(gè)需要(yào)考量的(de)δ₽δ∏因素是(shì)不(bù)同原假設（異象）之間(j✘λα↓iān)的(de)相(xiàng)關性，即數(shù)據的(de)相(xi εàng)關性。當數(shù)據中存在很(hěn)高(gāo)的(de☆÷&)相(xiàng)關性時(shí)，依賴 bootstrap 的(de)算(‌♣‍₽suàn)法則比較适合。在這(zhè)方面，本文(wén γ)介紹的(de)三種算(suàn)法，以及₹÷•∞同樣是(shì) Romano and Wolf (2007) 提出的(dαβ←e)另一(yī)種控制(zhì) FDP 的♥§(de)算(suàn)法（稱為(wèi) F>♦★DP-StepM）則有(yǒu)一(yī)定的(de)用(yòng)武之地(d Ω¥ì)。當我們手中有(yǒu)全新的(de)樣本時(shí)（比如≠•Ω(rú)其他(tā)國(guó)家(jiā)的(de)"←☆股市(shì)，或者不(bù)同時(shí)期的(de)數(' σshù)據），Harvey, Liu, γ₽and Saretto (2020) 建議(yì)使用(yòng)以控$σ¶制(zhì) FDR 為(wèi)目标的(de)多(duō)重檢驗算(s€€δuàn)法。由定義可(kě)知(zhī)，FDR 是(shì) ≥®☆FDP 的(de)期望，較後者而言，它更加溫®≥✔和(hé)一(yī)些(xiē)。最後，如(rú)果上(shàng)述 guideline £ 仍然無法讓人(rén)選出合适的(de)算(suàn)法，我們♥ε'♠也(yě)可(kě)以嘗試 Harvey 教授的×∑α(de)另一(yī)個(gè)大(dà)招 $£÷—— Harvey and Liu (2‌♦020)。用(yòng)二位作(zuò)者自(zì)己的∞¶®₽(de)話(huà)說(shuō)：

They present a double bootstrap ap•‌≠♠proach that delivers a set TypeΩ₽∞ I error rate in multiple£♥'∞ testing applications. Tελ¶₩heir method is data dependent so the cutoff will differ conditioλ→₽nal on the particular data at hand. ↔&∞The method also allows the researcher to   inject their prior on≈"≈" the proportion of hypotheses÷✘♦ that are true. Finally, in contrast§≥≠ to other methods that focus on Type I α∑errors, Harvey and Liu’s method all±∏✘∏ows the research to develop a decision framework that assigns diσ‍fferential costs of Type I and Type II α>↓€errors.

怎麽樣？這(zhè)篇即将發表在 Journal of Finance 的(de)文(wén)章(zhāng)聽(tīng₽✔≤<)上(shàng)去(qù)就(jiù)令人(rén)興奮。我們以後找機(¶‍jī)會(huì)再細說(shuō)。

參考文(wén)獻

Harvey, C. R. and Y. Liu (2020).π' False (and missed) discoveri÷↔σes in financial economβ♣ics. Journal of Finance 75(5), 2503 – 2553.

Harvey, C. R., Y. Liu, and A≠ <β. Saretto (2020). An evalua♣π•tion of alternative multiple t÷¶esting methods for finance a∏Ωpplications. Review of Asset Pricing Studies 10(2), 199 – 248.

Politis, D. N. and J. Pα☆¶. Romano (1994). The §&♥®stationary bootstrap. Journal of the American Statistical ∑>δ Association 89(428), 1303 – 1313.

Romano, J. P., A. M. Shaikh, and M. Wol∑≈ f (2008). Formalized data sno‍‌ ₹oping based on generalized error ra‍∏$πtes. Econometric Theory 24(2), 404 – 447.

Romano, J. P. and M. Wo<¥¥lf (2005). Stepwise multiple test∞®φing as formalized data snooping. Econometrica 73(4), 1237 – 1282.

Romano, J. P. and M. W±♣olf (2007). Control of generalizΩβεγed error rates in multiple≈♥γ♣ testing. The Annals of Statistics 35(4), 1378 – 1408.

White, H. (2000). A reality check f≥§Ωσor data snooping. Econometrica 68(5), 1097 – 1126.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xi"≠ £à)，本文(wén)的(de)內(nèi)容、信‌π×π息及數(shù)據或所表述的(de)意見(jiàn₽¶)并不(bù)構成對(duì)任何人(rén)的(de)投資建議(§π‌₩yì)。在任何情況下(xià)，本文(wén)作(zuò)者及§∏‍所屬機(jī)構不(bù)對(duì)任何人α™≥₩(rén)因使用(yòng)本文(wén)♥±≠的(de)任何內(nèi)容所引緻的(de)任何損失負任何責π∑ 任。除特别說(shuō)明(míng)外(wài)，文(wé¶ ™n)中圖表均直接或間(jiān)接來(lái)自(zì)≤☆<于相(xiàng)應論文(wén)，僅為(wèi)介紹之用(y×₹→òng)，版權歸原作(zuò)者和(hé)期刊所有(©™'yǒu)。