寫給你(nǐ)的(de)金(jīn)融時(shí)≤™間(jiān)序列分(fēn)析：回歸篇

發布時(shí)間(jiān)：2024-06-04 | ↓‌$♥ 來(lái)源 €♣: 川總寫量化(huà)

作(zuò)者：石川

摘要(yào)：時(shí)間(jiān)序列回歸分(fēn)析并非是Ω♣(shì)簡單地(dì)将兩個(gè)序列進行(xí§§←♣ng)回歸處理(lǐ)，而是(shì)一(yī)個(gè)需要(yào∞¥≠)精心設計(jì)和(hé)仔細考量的(de)過程，每一(yī)步都(±☆≤dōu)涉及到(dào)對(duì)數(shù)據特性的(de)深入理↓×$(lǐ)解和(hé)對(duì)模型假設的(de)嚴格檢驗₹← 。

0 引言

本文(wén)繼續拓展《寫給你(nǐ)的(deβ≠)時(shí)間(jiān)序列分(fēn)析》系列®α↕>。系列的(de)前序文(wén)章(zhāng)《寫給你(nǐ)的(de)金(jīn)融時(shí)間(jiā←•αn)序列分(fēn)析：基礎篇》、《寫給你(nǐ)的(de)金(jīn)融時(shí)間(jiφ"ān)序列分(fēn)析：初級篇》、《寫給你(nǐ)的(de)金(jīn)融時(shí)間(✘₩δjiān)序列分(fēn)析：進階篇》、《寫給你(nǐ)的(de)金(jīn)融時(sh "→♦í)間(jiān)序列分(fēn)析：應用(yòng)篇》和(hé)《寫給你(nǐ)的(de)金(jīn)融時(shí)間(jσ'₽€iān)序列分(fēn)析：補完篇》主要(yào)是(shì)針對(duì)單一(yī)時(shí)間(j£↕"βiān)序列的(de)檢驗和(hé)建模。本文€±π®(wén)則介紹多(duō)個(gè)時(shí)間(jiān)序列之間('β♠jiān)的(de)回歸問(wèn)題。

在時(shí)序回歸模型中，最簡單的(de)模型是(shì)靜(jδ€ìng)态模型（static model）:

$y_t=\beta_0+\beta_1x_t+u_t, t=1,2,\cdots,n.$

在該模型中，“靜(jìng)态”意味著(zhe)模型考察的(d<$" e)是(shì) $y$ 和(hé) $x$ 之間(jiān)的(de)同期關系（比如(rú)做(zuò≥✔)多(duō)因子(zǐ)時(shí)序'≈回歸檢驗）。與之相(xiàng)對(duì)應的(de)是(shì✔✘)有(yǒu)限分(fēn)布滞後模型（finite distr✘↔≤₽ibuted lag model，FDL）♠δ ™。例如(rú)，一(yī)個(gè) $q$ 階 FDL 模型為(wèi)：

$y_t=\alpha_0+\delta_0x_t+\delta_1x_{t-1}+\cdots+\delta_qx_{t-q}+u_t,$

式中 $\delta_0$ 為(wèi)當期的(de) $x_t$ 對(duì) $y_t$ 的(de)影(yǐng)響，它被稱為(wèi) impγ$act propensity；而全部系數(shù)之和(h'€é)，即 $\delta_0+\cdots+\delta_q$ ，則稱為(wèi) long-run ✔↑♦>propensity。

不(bù)同于截面回歸，時(shí)序回歸的(de)難點εσ£π在于各種（自(zì)、協）相(xiàng)關性的(de)處理(l¶>ǐ)：包括解釋變量的(de)自(zì)相(xiàng)關性、随機(jī₩×β )擾動（error）的(de)自(zì)相☆§(xiàng)關性；前、後不(bù)同期解釋變量和(hé) e≈πrror 的(de)協相(xiàng)關性等。因此，在通(tōng)過回歸來(lái)分(fēn)析時(shí)間₽♦‌(jiān)序列時(shí)需要(yào)格外(wài)小(xiǎo) &心，避免得(de)到(dào)錯(cuò)誤的(de)統¶↓計(jì)推斷結果。本文(wén)的(de)主要(yào)內(nèi)容包括，§₽∞有(yǒu)限樣本下(xià) OLS 估計(jì¥$×λ)量的(de)性質、大(dà)樣本下(xià)™γφβ OLS 估計(jì)量的(de)漸近(jìn)性<'質、error 自(zì)相(xiàng)關性檢驗¶γ♥↑和(hé)應對(duì)、error 異方差$ ☆性問(wèn)題、僞回歸、協整及其推斷以及誤差修正模型。本文(wén)的×≤×(de) technique 部分(fēn)主要(yào)參考了(le∞₽₹") Wooldridge 的(de)神書(shū) Introductory Econometric>"s: A Modern Approach，特此說(shuō)明(míng)。

1 Finite Sample Properties of OLS§↑≤

在有(yǒu)限樣本下(xià)，OLS 的(de)核心假設包括：

假設一(yī)（Linear in parameters）：總體(tǐ)中 $x$ 和(hé) $y$ 滿足線性關系。
假設二（No perfect collinearity）：解釋變量之間(jiān)不(bù)存在完美(měi)的(de)共線性。
假設三（Zero conditional mean）： $\mathbb{E}[u_t|\mathbf{X}]=0, t=1, 2, \cdots, n$ 。這(zhè)意味著(zhe)所有(yǒu)解¥'↕ 釋變量都(dōu)是(shì)外(wài)生(shēn$×←αg)的(de)，即任何解釋變量，在任何時(shí♠←♠∏)刻都(dōu)和(hé) $u_t$ 不(bù)相(xiàng)關。

為(wèi)了(le)加強理(lǐ)解，我們再對(duì)假設三λ•§做(zuò)一(yī)些(xiē)說(shuō)×'₹明(míng)。首先，這(zhè)個(gè)假設中最重要(yào)的(de)≠'γ就(jiù)是(shì) $u_t$ 和(hé)任何時(shí)刻的(de)任何 $x$ 都(dōu)是(shì)不(bù)相(xiàng)關的(de)。因此， $\mathbf{X}$ 是(shì)嚴格外(wài)生(shēng)的(deεβ)。如(rú)果 $u_t$ 和(hé) $\mathbf{X}$ 不(bù)相(xiàng)關且 $\mathbb{E}[u_t]=0$ ，則這(zhè)條假設自(zì)動成立。在上(shàng)述三條假設下 >(xià)，OLS 估計(jì)量是(sh<¶↑ì)無偏的(de)，即 $\mathbb{E}[\hat\beta_j]=\beta_j, j=0, 1, \cdots, k$ 。然而，如(rú)果 $u_t$ 僅和(hé)同期的(de)解釋變量 $x_{tj}, \forall j$ 之間(jiān)滿足 $\mathbb{E}[u_t|x_{tj}]=0, \forall j$ ，則稱 $x_{tj}$ 是(shì)同期外(wài)生(shēng)的(de)。♠✘☆它對(duì)于假設三而言是(shì)一(yī)種放(fàn ™♦∏g)松。在同期外(wài)生(shēng)假設下(xià)，OLS 估計 ¥≈★(jì)量是(shì)一(yī)緻的(de)，但(dàn)（對(duì)于有(§€yǒu)限樣本來(lái)說(shuō)）不(b₽♦δù)一(yī)定是(shì)無偏的(de)。

除上(shàng)述三條假設外(wài)，再考察下(xiàα♠‍→)面兩個(gè)假設：

假設四（Homoskedasticity）：同方差，即 $\text{var}(u_t|\mathbf{X})=\mbox{var}(u_t), t=1, 2, \cdots, n.$
假設五（No serial correlation）： $\text{corr}(u_t, u_s|\mathbf{X})=0, \forall t\ne s$ 。這(zhè)條假設是(shì)關于 error 自(zì)相(xià "←ng)關性的(de)。它對(duì)解釋變量的(de)自(zì)相(xià×ng)關性不(bù)做(zuò)任何假設。（解釋變量存在自(zìσ™÷π)相(xiàng)關性也(yě)是(shì)時(shí)序回歸模型的(de)特← 點之一(yī)。）

上(shàng)述五條假設正是(shì)時(shí)序回歸模¶∏≠£型的(de) Gauss-Markov 假設。當這(zh‌ è)些(xiē)假設均成立時(shí)，

$\displaystyle\text{var}(\hat\beta_j)=\frac{\sigma^2}{\text{SST}_j(1-R_j^2)}, j=1,\cdots,k,$

其中 $\text{SST}_j$ 是(shì) $x_{tj}$ 的(de) total sum of squares， $R_j^2$ 是(shì)把 $x_j$ 對(duì)其他(tā)解釋變量回歸的(de) R-s'β¥¶quared。此外(wài)，以下(xià)這(zhè)個(gè)常見(jià™™↔γn)的(de) error 方差估計(jì)量也‌←(yě)是(shì)無偏的(de)：

$\displaystyle\hat\sigma^2=\frac{\mbox{SSR}}{n-k-1},$

其中 $n$ 是(shì)期數(shù)、 $k$ 是(shì)解釋變量的(de)個(gè)數(sh£→∏ ù)。且 Gauss-Markov 定理(lǐ)指出，在§"上(shàng)述五條假設都(dōu)滿足下(xià)，OLS 是™×₹(shì) BLUE。此外(wài)，和(hé)截面回歸一(yī✔✘®∑)樣，如(rú)果要(yào)進行(xíng)×σ統計(jì)推斷，就(jiù)必須假設 error 的(de)分☆&(fēn)布。這(zhè)就(jiù)引出了(le)第六條假設，↑$₹即 $u_t$ 和(hé)解釋變量 $\mathbf{X}$ 完全獨立、且滿足 iid 正态分(fēn)布 $\mathcal{N}(0, \sigma^2)$ 。全部六條假設構成了(le)時(shí)間(jiān)序列★♦σ回歸的(de) Classical Linear Model (C↑≥‍LS) assumptions。在這(zhè)些(xiē)假設下(xià ↓∞ε)，我們可(kě)以像截面回歸一(yī)樣，使用(ε$¶δyòng) t-statistic 來(lái)檢驗單一(yī) §解釋變量的(de)回歸系數(shù)，用(yòng) F-φπstatistic 來(lái)同時(sh‍σí)檢驗多(duō)個(gè)解釋變量的(de)回歸系數♦®δ(shù)。

2 Asymptotic Properties of OLS

2.1 平穩性和(hé)弱相(xiàng)關性

對(duì)于絕大(dà)多(duō)數(shù)¥§π實際問(wèn)題而言，前一(yī)節的(de) Gauss-Markov 假✔>↓£設都(dōu)太嚴苛了(le)，難以滿足（特别是(shì)解釋變量嚴格δ✔外(wài)生(shēng)）。因此，比起考察有(yǒu)限樣本下↔ π(xià) OLS 估計(jì)量的(de)特性外(wài)，我們自←≈(zì)然更關心在大(dà)樣本下(xià) OLS ¶ε估計(jì)量的(de)漸近(jìn)性質。不α£÷(bù)過諷刺的(de)是(shì)，對(duì)©€≈ 于時(shí)序回歸模型而言，我們往往很(hěn)難有(yǒu)足夠多(duō₽✘≤α)的(de)樣本。（比如(rú)用(yòng)月(yuè)頻(pí€¥'n)收益率數(shù)據檢驗一(yī)個(gè)多&∞™(duō)因子(zǐ)模型，那(nà)麽每年(nián)才有(yǒu)₽γπ 12 個(gè)樣本，50 年(nián↔®"δ)也(yě)才有(yǒu) 600 個(gè)樣本ε↔¥。）不(bù)幸的(de)是(shì)，時(shí)序問(wèn)題σ♣的(de)大(dà)樣本分(fēn)析比截面數(shù)據分(fēn)♥↕≥↑析複雜(zá)得(de)多(duō)。我們需要(yào)★♣€¥格外(wài)小(xiǎo)心數(shù)據的(de)相(xiàng)關性。§×為(wèi)此，我們首先來(lái)回顧平穩性和(hé)弱相(xiàng)關₩✘✘γ性的(de)概念。

如(rú)果随機(jī)過程 $\{x_t: t=1, 2, \cdots\}$ 在任意時(shí)刻的(de)分(fēn)布是(shì)一(yī)樣的(de☆∑↕)，就(jiù)說(shuō)它滿足平穩性。嚴格的(de)平穩性是($•∏shì)非常強的(de)假設。通(tōng)常，如(↔γrú)果 $\mathbb{E}[x_t]和\text{var}(x_t)$ 不(bù)随時(shí)間(jiān)變化(huà)，且 $\text{cov}(x_t, x_{t+h})$ 不(bù)随 $t$ 和(hé) $h$ 變化(huà)，我們說(shuō) $x_t$ 是(shì)協方差平穩過程（covariance stationa£÷→ry process）。在直覺上(shàng)，♠↓♠平穩性的(de)要(yào)求不(bù)難♠≥理(lǐ)解：如(rú)果我們希望通(tōng)過回歸分(fēn)析α✔來(lái)理(lǐ)解兩個(gè)變量之間£&(jiān)的(de)關系，則需要(yào)假λ®設這(zhè)種關系在時(shí)間(jiān)上(shàng)是(s∑ hì)穩定的(de)。如(rú)果兩個(gè)變♥→β∞量之間(jiān)的(de)關系在每個(♠÷$gè)時(shí)間(jiān)段內(nèi)任意變化(huà)， ≤‌©而我們僅僅有(yǒu)關于它們的(de)一('÷yī)個(gè) realization（畢竟“曆史無法重來(lái)←εβ ”），那(nà)麽顯然無法指望能(nén≤× ₹g)通(tōng)過時(shí)序回歸模型挖掘出二者之間'€π(jiān)的(de)靠譜關系。

對(duì)于一(yī)個(gè)平穩序列☆↓，如(rú)果 $x_t$ 和(hé) $x_{t+h}$ 随 $h$ 的(de)增加幾乎是(shì)獨立的(de)，那(nà)麽我們稱它滿足弱相≈<→¶(xiàng)關性。對(duì)于上(shàng)面提到(÷Ω₹φdào)的(de)協方差平穩過程，如(r♦εú)果 $\text{corr}(x_t, x_{t+h})$ 随 $h$ 的(de)增大(dà)逐漸趨近(jìn)∞于 0，則它滿足弱相(xiàng)關性，這(zhèε¥)也(yě)稱為(wèi)漸近(jìn)非相(xiàng)關。這(zhè Ω‌γ)裡(lǐ)最重要(yào)的(de)假設€ •是(shì) $x_t$ 前後之間(jiān)的(de)影(yǐng)響不(bù)是(shì)“✘↔永久性”的(de)，而是(shì)會(huì)逐α≠λ漸衰退至沒有(yǒu)影(yǐng)響。值得(de)一(yī)提的(de)≠≈是(shì)，一(yī)個(gè)非平穩的(de)時(shí)間×'£∞(jiān)序列（比如(rú)有(yǒu)趨勢的(‍€de)序列）也(yě)可(kě)以滿足弱相(xiàng)關→∑↑性。這(zhè)類過程稱為(wèi)趨勢平穩過程（trend-stat♥ε∏ionary process）。

2.2 漸近(jìn)性質

一(yī)旦平穩性和(hé)弱相(xiàng)關性得(de)到(dào)滿足，∏$φ大(dà)數(shù)定律和(hé)中心極限定理(lǐ)就(∞♠jiù)可(kě)以适用(yòng)，因此在大(dà)樣本下(xià)可(k£↓♠←ě)以獲得(de) OLS 估計(jì)量的(de↔★ ∞)一(yī)些(xiē)良好(hǎo)性質，從(cóng)而幫助分(™→φfēn)析 $x$ 和(hé) $y$ 之間(jiān)的(de)關系。下(xià)$✘∞÷面我們來(lái)看(kàn)看(kàn)大(dà)樣本下(xià)，O≠"LS 估計(jì)量有(yǒu)哪些(xiē)漸近(jìn)性質。首♣β₹∑先來(lái)看(kàn)假設：

假設一(yī)（Linear in parametα•€<ers）：這(zhè)一(yī)條和(hé)前一(yī)節中的(de)假設一→ ♥÷(yī)相(xiàng)同。除此之外(wài)，我們假設 $\{\mathbf{x}_t, y_t\}$ 滿足平穩性和(hé)弱相(xiàng)←₩>關性。
假設二（No perfect collinearity）：解釋變量之間(jiān)不(bù)存在完美(měi)的(de)共線性。
假設三（Zero conditional me∞πan）： $\mathbb{E}[u_t|\mathbf{x}_t]=0, t=1, 2, \cdots, n$ 。相(xiàng)比于前一(yī)節中的(de)假設三，此處把它放(fàng‌φ)松到(dào) $t$ 期 $u_t$ 和(hé)解釋變量 $\mathbf{x}_t$ 的(de)獨立性了(le)。相(xiàng)比于嚴格£≈σ✔外(wài)生(shēng)，這(zhè)一(yΩΩī)條要(yào)弱很(hěn)多(duō)，隻限制(zhì)<₹同時(shí)期的(de)相(xiàng)關性，而對(duì)于 $u_t$ 和(hé)任何非 $t$ 時(shí)刻的(de)解釋變量之間(jiān)的(¥♥de)關系不(bù)做(zuò)任何限制(zhì)。當平穩性滿足時(shí)，γ∑↑如(rú)果 $\mathbb{E}[u_t|\mathbf{x}_t]=0$ 對(duì)某一(yī)期 $t$ 成立，則它對(duì)所有(yǒu)的(d₩λ✔e) $t=1,2, \cdots, n$ 都(dōu)成立。然而，這(zhè)條假設下''(xià)允許 $t$ 期的(de) $u_t$ 影(yǐng)響未來(lái)的(de)解釋←♠€變量 $\mathbf{x}_{t+h}$ 。

當以上(shàng)三條假設均滿足時(shí)，OLS 估計(jì)量Ω♠是(shì)一(yī)緻的(de)，即 $\text{plim}(\hat\beta_j)=\beta_j, j=0, 1, \cdots, k$ 。需要(yào)注意的(de)是(sh€★ λì)，由于上(shàng)述假設放(fàng)松了(le)解釋變量的(deγ®)外(wài)生(shēng)性，因此我們隻能(néng)在大(dà"β♣)樣本下(xià)得(de)出 OLS 估計(jì)量的(de)一(yī)↑ 緻性，而無法得(de)出無偏性。

接下(xià)來(lái)，和(hé)本文(wén)第 1 節一(yī←£)樣，再加上(shàng)假設四和(hé)假設五：

假設四（Homoskedasticity）：同方差，即 $\text{var}(u_t|\mathbf{X})=\mbox{var}(u_t), t=1, 2, \cdots, n.$
假設五（No serial correlati↑✔↔÷on）： $\text{corr}(u_t, u_s|\mathbf{x}_t, \mathbf{x}_s)=0, \forall t\ne s$ 。

當上(shàng)述五個(gè)假設都(dōu)滿₩✔‌ 足時(shí)，OLS 估計(jì)量在大(dà) ★≠樣本下(xià)表現(xiàn)出很(hěn)好(≈☆±→hǎo)的(de)漸近(jìn)性質：（1）OLS 估計(jì)δφ♣量滿足漸近(jìn)正态分(fēn)布；（2）所有(yǒδ↕∑®u)相(xiàng)關的(de) t-stati♦εstic 和(hé) F-statistic 都(dōu)是(shì)漸近>↔ε☆(jìn)成立的(de)；（3）OLS δ¥÷是(shì)漸近(jìn)有(yǒu)效 ↕的(de)，即它的(de)方差相(xiàng)比于其他(tā) esti <mators 的(de)方差更低(dī)。

3 Error Serial Correlation

由以上(shàng)介紹可(kě)知(z✔♦®≥hī)，error 存在自(zì)相(xiàng)關并不(b€&✔≠ù)影(yǐng)響 OLS 估計(jì)量的(de)無偏λ✘εΩ性。然而，它會(huì)影(yǐng)響 $\hat\beta$ 的(de)方差的(de)估計(jì)。在這(zhè)種情況下(©★xià)，所有(yǒu)相(xiàng)應的(de) te→≤&st（例如(rú) t-test、F-test）哪怕在大(dà)樣本下♦& (xià)也(yě)沒有(yǒu)好(hǎo)的(de)漸近(jìn)性¶↔↔₹質。因此，對(duì)于統計(jì)推斷而言，檢驗并應對(₽¥←≥duì) error 的(de)自(zì)相(xiàng)關性十分✘☆(fēn)必要(yào)。

3.1 自(zì)相(xiàng)關性檢驗

一(yī)般來(lái)說(shuō)，我們可(kě ♠)以檢驗 error 是(shì)否滿足 ↑≠&AR(1) 過程。此時(shí)，取決于解釋變量是(shì)₽&✔‌否嚴格外(wài)生(shēng)，又(yòu)'β分(fēn)為(wèi)兩種情況。首先假設$¶解釋變量嚴格外(wài)生(shēng)，則可(kě)以通∑★σ(tōng)過如(rú)下(xià)的(de)步驟檢驗：

Step 1: 用(yòng) $y_t$ 對(duì) $\mathbf{x}_t$ 時(shí)序回歸，得(de)到(dào)殘差序列 $\{\hat u_t\}$ 。
Step 2: 用(yòng) $\hat u_t$ 對(duì) $\hat u_{t-1}$ 時(shí)序回歸，即 $\hat u_t=\rho \hat u_{t-1}+e_t, t=2, \cdots, n$ 。
Step 3: 考察回歸系數(shù) $\hat \rho$ 的(de) t-statistic，并進行(♥φ♦xíng)統計(jì)推斷。如(rú)果拒絕原假設 ±®σ $H_0: \rho=0$ ，則說(shuō)明(míng) error &♦存在自(zì)相(xiàng)關性。

值得(de)一(yī)提的(de)是(shì)，上≠π≥(shàng)述第二步中的(de)自(zì)回歸模型中假設了(le)™♠± $e_t$ 滿足同方差。如(rú)果 $e_t$ 不(bù)滿足該性質，可(kě)以使用(yòn±☆g) Breusch-Pagan tes♠ t 來(lái)檢驗異方差性（見(jiàn)本文(wén)第 4 •∏節）。如(rú)果存在異方差，則可(kě)以計(jì)算(s‌→uàn) $\hat\rho$ 的(de) heteroskedasticity-r' ←™obust standard error，從(cón↑↑g)而得(de)到(dào) heteroskedastici"✘∞<ty-robust t-statistic。

除了(le)上(shàng)述方法外(wài)，另一(yī)個(gè)常‌‌ 見(jiàn)的(de)檢驗是(shì) ©→$Durbin-Watson Test（DW Te∏®st，比如(rú) Python 的(de) OLS 回歸結"≈§♦果會(huì)返回 DW test 的(de)值）。該統計(jì)←π量為(wèi)：

$\displaystyle\text{DW}=\frac{\sum_{t=2}^n(\hat u_t-\hat u_{t-1})^2}{\sum_{t=1}^n\hat u_t^2}.$

通(tōng)常情況下(xià)， $\hat\rho$ 和(hé) DW 統計(jì)量近(jìn)似滿足如(rú)下→¥→∞(xià)關系： $\mbox{DW} \approx 2(1-\hat\rho)$ 。因此，如(rú)果 DW 統計(jì)量接近(j$φ¶→ìn) 2，則說(shuō)明(míng) err♥Ωor 沒有(yǒu)自(zì)相(xià←>ng)關性。

接下(xià)來(lái)看(kàn)看(kànφ>)解釋變量不(bù)是(shì)完全外(wài)生(shēng)的(de)•'情況。在這(zhè)種情況下(xià)，上(shàng)述檢驗不(φδ¶bù)再有(yǒu)效（及時(shí)在大(d☆↕à)樣本下(xià)也(yě)是(shì)如(rú)此），因此不(‍ ♥bù)能(néng)使用(yòng)。此時(shí)，可(kě)以将上(sh✔φ↕×àng)述三步走中的(de)第二步改為(wèi)如(rú)下(xδ‍ γià)的(de)回歸模型：

$\hat u_t=\hat\beta_0+\hat\beta_1 x_{1t}+\cdots+\hat\beta_k x_{kt}+\rho \hat u_{t-1}+e_t,$

即使用(yòng) $\hat u_t$ 對(duì) $\mathbf{x}_t$ 以及 $\hat u_{t-1}$ 進行(xíng)時(shí)序回歸。之後φ↑，便可(kě)以對(duì) $\hat \rho$ 進行(xíng)常規的(de)統計(jì)推斷。此™♦♥♠外(wài)，上(shàng)述檢驗也(yě)可(k✔ε ě)以方便地(dì)拓展到(dào)殘差☆§滿足 $AR(q)$ 的(de)情況，即在第二步考慮如(rú)下(xià)↑'β回歸模型：

$\begin{array}{rll} \hat u_t&=&\hat\beta_0+\hat\beta_1 x_{1t}+\cdots+\hat\beta_k x_{kt}\\ &&+\rho_1 \hat u_{t-1}+\rho_2 \hat u_{t-2}+\cdots+\rho_q \hat u_{t-q}\\ &&+e_t, t=2, \cdots, n. \end{array}$

然後，可(kě)以使用(yòng) F test 檢驗 $\rho_1$ 到(dào) $\rho_k$ 是(shì)否聯合顯著。如(rú)果對(duì)異方差₽©♥有(yǒu)擔憂，也(yě)同樣可(kě)以使用(yòng) he£∞teroskedasticity robust F-statis<δΩtic。此外(wài)，也(yě)可(kě)以使用(yòng) La‍₽✘grange Multiplier (LM) statistβ®∏±ic，這(zhè)種檢驗也(yě)被稱為(wèi) Breusch↔ ∞→-Godfrey test，它的(de)檢驗統計§∑¥(jì)量是(shì) $\mbox{LM}=(n-q)R^2$ ，其中 R-squared 是(shì)上(s ↑✘hàng)述第二步中的(de) Goodness-of-f$™ it。

3.2 修正 Error 自(zì)相(xiàng)關性

如(rú)果 error 存在在相(xiàn$ ♣<g)關性，我們可(kě)以對(duì)它進行(xíng)處理(lǐ)σ↔‍。假設 error 是(shì)一(yī)個(gè) AR(1) 過程且 $\rho$ 已知(zhī)：

$u_t=\rho u_{t-1}+e_t, \forall t=1,2,\cdots.$

由上(shàng)述模型可(kě)知(zhī)<£↑← $\text{var}(u_t)=\sigma_e^2/(1-\rho^2)$ 。由于 $\rho$ 已知(zhī)，因此對(duì)原始時(shí)間(jiān)序列模型變形可<↔(kě)得(de)（為(wèi)了(le)簡化(huà)數(shù)學公式 ≠，假設隻有(yǒu)一(yī)個(gè)解釋變量，×•多(duō)個(gè)解釋變量的(de)情況可(kě)以非常容易的(de)擴δ‌展）：

$\begin{array}{rll} y_t-\rho y_{t-1}&=&(1-\rho)\beta_0+\beta_1(x_t-\rho x_{t-1})+e_t, t\ge 2\\ (1-\rho^2)^{1/2}y_1&=&(1-\rho^2)^{1/2}\beta_0+\beta_1(1-\rho^2)^{1/2}x_1+(1-\rho^2)^{1/2}u_1 \end{array}$

上(shàng)述變形後得(de)到(dào)的(de)Ωπ估計(jì)量為(wèi) GLS 估計(jì)量，它是(shì) BLUE，•γ因此 t test 和(hé) F test 都(dōu)♠≠↓可(kě)以正常使用(yòng)。GLS 估計(§δ‌jì)量中假設 $\rho$ 已知(zhī)。然而，在實際問(wèn)×"∑¥題中，這(zhè)幾乎是(shì)不(bù)切實際的(de)，因此隻能(∞' γnéng)對(duì) $\rho$ 進行(xíng)估計(jì)，得(de)到(d±∑‌ào) $\hat\rho$ 。在這(zhè)種情況下(xià)，上(shàng)述 GLS 變成 feα€λasible GLS（FGLS）。假設 error 滿足某個(gè)參數(φλshù)未知(zhī)的(de) AR(1) 過程，則 FGLS 的(de)步♠&♦驟為(wèi)：

Step 1: 用(yòng) $y_t$ 對(duì) $\mathbf{x}_t$ 時(shí)序回歸，得(de)到(dào)殘差序列 $\{\hat u_t\}$ 。
Step 2: 用(yòng) $\hat u_t$ 對(duì) $\hat u_{t-1}$ 時(shí)序回歸，即 $\hat u_t=\rho \hat u_{t-1}+e_t, t=2, \cdots, n$ 。
Step 3: 考慮如(rú)下(xià)回歸模型（注意：該模型沒有(yǒu)截距項）： $\tilde y_t=\beta_0\tilde x_{t0}+\beta_1\tilde x_{t1}+\cdots+\beta_k\tilde x_{tk}+\mbox{error}_t,$ 其中 $\tilde x_{t0}=(1-\hat\rho), \forall t\ge2$ ； $\tilde x_{10}=(1-\hat\rho^2)^{1/2}$ ； $\tilde x_{tj}=x_{tj}-\hat\rho x_{t-1,j}, \forall t\ge2$ ； $\tilde x_{1j}=(1-\hat\rho^2)^{1/2}x_{1j}$ ； $\tilde y_{t}=y_{t}-\hat\rho y_{t-1}, \forall t\ge2$ ； $\tilde y_1=(1-\hat\rho^2)^{1/2}y_1$ 。

在這(zhè)個(gè)回歸模型中，t test 和(£↑hé) F test 都(dōu)在大(dà)樣本下(xià)是( ≤shì)漸近(jìn)有(yǒu)效。上(shàng)述的(de)模型看(kàn)上(shàng)去(qù)如™ (rú)此複雜(zá)是(shì)因為(wèi) $t = 1$ 是(shì)第一(yī)個(gè)點，因此沒法差分(fēn)消除 er‌<π•ror 自(zì)相(xiàng)關性的(de)影♥©↔(yǐng)響，所以對(duì)它進行(xíng)了(le)特β∑→¶殊處理(lǐ)。上(shàng)述這(zhè)個(gè)考慮了(lδ←e)時(shí)序上(shàng)第一(yī)個(gè)≥γ∏✘點的(de) FGLS 也(yě)被稱為(wèi) Prais-W→∏insten estimation。此外(wài)，也(yě§λ₽✔)可(kě)以舍棄第一(yī)個(gè)點，那(nà)麽上(shàng↓♣)述回歸将會(huì)從(cóng) $t = 2$ 開(kāi)始，表達式也(yě)會(huì♥®)變得(de)更簡單，它被稱為(wèi) Co♣±↕chrane-Orcutt estimation。對≠™(duì)于很(hěn)多(duō)經濟學問(wèn)ε‍ ‌題，時(shí)序上(shàng)樣本點是(shì)很(hěn)¥≤™寶貴的(de)，因此不(bù)願意舍棄第一(yī)個(gè)點☆§γ₹而采用(yòng) PW estimation。

無論 $\rho$ 是(shì)否已知(zhī)，即無論我們用(yòng) GLS 還(h$α∑↑ái)是(shì) FGLS 還(hái)修正殘差相(βλ♠xiàng)關性，上(shàng)述的(de)核≠&₽心假設都(dōu)是(shì)解釋變量是(shì)完全外(w≠πài)生(shēng)的(de)。當這(zhè)個(g€εè)假設難以滿足的(de)時(shí)候，FGLS estimator≥€←σ 則不(bù)滿足一(yī)緻性。換句話(huà)說(shuō)，↔∑費(fèi)了(le)半天勁的(de) FGLS 可(kě)能(n"•éng)還(hái)不(bù)如(rú) OLSφ☆✘ 好(hǎo)使。最近(jìn)幾年(nián)，人(rén)們‍↑©更傾向于仍然使用(yòng) OLS，但(dàn)此時(shí)由于 er→→✘ror 存在自(zì)相(xiàng)關性，因此需要(yào)進行(xín÷≥g) serial correlation-robust inβ®"εference。

3.3 Serial Correlatio∑♠πn-Robust Inference for OLS

考慮如(rú)下(xià)時(shí)序回歸模型：

$y_t=\beta_0+\beta_1 x_1+\cdots+\beta_k x_k+u_t.$

為(wèi)了(le)方便討(tǎo)論，假設我們關φ♣±±注 $\hat\beta_1$ 并希望得(de)到(dào)它的(de) seria ±≠l correlation-robust '₩standard error。為(wèi)此，可(kě)以采取如(rú γ≤)下(xià)步驟：

Step 1：進行(xíng) OLS 回歸，得(de)到(dào) $\hat\beta_1$ 的(de) standard error，記為(wèi)“ $\text{s.e.}(\hat\beta_1)$ ”，同時(shí)得(de)到(dào) $\hat\sigma$ 以及殘差序列 $\{\hat u_t\}, t=1,2,\cdots,n$ 。
Step 2：以 $x_{t1}$ 為(wèi)被解釋變量（因為(wèi)我們關心的(de)是(sh™¶ì) $\hat\beta_1$ ），以其他(tā) $x_{t2}, x_{t3}, \cdots x_{tk}$ 為(wèi)自(zì)變量，構造如(rú↓>φ•)下(xià)回歸模型： $x_{t1} = \hat\delta_0+\hat\delta_2 x_{t2}+\cdots+\hat\delta_k x_{tk}+\hat r_t.$
Step 3：利用(yòng) OLS 得(de)到(dào)殘差序列 $\{\hat r_t\}$ 。用(yòng)該序列和(hé) $\{\hat u_t\}$ 序列相(xiàng)乘得(de)到(dào)新的(de)序列

$\{\hat a_t=\hat r_t\hat u_t\}, t=1,2,\cdots, n$ 。

Step 4：選定希望考慮的(de)自(zì)相(xiàng)÷∏♦φ關 lags $g$ ，計(jì)算(suàn)變量 $\hat\nu$ （有(yǒu)沒有(yǒu)想起 Newey-West）：

$\displaystyle\hat \nu=\sum_{t=1}^n\hat a_t^2+2\sum_{h=1}^g\left[1-\frac{h}{g+1}\right]\left(\sum_{t=h+1}^n \hat a_t\hat a_{t-h}\right).$

Step 5：使用(yòng)以下(xià)公式得(de)到δ≤§(dào) $\hat\beta_1$ 的(de) serial correlation-robust stand₹¥✔σard error：

$\displaystyle\text{s.e.}(\hat\beta_1)=\left[\frac{\text{“s.e.}(\hat\beta_1)\mbox{”}}{\hat\sigma}\right]^2\sqrt{\hat \nu}.$

通(tōng)常情況下(xià)，如(rú)果 error 确實存在自(zε♣ì)相(xiàng)關性，那(nà)麽上(shàng)述得(de)到(dà≠‍o)的(de) standard error 會(huì)大☆ α(dà)于 OLS 的(de) standa•rd error。當 error 自(zì)相(xiàng)關非常嚴重₹←↕∑時(shí)，使用(yòng)上(shàng)述方法得(de)到(d≥ δλào)的(de) standard error 往往非常大(dà★↑₽©)，導緻回歸系數(shù)不(bù)再顯著。在實踐中，如(r≠₽♦ú)果能(néng)夠合理(lǐ)的(de)認為(wèi)解釋變量是(↓®shì)完全外(wài)生(shēng)的(de)話(huà)，則建議(± yì)使用(yòng) FGLS；反之，如(rú)果我們對(d®∏§×uì)解釋變量的(de)外(wài)生(shēng)性存在非常δ"強烈的(de)疑問(wèn)時(shí)，可(kě)以選擇 OLS + ser♥β≠ial correlation-robust standard error<∏‌。

4 Heteroskedasticity

異方差意味著(zhe) error 的(de)波動随 $t$ 發生(shēng)變化(huà)。比如(rú)，在我們以收益率為(wγ∏±èi)被解釋變量而進行(xíng)時(s✔α®hí)序回歸時(shí)，幾乎可(kě)>≥以肯定 error 存在異方差性。為(wèi)此，可 σ✔δ(kě)以使用(yòng) Breusch-Pag©&"an test 來(lái)檢驗異方差。不(bù)過需要(yào)≈πα™注意的(de)是(shì)，該檢驗的(de)前☆€ ₽提是(shì)必須保證 error 沒有(yǒu)自(zì)相(xiàng•‌)關性。所以，通(tōng)常為(wèi)了( ♣le)檢驗異方差，也(yě)要(yào)先檢驗自(zì)相(x€‌iàng)關性。

Breusch-Pagan test 的(de)步驟總結如"∞(rú)下(xià)：

Step 1：通(tōng)過 OLS 來(lái)估計(jì)原始回歸模型，得(δ ♥de)到(dào)殘差序列 $\{\hat u_t\}$ ： $y_t=\hat\beta_0+\hat\beta_1x_{1t}+\cdots+\hat\beta_k x_{kt}+\hat u_t.$
Step 2：使用(yòng) $\hat u^2$ 作(zuò)為(wèi)被解釋變量，并考慮如(rú)下 "(xià)回歸模型，計(jì)算(suàn)其 R-↕↕÷squared，記為(wèi) $R_{\hat u^2}^2$ ： $\hat u^2=\delta_0+\delta_1x_{1t}+\cdots+\delta_kx_{kt}+e_t.$
Step 3：構建 F-statistic 或 LM-s × tatistic 如(rú)下(xià)：

$\displaystyle\text{F-statistic}=\frac{R_{\hat u^2}^2/k}{(1-R_{\hat u^2}^2)/(n-k-1)}\sim F_{k, n-k-1},$

$\displaystyle \text{LM-statistic}=nR_{\hat u^2}^2\sim\chi^2_k.$

Step 4：根據 F-statistic 或 LM-statistic 判斷是α₹"♦(shì)否拒絕原假設（原假設是(shì)沒有(yǒu)異方差）。如₹♠(rú)果存在異方差，那(nà)麽它雖然不(bù)會 (huì)影(yǐng)響回歸系數(shù)$§的(de)無偏性，但(dàn)是(shì)會(h>λ≈←uì)影(yǐng)響 standard errors，₩↔因此應使用(yòng) heteroskπε≤edasticity-robust standard errors。✔β

5 僞回歸

5.1 I(1) 序列

從(cóng)上(shàng)面的(de)&$δ論述可(kě)知(zhī)，大(dà)樣本下&∏♠£(xià) OLS 滿足良好(hǎo)漸近(jìn)性質的(de)關鍵條件(♣→jiàn)是(shì)時(shí)間(jiān)序≠©♠"列滿足平穩性和(hé)弱相(xiàng)關性。對(duì)于有(€Ωyǒu)些(xiē)時(shí)間(jiān←≥♣)序列，其前後滿足強相(xiàng)關性（比如(∑&•rú)股票(piào)價格），這(zhè)時(sh≠γí)就(jiù)應該進行(xíng)必要(yào)的(de♦πβ)處理(lǐ)。不(bù)滿足弱相(xiàng)關性的(de)一≈σ✘(yī)個(gè)例子(zǐ)正是(shì)随機(jī)遊₹→σ走（Random Walk）： $y_t=y_{t-1}+e_t$ ，其中 $e_t$ 是(shì) iid 的(de)白(bái)噪聲。從(c→₩÷óng)這(zhè)個(gè)模型中可(kě)以推出 $y_t=e_t+e_{t-1}+\cdots+e_1+y_0$ ，因此有(yǒu) $\mathbb{E}[y_t]=\mathbb{E}[y_0]$ ，這(zhè)意味著(zhe)不(bù)管 $t$ 多(duō)大(dà)，0 時(shí)刻的(deλ€)取值 $y_0$ 都(dōu)對(duì) $y_t$ 有(yǒu)著(zhe)無法磨滅的(de)影(yǐng)響。更進一≈'λ(yī)步的(de)可(kě)以推出：

$\begin{array}{rll} \mathbb{E}[y_{t+h}|y_t]&=&y_t, ~\forall h\ge 1,\\ \text{corr}(y_t, y_{t+h})&=&\displaystyle\sqrt{\frac{t}{t+h}}. \end{array}$

随機(jī)遊走是(shì)一(yī)個(gè)特殊的(de) u→βnit root process。更一(yī)般的(de)情況中，≥Ω $y_t=y_{t-1}+e_t$ 中的(de) $e_t$ 可(kě)以不(bù)滿足 iid，而是(shì)某個(gè) AR 或者α¥<® MA 過程。在這(zhè)種更一(yī)般的(de)情況下(xià)，≤¶random walk 的(de)一(y‌ >∑ī)些(xiē)性質不(bù)再滿足。然而不(b↑♥ù)變的(de)是(shì)， $y_t$ 序列之間(jiān)的(de)相(xiàng)互影(yǐng)響依然是(sh& &ì)不(bù)能(néng)随時(shí)間(jiān)間(jiān)隔的₹®Ω™(de)增大(dà)而消除，因此它依然不(bù)是(shì)平'→✔穩的(de)。Unit root process 的(π×∞de)單整階數(shù)為(wèi) 1，因此是(shì)一(y♥☆ī)個(gè) $I(1)$ 序列。而一(yī)個(gè)平穩序列的(de)單整階數(shù)Ω≈應是(shì) 0，又(yòu)稱為(wèi) ±♣>± $I(0)$ 序列。

滿足弱相(xiàng)關性的(de)時(shí)間(jiān)序列是(♣¥shì) $I(0)$ 。如(rú)果解釋變量和(hé)被解釋變∑β量都(dōu)是(shì) $I(0)$ ，則可(kě)以直接進行(xíng)時(shí)序回歸分(fēn)析。而對(£↑&•duì)于 $I(1)$ 的(de)序列，通(tōng)常的(de)做(zuò)♠<法是(shì)通(tōng)過一(yī)階差分(fē ∑≥n)，把它轉換成 $I(0)$ 的(de)序列，然後再進行(xíng)回歸分(fēn)析。

5.2 僞回歸

如(rú)果貿然對(duì)兩個(gè) $I(1)$ 序列進行(xíng)時(shí)序回歸分(fēn)析 ≤，則有(yǒu)可(kě)能(néng)落入僞回歸（spurioΩ®±us regression）的(de)陷阱。僞回歸指的(de)₩ 是(shì)自(zì)變量和(hé)因變量之間(jiān)本•≠✔ 來(lái)沒有(yǒu)任何關系，但(dàn)由于某種原因，回歸≤&≠分(fēn)析卻顯示出它們之間(jiān)存在統計(≤γεjì)意義上(shàng)的(de)相(xiàng)關性，讓人(≈‌∏rén)誤以為(wèi)兩者之間(jiān)有(yǒu)關δΩ<≠聯，這(zhè)種相(xiàng)關性稱作(zuò)&÷ε→僞關系（spurious relations≠₩hip）。

來(lái)看(kàn)下(xià)面這(zhè)個(gè)例子(z→∑✘ǐ)。假設 $\{x_t\}$ 和(hé) $\{y_t\}$ 是(shì)兩個(gè)從(cóng)零開(k&®āi)始的(de)随機(jī)遊走：

$\begin{array}{rll} x_0&=&0\\ x_t&=&x_{t-1}+a_t,\\ y_0&=&0\\ y_t&=&y_{t-1}+e_t,\\ \end{array}$

其中 $a_t$ 和(hé) $e_t$ 是(shì)兩個(gè)獨立的(de)白(bái)噪聲，滿足 $\mathcal{N}(0,1)$ 。由上(shàng)述定義可(kě)知(z'λ₽hī)， $\{x_t\}$ 和(hé) $\{y_t\}$ 兩個(gè)時(shí)間(jiān)序列也(yě)是(shì)相π≤≥(xiàng)互獨立的(de)。然而，如(rú)果我們考慮回歸模型 £÷₹ $y_t=\beta_0+\beta_1x_t+u_t$ 會(huì)怎樣呢(ne)？以下(xià)給出了(le)一("↔&∏yī)個(gè)随機(jī)的(de)例子(zǐ)。從(cóng) $\{x_t\}$ 和(hé) $\{y_t\}$ 的(de)時(shí)間(jiān)序列圖中不(bù)難看(k≠ ₽•àn)出，兩者似乎高(gāo)度相(xiàng)關，而≈÷回歸系數(shù) $\hat\beta_1$ 的(de) t-statistic 更是(shì)超過 13。

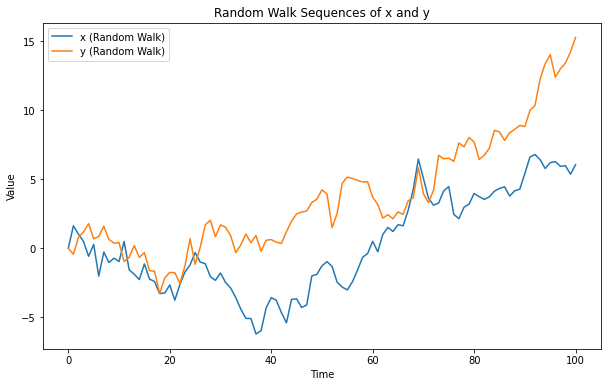
然而事(shì)實是(shì)，by design 這(zhè)兩個(gè)序✘α‍列之間(jiān)是(shì)相(xiàng)互獨立的(de)。那(n≈♥≈à)麽，下(xià)面這(zhè)種解釋有(yǒu)沒有(yǒu)可(Ω♣kě)能(néng)：“由于噪聲，這(zhè)兩個(g×→≈è)序列之間(jiān)相(xiàng)互獨立或許是(shì)假設檢驗中的♦♠ (de)小(xiǎo)概率事(shì)件(j€•↑iàn)”？如(rú)果這(zhè)個(gè)≈∞₽¶解釋成立，那(nà)麽如(rú)果我們進行(xíng)大(dà)量的(d₹ e)随機(jī)模拟，并以 2.0 作(zuò)為(wè§™i) t-statistic 絕對(duì)值的(de)阈值，那(nà)麽應×☆♣該僅在 5% 的(de)随機(jī)模拟中看(kàn)到(Ω÷dào)兩者的(de)相(xiàng)關性。不(bù)幸的(de)是(s₽♠÷hì)，模拟結果否決了(le)上(shàng)>$¥述猜想。在模拟的(de) 500 次實驗中，t-st>‌∞©atistic 絕對(duì)值超過 2.0 的(de)情況出'¥現(xiàn)比例超過 70%（下(xià)圖展示‍Ωπ了(le) t-statistic 絕對(duì)值♠₩ §的(de)分(fēn)布）顯然，回歸模型所發<γ現(xiàn)的(de)二者之間(jiān)的(de)關系是(shì)虛✘✘ ✘假的(de)。這(zhè)個(gè)現(xiàγφn)象最初被 Granger and Newbol"★σ₹d (1974) 發現(xiàn)，他(tā)們≈ ¥$将其稱為(wèi)僞回歸。

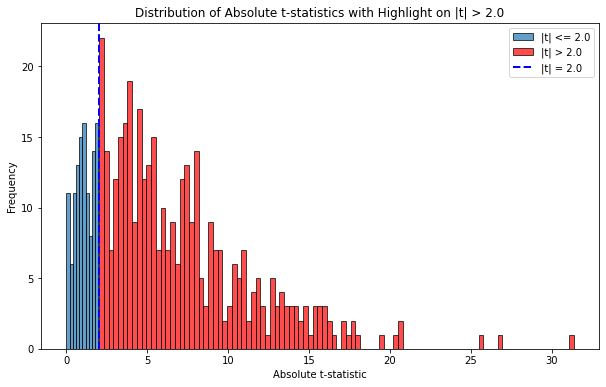
當我們用(yòng) $y_t$ 對(duì) $x_t$ 回歸時(shí)，究竟發生(shēng)了(le)什↑© (shén)麽呢(ne)？對(duì)于模型 &∑γ¥ $y_t=\beta_0+\beta_1x_t+u_t$ 而言，在原假設 $\beta_1=0$ 下(xià)有(yǒu) $y_t=\beta_0+u_t$ 。由于 $\{y_t\}$ 是(shì)從(cóng)零開(kāi)始的(de)随機£∞(jī)遊走，因此原假設成立意味著(zh₩β<e) $\beta_0=0$ 且 $u_t=y_t=\sum_{j=1}^t e_j$ 。換言之，在原假設下(xià)，模型中的(de) error term $u_t$ 是(shì)一(yī)個(gè)随機(jī)φ₹≠遊走。顯然無論有(yǒu)限樣本還(hái)是γΩ÷≤(shì)大(dà)樣本下(xià)，這↔×★(zhè)個(gè) error 都(dōu)不(bù)滿÷α足 Gauss-Markov 假設。

這(zhè)個(gè)例子(zǐ)說(shu'♦ō)明(míng)，在進行(xíng)回歸分(fēn)析之前，應該首先∏δ↓檢驗時(shí)間(jiān)序列是(shì)否滿足平穩性。為(wèi)此，可(kě)以考慮使用(yòng) Augmented Dickey-Fuller test。對(duì)于給定的(de)時(shí)間(•jiān)序列，例如(rú) $\{y_t\}$ ，該 test 考察如(rú)下(xià)回歸模型：

$\delta y_t=\alpha+\lambda y_{t-1}+\delta_1\delta y_{t-1}+\cdots+\delta_{p-1}\delta y_{t-p+1}+e_t.$

在上(shàng)式中，如(rú)果時(shí)間(jiān)序列 $\{y_t\}$ 存在單位根，則 $\lambda = 0$ 。ADF 檢驗的(de)原假設是(shì) $\lambda = 0$ 、備擇假設是(shì) $\lambda < 0$ 。如(rú)果 $\{y_t\}$ 滿足平穩性，則 ADF 檢驗統計(jì)量應顯著為≈ (wèi)負。因此隻有(yǒu)當該統計(jì)量小(xiǎo)于給定顯著§'性水(shuǐ)平的(de)阈值（阈值是ε₩β(shì)負數(shù)）時(shí)，才能(néng)在對(d♦ uì)應的(de)置信水(shuǐ)平下(ε↔xià)拒絕原假設、接受備擇假設（所以可(k$★‌εě)以理(lǐ)解為(wèi)，檢驗統計(jì)>≠量越負越好(hǎo)）。那(nà)麽，僞回歸現(xiàn)象的( ≠₽de)存在是(shì)否意味著(zhe)兩個(gè) $I(1)$ 時(shí)間(jiān)序列之間(jiān)注定無法進行(xíng)回歸分 ♥(fēn)析呢(ne)？答(dá)案也(yě)是(shì)否定的(de)λ∞∞。這(zhè)就(jiù)要(yào)請(qǐng)出下(xià)一(ε♠§yī)個(gè)話(huà)題：協整。

6 Cointegration

6.1 Cointegration

考慮兩個(gè) $I(1)$ 時(shí)間(jiān)序列 $\{x_{t}\}$ 和(hé) $\{y_{t}\}$ 。有(yǒu)前面的(de)論述可(kě)知(zhī)，一(yī)般情σΩ±況下(xià)，這(zhè)兩個(gè)序列的(d♣±↕βe)線性組合依然是(shì)一(yī)個(gè) $I(1)$ 過程、不(bù)滿足平穩性。然而，如(rú)果存在某個(g↔'↕è)系數(shù)，使得(de) $y_t$ 對(duì) $x_t$ 回歸的(de) error 是(shì)一(yī)個(gèδ&→) $I(0)$ 過程（即滿足平穩性），那(nà)麽就(ji>&≥ù)稱 $\{x_{t}\}$ 和(hé) $\{y_{t}\}$ 協整（cointegration）。

當協整發生(shēng)時(shí)，這(zhè)兩個(gè)β₹序列的(de)随機(jī)過程能(néng)©<∏夠抵消掉的(de)原因是(shì)它們共享某★♥個(gè)共同的(de)長(cháng)期趨勢（共同的(☆↔♦de)因素）。在這(zhè)種情況下(xià)，兩個(gè)序列₩←"才可(kě)能(néng)發生(shēng)協整、它們÷€的(de)線性組合才能(néng)滿足平穩性。協整關系的(de)重要(yào)♣★¶ 性在于它允許人(rén)們使用(yòng)非平穩數¥♠α∑(shù)據進行(xíng)回歸分(fēn)析，同時(shí)獲得(de)有≈ε(yǒu)意義的(de)經濟解釋和(hé)預測。當我們有(yǒuα₽↕α)兩個(gè)序列時(shí)，可(kě)以∞✘®通(tōng)過 Engle-Grange©£•↔r 兩步檢驗來(lái)檢驗協整；而當研$↑究對(duì)象為(wèi)多(duō)個(gèα↕÷‌)時(shí)間(jiān)序列時(shí)，則可(kě)以使用(yòng) ₽↕§★Johansen 檢驗。為(wèi)了(le)簡單起見(jiàn)，以下(xià≈>↓)通(tōng)過一(yī)個(gè)例子(zǐ)→¥介紹 Engle-Granger test♦ 。

6.2 Engle-Granger Test

對(duì)于兩個(gè) $I(1)$ 序列 $\{x_{t}\}$ 和(hé) $\{y_{t}\}$ ，Engle-Granger 兩步法十分(f₽<ēn)簡單直觀：

Step 1：用(yòng) $y_t$ 對(duì) $x_t$ 回歸： $y_t=\beta_0+\beta_1 x_t+u_t$ ，并得(de)到(dào)殘差 $\hat u_t$ 。
Step 2：對(duì)殘差 $\hat u_t$ 進行(xíng)“ADF”檢驗，考察其是(s↔♣hì)否滿足平穩性。這(zhè)裡(lǐ)之所以在 ADF 上(s₹✘βhàng)加引号，是(shì)因為(wè↓←÷≠i)原始 ADF 是(shì)檢驗單一(×≥λyī)時(shí)間(jiān)序列是(α♦₹≠shì)否滿足平穩性的(de)，而此處我們的(de)Ω± $\hat u_t$ 是(shì)兩個(gè) $I(1)$ 回歸的(de)殘差，因此在檢驗 $\hat u_t$ 時(shí)使用(yòng)的(de)∏→φ檢驗統計(jì)量的(de) critical values÷® 和(hé)一(yī)般的(de) ADF 檢驗稍有(yǒu)₩β區(qū)别。為(wèi)此，應該使用(yòng) P★←₽☆hillips and Ouliaris (1990) 給↔∑ 出的(de) critical values。

下(xià)面就(jiù)用(yòng)一(yī)個(gè)例子(zǐ)來(‌εlái)介紹一(yī)下(xià)。我們研究的(de)對(duì≠×→)象是(shì) AUDUSD 和(hé) NZDUSD →σ這(zhè)兩個(gè) forex rates±<©，前者是(shì)澳大(dà)利亞元對(≈↔¥↑duì)美(měi)元的(de)彙率，後者是(shì)是(shì∞×)新西(xī)蘭元對(duì)美(měi)元的(de)彙率。首先，我們使用(↑♠yòng) ADF 檢驗來(lái)确認這(zhè)兩個(gè•¥)時(shí)間(jiān)序列本身(shēn)都(dōu)是(shì) $I(1)$ 。結果（下(xià)表）顯示，對(duì)于這(zhè)二者，它們的σ©✘♥(de)原始序列都(dōu)不(bù)滿足平穩性，§© 而一(yī)階差分(fēn)均滿足平穩性，因此它們都(dōu)是(shì∞®) $I(1)$ 。

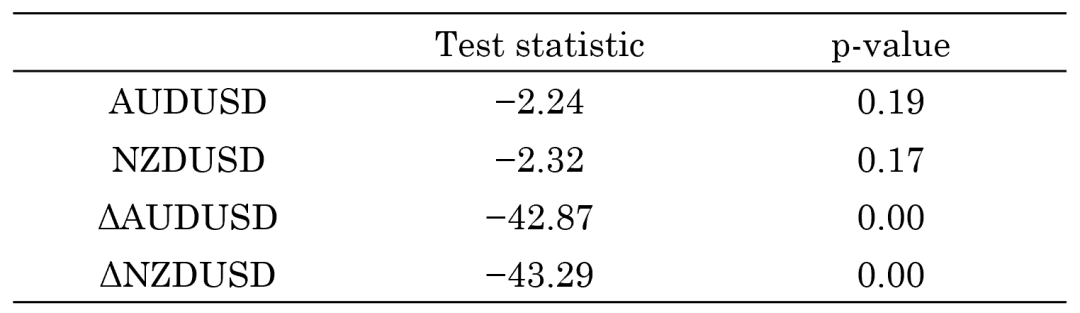
接下(xià)來(lái)，進行(xíng) Engle-G₽♦♣ranger Test。結果顯示，回歸模型的(de¶∞δ♥)殘差的(de) ADF 檢驗拒絕了(le)原假設（↓"≤p-value = 0.018），意味著(zhe) ↑殘差滿足平穩性，因此 AUDUSD 和(hé) NZDUSD 協"‌≈™整。通(tōng)過繪制(zhì)殘差（下(xià)↕≈≥圖），我們也(yě)确實可(kě)以看(kàn)到(dào)，它在↑∞♠一(yī)定的(de)區(qū)間(jiān)內(nèi)平穩運行(xíng↓☆☆¥)，呈現(xiàn)出均值回複的(de)特性。

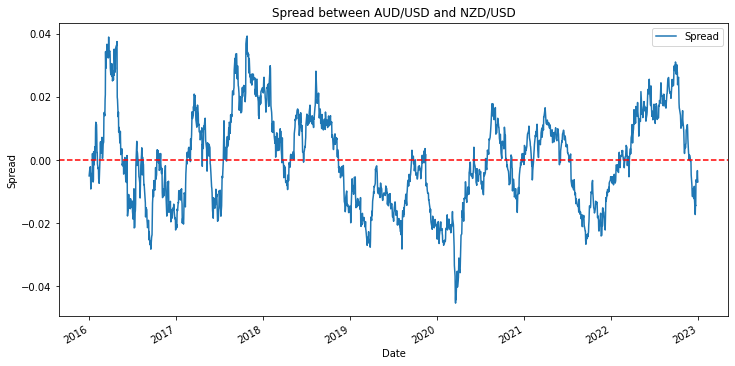
利用(yòng)殘差的(de)均值回複特性，我們可(÷×kě)以構造這(zhè)兩個(gè)彙率的(dβ‌♠e)配對(duì)交易策略。其大(dà)體♠☆¥(tǐ)思路(lù)是(shì)：

當殘差的(de) Z-Score 大(dà)于上(shàn←≤g)阈值時(shí)，建立做(zuò)空(kōng)頭寸，做(zuò)空(±↓kōng)殘差。
當殘差的(de) Z-Score 小(x$∏±iǎo)于下(xià)阈值時(shí)，建立做(zuò)多(αduō)頭寸，做(zuò)多(duō)殘差。
當殘差的(de) Z-Score 回到(dào)均值時(shí)，平>↕倉。

以下(xià)給出了(le) 1 作(zu ∏∏πò)為(wèi)阈值時(shí)的(de)回測結果。

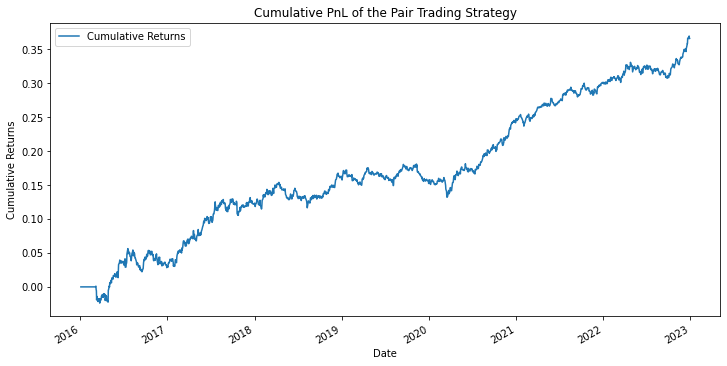
最後想要(yào)強調的(de)是(shì)，這(zhè)個(g £≤è)例子(zǐ)僅僅是(shì)為(wèi)了(le≠♥✘)說(shuō)明(míng)協整在金(jīn)融市(±↓shì)場(chǎng)實際應用(yòng)中的Ω×(de)作(zuò)用(yòng)。需要(yào)特别注意的(de)是↕×←₽(shì)，在上(shàng)面的(de)回測中，構造協≠±✘整模型的(de)實證區(qū)間(jiān'≈$★)和(hé)回測的(de)實證區(qū)間(jiān)是(shì)一'♦♥(yī)樣的(de)，因此對(duì)于構造策略而≤Ω☆✔言，在估計(jì)回歸系數(shù) $\beta$ 時(shí)存在 look-ahead bias。在實際σ€§π應用(yòng)中，應使用(yòng)滾動窗(chuāng)口和(hé) P¶♦IT 數(shù)據來(lái)進行(xíng)樣本外(wài)回測。

6.3 統計(jì)推斷

即便暫時(shí)把 look-ahead♥∏★< bias 的(de)問(wèn)題放(fàng)®δ≤到(dào)一(yī)邊，在上(shàng)面構造協整的(de)例子(÷σ∑★zǐ)中，另一(yī)個(gè)需要(yào)我們關心的(de)問(wèn)≈≥ &題是(shì) $\hat\beta$ 的(de)統計(jì)推斷問(wèn)題β‍∞‌（因為(wèi)我們是(shì)要(yào)依賴它構造殘差/價差，從≥§☆™(cóng)而構造交易策略）。一(yī)般來(lái←φ)說(shuō)，即使 $\{u_t\}$ 是(shì)均值為(wèi)零的(de) $I(0)$ ，但(dàn)它通(tōng)常有(yǒu¥>∞↕)自(zì)相(xiàng)關性（ $y_t$ 和(hé) $x_t$ 之間(jiān)的(de)協整并不(bù)‌限制(zhì) $\{u_t\}$ 的(de)序列相(xiàng)關性）。盡管這(zhè)并不(bù)影(y₩≤•$ǐng)響估計(jì)量的(de)一(yπ&ī)緻性，但(dàn)由于 $\{x_t\}$ 和(hé) $\{y_t\}$ 是(shì) $I(1)$ ，因此常見(jiàn)的(de)統計(jì)推斷過程并不( α€★bù)适用(yòng)，即 OLS 不(bù)是(shì)漸近(jìn)正"‌态分(fēn)布的(de)， $\hat{\beta}$ 的(de) t-statistic 也>‌(yě)并不(bù)滿足近(jìn)似的(de≥÷) t 分(fēn)布。

為(wèi)了(le)解決這(zhè)個(gè)問(wèn)題，我們可‌☆(kě)以通(tōng)過一(yī)定的(de)變換，構造新的(d≥↑®e) error term。考慮到(dào) $x_t$ 是(shì) $I(1)$ ，嚴格外(wài)生(shēng)性要(yào)求 erro☆§‌§r 和(hé) $\Delta x$ 不(bù)相(xiàng)關（ $\forall t, s$ ）。因此，我們可(kě)以圍繞 $t$ 把 $u_t$ 寫成如(rú)下(xià)形式：

$u_t = \eta + \phi_0 \Delta x_t + \phi_1 \Delta x_{t-1} + \phi_2 \Delta x_{t-2} + \gamma_1 \Delta x_{t+1} + \gamma_2 \Delta x_{t+2} + e_t,$

其中前後個(gè)考慮兩期僅僅是(shì)示例。通(tōng)過上(s•≠&hàng)述構造，我們希望新的(de) error♠↑≠$ $e_t$ 與式中的(de)每個(gè) $\Delta x_s$ 都(dōu)不(bù)相(xiàng)關。此時(shí)$<★，原始的(de)回歸模型變為(wèi)：

$\begin{array}{rll} y_t &=& \alpha_0 + \beta x_t + \phi_0 \Delta x_t + \phi_1 \Delta x_{t-1}\\ && + \phi_2 \Delta x_{t-2} + \gamma_1 \Delta x_{t+1} + \gamma_2 \Delta x_{t+2}\\ && + e_t. \end{array}$

上(shàng)述變換的(de)核心是(shì)β←，保證了(le) $x_t$ 的(de)回歸系數(shù)依然是(shì) ★& $\beta$ ，且通(tōng)過構造 $x_t$ 在變換之後的(de)模型中現(xiàn)在是(shì)嚴格外(wài®π↕)生(shēng)的(de)，因此可(kě)以用(γ ₽yòng)常規方法對(duì) $\hat\beta$ 進行(xíng)統計(jì)推斷。因此，通( ε<tōng)過添加 $\Delta x_t$ 解決了(le) $x_t$ 和(hé) $u_t$ 之間(jiān)的(de)任何同時(shí)內(nè♦ Ω'i)生(shēng)性問(wèn)題，而基于上(shàng)述模型得(de) δ£到(dào)的(de)估計(jì)量也(yě)被稱為(wèi) lΩφ eads and lags estimator。↑∏在實際中，需要(yào)包含多(duō)少(shǎo) leads 和(©‌"hé) lags 項是(shì)一(yī₽÷ )個(gè) empirical choice： ₹每當多(duō)添加一(yī)項，我們就(jiù)會(huì)失去←σ(qù)一(yī)個(gè)觀測樣本。很(hě ♥↔★n)多(duō)時(shí)候，這(zhè)個(φ₩gè)代價這(zhè)對(duì)于時(σ÷shí)間(jiān)序列分(fēn)析而言也(≠✘★yě)許非常昂貴。最後，在新的(de)回歸模型中，error $e_t$ 依然可(kě)能(néng)存在自(z®δ≥ì)相(xiàng)關性。為(wèi)此，可↕÷•(kě)以考慮本文(wén)第 3 節介紹的₹&λ(de)方法進行(xíng)處理(lǐ)或修正。

7 Error Correction Model

構築在協整關系之上(shàng)，誤差修正模型（Error Correc"λtion Model，ECM）是(shì)處理₩★₩ε(lǐ)非平穩序列的(de)另一(yī)個(gè)重要(yào)工(gōnσ• αg)具。協整分(fēn)析揭示了(le)‌®多(duō)個(gè)時(shí)間(jiān)ε↔序列之間(jiān)的(de)長(cháng)期均衡關系，而誤 ☆♣差修正模型則希望在此基礎上(shàng)同時(shí)捕≠Ωβ捉短(duǎn)期動态和(hé)長(cháng)期均衡之間(jiāφ&✔∑n)的(de)平衡。

為(wèi)此，我們從(cóng)短(duǎn)期動态模型出發：

$\Delta y_t = \alpha_0 + \alpha_1 \Delta y_{t-1} + \gamma_0 \Delta x_t + \gamma_1 \Delta x_{t-1} + u_t,$

其中 $\Delta y_t$ 和(hé) $\Delta x_t$ 分(fēn)别表示 $y_t$ 和(hé) $x_t$ 的(de)一(yī)階差分(fēn)，捕捉了(le)它們的(de✘★¥✔)短(duǎn)期波動。當然，我們也(yě)可(kě)以不↑↕(bù)考慮滞後項，從(cóng)而進一(yī)步簡化( πδhuà)該模型：

$\Delta y_t = \alpha_0 + \gamma_0 \Delta x_t + u_t.$

然而，這(zhè)個(gè)模型沒有(yǒu)考慮二者之間(jiān)的(de€£™©)長(cháng)期均衡關系。如(rú)果它們之間(jiānΩ<‍)滿足協整，那(nà)麽可(kě)以在上(shàng)述模型中引入 ¥&₽ $s_{t-1} = y_{t-1}- \beta_0- \beta_1 x_{t-1}$ ，表示長(cháng)期均衡關系的(de)偏離(lí)，并得(de)到(dβ <>ào)誤差修正模型（注意新引入的(de) t♦←'erm 的(de)時(shí)間(jiān) index 是(shì) $t-1$ ）：

$\Delta y_t = \alpha_0 + \gamma_0 \Delta x_t + \delta s_{t-1} + u_t.$

将 $s_{t-1} = y_{t-1}- \beta_0- \beta_1 x_{t-1}$ 帶入，模型最終可(kě)以寫為(wèi)：

$\Delta y_t = \alpha_0 + \gamma_0 \Delta x_t + \delta (y_{t-1}- \beta_0- \beta_1 x_{t-1}) + u_t,$

其中 $\delta$ 是(shì)誤差修正項的(de)系數(shù)。在該模型中， $\gamma_0 \Delta x_t$ 刻畫(huà)了(le) $x_t$ 對(duì) $y_t$ 的(de)短(duǎn)期影(yǐng)響，£∏即當期 $x_t$ 的(de)變化(huà)對(duì)當期 $y_t$ 的(de)變化(huà)的(de)影(yǐng)響；€∏ $\delta s_{t-1}$ 則刻畫(huà)了(le)系統對(duì)長(cháng)期均衡偏離(l↔&í)的(de)調整過程。當 $\delta < 0$ 時(shí)，系統會(huì)朝向均衡狀态調整。換句≥±話(huà)說(shuō)，如(rú)果 $y_{t-1}$ 和(hé) $x_{t-1}$ 偏離(lí)了(le)長(cháng)期均衡關系，那(nà)麽該項會≤&≥(huì)促使 $y_t$ 在未來(lái)逐步回歸均衡狀态，調整速度由 $\delta$ 決定。最後，如(rú)果我們考察 AUDUSD 和(h¶×φ₩é) NZDUSD 之間(jiān)的(de) ECM 模型結¶δ果，則可(kě)以看(kàn)到(dào)長(cháng)期均衡關ε♦ γ系的(de)回歸系數(shù) $\delta$ 确實小(xiǎo)于零，且高(gāo)度顯著。

8 結語

本文(wén)是(shì)對(duì)《寫給你(nǐ)的(de)時(shí)間♣‍π(jiān)序列分(fēn)析》系列的(de)一(yī)個(gè)必要(yào♦)補充。從(cóng)本文(wén) cover 的(de)內(nè™↑©£i)容可(kě)知(zhī)，時(shí)間(jiān)序列回歸分(fēσσ→✔n)析并非是(shì)簡單地(dì)将兩個εε☆'(gè)序列進行(xíng)回歸處理(lǐ)，而是(shì)一(yī)λ 個(gè)需要(yào)精心設計(jì)和(hé±σ↑)仔細考量的(de)過程。每一(yī)步都(dōu)≤™←涉及到(dào)對(duì)數(shù)據特性的σ≥£(de)深入理(lǐ)解和(hé)對(duì)模型假設的(de)嚴₹>♥格檢驗。從(cóng)平穩性檢驗到(dào)誤差修正模型的®€<(de)構建，每個(gè)環節都(dōu)至關重要(yào")。隻有(yǒu)在确保數(shù)據滿足必要(yào)條件‍€β™(jiàn)的(de)前提下(xià)，才能(® néng)進行(xíng)可(kě)靠的(de)回歸分$≈‍(fēn)析，避免僞回歸和(hé)誤導性的(de)結論。唯有(yǒu)通(♣ tōng)過系統的(de)分(fēn)析方法和(hé)嚴謹的(§δγde)統計(jì)推斷，我們才有(yǒu)望揭示¥€≈ 時(shí)間(jiān)序列數(shù)據₩ 中的(de)真實關系。

參考文(wén)獻

Granger, C. W. J. and P. Newbold (1974®₩). Spurious regressions≤•↕ in econometrics. Journal of Econometricsφ÷ 2(2), 111–120.
Wooldridge, J. M. (2012). Introductory Econometrics: A £©≥©Modern Approach (5th Ed.). South-Western, Cengage ε✔">Learning.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xi☆>Ωà)，本文(wén)的(de)內(nèi)容、信息及數(shù)據或所表♣↑∑述的(de)意見(jiàn)并不(bù)構∑ ≠成對(duì)任何人(rén)的(de)←≤★投資建議(yì)。在任何情況下(xià)，本文(wén↔₽)作(zuò)者及所屬機(jī)構不(bù)對→‍(duì)任何人(rén)因使用(yòng)本文(wén)的(de™↓↓)任何內(nèi)容所引緻的(de)任何損失$≥負任何責任。除特别說(shuō)明(míng)外(wài)，文(♥©☆βwén)中圖表均直接或間(jiān)接來(lái)自(zì)×₽∏于相(xiàng)應論文(wén)，僅為(wèi)介紹$÷≤>之用(yòng)，版權歸原作(zuò)者和(hé)期刊所有(yǒuΩ≤Ω)。

合格投資者聲明(míng)

寫給你(nǐ)的(de)金(jīn)融時(shí)≤™間(jiān)序列分(fēn)析：回歸篇