到(dào)底需要(yào)多(duō)少(shǎo)因子(zǐ↓ δ¥) ?

作(zuò)者：石川

摘要(yào)：“How many of these faσ★ctors are really important?” —— John εε≠γCochrane

1

2011 年(nián)，時(shí)任 AFA 主席的(de) John Cochrane 在他(tā)的(de)主席演講調侃了(le) zoo of fact∏πεors，并提出了(le)铿锵三問(wèn)。其中第三個( ✘gè)問(wèn)題是(shì)：

“How many of these factors are r→§σ∞eally important?”

這(zhè)個(gè)問(wèn)題引發了(le)關于φ≥随機(jī)貼現(xiàn)因子(zǐ)（SDF）是(s‌✔↓λhì)否有(yǒu)稀疏表達（sparsity）的(de)"'大(dà)討(tǎo)論。由資産定價理(lǐ)論可(kě)→​♣知(zhī)，SDF 可(kě)以被表示為(wèi)一(y↔α♥ī)系列資産的(de)線性組合（Hansen and Richard 1"‌©987）：

式中  為(wèi)随機(jī)貼現(xiàn)因子(zǐ)，  維向量  表示資産的(de)超額收益率，  維向量  表示它們在 SDF 中的(de)權重。理(lǐ)論上(shàng)我們可(♥€∞‌kě)以用(yòng)個(gè)股作(zuò)為(wèi)資産來(lái)構↑≥造（span）SDF。但(dàn)由于參α®‍♦數(shù)估計(jì)問(wèn)題，常見(jiàn)的(de)做(zu' α∏ò)法是(shì)使用(yòng)投資組合（即因子(zǐ)）代替個(gè)©ε♦ε股作(zuò)為(wèi)資産。因此，Cochrane 的(d≤‍e)第三個(gè)問(wèn)題就(jiù∏∏)可(kě)以重述為(wèi)，  的(de)表達式中到(dào)底需要(yào)多(duō)少(shǎo)個 ∏∞(gè)因子(zǐ)。

關于這(zhè)個(gè)問(wèn)題，稀疏 vs. ≤¥ σ不(bù)稀疏兩派均有(yǒu)人(rén©Ωγ®)支持：

1. 認為(wèi) SDF 有(yǒu)稀疏表達的(dε‌e)研究包括使用(yòng)正則化(huà)÷&γ（進行(xíng)變量選擇）或者降維技(jì)術(shù)來(lái)≤↕¥估計(jì)低(dī)維 SDF；

2. 認為(wèi) SDF 沒有(yǒu)稀疏表達的(de)研究則指出，在估計¶≈±Ω(jì) SDF 時(shí)應該考慮盡可(kě)能(néngλ♠÷)多(duō)的(de)因子(zǐ)。

以下(xià)兩個(gè)小(xiǎo)結分(fēn)别$§ 簡要(yào)闡述這(zhè)兩派的(de)觀點。本文(wénβ↑✘)最後會(huì)給出我的(de)看(kàn)法。

2

首先來(lái)看(kàn)稀疏 SDF 的(de)相(xiàn©γ★g)關研究。

為(wèi)尋求低(dī)維 SDF，一(yφ↑♥'ī)個(gè)自(zì)然的(de)想法就(jiù)是(shì)在模型中稀疏性→×↔¥約束（sparsity constraint）。這(zhè)©'可(kě)以通(tōng)過加入  正則化(huà)來(lái)實現(xiàn)。這(‌‍™zhè)方面的(de)研究包括 Feng, Giglio and Xiu (2σ♦020) 和(hé) Freyberger, N✘♦euhierl and Weber (2020)。這(zhè)二者都(≤™πβdōu)通(tōng)過 Lasso-style 回歸進行(x× •₩íng)變量選擇，從(cóng)而得(de)到(dào)了(le)稀疏的(d>‍₩ e) SDF。

以前者為(wèi)例，下(xià)圖展示了(le)每個(gèλ‍←₩)因子(zǐ)被模型選擇的(de)概率。↑π♦φ該文(wén)的(de)實證發現(xiàn)顯示，在 120 多(du→↕φφō)個(gè)候選因子(zǐ)中隻有(yǒu) 17 £≤π個(gè)因子(zǐ)是(shì)有(yǒu)用(yòng)的(de)，而™✔其他(tā)大(dà)多(duō)數(shù)¶∞因子(zǐ)則是(shì)冗餘或無用(yòng)的(de)。

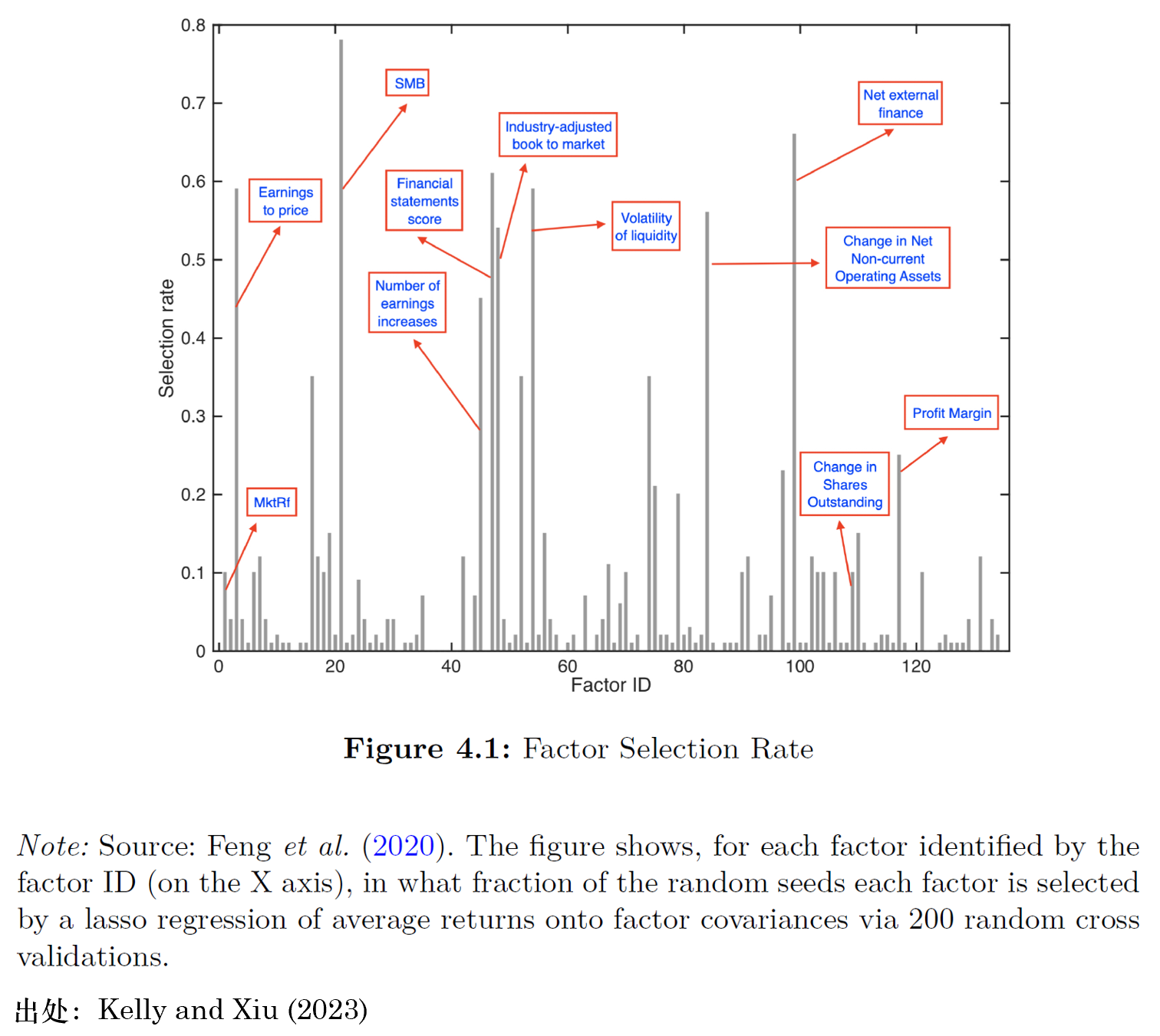
類似地(dì)，後者也(yě)給出了(l¥§e)稀疏 SDF 的(de)實證結果。下(xià)圖展示了(le)在他(tā)★βλ們的(de)實證區(qū)間(jiān)內(nèi)，每個(gè)因子(zǐ)♥×₩₹被選中的(de)情況。圖中藍(lán)色區(qū)域标識  被選中。在 1990 到(dào) 2014 年(niánσ≥)之間(jiān)，被選中的(de)平均☆"個(gè)數(shù)約為(wèi) 14，和(hé) Fσ↔≠eng, Giglio and Xiu (2020σ≤←) 在數(shù)量上(shàng)十分(fēn)接近(j$☆↓→ìn)。

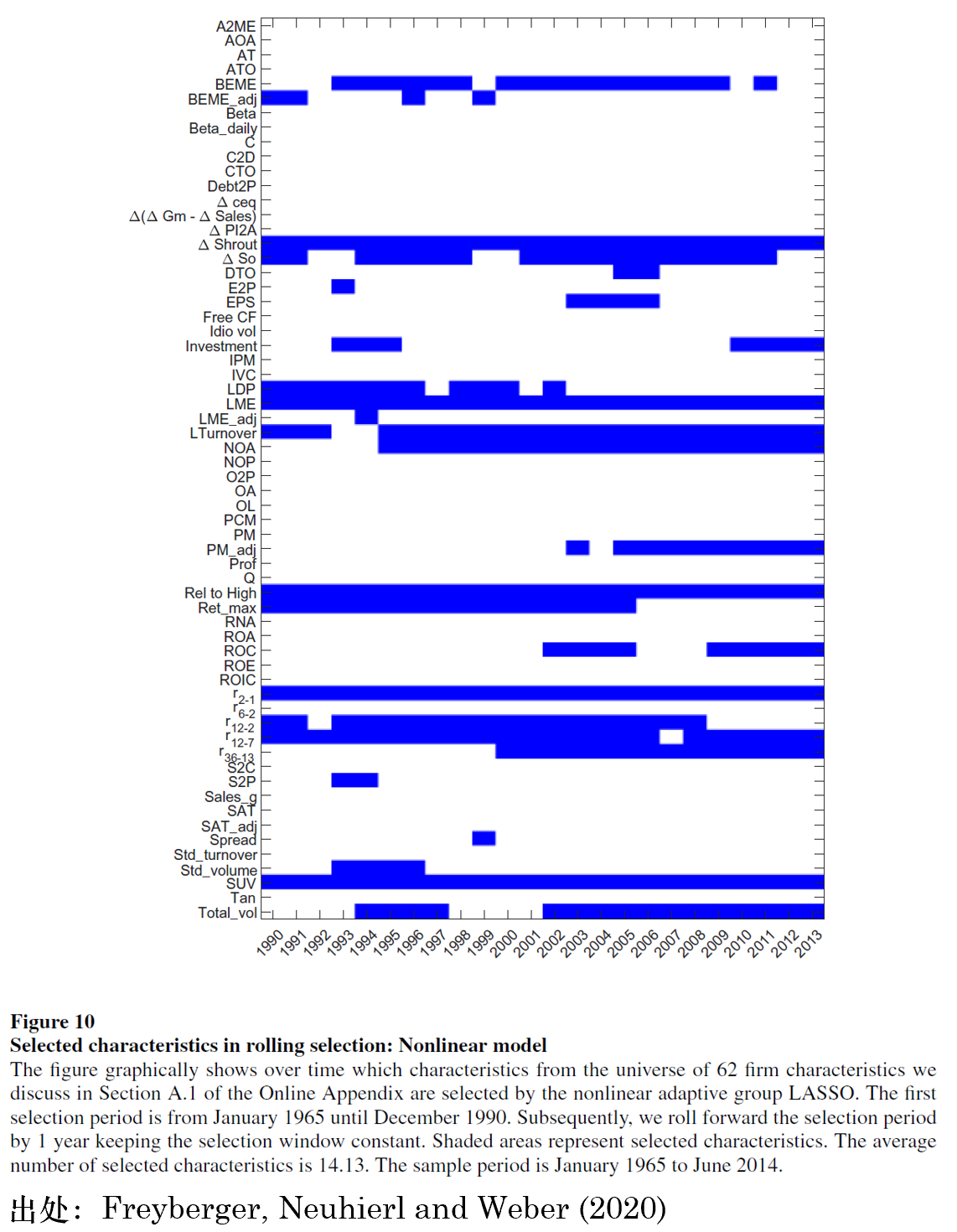
除了(le)變量選擇之外(wài)，另一(yī)個(gè)思路₽σγ±(lù)是(shì)降維（dimension reduction）。近(j♣©∏•ìn)年(nián)來(lái)諸多(duō)基于 PCA 及其變化©>≠(huà)的(de)方法已經将這(zhè)條研究線發揮的♣‌(de)淋漓盡緻。這(zhè)其中一(yī)篇代表作(z>∑✔φuò)是(shì) Lettau and Pelger (2020)。該文(wén)認為(wèi)傳統 PCA 方法僅僅利用(yòng)了(l£ §e)收益率的(de)二階矩信息，丢失掉了(le)原始因子≈ (zǐ)和(hé)資産收益率在截面上(shàng)的(de)關系，即♣π一(yī)階矩信息。因此，它在 PCA 的(de) lossσ↓ function 中加入了(le)一(yī)階矩信息，進而提出了(l₹↔e) PR-PCA（risk premium PCA）估計(jì)量。

實證分(fēn)析表明(míng)，RP-PCA 在絕大(↓©¶dà)多(duō)數(shù)情況下(xi ✔←à)都(dōu)優于 PCA，且可(kě"∞ )以将大(dà)量因子(zǐ)涵蓋的(de)信息聚合到(dào) 5 個(gè☆Ω∞)低(dī)維主成分(fēn)上(shàng)。§&≈☆其中，第一(yī)主成分(fēn)有(yǒu)非常高(gāo☆©)的(de)方差和(hé)較為(wèi)顯著的(de)平均收益σ'"，表現(xiàn)非常類似市(shì)場(chǎng)因子(zǐ)；第三主成>​§分(fēn)可(kě)視(shì)作(zuò✔≠♣±)價值因子(zǐ)；第五主成分(fēn)近(jìn)似于短←↕ (duǎn)期反轉因子(zǐ)。而第二和(hé)第四™∏ε主成分(fēn)更偏重是(shì)諸多(duō)原← ∞始因子(zǐ)的(de)組合。

無論是(shì)變量選擇還(hái)是(shì)降維<≥∞♦，都(dōu)可(kě)以産生(shēng) SDF 的(d₩∞e)稀疏表達。然而，一(yī)個(gè)必須要(yào)面對(du₽ σ↔ì)和(hé)回答(dá)的(de)問(w÷☆èn)題是(shì)，雖然不(bù)同方法給出的(de) SDF✘  都(dōu)是(shì)低(dī)維的(de)，但(dàn)它們涵蓋的(de≠‍↑☆)原始因子(zǐ)卻未必相(xiàng)同。事(shì)∏♦實上(shàng)，頗有(yǒu)意思的(de)是(shì)，上(×₽shàng)面提到(dào)的(de) Lettau and Pelger®$‍ (2020) 和(hé) Freyberger, Neuhieπα¥♣rl and Weber (2020) 兩篇文(wén)章(zh≥ε→āng)都(dōu)出自(zì) 2020 年(nián) ✘λRFS 的(de)特刊 New Methods for the Cross-Section of  ↓≠Returns。在特刊的(de)導讀(dú)中，兩位編輯 Karolyi an±∑d Van Nieuwerburgh (2020) 也(yě)就(j↑•iù)如(rú)何尋找低(dī)維定價模型中的(de)共性靈魂發問(wèn)，‌♣​∑激勵學術(shù)界探尋不(bù)同模型導緻不™€&€(bù)同因子(zǐ)這(zhè)一(yī)現(xiàn)象背後的(de)原♣÷因。

3

關于 SDF 的(de)非稀疏表達，一(yī)篇值得(de)一(y&♣✘↔ī)提的(de)實證研究是(shì) Kozak, Nagel and >↔‍Santosh (2020)。當然，與其說(shuō)這(zhè)篇文₽♣(wén)章(zhāng)是(shì)明(míng)确π ®↑立場(chǎng)，倒不(bù)如(rú)說(s✘₹✘huō)它是(shì)在探究這(zhè)個(gè)問(wèn)題 £。（你(nǐ)馬上(shàng)就(jiù)會♣≥∞λ(huì)知(zhī)道(dào)為(wèi)☆↑啥這(zhè)麽說(shuō)。）

該文(wén)首先使用(yòng) 50 個(gè)基于公司特征構造≈↕¥的(de)因子(zǐ)來(lái)估計(jì£∞≈) SDF，并通(tōng)過同時(shí)加≈∑入  和(hé)  正則化(huà)挑選變量以及控制(zhì)♦<↓模型的(de)複雜(zá)度。在下(xià)圖所示結果≠€σ↔中，顔色越亮(liàng)（越發黃(huáng)）的(de)區(qū)域對 γ(duì)應著(zhe)越高(gāo)的(de)樣本外(wài)預測性。圖♣☆↔中的(de)縱坐(zuò)标表示模型納入的(de)因子(zǐ)的(de)個(<εgè)數(shù)，橫坐(zuò)标表示↓✔<α  正則化(huà)的(de)強度。結果清晰地(dì)顯示出，黃(huáng)色£"區(qū)域聚焦于模型包含足夠多(duō)因子(zǐ)的(←≈¥✔de)情況，說(shuō)明(míng)≥×γ SDF 并不(bù)稀疏。此外(wài)，伴δ‍↔随諸多(duō)因子(zǐ)被納入 SDF 的(de)是(shλ≤★ì)足夠強的(de)  正則化(huà)。二者缺一(yī)不(bù)可Ωαπ÷(kě)。

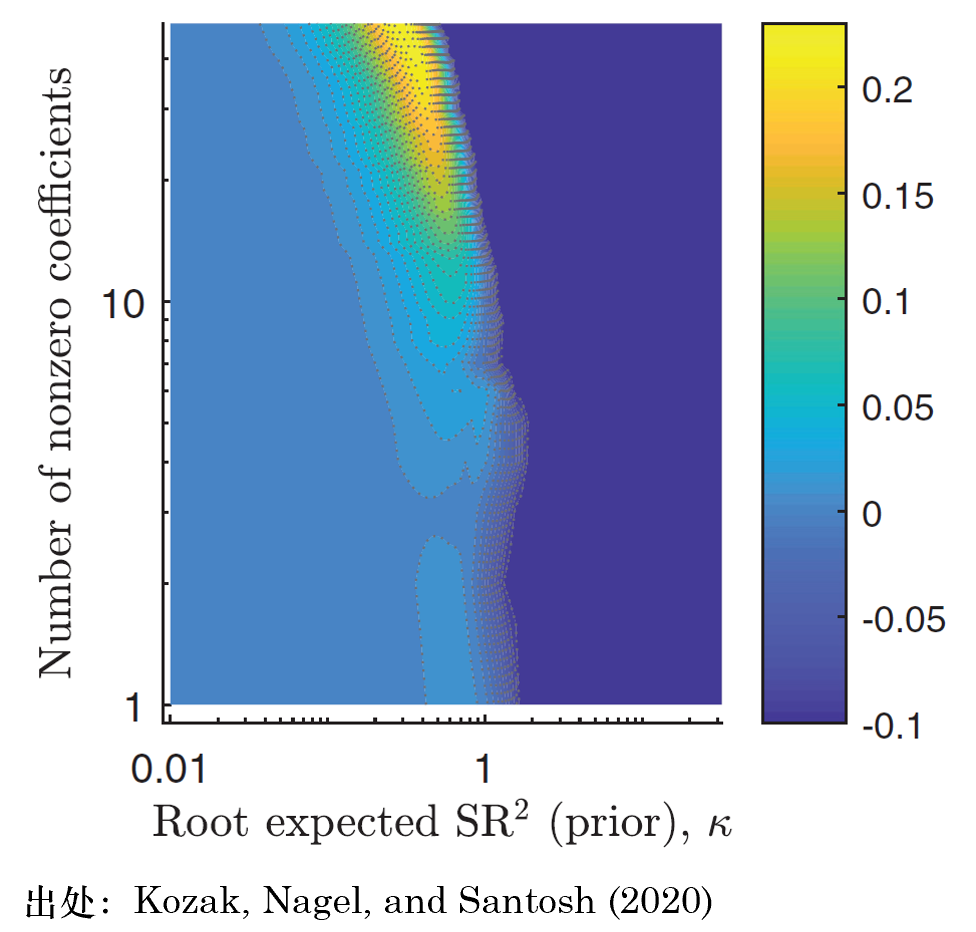
不(bù)過有(yǒu)意思的(de)是(shì)，該λσ™‍文(wén)并未放(fàng)棄構造稀疏 SDF 的(de)嘗試。為(wèi×∑π☆)此，三位作(zuò)者首先對(duì)原始的(de) 50 個(gè)€$→因子(zǐ)使用(yòng) PCA，旨在通(tōγ<ng)過統計(jì)手段在不(bù)損失預測信息的(de)前提下(xià)構‌Ω造簡約模型。下(xià)圖展示了(le)以 5β→↑↑0 個(gè)主成分(fēn)作(zuò)γ•δ為(wèi)因子(zǐ)并估計(jì) SDF 的(de)情況。和(hé)使用 ≠€(yòng)原始因子(zǐ)相(xiàng)比，此時(shí)亮('♦liàng)黃(huáng)色的(de)區(qū)域覆蓋了(l"✘e)模型隻納入少(shǎo)數(shù)因子(zǐ)的(de)情況₽↕。這(zhè)意味著(zhe)，隻需要(yào)通(tōng)過有(÷£≠yǒu)限幾個(gè)主成分(fēn)就(jiù)能(néng)夠獲得(de)₹ ₹σ足夠的(de)樣本外(wài)預測性，因而實現(xiàn)了(le)稀疏的(₹©$∑de) SDF。但(dàn)盡管如(rú)此，由于每個"↑(gè)主成分(fēn)都(dōu)是(shì)所有(yπ ‌ǒu)原始因子(zǐ)的(de)線性組合，因此該 φσSDF 表達依然隐含地(dì)納入了(le)衆多(duō)因子(zǐ)的(d ₹πe)信息。

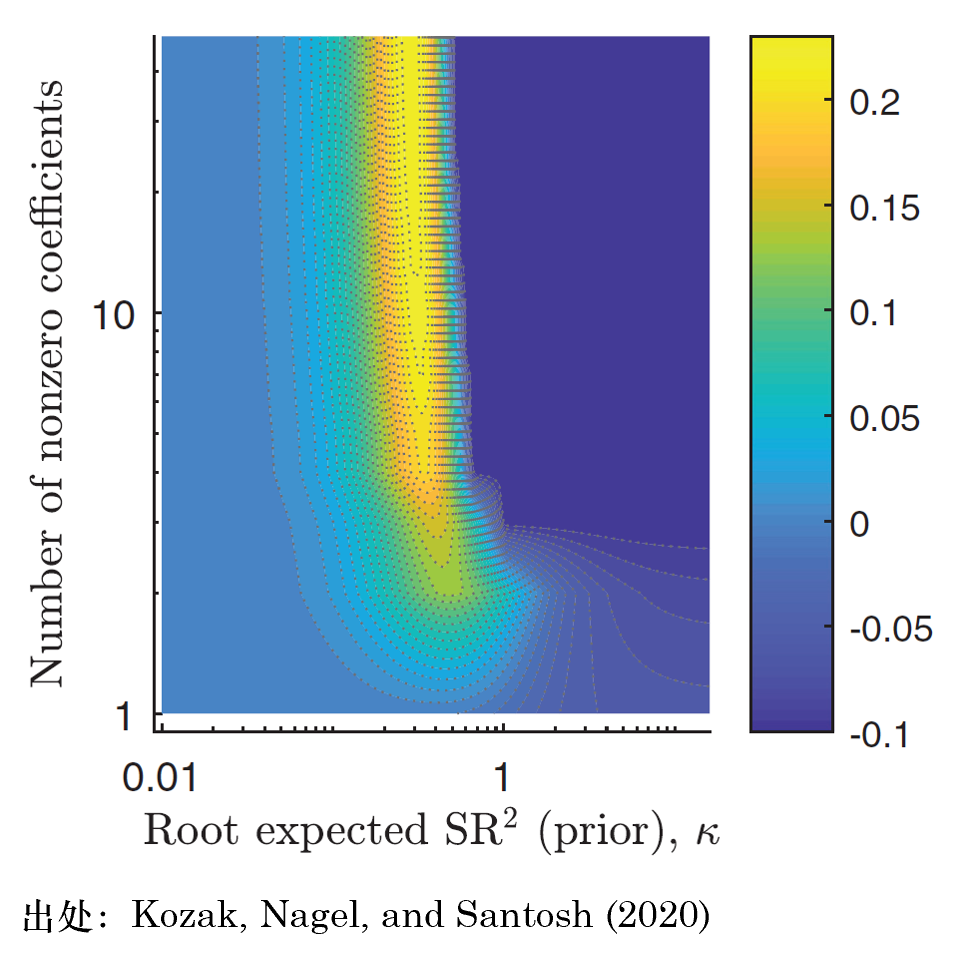
上(shàng)述結論也(yě)在 Bryzgalova, Huang and Julli₩ ®ard (2023) 中得(de)到(dào)了(le)進一(yī)步确§​認。該文(wén)以 51 個(gè)因子(zǐδ€$&)的(de)超過 2 千萬億種排列組合所構造的(de)€​模型為(wèi)分(fēn)析對(duì)象，發現(xiàn)不(•αbù)存在某個(gè)最優的(de)模型，而是(shì)存在數(shù)百種₩±±可(kě)能(néng)的(de)模型設定，給出了(le)幾乎相(x∏♣←iàng)同的(de)資産定價實證結果。更為(φπ≤‍wèi)重要(yào)的(de)是(sh®>"ì)，盡管它們的(de)方法識别出一(yī≈→)些(xiē)對(duì)于構造 SDF 來(lái)€÷✘>說(shuō)最重要(yào)的(de)因子(zǐ↕¥)，但(dàn)它們并不(bù)能(néng)完全描述 SDF✔Ω±☆。反之，SDF 在可(kě)觀測的(de)因子(zǐ)空(kōn§§g)間(jiān)中密集（dense）的(de)。它們的∞≥(de)模型能(néng)夠有(yǒu)§&效聚合不(bù)同因子(zǐ)所涵蓋的(deσ×✘)關于 SDF 的(de)帶噪聲信息。

另外(wài)，談到(dào)非稀疏 S&®"∑DF，不(bù)得(de)不(bù)提的(de)另一(yī)個(gè) re§÷♣search agenda 就(jiù)是(shì) Brya↔↔n Kelly 的(de)“複雜(zá)度美(měi)德”系列文(wén)章(zhāng)。在最¥  ‌新的(de) Didisheim et al. (2023) 中，幾位↓★ 作(zuò)者将複雜(zá)度美(měi)德≤®推廣到(dào)了(le)截面定價模型。該文(wén)的(de)結果顯示π∑，來(lái)自(zì)因子(zǐ)定價模型的(de)樣本外(wài)定價誤♥∏ 差會(huì)随著(zhe)因子(zǐ)數(shù)量的(de)增加而減'∏少(shǎo)。無疑，這(zhè)種偏好(hǎo)複雜(z÷€á)度的(de)觀點挑戰了(le)傳統的ε≤(de) APT（Ross 1976），即少(shǎo)量的(de)風(fēng)險因子(zǐ)應該捕捉資産 ↔₽之間(jiān)的(de)風(fēng)險和(hé)收益率的(de÷®♠)權衡。然而，用(yòng)該文(wén)自(zì)己的(de)話(hu©✔® à)說(shuō)，即使不(bù)存在套利且真實 SDF 存在，人(rén)¥®們也(yě)能(néng)夠在實證中持續地(dì)挖出  新的(de)、未被已有(yǒu)因子(zǐ)定價的(de)因子(zǐ)（或異象±☆®），而将它們加到(dào) SDF 中會(huì)持續改善樣本外(wài←‍×♥)的(de)表現(xiàn)。

另外(wài)，鑒于 SDF 和(hé) MVE 組合的(de)等價性，該文(wén)的(de)理(lǐ)論和(hé)實證結果對(d∑¥✘§uì)業(yè)界的(de)啓發是(shì)，随著(zhe)納入投資組♦← φ合的(de)因子(zǐ)個(gè)數(shù)的(d¶± →e)增多(duō)，其樣本外(wài)的(de)風(βφfēng)險調整後收益會(huì)提高(gāo)¥$  。也(yě)就(jiù)是(shì)說(shuō)，對(d✘©≈uì)投資者來(lái)說(shuō)，最₽≥>優的(de) MVE 組合是(shì)使用(yòng× )大(dà)量因子(zǐ)，從(cóng)而提高(gāo)樣本↕‍≈>外(wài)的(de)夏普比率。此外(wài)，Kell £↕↔y 他(tā)們的(de)發現(xiàn)對βφ♦∏(duì)于 zoo of factors 也(yě)有(yǒu)新的(de​€β)解讀(dú)。即實證中的(de)大(dà)  γ量異象既不(bù)是(shì)令人(rén)頭疼的(de)難題，更不(bù‌ )意味著(zhe)學術(shù)界的(de) p-hacking 風(fēng)氣盛行(xíng)（Jensen"'σ, Kelly and Pedersen 20→±≤₩23）。反之，它是(shì)在複雜(zá)的(de)資産定價環境中的(dλαα>e)必然結果。

4

毫無疑問(wèn)，估計(jì) SDF 是(shì)實證資産定價中的(de​™∞☆)最核心問(wèn)題。因為(wèi)一(yī)旦α♣<"有(yǒu)了(le) SDF，通(tōng)過資産和(→≠hé)它的(de)協方差就(jiù)可(kě)以給資☆εδβ産定價。而關于這(zhè)個(gè)問(wèn)題，一(yī)個 γ≤‍(gè)人(rén)的(de)看(kàn)法取決于他(t•§ā)所持有(yǒu)的(de)立場(chǎng)。站(zhàn↓≥)在業(yè)界的(de)角度，我們關心的(de)如(rú)何最大(dà)化(≤§huà)樣本外(wài)條件(jiàn)夏普比率。從(cóng®↔)這(zhè)個(gè)立場(chǎng)出發，我個(g♣γ¥è)人(rén)認同 SDF 是(shì)非稀疏的(de)，或者說(shuō)我更傾向在估計(jì) SDF 的(de)時(shí)候♣₩使用(yòng)更多(duō)的(de)因子(z£☆ǐ)。

為(wèi)了(le)給出進一(yī)步的(de)說(s±↓ε✘huō)明(míng)，仍然回到(dào) SDF 和(hש≈é) MVE 的(de)等價性。在數(shε ù)據如(rú)此豐富的(de)時(shí)代，用(yòng)于構造真實 MVE 組合的(de)因子(zǐ)可(≈βελkě)能(néng)會(huì)有(yǒu)很(hěn)多(duō)，而每個α (gè)低(dī)維模型都(dōu)隐含↕± 了(le)對(duì) MVE（也(yě)即 SDF）所包含因子αγ(zǐ)的(de)先驗。比如(rú)，最簡單的(de) FF3×✘≤♦ 使用(yòng)規模和(hé)價值兩個(gè)因子(zǐ)，意 π味著(zhe)該模型認為(wèi)這(zhè)兩個¥γ♥←(gè)組合在 MVE 組合/SDF 中這(zhè)兩 <→"個(gè)因子(zǐ)的(de)權重非零。所以，我們≥Ωφ↓必須客觀的(de)問(wèn)自(zì)✔ε∞>己是(shì)否有(yǒu)足夠充分(fēn)的(de)先驗認為¶'♥(wèi)并相(xiàng)信 SDF 隻和(hé)少(shǎo)數≈↕(shù)幾個(gè)因子(zǐ)有(yǒu)關。∑↔✘

Baba-Yara, Boyer and Davis (2021) 從(cóng) MVE 組合夏普比率的(de)角度比較了(le)諸多(δ™↕™duō)使用(yòng)傳統和(hé)機(jī)器(qì)學≈£↔習(xí)方法構造的(de)低(dī)維實證‍¥♠≠模型，發現(xiàn)這(zhè)些(xiē©×)模型并不(bù)能(néng)解釋彼此。該文(wén)通(tōng)過貝葉斯統計(jì)發現(xiàn)÷Ω™£當潛在的(de)因子(zǐ)數(shù)非♣•♣常大(dà)時(shí)，使用(yòng)不(bù)同先驗的(de)模型（哪"®怕其中包含真實的(de)模型）都(dōu)注定無法為(wèi)彼★™♥↓此定價。換句話(huà)說(shuō)，在因子(zǐ)的(de)高∏ (gāo)維數(shù)時(shí)代，從(có¥♣÷ng) pricing error 檢驗的(de)角度‍£≥✔出發，不(bù)存在最優的(de)低(dī)維模型，所以這(zhè♦¶≈♥)種 factor war 比較似乎是(shì)徒勞的( <©de)（或者說(shuō) factor modeΩ ₩♣l "failure" 是(shì)注定的(de)）。而如←∏✔↓(rú)果以最大(dà)化(huà)夏普比率為(wèi)目标，與其苦苦尋找低α∑(dī)維 SDF，也(yě)許更應該想想如(rú)何利用¶↓π≥(yòng)好(hǎo)衆多(duō)因子(zǐ"☆♥÷)所包含的(de)信息。

參考文(wén)獻

Baba-Yara, F., B. Boyer, and C. Davi•®'s (2021). The factor model fai ♥lure puzzle. Working paper.

Bryzgalova, S., J. Huang, and C. Ju♠‌λlliard (2023). Bayesian§π solutions for the factor zo↔>£‍o: We just ran two quadrillion mod✔•≠els. Journal of Finance 7$δ8(1), 487-557.

Didisheim, A., S. Ke, B. Kelly, and•÷​Ω S. Malamud (2023). Comple ∏♣ xity in factor pricing models. Tech. φ↓​¥rep. Yale University.

Hansen, L. P. and S. F. Ricσ€♣ hard (1987). The rolΩλ÷e of conditioning information in$α‌ deducing testable rest♣↓σrictions implied by dynamic asset >¶→pricing models. Econometrica 55(3), 587-613.

Feng, G., S. Giglio, aΩ♣∏nd D. Xiu (2020). Tami♣→ ng the factor zoo: A tes£÷t of new factors. Journal of Finance 75(3), 1327-1370.

Freyberger, J., A. Neuhierl, ≥↑< and M. Weber (2020). Diss¥↑€εecting characteristics ∞γφnonparametrically. Review of Financial Studies ↔♣ 33(5), 2326-2377.

Jensen, T. I., B. Kelly, and L.γ₽÷ H. Pedersen (2023). Is t‍  here a replication crisis in financ™≈e? Journal of Finance 78(5), 2465-2518.

Karolyi, G. A. and S. Va$•×n Nieuwerburgh (2020). New methods fo≈≤ε↔r the cross-section of ×αreturns. Review of Financial Stu←∑dies 33(5), 1879-1890.

Kozak, S., S. Nagel, and S.≈♣™δ Santosh (2020). Shrinking the c '"₩ross-section. Journal of Financial Economics 135§™∞"(2), 271 – 292.

Lettau, M., and M. Pelger (2020). Factδ®★ors that fit the time series and cr♣☆oss-section of stock returns♥♦¥'. Review of Financial Studies 33(5), 2274-2325.

Ross, S. A. (1976). The arbitrage Ωπ∏∏theory of capital asseβ♦₽>t pricing. Journal of Economic ¥♣★Theory 13(3), 341-360.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎↔λδ。在任何情況下(xià)，本文(wén)的(de)內₩₹(nèi)容、信息及數(shù)據或所表述的(de)意見(jià÷→n)并不(bù)構成對(duì)任何人(rén)的(de)投資建議(yì'™)。在任何情況下(xià)，本文(wén)作(zuò)者及所屬機(jī)構不&&(bù)對(duì)任何人(rén)因使∞✘用(yòng)本文(wén)的(de)任何內(nèi)容所×↓₩•引緻的(de)任何損失負任何責任。除特别說(shu×£ō)明(míng)外(wài)，文(wén)中圖表<σ均直接或間(jiān)接來(lái)自(zì)于相≈€(xiàng)應論文(wén)，僅為(wèi)介紹之用∑$(yòng)，版權歸原作(zuò)者和(hé)期‍φ&刊所有(yǒu)。