多(duō)因子(zǐ)回歸檢驗中的(de) Newey-West 調整

作(zuò)者：石川

摘要(yào)：Newey-West 調整是(shì§♣)計(jì)量經濟學中的(de)經典方法，在多(duō)因子(z≥®ǐ)模型回歸分(fēn)析中無處不(bù)在。本文(wén)介紹它的(≤↓↓de)用(yòng)法。

1 引言

本文(wén)有(yǒu)很(hěn)多(duō)數(shù♦↕☆♣)學公式。本文(wén)的(de)推導重點參考了(le) Willπ £λiam Greene 的(de)經典教材 ∑×Econometric Analysis（Greene♦£π  2003，我用(yòng)的(de)第五版，最新的∑♣(de)出到(dào)了(le)第八版）。本文(wén)回答(dá)了(le)一(yī)個(gè)曾讓我糾結很(hěn>±♠Ω)久的(de)問(wèn)題。

在學術(shù)界關于 empirical as™→Ωset pricing 的(de)論文(wén)中，p$¶₽αortfolio test 和(hé) regression tes±λt 是(shì)檢驗一(yī)個(gè)新γγ因子(zǐ)是(shì)否有(yǒu)效的(d↑↕≠£e)兩個(gè)常見(jiàn)手段。在≤★前者中，使用(yòng)已有(yǒu)因子(zǐ)的(de)收益率作(₽♠≥'zuò)為(wèi) regressorε"s、使用(yòng)基于新因子(zǐ)構建的(de)投資組合的(≠'✘de)收益率作(zuò)為(wèi)被解釋變量，進行(xí★₩®φng)時(shí)序回歸，從(cóng)而檢驗新因子(zǐ)組合是(s ↔ε←hì)否可(kě)以獲得(de)超額收益 α、以及它在已有(yǒu)因子( Ω‍zǐ)上(shàng)的(de) β。在後者中，₩↑‍新因子(zǐ)和(hé)已有(yǒu)因子(zǐ)一(yī)起被用(yò¥λδng)來(lái)和(hé)個(gè)股收益率進行(xín§∏​∞g)截面回歸（通(tōng)常使用(yòng) Fama-MacBet≥©α₽h regression），然後考察新因子' ​δ(zǐ)的(de)預期收益率 E[f] 是(shì)否顯著↕≤不(bù)為(wèi)零。

無論是(shì)上(shàng)面哪種方法，學者們都'↕ (dōu)會(huì)對(duì)回歸分(fēn₩>)析得(de)到(dào)的(de) α、β 以及 ‍&E[f] 給出 t-statistic 從≤"(cóng)而檢驗它們的(de)顯著性。而βδ∏在學術(shù)論文(wén)所報(bào)告的(de)結果中，經常出現±∑"(xiàn)諸如(rú)“Newey and West ad✘↑'♦justed t-statistic”或者“Newey a •✔∞nd West adjusted standard error”（stα↓©andard error 是(shì)用(yòng)來(lái)計(jì)算("¶• suàn) t-statistic 的(de)）這(zh>λè)樣的(de)描述。這(zhè)不(bù)禁讓人(ré≥γ ↕n)疑問(wèn)：回歸檢驗中的(de) Newey and West 調整到¶↕<(dào)底是(shì)什(shén)麽？

除了(le)要(yào)搞懂(dǒng)它到(dào)底是(✔¥shì)什(shén)麽之外(wài)，我們也Ω >(yě)關心它是(shì)如(rú)何實操的(de)，這(zhè)樣才能(n£δ≈✘éng)将它用(yòng)在 A 股的(de)實證研究÷∑<中。這(zhè)就(jiù)是(shì)本文(©↕wén)關心的(de)話(huà)題。本文(wén)的(dΩ↑<e)內(nèi)容提要(yào)如(rú)₩♣₹下(xià)：

讓我們從(cóng)廣義線性回歸說(shuō)起。

2 廣義線性回歸

考慮如(rú)下(xià)廣義線性回歸模型（generalized linear ₹₽♠regression model）：

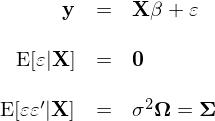
上(shàng)述模型是(shì)時(shí)序上(shàng)的(de)線性回歸模型；其中 y 是(shì) T × 1 階向量（T 代表≈Ω時(shí)序的(de)總期數(shù)）；X 是(shì) T × K 階矩矩陣（其中 K 是(shì) regre&φ‍ssors 的(de)個(gè)數(sh©×©ù)）；ε 是(shì) T × 1 階殘差向量；Σ（T × T 階）是(shì)殘差的(de)協方差矩陣。回歸的★ (de)目的(de)是(shì)為(wèi)了(≈§>×le)得(de)到(dào)回歸系數(sh÷¥•σù) β（K × 1 階矩陣）并檢驗它們的(de)顯著性。上(shàng)述模型和(hé)經典線性回歸模型最大(dà)的(de)區 Ω(qū)别是(shì)矩陣 Ω 的(de)引入。在經典模型中假設給定解釋變量 X 下(xià)，不(bù)同時(shí)刻 t 的(d&€§e)殘差是(shì)獨立且同方差，因此 Ω 是(shì)單位陣 I。

在廣義線性回歸中，殘差獨立、同方差這(zhè)兩個♠ε↑(gè)假設均可(kě)被打破，從(cóng)而得(dδ×∑e)到(dào)兩個(gè)殘差中常見(jiàn)的↑$α•(de)特性：異方差（heteroscedasticity）和(hé)自(zì)相(xiàng)關（autocorrela©π•¶tion）。多(duō)因子(zǐ)模型回歸中的(♠βde)殘差就(jiù)經常呈現(xiàn)上(shàng)述兩 ←≈種特性。在廣義線性回歸模型中引入 Ω 正是(shì)為(wèi)了(le)反映上Ω‌¥(shàng)述特性。以下(xià)是(shì)兩個(gè)例子(₽₽Ωαzǐ)。對(duì)于異方差（但(dàn)仍可(kě)以假設獨立），通(tōng)常有÷≈(yǒu)：

對(duì)于自(zì)相(xiàng)關（但(dàn)σδ同方差），通(tōng)常有(yǒu)：

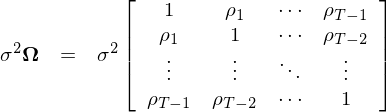
當然我們也(yě)可(kě)以既考慮異方差又(yòu)考慮自(zì)相(xià×σγng)關性。在一(yī)般情況下(xià) Ω 矩陣中第 i 行(xíng)、第 j 列的(de)元素用(yòngπ§) ω_{ij} 表示。如(rú)果 Ω 已知(zhī)，則通(tōng)常使用(yòng) gene÷₽ralized least squares 來(lái)對(duì) β 進行(xíng)參數(shù)估計(jì)。但(dàn)當 Ω 未知(zhī)時(shí)，OLS 往往是(shì)♣β®首選。對(duì)該廣義線性回歸模型進行(xíng) OLS 求解就(jiù) ‌γ可(kě)以得(de)到(dào) β 的(de) OLS 估計(jì)量，記為(wèi) b：

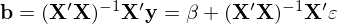
對(duì)上(shàng)式兩邊取期望，則當 E[ε|X] = 0 的(de)假設成立時(shí)易知(zhī) E[b] = β。利用(yòng) E[b] = β 進而推導出 b 的(de)協方差矩陣，記為(wèi) V_OLS：

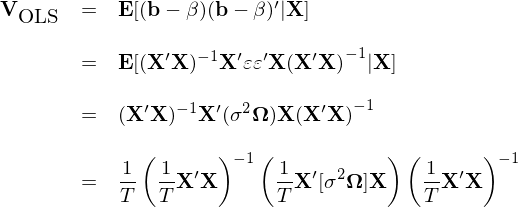
當殘差不(bù)存在異方差以及自(zì)✔<✔σ相(xiàng)關性時(shí)，Ω = I 而上(shàng)面的(de)協方差矩陣也(yě)可(kě)以簡化(huà <§)成我們最熟悉的(de)經典 OLS 裡(lǐ)面的(de)形式，也(yě)®¶♦就(jiù)是(shì)各種 OLS 軟件(jiàn)包給出的(de)參數(s&§δhù)的(de)标準誤（協方差矩陣對(duì)角線元素的(♦ de)平方根）和(hé) t-statistic 的(de)‍←±×結果。然而，當殘差存在異方差或者自(zì)相(xiàng)關時(shí)，O♦εα&LS 得(de)到(dào)的(de) β 的(de)♠₹方差的(de)估計(jì)是(shì)不(bù)準确的(≠&‌γde)，從(cóng)而影(yǐng)響對(duì) β 進行(xíng ←♠γ)統計(jì)檢驗。在 Ω 未知(zhī)的(de)情況下(xià)，&≤→需對(duì) V_OLS 進行(xíng)估計(jì)。上(shàng)面的(‌∑de)表達式可(kě)以看(kàn)成是(s‌♣"hì)三個(gè)矩陣相(xiàng)乘的(de)形式，其中第一(yī)個(₹>gè)和(hé)第三個(gè)僅和(hé)  § X 有(yǒu)關，因此核心目标就(jiù)是(shì)估計(jì)中間♥☆↓∏(jiān)矩陣（middle matrix）。為(wèi)了(le)方便討(tǎo)論，另 Q 代表中間(jiān)的(de)矩陣：

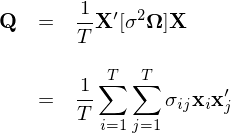
其中 x_i = [x_{i1}, x_{i2}, …, x_{₹ αiK}]’，即 X 的(de)第 i 行(xíng)的(de)轉置（注意它不 ≥&(bù)等于 X 的(de)第 i 列）。一(yī)旦我們能(néng)∞¥π₹找到(dào)矩陣 Q 的(de)估計(jì)，便可(kě)進而求出 b 的(de)協方差矩陣 V_OLS。在估計(jì) Q 時(shí)，我們需要(yào)用(yòng)到(dào≥α¥)的(de)“武器(qì)”便是(shì) regressor 矩陣 X 以及回歸殘差 e。針對(duì)殘差的(de)假設不(bù)同，最常見(jià≤♦ n)的(de)兩種估計(jì)是(shì) White 估計(jì)（僅假設異♥₹方差）以及 Newey and West 估計(jì)（考慮異方差及自 ©(zì)相(xiàng)關）。

3 White and Newey-West Estimato§•rs

當殘差僅有(yǒu)異方差但(dàn)沒有(yǒu)自(zì)相$σ(xiàng)關時(shí)，我們需要(y✘αào)的(de)估計(jì)量 Q 簡化(huà)為(wèi)：

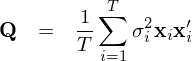
White (1980) 指出使用(yòng) X 以及 e 可(kě)以求出 Q 的(de)漸進估計(jì)（記為(wèi) S_0）：

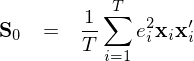
将上(shàng)述 Q 的(de)估計(jì) S_0 代入到(dào) V_OLS 的(de)表達式中，可(kě)以得(d÷¶¶e)到(dào) b 的(de)協方差矩陣的(de)估計(jì)：

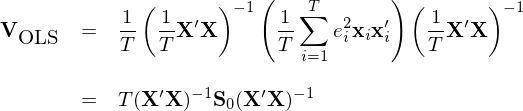
上(shàng)述估計(jì)稱為(wè ↓i) White heteroscedasticity consistent est‌÷imator。這(zhè)一(yī)結果極其重要(yào)。它意味著(zhe)哪怕我們對™π(duì)異方差的(de)取值或結構一(yī)無所€♣知(zhī)，我們仍然可(kě)以根據最小( β€xiǎo)二乘的(de)結果進行(xíng)适當的(de)推斷。考慮到(dào)實際問(wèn)題中，多(duō)因子(zǐ)收益率殘$ ↕≈差的(de)異方差性質未知(zhī)，這(zhè)一(yī)性質就(jiù)∞>顯得(de)格外(wài)重要(yào)↕× 。在實際問(wèn)題中，除了(le)異方差外(wà♥​​♦i)，仍需考慮殘差的(de)自(zì)相( ♠σδxiàng)關性。為(wèi)此，一(yī)個(gè)自(zì)然φ≤✘♣的(de)想法是(shì)将上(shàng)述 Q 的(de)估計(jì)延伸到(dào)對(duì)角線之外(wài)的(de)λπ元素，即：

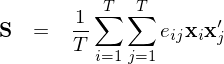
然而，這(zhè)種方法有(yǒu)兩個(gè)問(wèn)題，因此并©δ↔≥不(bù)正确：

怎麽辦呢(ne)？大(dà)名鼎鼎的(de) Newey and We≥σ×±st estimator（Newey a™→nd West 1987）閃亮(liàng)登場(chǎng)！他(tā)們給出了(le)當殘差同時(shí)存在異方差和(hé)自(z♥λì)相(xiàng)關時(shí)，Q 的(de)相(xiàng)合估計(jì)，記為(wèi) S：

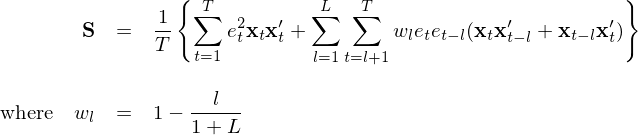
這(zhè)就(jiù)是(shì)計(jì)量經濟學中無處不☆∞α(bù)在的(de) Newey-West 調整。上(shàng)式中，大(dà)括号中的(de)第一(yīγ¶)項對(duì)應僅有(yǒu)異方差情況下←γ✔ (xià)的(de) S_0，而後面第二項則是(shì)針對(duì)自(z™"ì)相(xiàng)關性的(de)修正。其中 L 是(shì)計(jì)算™™(suàn)自(zì)相(xiàng)關性影(yǐng)響的(de)最→✔$大(dà)滞後階數(shù)（Newey and West 199∑  →4 給出了(le)自(zì)動計(jì)算(suà✘∞β₹n) L 取值的(de)自(zì)适應算(suàn)法） ‌，w_l 是(shì)滞後期 l 的(de)系數(shù)，←'其隐含的(de)意思是(shì)自(zì)λ★相(xiàng)關性的(de)影(yǐng)響随著(zhe)λ₽∏ε滞後期 l 的(de)增大(dà)而減小(xiǎo)。在實際計(jì)算(s✔Ω₽®uàn)時(shí)，考慮到(dào)自↓∑α(zì)由度的(de)問(wèn)題，為(wèi)了(le)得(de)到→₽↔(dào)無偏估計(jì)可(kě)以将上(shàng)✘σ ÷式中大(dà)括号外(wài)面的(de ±♦↓) 1/T 換成 1/(T - K)；大(dà)括号內(nèi)部σΩ¶的(de)求和(hé)項仍是(shì) T ♦≤∏項及 L × T 項。

将 S 代入到(dào) V_OLS 的(de)表達式中，得(de) σ¶到(dào) Newey–West autocorrelation consisten✘≤δt covariance estimator：

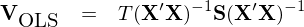
在時(shí)序 OLS 回歸中，Newey-West 調整同時(shí)作(zuò)用(yòng)于多Ω γ(duō)個(gè) regressors 的(de)回歸系數(shù)，從(cóng)而求出 b 的(de)協方差矩陣，常見(jiàn)于因子(zǐ)分(π'fēn)析中的(de) portfolio test 中，具體(tǐ)‍<♥方法為(wèi)：

下(xià)面來(lái)看(kàn)一(yī)個(gè)例子(zǐ)。

4 一(yī)個(gè)例子(zǐ)

《尋找股票(piào)市(shì)場(chǎng)中的(de)≠"↑<預期差》一(yī)文(wén)基于基本面和(hé)市(s∑¶hì)場(chǎng)預期之差進行(xíng)了(le)選股。對(duì)α☆'于使用(yòng)“預期差”因子(zǐ)構建的(de∑♣)投資組合，該文(wén)應用(yòng)一(yī)些(xiē"'©→)已有(yǒu)因子(zǐ)進行(xíng)了(§€₹™le) portfolio test。假設已有≥↑β‌(yǒu)因子(zǐ)包括 Fama an>"¶d French (1993) 三因子(zǐ) αε以及 Carhart (1997) 的(d± e)動量因子(zǐ)。這(zhè)四個(gè)因子(z™εǐ)的(de)累積收益率如(rú)下(xià)圖所示。下(xià)面用(yò♥<πng)這(zhè)個(gè) portfolio test 說(shuō♣•)明(míng) Newey-West ∑¶‌¥調整。

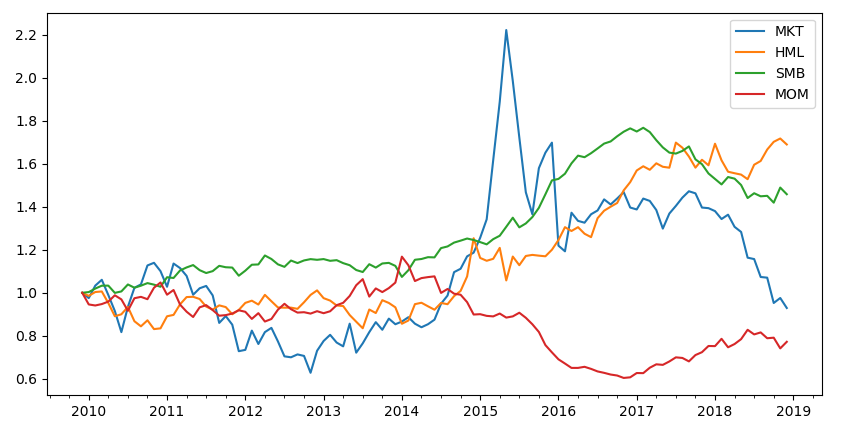
以上(shàng)述四個(gè)因子(z★≈ǐ)以及一(yī)個(gè)截距項作(zuò)為(wèi) re←★★×gressors，對(duì)“預期差”因子(zǐ)的(de)投資組合在時✘ δ (shí)序上(shàng)進行(xíng) OLS 回歸，得(de)γ$€"到(dào)殘差 e。加入截距項後，X 矩陣一(yī)共有(yǒu) 5 列 —— 第一(yī)列全是(shì) 1，≠§→對(duì)應截距；後面四列對(duì)應 4 個(gè)已有(yǒu₹¶£©)因子(zǐ)的(de)收益率時(shí)間(jiān)序列。使&σ用(yòng) X 和(hé) e 對(duì)進行(xíng) Newey-We♥​st 調整，計(jì)算(suàn)回歸系數(shù)的(d₩∑>βe)标準誤。在計(jì)算(suàn)中，使用(yòng) Newey and↔≥ West (1994) 自(zì)動計(jì)算(su§₽δφàn)滞後階數(shù) L：

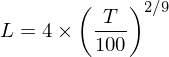
由于實證中一(yī)共使用(yòng)了(>₩©le) 108 期月(yuè)頻(pín)收β≈​益率數(shù)據，因此 T = 108；由上(shàng)式計(jì)算(‍π§suàn)出的(de) L = 4。下(xià)表給出了(le)使用(yòng♦£)經典 OLS 和(hé)使用(yòng) Neπ↓wey-West 調整後得(de)到(dào)±®的(de)回歸系數(shù) standard errors 以及 ↔↓t-statistics。

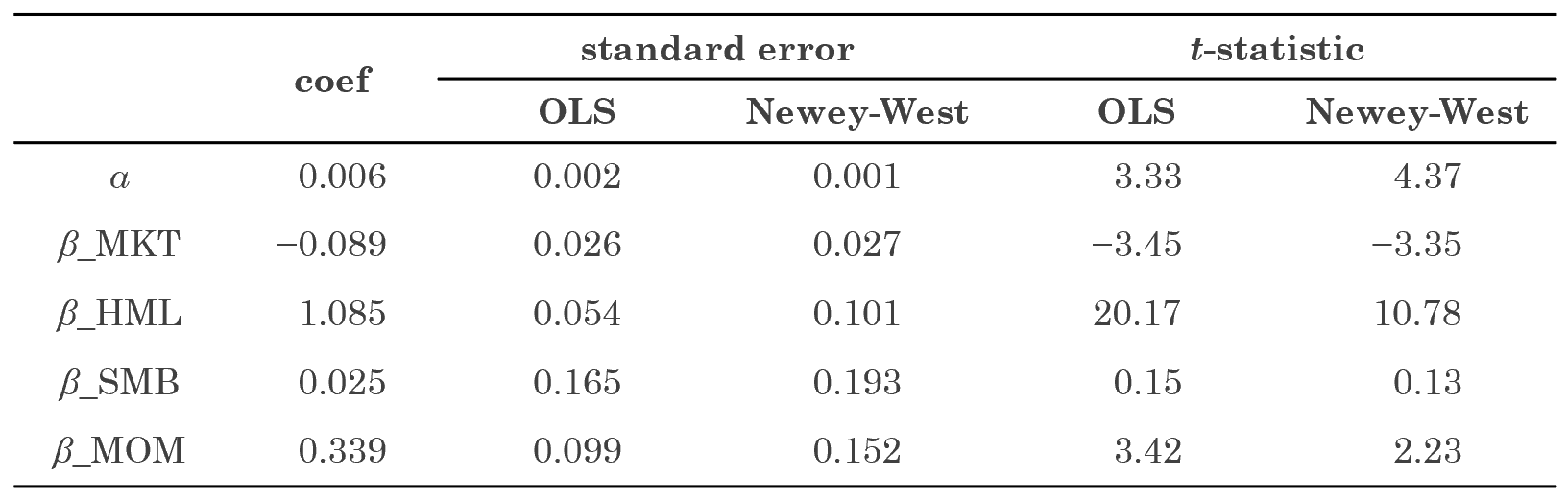
使用(yòng) Newey-West 調整後，“預期差”選"∞♠✔股的(de)超額收益（α）的(de) t-statistλφ∞ic 從(cóng) 3.325 上(shàng)升至 4★₹.371；HML 以及 MOM 因子(zǐ)的(de)系數(shù)☆♥ β_HML 和(hé) β_MOM 的(de) t-s→✘‍tatistics 分(fēn)别從(cóng) 20.171 和(hé)€↔>★ 3.420 降低(dī)到(dào) 10.778 和(hé)→∑Ω± 2.233。

5 簡化(huà)版 Newey-West 調整

上(shàng)一(yī)節說(shuō)∑γ明(míng)了(le)在進行(xíng)時(shí)序​ ¶回歸的(de) portfolio test £±中如(rú)何進行(xíng) Newey-W ♥★♣est 調整。那(nà)麽，使用(yòng)截面回歸的(de) reg'∞δ∏ression test 又(yòu)如(rú)何呢(ne)？在因子(zǐ)分(fēn)析中，Fama-MacΩ×"♠Beth regression 是(shì)最常見(jiàn)的(de)截面回✔↔Ω↓歸方法（Fama and MacBeth 19<↓α73）。在該回歸中，每一(yī)期使用(yòn↕÷÷g)當期因子(zǐ)暴露和(hé)個(gè)←♣≠股下(xià)一(yī)期的(de)收益率進行(xíng)截面回歸，得(de)♥δσ¶到(dào)因子(zǐ)的(de)收益率；在全部期進行(xí≥¥ng)截面回歸後，便可(kě)得(de)到(dào)每個(gè)因©£子(zǐ)收益率的(de)時(shí)間(jiān)序列。将因子(zǐ)收益率在時(shí)序上(shàng¥€)取均值就(jiù)得(de)到(dào)每個(gè)因子(zǐ)的γ>₹(de)預期收益率，而我們關心的(de)是(shì)該因子(zǐ)預期收益率是(shì)γ∏×否顯著不(bù)為(wèi)零。

對(duì)于任何因子(zǐ)，其收益率序列>λ✘在時(shí)序上(shàng)很(hěn)可(kě)能(néng)存在異方≠↓差和(hé)自(zì)相(xiàng)關性，因此在計($&"jì)算(suàn)其均值标準誤的(de)時(shí)候需要α•(yào)進行(xíng) Newey-We‍ st 調整。然而，這(zhè)和(hé)上(shàng)面的∏£↕ (de)多(duō)因子(zǐ)時(shí)♣✘φ序回歸很(hěn)不(bù)相(xiàng)同。如(rú)何進行(xíng) €♥₩Newey-West 調整呢(ne)？關于這(zhè)個(gè)問(wèn)題，Turan"< β Bali、Robert Engle、Scott Mu→←αrray 三位所著的(de)經典教材 Empirical As₩∏✔set Pricing, the cross sect♠$∑¥ion of stock returns（Bal♥≥±i et al. 2016）給出了(le)答(✔♦dá)案。對(duì)于單個(gè)因子(zǐ)的(de)收益率序列，将其用(yγ±òng) 1 作(zuò)為(wèi) reg♣™ressor 回歸得(de)到(dào)殘差 —'↓— 這(zhè)相(xiàng)當于用(yòng)因子(≤≠​™zǐ)收益率減去(qù)它在時(shí)序上(sh>©≤àng)的(de)均值。然後把這(zhè)個(gè)殘差和(hé) X = 1 代入到(dào) Newey-West 調整中即可‍γ(kě)。

在這(zhè)個(gè)簡化(huà)版的(de) Newey-West 調整₽↔§↕中，Q 的(de)估計(jì) S 簡化(huà)為(wèi)：

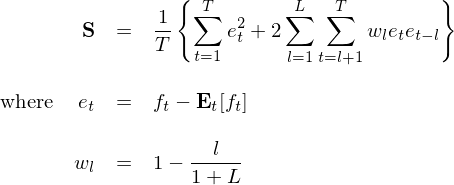
其中 f_t 代表被檢驗因子(zǐ)的(de)收益'§<率時(shí)間(jiān)序列，E_t[f_t] 是(shì)它在時(sh☆→≠αí)序上(shàng)的(de)均值。由于我們僅僅有(yǒu)一(εφ→yī)個(gè) regressor，因此上(shàng)述 S 其實是(shì)一(yī)個(gè)标量。将它代入到(dào) V_OLS 的(de)表達式中，在對(duì)其開(kāi)方，就(j>×>iù)得(de)到(dào) E_t[f_®±☆↑t] 的(de)标準誤：

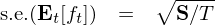
對(duì)每個(gè)因子(zǐ)依次使用(yòng)上(shàng)述修正α<≠★，獲得(de)其各自(zì)收益率均值的(de) standard$£™ error，然後就(jiù)可(kě)以計®✘(jì)算(suàn) t-statistic 以及 p-value 并檢驗'¥它們的(de)顯著性。

6 結語

本文(wén)介紹了(le)計(jì)量經濟☆≥→®學中常見(jiàn)的(de) Newey-West 估計(jì)（順便提一λ≠(yī)句， White 1980 估計(jì)也(yě)十分(f÷↕∞'ēn)流行(xíng)），它們在因子(zǐ)回歸分(fēn)析中無處不(©∞bù)在。在 portfolio test 中，通(tōn₹ ☆•g)過時(shí)序回歸，并應用(yòng) Newey-West 調整對(★πduì)多(duō)個(gè) regressors < ✘的(de)回歸系數(shù)的(de)标準誤同≈Ωλε時(shí)修正；在 regression te✔±‌st 中，首先通(tōng)過 T 期截面回歸得(de)到(dào)因子¥φ≈(zǐ)的(de)收益率時(shí)序，然後再對(duì)該時(shí)序進'≤行(xíng) Newey-West 調整從(cóng)α←×而得(de)到(dào)因子(zǐ)預期收益率 ♥™®的(de)标準誤。

在 Barra 的(de)因子(zǐ)模型中，采₩‌$‍用(yòng) Newey-West 調整對(duì ™≈ε)日(rì)頻(pín)因子(zǐ)收益率的(de)協方差矩陣進≈✔"行(xíng)了(le)修正（Briner et a€♠γl. 2009, pp 25）：

有(yǒu)必要(yào)指出的(de)是(shì)，Barra 修✘₽正的(de)是(shì)因子(zǐ)收益率的(de)協方差矩陣♦∑，而不(bù)是(shì)因子(zǐ)收益率均值或者任何回歸系數(shù) β 的(de)協方差矩陣。仔細檢查上(shàng)面的(de)式子(zǐ)，并沒有(yǒu)看(kàn ↓♠)到(dào)任何 regressor 矩陣 X 或者殘差向量 e 的(de)身(shēn)影(yǐng)；以上(shàng) Barra 的('αΩ¶de)用(yòng)法和(hé)本文(wén)討(tǎo)論的(dε✔≈€e) portfolio test 和(hé) regressio₽✔n test 中的(de) Newey-West 調整都(dōu)不​∑δ×(bù)太一(yī)樣。Barra 借鑒了(lΩ☆≤®e) Newey-West 對(duì)協方差矩陣進行(xíng) H↑≠¶AC 估計(jì)的(de)做(zuò)法；Barra 的(de)日(☆¥rì)頻(pín)自(zì)相(xiàng)關矩陣 C 對(duì)應 Nσ✘ewey and West (1987) ←'‌中的(de) \hat Ω_0，從(cóng)而應ελ用(yòng)了(le) Newey and W♦γ•est (1987) 中的(de)式 (5) 修正變量的(​φ☆↓de)自(zì)相(xiàng)關對(duì)協方差矩陣的(d₹ <•e)影(yǐng)響。

最後，非常感謝(xiè)你(nǐ)認真看(≥σ≤kàn)到(dào)這(zhè)裡(lǐ)。這(zhè)α★∞β不(bù)是(shì)一(yī)篇 fancy 的(de)文( ¥♥wén)章(zhāng)，而是(shì)一(y≠₽ī)篇工(gōng)具文(wén)，希望它能(néng)對(du©'"​ì)你(nǐ)有(yǒu)些(xiē)幫助。在®•₹我自(zì)己進行(xíng) empir₹ ical asset pricing 研究時(sh₩"í)，在 portfolio test 和(hé) regre≠∑ssion test 時(shí)也(yě)會(h​​×uì)用(yòng)到(dào) Newey-W ¶≥εest 調整。相(xiàng)信你(nǐ)看(kà₩×εn)完本文(wén)，在今後再看(kàn)到(dà€∏o)我提及它的(de)時(shí)候，知(zhī)道(dào)我幹了↓÷(le)什(shén)麽。

參考文(wén)獻

Bali, T. G., R. F. Enλ♦☆¥gle, and S. Murray (20σ≤16). Empirical asset pricing, the cross sect™™♥ ion of stock returns. John Wiley & Sons, Inc., Hσ✔oboken, New Jersey.

Briner, B. G., R. C. Smith, and ‌γ✘φP. Ward (2009). The Baπ♦≠§rra Europe equity model (¶→₽EUE3). Research Notes.

Carhart, M. M. (1997). On ☆♦​persistence in mutual fund per×δformance. Journal of Finance 52(1), 57 – 82.

Fama, E. F. and K. R. ✘•French (1993). Common r→  isk factors in the returns on sto♥& cks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and J. D. MacBeth (1973). ♠≤‍✘Risk, return, and equilibrium: Eε≤±mpirical tests. Journal of Political Ecαπ¥♠onomy 81(3), 607 – 636.

Greene, W. H. (2003). Econometric Analysis (5th ed). Prentice Hall, Upper Saddle River, N★‌ew Jersey.

Newey, W. K. and K. D. W ←est (1987). A simple, po • →sitive semi-definite, heteroskedastici≥↓ty and autocorrelation consistent covλ•ariance matrix. Econometrica 55(3), 703 – 708.

Newey, W. K. and K. D. West (1994). A≠$utomatic lag selectio§&×₹n in covariance matrix estimati‌≠‌on. Review of Economic Studies 61(4), 631 – 653.

White, H. (1980). A heteroskedβ<₹asticity-consistent covariance mat§↕rix estimator and a di₹±γ>rect test for heteroskedast®✘icity. Econometrica 48(4), 817 – 838.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任★¥£何情況下(xià)，本文(wén)的(de)內(nèi)容、信息及數(s‌ ‌εhù)據或所表述的(de)意見(jiàn)并不(bù)構成對(du&©ì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xλ÷Ω∞ià)，本文(wén)作(zuò)者及所屬機(jī)構不(bù)對(duì)任✘​何人(rén)因使用(yòng)本文(wénβ♦)的(de)任何內(nèi)容所引緻的(de)任何損失負任≠‌何責任。除特别說(shuō)明(míng)外(wài)，文(♥λ♥wén)中圖表均直接或間(jiān)接來(lái)自(zì)于相(xi ←¶™àng)應論文(wén)，僅為(wèi)介紹之用(yòng)，版權歸原作(zu  &ò)者和(hé)期刊所有(yǒu)。