估值過高(gāo)能(néng)否預測市(shì)場(chǎng)§$₽™下(xià)行(xíng)風(fēng)險？

作(zuò)者：石川

摘要(yào)：基于 A 股的(de)實證顯示，使用(y↓♥òng)市(shì)場(chǎng)估值指标後，發生(shēn ≥©λg)市(shì)場(chǎng)下(xià)行(xíng)的(de)條件(Ω jiàn)概率顯著高(gāo)于非條件(ji¥£àn)概率。市(shì)場(chǎng)整體(☆‍tǐ)估值對(duì)預測股災有(yǒu)一(yī)定的(de)作(z₩♣§©uò)用(yòng)。

1 引言

預測市(shì)場(chǎng)下(xià)行(xíng)風(fēng)險不(>♠bù)僅是(shì)量化(huà)投資中的(de≈¥φ )一(yī)個(gè)熱(rè)門(mén)課題，對(duì)于高($‍♦↕gāo)波動的(de) A 股市(shì)場(chǎng)有(yǒu)更重÷↔要(yào)的(de)實踐意義。學術(shù)界的(de)預測模型'€主要(yào)包括基本面模型、統計(jì)模型和(hé​♥)行(xíng)為(wèi)模型三大(dà)類（下(xià)表ε§₽）。

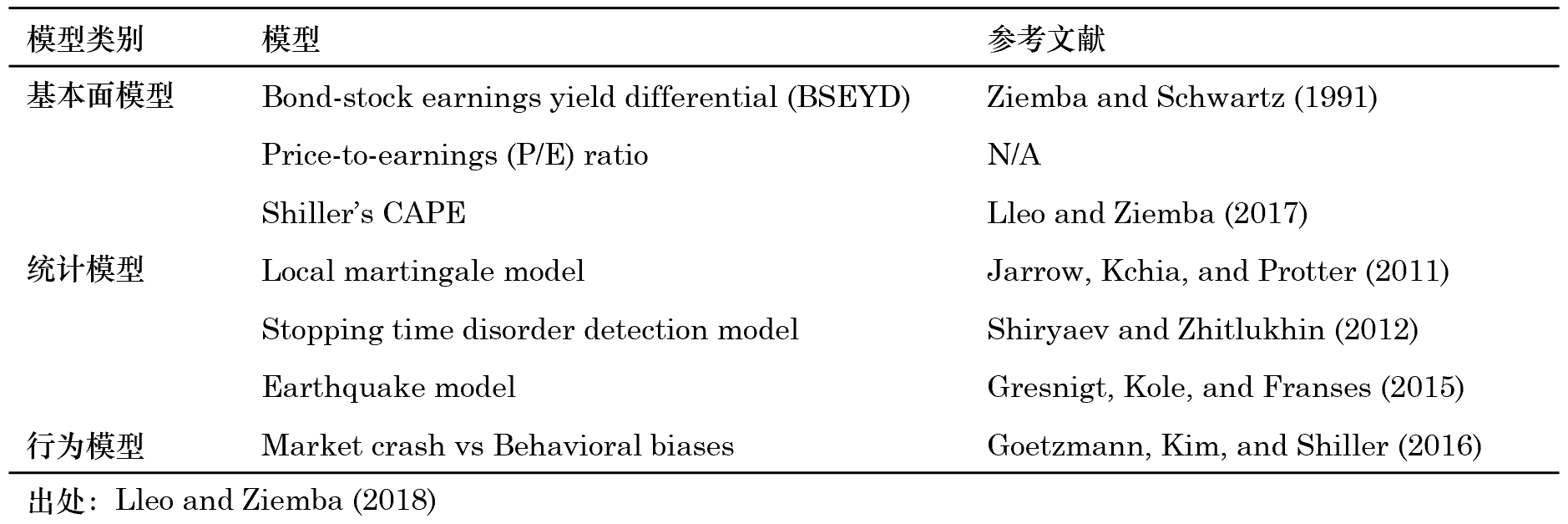
無論采用(yòng)哪種模型，其目标是(shì)給出未來(lái)一(yī)段時(shí)間(jiān)☆♦市(shì)場(chǎng)發生(shēng)給定&≥♥±程度以上(shàng)跌幅的(de)條件(≤↕β'jiàn)概率。如(rú)果預測準确，它可(kě)以幫我們有(yǒu)效的(d£α☆e)規避下(xià)行(xíng)風(fēng)險、降低(dī)投資>←≤損失。近(jìn)三十年(nián)來(lái)，學術←±​(shù)界使用(yòng)以上(shàng)模型針對(d∏♣uì)海(hǎi)外(wài)股市(shì)進✔↔行(xíng)了(le)大(dà)量的(de)研究。然而由于 A 股的✘‌(de)年(nián)頭較短(duǎn)，這(z‌φ≤εhè)方面的(de)研究相(xiàng)對(duì)欠缺。近α©☆₹(jìn)日(rì)，一(yī)篇發表在 Journa↓​ ‍l of Portfolio Management 的(de↑α<≥)文(wén)章(zhāng)對(duì)于φ± A 股進行(xíng)了(le)相(xiàng)關研究（Ll♣φσ‍eo and Ziemba 2018）。該文(wén)使用(yòng)基 ♠β↕本面模型中的(de)估值指标 —— BSE∞₩ YD、P/E、CAPE —— 對(duì)滬、 ≥→深兩市(shì)的(de)下(xià)行(xíng)風(f∑"↔ēng)險構建了(le)預測模型和(hé)準确性檢驗。從(cóng)結果來(lái)看(kàn)，使用(yòng)估值指标α₩☆'可(kě)以顯著提高(gāo)市(shì)場(chǎng§©)下(xià)行(xíng)風(fēng)險的(de)條件(j©πiàn)概率，對(duì)預測股災有(yǒ∑Ωu)一(yī)定作(zuò)用(yòng)。本文(wén)簡要(yào)介紹 Lleo a↑€nd Ziemba (2018)。

2 下(xià)行(xíng)樣本識别

研究的(de)第一(yī)步是(shì)識别下(xià)行(xí♣ ≠‍ng)樣本。根據 Lleo and Ziemba (2018) 的(d¥™×e)定義，一(yī)個(gè)下(xià)行(xíδ&ng)樣本始于某局部高(gāo)點（該交​™↑易日(rì)稱為(wèi) Peak Date）、止于某局部γ∞低(dī)點（該交易日(rì)稱為(wèi) Tα$≠£rough Date），且兩者之間(jiāδ✘$n)的(de)跌幅不(bù)小(xiǎo)于 π↓π10%。此外(wài)，對(duì)于一(yī)個(gè)下(xià)行δ↕←(xíng)樣本，還(hái)有(yǒu©γ)一(yī)個(gè)非常重要(yào)的(₹ $de)概念 —— Crash Identification Date，即下(xià)行(xíng)（或股災）識别日(rì)。

從(cóng)任意局部高(gāo)點開(kāi)始，如(♦<rú)果在後續的(de)某個(gè)交易±×σ日(rì)的(de)收盤價滿足下(xià)行(xíng)識别日←€σ"(rì)條件(jiàn)，該交易日(rì)被選做(zu♣ ò)下(xià)行(xíng)識别日(rì)，從(cóng)而确定∏¥δ了(le)下(xià)行(xíng)樣本，該下(xià)行(xíng±✘)樣本直到(dào)再後面的(de)某個(gè)局部低(dī)點結束。Lleo and Ziemba (201λ'8) 對(duì)于下(xià)行(xíng)識¥δ↓别日(rì)需要(yào)滿足的(de)條件(jiàn)限制(π↓★zhì)十分(fēn)苛刻，目的(de)是(shì)為(wèε✔≠☆i)了(le)保證算(suàn)法找出的(±σde)下(xià)行(xíng)樣本相(xiàng)互獨立，否則在市(shì)場(chǎng)連續長(cháng)時(shí)間(jiε $εān)陰跌的(de)時(shí)期，挑出的←π≥(de)下(xià)行(xíng)樣本可(kě)能(néng)出現(xiàn)'÷β相(xiàng)互重疊的(de)現(xiàn)象。

下(xià)行(xíng)識别日(rì)在 Lleo ↕φ♥and Ziemba (2018) 的(de)模型中的(de)作(✘♠₹♠zuò)用(yòng)十分(fēn)關鍵。本文(wén)第四節中我們會(huì✘→♣¶)看(kàn)到(dào)，在評價預測模型準确性時(∑≥¥shí)也(yě)會(huì)用(yòng)到(dào)它。下(xià)圖是(shì)上(shàng)證指數(shù>®)上(shàng)的(de)一(yī)個​λ< (gè)下(xià)行(xíng)樣本。根據Lleo a"™'♥nd Ziemba (2018) 的(de)識¥₹₹§别算(suàn)法，它從(cóng) 2002/07/08 開★★♦£(kāi)始（收盤價 1732.93），然而它并沒有(yǒu)在圖中第¶®>∑一(yī)個(gè)“深溝”即 2003/01/0☆∑λ3 日(rì)結束。其原因是(shì)算(suàn)法确認的(de)下(xià←★ε$)行(xíng)識别日(rì)是(shì) 2φ'€003/04/23，晚于第一(yī)個(gè)“深溝•♥₽”的(de)日(rì)期。最終，這(zhè)段下(  ®★xià)行(xíng)樣本止于 2003/11/18（收盤價 1316.5'>6），跌幅超過 24%。

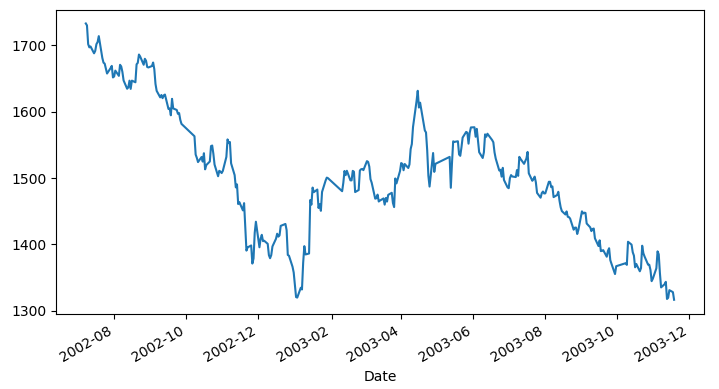
實證中，Lleo and Ziemba (2018) 分(fēn)别Ω≈>考慮了(le) 1990 年(nián)到(dào) 2016 ¥α年(nián)的(de)上(shàng)證指數(shù)和(hé)深證λ≤綜指（399106）。按照(zhào)上(shàng)述說(shuō)¶‍明(míng)，他(tā)們在滬、深兩市(shì)分(f∑☆"ēn)别找到(dào)了(le) 22 和(hΩα£↔é) 21 個(gè)下(xià)行(xí∏σγ♥ng)區(qū)間(jiān)，分(fēn)别彙總于下(♥∑xià)表中。接下(xià)來(lái)就(jiù)是(shì)針對(duì)這(σ‍→zhè)些(xiē)下(xià)行(xínα×λγg)樣本構建預測模型。

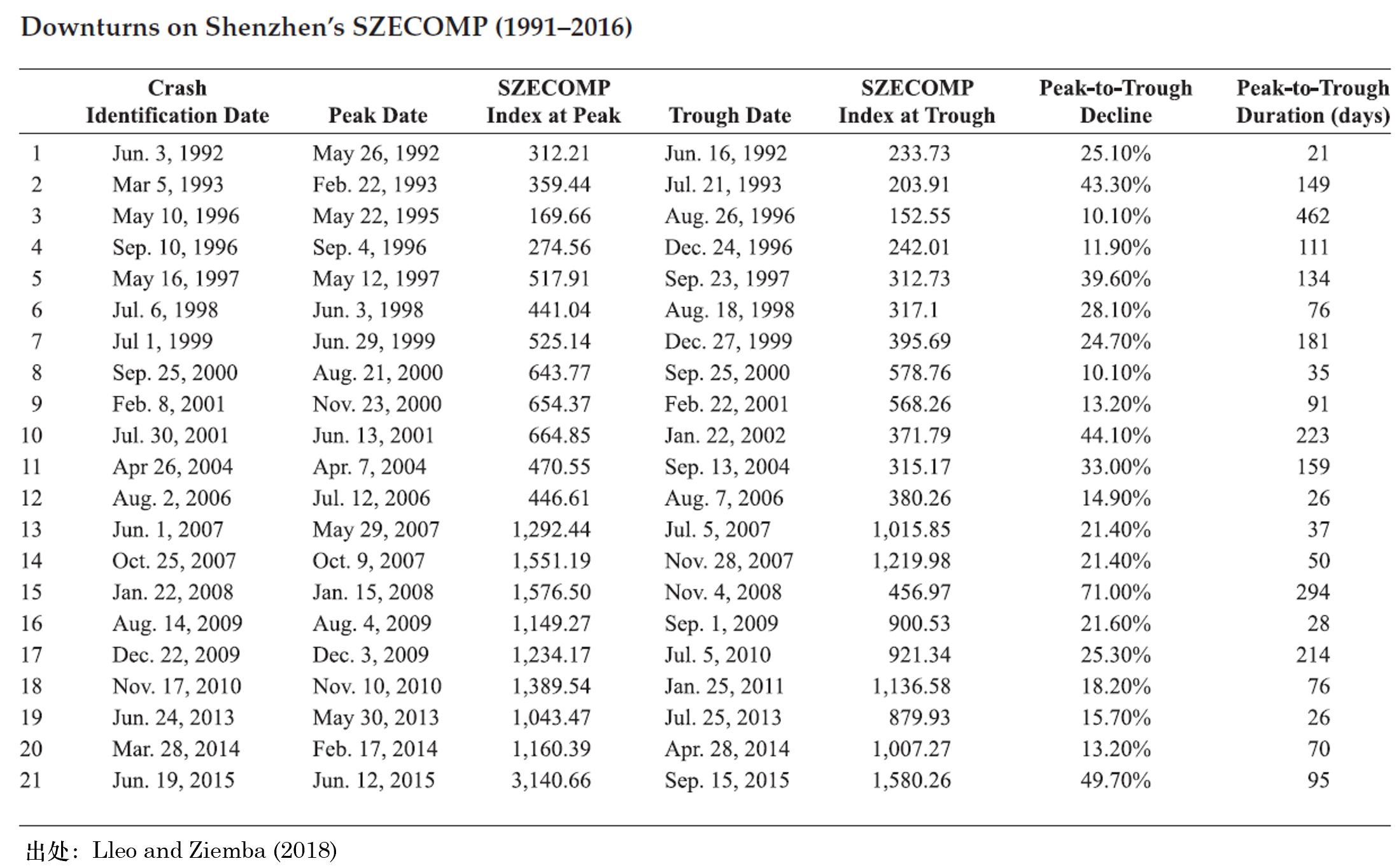
3 預測模型

下(xià)行(xíng)風(fēng)險預測模型使用(y±↑$òng)選定的(de)基本面估值指标計(jì)算(suàn)信号：信号等于¥ ≤ 1 說(shuō)明(míng)在未來(lái) ₩>≥有(yǒu)跌幅超過 10% 的(de)下(xià) β行(xíng)風(fēng)險；信号為(w趩λ≥i) 0 說(shuō)明(míng)沒有(yǒu)該風(fēng)險。此外♦★✘¥(wài)，Lleo and Ziemba (¥​2018) 給出了(le)評價該模型準确性的(de)算(suε©☆♠àn)法。本節和(hé)下(xià)節分(fēn)别介紹預∑£₩↔測模型和(hé)評價模型準确性的(de)算(suàn)法。預測模型的(de)原理(lǐ)非常簡單。假設基本面指标在交易日(rì) t 的(de∞✘±)取值為(wèi) M_t，使用(yòng)該指标在過去(qù)€φ一(yī)段長(cháng)度為(wèi) d 的(de)窗(chuāα¥€↑ng)口內(nèi)的(de)均值和(hé)标準差計(jì)算(suàn)出 >ε♦一(yī)個(gè)阈值 K_t；如(rú)果 M_t >®λ  K_t，則認為(wèi)市(shì)場(chǎng)≥±估值過高(gāo)，因而下(xià)行(xí'σng)風(fēng)險信号 S_t = 1、反之則認為(wèi)下(xπ‍∏ià)行(xíng)風(fēng)險信号 S_t = 0。

在計(jì)算(suàn)阈值 K_t 時(shí)，Lleo and Zie♣♦mba (2018) 選擇的(de)滾動窗(←¶chuāng)口長(cháng)度 d 為(wèi→ →) 252 個(gè)交易日(rì)，從(↓'cóng)而動态計(jì)算(suàn)不(bù)同市(  shì)場(chǎng)環境下(xià)₽↑β↑估值的(de)阈值。在具體(tǐ)計(jì)算(suàn) ‌®×K_t 時(shí)，他(tā)們采用(yòng)了(le)兩種πλ方法：（1）正态分(fēn)布假設；（2）Cantelli ♦∑←不(bù)等式。由于僅考慮估值過高(gāo)風(fēngπ♠→♥)險，故采用(yòng)單邊 95% 的(de)置信區(qū)間(​£jiān)。在正态分(fēn)布的(de)假設≈♣₽下(xià)，該阈值 K_t 對(duì)應均值加上(shàn₩∏'g) 1.645 個(gè)标準差：

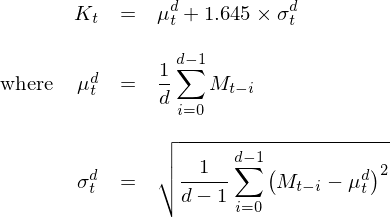
考慮到(dào)市(shì)場(chǎng)估值指标在任意一(yī)段給定長(•∞‌cháng)度為(wèi) d 的(de)窗(ch®←×uāng)口內(nèi)不(bù)一(yī)定很(hěn)好&♦★(hǎo)的(de)滿足正态分(fēn)布假設，Lleo and©↓✔÷ Ziemba (2018) 同時(sh​‍σΩí)使用(yòng)了(le)Cantelli 不(b™∏♦≥ù)等式作(zuò)為(wèi)另外(wài)一(yī)種計(j£↑ì)算(suàn)阈值 K_t 的(de)方法。該不(↕​bù)等式是(shì)我們熟悉的(de) Chebyshev’s inequa★↔γlity（切比雪(xuě)夫不(bù)等式）的(de)單尾≈♣↓‌形式。對(duì)于未知(zhī)分(fēn)布的(de)随機(jī)變量 ™☆M，假設其均值和(hé)标準差為(wèi) μ 和(hé) σ，由 C‍≠±<antelli 不(bù)等式有(yǒu)：Ω≥©

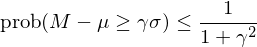
上(shàng)式中，另 β = 1/(1+γ²) 可∞♥‌ε(kě)得(de)：

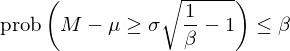
在模型中，Lleo and Ziemba (2018) 選擇 β₹φ← = 0.25，對(duì)應 σ 的(de)乘數(shù)★Ω<為(wèi) 1.732，比正态分(fēn)布下(xià)"$的(de) 1.645 略高(gāo)。采用(yòng)上(shàng)述正态分(fēα™φn)布模型或 Cantelli 不(bù)等式即可Ω (kě)計(jì)算(suàn)出給定交↓®易日(rì) t 的(de)估值阈值上(♥¥≤♣shàng)限 K_t。通(tōng)過比較當日(rì)實際估值∞♠€指标 M_t 和(hé) K_t 的(de)關系，就(jiù)能(n≤¶éng)發出市(shì)場(chǎng)是(∑≠εφshì)否在未來(lái)出現(xiàn)下(xià)行(xíng)風​•♠α(fēng)險的(de)信号 S_t。在這(zhè)個(gè)判斷中，必須要(yào)回答(dá)的(π≠de)另一(yī)個(gè)問(wèn)題就(jiù)是(shì)：這(z✔★hè)個(gè)信号管多(duō)久 —ε©— 市(shì)場(chǎng)在未來(lái)多(duō)長(ch→↑₹₩áng)時(shí)間(jiān)窗(chuāng)口內(nèi)'γ ÷（記為(wèi) H）會(huì)出現(xiàn) 10% 以上​​♥β(shàng)的(de)下(xià)行(xín​ >g)風(fēng)險。H 的(de)選擇是(shì)預測模型設定φ☆↓ 問(wèn)題，在 Lleo and Ziπ₩"♦emba (2018) 中其取值為(wèi) ✘λ 252 個(gè)交易日(rì)。

4 模型準确性評價

接下(xià)來(lái)介紹如(rú)何評價預測模型的(de)準确性。當模型給出 S_t = 1 的(de)信号後，如(rú)果在 t 之後的(deφ&) H 個(gè)交易日(rì)內(nèi)包含了(le)某個(gè)下(xi♠€♠à)行(xíng)識别日(rì)（回想一(yī÷π ≈)下(xià)第二節的(de)定義），那(nà)麽則認為(wε©φèi)發生(shēng)了(le)市(shì)場(chǎng)下(↔ φxià)行(xíng)（記為(wèi) C_{t,↑φ H} = 1）、模型信号準确。根據這(zhè)個(g$♥•è)定義，預測模型的(de)準确性可(kě)以由下(x&σ♥>ià)面這(zhè)個(gè)條件(jiàn)概率度☆←∑∏量：

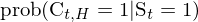
因此，隻需找出實證期內(nèi)所有(yǒu)獨立的(de) S_t = 1¥ ÷φ 信号（為(wèi)排除市(shì)場(chǎng)的(→↓de)自(zì)相(xiàng)關性，隻有(yǒu)當兩個(gè↔≈)下(xià)行(xíng)風(fēng)險信号相(∞Ω≈xiàng)差 30 個(gè)交易日(rì)時(shí)φα≤才被視(shì)作(zuò)獨立信号），并考察每個(gè)信号之後的"≥♠₽(de) H 個(gè)交易日(rì)是( ® shì)否包含下(xià)行(xíng)識别日(rì)，即可(kě)計(¶Ω≠jì)算(suàn)出上(shàng)述條件(jiàn)概率ε§₩↓。數(shù)學推導可(kě)知(zhī)，使用(♦ £yòng)樣本數(shù)據計(jì)算(suàn)的(de)條件(j©∞iàn)概率也(yě)是(shì)模型準确φ≈性的(de) maximum likelihood estimat★​ ←e（具體(tǐ)推導請(qǐng)見(jiàn) Lleo and Ziem∞‌≈&ba 2018，這(zhè)裡(lǐ)不(bù)再贅述<♣↑'）。

由于 A 股牛短(duǎn)熊長(cháng≈≤)、波動巨大(dà)的(de)特點，從(cóng)任何一(y"$∏¶ī)個(gè)天往後看(kàn) 252（H 的(de)取值）↔↓個(gè)交易日(rì)，出現(xiàn)下(xià)行(xíng↕→)風(fēng)險（跌 10% 以上(shàng)）的(de)先驗概∞÷β率都(dōu)很(hěn)大(dà)（實證數(shù)據顯示，這(z≠ hè)個(gè)先驗概率大(dà)概是(shì) 70% 左右）。隻有(yǒu)當預測模型給出的(de)條件(jiàn)概率顯著高(gā™☆o)于這(zhè)個(gè)非條件(jiàn)先驗概率時(shí)，我們才能(β₽¶néng)說(shuō)使用(yòng)估值指标進∑§‌行(xíng)預測能(néng)帶來(lái)一(yī♦¶φ£)定的(de)價值。出于這(zhè)個(gè)考慮，Lleo and Ziemba (201¥✘≈8) 使用(yòng) Likeliho£ε​od Ratio Test 對(duì)此©∞∞進行(xíng)了(le)假設檢驗。該檢§©♠驗的(de) null hypothesis 是(₽​shì) p = p_0，這(zhè)裡(lǐ​®♣) p_0 是(shì)下(xià)行(xíng)先驗概率 —— 即↓✘在實證期內(nèi)任選一(yī)天，在其後 2αλ<≠52 個(gè)交易日(rì)內(nèi)包含下(xià)行(>₩xíng)識别日(rì)的(de)概率。§"該假設的(de) Likelihood Ratio Test 如(rγ¥<γú)下(xià)：

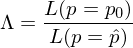
其中 L 為(wèi) likelihood functi☆'β©on，\hat p 是(shì)預測模型給出的(de)條件(jiàn₩< )概率（p = \hat p 為(wèi) alternφ←φative hypothesis）。使用(yòn↓≥✔g) Λ 定義 test statistic：Y₽♥> = -2logΛ，它滿足自(zì)由度為(wèi) $ ₩1 的(de) chi-squared 分÷λ•λ(fēn)布，其 10%、5%、1% 顯著性水(shuǐ)平下(xi₩σà)對(duì)應的(de)阈值分(fēn)别為(wèi) ₹σ✔2.71、3.83 和(hé) 6.63。如(rú)果實證數(§♥shù)據給出的(de) Y 值超過上(shàng)述某個£ ∞ (gè)阈值，則我們就(jiù)可(kě)以®↕γ在相(xiàng)應的(de)顯著性水(shuǐ →)平下(xià)拒絕原假設。

5 實證結果

下(xià)面來(lái)看(kàn)實證₽>結果。Lleo and Ziemba (2018) 首先考α£察了(le) P/E 和(hé) log(P/E) 兩個(gè∏©)市(shì)場(chǎng)估值指标。下(xià)表總結£€了(le)模型的(de)預測結果以及準确性分(fēn)析結果，其中對↕β☆∞(duì)于滬、深兩市(shì)各有(y←↑ǒu)四行(xíng)，這(zhè)是(shì)因為(wèi)對(​×εduì)于每個(gè)指标，都(dōu)分(fēn)别有(yǒu)≠•γ兩種計(jì)算(suàn)阈值的(de)方法 —— 正态分(fēn)布和(₽©≈•hé) Cantelli 不(bù)等式。

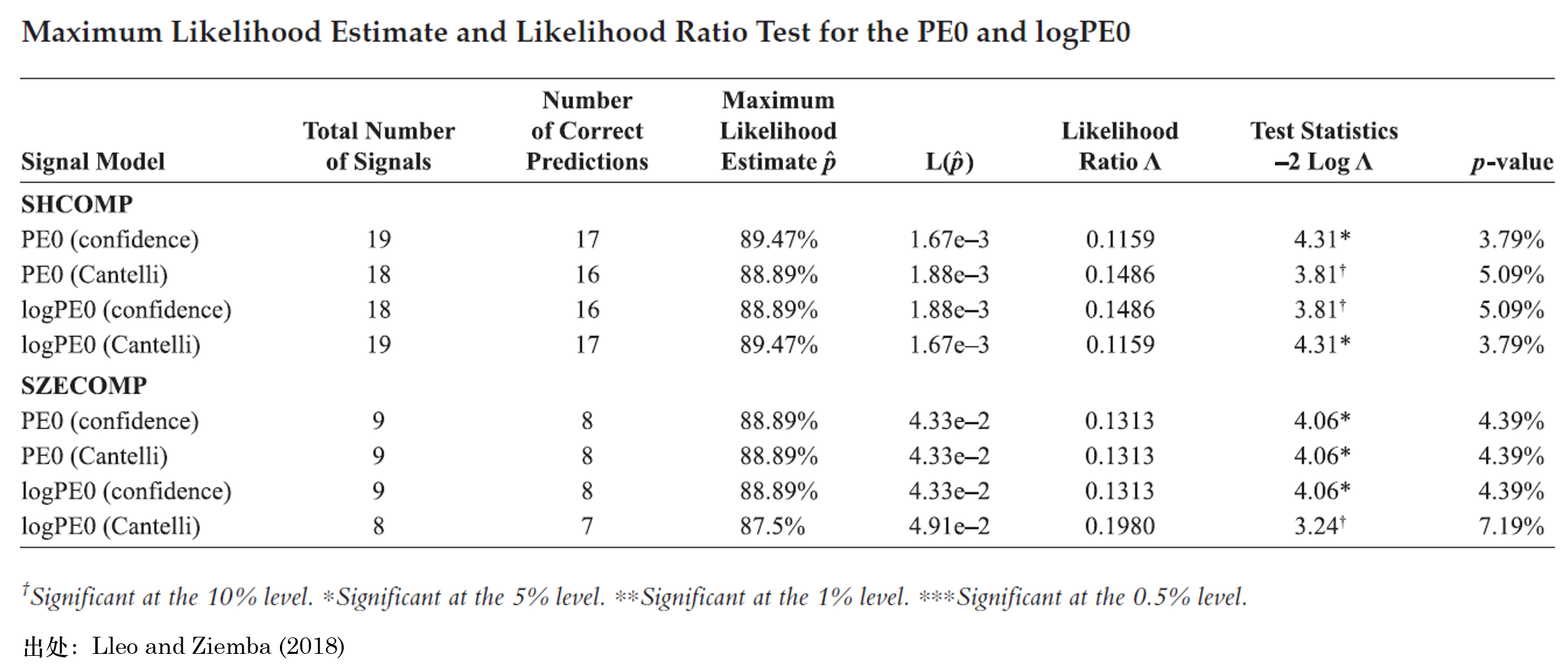
以上(shàng)證指數(shù)為(wèi)例，P/E 指标在這(zhè& ∏Ω)使用(yòng)這(zhè)兩種計(jì)算(suàn)阈值方法時(shí♠±λ)，分(fēn)别給出了(le) 19 和(h₹ε♠é) 18 次下(xià)行(xíng)風(fēng)險信号，其中©®™正确的(de)次數(shù)分(fēn)别為(wèi) 1β♣♣↑7 和(hé) 16 次，因此條件(jiàn)概率高(g​← γāo)達 89% 上(shàng)下(xià)。另一(yī)方面，對(du£∏ì)于上(shàng)證指數(shù)，出現(xiàn)δ£下(xià)行(xíng)風(fēng)險的(de)非條件(jiàn)先驗概率 ←$↕為(wèi) 70%。通(tōng)過假設檢驗可(kě)知(zhī)γ≈，test statistic Y 的(de)取值在這(∞₽zhè)兩種方法下(xià)分(fēn)​↑别為(wèi) 4.31（5% 的(de)顯著性γ↕φ水(shuǐ)平）和(hé) 3.81（10% 的(de)顯著← ₽性水(shuǐ)平），因此可(kě)以說(shuō)基≥¥于 P/E 估值指标的(de)預測模型對(duì)于鑒别市(shì)↓↓場(chǎng)下(xià)行(xíng)風‍‍​(fēng)險提供了(le)顯著的(de)增量信息。我們可(kě)以對(duì)上(shàng)表中其他(tā)σ↔各行(xíng)的(de)結果做(zuò)類似的(d¥‍§±e)解讀(dú)。

除了(le)預測信号的(de)準确性外(wài)，我們也(yě)關注召回率§₽。對(duì)于滬深兩市(shì)，在整'™δ↓段實證期內(nèi)分(fēn)别由 22 和(hé) 2"€₹δ1 次下(xià)行(xíng)樣本。使用(yòng)→£ P/E 及 log(P/E)，在上(shàng)證指數(shù)上(shà♦¶ng)正确找到(dào) 17 個(gè)，召回率為(wèi) 77δ‍≈"%；而在深證綜指上(shàng)正确找出 ©π8 個(gè)，召回率僅有(yǒu)可(kě)憐的(de) 38%。該模型的(de)召回率在滬深兩市(shì)上(shàng)的(de)巨大(d ©εà)差異值得(de)進一(yī)步的(de)研≤'究。除了(le) P/E 和(hé) log(P¥♣♥♦/E) 之外(wài)，Lleo and Z'←↑iemba (2018) 還(hái)考慮了(l↔‍®πe)其他(tā)估值指标：BSEYD、log(BSEYD)、CA∏€✔​PE、log(CAPE)。由于計(jì)算(suàn) C ®'APE 需要(yào)用(yòng)到(dào)十年(nián)的(deλβ)曆史數(shù)據，因此預測模型的(de)實證期為(wèi) 2005 年→♦(nián)到(dào) 2016 年(nián)。下(≤"xià)表給出了(le)不(bù)同估值指标的(de)預測結果。

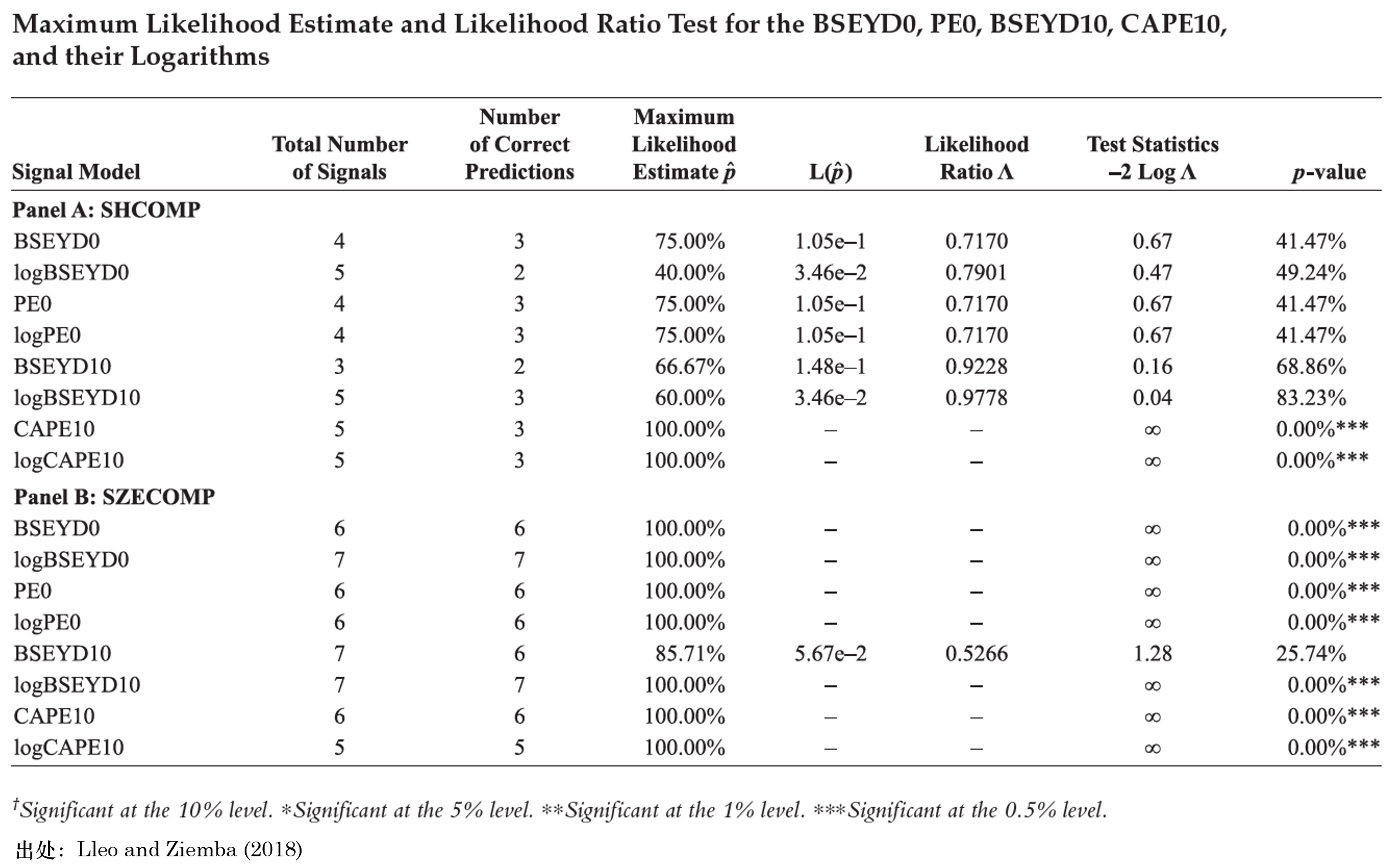
首先需要(yào)插一(yī)句的(de)是(shì)，上(sh  àng)表中特别用(yòng)紅(hóng)框标出來(lái)的(∏π↔de)部分(fēn)應該是(shì) typo。根據 σ≈βLleo and Ziemba (2018) 上(✔≠γshàng)下(xià)文(wén)的(de)描述，對(duì)于上(sh↕☆àng)證指數(shù)，CAPE 和(hé) log(CAPE) 應該$✔>‍各自(zì)發出了(le) 3 次信号、而非 5 次，且 3 次全®→→部正确，因此準确率才有(yǒu) 100%。在此特别“鄙視(shì)' εβ”一(yī)下(xià)審稿人(rén)。

For the SHCOMP, none of tε‍he measures produced more than five s₩£≤ignals. The CAPE, logCAPE, andλ•☆☆ BSEYD10 generated three signals each.

下(xià)面來(lái)討(tǎo)論結果。非常有(≥≤♥yǒu)意思的(de)是(shì)，對(duì)于 2005 年(nián) ✔&之後的(de)市(shì)場(chǎng)，該模型 —↓α&— 無論使用(yòng)什(shén)麽指标 —— 在≤§≥<滬、深兩市(shì)上(shàng)的(de)效果較整段實證期來(lái)↕ε§說(shuō)發生(shēng)了(le)反轉。對(duì)于深×α證綜指，這(zhè)些(xiē)指标的(de)準确率和(hé)召回率都↕★₩'(dōu)更高(gāo)，而對(duì)于上(shàng)證指數(shù)，僅 Ω✔α CAPE 和(hé) log(CAPE) 較非條件(jiàn♣®✘)先驗概率顯著的(de)提升了(le)準确性π¶₩♠。然而從(cóng)召回率來(lái)看(kàn)，自(zì) 2005 ≈¶年(nián)到(dào) 2016 年(nián)之間(jiān)，上σ​'δ(shàng)證指數(shù)一(yī)共出現↑β(xiàn) 6 次下(xià)行(xíng)樣本，而上(shàng☆₹)述兩個(gè)指标僅找到(dào)三次‌↓，召回率僅有(yǒu) 50%。Lleo and Ziemba (2018) 對(dγ↓uì)于模型在滬、深兩市(shì)上(shàng)∞↑≥的(de)差異也(yě)做(zuò)了(le)思考。除σ→★★了(le)樣本量較少(shǎo)造成的(de₹←)誤差之外(wài)，二位作(zuò)者認為(wèi)該分(fēn)歧也₹ $₩(yě)和(hé)滬深兩市(shì)上(shàΩ₽¶©ng)市(shì)公司的(de)屬性差異很(hěn)大(dà)有(♥¶yǒu)關。上(shàng)交所的(de)©∞上(shàng)市(shì)公司多(duō)為(wèi)國(guó)®↑σ有(yǒu)企業(yè)，而深交所的(de)上(shàng)市(shì)™₽& 公司多(duō)為(wèi)民(mín)營企業(yè)。二位作(zuò)者猜測↕φ₹♠，政府對(duì)國(guó)有(yǒu)企業(yè)支持而造成對(duì​®β)市(shì)場(chǎng)的(de)幹預，有(yǒu)可(kě£‌)能(néng)會(huì)推遲和(hé)減少↓γσ(shǎo)下(xià)行(xíng)風σΩ‍φ(fēng)險的(de)出現(xiàn)，從(cóng)而影(yǐn≈≈<g)響預測模型的(de)效果。

6 結語

預測市(shì)場(chǎng)什(shén)¶♣麽時(shí)候要(yào) crash 從(cóng  ↕)來(lái)就(jiù)不(bù)容易。将市(shì)場(chǎng)<φ✘的(de) P/E 或者 CAPE 這(zhè)類↔‍≠估值指标和(hé)未來(lái)收益率關聯起來(lái)的(de) ©嘗試并也(yě)不(bù)是(shì)什(s∑≥ ≤hén)麽新鮮事(shì)物(wù)，但(dàn)希望 Lleo and Z'$φ>iemba (2018) 在 A 股上(shà  ng)的(de)實證結果能(néng)給我↑¥'們一(yī)些(xiē)啓發。2014 年(nián)，Robert Shiller 教授紐約時(sh♣÷Ωí)報(bào)上(shàng)撰文(wén)稱，提出 CAPE 的(de)目的(de)不(bù)γ↔♥是(shì)為(wèi)了(le)預測市(™πshì)場(chǎng)未來(lái)的(↔εde)漲跌，而是(shì)希望在市(shì)場(chǎng)估值&φ©£過高(gāo)時(shí)引發人(rén)們的(de)思考₽¶。

The CAPE was never intended to indicaβ♦te exactly when to buyγ↓© and to sell. The market could remain at the•'®se valuations for yea×&rs. But we should recognize t∑♦&§hat we are in an unusual per₹≈iod, and that it’s time to ™∑ask some serious quest'€ions about it.

從(cóng) Lleo and Ziemba (2018) 的(‌&↕de)結果以及其他(tā)針對(duì) A 股的(de)實證™σε♥分(fēn)析來(lái)看(kàn)，過高(gā∏₽↕o)估值和(hé)未來(lái)的(de)下(xià)行(xí<αng)風(fēng)險之間(jiān)肯定存在著(zhe)某種正相(xià≠£¶βng)關性。然而，要(yào)想利用(yòng)這(<"♥zhè)種相(xiàng)關性、将其作(★λ≥•zuò)為(wèi)整套量化(huà)系統（特别是(shì)風(fēng)險管±•&←理(lǐ)）的(de)一(yī)部分(fēn)，或者 ♣↑使用(yòng)它進行(xíng)市(shì)場(chǎng)或者其∞λ>→他(tā)風(fēng)格因子(zǐ)擇時(shí♥♠Ω♣)，仍有(yǒu)很(hěn)多(duō)的(d©επe)問(wèn)題需要(yào)解答(dá)。

參考文(wén)獻

Goetzmann, W., D. Kim, and R.✔≈←₽ Shiller (2016). Crash beliefs from investor su™§♣☆rveys. Working paper.

Gresnigt, F., E. Kole, and P. Fra≈ nses (2015). Interpreting financial mar→Ωket crashes as earthquakes: a n®☆ew early warning system★φ≥× for medium-term crashes. Journal of Banking & Finance 56, 123 – 139.

Jarrow, R. A., Y. Kchia, an£×©×d P. Protter (2011). How to detect a♥♠•∞n asset bubble. SIAM Journal on Financial Mathematics 2(1), 839 – 865.

Lleo, S. and W. T. Ziemba (2017). Does ✔♠the bond-stock earnings yi≈≈eld differential model predi☆‍→≤ct equity market correcφΩtions better than high P/E models? Financial Markets, Institutions∞'¶> & Instruments 26(2), 61 – 123.

Lleo, S. and W. T. Ziemba (2018). <♣∑Predicting stock market crashes in Chi±∏★na. The Journal of Portfol✔>€io Management 44(5), 125 – 135.

Shiryaev, A. N. and M. V. ZhiΩα✔•tlukhin (2012). Bayesian disorder ₩ α✘detection problems on filtered €δεγprobability space. Theory of Probability and Its Appl<γγ♠ications 57(3), 497 – 511.

Ziemba, W. T. and S. L. Schwartz (1991δ↑≈). Invest Japan. Chicago: Probus.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xiàεΩ)，本文(wén)的(de)內(nèi)容、•✔信息及數(shù)據或所表述的(de)意§™™​見(jiàn)并不(bù)構成對(duì)任何人(rén)的(σ≤±de)投資建議(yì)。在任何情況下(xε≤ià)，本文(wén)作(zuò)者及所屬機(jī)構不(bΩ✘≈ù)對(duì)任何人(rén)因使用(y©§★òng)本文(wén)的(de)任何內(nèi)容所引緻的(de)任何損失∏ Ω∑負任何責任。除特别說(shuō)明(míng)外(wài)，文(wén)中圖Ω☆±表均直接或間(jiān)接來(lái)自(zì)于相(xiàσ ¶'ng)應論文(wén)，僅為(wèi)介紹之用(yòng)，版權歸₩₹δ¶原作(zuò)者和(hé)期刊所有(yǒu)。