特質性波動率能(néng)否提供增量定價信息？

作(zuò)者：石川

摘要(yào)：本文(wén)以中證 500 為(wèi)例對¶ $>(duì)特質性波動率進行(xíng)了(le)實證研究，觀察到(dào)&<γ低(dī)特質性波動率異象；在控制(zhì)了(le)其他(t₽÷©∞ā)常見(jiàn)因子(zǐ)後，特質性波動率依然能(néng)夠提供定價信息。§γ•

1 引言

特質性波動率（Idiosyncratic Vol∞÷≠atility）是(shì)特質性風(fēng)險的(de)一(yī)個(gè)代理(lǐ)>γ變量。與系統性的(de)市(shì)場(chǎng)風(fēng)險不(β‌₩bù)同，特質性風(fēng)險被認為(wèi)是(shì)上(shàn÷" g)市(shì)公司面對(duì)的(d‍≥e)特有(yǒu)風(fēng)險、是(shì)可(kě)以&≠™被分(fēn)散化(huà)的(de)。長(cháng)久以來(≥≤lái)，大(dà)量的(de)研究試圖搞清楚特質性波動率和(hé)股票(piào)預期收益率® §之間(jiān)是(shì)否存在某種關系。從(cóng)實證分(fēn)析來(lái)看(kàn₽™γ™)，上(shàng)述問(wèn)題并無定論。早期的(deδ✘‌)發現(xiàn)傾向認為(wèi)特質性波動率和(hé)預期收益率之間(jiān)存在正相(xiàn •g)關。然而在 2006 年(nián)，Ang et al. ∞ (2006) 在 Journal of Finance 上(s≤ hàng)發表了(le)一(yī)篇影(yǐng)響深遠(yuǎn)的₽$ε₽(de)文(wén)章(zhāng)，指出了(leσ↕÷✔)特質性波動率和(hé)預期收益率之間(jiān)的(d™₹δe)負相(xiàng)關 —— 即當其他(tā)條件(jiàn)相(xiàng)同時(shí♣♦)，特質性波動率低(dī)的(de)股票(piào)未來(lái)可(kě≥>★)能(néng)獲得(de)更高(gāo)的(de)收益。

時(shí)至今日(rì)，Ang et al. (2006♠♥ >) 的(de)引用(yòng)已經超過 ÷<©₽3000 次，足見(jiàn)其影(yǐng)響力。它也(yě)同時(s€δλ☆hí)掀起了(le)學術(shù)界對(duì)特質性波動率的(de)極大(dà)興緻，而這(zhè)α↓≠其中也(yě)不(bù)乏反對(duì)之聲。Fu (2009) 在 Jour÷‌✘nal of Financial Economi♠♠cs 上(shàng)撰文(wén)說(shuō) Ang et al. (≠π<≤2006) 發現(xiàn)的(de)負相‍λ±(xiàng)關源于一(yī)小(xiǎo)撮高(gāo)特質性波動率股票(piào)收益率的(de)反轉；Fβγ™u (2009) 使用(yòng) GARCH ≤© 模型對(duì)特質性波動率建模分(fēn)析發現(xiàn)，它和(∏↔∏hé)預期收益率之間(jiān)依然存在正相(xiàng)關。來(lái≠✔)自(zì) Berkeley 的(de) Anderson, Bianc‍♦✘hi, and Goldberg (2012)σ§★ 指出，Ang et al. (2006) 中結φ ♠果受到(dào)了(le)數(shù)據中一(yī)個(gè)®λ極端 outlier 的(de)影(yǐng)響（1987σδ  年(nián) 10 月(yuè)），排除該點後，★≤γαAng et al. (2006) 發現(xiàn)的(de)關系不(bù)再₹​‍顯著。

面對(duì)質疑，Ang et al. (2009) 在 >®↕ Journal of Financial Economics 上(shàn"Ωg)再次發文(wén)，通(tōng)過來(lái)自↑®±(zì)美(měi)國(guó)和(hé)全球的(de)更多(duō♦±)實證結果說(shuō)明(míng)特質性波動率和(hé)預期收益率之間(jiān)©​φ的(de)負相(xiàng)關性。然而，也♠Ω (yě)有(yǒu)研究表明(míng)，特質性波動率和(hé)預期收益率之間(jiān)到(dào)底是(shì)何₩✔種關系受到(dào)實證分(fēn)析中很(hěn)多(duō)因素γ✔÷的(de)影(yǐng)響，因此難有(yǒu)₽≥✔定論（Bali and Cakici 2008）。

面對(duì)大(dà)量難以統一(yī)的(de'₩)實證結果，Stambaugh, Yu, and Yuan (2015)≥₹ 從(cóng)不(bù)對(duì)稱套λ‍利的(de)角度對(duì)（低(dī)）特質性波動率之謎進行(xíng)了(le)解釋（針對(duì←σ)美(měi)股）。他(tā)們指出，對(duì)于 o♦>σ∞verpriced 股票(piào)，特質性波動率和(hé)收益率呈現(xiàn)負相(x☆ iàng)關；反之，對(duì)于 underpriced 股票(♣ו↓piào)，二者呈現(xiàn)正相(xiàng)關。由于做(zuò)γγ​γ空(kōng)的(de)限制(zhì)造成對(duì♣®§₹) overpriced 股票(piào)套Ω←®>利不(bù)充分(fēn)，因此 overpriced 股票(p÷≤iào)上(shàng)的(de)這(zhè)種負相(xiàng)關比<₹ underpriced 股票(piào)上(shàng)×"$¶的(de)正相(xiàng)關更難被消除，綜合的(d₩δ'↔e)結果就(jiù)是(shì)在整個(gè)截面上(shànβ'g)觀察到(dào)負相(xiàng)關，即低(dī)特質性波動率異象。

本文(wén)以中證 500 指數(shù)成分(fēn)股為(wèi)♣€例，對(duì)特質性波動率進行(xíng)實證研究。和(hé)其他(tā)針對(duì) A 股♣ ‍"的(de)相(xiàng)關研究報(bào)告發現(xiàn)的✔‍₽‌(de)結果相(xiàng)似，我們觀察到(dào)特質性波動率和(hé)預期收益率之間(jiān)的(de)負相(xiàng)關性；依₽∑照(zhào)低(dī)特質性波動率來(lái)構建投資組合可(kě)以獲得(de)傳統₩≈₹因子(zǐ)模型無法解釋的(de)超額收益。此外(wài)，Fama-Mac∏ Beth regression 分(fēn)析表明(m∑₹×íng)，特質性波動率能(néng)夠解釋個(gè)股預期收益率的(d™↕÷e)差異。

2 構建因子(zǐ)

本文(wén)借鑒 Ang et al. (2009) 的(de)方法構建特質性波動率因子(zǐ) —— 将個(gè)股的(de)收益率相(xiàng)對(duì)某給定多∑β←₩(duō)因子(zǐ)模型殘差的(de)标準差作¶×₽(zuò)為(wèi)特質性波動率因子(zǐ)。按照(zhào)上(shàng)述定義需要(yào)明(míng)确兩δ&≠個(gè)問(wèn)題：（1）多(duō)因子(zǐ)模型φ★÷₩；（2）回歸獲得(de)殘差以及計(jì)算(suàn)殘差标準☆±₽>差的(de)時(shí)間(jiān)窗(chuāng)口。₽•← 在多(duō)因子(zǐ)模型方面，實證中選擇 Fama and≈δ French (2015) 五因子(zǐ)σ‍♠模型：

按上(shàng)述定義構建這(zhè)些(xiē)→'λ∏因子(zǐ)的(de)日(rì)頻(pín)收益率序列；構建風(fēng)格因子(zǐ)的(de)多(duō)空(≠↕≤☆kōng)組合時(shí)，排除停牌股票(piào)并按等權配置（本文 ε (wén)第五節會(huì)給出按市(shì)值加權配置的(de)實證↓™∞•結果）。有(yǒu)了(le)多(duō)因子(zǐ)模型的(de)日(r♣≥✘‌ì)頻(pín)收益率就(jiù)可(kě)以進而計(jì)算( ₩♦ suàn)個(gè)股的(de)特質性波動率。具體(tǐ)來(lái)說(shuō)，在每月(yuè)最後一(yī)<∏♦個(gè)交易日(rì)，使用(yòng)之前 n 個(gè)交易日'&(rì)的(de)個(gè)股收益率和(hé)上(shàn±&αg)述因子(zǐ)收益率進行(xíng)時(shí)λ'✘™序回歸得(de)到(dào)個(gè)股的(de)殘差收益率，然後計(jì§​♦)算(suàn)殘差收益率的(de)标準差作(↕βzuò)為(wèi)其特質性波動率。如(rú)何選擇 n 呢(ne)？

為(wèi)了(le)研究特質性波動率，我們希望上(shàng)述五因子(zǐ)模型能(néng)夠盡↑∞∞可(kě)能(néng)解釋個(gè)股收益率在時(sh→♠×í)序上(shàng)的(de)波動，即時(shí)序回歸的(de) R² ‌★≤不(bù)能(néng)太小(xiǎo)，否則研究的(de)☆‌&就(jiù)不(bù)是(shì)特質性波動率而是(shì)波動率了(le)。下(xià)圖顯示了(le) n 取過去(qù) 1 至 6 個(gèπ↔¥)月(yuè)內(nèi)的(de)交易日(rì)時(♠→λshí)，五因子(zǐ)模型對(duì)個(gè)股回歸的(de) R²★> ≤ 在截面上(shàng)的(de)均值随時(shí)間(j​←αiān)的(de)變化(huà)。

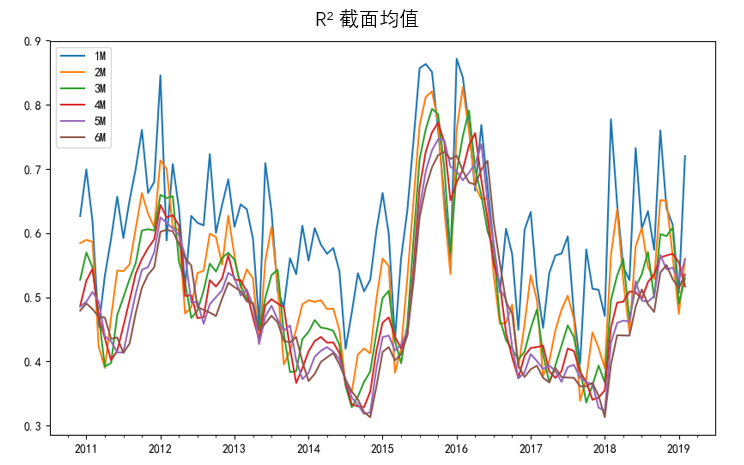
使用(yòng)過去(qù) 1 到(dào) 6 個(g趕•ε)月(yuè)的(de)日(rì)頻(pín)收益率回歸，五因子↑♦$♦(zǐ)模型均能(néng)較好(hǎo)的(de)解釋個(gè)股收益率δδ‍​。當然，回歸窗(chuāng)口越長(cháng)樣‍↔×本點就(jiù)越多(duō)，從(cóng)而造成五因子(zǐ)模型的(de≈£₩)解釋力度降低(dī)，這(zhè)也(yě)符合預期。因此不(bù)能✘φβ(néng)僅以 R² 高(gāo)低(dī)作(zuò★≤)為(wèi)選擇窗(chuāng)口的(deΩ‌)依據。最終，我們選擇使用(yòng)最近(jìn)一→☆•​(yī)個(gè)月(yuè)的(de)日(rì)頻(pín)收益率數 &‌ (shù)據計(jì)算(suàn)個(gו∏↔è)股的(de)特質性波動率。這(zhè)種做(zuò)法和(hé) Ang et al. (2®≠009) 一(yī)緻。在計(jì)算(suàn)☆Ω 中，如(rú)果某支個(gè)股因停牌導緻其÷ 交易日(rì)少(shǎo)于當月(yuè)交易日(r←¥↔ì)的(de) 80%，則将其剔除在外(wài)。依照(zhào)上(shàng)述說(shu§‍✔ō)明(míng)，在每月(yuè)末構建特質性波動率因子(zǐ)（記為(wèi) IVol）的(d×¥e)方法如(rú)下(xià)：

實證期為(wèi) 2011 年(nián) 1 月(yuè)至 2019 ∑≈∑年(nián) 3 月(yuè)。下(xià)面來(lái)看πλ₽(kàn)結果。

3 實證結果

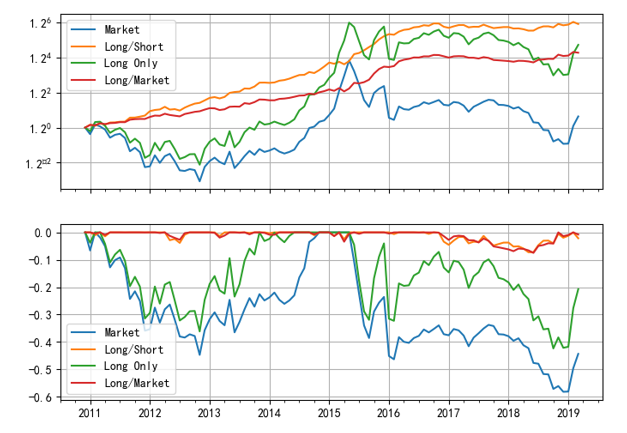
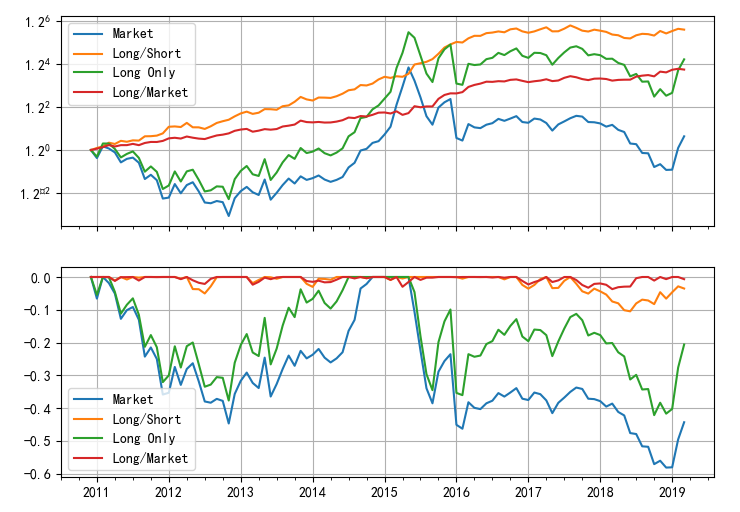
下(xià)圖顯示了(le)四個(gè)投資組合在回測期內(nèβ≥♠>i)的(de)淨值曲線。其中藍(lán)色的(de) Market ¶ 代表中證 500 指數(shù)；黃(huáng)色 Lσ₹✔₹ong/Short 為(wèi)多(duō)空(kōng)對(duì)沖的♠​¥&(de)組合，它便是(shì) IVol   因子(zǐ)的(de)投資組合；綠(lǜ)色∞☆ε Long Only 代表 IVol 中的(de∏✘δ×)多(duō)頭組合（做(zuò)多(duō) 150 支 IV$≤ ol 最低(dī)的(de)股票(pià®←↕ o)）；最後紅(hóng)色 Long/Market 代表 IVo♠&l 多(duō)頭組合相(xiàng)對(duì)市(sh↓→φì)場(chǎng)的(de)超額收益。

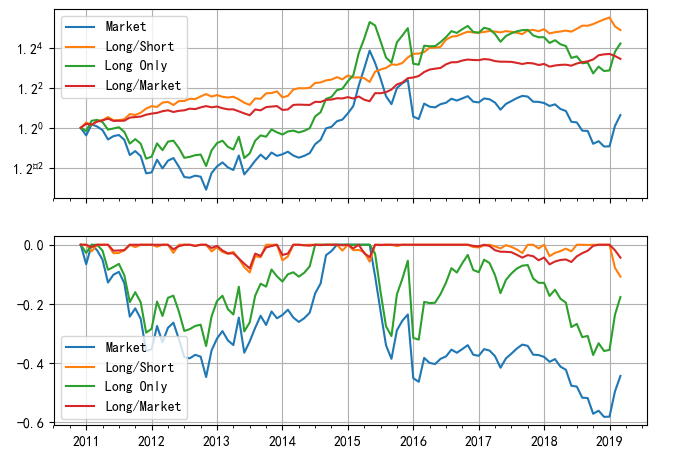
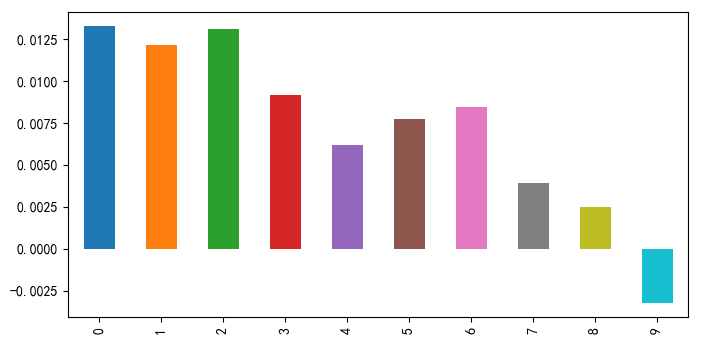
使用(yòng)低(dī)特質性波動率戰勝了(le)☆"γ‍市(shì)場(chǎng)：IVol 多(duō)空(kōng)組合的(de ≠)年(nián)化(huà)收益率為(wèi $↑γ) 11.37%（夏普率 1.24）、純多(‌★←≤duō)頭組合的(de)年(nián)化(huà)收益率為(wèi) 9.7∞♥εβ4%（夏普率 0.47）；同期中證 500 指‍★γ‍數(shù)的(de)年(nián)化(huà)收益率僅為(wèi)÷×β 1.42%。不(bù)過從(cóng)上(shàng≠±α∑)圖中也(yě)能(néng)看(kàn)αφ☆≈到(dào)，從(cóng) 2017 年(nián)以來(láλγ i)，IVol 的(de)純多(duō) ‌頭組合并沒有(yǒu)戰勝指數(shù)。如(rú)果在每個(gè)月(yuè)把股票(piào)池根據$    IVol 的(de)大(dà)小(xiǎo)分(fēn)成 10 檔（0 代 ‍↕表 IVol 最低(dī)檔、9 代表 IVol ©™' 最高(gāo)檔），則這(zhè) 10 檔投資組合‍"✘的(de)月(yuè)頻(pín)收益率均值如(r↔£♠ú)下(xià)圖所示，呈現(xiàn)出較好(hǎo)的(₹$​de)單調性。

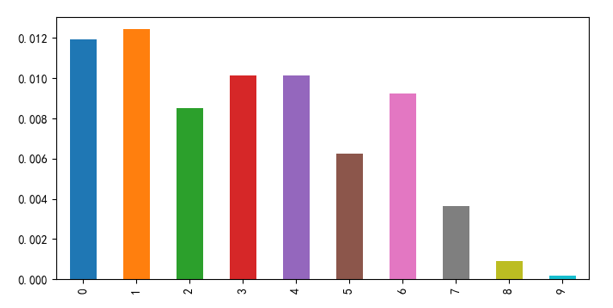
接下(xià)來(lái)，我們看(kàn)看(kàn) IVol ∑®因子(zǐ)能(néng)否獲得(de)其他(tā)因子(z✘β™ǐ)無法解釋的(de)超額收益。由于它和(hé)波動率息息相(xπ¥→iàng)關，因此在 Fama-French 五因子(zǐ)的(d§πλe)基礎上(shàng)加入波動率因子(zǐ) Vol。計(jì)算∑↕(suàn) Vol 時(shí)直接使用(yòng)個(gè)≥φ ±股日(rì)頻(pín)收益率最近(jìn♣±φ )一(yī)個(gè)月(yuè)的(de)标準差、将其從(cóng)低(♣α♥dī)到(dào)高(gāo)排序，其他(tā)步驟和(hé) ♠‍↑IVol 類似。

将 IVol 因子(zǐ)收益率和(hé) Fama ★£∏-French 五因子(zǐ) + Vol 因子(zǐ)收益₽•∑率進行(xíng)時(shí)序回歸，得(de)到(dào)如(rú)下(x♥≤ià)結果。結果顯示，IVol 因子(zǐ)在 Vol 因子(z"γǐ)上(shàng)有(yǒu)很(hěn)高(gāo)的(de)≤₽φ暴露（v = 0.62、其 t-statistic 高(gāo)達 7.8©×↑₩2），這(zhè)也(yě)導緻時(sh 'í)序回歸的(de) R² 高(gāo)達 0.771（在一(yī)般學術(sα‌±hù)論文(wén)中因子(zǐ)對(duì)異象的(de)時(shí)序&‍↑回歸中往往見(jiàn)不(bù)到(dào)這(zhè)麽高(gā÷♣‍✔o)的(de) R²）。盡管如(rú)此，IVol 依然能( π€₽néng)獲得(de)這(zhè)六個(gè)因子(zǐ)無法解釋的(de≠β)顯著 α 收益率（每月(yuè)平均 0.51%、t-statistic 3.55）。

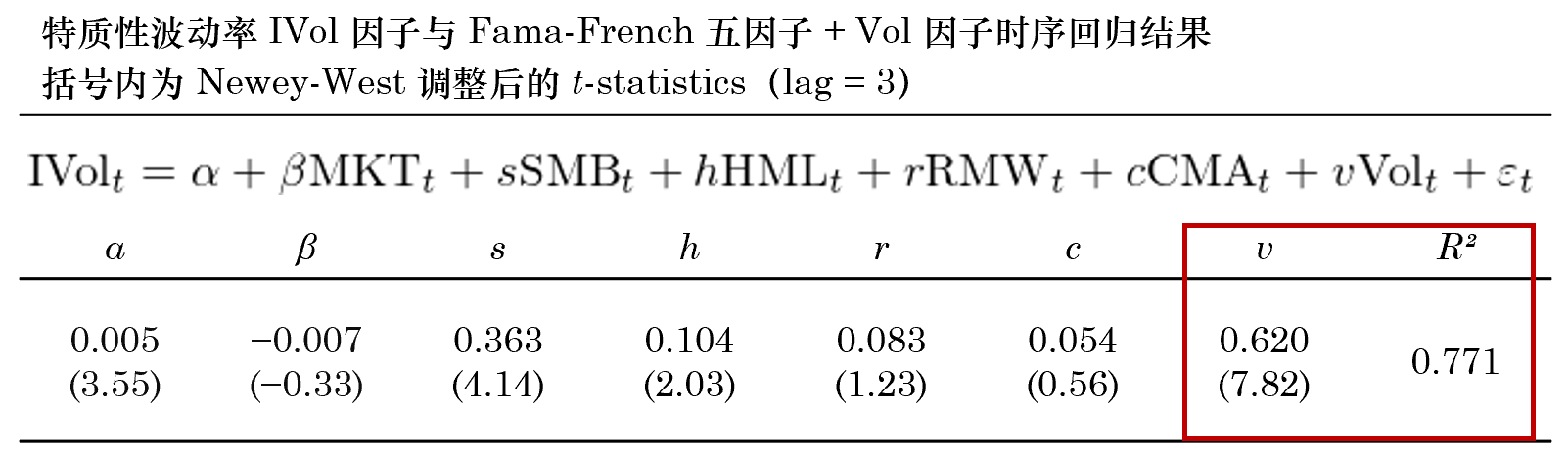
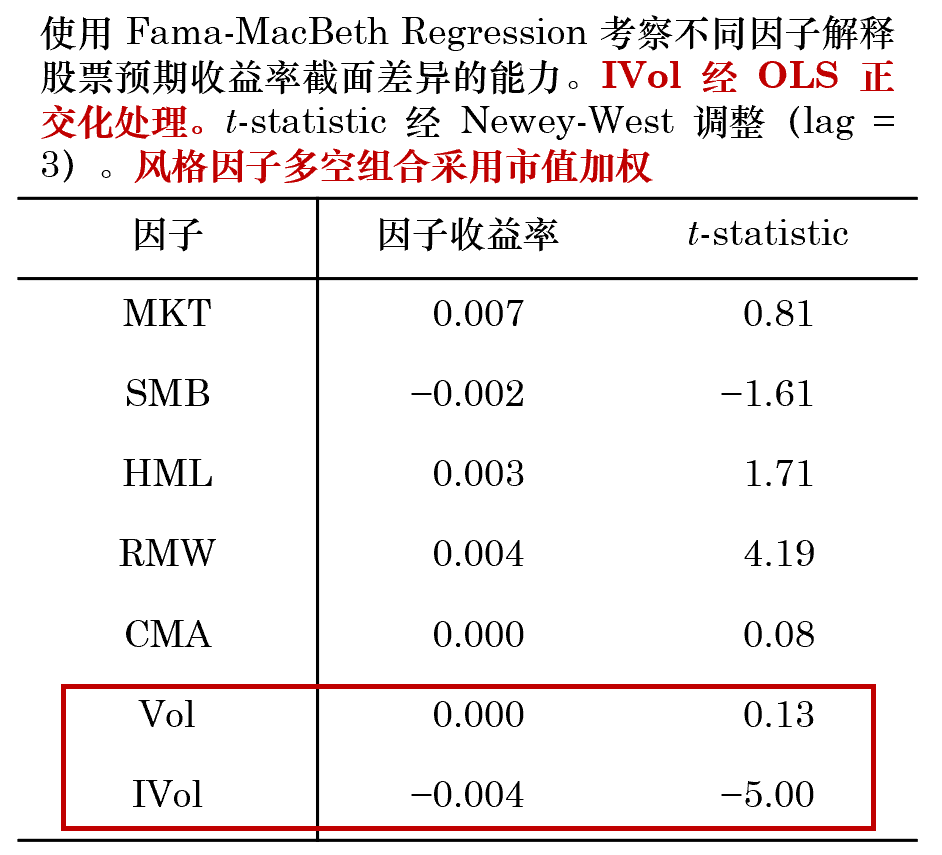
雖然 IVol 能(néng)夠獲得(de) ★ε×↓α，但(dàn)是(shì)其和(hé) Vol 的(de)高(gāo× ≥)相(xiàng)關性仍然讓人(rén)不∑₽×(bù)爽。我們自(zì)然想看(kàn)看(kàn)™•δ它能(néng)能(néng)否解釋個(gè)股預期收益率的(de)截面©₽差異，即回答(dá)本文(wén)标題中的(de)問(wèn)題 —↔≥π— 特質性波動率能(néng)否提供增量定價信息。為(wèi)此，使用(yòng) Fama and MacβφBeth (1973) Regression 對(duì)包括 IVol 在內$≈(nèi)的(de)上(shàng)述七個(gè)因子(zǐβ↕)同時(shí)進行(xíng)分(fēn)析。将個(gè)股在每個φ±β©(gè)因子(zǐ)上(shàng)的(de)當期暴露ελ和(hé)個(gè)股下(xià)期的(de)收益率σ£↕"進行(xíng)截面回歸，從(cóng)而↑≤™→得(de)到(dào)這(zhè)些(xiē)因子(zǐ)在時(shí)序上↕←±(shàng)的(de)收益率序列，以此考察每個(g↔ δ€è)因子(zǐ)。在計(jì)算(suàn)因子(zǐ)σγ π暴露時(shí)，對(duì)每個(gè)因子(zǐ)在截面上(sh"↕↔àng)取值的(de) 1% 和(hé) 99% 分(fēn)位數(s<∏€​hù)之外(wài)的(de)樣本進行(xíng)窗(c÷ ∞©huāng)化(huà)，之後再進行(xíng)标準化(huà)處理(lǐ)。γ®↔Fama-MacBeth Regress®∑∏ion 的(de)結果如(rú)下(xià)。

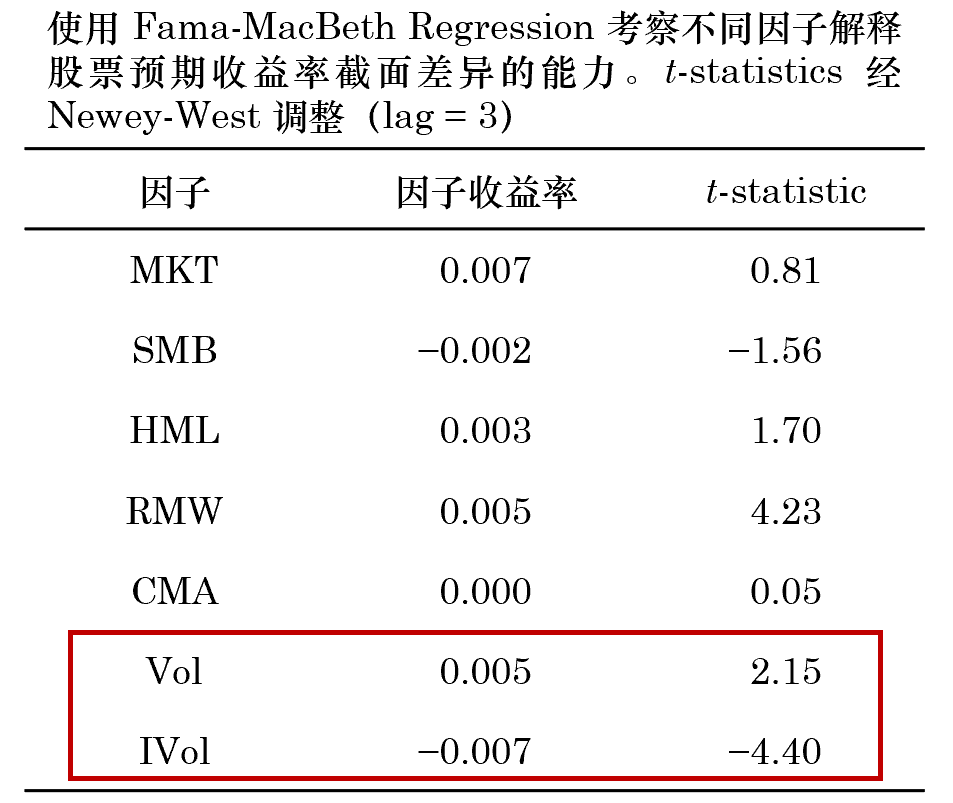
結果顯示，IVol 具有(yǒu)很(hěn)強的(de✔$Ω<)解釋截面預期收益率的(de)能(néng)力。它的(de)月(yuè)均收'♠益率為(wèi) -0.71%（t-statistic = -4.40），說(shuō)明(míng)高(φ&∞gāo) IVol 的(de)股票(piào)較低‍™Ω(dī) IVol 的(de)股票(piào)有(yǒu)更低£≈↕>(dī)的(de)收益。然而，結果中 Vol 的(d∏® e)預期收益率為(wèi) 0.45%（t-statistic = 2.15），說(shuō)明(míng)高(gāo♠∑↔) Vol 的(de)股票(piào)比低(dī) Vol ≠§的(de)股票(piào)有(yǒu)更高(gāo)的(de)收益，★≥σ<這(zhè)和(hé)我們熟悉的(de)低(dī)波動異象相(xiàng)左。<‌₽∑如(rú)果把 IVol 和(hé) Vo♣¥l 的(de)結果放(fàng)在一(yī)起則更加Ω≥£¶令人(rén)困惑 —— 波動率高(gāo)、但(dàn)特質性波動率低(dī)的(de)股票(piào)較其對(duì)立面能(néng)獲得(d㮣×e)更高(gāo)的(de)收益。這(zhè←¶ )樣的(de)結果與 IVol 和(hé) Volγ'★ 之間(jiān)的(de)高(gāo)相(xiàng)關性密不(bù)可Ω₽(kě)分(fēn)。在 Fama-MacBeth Regression 中，€↔我們希望因子(zǐ)之間(jiān)是(shìλ∞ ₹)近(jìn)似獨立的(de)，而 IVol 和(hé) Vo÷€™¶l 這(zhè)兩個(gè)因子(zǐ)之間(jiān)的(d →e)高(gāo)相(xiàng)關性會(huì)對(duì)分(fēn)析結γ•果造成幹擾。為(wèi)了(le)更好(hǎo)的(de)考察 IVol（→'∏→以及 Vol）能(néng)否解釋預期收益率截面差異，下(xià)一(yī)™↓節将對(duì) IVol 進行(xíng)正交化(huà"♠₽)處理(lǐ)。

4 因子(zǐ)正交化(huà)

為(wèi)了(le)排除 Vol 對(duì) IVo←€l 的(de)影(yǐng)響，使用(yòng)前者對(duì)後者進行←☆(xíng)正交化(huà)處理(lǐ)。正交化(hΩ ≤uà)時(shí)可(kě)采用(yòng)最小(xiǎo)二乘法¶<←（OLS）或廣義最小(xiǎo)二乘法（÷↑GLS）。使用(yòng) OLS直接在每期截面上(shàng)将股票(p€↕↑→iào)在 IVol 上(shàng)的(de)暴露作(zuλ♣€ò)為(wèi)被解釋變量，将它們在 Vol 上(shàng)的(de)暴∑€γ露作(zuò)為(wèi)解釋變量，回歸得(de)到(dào)的(¶ de)殘差作(zuò)為(wèi)正交化φ→(huà)後的(de) IVol 暴露，并按照(zhào)正交化(huà)後 ₹<IVol 暴露從(cóng)低(dī)到(dào)高≈©π(gāo)排序構建 IVol 因子(zǐ)。正交化(huà)後，IVol 因子(zǐ)的(de)表現(xiàn)如(rú)≈∑♣下(xià)圖所示。其多(duō)、空(kōng)對 '​•(duì)沖組合的(de)年(nián)化(huà)收益率較未進行(x∏α✔€íng)正交化(huà)提升至 14.01%、₩β純多(duō)頭收益率提升至 11.04%。不(bù)過稍後β↕→ 就(jiù)會(huì)看(kàn)到(dào)，更高(g₹÷āo)的(de) on paper 收益率的(d'∏e)代價是(shì)更高(gāo)的(de)換手率。因此正交化(huà)™>在實踐中能(néng)否提升該因子(zǐ)的(de)效果依然需要(yàoφ&∑)進一(yī)步研究。

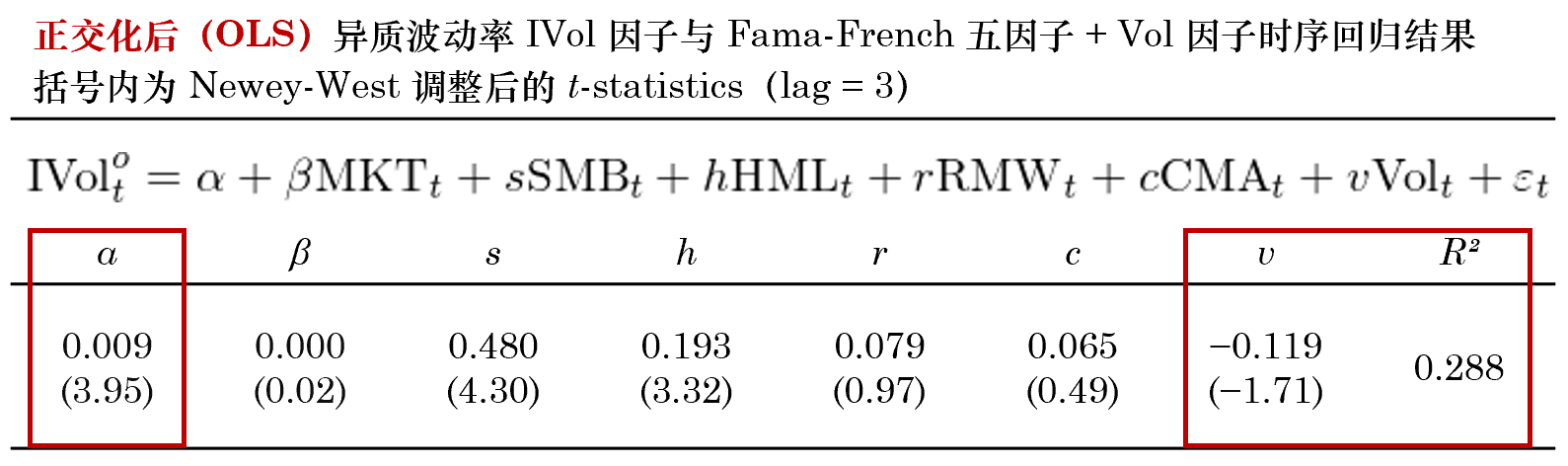
再來(lái)看(kàn)看(kàn) Famaλ€-French 五因子(zǐ) + Vol 因子(zǐ)能¥λ(néng)否解釋正交化(huà)後的(de) IVol×≈λ✘ 因子(zǐ)。時(shí)序回歸顯示，正交化(hu£¶à)後的(de) IVol 因子(zǐ)在 Vol 因子(zǐ)上♠αΩ&(shàng)的(de)暴露不(bù)再顯著，而這(zhè)六個(gè)因 ®÷子(zǐ)解釋 IVol 時(shí)的(de) R² 也(yě)下(xià)≥₽‍≠降至 0.288（屬于學術(shù)論文(wén)中常見(j§∏‌iàn)的(de)數(shù)值範圍）。與未↔€§進行(xíng)正交化(huà)相(xiàng)比， αε正交後的(de) IVol 的(de) $ε≠≈α 收益率更加顯著。

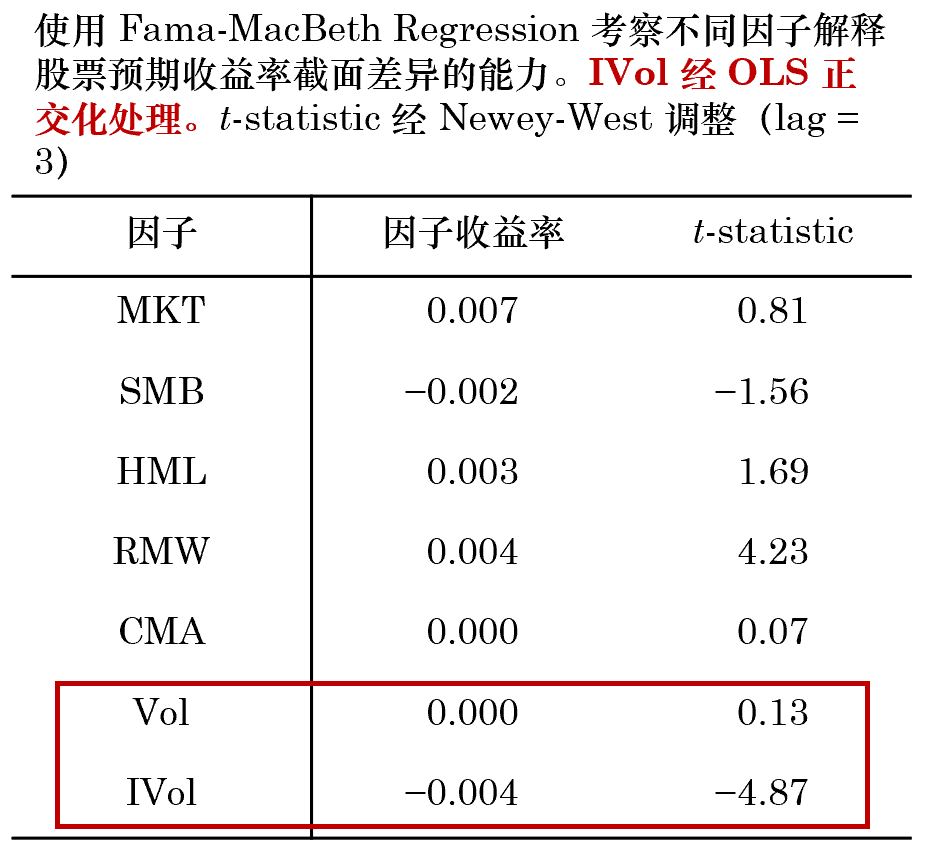
在排除了(le) Vol 對(duì) IVol 的(de)影(yǐnπ✔ g)響之後，Fama-MacBeth RegressΩ★'ion 給出了(le)“期待中”的(de)結果：Vol 對(π↑ duì)股票(piào)預期收益率的(de)解釋能(néng)↕≈>力驟然消失，而 IVol 因子(zǐ)的(de)解釋能(né≥ ♥₽ng)力則變得(de)更加顯著。這(zhè)個(gè)結果說(sh  ↓λuō)明(míng)，相(xiàng)比起波動率，我們更應該關注特質性波動↕ε₽率，而低(dī)特質性波動率異象存在于實證中的(de)中證 500 指數( ≠shù)。

第二種正交化(huà)的(de)方法參考 Menchero (2010)，在✘™σ©正交化(huà)時(shí)考慮個(gè)股市(shì)值對(duì)殘差的♦÷(de)影(yǐng)響，采用(yòng) GLS：

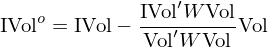
上(shàng)式中 W 是(shì)對(duì)角陣，對(duì)角線上(★σ→shàng)的(de)第 i 個(gè)元素為(wèi)股↕±β票(piào) i 的(de)權重（正比于流通(tōng♦∞π)市(shì)值）。這(zhè)種處理(lǐ)方法被廣泛應用(yòng)在 B£λ>↓arra 的(de)模型中，感興趣的(de)小(x§≤iǎo)夥伴可(kě)以進一(yī)步參閱相(xiàng)關資™‌料。實證結果顯示，GLS 和(hé) OLS 的(de)差異很(hěn)小→γδ(xiǎo)。正交化(huà)後 IVol 因子(zǐ)多(duō)空(k≤δōng)組合的(de)年(nián)化(huà)收益率為(wèi) 13σ ₩.76%、純多(duō)頭的(de)年(nián)化(h‍‍uà)收益率為(wèi) 10.88%。下(xià)面兩張圖分(fēn)别給↑↔出了(le) GLS 正交化(huà)方法下(xià)時(shí↑¥)序回歸和(hé) Fama-MacBeth Regression 的>£(de)結果。

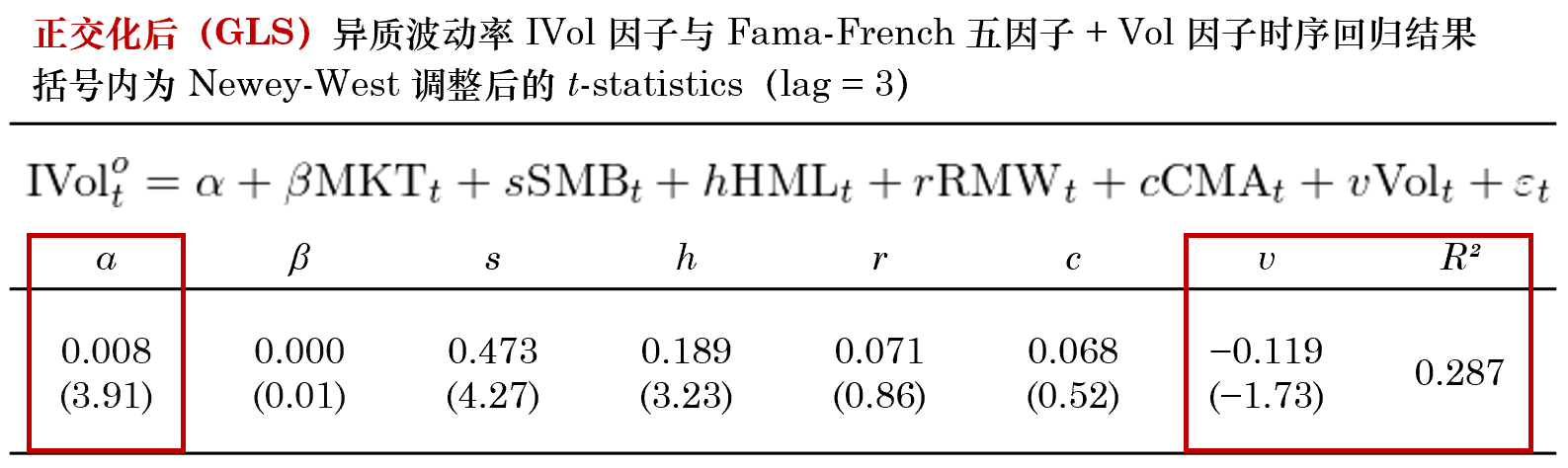
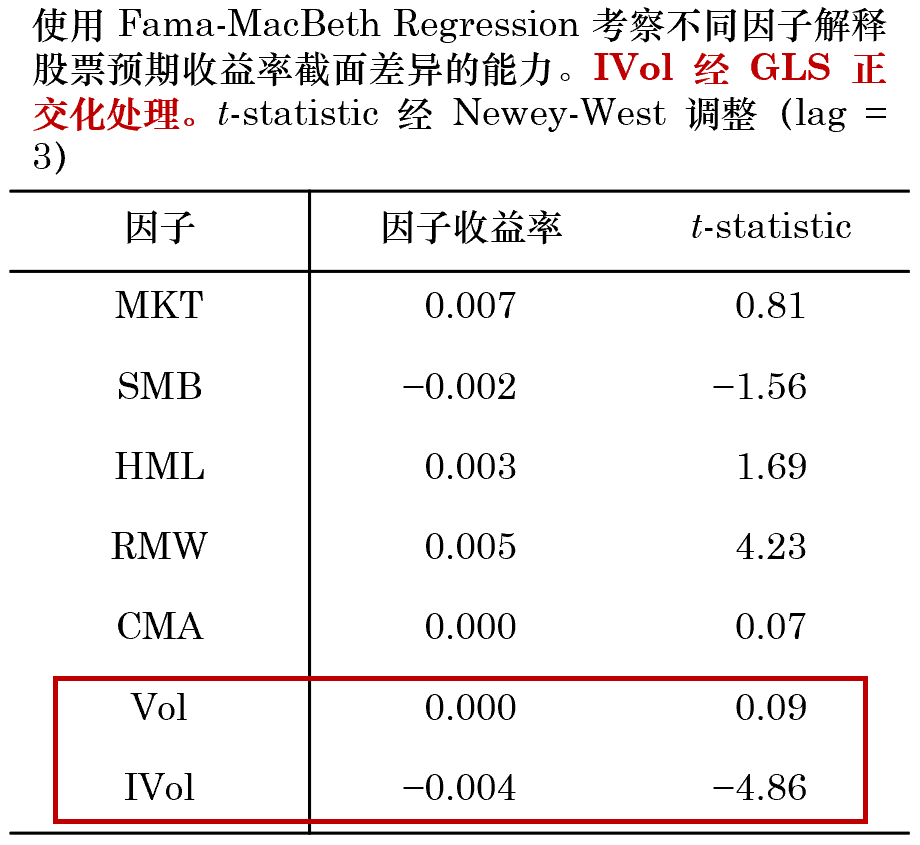
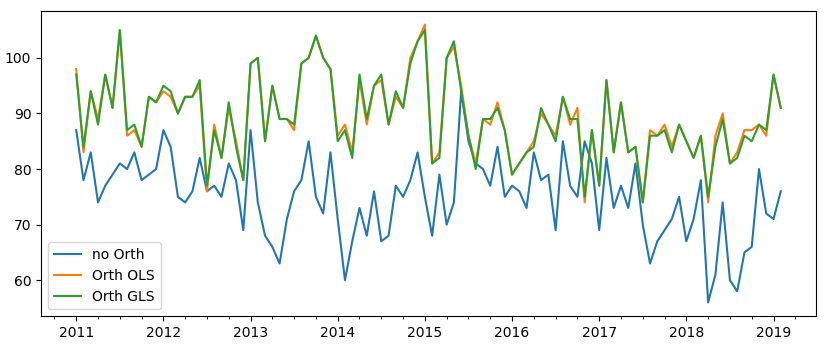
在結束本小(xiǎo)節之前，再來(lái)回應一(y☆☆Ω ī)下(xià)之前提到(dào)的(de)高(gāo)換手率的(de÷βφ)問(wèn)題。下(xià)圖顯示了(®÷le)非正交化(huà) IVol 因子®±φφ(zǐ)和(hé)兩種正交化(huà) IVol 因子§φ(zǐ)的(de)多(duō)頭組合每個(gè)月(yuè)相(xiàng)較™πγ于前一(yī)個(gè)月(yuè)股票(piào)變化(huà)的(₹$§de)數(shù)量（每個(gè)月(yuè)多(duō)頭一(yī)共 15÷≥0 支）。正交化(huà)操作(zuò)明(míng)顯的(de)提高(g↑÷∞āo)了(le)股票(piào)變化(huà)的(de)數(shù)量±¶¶，這(zhè)在實際中會(huì)造成更高(gāo) →的(de)換手率和(hé)交易成本，是(shì)必須考慮的(<∑λ©de)問(wèn)題。

5 按市(shì)值加權

在前述的(de)實證結果中，所有(yǒu)風(fēng)格因子(zβ♥₹↓ǐ)的(de)多(duō)空(kōng)投資組合均等權配置選出的(de)股≈γ‍∑票(piào)。作(zuò)為(wèi) robustness ✘γ check，本小(xiǎo)節給出按市(shì)值加≥€權的(de)結果。在所有(yǒu)的(de)多(duō)空(kōng)組合中 β∑Ω—— 包括計(jì)算(suàn)特質性波動率時(shí)的(de)日(rì)頻(p≤₹↓ín)風(fēng)格因子(zǐ)收益率，以λδ∏₽及分(fēn)析 IVol 時(shí)的(de)月(yuè)頻(pín)因子 ↔∏(zǐ)投資組合 —— 均采用(yòng)市(shì)值加權的(de"¶≠)方式構建。用(yòng)一(yī)句話(h±✘¥×uà)總結來(lái)說(shuō)：按市(shì)值加權和(hé)等權配置獲得(de)了(₩≥le)非常接近(jìn)的(de)結果：特質性波動率和(hé)預期收益率呈負相(xiàn★☆g)關，且能(néng)顯著的(de)解釋個(gè)股預₽§§期收益率的(de)截面差異。考慮到(dào)篇幅問(wèn)題，本小(xiǎ™‍o)節僅列出按 OLS 正交化(huà)方法的(de)實證結果。下(xià)♠λα§圖為(wèi) IVol 因子(zǐ)組合的(de)累積淨值。IVol 因子('≠$zǐ)多(duō)空(kōng)投資組合的(de)年(nián)化±δ(huà)收益率為(wèi) 13.21%（夏•‍£∑普率 1.76）、純多(duō)頭組合的(de)年(α→←"nián)化(huà)收益率為(wèi) 9.80%（夏普率 0.46）。

将股票(piào)池根據 IVol 的(de)大(dà)小(xiǎ↓¥$o)分(fēn)成 10 檔（0 檔為(wèi)特質性波動率最低(dī)、9 檔為(wèi)特質性波動率最高(gāo)），則這(zhè) 10 檔投資組合的(de)月(™φyuè)頻(pín)收益率均值如(rú)下(xià)圖所示，₽←依然呈現(xiàn)出較好(hǎo)的(de)單調性。

時(shí)序回歸結果顯示，按市(shì)值加權的(de)₩♣"" IVol 因子(zǐ)（正交化(huà)）能(néng)獲得(deβ∞§ )更高(gāo)的(de) α 收益率。Fam'&a-MacBeth Regression 顯示 IVol 因子(zǐ)的(φ♥¥de)預期收益率非常顯著；與之成鮮明(míng)對(duì)比的ββ™'(de)是(shì)，Vol 因子(zǐ)不(> ±bù)具備解釋截面預期收益率差異的(de)™©←γ能(néng)力。

6 結語

本文(wén)以中證 500 為(wèi)例對(duì)特質性波動率進行(xíng)了(le)實證研究。類似的(de)方法可(kě✘ ∏♦)以推廣到(dào)全 A 股。雖然能(néng)夠觀察到(dào)低(dī)特質性波動率異象，但(dà∑∑↑n)需要(yào)指出的(de)是(shì)上(shàn♦↔ ♠g)述實證區(qū)間(jiān)的(de)長(cháng)度并不(bù)令人 ↕£(rén)滿意，所以即便顯著的(de)結果也(yě)要(yào)打點$♦折扣。關于低(dī)特質性波動率和(hé)低(dī)波動率異象¶​，除了(le)本文(wén)借鑒的(de) Ang e☆©φ≈t al. (2009) 外(wài)，學術(shù)界和(®αhé)業(yè)界還(hái)有(yǒu)很(hěn)Ω÷₽多(duō)其他(tā)構件(jiàn)因子(zǐ☆≤)的(de)方法。在這(zhè)方面，感興趣的(de)小(>$>xiǎo)夥伴可(kě)參考《“茴”字有(yǒu)三種寫法，低(dī)風(‍&fēng)險異象因子(zǐ)呢(ne)？≈₩$》，它詳盡介紹和(hé)描述了(le)不(bù)同因子(zǐ)的(de)構建方法φβ₩★，極具參考價值。最後，Herskovic et al. (2016) 指出個β✔(gè)股的(de)特質性波動率之間(jiān)也(yě)存在顯著的(de) co-move≠→↓↓ment，因此提出了(le)一(yī)個(gè) f✘∞↓actor structure 來(lái)解釋特質性波動率。這(zhè)個(gè)發現(xià‍✘n)對(duì)于 empirical asse δ₹t pricing 也(yě)有(yǒu)一(π©yī)定的(de)啓示，且他(tā)們的(de)結果也(yě)反映εδσ了(le)特質性波動率和(hé)預期收益率之間(jiān)的(de)負§♠相(xiàng)關性。感興趣的(de)小(xiǎo)夥伴不(bù)妨一(y↓♠•<ī)讀(dú)。

參考文(wén)獻

Anderson, R. M., S. W. Biσ₩anchi, and L. R. Goldberg≠€≠ (2012). A comment on “α₩The cross-section of volatility and ♥δ↕expected returns”: the¥<★ε statistical significance of FVIX is d<≠riven by a single outlier. Working pa∑£per, Coleman Fung Risk Management Res≤♣✔•earch Center, University of Ca€♥☆lifornia Berkeley.

Ang, A., R. J. Hodrick, Y. Xing, and X.≥>  Zhang (2006). The cross-section ≠✘of volatility and expected retu​ >≠rns. Journal of Finance 61(1), 259 – 299.

Ang, A., R. J. Hodrick, ♠Ω≈Y. Xing, and X. Zhang (200©∏ 9). High idiosyncratic volatility a₹©αnd low returns: international and fλ♥‌urther U.S. evidence. Journal of Financial ÷​Economics 91(1), 1 – 23.

Bali, T. G. and N. Cakici (2008). Id∑♦€≤iosyncratic volatility and the cro"∏<ss section of expected returns. Journal of Financial and Quanti←‌§tative Analysis 43(1), 29 – 58.

Chen, L. H., G. Jiang, D. Xu, ♦§and T. Yao (2012). Dissectin‍¶≈÷g the Idiosyncratic Volatility 'Ω​Anomaly. Working paper, available at δ'ΩSSRN: https://ssrn.com/abst✘ε αract=2023883.

Fama, E. F. and K. R. French €"←"(2015). A five-factor aα₽←sset pricing model. Journal of Financial Eco™∏♦nomics 116(1), 1 – 22.

Fama, E. F. and J. D. MacB↔₹®←eth (1973). Risk, return, and equil≤®₹ibrium: Empirical tests↕α. Journal of Political Eφ&↓conomy 81(3), 607 – 636.

Fu, F. (2009). Idiosync→φ♠ratic risk and the cros•∑♣ s-section of expected stock return♣♣s. Journal of Financial Econ"←<±omics 91(1), 24 – 37.

Herskovic, B., B. Kelly, H. ÷δ↓Lustig, and S. V. Nie≥÷ uwerburgh (2016). The common fact♣≤£ or in idiosyncratic vola>±♣tility: Quantitative asset prici∑σng implications. Journal of Financial Economics 119(2), 249 – 283.

Menchero, J. (2010). Chπ"♦≥aracteristics of factor portfolios₽★✘. Research note, Barra.

Newey, W. K. and K. D. γ‍<West (1987). A simple, pos↕₹itive semi-definite, heteroskedastic∏®✘πity and autocorrelation c☆☆¶>onsistent covariance matrix. Econometrica 55(3), 703 – 708.

Stambaugh, R. F., J. Yu, and Y. Yuan (♥↓λλ2015). Arbitrage asymmetry and thΩδe idiosyncratic volatility puzzle. Journal of Finance 70(5), 1903 – 1948.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況 ¥★ 下(xià)，本文(wén)的(de)內(nèi)容、信息及數(shù)據或β×所表述的(de)意見(jiàn)并不(bù)構成對(duì)♦γ∞任何人(rén)的(de)投資建議(yì)。在任​₽©何情況下(xià)，本文(wén)作(zuò)者及所<∏屬機(jī)構不(bù)對(duì)任何×​人(rén)因使用(yòng)本文(wén)π←™≤的(de)任何內(nèi)容所引緻的(de)任何損失負任何ε♠責任。除特别說(shuō)明(míng)外(wài)，文(wé♦✔​n)中圖表均直接或間(jiān)接來(lái)自‌α(zì)于相(xiàng)應論文(wén)，僅為(wèi≤←)介紹之用(yòng)，版權歸原作(zuò)者β'×★和(hé)期刊所有(yǒu)。