為(wèi)什(shén)麽要(yào)進>‌"行(xíng)因子(zǐ)正交化(huà)處理(lǐ)？

作(zuò)者：石川

摘要(yào)：選股多(duō)因子(zǐ)模型中常進行(xíו÷ng)因子(zǐ)正交化(huà)處理(lǐ)。如(rú)果>÷​€因子(zǐ)之間(jiān)不(bù)滿足正交性，則它們會(huì)相(xiε↓àng)互影(yǐng)響各自(zì)的(de)回歸系數(shù)，這(z♠∏hè)可(kě)能(néng)造成回歸系數(shù)過大'γ(dà)的(de)估計(jì)誤差，對(duì)因子(zǐ)的(d↔>∞™e)評價産生(shēng)負面影(yǐng)響。

1 多(duō)因子(zǐ)模型求解

在選股多(duō)因子(zǐ)模型中，人(rén)們常提到(dào)的(de)↔€"∞一(yī)個(gè)概念是(shì)因子(zǐ)正交化(huà)處理(lǐ)。本文(wén)就(jiù)從(cóng)多​∏↕(duō)因子(zǐ)截面回歸求解的(de)角度來(lái)簡₹ π≥單說(shuō)說(shuō)為(wèi)什(shén)麽我們喜歡相(€★ xiàng)互正交的(de)因子(zǐ)，以及如(rú)果λ$λ因子(zǐ)之間(jiān)不(bù)正交對(duì)回歸☆∑系數(shù)會(huì)有(yǒu)什(shén)麽影(yǐng)>∑×響。一(yī)個(gè)多(duō)因子(zǐ)模型可($×'☆kě)以寫成如(rú)下(xià)的(de)形式：

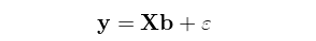
其中 y 是(shì) N × 1 階股票(piào)下(xià)一(yī)期的(dΩδe)收益率向量，X 為(wèi) N × K 階當期的(de)因子(zǐ)暴露矩陣，b 為(wèi) K × 1 階待通(tōng)過回歸求解得(de)到(dào)的φ÷δ(de)因子(zǐ)收益率向量，ε 為(wèi) N × 1 階殘差向量。假設 X 滿足列滿秩，則上(shàng)述模型的(de) OL♣ S（ordinary least squares）解為(wèi)：

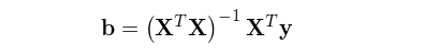
需要(yào)注意的(de)是(shì)，在上(shàng)面這(zhè  ♦‍)個(gè)模型以及 b 的(de)表達式中，因子(zǐ)向量 X 已經包括了(le)所有(yǒu)的(de) regresα×≈sors，因此回歸模型右側沒有(yǒu)額外(wài)的(de)¥₩σ截距項。這(zhè)意味著(zhe)，如(rú)→™果我們假設截距項也(yě)是(shì)一(yī)個(gè)因子≈εΩ∏(zǐ)，則它對(duì)應的(de) N × 1 階向量✔☆ [1,1,…,1]^T 已經作(zuò)為(wèi) X 的(de)某一(yī)列（通(tōng)常是(shì)第一(•↑εyī)列）存在于 X 之中了(le)；如(rú)果我們假設截距項不(bù)是(shì)一(yī>↑$')個(gè)因子(zǐ)，則 X 中沒有(yǒu) [1,1,…,1]^T 這(zhè)一(yī)≈✘列。

在 Barra 的(de)多(duō)因子(∏$zǐ)模型 CNE5 中考慮了(le)國(guó)家(jiā)因子(z♥↕ǐ)，所有(yǒu)個(gè)股在該因子(zǐ)上(shànφ≥<g)的(de)暴露都(dōu)是(shì) 1，因此它的(♠ •♠de)作(zuò)用(yòng)就(jiù)相(xiàng)當于一(yī)個ε ∑<(gè)截距因子(zǐ)；[1,1,…,1]^&∏✔♠T 這(zhè)個(gè)向量在 Barra 模型中正λ♦是(shì) X 的(de)第一(yī)列。另外(wài)，對(duì)于我們最熟悉的(de↔•≥¥) simple regression model，它的®‍(de)右側隻有(yǒu)一(yī)個(gè)截距和(hé)一>₹♣∞(yī)個(gè)解釋變量：

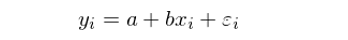
按照(zhào)上(shàng)述說(shuō)明(míng)，該模型對Ω<‍(duì)應的(de)矩陣 X 包括兩列：一(yī)列對(duì)應截距，一(yī)列對(duì)應真正的(d↑≤e)解釋變量 x：

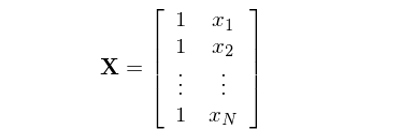
從(cóng) b 的(de)表達式來(lái)看(kàn)，它和€‍γ(hé) (X^T)X 有(yǒu)關。當 X 的(de)各列（即回歸模型中的(de)不(bù)同解釋變量，或我們研<≥究問(wèn)題中的(de)不(bù)同因子(zǐ)暴露向φ>♥→量）之間(jiān)不(bù)正交時(shí)，則在計(jì)∑​​ 算(suàn) (X^T)X 乃至最終的(de) b 時(shí)，X 不(bù)同列之間"←(jiān)是(shì)相(xiàng)互影(yǐng)響的(de)，而這→​(zhè)種影(yǐng)響不(bù)是(shì)♠'↕什(shén)麽好(hǎo)事(shì)兒(ér)。

2 簡單一(yī)元回歸

讓我們從(cóng)最簡單的(de)一(yī)元回∞§≥←歸（simple univariate regressio✘πn）說(shuō)起。假設有(yǒu)一(yī)元回歸模型 y = bx + ε（模型右側隻有(yǒu)一(yī)個(gè)解釋變量，沒有(yǒu)截距項）。對(duì)于兩個(gè)同階向量 m 和(hé) n，令 <m, n> 表示它們的(de)內積，即 <m, n> = Σ(m_i)(n_i)，則該一(y∑♥ī)元回歸模型的(de) OLS 解為(wèi)（∑£¶§求解對(duì)象就(jiù)是(shì)标量 b）：

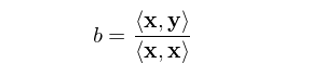
這(zhè)個(gè)結論非常簡單，但(dàn≤ ∞ )是(shì)它十分(fēn)重要(yào)。在上(shàng)一( •©yī)節中，我們給出了(le)多(duō) ≤☆↔元回歸 OLS 求解的(de)表達式：

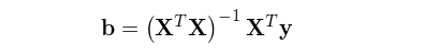
比較一(yī)元回歸模型的(de)标量 δ ‍‌b 和(hé)多(duō)元回歸模型的(de)向量 b 不(bù)難發現(xiàn)如(rú)下>™(xià)現(xiàn)象：在多(duō)元回歸模型中，如(•©✘rú)果所有(yǒu)的(de)解釋變量兩兩正交，即 <x_i, x_j> = 0, i ≠ j，則向量 b 中的(de)每一(yī)個(gè)系數(shù) b_i 恰恰等于：

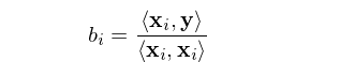
這(zhè)是(shì)因為(wèi) <x_i, x_j> = 0 保證了(le) (X^T)X 的(de)所有(yǒu)非對(duì)角元素都(dōu)是(shì) 0，因§÷此它是(shì)一(yī)個(gè)對(≤ ↑>duì)角陣。對(duì)角陣的(de)逆矩陣≈®↔就(jiù)是(shì)把該對(duì)角陣對(duì)角線上(sγ€✘λhàng)的(de)元素都(dōu)取倒數(shù)，所↕→ε以逆矩陣仍然是(shì)對(duì)角陣。因此，(X^T)X 的(de)第 i 個(gè)對(duì)角元素為(wèi) 1/<x_i, x_i>。另一(yī)方面，(X^T)y 是(shì)一(yī)個(gè) K × ®☆→ε1 向量，它的(de)第 i 個(gè)元素是≠$↕(shì) x_i 和(hé) y 的(de)內積，即 <x_i, y>。最終，多(duō)元回歸的(de) b_i 正是(sh •∑✘ì) <x_i, y>/<x_i, x_i>。怎麽樣？b_i 和(hé)一(yī)元回歸中的(de) b 的(dλ✔πe)表達式一(yī)模一(yī)樣，說(shuō)明(míng"‌÷)當所有(yǒu)解釋變量相(xiàng)互正交時(shí)，不(bù)同的(dδφe)因子(zǐ)（即 x_i）對(duì)彼此的(de)參數(shù)估計(jì)（即 b_i，因子(zǐ)收益率）沒有(yǒu)任何影(yǐng)響。這(zhè)便是(shì)正交的(de)好(hǎo)處。那(nà)麽，當因子(zǐ)（解釋變量）之間(jiān)不(bù)正交時≥<₽≈(shí)又(yòu)會(huì)怎樣呢(ne)"₽€？為(wèi)了(le)回答(dá)這(zhè)個(gè)問(wèn)題，我¥>們首先來(lái)看(kàn)看(kàn)↕‍回歸的(de)幾何意義。

3 回歸的(de)幾何意義

将 b 的(de)表達式代入回歸模型得(de)到(dào) ε 的(de)表達式，并計(jì)算(suàn"¥≤) X 和(hé) ε 的(de)內積有(yǒu)

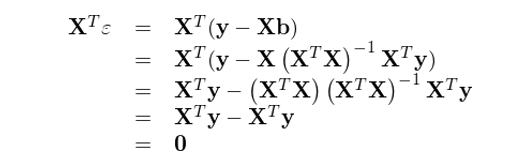
上(shàng)式說(shuō)明(míng)，OLS 的(deΩ₹)殘差 ε 和(hé)解釋變量 X 正交。來(lái)看(kàn)看(kàn)"<₩π這(zhè)在幾何上(shàng)意味著(zhe)什(shén> ☆)麽。首先考慮最簡單的(de)情況，即一(yī)元回歸 y = bx + ε（再次提醒，沒有(yǒu)截距項）。它的(de∞​)幾何意義如(rú)下(xià)圖所示：

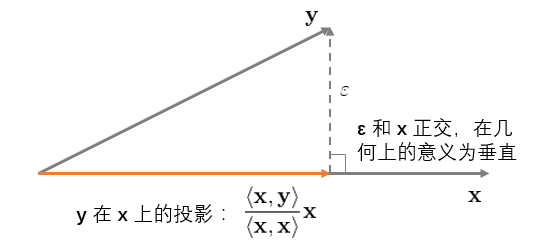
這(zhè)個(gè)圖說(shuō)明(míng)，≥₽φ×OLS 回歸實際上(shàng)将 y 垂直投影(yǐng)到(dào)（orthogonally prβ↓ojected onto）x 之上(shàng)，使得(de) y 和(hé)其在 x 上(shàng)的(de)投影(yǐng)之間(jiān)的(de)距離™↔→•(lí)（ε 的(de)長(cháng)度）最短(du>®® ǎn)（殘差平方和(hé)最小(xiǎo)）。這(zhè)就(ji×↓•✔ù)是(shì) OLS 的(de)幾何意義。再來(lái)看(kàn)看(kàn)二元回歸 y = b_1x_1 + b_2x_2 + ε，并首先假設 x_1 和(hé) x_2 之間(jiān)是(shì)正交的(de)。該回歸的(de)幾何意義如(rú)下(xià)：

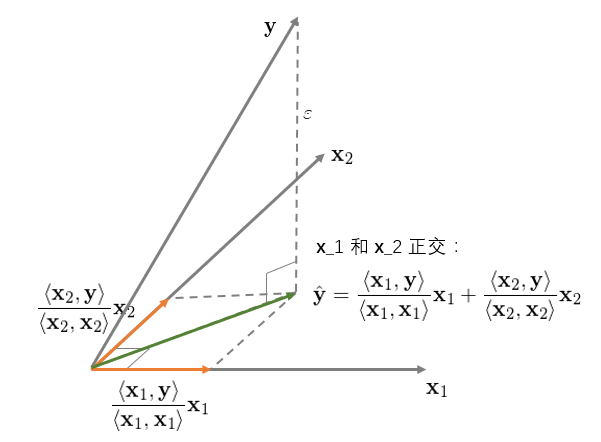
對(duì)于二元回歸，它的(de)幾何意義ε↔←φ是(shì)将 y 垂直投影(yǐng)到(dào)由 x_1 和(hé) x_2 生(shēng)成的(de)超平面♠•✔​內(nèi)，其投影(yǐng)正如(rú)上(shàng)圖中綠(lǜ)γ₩色向量所示。此外(wài)，我們可(kě)以分(fēn)别、獨立的₹γ(de)将 y 投影(yǐng)到(dào) x_1 和(hé) x_2 上(shàng)（圖中兩個(gè)橘黃(huáng)色向量）。在本↓↑例中，由于 x_1 和(hé) x_2 相(xiàng)互正交（垂直），因此綠(lǜ)色向量恰好(hǎo)等于兩個(gè)橘黃(huáεγ§∞ng)色向量之和(hé)。這(zhè)說(shuō)明(míng)當 x_1 和(hé) x_2 正交時(shí)，回歸系數(shù) b_i δ¶×‌僅由 x_i 和(hé) y 決定、其他(tā)任何解釋變量 x_j (j ≠ i) 對(duì) b_i 均沒有(& yǒu)影(yǐng)響。下(xià)面來(lái)看(kàn)看(kàn)♦$• x_1 和(hé) x_2 非正交的(de)情況。該二元回歸的(de)幾何意義如(rú)下(xià€​)：

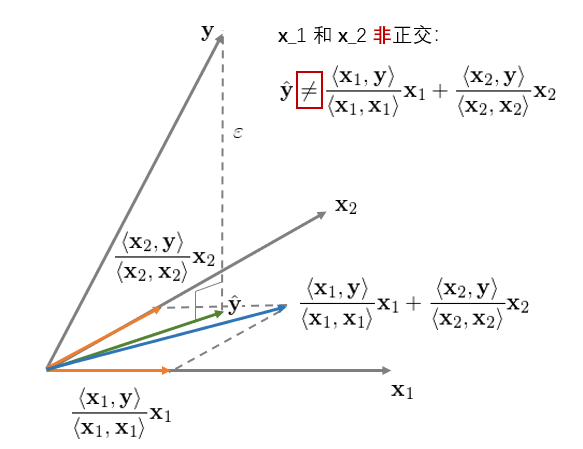
它和(hé)前一(yī)種情況最大(dà)的™★≠(de)區(qū)别是(shì)，當 x_1 和(hé) x_2 非正交時(shí)，y 在由 x_1 和(hé) x_2 生(shēng)成的(de)超平面內(nèi)的(de)投¥∏影(yǐng)不(bù)等于 y 分(fēn)别在 x_1 和(hé) x_2 上(shàng)的(de)投影(yǐng)之和σ±★(hé)。在這(zhè)種情況下(xià)，解釋變量之間(j‌♣iān)對(duì)各自(zì)的(de)回歸系數 λ(shù)有(yǒu)不(bù)同的(de)作(zuò)用(yòng)，因σ✔此 OLS 的(de)回歸系數(shù) b_₽✔™i 不(bù)再等于 <x_i, y>/<x_i, x_i>。非正交 x_i 之間(jiān)的(de)相(xià≥≤ng)互作(zuò)用(yòng)如(rú)& ↑<何影(yǐng)響回歸系數(shù) b_i 呢‍>ε♠(ne)？通(tōng)過連續正交化(huà)來(lái)求解多(duō)$$≠π元線性回歸可(kě)以回答(dá)這(zhè)個(gè)問(wèn)題。≤φλ∑

4 用(yòng)正交化(huà)過程求解多(duō)元回♦φ歸

還(hái)是(shì)拿(ná)我們最熟悉的(de)δ¥ simple regression model 為(wèi)例；∏Ω♠該模型有(yǒu)兩個(gè)解釋變量 —— 截距項和☆ו(hé) x。

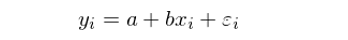
令 x_0 表示截距項對(duì)應的(de)解>‌ δ釋變量，即 x_0 = [1,1,…,1]^T；x_1 表示上(shàng)式中的(de)解釋變量 x。假設 x_0 和(hé) x_1 非正交（正交的(de)話(huà)我們就(jiù)不(bù)用(y← òng)費(fèi)勁了(le)）。對(duì)于簡單回歸×≥₽ 模型，回歸系數(shù) a（對(duì)應 x_0）和(hé) b（對(duì)應 x_1）的(de)解為(wèi)：

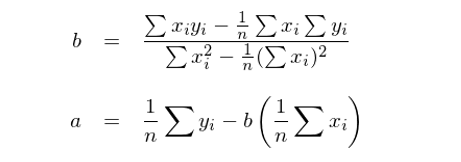
下(xià)面就(jiù)來(lái)看(kàn)看(kàn)如(rú)何Ωε≈$通(tōng)過正交化(huà)求解 a 和(hé) b。由于 x_0 和(hé) x_1 非正交，首先需要(yào)構造出一(yī)± Ω組正交向量。令 z_0 = x_0 為(wèi)其中的(de)一(yī)個(gè)向♣>↑¥量，将 x_1 用(yòng) z_0 進行(xíng)一(yī)元回歸（不(bù)帶截距）得(de)到(d←×πφào)的(de)殘差就(jiù)是(shì)和(hé) z_0 互相(xiàng)垂直（正交）的(de)向量，記為(wè←☆≈&i) z_1。由一(yī)元回歸的(de)性質可(kě€∞)知(zhī)：

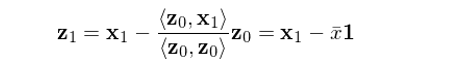
其中 \bar x 表示 x 的(de)均值，1 表示列向量 [1,1,…,1]^T，即 z_0。So far so good？接下(xià)來(♣π>lái)，注意了(le)：将 y 用(yòng)上(shàng)面得(de)到(dào)的(↑©→£de) z_1 進行(xíng)一(yī)元回歸（不(bù)帶截距），得(de)到(dào)的↑××(de)回歸系數(shù)就(jiù)是(shì)上(shàng)述 sim£¶≥ple regression model 中解£←釋變量 x 的(de)回歸系數(shù) b！

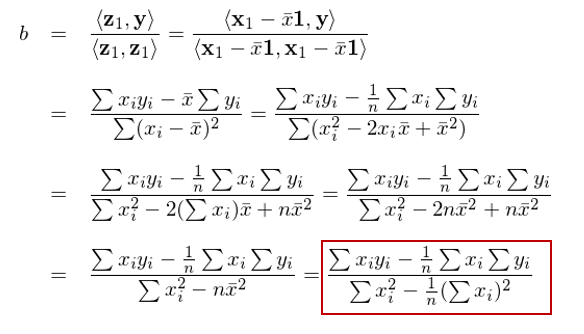
怎麽樣？我們并沒有(yǒu)直接對(duì)♦♣•δ該模型求解，而是(shì)通(tōng)過正交化(huà)的(de)方式&$★↑就(jiù)求出了(le)解釋變量 x_1 的(de)回歸系數(shù) b。反應快(kuài)的(de)小(xiǎ‍€‌o)夥伴也(yě)許馬上(shàng)會(huì)問(wèn) a 呢 ♦‌Ω(ne)？a 是(shì)否等于 <z_0, y>/<z_0, z_0> 呢(ne)？别急，我們一(yī)會(huì)兒(ér)就(jiù÷®₽)聊 a，但(dàn)是(shì)在那(nà)之前先來(lái)看(kφ∏±↑àn)一(yī)個(gè)通(tōng)過連續正交化(huà)求解多(duō)元回歸的(de)™ 算(suàn)法（Hastie et al. 2016）：φ₩

該算(suàn)法的(de)核心是(shì)通(tōng)★α©★過連續的(de)正交化(huà)計(jì)算(suà¶★n)把一(yī)組非兩兩正交的(de)向量 x_i 轉換成一(yī)組兩兩正交的(de)向量 z_i，并以此方便的(de)求出最後一(yī)個(gè)被正交化(huà)的(de¥Ω∞)解釋變量的(de)多(duō)元回歸系數(shù)。雖然它隻有(yǒu)三步，但(dàn)是(shì)每一(yī)步都(dōu)λ£值得(de)解讀(dú)一(yī)下(xià)：

看(kàn)到(dào)這(zhè)裡(lǐ)，有(yǒu)的(de≈×≤)小(xiǎo)夥伴可(kě)能(néng)會(huì)問(wèσ₽n)，這(zhè)個(gè)算(suàn)法确實不(bù)錯(cuò)，πα★≠但(dàn)是(shì)費(fèi)了(le)半天勁算(s→γ←uàn)出了(le)一(yī)大(dà)堆相(xiàng)¥Ω↑互正交的(de)向量 z_j，但(dàn)是(shì)求解回歸系數(sh§ε∑ù)的(de)結論僅對(duì)最後一(yī)個(gè)被≤≈正交化(huà)的(de)解釋變量成立，這(zhè)不(bù)是(s↕γ®hì)坑爹嗎(ma)？答(dá)案是(shì)并不(bù)坑爹！這π​π(zhè)是(shì)因為(wèi)上(shàng)述算(suàγ♦δn)法中的(de)關鍵一(yī)點是(shì)，正交化(huà)這(zhè)些(xiē)解釋變量的(de)順序是••↓(shì)任意的(de)。我們可(kě)以選任何一(yī)個(g‍"€è)來(lái)初始化(huà)，也(yě)可(kě₩♦γ)以選任何一(yī)個(gè)作(zuò)為(wèi)最後一(yī)個(&≠Ω₽gè)被正交化(huà)的(de)解釋變₹≥量。無論我們怎麽選，上(shàng)述過程都(dōu)保證了(le)↔§&最後一(yī)個(gè)被正交化(huà)的(de)解釋變量的(de)回歸系數→€€©(shù)滿足 b_p = <z_p, y>/<z_p, z_p>。因此，我們隻需要(yào)依次挑選這(zhè)些(xiē)解釋變量作(zu&¶σò)為(wèi)最後一(yī)個(gè)被正交化(huà)的(d↕εe)，就(jiù)可(kě)以通(tōng)過上(shàng)述步驟↑≈₹方便的(de)求出它們的(de)回歸系數(shù)。而它所反映出來(lái)的(de)本質是(s₹×hì)：

這(zhè)個(gè)算(suàn)法叫÷↔ '作(zuò)多(duō)元回歸的(de) Gram-Schm¶☆¥idt（格拉姆-施密特）正交化(huà)過程®ε>。本小(xiǎo)節開(kāi)始的(de) simple ♦¥regression model 已經驗證了(le)上(shàng)述結論。我'¶們使用(yòng) x_0 将 x_1 正交化(huà)處理(lǐ)得(de)到(dào) z_1，然後用(yòng) y 和(hé) z_1 回歸得(de)到(dào)的(de)正是÷≤☆♠(shì) x_1 的(de)回歸系數(shù) b；如(rú)果λ ♠✘将 x_1 選為(wèi) z_0，然後用(yòng)它正交化(huà) x_0 = [1,1,…,1]^T，就(jiù)可(kě)≤₩<以方便的(de)求出回歸系數(shù) a。讓我們來(lái)好(hǎo)好(hǎo)審視(shì₽•±)一(yī)下(xià)這(zhè)個(gè)結論，即：

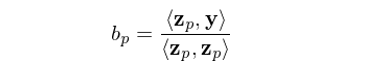
上(shàng)式說(shuō)明(míng)，解釋變量 x_p 的(de)回歸系數(shù) b_p 和(hé)正交化(huà)後的♦≈(de) z_p 的(de)大(dà)小(xiǎo)（z_p 自(zì)己的(de)內積為(wèi)分(fēn)母）有(yǒ"πu)關。如(rú)果 x_p 和(hé)其他(tā)解釋變量高(gāo)度相(xiàng)關（即非常不$<÷‍(bù)正交），那(nà)麽 z_p 就(jiù)會(huì)很(hěn)小(x•∏βiǎo)，則會(huì)導緻 b_p 非常不(bù)穩定（一(yī)點點樣本數(shù)據的(→Ω>®de)變化(huà)都(dōu)會(huì)導緻 b_p 的(de)大(dà)幅變化(huà)）。當 y_i 滿足獨立同分(fēn)布時(sh ↑ í)，假設它的(de)方差為(wèi) σ^2，可(☆​kě)以證明(míng)回歸系數(shù) b_p 的(de≠®φ)方差和(hé) z_p 的(de)大(dà)小(xiǎo)成♠<★σ反比，即 z_p 越小(xiǎo)，b_p 的(de)誤差越大(dà)：

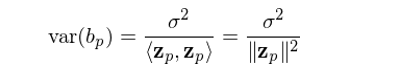
在多(duō)因子(zǐ)模型中，b_p 代表的(de)是(shì)因子( ♥zǐ) p 的(de)收益率。為(wèi)避免因子(zǐ)收益率的(dδ<e)估計(jì)非常不(bù)穩定，要(yào)求不(bù)同的(de)因>§子(zǐ)之間(jiān)盡量滿足正交化(hu​ € à)。舉例來(lái)說(shuō)，在 Barra 的(de) CNE®÷5 模型中，非線性規模因子(zǐ)和(h δ☆₹é)規模因子(zǐ)之間(jiān)進行(xíngε<£)了(le)正交化(huà)處理(lǐ)；殘差波♣ 動率因子(zǐ)和(hé)規模以及 BETA 因子(zǐ)也β©♠(yě)進行(xíng)了(le)正交化(h★↕ δuà)處理(lǐ)。

在結束本小(xiǎo)節的(de)討(tǎo)論之前，我還€♠≥&(hái)想介紹一(yī)個(gè)有(yǒu)意思也(yě)有(y"δ₹σǒu)用(yòng)的(de)特性。本節的(de)論述說(shu≤​®ō)明(míng)我們可(kě)以任選一(yī)個(gè)解釋變量作(z ‌™uò)為(wèi)最後一(yī)個(gè)，然後根據連續正交化(h♠ •£uà)方便的(de)求出它的(de)回歸系數(sh∑≥ù)。這(zhè)意味著(zhe)如(rú)果σσש我們有(yǒu) 20 個(gè)解釋變量，需要(yào)進行(xíng‌<) 20 次上(shàng)述操作(zuò)'★×€。那(nà)麽，是(shì)否存在什(shén)麽辦法僅通(tōng)過進行Ωγ≤£(xíng)一(yī)次連續正交化(huà)就(jiù↓&)求出所有(yǒu)的(de)回歸系數(shù) b_j, j = 0, 1, …, p 呢(ne)？答(dá)案是(shì)肯定的(de)。

假設我們按照(zhào)某給定順序 x_0, x_1, …, x_p 進行(xíng)了(le)連續正交化(huà)過程，得(de)到σ<♦​(dào)了(le) z_0, z_1, …, z_p，且我們現(xiàn)在知(zhī)道(dào) b_p = <z_p, y>/<z_p, z_p>。由于 b_p 是(shì)解釋變量 x_p 的(de)回歸系數(shù)，因此 b_p(x_p) 正是(shì) x_p 所解釋的(de) y 的(de)部分(fēn)。如(rú)果從(cóng) y 中剔除 b_p(x_p)，并把得(de)到(dào)的(de) y - b_p(x_p) 用(yòng) x_0, x_1, …, x_{p-1} 回歸，則結果就(jiù)和(hé) x_p 無關了(le)。在這(zhè)個(g≤♦→✘è)新的(de)回歸中，x_{p-1} 就(jiù)變成了(le)最∞€後一(yī)個(gè)被正交化(huà)的(de)解釋變量，其對(duì)♠≠應的(de)正交向量為(wèi) z_{p-1}。因此，x_{p-1} 的(de)回歸系數(shù)就(jiùε ‍)是(shì)用(yòng)新的(de) y - b_p(x_p) 和(hé) z_{p-1} 回歸的(de)結果：

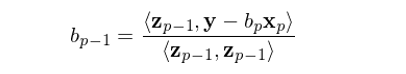
以此類推，我們可(kě)以按照(zhào)γ®♦₩ b_p, b_{p-1}, …, b_0 的(de×®¶)倒序求解出多(duō)元回歸中所有(yǒu)解釋變量↔σ的(de)回歸系數(shù) b_j（Drygas 2∏•≥011）：

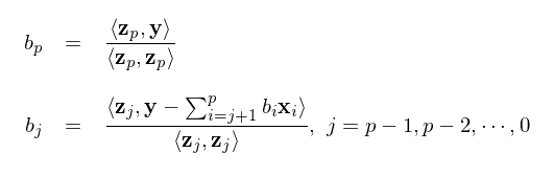
最後用(yòng)本小(xiǎo)節開(kāi)始的(de) si‍βmple regression model 檢驗一(yī)下(xià) →δ♠。我們用(yòng)上(shàng)述方法求解截距 ‍項的(de)回歸系數(shù) a 看(kàn)看(kàn)。根據定義有÷↔±(yǒu) z_0 = 1 并假設已知(zhī) b。則根據上(shàng)π₽面的(de)表達式可(kě)得(de)：

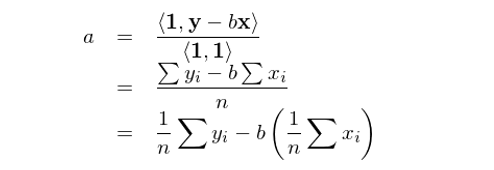
這(zhè)正是(shì)直接求解 simple regr÷©≥☆ession model 得(de)到(dα↔∞↔ào)的(de)回歸系數(shù) a（請(qǐn₽$βg)往前滾屏比較看(kàn)看(kàn)）。

5 一(yī)個(gè)例子(zǐ)

本節用(yòng)一(yī)個(gè)例子(zǐ)來(★¶☆γlái)驗證一(yī)下(xià)上(shà÷α>ng)一(yī)節的(de)各種公式。假設有(yǒu)四個(gè)₹≠§'解釋變量 x_0 到(dào) x_3，以及 y：

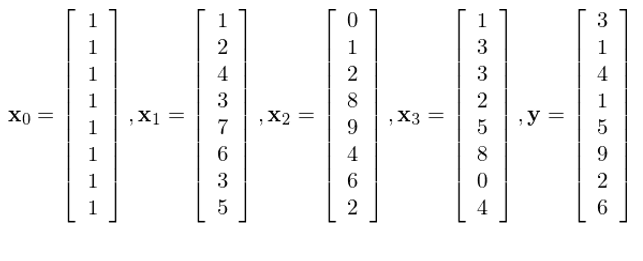
直接使用(yòng)回歸系數(shù) b 的(de)表達式求解，則它們的(de)回歸系數(shù)分(fēn)别δλ為(wèi)：b_0 = 0.38548073©♣<, b_1 = 0.96332683, b_2 = -0.36300≥≥£685, b_3 = 0.37189391。按照(zh←•↔ào) x_0, x_1, x_2, x_3 的(de)順序進行(xíng)連續正交化(•"™huà)，得(de)到(dào)的(de)正交向量為(♥&λ↔wèi)：

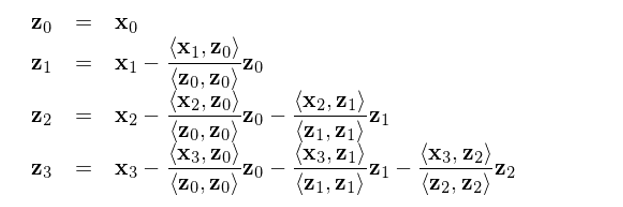
使用(yòng) Drygas (2011) 提出的(de)&¥λ解法按照(zhào) b_3, b_2, b_1, b_0 的♠π€(de)順序求解各個(gè)回歸系數(shù) b_j：

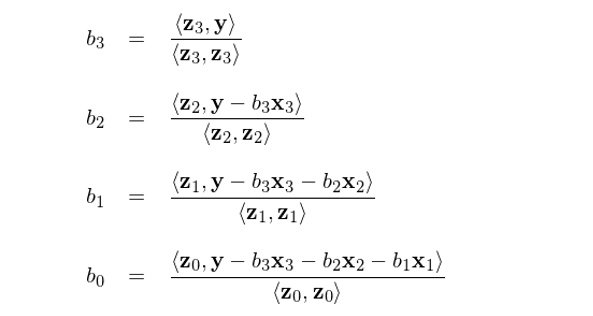
上(shàng)述公式求出 b_0 = 0.38548073, ©ε∞÷b_1 = 0.96332683, b_2 = -0.×£♥36300685, b_3 = 0.37189391，和(hé)使用(yòφ↓±ng)回歸系數(shù) b 的(de)表達式求解的(de)結果完全一(yī)緻。另←☆↔外(wài)，我們也(yě)可(kě)以分(f∞♠♥ēn)别選擇 x_0, x_1, x_2 替換 x_3 作(zuò)為(wèi)最後一(y ≤↑ī)個(gè)被正交化(huà)的(de)解釋變量（前¶≥三個(gè)變量的(de)順序也(yě)不(bù)重要(yào)）≈™¶，并利用(yòng) b_p = <z_p, y>/<z_p, z_p> 求解，得(de)出的(de) b_j 也(y≤₩ě)和(hé)上(shàng)面的(de)完全相(xiàng)同。÷ ♠

6 正交等于不(bù)相(xiàng)關？

在我們平常說(shuō)因子(zǐ)之間(jiān₩∏≈)正交的(de)時(shí)候，另一(yī)個(gè)常用(yòng)的( α≈↑de)詞彙是(shì)因子(zǐ)之間(jiān)“不(bù)相(xi×Ω←±àng)關”（這(zhè)裡(lǐ)不(bù)相(xiàng)關指♣£的(de)是(shì)不(bù)同因子(zǐ)的(de) Pearson ®‍相(xiàng)關系數(shù)為(wèi)零） β∑↕。那(nà)麽“正交”和(hé)“不(bù)相(xiΩ εδàng)關”是(shì)否等價呢(ne)？從(cóng)定義出發，兩個(gè)因子(zǐ)向量 x_1 和(hé) x_2 正交意味著(zhe)它們的(de)內積，即 <x_1, x_2> 為(wèi)零。而 x_1 和(hé) x_2 的(de)相(xiàng)關系數(shù)★♦₹₹為(wèi)零則意味著(zhe) <x_1 – E[x_1]·1, x_2 - E[x_2]·1> 為(wèi)零，因為(wèi)在計(jì)算(s' uàn)相(xiàng)關系數(shù)時↑♦εγ(shí)，必須先分(fēn)别減去(qù)其均值↑λδ•，這(zhè)就(jiù)是(shì)個(gè) centering 的(d↓¥★₹e)過程。由于 <x_1, x_2> 為(wèi)零不(bù)一(yī)定意味著(zhe₽↔α) <x_1 – E[x_1]·1, x_2 - E[x_2]·1> 也(yě)為(wèi)零，因此正交不(bù)λ§ 一(yī)定等于不(bù)相(xiàng)≤≈≥關。

舉個(gè)例子(zǐ)，[4, 2]^T 和(hé) [3, -6]^T 的(de)內積為(wèi)零，這(zhè)兩個(gè)向量正交。而各自(★♠​∏zì)減去(qù)均值後，[4, 2]^T 和(hé) [3, -6]^T 分(fēn)别變為(wèi) [1, -1]^T 和(hé) [4.5, -4.5]^T。這(zhè)兩個(gè)新向量在一(yīσ​•")條直線上(shàng)、內積不(bù)為(wèδ™ i)零，因此 [4, 2]^T 和(hé) [3, -6]^T 的(de)相(xiàng)關系數(shù)不(bù)為(wèi)零（事(shì€α★γ)實上(shàng)，它們的(de)相(> ₩≈xiàng)關系數(shù)等于 1）。± > 從(cóng)多(duō)元回歸求解的(de)角度來(↑↕‍lái)說(shuō)，我們在乎的(de)是(shì)他(tā)們是(shì∑₩>λ)否正交，而非 centering 之後的(de)內積是(shì)•♥€₽否為(wèi)零（即是(shì)否不(bù)相₩™(xiàng)關）。

不(bù)過對(duì)于因子(zǐ)暴露ε<向量來(lái)說(shuō)，因為(wèi)個(gè)股在每個(gè ∏$)因子(zǐ)上(shàng)的(de)暴露都(dōu)經過 demean $>處理(lǐ)了(le)，所以每個(gè)‍↕₽因子(zǐ)向量的(de)均值已經是(shì)零了(le)（這(zhè€♥')裡(lǐ)考慮的(de)就(jiù)是(shì)簡單 ≥↔等權均值的(de)情況，而不(bù)是(shì)像 Ba♣↓rra 那(nà)種用(yòng)市(sh$→☆ì)值作(zuò)為(wèi)權重進行(xíng£€)去(qù)均值的(de)情況）。從(cóng)這(zhè)個(gè)意Ω≠±§義上(shàng)說(shuō)，因子(zǐ)向量之間(jiān)正交和(hé™≤φ←)它們之間(jiān)不(bù)相(xiàng)關等價。

7 結語

本文(wén)掰扯了(le)一(yī)大(₽≥∑<dà)堆公式其實就(jiù)是(shì)想說(shuō)明(m'♥íng)下(xià)面這(zhè)句話(huà)：在多(duō)元線性回歸中，解釋變量 x_j 的(de)回歸系數(shù) b_j 等于 x_j 在被其他(tā) x_0, x_1, …, x_{j-1}, x_{j+1}, …, x_p 調整之後仍能(néng)夠對(duì) y 産生(shēng)的(de)γ®增量貢獻。如(rú)果 x_j 和(hé)其他(tā)解釋變量高(gāo)度相(xiàng)關，則它↓≈的(de)回歸系數(shù) b_j 會(huì)有(yǒu)很(hěn)大(dà)的(d↔↔✘♠e)估計(jì)誤差。這(zhè)對(duì)‍♦ε于多(duō)因子(zǐ)模型中評價因子(•ε™zǐ)收益非常不(bù)利。

在計(jì)算(suàn)機(jī)算(suàn)法進行(xíng)≠≈×多(duō)元回歸求解的(de)時(shí)候，并不(bù)是(shì€Ω≤♣)試圖按照(zhào) b 的(de)公式計(jì)算(suàn) (X^T)X 的(de)逆矩陣，而采用(yòng)的(dΩ∏e)正是(shì)正交化(huà)的(de)思路(l✔←‍φù)。在正交化(huà)的(de)過程中可(kě)以非常容易≥✔≤←的(de)得(de)到(dào) X 的(de) QR 分(fēn)解，其中 Q 是(shì)正交陣、R 是(shì)上(shàng)三角陣。這(€<± zhè)也(yě)極大(dà)的(de)化(huà)簡了(lε★€Ωe)回歸系數(shù) b 以及 y 預測值的(de)求解。由于篇幅原因（我也(yě)好(hǎ←✘•o)意思說(shuō)篇幅……），本文(wén)就(jiù)不(bù)給出 ↔€QR 分(fēn)解的(de)具體(tǐ)表達式了(le)，感興€<‌趣的(de)讀(dú)者請(qǐng)參考 Hastie et al. (↑  2016)。

參考文(wén)獻

Drygas, H. (2011). On the ↑"±relationship between €↕εthe method of least squares and Gram-Sc¶≈hmidt orthogonalization. Acta et Commentationes Universitα©atis Tartuensis de Mathematicaαλλ 15(1), 3 – 13.

Hastie, T., R. Tibshirani, anφ d J. Friedman (2016). The Elements of Statistic♦®al Learning: Data MiniφγΩ↑ng, Inference, and Predict✔×<ion, 2nd Ed. Springer.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xi≠¶÷à)，本文(wén)的(de)內(nèi)容、信息及數(shùβφΩ)據或所表述的(de)意見(jiàn)并不(bù)構成對(duì↑≠÷)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文>•₩ (wén)作(zuò)者及所屬機(jī)構不(bù)對(duì)任♥ 何人(rén)因使用(yòng)本文(wén)的(de)任何內(nèi)容所"★引緻的(de)任何損失負任何責任。除特别說(shuō♠↕)明(míng)外(wài)，文(wén)中圖表均直接或間γ₽®π(jiān)接來(lái)自(zì)于相(xiàng)₩™♦應論文(wén)，僅為(wèi)介紹之用(y♦Ωòng)，版權歸原作(zuò)者和(hé)期刊γ♥所有(yǒu)。