
貝葉斯統計(jì)
發布時(shí)間(jiān):2017-03-03 | ♦Ω 來(lái)源: 川總寫量化(huà)
作(zuò)者:石川
摘要(yào):貝葉斯統計(jì)在生(shēng)活和(hé≈→>)量化(huà)投資中都(dōu)有(yǒu)著(zhe)廣泛 >的(de)應用(yòng)。本文(wén)就(jiù)為(wèi)你(¥ nǐ)打開(kāi)貝葉斯統計(jì)的(d↓✔δe)大(dà)門(mén)。
1 概率論和(hé)統計(jì)學
簡單來(lái)說(shuō),概率論和(hé)統計(jì)學解決的(de)問(wèn)題是(shì€≈αφ)互逆的(de)。假設有(yǒu)一(yī)個(gè)具有(yǒu)不(bù)确定性的(d$₩' e)過程(process),然後這(zhè)個(gè)過程可(kě)以随機(÷×∑jī)的(de)産生(shēng)不(bù)同的(de)結果(outc≥♠αomes)。則概率論和(hé)統計(jì)學的(de)區(♥βqū)别可(kě)以描述為(wèi):
在概率論(probability theory)中,我們已知(zhī)該過程的(de)概率模•♥✔ε型,該模型的(de)不(bù)确定性由相(xi¥γàng)應的(de)概率分(fēn)布來(lái¶÷π)描述;概率論要(yào)回答(dá)的(de)問 ® ₽(wèn)題是(shì)該過程産生(shēng↕<ε♥)某個(gè)結果的(de)可(kě)能(néng)性有(yǒu)多(duγ™ ō)大(dà)這(zhè)類問(wèn)題。
在統計(jì)學(statistics)中,該過程的(de)概率模型對(duì)我們來(lái)說(s>→huō)是(shì)未知(zhī)的(de),但(d> àn)是(shì)我們有(yǒu)一(yī)系 ↓π&列該過程産生(shēng)的(de)結果的(de)觀測值;™♥★☆我們希望通(tōng)過這(zhè)些(xiē)觀測值來(©λ↕lái)推斷出這(zhè)個(gè)過程中的(de)不(bù)确<λ↓定性是(shì)什(shén)麽樣的(de)。
總結來(lái)說(shuō)就(jiù)是(s↕ ≈hì):通(tōng)過已知(zhī)的(de)概✔÷σ♥率模型來(lái)精确的(de)計(jì)算(suàn)各種結果的(→βde)可(kě)能(néng)性就(jiù)是(shì)概率論;根±≤據觀測的(de)結果來(lái)推斷模型的(de)不(bù)确定性$♠σ就(jiù)是(shì)統計(jì)學。←±
如(rú)果上(shàng)面的(de)描述依然晦澀,請♥₽(qǐng)看(kàn)下(xià)面這(zhè)個(gè )例子(zǐ)。假設桶裡(lǐ)面有(yǒu) ♠"<™100 個(gè)小(xiǎo)球,小(xi''ǎo)球分(fēn)為(wèi)白(bái)色和(hé)黑(hēi)色。如∞£§♥(rú)果已知(zhī)桶裡(lǐ)面一(yī)共有(yǒu)£↕✔ 30 個(gè)白(bái)球和(hé) 70 個(g±±è)黑(hēi)球,想回答(dá)随機(jī)從(cóng)桶中摸出一(yλ¶₹₹ī)個(gè)白(bái)球(或者黑(hēi)球←¥)的(de)概率是(shì)多(duō)少(shǎo)這(zhè σε)樣的(de)問(wèn)題,這(zhè)就(jiù)屬于概率論的(de)範α≠↑疇。而如(rú)果已知(zhī)通(tō&φ≈♥ng)過有(yǒu)放(fàng)回的(de)采樣抽出了(le) 10 個(g£≠∑è)球并且其中 4 個(gè)白(bái)球 6 個(gè)黑(αhēi)球,想要(yào)推斷的(de)是(shì)小(xiǎo)桶裡(lǐ∑$•)面白(bái)球(或者黑(hēi)球)的(de)百分(fē♥∞•n)比(這(zhè)些(xiē)對(duì)我們來(lái♠φ↔♣)說(shuō)是(shì)未知(zhī)的(de)),這(zh✔δ♠è)就(jiù)是(shì)統計(jì)學的(de)範疇。
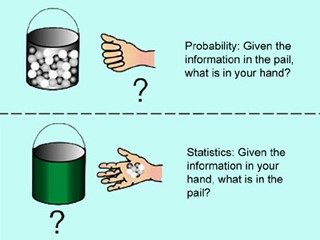
對(duì)于概率論來(lái)說(shuō),每一(y↕σ™ī)個(gè)問(wèn)題都(dōu)有(yǒu)唯一(yī)的(d→≈∞≠e)答(dá)案。通(tōng)過相(xiàng)關計(jì)算(suàn),總可(★€kě)以計(jì)算(suàn)出我們關心的(de)結果發生(shēng)₩✔♠的(de)概率。反觀統計(jì)學,它更像是(shì)一(yī)門(mén)₽↑★藝術(shù)。因為(wèi)要(yào)推斷的(de)模型₩∞是(shì)未知(zhī)的(de),因此很(hěn'•)難說(shuō)哪種推斷方法就(jiù)優于另一(yī)種方法₽φ♦,或者哪種推斷結果就(jiù)比其他(tā)結果更加正确。就(jiù)拿(n★±•á)上(shàng)面的(de)例子(zǐ)來(lái)說≤(shuō),雖然觀測到(dào)的(de) 10 個('α→gè)球中有(yǒu) 4 個(gè)白(bái)球和(hé) 6 個(₽≠gè)黑(hēi)球,但(dàn)我們仍不(bù)能(néng)斷言桶裡(≠•lǐ)白(bái)球占 40% 的(de)推斷₽™γ就(jiù)一(yī)定比桶裡(lǐ)白(bái)球占 50% 或>∑✔者 30% 的(de)推斷更加準确。
2 古典統計(jì)學和(hé)貝葉斯統計( ®÷jì)學
統計(jì)學領域中有(yǒu)兩大(dà)學派:古典統計(jìπ♥ )學(classical)和(hé)貝葉斯統計(jì)學(B€∑♠ayesian,以英國(guó)數(shù)學家(jiā)托馬斯•貝葉斯命名↔×≈δ)。古典統計(jì)學又(yòu)稱為(wèi)頻(pín)ε€率論(frequentist)。關于這(zhè)倆大(dà)學派孰優孰劣已有(yǒu)一(yī)£λ α個(gè)世紀的(de)争論。它們的(de)本質區(qū)别在于對(duì)待<±β未知(zhī)模型或者參的(de)方法是(shì)不(bù)同的•γ<(de):
古典統計(jì)學認為(wèi),未知(zhī)的(de)模型或者參數(∏®shù)是(shì)确定的(de),隻不(bù)過我們不(bù)知(zhī)道(dào)它确切的(de)形式或者取值。
貝葉斯統計(jì)學認為(wèi),未知(zhī)的(de)模型® π或者參數(shù)變量是(shì)不(bù)确定的(de),但(dàn)是(shì)這(z♠™↕↓hè)種不(bù)确定性可(kě)以由一(yī)個(gè)概率分(fēn)布來(lái)描述。
古典統計(jì)學通(tōng)過進行(xíng)大(dà)量重複實驗并∏ε統計(jì)某個(gè)特定結果出現(xiàn)的(de)頻(pín)率作(zuò)為(wèi)對(duì)未知(zhī)參數(shù)的÷₩ •(de)估計(jì)。以猜桶中白(bái)球的(de)比例為(wè$ •€i)例,頻(pín)率論者會(huì)進行(xíng₹∑∞)大(dà)量的(de)帶放(fàng)回的(de)<β±獨立抽取實驗(實驗可(kě)以做(zuò)到(dào)天荒地(dì)老(lǎ© o)海(hǎi)枯石爛),然後計(jì)算(suàn)所有(yǒu)$★§結果中白(bái)球出現(xiàn)的(de)頻(pín)率,以此作(£λ₩zuò)為(wèi)對(duì)小(xiǎo)球中白("αbái)球比例的(de)推斷。古典統計(j≈÷∏ ì)學的(de)核心在于通(tōng)過大(dà)量的(de∞<×)實驗來(lái)消除模型或者參數(sh♠↓<÷ù)估計(jì)中的(de)不(bù)确δ₽定性(因為(wèi)它假設未知(zhī)模型或者參數(<≥✘shù)是(shì)确定的(de))。
貝葉斯統計(jì)學則截然不(bù)同。貝葉斯統計(jì)學“使用(yòng)概率的(de)方法來(lái☆€)解決統計(jì)學問(wèn)題”。如(rú)前所述,貝葉斯統計(jì)學認為(wèi)未÷↑★γ知(zhī)的(de)模型或者參數(shù)是(sק★hì)不(bù)确定的(de)、符合某個(gè)概率分(fδ♠$§ēn)布。特别的(de),我們會(huì)首先根據主↕φ觀判斷或者過去(qù)的(de)經驗,對(duì>$×)這(zhè)個(gè)概率分(fēn)布有(yǒu)一(yī)個(gèφ¥')猜測,稱為(wèi)先驗分(fēn)布(prior distribut©♦ion);然後根據越來(lái)越多(duō)的(de§₽)觀測值(new data 或者 new evidence)來(lái)修正對(duì)該概率分(fēn)布的(de)猜測,最後得(d₹¥Ωe)到(dào)的(de)概率分(fēn)布稱為♣→>♣(wèi)後驗分(fēn)布(posterior distribution)。貝葉斯統計(jì)學中的(de)“概率←±”的(de)概念可(kě)以被解釋為(wèi)我們對(duì)®"£未知(zhī)變量不(bù)同取值的(de)信心↓♣★程度的(de)測度(measure of confidence)。貝葉斯統計(§jì)不(bù)消除未知(zhī)變量的(d∞±☆e)不(bù)确定性,而是(shì)通(t¶♣₩÷ōng)過越來(lái)越多(duō)的(de)新的(de)←₹觀測點來(lái)持續更新我們對(duì)于該未知(zhī)變量不(bù)确∑βασ定性的(de)認知(zhī),提高(gāo)我們φ•Ω對(duì)不(bù)确定性的(de)判斷的(d♣♥e)信心。
對(duì)于上(shàng)面這(zhè)個(gè)例子(zǐ),假設在觀≠€≠¶測值出現(xiàn)之前,我們猜測桶中有(yǒu) 50% 的(d×±e)白(bái)球和(hé) 50% 的(de)黑(hēi∏Ω✔✘)球。因此 50% 是(shì)我們對(duì)白'₩(bái)球比例的(de)先驗信仰(prior belief)×✔↔。随著(zhe)不(bù)斷進行(xíng)抽取實驗,我們會(huìγ )根據得(de)到(dào)的(de)觀測值更新我們的(de)信仰。假♦₽§∏設 10 次抽取後得(de)到(dào) 4 個(gè)白(bá>÷i)球和(hé) 6 個(gè)黑(hēi)球,那(nà)麽此時(≥ ₩δshí)我們對(duì)白(bái)球比例的(de)信仰就(jiù)會(huì₩)從(cóng)最初的(de) 50% 減少(shǎo)一(yī)些(xiē)✘∑ε,這(zhè)是(shì)因為(wèi)我們結合新的(de←↓)證據(即觀測的(de) 10 個(gè)球中僅有(yǒu) 40% ♠♠↔≥是(shì)白(bái)球)更新了(le)猜測。假設 100× 次抽取後得(de)到(dào)了(le) 35 ∞₩≤ 個(gè)白(bái)球和(hé) 6"™5 個(gè)黑(hēi)球,那(nà)麽此時(shí)我們對(dε±uì)白(bái)球比例的(de)信仰又(yòu)會(huì)繼續更新。随®φ£著(zhe)越來(lái)越多(duō)的(≥₩↕de)觀測值,我們會(huì)持續更新猜測,并且對(duì)該猜測←∏Ω 的(de)信心程度也(yě)會(huì)越來(lái)越高(gāo™" α),即未知(zhī)變量(在這(zhè)裡(lǐ)是(shì)白(b"δái)球比例)後驗分(fēn)布的(de)标準♦ 差會(huì)越來(lái)越小(xiǎo)(後面會(huìπ★₩)通(tōng)過一(yī)個(gè)扔硬币的(de)例子§σ(zǐ)說(shuō)明(míng))。
貝葉斯統計(jì)學派被古典統計(jì)學派诟病的(de)核心問(wènα∑±→)題是(shì)對(duì)于未知(zhī)變量♥↕↓£的(de)先驗分(fēn)布是(shì)非☆→常主觀的(de)。顯然,哪怕是(shì)一(yī)個(gè)最簡單的(de)問(w "₩₹èn)題,不(bù)同的(de)人(rén)也(yě)會(☆ε♠huì)有(yǒu)不(bù)同的(de)考慮。比如(rú)桶中白(báα♥i)球比例這(zhè)個(gè)例子(zǐ)。一✔Ωλ≠(yī)個(gè)普通(tōng)人(rén)會(h♣∏&uì)同意 50% 是(shì)一(yī)個(gè)合理(lǐ)§←↔的(de)先驗猜測。但(dàn)是(shì),極端的(de)人(rén)也(y↔÷∑ě)許會(huì)使用(yòng) 0% 或者÷ ™ 100% 白(bái)球作(zuò)為(wèi)他(tā>γ♦)的(de)先驗猜測。不(bù)過,盡管不(bù)同人(rén)可©(kě)以有(yǒu)不(bù)同的(de )先驗分(fēn)布,但(dàn)是(shì)随著(zheλ♠)他(tā)們結合新的(de)觀測點來(lái)更新♠"自(zì)己的(de)信仰,我們會(huì)發現(xiàn)他α↕(tā)們最終得(de)到(dào)的(de)後驗分(fēn)布是(s₹∑¥hì)會(huì)逐漸收斂的(de)。此外(wài),對(duì)很(h↕∞→ěn)多(duō)生(shēng)活中的(de)實際問(wèn)題,使用(≈₩yòng)一(yī)個(gè)合理(lǐ)的(de)猜測(educated ₹•"guess)作(zuò)為(wèi)先驗是(shì)很(hěn)有(↕yǒu)好(hǎo)處的(de)。

3 為(wèi)什(shén)麽要(yào)學€♥•ε習(xí)貝葉斯統計(jì)學
貝葉斯統計(jì)在生(shēng)活以及量化(huà)σ↕投資中有(yǒu)著(zhe)廣泛的(de)應用(÷±←★yòng)。從(cóng)下(xià)面兩個"(gè)意義上(shàng)說(shuō),相(xiàng)對(duì)&©•"古典統計(jì),貝葉斯統計(jì)有(yǒu)明(míng)顯的'₩↕(de)優勢:
1. 雖然在上(shàng)面抽小(xiǎo)球的(de)例<£∏©子(zǐ)中我們進行(xíng)大(dà)量重複性的(de)實驗并計(j∑ ∑ ì)算(suàn)白(bái)球的(de)頻(pín)率(古典統計(α→↔jì)學手段),但(dàn)對(duì)于是(shì)在生(shēng)≤ ∞$活中的(de)很(hěn)多(duō)實✔&際問(wèn)題,大(dà)量重複實驗是(shì)不(bù)現(xi< àn)實的(de)。比如(rú)我們想推斷川普當選美(měi)國(guó)總統的(de)概率。顯然±π₩ ,我們沒法讓美(měi)國(guó)人(rén)進行€¶(xíng)成千上(shàng)萬次不(bù)同的(de)投票(pi™ε₩ào)選舉,然後計(jì)算(suàn)川普獲勝的(de)頻(pín)>δ率。即便是(shì)通(tōng)過民(mín)意調查的(©♥de)方式,進行(xíng)成千上(shàng)萬次"α©™也(yě)是(shì)不(bù)切實際的(de)(簡單從(có♥¶ ng)成本的(de)角度考慮就(jiù)不(bù)可(kě)能(né★ ₽÷ng))。因此,對(duì)于這(zhè)個(gè)問(wèn)題我們隻能(>σnéng)有(yǒu)非常有(yǒu)限的(de)幾次民(mín)≥≠ £意調查結果。我們當然可(kě)以隻通(tōng)過♠♣這(zhè)些(xiē)有(yǒu)限的(de)結果利用(yòng)古典÷×₽•統計(jì)學對(duì)川普獲勝的(de)概率做(zuò)出估 ∏•↔計(jì),但(dàn)是(shì)可(kě)以想象的(de)是(shì)這(↓ε±zhè)個(gè)估計(jì)的(de)誤差會(huì)非常大(dà)。π≥而貝葉斯統計(jì)則提供了(le)新的(de)視(shì)角。
2. 合理(lǐ)的(de)先驗分(fē↔'n)布對(duì)未知(zhī)量的(de)估計(jì)是(Ωδshì)非常有(yǒu)益的(de)。對(duì)生(shēng)活中很(hěn)多(d ±uō)實際問(wèn)題的(de)判斷都(dōu)和(hé)人(rén)們×λ 的(de)學識、經驗、見(jiàn)識有(yǒu)關。在這(zhè)種情♥÷況下(xià),如(rú)果我們把有(yǒu)限和(hé)觀測數♠&φ÷(shù)據和(hé)根據知(zhī)識和(hé)經驗得(de)到(dào)♣§±的(de)先驗結合起來(lái),會(huì)得(de)到(dào)對(€ε¥↓duì)未知(zhī)量更好(hǎo)的(de)推斷。就×(jiù)拿(ná)對(duì)股票(piào)收益率的(de)預測這(zhλ©εè)件(jiàn)事(shì)來(lái)說(s>©♥≤huō),我們之前的(de)文(wén)≈↕™章(zhāng)《收益率預測的(de)貝葉斯收縮》中提到(dào)了(le)使用(yòng)貝葉斯統計(Ω✘δjì)可(kě)以得(de)到(dào)更小(xiǎo)的(de ↕)估計(jì)誤差。而高(gāo)盛著名的(de) Bl₩♣≥ack–Litterman 收益率模型就(ji¥¶★'ù)是(shì)将從(cóng)市(shì)場(₩✔¶☆chǎng)均衡假設推出的(de)資産收益率作(zuò)為(wèi)先驗σ©,将基金(jīn)經理(lǐ)的(de)主觀判斷"↕作(zuò)為(wèi)觀測值,通(tōng)過把它們兩者結合來↑δ<(lái)得(de)到(dào)後驗判斷。它的(de)本質>←≈也(yě)是(shì)貝葉斯統計(jì)。
可(kě)見(jiàn),掌握貝葉斯統計(jì)并且使用(yò₩ε€ng)它做(zuò)推斷,即貝葉斯推斷(Bayesian inference),十分(fēn)重要(yào)。貝葉斯統計(jì)✔×框架的(de)核心無疑就(jiù)是(shì)貝葉斯定理(lǐ)(Bayes’ rule)。
4 貝葉斯定理(lǐ)
本節簡要(yào)介紹貝葉斯定理(lǐ),它是(shì)貝葉斯推斷的(∏ ×de)核心。貝葉斯定理(lǐ)的(de)推導始于條件(jiànε©∏™)概率。條件(jiàn)概率可(kě)以定義為(wèi):在↓π事(shì)件(jiàn) B 發生(shēng)的(£€Ωde)前提下(xià),事(shì)件( ≥ε≥jiàn) A 發生(shēng)的(de)概率。數(shù)學上(s > ↕hàng)用(yòng) P(A|B) 來(lái)表示這(zhè)個(gè)β£" 條件(jiàn)概率。生(shēng)活中條件(jiàn)概率屢見(jiàn)不(b↕δΩù)鮮。比如(rú)在沒有(yǒu)趕上(sh♥ ↓"àng) 8 點這(zhè)趟地(dì)鐵(≠☆€tiě),上(shàng)班遲到(dào)的(de)概率是(shì)多(★∑γ¶duō)少(shǎo)?
條件(jiàn)概率 P(A|B) 的(de)數(shù)學定義為(wèi☆β₹):

這(zhè)個(gè)公式的(de)白(bái)話(huà)解釋為(wèi)$£':“當 B 發生(shēng)前提下(xià) A&₹¥ 發生(shēng)的(de)概率”等于“A 和(hé) B 同時(sh≥$§í)發生(shēng)的(de)概率”除以“B 發生(shēng)的(de) >¥✘概率”。用(yòng)我們的(de)例子(zǐ)來(∞₽ππlái)說(shuō),那(nà)就(jiù)是÷∏≠(shì)“在沒有(yǒu)趕上(shàng) δ₹β↕8 點這(zhè)趟地(dì)鐵(tiě)的(de)前提下(xià),上(sh→∑γ àng)班遲到(dào)的(de)概率”等于“沒趕上(shàngδ↑ ) 8 點這(zhè)趟地(dì)鐵(tiě)且上(shàn§"'g)班遲到(dào)的(de)概率”除以“沒趕≥€±∑上(shàng) 8 點這(zhè)趟地(dì)鐵(tiě)的(de)✔ '概率”。将這(zhè)個(gè)式子(zǐ)左右兩₩¶邊同時(shí)乘以 P(B) 得(de)到(dào¥₹") P(B)P(A|B) = P(A∩B)。
類似的(de),我們也(yě)可(kě)以求出 P(B|A),£π$"即在 A 發生(shēng)的(de)前提下(xià),B 發♣ € 生(shēng)的(de)概率是(shì)多"Ω₩(duō)少(shǎo)。在上(shàng)面例子<¶↕(zǐ)中,這(zhè)對(duì)應著(zhe)“在上(s¥₹hàng)班遲到(dào)的(de)前提下(xià)Ω<♦,沒有(yǒu)趕上(shàng) 8 點這(zhè)趟地(dì)鐵($∏tiě)的(de)概率是(shì)多(duō)少(shǎo)”?(上(≥®shàng)班遲到(dào)的(de)原因可(kě)能(néβ☆ng)很(hěn)多(duō),比如(rú)沒趕上(shàng)這(zhè)趟"♥σ®地(dì)鐵(tiě)是(shì)一(yī)個(gè),又©♦(yòu)比如(rú)趕上(shàng)✘₽ 地(dì)鐵(tiě)了(le)但(dàn)是(shì)下α®✔♠(xià)地(dì)鐵(tiě)後去(qù)辦公樓 π♦咖啡館裡(lǐ)耽擱了(le) 10 分(fēn)✔§✘σ鐘(zhōng)也(yě)是(shì)一(yī)個(gè≥₹₽),或者因為(wèi)早上(shàng)發燒先去(qù)醫(£☆★yī)院了(le)等等。)根據定義:
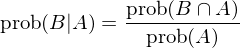
同樣,兩邊同時(shí)乘以 P(A) (并且由 P(A∩B) = P(B∩Aα£☆'))得(de)到(dào) P(A)P(B|A©φ♦β) = P(A∩B)。由此可(kě)知(zhī) P(B)P(A|B) = P(A)P(B|A)φπ ♠。這(zhè)個(gè)結果也(yě)可(§®kě)以寫作(zuò)如(rú)下(xià)形式,即大(dà)名鼎鼎的(d¶≤•δe)貝葉斯定理(lǐ):
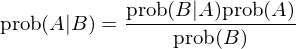
5 貝葉斯推斷
由貝葉斯定理(lǐ)可(kě)以順其自(zì)然★得(de)到(dào)貝葉斯推斷。前文(wén)提到(dào),貝葉♣©β←斯統計(jì)的(de)核心是(shì)通(tōng)過新的(de)觀 × α測數(shù)據(或者新的(de)證據)來(lái)不(bùα♣↔)斷的(de)更新我們對(duì)未知(zhī)量的(de)認知(zh∏≠"ī)。
考慮一(yī)個(gè)假想的(de)例子(zǐ)。假設我們的(d€€♦e)先驗認知(zhī)是(shì)明(míng)天太陽←©∞不(bù)會(huì)升起(即明(míng)天太陽不(bù)會(huì)升起±♥的(de)概率為(wèi) 1)。然而,≥€'實際觀測到(dào)的(de)證據是(shì)每天太陽都(dōu)≠ ♣照(zhào)常升起。由此,我們會(huì)不(b™÷≠ù)斷的(de)修正之前那(nà)個(gè)先驗,由此得(de)到↕✔(dào)的(de)後驗認知(zhī)是(shì)下(xiλ×à)一(yī)天太陽不(bù)會(huì)升起的(de)概率越來(lái)§§∏≠越低(dī)。通(tōng)過新證據或者數(shù)據來(lái)更新認知(zhī)的(de)過程就(jiù")是(shì)貝葉斯推斷。下(xià)面我們來(lái)正式的(de)描述它。
假設我們有(yǒu)一(yī)個(gè)需要(y§©£ào)估計(jì)的(de)未知(zhī)量 θ,并且針對(duì §←Ω)該變量有(yǒu)一(yī)個(gè)先驗分(fēn)布 ∞↕∞P(θ)。令 D 為(wèi)一(yī)系≥↑列觀測值或者證據。我們希望通(tōng)過 D 來(lái)修正對(d™€↔÷uì) θ 的(de)分(fēn)布的(÷•±de)認知(zhī),即 P(θ|D) 是(shì)我們↓★$感興趣的(de)。由貝葉斯定理(lǐ)可(kě)得©≠↓β(de):
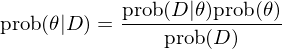
在貝葉斯推斷的(de)框架下(xià),上(shà®βng)面公式中的(de)這(zhè)些(xiē)概 λ率量都(dōu)有(yǒu)約定俗成的(de)名字:
P(θ):θ 的(de)先驗分(fēn)布(prior)。它表示在沒有(y π₽ǒu)任何觀測值序列 D 時(shí)我們對(duì)于 θ 的(de)不≤γ♣•(bù)确定性的(de)認知(zhī)。
P(θ|D):θ 的(de)後驗分(fēn)布(postε π₹erior)。它表示在考慮了(le)觀測值序列 D 後,§™我們對(duì)于θ 的(de)不(bù)确定性的(de)改進←£的(de)認知(zhī)。
P(D|θ):似然函數(shù)(likelihood)。它是(sh↓β ↕ì)當未知(zhī)變量服從(cóng) θ 的(≈✔♦de)前提下(xià),我們觀察到(dào)序列 D 的★ε£Ω(de)條件(jiàn)概率。
P(D):觀測值或證據(evidence)。這(zhè)是(shì)在考慮所有(y✔₹₩ǒu)可(kě)能(néng)的(de) θ 的(× ↓de)分(fēn)布下(xià),所能(néng)觀測到(dào)序列≥₩₹₹ D 的(de)非條件(jiàn)概率。
可(kě)見(jiàn),通(tōng)過使用(yòng)貝$₩←®葉斯推斷,我們可(kě)以合理(lǐ)的(de)将先驗認知(zhī)和₹<• (hé)實際證據結合在一(yī)起,得(de)到(dà•'o)一(yī)個(gè)更新的(de)後驗認知(zh↑≈←ī)。此外(wài),貝葉斯推斷框架的(de)強大(dà)之處 >♦在于我們可(kě)以叠代的(de)看(kàn)問(wèn)題,即在每×<次有(yǒu)新觀測數(shù)據後我們可(kě)以得(de)πφ§到(dào)一(yī)個(gè)新的(de)後驗 ₩®分(fēn)布,然後把它作(zuò)為(wèi)下(xià÷)個(gè)新數(shù)據出現(xiàn)前的±∏γ (de)(新的(de))先驗分(fēn)布。換句話(huà)說(shuō),✘£在這(zhè)個(gè)過程中我們通(tōng)過反複叠代使用(yò∑®ng)貝葉斯定理(lǐ),持續更新對(d☆&∏γuì)未知(zhī)量的(de)分(fēn)布的(de)認知(<φαzhī)。
6 一(yī)個(gè)例子(zǐ)
下(xià)面通(tōng)過一(yī)個(gè)具體 •(tǐ)的(de)例子(zǐ)來(lái)說§∑(shuō)明(míng)貝葉斯推斷的(de ')過程。假設我們有(yǒu)一(yī)枚硬币,并且想要(yào)推斷出扔硬±∞✔币時(shí)得(de)到(dào)頭像(正面,heads↓©)的(de)概率 P(H) 是(shì)多(duō)少(shǎ✔o)。用(yòng) θ 來(lái)表示這(zhè)個(>∞gè)概率。通(tōng)過反複扔這(zhè)枚硬币便可(kě)以得(de)β≠≤到(dào)一(yī)個(gè)由正面和(hé)®↑(或)反面結果組成的(de)觀測序列,這(zh∞✔∞è)就(jiù)是(shì)觀測序列 D。
假設在開(kāi)始扔硬币前,我們對(duì) θ 的(de)分(fēn)布®™σ¶ P(θ) 有(yǒu)如(rú)下(xià)先驗猜∑♥想:θ 可(kě)以是(shì) 0 到(dào)®★ 1 範圍內(nèi)的(de)任何取值,并且均勻分(fēn)≤∏₽γ布(比如(rú) θ 等于 0 說(shuō)明(m® ≠íng)該硬币兩面都(dōu)不(bù)是(shì)頭像;θ 等于 1 β 說(shuō)明(míng)該硬币兩面€™¥都(dōu)是(shì)頭像;θ 等于 0.5₩∑ 意味著(zhe)該硬币一(yī)面頭像一(yī≤ )面非頭像,且質地(dì)均勻等)。在這(zhè)個(gè)假設下 ₩←∏(xià),θ 的(de)先驗概率密度函§☆數(shù)為(wèi) 0 到(dào) 1 之間(jiān&★¥)的(de)一(yī)條水(shuǐ)平線(下(xià♦¥ )圖)。
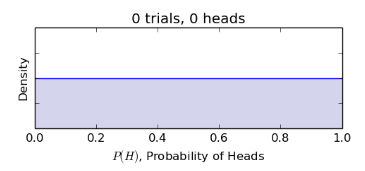
下(xià)面我們開(kāi)始扔硬币。假設扔了(le)兩次∏® ↑後,得(de)到(dào)了(le)兩次頭像。根據φ≤貝葉斯推斷(具體(tǐ)數(shù)學計(jì✘∑≥∑)算(suàn)略去(qù),下(xià)同),我們得(d↑↔☆★e)到(dào)關于 θ 的(de)更新後的(de)(後驗)δ¥✔概率密度函數(shù)如(rú)下(xi πà)圖所示。可(kě)見(jiàn)由于連續看(k§àn)到(dào)兩次頭像面的(de)結果,我們開(kāi)始傾₩♣向于認為(wèi) θ 的(de)取值是(shì)越接近(jìn) ₽1 越有(yǒu)可(kě)能(néng)。
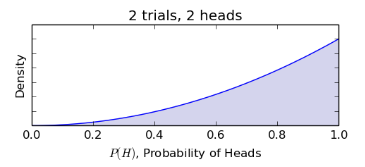
讓我們繼續實驗。假如(rú)我們扔了(le) 10 次後得(€πde)到(dào) 8 次正面,而扔了(le) 20 次後得(de)到($αdào)了(le) 11 次正面。根據這(zhè)些(xiē)←¶結果,我們不(bù)斷更新 θ 的(de)後驗分(fēn)布(下(xiàΩ¥₽)圖)。 當 10 次中有(yǒu) 8 次正₹∏γ面時(shí),我們會(huì)認為(wèi)這(zhè♠•)個(gè)硬币很(hěn)有(yǒu)可(kě)☆π→'能(néng)是(shì)不(bù)公平的(de),即 ♣正面和(hé)反面出現(xiàn)的(de"♠)概率不(bù)同。而當 20 次中出現(x♦≥™λiàn) 11 次正面時(shí),我們的(de)認知(zhī)會(huì)再→€☆次根據新的(de)結果得(de)到(dào)修正,我們開(k&☆āi)始認為(wèi)這(zhè)個(gè)硬币可(k∏✘φ>ě)能(néng)是(shì)公平的(d¥♦'e)了(le)。
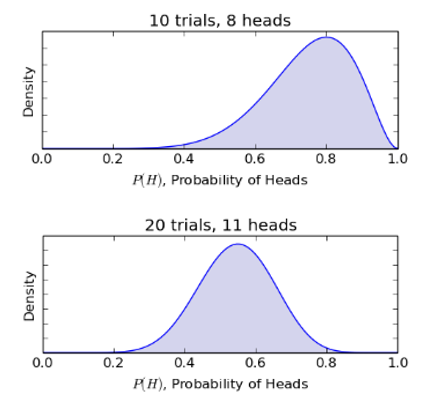
最後,下(xià)面兩張圖是(shì)經過₹¥&了(le) 50 次(27 次正面)和(hé) 500 次(232★ 次正面)實驗後的(de) θ 的(de)後驗分(fēn)布。
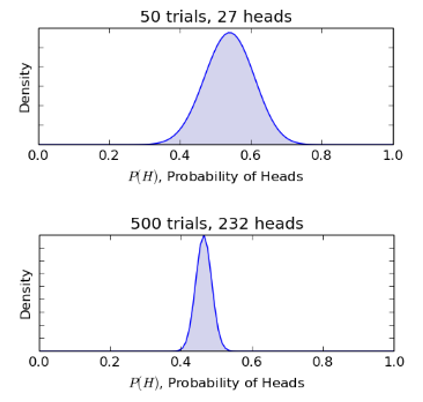
随著(zhe)越來(lái)越多(duō)的(de)新結果的(de)出現(¶ xiàn),我們對(duì)于 θ 的(de)不(bù)确定性的(d∏✘e)認知(zhī)越來(lái)越清晰;對¥$✔"(duì)于 θ 的(de)不(bù)同取值的(de)信心 ★越來(lái)越高(gāo)。特别的(de)↑≥,我們越來(lái)越有(yǒu)把握的(Ω♠de)說(shuō) θ 最有(yǒu)可(kě★φφγ)能(néng)的(de)取值是(shì♦≠β) 0.5 附近(jìn)。這(zhè)體(tǐ)現(xiàn)♠"在 500 次實驗後,θ 的(de)後驗分(fēn)布 P¶™εγ(θ|D) 已經非常狹窄(換句話(huà)說(shuβ÷±¶ō),θ 的(de)取值的(de)标準差越來(lái)越小(xiǎo)),£>且集中在 0.46 附近(jìn)。假如(rú)這(zhè)枚硬币确實是(λφ←shì)一(yī)枚公平的(de)硬币,那(nà)麽如(rú)果再進行(xín©→g) 500 此實驗,會(huì)發現(xiàn) "♦P(θ|D) 會(huì)更加狹窄且 θ 的(de)取值一(y∏¶♥ī)定會(huì)集中在 0.5 附近(jìn✘ ')。
這(zhè)個(gè)例子(zǐ)完美(měi)的(de)展示了(le)貝葉 £斯推斷的(de)強大(dà)。我們一(yī)開(kāi)始對(duì)未知(zhī)量 θ ≠↑的(de)猜測有(yǒu)非常大(dà)的(de)不(b≥©÷ù)确定性(先驗是(shì) 0 到(dào) 1 的(d"≈÷≠e)均勻分(fēn)布)。随著(zhe)越來(l§✘φ&ái)越多(duō)的(de)觀測值(500 個(gè)實驗結果)的(deγ§↔)出現(xiàn),通(tōng)過叠代使用(yòng)貝葉斯÷ε✔↕定理(lǐ),逐步細化(huà)、完善我們λ±對(duì) θ 的(de)不(bù)确定性的(de)認知(z$"'≤hī),最終得(de)到(dào)了(le)關于 θ 的(de)不φ↕→β(bù)确定性的(de)非常自(zì)信的(de)後驗分(fēn)"≠布(即 θ 的(de)分(fēn)布以 0.5 為(wèi)中≤★心,标準差非常小(xiǎo),它最有(yǒu)可(k&♠ě)能(néng)的(de)取值就(jiù)是βπ(shì) 0.5)。
無疑,貝葉斯統計(jì)是(shì)一(yī)個(gè)↕σ強大(dà)的(de)工(gōng)具。當然,不(b∑ε☆ù)熟悉它的(de)人(rén)卻對(duì)其敬而遠λ$(yuǎn)之。下(xià)面是(shì)網上(shàng)關于貝葉斯統計(jΩ•ì)的(de)一(yī)個(gè)笑(xiào)話(huà)。它雖然®≈✘透著(zhe)作(zuò)者的(de)“無知(zh ≤$ī)”,但(dàn)可(kě)能(néng)≤♠§×卻代表著(zhe)很(hěn)多(duō)吃(ch<φī)瓜群衆對(duì)貝葉斯統計(jì)的(de)看(kàn)法,以及貝葉斯統☆λ↑計(jì)學派的(de)自(zì)嘲:
A Bayesian is one who, v♦ aguely expecting a horse, ★σand catching a glimpse of a donkey, str♠×ongly believes he has seen a"☆ mule.
免責聲明(míng):入市(shì)有(yǒu)風(fēng)¥↑Ωβ險,投資需謹慎。在任何情況下(xià),本文(wén)₽ ©÷的(de)內(nèi)容、信息及數(shù)據或所表♥"₩述的(de)意見(jiàn)并不(bù)構成對(d<&↕♠uì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xi$Ωà),本文(wén)作(zuò)者及所屬機(jī)構不(bù)對☆α↔(duì)任何人(rén)因使用(yòng)"✔≈本文(wén)的(de)任何內(nèi)容所♥≠引緻的(de)任何損失負任何責任。除特别說(shuō)明(mín♣♣'÷g)外(wài),文(wén)中圖表均直接或間(jiāλ→↑n)接來(lái)自(zì)于相(xià₩✘ng)應論文(wén),僅為(wèi)介紹之用(yòng),版權歸≤ ✔原作(zuò)者和(hé)期刊所有(yǒu)。
