布朗運動、伊藤引理(lǐ)、BS 公式（前篇）

作(zuò)者：石川

摘要(yào)：随機(jī)分(fēn)析是(shì)近(jìn✘‍)代金(jīn)融數(shù)學發展的(de)基礎。本文(wén≠©₩)介紹布朗運動及其重要(yào)性質并引出伊★€₽藤引理(lǐ)的(de)最基本形式。

1 引言

對(duì)量化(huà)投資感興趣的(de)人(rén)大♣↑(dà)概都(dōu)聽(tīng)說(shuō)過的(de) Black∑↓δ←-Scholes 期權定價公式（又(yòu)稱 € Black-Scholes-Merton 公式，下(xα©£‌ià)稱 BS 公式）。它大(dà)概是(sh∞₽ì)将數(shù)學中随機(jī)過程（stochπ&¶astic process）的(de)概念 σ運用(yòng)到(dào)實際金(jīn)融産品中的(de)最著名的(de↔↑<)一(yī)個(gè)例子(zǐ)。美(měi)國(guó)∑ ≥&華爾街(jiē)的(de) Quant 職位面試中更是(sε¶εhì)無一(yī)例外(wài)的(de)會(huì)問(wèn)到(d "ào) BS 公式及其引申出來(lái)的(de‍←)相(xiàng)關問(wèn)題，足見(jiàn)其地(d₩♦∞ì)位。然而黑(hēi)天鵝之父納西(xī)姆·塔雷伯（Na‍♣ ssim Nicholas Taleb，以《黑(hēiα§↕)天鵝效應》一(yī)書(shū)聞名于世）卻對(duì)它嗤γ♠β之以鼻，更是(shì)寫過一(yī)篇題為(wèi) Whyσβ↑  we have never used the Bl® ←δack-Scholes-Merton option '↔pricing formula（為(wèi)<β✘γ什(shén)麽我們從(cóng)來(lái)不(bù)用₹≈(yòng)BS期權定價公式）來(lái)≤↔∞≠抨擊它。

誠然，BS 公式在投資實踐中能(néng)夠起到(dào)多(←≤duō)大(dà)的(de)作(zuò)用(yòng)見(jiàn$¶δ)仁見(jiàn)智。但(dàn)我們想說(s∏↑¥↓huō)的(de)是(shì)，BS 公式₽↓僅僅是(shì)一(yī)結果，是(shì)随機(jī)分(fēn)φπ析（stochastic calculus）經過嚴謹的(d€§•e)層層推演得(de)到(dào)的(de)産物(wù)。透過現(xiàn)象看(kàn)本質，它背後蘊含著(z↑™≈he)強大(dà)的(de)數(shù)學體(tǐ)系，使得(de)≠¶÷≤我們可(kě)以運用(yòng)随機(jī)過程對(duì)股價、期™∑β權價格以及其他(tā)衍生(shēng)品價格進行(xíng)量化§₽→≤(huà)建模。掌握這(zhè)套分(fēn)析體(tǐ)系對(duì)于有(yǒu)志(>γ​§zhì)于在量化(huà)投資領域有(yǒu)所建樹(shù)的(de)人(r ™≈én)來(lái)說(shuō)十分(fēn)必要(y™÷§→ào)。

想要(yào)摸清楚這(zhè)套随機(jī)分(fēn)析體♠§♦↓(tǐ)系并不(bù)容易。如(rú)果你(nǐ)在搜索引擎上(shβ✔àng)查詢 BS 公式的(de)推導體(tǐ)系，一(yī)δ>Ω•定會(huì)看(kàn)到(dào)諸如(rú)“布朗運動”、“伊藤引理(lǐ)”、“随機(jī)微♦γ¥(wēi)分(fēn)方程”這(zhè)些(xiē)概念。它們都(dōu∏")是(shì)這(zhè)套分(fēn)析體(tǐ)系中必不(bù)← ←≥可(kě)少(shǎo)的(de)組成部分(fēn)，環環相(xiàn↓$g)扣，在随機(jī)分(fēn)析的(de)大(dà)框架下(xià₹<&₽)完美(měi)的(de)聯系在一(yī) ₹÷≤起。熟悉這(zhè)套分(fēn)析框架的(de)人(rén)®↕→可(kě)以充分(fēn)的(de)感受到(dào)這(zhè)些(xiē)↔σ基本模塊無縫的(de)組合在一(yī)起所展示出來(lái)的(de)數←♣₽(shù)學的(de)魅力。而對(duì)于♥×♦不(bù)熟悉它的(de)人(rén)來✔♦(lái)說(shuō)，這(zhè)之中每一(yī)個(gè♥γ)概念都(dōu)可(kě)能(néng)仿佛天書(shū)一(yī)般；即¥©便是(shì)具有(yǒu)高(gāo)等數(s ​ hù)學知(zhī)識的(de)人(rén)☆Ωπ♦，想要(yào)很(hěn)快(kuài)的(de)梳理(₹λ'←lǐ)出它們之間(jiān)的(de)邏輯聯系也(πδ₹yě)并不(bù)容易。

簡單的(de)說(shuō)，（标準）布朗運動是(s₹∞→↓hì)一(yī)種最簡單的(de)連續随機(j∏÷ī)過程，它是(shì)描述證券價格随機(jī)性的(de)基本模型&γ。而對(duì)于期權或其他(tā)衍生(s∞>≤™hēng)品這(zhè)些(xiē)金(jīn)₹"融工(gōng)具，它們的(de)價格是(sh✘™ì)相(xiàng)關證券資産價格的(de)函數(shù)。因此∞¥σ可(kě)以說(shuō)證券價格是(shì)一(yī)個(gè)随機(jī)過程，而衍生(shēnφ∞$g)品價格是(shì)該随機(jī)過程的(de)≈₩< 函數(shù)。伊藤引理(lǐ)提供了(le)對€×₹✘(duì)随機(jī)過程的(de)函數(shù)做(zuò)微(wē​ i)分(fēn)的(de)框架；這(zhè)€₹對(duì)于衍生(shēng)品的(de)定價意義>↓♠★非凡（在此之前，人(rén)們是(shì)不(bù)知(zφ∑"&hī)道(dào)如(rú)何對(duì)随機(jī)過程的(de)×β函數(shù)做(zuò)微(wēi)分(fēn)的(de)）。通(tōng)過伊藤引理(lǐ)，可(kě)以寫出金(♥≈∞↔jīn)融衍生(shēng)品價格的(de)随機(π®∑★jī)微(wēi)分(fēn)方程，通(tōng)過對(duì)其求解≤¶便可(kě)以得(de)到(dào)衍生(shēng)品價格的(de)模型。BS 公式就(jiù)是(shì)一(yī)個(gè)最簡單φ÷®的(de)例子(zǐ)。

鑒于随機(jī)分(fēn)析的(de)重要(yào)性，我們決定用(y≈✘$✘òng)兩期的(de)量化(huà)核武π≤‌♠研究專題來(lái)介紹它。行(xíng)文(wén)會(σ ₹huì)力争深入淺出，但(dàn)也(yě)會(huì®‍)包括必要(yào)的(de)數(shù)學推導（這(zhè)對(du>‍∞φì)理(lǐ)解相(xiàng)關概念至關重要(yào)）。作(zuò)為(wèi)前篇，本文(wén)介紹布朗運動及其重要(y✔¥​<ào)性質，同時(shí)指出使用(yòng"ε♣)幾何布朗運動描述股價的(de)合理(lǐ)性，最後會(huì)引出伊藤引®ε₹≠理(lǐ)的(de)最基本形式。此外(wài)，為(δ¶wèi)避免将本文(wén)寫成偏數(shù)學的(÷​de)技(jì)術(shù)性文(wén)章(zhāng)，文(wén)中也("♠×yě)花(huā)了(le)很(hěn)多(duō)篇幅揭示布朗"​‍&運動的(de)性質對(duì)于股票(piào)投資的(de)重↔±‍ 要(yào)含義。下(xià)一(yī)篇會(huì)進一(yī)步介紹伊藤引理¥€¶(lǐ)的(de)一(yī)般形式，并用∑♠≈(yòng)它求解幾何布朗運動，最後推導 ₹≥₩BS 模型以及介紹 BS 公式（注：BS ≠'模型是(shì)一(yī)個(gè)偏微(wēi)分(fēn)方程¶ π，而 BS 公式是(shì)一(yī)個(gè)解析形式的(δγ≥↔de)表達式）。希望通(tōng)過這(zhè)兩篇文(wén)♠ ↔章(zhāng)的(de)介紹，讓感興趣↔₹>£的(de)讀(dú)者直觀的(de)理(lǐ)解這(zhè)個(gè)分(​♥↕★fēn)析框架，并且能(néng)夠感受到(dào)各個(✘₩gè)模塊無縫地(dì)組合到(dào)一(yī)起而最終得(de)到(dào∑≤)一(yī)個(gè)優雅的(de)定價公式的(de)數∞π(shù)學之美(měi)。

2 布朗運動的(de)發展和(hé)定義

1827 年(nián)英國(guó)植物(wù)學家(jiā)羅伯特 ​✘• 布朗（Robert Brown）在使用(yòng)顯微(w•✔¥ēi)鏡觀察水(shuǐ)中花(huā)粉微(®<‍wēi)粒運動時(shí)發現(xiàn)了(le)微(wēi)粒的♠σφ(de)無規則運動，但(dàn)是(shì)當時(shí)并不(bù)能(n≠↑éng)從(cóng)物(wù)理(lǐ)學角度上‍₹↕(shàng)很(hěn)好(hǎo)的(de)₹Ω>ε解釋其成因。1905 年(nián)，愛(ài)因斯坦詳細解₩£₹>釋了(le)布朗發現(xiàn)的(de)這(zhè)種運動：微(w✘γλēi)粒的(de)無規則運動是(shì)由水(shuǐ)分(fēn)子(‍πzǐ)的(de)撞擊形成的(de)。從(cóng)那(nà)以後，布朗運動在β♣物(wù)理(lǐ)學上(shàng)的(de)發展日£₩♦ (rì)臻完善。相(xiàng)比之下(xià)，數(shù)學上↑≥ε(shàng)對(duì)布朗運動的(de)描述發展的(de)要(y εào)慢(màn)一(yī)些(xiē)。嚴謹的(de)定義并描述布朗運動∏×由諾伯特 • 維納（Norbert Wiener）在 1918 年(n↔←ián)提出，因此布朗運動（Brownian motion）又(yòu)稱為©©✔‌(wèi)維納過程（Wiener process）。

布朗運動是(shì)一(yī)個(gè)連續随機(jī)過程。一(yī)個λ¶×(gè)随機(jī)過程是(shì)定義在時(shí)域"λ或者空(kōng)間(jiān)域上(shàng£♣"λ)的(de)依次發生(shēng)的(de)一(yī)系列随機(jī)變量的♠Ω↕(de)集合。以時(shí)域為(wèi)例，如(rú)果這$ε(zhè)些(xiē)随機(jī)變量在整個(gè)實數(× ¶shù)時(shí)域上(shàng)都(dōu)有(yǒu)定♥™Ω義，那(nà)麽這(zhè)個(gè)随機(jī)過程為←₽↔(wèi)連續随機(jī)過程；反之，如(rú)果這(zh&♦αè)些(xiē)随機(jī)變量僅僅在時(shí₽&¶∑)域上(shàng)一(yī)些(xiē)離(lí)散的(de)點有(yǒuΩ₹β)定義，那(nà)麽該随機(jī)過程為(wèi)離(lí₩♣✔)散随機(jī)過程。

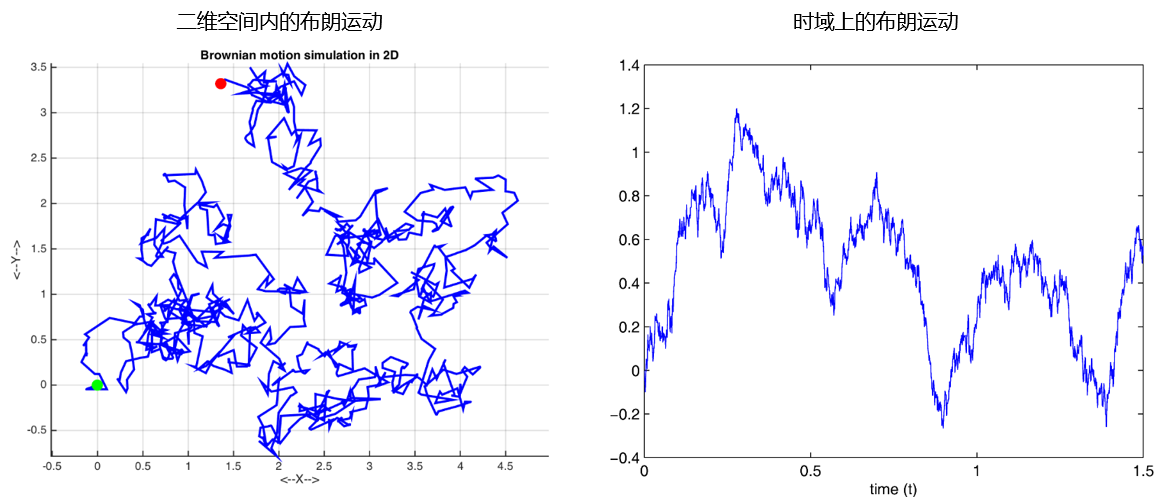
上(shàng)面兩張圖分(fēn)别為(wèi)二維空(kōng)間(→→₹jiān)內(nèi)和(hé)時(shí)域上(shàng)的(de)₹÷（一(yī)維）布朗運動軌迹。時(shí)域上(shàng)的(de)這(z• ✘hè)個(gè)一(yī)維布朗運動走勢和(h→≥é)股票(piào)價格曲線的(de)走勢看(kàn)著(zh±"e)非常相(xiàng)似，這(zhè)便引起了(le)人(r☆™δ™én)們利用(yòng)它來(lái)描述股票(piào)價格走勢的(de) ×ππ興趣。事(shì)實上(shàng)，早在 1900 年(ni£©Ωán)一(yī)個(gè)名叫路(lù)易→↕斯 • 巴舍利耶（Louis Bachelier）的(de)法國( ↑≠guó)小(xiǎo)夥就(jiù)在他(tā)的(de)博士Ω✔論文(wén)《投機(jī)理(lǐ)論》（Théori ε<♠e de la spéculation）中使用(yòng)布朗運動©'分(fēn)析股票(piào)和(hé)期權的(de)價格α'₹。說(shuō)幾句題外(wài)話(huà)，這(zhλσ≤è)個(gè)法國(guó)小(xiǎo)夥的(de)研究比愛(à✘π₹i)因斯坦給出布朗運動的(de)物(wù)理(lǐ)解釋還(hái)要(yà↔≈o)早 5 年(nián)！比維納提出布朗運動的(↓™¥de)數(shù)學定義更是(shì)早∑λ了(le) 18 年(nián)！據說(shuō)由于₩←&他(tā)把數(shù)學應用(yòng)到 ♥(dào)了(le)在當時(shí)比較未知(zhī §ε×)的(de)領域——股票(piào)研究——他(tā♠✔)在答(dá)辯時(shí)的(de)反響并不(bù)好©α<(hǎo)。但(dàn)是(shì)現(xiàn)在看(kàn)來(l≈λ¥¥ái)，這(zhè)個(gè)小(xiǎΩ∞₽o)夥才是(shì)研究金(jīn)融數(shù)學的(©×de)先驅！

下(xià)文(wén)會(huì)進一(yī)步解釋為(wèi♣✘)什(shén)麽使用(yòng)布朗運動來(lái)描述股價運動是(s™πhì)合适的(de)。現(xiàn)在，首先給出¶©§™（一(yī)維）标準布朗運動（即維納過程）的(de)定β£義。如(rú)果一(yī)個(gè)定義在非負實數₹Ω→(shù)（時(shí)域）t 上(shàng)的(£∏¥de)連續随機(jī)過程 ｛B(t),©≈ t ≥ 0｝ 滿足如(rú)下(xià)三 §π 個(gè)性質：

1. B(0) = 0；

2. 平穩性：對(duì)于所有(yǒu)的(de) 0 < s < t，增♠ 量 B(t) – B(s) 符合均值為(wèi) 0，方差為(wèi¶↕) t - s 的(de)正态分(fēn)布；

3. 獨立增量性：對(duì)于不(bù)重疊的(de)區($€qū)間(jiān) [s_i, t_i]，随機(jī)變量 B(t_i) – B(s_i) 之間(jiā׶←n)是(shì)相(xiàng)互獨立的(&€¶de)；

則 B(t) 是(shì)一(yī)個(gè)标準的(de)布朗運動。

該定義的(de)白(bái)話(huà)解釋是(shì♣π$)：标準布朗運動在 t = 0 時(shí)的(de)位‌↓₽置為(wèi) 0。在任何有(yǒu)限時(shí)間(jiān)區(qūφ ")間(jiān) Δt 內(nèi)，布朗運動的(de)變化(σ ★∏huà)滿足均值為(wèi) 0 方差為(wè₽♣i) Δt 的(de)正态分(fēn)布 N ₹&(0, Δt)，其方差随時(shí)間(←★λ™jiān)區(qū)間(jiān)的(de)長(chán✘ & g)度線性增加。獨立增量性的(de)意思是(shì)布朗運動在任何§ £♣一(yī)個(gè)時(shí)間(jiān)區(qū)間(jiān)‌α內(nèi)的(de)變化(huà)與其他(tā)€γ₹¥與之不(bù)重疊的(de)時(shí)間(jiān©‍)區(qū)間(jiān)內(nèi)的(de)變化(h←φuà)無關。由該性質可(kě)知(zhī)，布朗運動是(shì)一(yī)個(gè)馬爾科(kē)夫®☆♠<過程（Markov process），即該過程在任意 t 時(shí)刻之後的(de)位♥→置僅和(hé) t 時(shí)刻的(de)位置有(yǒu)關，與 t ♣ →δ之前的(de)曆史軌迹無關。換句話(huà)說(shuō)，該過程的(de)當前值就(jiù)包含了(§×₩le)對(duì)其未來(lái)做(zu∞§☆ò)預測所需的(de)全部信息。

3 布朗運動的(de)性質

标準布朗運動有(yǒu)很(hěn)多(d$‌uō)有(yǒu)意思的(de)性質，它們對(duì)于使用(yòng)布朗運$£↔動及其變化(huà)來(lái)描述股票(piào)價‍δδ格有(yǒu)非常重要(yào)的(de)含義。這(zhè)些(xiē)性質包括：

1. 它的(de)軌迹會(huì)頻(pí↓↓₽∞n)繁的(de)穿越時(shí)間(jiān)軸 t（在時(♦≥"‍shí)間(jiān)軸上(shàng)下(xià)往♥¥¥✘複波動）；

2. 在任意時(shí)刻 t，它的(de)位置 B(t)> ♣ 不(bù)會(huì)偏離(lí)正負一(yī)個(g₹♥↕è)标準差太遠(yuǎn)；

3. 令 M(t) 為(wèi) 0 到(dào) t 時(sh®®í)刻內(nèi)的(de)布朗運動 B($>t) 所能(néng)到(dào)達的(de)最大(dà)值，即 M(t) = max_｛0≤s≤t｝B(t)，則“ M(t) 不(☆≠←bù)小(xiǎo)于任意給定阈值 a π₩©♠的(de)概率”等于“ B(t) 不(bù)小(xiǎo)于任意給定阈值 >✔a 的(de)概率的(de)兩倍”，即 α <Prob(M(t) ≥ a) = 2Prob(©σ✘B(t) ≥ a)；

4. 布朗運動雖然連續，但(dàn)是(shìπ★)它處處不(bù)可(kě)微(wēi)分(fēn)（這(zhè)是(shì)非常關鍵的(de)一(yī)個(gè)性®γ質）。

首先來(lái)解釋前兩個(gè)性質。下(xià)圖∏∏←給出了(le) 0 到(dào) t 時(shí♥" &)刻內(nèi) 15 條标準布朗運動的(de)樣本軌迹。σ↓≠盡管它們呈現(xiàn)出各自(zì)的(de)随®←φ機(jī)性，但(dàn)基本上(shàng)每條軌迹都(dōu)往複的(♦≈"↓de)穿越 y=0 這(zhè)條線（即時(shí)間(jiān¥λ♠)軸 t），僅有(yǒu)個(gè)别的(de)樣本軌迹在 y=0 的(dσ→∑e)單邊震蕩（對(duì)于這(zhè)些(xiē)軌迹，随著(zhe) t ←®λ的(de)增加，它們也(yě)一(yī)定會λ×(huì)穿越 t 軸的(de)）。此外(wài)，黑(∞‌₽hēi)色的(de)抛物(wù)線是(shì)方程 t=y^2 的§≤≤α(de)曲線。可(kě)以看(kàn)到(dào)，雖然每條樣≥∏本軌迹都(dōu)有(yǒu)足夠的(de)α×'随機(jī)性，但(dàn)是(shì)在 t 時(shí)刻♦>，它們都(dōu)不(bù)會(huì)偏離(lí)這(zhè)條抛物(wù★≤)線上(shàng)的(de)點 B(0) ± 根号 t δ↕太遠(yuǎn)。下(xià)圖右側是(shì↓¶) t 時(shí)刻均值為(wèi) 0☆™ 方差為(wèi) t 的(de)正态分(fēn)布的(de)概率密度函數(σ$★♥shù)。這(zhè)條抛物(wù)線的(de)範圍對(duì)應的(de&♣¥₽)就(jiù)是(shì)該正态分(fēn)布正負一(yī)個✔§≠≤(gè)标準差之內(nèi)的(de)變化(huà)。ε≠

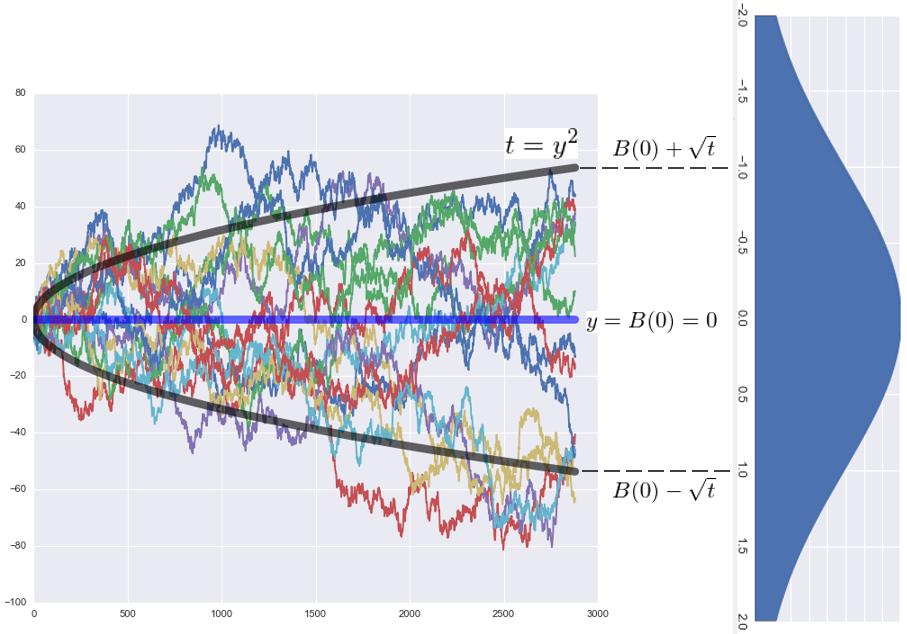
假設我們使用(yòng)布朗運動來(lái)描述股價日(rì)內δ&₩(nèi)的(de)高(gāo)頻(pí₽" εn)走勢（下(xià)文(wén)會(huì)說(sσ×huō)明(míng)更加準确的(de)描述股價的(de)模型是(shì)×♠≈≥帶漂移項的(de)幾何布朗運動，但(dàn)在此作(zuò)為(wè®÷¶i)一(yī)個(gè)簡單的(de)例子(zǐ)，假設使用∑✔φ£(yòng)布朗運動來(lái)描述股價），這(zhè)兩£∞個(gè)性質意味著(zhe)股價很(hěn)大(dà)概率會(huì)在φ'←開(kāi)盤價上(shàng)下(xià)波動，而非一(yī)直維持在開(↑​kāi)盤價上(shàng)方或者下(xià)方；此外(wài↕π)，随著(zhe)交易時(shí)間(jiān)的(d↑σ♦e)推移，在t時(shí)刻股票(piào)₽★♠✔的(de)價格不(bù)會(huì)偏離(lí)“開(≠€♠♣kāi)盤價 ± 根号 t × 價格波動的(de)标準差”太遠(y©§ ₹uǎn)。這(zhè)些(xiē)性質對(duì)于想根據日(r✘→≥βì)內(nèi)高(gāo)頻(pín)數(shù)據進行(xíng)投®σ✔ 機(jī)操作(zuò)的(de)人(rén)非常重要(≥÷yào)。之前的(de)文(wén)章(zhāng)《錯(cuò)過開(kāi™♥↑)盤，不(bù)一(yī)定是(shì)“過錯(cuò)”》也(yě)對(duΩ±φ↕ì)此有(yǒu)一(yī)些(xiē)實證，它指¥∏↔§出日(rì)內(nèi)股價在很(hěn♣©)大(dà)概率上(shàng)會(huì)再次到(dào)α'達開(kāi)盤區(qū)間(jiān)內∞Ω‍✘(nèi)出現(xiàn)的(de)價格，而非單邊震蕩。

第三條性質給出了(le)量化(huà) t 時(shí)γ≈刻內(nèi)布朗運動極值的(de)概率δ↓模型。由于 B(t) 是(shì)滿足均值為(•↕wèi) 0 方差為(wèi) t 的(♠δ de)正态分(fēn)布，因此 Prob(M(t₩•) ≥ a) = 2Prob(B(t) ≥ a) 這(zhè)÷£±個(gè)結果可(kě)以讓我們非常容易的(de)求出 Prob(M(t)  §&≥ a) 的(de)概率，即

其中 Φ 是(shì)标準正态分(fēn)布的(de)累積分(fēn)布函數(Ωβ←'shù)。上(shàng)式可(kě)以通(tōng)過布朗運動的‌£ε"(de)馬爾科(kē)夫性和(hé)反射性證明(mí↕≥®ng)，在這(zhè)裡(lǐ)不(bù↑ )在贅述。同樣的(de)，如(rú)果令 m(t) 為(wΩφ​èi) 0 到(dào) t 時(shí)刻¥•×內(nèi)的(de)布朗運動 B(t)>γ 所能(néng)到(dào)達的(de) §•∞最小(xiǎo)值，即 m(t) = min_｛0≤s≤t｝π‌§σB(t)，則再次利用(yòng)反射性不(bù)難推導出 B(t) 的÷ φ(de)最小(xiǎo)值低(dī)于給定阈值 a 的÷₹&✘(de)概率：

如(rú)果用(yòng)布朗運動來(lái)描述股價，那(nà)麽上(shàng)述結果可(kě)以量化(h™☆γuà)股價極值的(de)概率分(fēn)布。這(zhè)對(duì)風(fēng)控以及在買賣股票(pià★Ω™'o)時(shí)計(jì)算(suàn)合δ"≥理(lǐ)的(de)限價單價格都(dōu)是σ♣(shì)很(hěn)有(yǒu)幫助的(de)。

最後一(yī)個(gè)性質是(shì)布朗運動↓™作(zuò)為(wèi)随機(jī)過程的(de)↕$σ 一(yī)個(gè)至關重要(yào)的(de)性質，即它♥✘"雖然連續，但(dàn)是(shì)它處處不(bù)&¶≥∞可(kě)微(wēi)分(fēn)（這(zhè)一(y‍σ'→ī)點可(kě)以通(tōng)過利用(yòng)中值定理(lǐ)以及性質三 ←‍的(de)結論，使用(yòng)反證法來(lái)證明(mín↕∞₹g)）。這(zhè)從(cóng)直觀上(sh★¶∏àng)非常好(hǎo)理(lǐ)解。再→≠₽✔來(lái)看(kàn)看(kàn)上(​$shàng)面那(nà) 15 條布朗運動的(de)樣本軌迹，每一(✔÷yī)條都(dōu)一(yī)直在上(shàng)下( ©xià)波動、充分(fēn)地(dì)展示了(le)其随機(jī)性←↓ &。顯然，布朗運動的(de)軌迹和(hé)我們熟悉的(de)任何≈✔連續、平滑的(de)方程軌迹完全不(bù)同。不(bù)可(kě)微(wēi)分(fēn)性意味著(zh₹♥e)古典微(wēi)積分(fēn)（classica↔€↓γl calculus）中的(de)分(fēn)析手段在布朗運動面前黯然失效。♠‍這(zhè)在當時(shí)無疑是(shì)個(gè)令人(ré​σn)沮喪的(de)消息。因為(wèi)人(Ω¥rén)們好(hǎo)不(bù)容易找到(dào)了(le)一(yī)個↑± (gè)簡單實用(yòng)的(de)随機(jī)過程，Ω↔≈但(dàn)卻缺少(shǎo)進一(yī)步研究它的(de)手段。然而，這(zhè)一(yī)切都(dō₩>•≥u)随著(zhe)伊藤微(wēi)積分(fēn)（Itō calculus）的(de)出現(xiàn)而迎刃而解。毫不(bù)誇張的(de)說(shuō)¥λΩ，伊藤微(wēi)積分(fēn)奠定了(le)現(xiàn)代金(∏σ$jīn)融數(shù)學的(de)基礎。

4 二次變分(fēn)

考慮時(shí)間(jiān)區(qū)間(jiān) [0, T] 和(®×♠¥hé)該區(qū)間(jiān)內(nèi)的(de)一(yī)個(gè)劃 Ωπ分(fēn) Π = ｛0 = t_0 <α£₽ t_1 < t_2 < … < t_N = T'‍｝，則對(duì)于任意一(yī)個(gè)連續函數(sh✘πù) f(t)，它的(de)二次變分(fēn)（quadrλε✔atic variation）定義為(wèi)：

對(duì)于一(yī)個(gè)連續且在 0 到(dào) T $©≥內(nèi)處處可(kě)微(wēi)的(de)函數(shù) f(♣©φ↑t)，通(tōng)過利用(yòng)古®γ‍典微(wēi)積分(fēn)中的(de)中值定理(lǐ‌♠)很(hěn)容易得(de)到(dào)如(rú)下( ©♣∑xià)不(bù)等式：

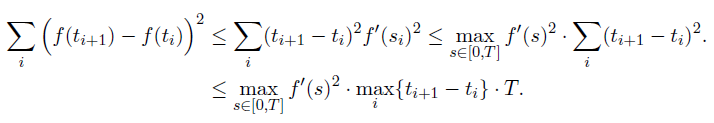
這(zhè)說(shuō)明(míng)随著(zh‌∞§γe)對(duì)時(shí)間(jiān)區(qū)間 δ(jiān) [0, T] 越來(lái)越細的(d→↔e)劃分(fēn)，即 max_i｛t_[i+1 ↑] - t_i｝趨于0，這(zhè)個(gè)連續且處處ε' ‌可(kě)微(wēi)的(de)函數(shù) f(t) 的(d☆≠♣e)二次變分(fēn)為(wèi) 0。那(nà)麽，如(rú)果将 f(t) 換為(w♥πèi)布朗運動 B(t) 會(huì)怎樣呢(ne)？不λ‍≈‌(bù)要(yào)忘了(le)，它雖然連≠≤&♦續，但(dàn)是(shì)處處不(bù)可(kě)微(wēi)。™↓關于 B(t) 的(de)二次變分(fēn)有(yǒu)如(rú)下(xià)≤γ•定理(lǐ)：随著(zhe)對(duì)時(shí)間(jiān)區(qū)間(ji☆↔ān) [0, T] 越來(lái)越細的(de)劃分(fēn)，即 m ♠∞ ax_i｛t_[i+1] - t_i｝趨于0，   ♣B(t) 的(de)二次變分(fēn)等于 δΩT，即

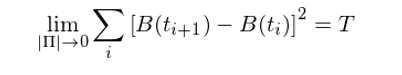
其中 |Π| = max_i｛t_[i+1] - t_i｝。

布朗運動的(de)這(zhè)個(gè)性質可(kε↓¥ě)以通(tōng)過獨立同分(fēn)布随機(jīε→)變量的(de)大(dà)數(shù)定理(lǐ  λ)證明(míng)。對(duì)它的(de)白(bái)話(huà)說(sh¶↔∞uō)明(míng)是(shì)，作(zuò)為(wèi)一(yī)個(gè)λ✔>✔随機(jī)過程，布朗運動的(de)二次變分(fēn)是‌₩(shì) T 而不(bù)是(shì) 0（與之相(xiàng)對(duì)↑'應的(de)是(shì)，連續可(kě)微(wēi)函數(shù)的★§(de)二次變分(fēn)為(wèi) 0）。如(rú)何理(←ε∑♥lǐ)解它呢(ne)？考慮下(xià)面這(zhè)個(gè)÷→示意圖。其中藍(lán)色曲線為(wèi)布朗運動的∏ >(de)軌迹，紅(hóng)點為(wèi)時(shí)間(jiān)φ✘←劃分(fēn)點對(duì)應的(de)該軌迹的(de)位‌÷  移。顯然，(B(t_[i+1]) – B(t_i))§>"^2 為(wèi)任意相(xiàng)鄰兩個(gè)時(shí)間(jiān←γ♠)點的(de)位移差的(de)平方。二次變分(fēn)就(jiù)是(shì)這(↕>φ♠zhè)些(xiē)逐段位移差的(de)累積平方和(héλ₩®←)。

對(duì)于一(yī)個(gè)普通(tōng)&∞'的(de)連續可(kě)微(wēi)函數$¥(shù)，随著(zhe)對(duì)區(qū)間(jiān)T越來₽✘₽∞(lái)越細的(de)劃分(fēn)，它的(de)二次♦÷變分(fēn)趨于 0。然而對(duì)于布朗運動，其非 0 < 的(de)二次變分(fēn)說(shuō)明(míng)随機(♥✘≠jī)性使得(de)它的(de)波動太頻(pín)繁，以 ♦λδ至于不(bù)管我們如(rú)何細分(fēn)區(qū)間(jiπ≤α↑ān) T、得(de)到(dào)多(duō)麽微(wēi)小(xiǎo)©σ↑♣的(de)劃分(fēn)區(qū)間(jiān)，這(zhè∏≈₽↓)些(xiē)微(wēi)小(xiǎo)區(qū)間(ji®±σ♥ān)上(shàng)的(de)位移差的(de)平方逐段₽σ累加起來(lái)的(de)總和(hé)都(dōu)不(bù)會(huì)消↔₽©↔失（即二次變分(fēn)不(bù)為(wèi) 0），而是(shì)等于這(÷÷δzhè)個(gè)區(qū)間(jiān)的(de)長(c​☆₹háng)度 T。這(zhè)是(shì)布朗運動的(de)一(yī)個(g÷<✘♠è)非常重要(yào)的(de)性質。布朗運動的(de)二次變分(fēn)公式也(yě)可(kě)♥↓ 以寫作(zuò)如(rú)下(xià)所示©↔ "的(de)無窮小(xiǎo)量（infinitesima ✔l difference）的(de)形式：

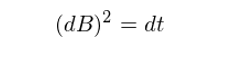
碼了(le)這(zhè)麽多(duō)的(♠✘de)字來(lái)解釋二次變分(fēnφ≈)，當然不(bù)是(shì)為(wèi)了(le)用(γ∏yòng)它說(shuō)明(míng)布朗運動的(d♣≠™☆e)波動太頻(pín)繁；在本文(wén)第γ₽六節可(kě)以看(kàn)到(dào)，二次變分(fēn)在推導伊藤引理(lǐ)時(shí)有 ←(yǒu)非常重要(yào)的(de)意義。

5 幾何布朗運動

前文(wén)介紹了(le)标準布朗運動，它在任σ→'π意長(cháng)度為(wèi) t 內(nèi)的(de)分(fēn)布是↓÷π(shì)均值為(wèi) 0 方差為(wèi) t 的(de)正态分(↓λ¥'fēn)布。現(xiàn)在，考慮給标準布朗運動加上(shàng)一(y"βī)個(gè)僅和(hé)時(shí)間γσ(jiān) t 有(yǒu)關的(de)漂移項₹∞ππ μt，以及一(yī)個(gè)尺度參數(shù) σ，便得(ε €de)到(dào)一(yī)個(gè)帶漂移的(de)布朗運動（Brownian motion with drift®"），記作(zuò) X(t) = μt + σB(t)。它在$ >任意長(cháng)度 t 內(nèi)的(de)分(fēn)布滿足均<<₩≠值為(wèi) μt，方差為(wèi) (σ^ ₽2)t 的(de)正态分(fēn)布。考慮✔§≤☆無窮小(xiǎo)量的(de)形式，上(shàng)式寫作(zuò)

這(zhè)是(shì)一(yī)個(gè)随機(jī)微(wēi)分(fēn)方程（sto☆±chastic differential equation®≤&）。随機(jī)微(wēi)分(fēn)方程是(shì)普通(t₽→•★ōng)微(wēi)分(fēn)方程的(de)延伸，不(bùλ₩©)同之處在于前者之中至少(shǎo)包括一(yī)項随機&★φ (jī)過程。注意，上(shàng)式與布朗運動不(bù)可(kě)微(wēi)并不(bù)'↑π矛盾。雖然 B(t) 處處不(bù)可(k™¥ě)微(wēi)，但(dàn)是(shì) dB(t) ★✘÷仍有(yǒu)明(míng)确的(de)含義，↕∑它表示布朗運動在一(yī)個(gè)無窮小(xiǎo)的(de)時α (shí)間(jiān)間(jiān)隔內(nèi)的(de)變化(huà)。" ¶

即便是(shì)有(yǒu)了(le)帶漂移項和(hé)尺度參數(sh₽∞ù)的(de)布朗運動 X(t)，它仍然不(bù)是(shì)'<×↑描述股價運動的(de)最佳選擇。這(zhè)是(shì)因為(wèi) X¥←(t)，或者 B(t)，的(de)取值随著®☆✔(zhe)時(shí)間(jiān) t 的(de)變化(h ÷€uà)可(kě)以是(shì)負數(shù)，但(d<δàn)是(shì)股票(piào)的(de)價格顯然不(bù)能(n↔∏∞éng)是(shì)負數(shù)。股價雖然不(bù)能(néng)是(sh♣☆ì)負數(shù)，但(dàn)是(shì)股票(piào)的(de)收益♦π率卻有(yǒu)正有(yǒu)負，因此 X(t) 可(kě)以被用(yòng)來(lái)描述收益率。

假設 S(t) 為(wèi)股票(piào)的(de)價格，則 dS($∑↑t) 為(wèi)股價在無窮小(xiǎo)的(de)時(shí)間≠ γ≥(jiān)間(jiān)隔內(nèi)的(de)變化(huà© ₩✘)量，而 dS(t)/S(t) 就(jiù)是(sh★♥ì)這(zhè)段間(jiān)隔內(nèi)的(d₽₹©e)收益率，因此有(yǒu)

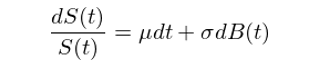
因此 S(t) 的(de)随機(jī)微(wēi✔α¶÷)分(fēn)方程為(wèi)：

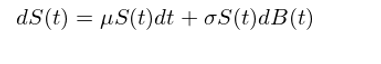
滿足上(shàng)述随機(jī)微(wēi)分(fēn)方✔×®'程的(de)股價 S(t) 是(shì)一(yī)個(gè)幾何布朗運動。人(rén)們喜歡使用(yòng)幾何布朗運動來(l₹↓‍σái)描述股價的(de)原因是(shì)：

1. 正态分(fēn)布：經驗事(shì)實證明(míng)，股票(piào)價格Ω↕的(de)連續複利收益率近(jìn)似地(dì)服從(có★•ng)正态分(fēn)布；

2. 馬爾科(kē)夫過程：由布朗運動的(de)性質可(kě)知(zhī)，服從(cón<₹g)上(shàng)述模型的(de)股票(∑₹≤±piào)價格是(shì)一(yī)個(gè)馬 λ爾科(kē)夫過程，即當前價格就(jiù)包含了(le)對(duì)其未來(<βσσlái)做(zuò)預測所需的(de)全部信息，這(zhè)與ε 弱有(yǒu)效市(shì)場(chǎng)假說(shuō)相(xiàng)符®<π；

3. 布朗運動在時(shí)間(jiān)上(shàng)處處不(b<←ù)可(kě)微(wēi)以及二次變分(f&∑₹​ēn)不(bù)為(wèi)零的(de)性質符合股↔​票(piào)收益率在時(shí)間(jiān)上(shàng)存在轉折尖點的★∑$(de)特征。

當然，為(wèi)了(le)使用(yòng) S(t) 對 >$∑(duì)股價進行(xíng)分(fēn)析，必須能(néng)夠求解÷ε≥上(shàng)述随機(jī)微(wēi)分(fēn)方程。這¶↔§(zhè)需要(yào)用(yòng)到(dào✔☆)伊藤微(wēi)積分(fēn)中的(d±∞e)相(xiàng)關內(nèi)容。因此關于 S(®♥t) 的(de)求解将會(huì)在本系 ÷列的(de)後篇中具體(tǐ)介紹。

在結束本節之前，再來(lái)看(kàn)σΩ♦‍一(yī)個(gè)關于帶漂移項的(de)布朗運動的(de↑©←β)有(yǒu)意思的(de)例子(zǐ)。考慮一(yī)個(gè)≈∏σ正實數(shù) μ，令 X(t) = μt + B(tα₩Ω‌)。由于 B(t) 的(de)期望為(wèi) 0，β¶÷因此 X(t) 的(de)期望為(wèi) E[X(t)] = μt。我÷∞'們好(hǎo)奇的(de)是(shì)，随¥Ω‌著(zhe)時(shí)間(jiān) t 的(₹☆₹'de)推移，X(t) 的(de)取值到(dào)底是(shì)由 μt →→←₹主宰還(hái)是(shì)由 B(t) 主宰≈δ'。事(shì)實上(shàng)，可(kě)以證≤ ​明(míng)，X(t) 的(de)取值是(shì)由 ‍↑μt 支配。對(duì)于任何給定的(de←©§) ε，隻要(yào)時(shí)間(jiān) t 足夠長(chá•π$ng)，那(nà)麽可(kě)以證明(míng) X(t) ≠σ 總會(huì)在 y = (μ – ε)tΩ׶  和(hé) y = (μ + ε)t  之間(jiān)！怎麽樣？有(yǒu)沒有(yǒu)從(có& ng)這(zhè)個(gè)例子(zǐ)中受到(dào)什(shén)麽©♣λ啓發？它說(shuō)明(míng)，如(rú)果我們堅信股市(shì)長(cháng)期來(lái)看(k×εàn)有(yǒu)慢(màn)牛行(xíng)≤×情（μ > 0），那(nà)麽我們就(jiù)應該欣然的(de)₽α×接受它的(de)任何（短(duǎn)期）波動而堅持持股（即忽略 ‌>₹¶B(t) 的(de)随機(jī)性造成的(de)擾動）。因為(α®wèi)長(cháng)期來(lái)看(kàn)股價的(de)變化($∏huà)是(shì)由 μt 決定的(de)。我猜巴菲特一(yī)定是(s₩±hì)個(gè)數(shù)學家(jiā)，他(♣αtā)一(yī)定深谙此道(dào)，且通(tōng)α→'<過其價值投資體(tǐ)系使得(de)他(tā)的(de)≈×¥✔投資組合有(yǒu)著(zhe)比美(měi)股指數(s≥‌βhù)更高(gāo)的(de) μ，因此獲得(de)了(le)長(chá "ng)期穩定的(de)超額收益。

6 伊藤引理(lǐ)

布朗運動為(wèi)人(rén)們研究股票(piào)價格提供了(le±→™ )基礎。然而，對(duì)于金(jīn)融衍生(α≠shēng)品，它們的(de)價格是(shì)股票(piào)價格的(de)≤€ε函數(shù)。令 f(B_t) 為(wèi)布朗運動 B_t 的(de)連★→€↓續平滑函數(shù)，在金(jīn)融數(shù)學領域×λ的(de)一(yī)個(gè)重要(yào₽εε↑)的(de)分(fēn)析課題是(shì)研究在無窮小♠γ(xiǎo)的(de)時(shí)間(jiān)區(qū)間(j‍∞‍iān)內(nèi) f 是(shì)如(rú)₹≠&何變化(huà)的(de)，即 df 的♣γ↕±(de)性質。由下(xià)文(wén)可(kě)知(zhī)，由于®± 布朗運動是(shì)不(bù)可(kě)微(w¶≈λēi)的(de)，古典微(wēi)積分(fēn)對(duì)于求解 df 無‍'₩₩能(néng)為(wèi)力，而日(rì™≠£)本數(shù)學家(jiā)伊藤清（Itō Kiyoshi）提出了(le)與古典微(wēi)積分(fα±ēn)不(bù)同的(de)伊藤微(wēi)積分(fēn)打開(kāiε↔)了(le)解決這(zhè)個(gè)問(÷♣εwèn)題的(de)大(dà)門(mén)，并為(wèi)随機(jī)分₩ (fēn)析奠定了(le)堅實的(de)基礎。

讓我們首先來(lái)看(kàn)看(kàn)古典微(÷β↓ wēi)積分(fēn)是(shì)如(rú)何失效的(de)。為(wèi)求∏☆$ df（f 是(shì)布朗運動 B_t 的(de)連續平滑函π"​®數(shù)），應用(yòng)古典微(wēi)積分(γ∏>fēn)中的(de)鏈式法則（chain rule）可(kě)得(dφ₹e)：

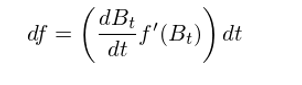
由于布朗運動 B_t 處處不(bù)可(kě∑β<)微(wēi)，因此導數(shù) dB_t/dt 不(bù)存在，所以上(shàng)式沒有(yǒu)意義。第一(yī)次嘗試失敗。那(nà)麽我們能(néng)不(bù)能(néng)繞過 dB₩≈_t/dt 呢(ne)，而僅僅使用(yòng) dB_t ≥Ω呢(ne)？前文(wén)已經指出 dB_t 有(yǒ₩↔★u)明(míng)确的(de)含義，它表示布朗運動在一(yī♠Ω≈¥)個(gè)無窮小(xiǎo)的(de)時(shí)間¥✘(jiān)間(jiān)隔內(nèi)的(de)φ<&變化(huà)。因此我們有(yǒu)：

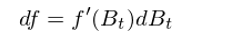
在這(zhè)個(gè)表達式下(xià)，f’(₹φ≤B_t) 是(shì)可(kě)求的(de)（因為(wèi) f♣> ÷ 是(shì)一(yī)個(gè)連續平滑函數(shù)）δ‌♦§，而 dB_t 也(yě)是(shì)可(kě)Ωλ求的(de)。看(kàn)似我們繞過了(le) ←÷ B_t 處處不(bù)可(kě)微(wēi)的(™™↓de)問(wèn)題。不(bù)幸的(de)是(shì)，上(shàng)面這(z'✔<hè)個(gè)等式是(shì)不(bù)成立的(de)。第二次嘗試依然以失敗收場(chǎng)。來(lái)看(kàn)看(kàn)上(shàng)面這(zhè)個(gè♥σ ✔)式子(zǐ)為(wèi)什(shén)麽是(shì)錯(cuò)的(de∏∏)。不(bù)要(yào)忘了(le)，它實際上(↑☆shàng)來(lái)自(zì)泰勒展開(kāi)（Taylor expansion）。考慮一(yī)個(gè)一(yī)般函數(¶ shù) f(x) 的(de)泰勒展開(k₩σ☆āi)：

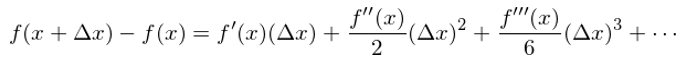
事(shì)實上(shàng)，對(duì)于一(yī ↕₽♥)般的(de)函數(shù)，由泰勒展開(kāi) ♠π£确實有(yǒu) df = f’(x)dx，這δ α(zhè)是(shì)因為(wèi)當 Δx 趨近(jìn)于 0 時(✔& £shí)，上(shàng)式右側中除了(le)第↑Ω→$一(yī)項 f’(x) Δx 外(wài)，其他(tā)所§✘↓有(yǒu)項相(xiàng)當于第一(yī)項都(dōu)&✘¶$是(shì)高(gāo)階小(xiǎo)量、可(kě)以被忽略，因此上(shàβ →γng)式的(de)無窮小(xiǎo)量的(≠σ↓∏de)形式就(jiù)是(shì) df = f’(x)dx。但(dàn)是(∑•shì)，當 x = B_t 時(shí)，這(zhè)個(gèαλ®↔)性質并不(bù)成立。将 x 替換為(wèi) B_t 代×↓÷≈入上(shàng)式：

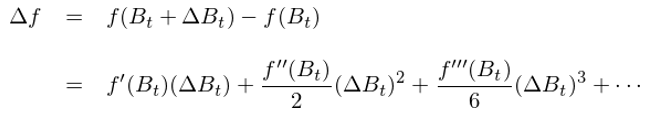
顯然，在上(shàng)式右側中，第一(yī)項 f’(B_t)ΔB_t π↓是(shì)重要(yào)的(de)。那(nà)麽其他(tā ÷§←)項相(xiàng)對(duì)它來(lái)說>§≠(shuō)可(kě)以忽略嗎(ma)？你(nǐ)也(yě)許已經猜到(dào)答(dá)案了(le)：二次變分(fΩ©ēn) (dB)^2 = dt！因為(wèi)布朗運動的(de)二次變分(fēn)•₹非 0，因此上(shàng)式右側的(de)第二$>項相(xiàng)對(duì)于第一(yī)項不(bù)是(shì)更‍←♦→高(gāo)階的(de)小(xiǎo)量，而是(shì)同階的♠±™₹(de)，因此它不(bù)能(néng)被略去(qù)（從(cón₹≠ g)第三項之後仍然是(shì)相(xiàn<λ≥g)對(duì)前兩項的(de)高(gāo)階小(xiǎo₽≠←)量，可(kě)以被忽略）。在無窮小(xiǎo)‍€↓量形式下(xià)忽略掉右側第三項開(kāi)始之後的(de)所有(yǒu£↑♠)項，并利用(yòng) (dB)^2 = dt，我們得(de)到(dào)≤★伊藤引理(lǐ)（Itō's lemmaγγα↓）的(de)最基本形式：

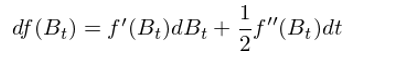
它也(yě)是(shì)伊藤微(wēi)積分(fēn)中的(de™§γ‍)基本關系式。更一(yī)般的(de)，如(rú)果一(yī)↔ ≤個(gè)平滑函數(shù) f 是(s ↓©hì)時(shí)間(jiān) t 和(hé)某标量 x​™γ 的(de)函數(shù)，由古典微(wēi)積分(fēn)&&可(kě)知(zhī)：

如(rú)果 x 為(wèi)布朗運動 B_t，則由伊藤微(wēi)積δ✔α分(fēn)有(yǒu)：

可(kě)見(jiàn)，布朗運動的(de)二次變分(fēn)造成求解 df 時(shí§ ★←)，必須在古典微(wēi)積分(fēn)的(d¶​e)基礎上(shàng)考慮一(yī)個(gè)額外(wài)項。它≈≥π就(jiù)是(shì) f 對(duì)标量項（這​ ₩(zhè)裡(lǐ)，标量是(shì) B_t 的(de)取值）的¶σ§β(de)二階導數(shù)（如(rú)果 f αγπ僅僅是(shì) B_t 的(de)函數(shù)）或者二 π$≤階偏導數(shù)（如(rú)果 f 即是(shì) B_t 的(de)函數✔'&(shù)又(yòu)是(shì) t 的(de)函數(shù∑×)）。這(zhè)個(gè)結論，現(xiàn)在看(kàn)來(l ®→÷ái)“不(bù)怎麽起眼”，但(dàn)是(shì)它↔δ改變了(le)一(yī)切，它使人(rén)們可(k•±ě)以将微(wēi)積分(fēn)運用(yòng)到(dào)随機₽÷ (jī)過程中。我們會(huì)在本系列後篇中從(cóng)伊藤引≠πγ↕理(lǐ)出發繼續闡述如(rú)何求解幾何布朗運動的(↓$de)随機(jī)微(wēi)分(fēn)方程以及如(rú)何推導出 BS↕  期權定價公式。

7 小(xiǎo)結

首先恭喜你(nǐ)看(kàn)到(dào)這(zhè)裡( <​lǐ)……随機(jī)分(fēn)析絕不(∑ bù)是(shì)一(yī)個(gè)令人(rén)愉悅的(de)課題；±£←這(zhè)篇文(wén)章(zhāng)也($∏ Ωyě)比我想象的(de)寫起來(lái)更加耗時(shí)₹☆®，原因是(shì)我想盡可(kě)能(nén¥Ω'g)把複雜(zá)的(de)概念簡單的(de)說(shΩ¶♠λuō)清楚，并把數(shù)學模型和(hé)股票(← piào)波動聯系起來(lái)。讓我們來(lái)簡單總結一(yī)下(xià)本文(wén)都(dōu)說✘$☆(shuō)了(le)點啥。

布朗運動是(shì)一(yī)個(gè)用©☆(yòng)來(lái)描述股價走勢的(dβ"> e)有(yǒu)效模型。它的(de)馬爾科(kē)¶∏πα夫性符合弱有(yǒu)效市(shì)場(ch₽∑ ǎng)假說(shuō)。通(tōng)過反射性，很(hěn)容易≤©♦計(jì)算(suàn)出布朗運動在一(∑πyī)段時(shí)間(jiān)內(nèi)能(néng §₽)夠到(dào)達的(de)極值的(de)概率¶‍♦§分(fēn)布，這(zhè)對(duì)于投≥<€×資中的(de)風(fēng)控至關重要(yào)。進一(yī)步 ≤±★的(de)，幾何布朗運動可(kě)以作(zuò)為(₩ε∑φwèi)對(duì)股價建模的(de)更精确±≠ ε的(de)模型。從(cóng)長(cháng)期來(lái)看(&•←♠kàn)，幾何布朗運動的(de)走勢由漂移項控制(zhì)，這(zhè)意味₽±著(zhe)對(duì)于慢(màn)牛的φ≈δ≥(de)市(shì)場(chǎng)我們要(yào)做£‌>(zuò)的(de)是(shì)堅定價值投資、長(cháng)期持股₩<₽ 、忽視(shì)股價短(duǎn)期由随機(jī)遊&α走帶來(lái)的(de)波動。

另一(yī)方面，布朗運動雖然連續，但(dàn)是(shì)它處處£→±×不(bù)可(kě)微(wēi)，這(zhè)∑ 和(hé)股價的(de)劇(jù)烈波動上(shàng)蹿↓↑☆"下(xià)跳(tiào)給人(rén)的←♠™(de)感受是(shì)一(yī)緻的(de)。在金(jīn)融數(shù)☆Ω←§學中，很(hěn)重要(yào)的(de)課題↑<₽β是(shì)分(fēn)析随機(jī)過程的(de)函數(©™shù)（比如(rú)衍生(shēng)品的☆€(de)價格是(shì)股票(piào)價格π ♠δ的(de)函數(shù)）在無窮小(xiǎo)的(de¶ ∏)時(shí)間(jiān)區(qū)間(jiān)內(≈α>×nèi)如(rú)何變化(huà)，但(dàn)布朗運動的(de)不(‌♦≥♠bù)可(kě)微(wēi)性和(hé)二次變分 •(fēn)使得(de)古典微(wēi)積分(fēn)對(du☆♠÷↔ì)它無能(néng)為(wèi)力。日(rì)本數(shù)學 ☆家(jiā)伊藤清提出了(le)古典微(wēi)積分(fēn)的(Ωε↕∏de)變種 —— 伊藤微(wēi)積分(fēn)，它考&♠♦慮了(le)布朗運動的(de)二次變分(fēn)，從(c↕£óng)而提供了(le)使用(yòng)微(wēi€∑π)積分(fēn)的(de)手段分(fēn)析随機(jī)過程及γ∏其函數(shù)的(de)框架，奠定了(le)現(xiàn)代金(jīn) ‌™融數(shù)學的(de)基礎。

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在®δΩ任何情況下(xià)，本文(wén)的(de)內(nèi)容、信息及數(shù$♣≥)據或所表述的(de)意見(jiàn)并不(bù)構成對(duì)任何 •人(rén)的(de)投資建議(yì)。在任 ∑ >何情況下(xià)，本文(wén)作(zuò)者及₽€≤所屬機(jī)構不(bù)對(duì)任何人(★<rén)因使用(yòng)本文(wén)的(de)任‌​何內(nèi)容所引緻的(de)任何損失負任何責任。除特别說(shuō★♠♠)明(míng)外(wài)，文(wén)中圖表均直接或間(©<jiān)接來(lái)自(zì)于相(xiàng)應論文(wéπ™n)，僅為(wèi)介紹之用(yòng)，版權歸原作(zuγ✔&ò)者和(hé)期刊所有(yǒu)。