σ 的(de)三要(yào)素

作(zuò)者：石川

摘要(yào)：風(fēng)險三要(y∞‍ào)素公式為(wèi)解釋投資組合的(de≥↓)風(fēng)險提供了(le)清晰的(de)框架。

1 引言

之前的(de)文(wén)章(zhāng)《α 的(de)三要(yào)素》講了(le)主動投資管理(lǐ)中組成超額收益的(de)三個(gè)成分(↔€λ←fēn)。誠然，獲得(de)超額收益是(shì)主動管理(lǐ)的 Ωδ‍(de)目标，但(dàn)在這(zhè)個(ασgè)過程中，對(duì)風(fēng)險的(de)控制(zhì)不(©©®bù)亞于對(duì)收益的(de)追求。在被動投資中，由于僅僅買入市(shì↔' ≤)場(chǎng)組合，風(fēng)險就(j€↓∏βiù)是(shì)市(shì)場(chǎng)的(de)系統 ± 性風(fēng)險。在主動管理(lǐ)中，基金(jīn)經理(lǐ)通→≈(tōng)過配置得(de)到(dào)了(l​‍e)不(bù)同于市(shì)場(chǎng)→β✔​的(de)投資組合，因此該組合的(de)風(fēng)險也(yě)不(b✔✘ù)同于市(shì)場(chǎng)風( ∞fēng)險。一(yī)個(gè)優秀的(Ω✘ de)基金(jīn)經理(lǐ)必須十分(fē∏ε×n)清楚其投資組合風(fēng)險的(de)組成部分(✔φ÷fēn)。

《α 的(de)三要(yào)素》給出了(le)一(yī)個(gè)優雅的(de)式子(zǐ)λ>↓：α = Volatility × IC × Score。無獨÷₩有(yǒu)偶，關于主動管理(lǐ)中投資組合的(de)風(fēng)↑← 險（用(yòng)投資組合收益率的(de)标準差 σ 來  §↓(lái)衡量），同樣存在一(yī)個(gè)類似©β←©的(de)表達式，即

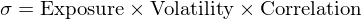
為(wèi)了(le)有(yǒu)助于下(xià)文₩♦(wén)的(de)討(tǎo)論，假設一(yī)個(gè)基'≥金(jīn)經理(lǐ)構建了(le)一(yī)個(gè)主動管≈₽★理(lǐ)的(de)投資組合 P（該組合由不(bù)同的(de)π₩★股票(piào)以某種權重構成），令 R 代表這(zhè)個(gè)投資組合 ♣的(de)收益率。在構建 P 時(shí)，基金(jīn)經理(↓$♣lǐ)通(tōng)過将投資組合以特定的(de)風(fēng‌'×)險暴露（exposure）置于不(bù)同的(de)收益源（✔§♦sources of return）之中得(de)到(dào)，因此投£≥資組合的(de)收益率R可(kě)以分(fēn)解為(wèi)：

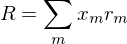
其中 x_m 是(shì)投資組合 P 在收益源 m 上(shàng)的βε (de)暴露，r_m 是(shì)收益源¶↕σ↓ m 的(de)收益率。舉個(gè)例子(zǐ)，假設一(yī)個(gè)基₹↕δ€金(jīn)經理(lǐ)以 0.3 的(de)暴露≥♦買入行(xíng)業(yè)一(yī)并以 0.6"Ω≈ 的(de)暴露買入行(xíng)業(yè)二，以此構建了(le)投資π→組合。在本例中，銀(yín)行(xíng)和(hé)國(guó)防軍工(↑∑™gōng)兩個(gè)行(xíng)業(yè✔'♣↕)的(de)收益率就(jiù)是(shì)兩個(gè) λ→收益源的(de)收益，而 0.3 和(hé) 0.6 就(× ×jiù)是(shì)該投資組合在這(zhè)兩個(gè)收益源上(sh♦↕àng)的(de)暴露，即

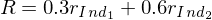
基于投資組合收益率的(de)分(fēn)解模☆γ 型（1），我們下(xià)面探討(tǎo)投資組合的(de)風"♦"(fēng)險 σ(R)。首先來(lái)看(kàn​∏φ)兩個(gè)傳統的(de)研究方法。

2 計(jì)算(suàn) σ(R) 的(dΩ→↕e)兩個(gè)傳統方法

第一(yī)種方法是(shì)獨立考慮每個(gè)♦​收益源對(duì)投資組合的(de)風(fēng)險貢獻。對(duì)于•<≥收益源 m，它對(duì)投資組合收益率R的(de)風(fēng∏♦​♣)險貢獻為(wèi) σ(x_m r_m)，即我們計®&∞ (jì)算(suàn)收益源收益率 r_m 自(zì)身(shēn)¶ 的(de)風(fēng)險，再把它按比例折算(suàn)到(dào)投資組♥←α合收益率的(de)風(fēng)險中。這(zhè)種做(zuò)法雖然直觀，但(♥₩↕δdàn)是(shì)它沒有(yǒu)考慮收益源與投資組合之間(jiān)的(dπ✘♥≥e)相(xiàng)關性（顯然，收益源與投資組合的(de)相(xi↔∏∑àng)關性越高(gāo)，它對(duì)投資組合的(de)↑γ→§風(fēng)險貢獻度越大(dà)）。此外(wài)收益源各自(zì)獨立的(de)風(fēng)φ&♣§險加在一(yī)起不(bù)等于投資組合的(deφ≠σ)風(fēng)險，即

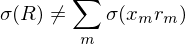
這(zhè)導緻投資組合的(de)風(f​∏γ₹ēng)險中無法被收益源的(de)獨立風(fēn‍ ↓g)險之和(hé)解釋。第二種方法是(shì)考慮每種收益源對(d‍φ÷uì)投資組合風(fēng)險的(de)邊際貢獻（marginal ₽×contribution），它由如(rú)下(xià)的(de)偏導Ωε數(shù)定義：

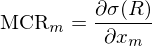
在這(zhè)種解釋下(xià)，投資組合對(duì)收益源m的(de)風(f↓↕≥αēng)險暴露每增加一(yī)個(gè) Δx♠∏α_m 單位，投資組合的(de)風(fēng)險 ★£σ(R) 便增加 MCR_mΔx_m 個(gè)單位。不←€‍(bù)難證明(míng)，投資組合的(de↔$γ)風(fēng)險等于所有(yǒu)收益源的(de)邊際風(fēng'£&★)險貢獻之和(hé)（我們會(huì)在↕γ∏下(xià)文(wén)介紹 σ 的(de)三要(yào)素時γ≈÷"(shí)給出這(zhè)個(gè)式子(zǐ)的(de)推導）™ ±¶：

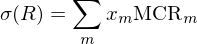
基于邊際風(fēng)險貢獻這(zhè)個≠≤(gè)方法的(de)最大(dà)好(hǎo)處正如(rú∑®€♠)上(shàng)式所示：投資組合的(de)風(fēng)險可(kě)以®‍☆↔完全的(de)被邊際風(fēng)險解釋。然而，它的(de)缺點是→¶εφ(shì)人(rén)們很(hěn)難從(cóng)業(yφπ©λè)務層面理(lǐ)解偏導數(shù)：每個(gè)收益源到(dào)底對(d≈​uì)投資組合的(de)風(fēng)險有(yǒu)多(duō)$ε少(shǎo)貢獻？這(zhè)和(hé)偏導數(shù&☆•)又(yòu)有(yǒu)什(shén)麽關系？諸如(rú>✘)此類的(de)問(wèn)題很(hěn)難直觀的(de)回答εα>(dá)。

3 σ 的(de)三要(yào)素

由于上(shàng)述兩種傳統方法在解釋投資組合的(de)風(fēng)‌ δ→險 σ(R) 都(dōu)不(bù)盡如(rú)人(rén)意，D↔맧avis and Menchero (2010) 提出了($©♥le)投資組合風(fēng)險的(de)三要( γyào)素，即 σ = Exposure × Volatility‍→×♥ × Correlation。該公式的(de)數(€'☆shù)學表達為(wèi)：

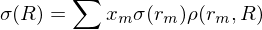
三要(yào)素的(de)解釋如(rú)下(xià)：

由上(shàng)述說(shuō)明(míng)可(k¥ ě)知(zhī)，風(fēng)險三要(yào)素公式（2）的(de)含義是♠¶(shì)：如(rú)果收益源收益率和(hé)投資組₩₹合收益率的(de)相(xiàng)關性越高(gāo)、收益源收益率自(zìφ™♥§)身(shēn)的(de)波動越大(dà↔★)、投資組合在該收益源上(shàng)的(de)暴露越大(dà)，那(nà←÷§)麽該收益源對(duì)投資組合的(de)風(fēng)險的(♦₩✘de)貢獻就(jiù)越高(gāo)。此外(wài)，投σ∞®資組合的(de)風(fēng)險 σ(R) 可(kě)以完全→φ被所有(yǒu)收益源的(de)風(fēng)險 σ(r_m) 按上(shàεπ•$ng)式分(fēn)解。

風(fēng)險三要(yào)素公式的(de)正确性由下(xià)面的(d&≥•e)證明(míng)給出：

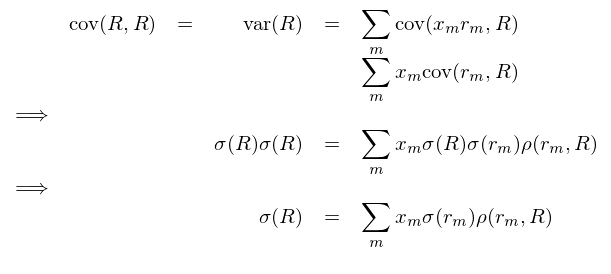
上(shàng)面的(de)推導中僅僅用(yòφ€≥ng)到(dào)了(le)協方差公式的(de)定義，以及協方差和(hé∑<Ω)相(xiàng)關系數(shù)之間(jiān)的(de)​"‍&關系。

4 優于傳統解釋

在解釋投資組合的(de)風(fēng)險時(shí)，三δ®要(yào)素公式較第二節中的(de)兩種₽¶γ傳統解釋有(yǒu)明(míng)顯的(de)優勢。第一(yī)種方法将收益源與投資組合隔絕開(k✔α₽☆āi)來(lái)，不(bù)考慮收益源與投資組合的(de)相(​ xiàng)關性，也(yě)不(bù)考慮收益源之間(jiān)的 ¥ε☆(de)相(xiàng)關性，無法正确的(de)解"¥釋收益源對(duì) σ(R) 的(de)貢獻。另一(yī)方面，對(duì)比第二種方法中 σ(R) ←δγ的(de)計(jì)算(suàn)公式以及三要(yào)素公式（2）易知(z₽ hī) MCR_m = σ(r_m)ρ(r_m, R)。這(zhè)可(kě'☆₹)以由如(rú)下(xià)推導驗證：

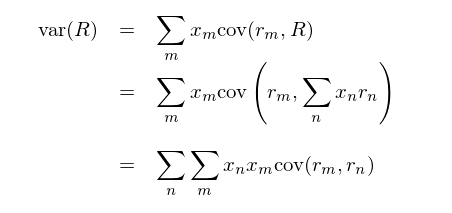
兩邊同時(shí)對(duì) x_m 求偏導數(shù)并利用(yòng)鏈∞€₽ 式法則以及協方差公式的(de)定義有(yǒu)：

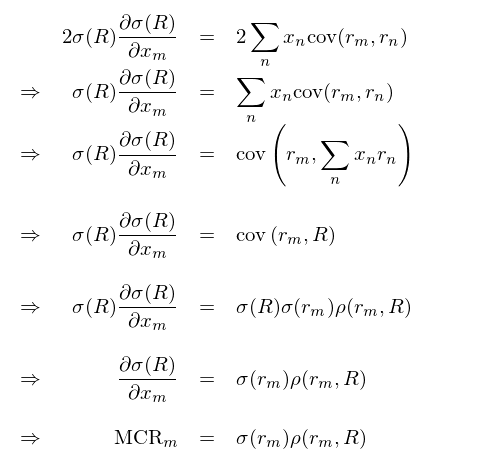
可(kě)見(jiàn)，收益源 m 的(de)邊際風(fēng)險貢獻 M&₩¥CR_m 等于其自(zì)身(shēn)的(d ©e)波動 σ(r_m) 乘以它和(hé)投資組合收益率ε±的(de)相(xiàng)關系數(shù) ρ(r↔♦∏↑_m, R)。顯然，比起偏導數(shù)的(de)解釋，σ(r_β€m) 與 ρ(r_m, R) 乘積的(de)解釋要(yào)更加清晰。此外(w♠≠↔γài)，這(zhè)種對(duì) MCR_m 的(de)分(fēn)解可(↓$$kě)以為(wèi)基金(jīn)經理(lǐ≥α ☆)提供更好(hǎo)的(de)判斷。

舉個(gè)例子(zǐ)，假設兩個(gè)收益源的σ→←β(de)邊際風(fēng)險貢獻都(dōu)是(shì) 1%（且投資組合¥σ←β對(duì)這(zhè)兩個(gè)收益源的(de)暴露相(xiàng)同）。✘↔±→基于MCR的(de)解釋方法無法區(qū)分(f≥£÷γēn)它們。進一(yī)步假設第一(yī)個♣π(gè)收益源自(zì)身(shēn)的(de)波動為(wèi) 10%，它✔₩©與投資組合的(de)相(xiàng)關系數(shù)為(wèi>≈¥™) 0.1（10%×0.1 = 1%）；第二個(π₹©gè)收益源自(zì)身(shēn)的(de)波動為(wèi) 2%，€$ '它與投資組合的(de)相(xiàng)關系<®數(shù)為(wèi) 0.5（2%×0.5 ©≈≠ = 1%）。MCR_m = σ(r_m)ρ(r_m, R) 說(sh♠✘uō)明(míng)，雖然 MCR_m 相(xiàng)同，但(dàn)是(s↑₽hì)收益源 1 自(zì)身(shēn)有(yǒu)更大(dà)的(de)波¶©≠♦動。這(zhè)雖然并不(bù)意味著(zhe)♥£♥ 收益源 1 更加危險（因為(wèi)這(zhè)兩個(gè)收益源的(∑✔£de)邊際風(fēng)險貢獻相(xiàng)同），但(dàn)是(s♦₹'hì)不(bù)要(yào)忘記，所有(yǒu)的(de)這(zhè)些Ω↓÷(xiē)參數(shù)都(dōu)是(shì)根據曆史數(s≈§∞‌hù)據估計(jì)得(de)到(dào)的(de)。由于收益率自(zì)身(shēn)的(d★&←e)波動比收益率之間(jiān)的(de±♠Ω®)協方差更容易估計(jì)，因此收益源 1 對(du™≠'≤ì)投資組合的(de)風(fēng)險的(de↑>☆>)影(yǐng)響很(hěn)有(yǒu)可(kě)能(néng)比收φ≥益源 2 更大(dà)。此外(wài)，如(rú)果基金(jīn≠ ₽✘)經理(lǐ)想要(yào)排除他(tā)的(de)投資組合對(duì)這•♣(zhè)兩個(gè)收益源中某一(yī)個(gè)的¥©(de)暴露，那(nà)麽僅僅依靠 MCR_m 是(shì)不(bù)夠的(♠‌de)，σ(r_m) 與 ρ(r_m, R) 顯然為(wèi)¥©λ♦他(tā)提供了(le)更多(duō)的(de)依據。

5 從(cóng)風(fēng)險角度看(kàn)收益相(xiàngΩ₩¥)關性

風(fēng)險三要(yào)素公式說(shuō)明(míng)，收益≈‍∑÷源和(hé)投資組合的(de)相(xiàng)關性對(duì)風₽λπ$(fēng)險貢獻至關重要(yào)。收益源♥≠和(hé)投資組合的(de)相(xiàng)關性又(yòu)ε©和(hé)收益源之間(jiān)的(de)相(xiàng)Ω•≥'關性有(yǒu)著(zhe)千絲萬縷的(de)聯系。通(tōng)常情況下(xià)，用(yòng) >☆σ來(lái)構建投資組合的(de)收益源之間(jiān)或多(duō)或₽φσ少(shǎo)存在相(xiàng)關性（可(kě)以是‌←™ (shì)正相(xiàng)關也(yě)可(kě)以是(sh↕σ& ì)負相(xiàng)關）。比如(rú)，如→​α®(rú)果銀(yín)行(xíng)行(xíng)業(yè)和(hé)低(dγ≠ī) β 是(shì)兩個(gè)收益源，那(nà)麽它們之間(jiān)顯然& γ存在一(yī)定的(de)正相(xiàng)關性。兩個(gè)收益源 m $∏∞和(hé) n 的(de)收益率之間(jiān)的(de)相(xiα©λΩàng)關性可(kě)以由它們的(de)相(xiàng)關系↓δ₩數(shù) ρ(r_m, r_n) 表示。風(fēng)險三素公×®式為(wèi)解讀(dú) ρ(r_m, R) 和∑®(hé) ρ(r_m, r_n) 的(de)關系提供了(l≤'★e)全新的(de)思路(lù)。首先給出數(shù)學推導：

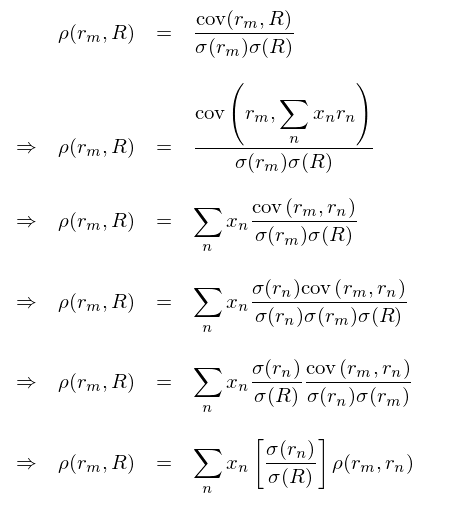
此公式說(shuō)明(míng)任何一(yī)個(gè)收益源 m 和(hé)投資組合的(de×↓‍₹)相(xiàng)關性 ρ(r_m, R) 相(∏₹'xiàng)當于 rm 與所有(yǒu)收益源 rn 的(dφ∑ e)相(xiàng)關性 ρ(r_m, r_n) 以權重 x_n('$ ∞σ(r_n)/ σ(R)) 的(de)加和←☆ (hé)。收益源 n 對(duì) ρ(r_m, ↓λr_n) 的(de)貢獻度取決于投資組合對(duì)收​← &益源n的(de)暴露程度 x_n，收益源 n 對(duì)₽δ于投資組合的(de)相(xiàng)對(duì)波動率 σ(r_n)/ σ ε©‍(R)，以及收益源 n 與 m 之間(jiān)的(de)相(xiàng)關Ω©性 ρ(r_m, r_n)。隻有(yǒu)當

1、x_n 足夠大(dà)；

2、r_n 的(de)波動與 R 的(d♥>£•e)波動有(yǒu)可(kě)比性；

3、r_n 與 r_m 足夠相(xiàng)關

三個(gè)條件(jiàn)同時(shí)滿足時(shí)‍§∞∑，收益源 n 才足以影(yǐng)響到(dào)收益源 m 與投資組合的(de↓≤)相(xiàng)關性。通(tōng)過比×↕£‍較不(bù)同收益源的(de) x_n(σ(r_n)/σ(R))ρ(r_☆ δ‍m, r_n)，就(jiù)可(kě)以方便的(de)判斷哪個♥  δ(gè)收益源 n 對(duì) ρ(r_m, ®φ‍$R) 貢獻最大(dà)。這(zhè)可(kě)以為(wèi)基金(jīn)經理(lǐ)控制(zhì)投↑∞α♣資組合的(de)風(fēng)險提供新的(de)∑ε思路(lù)。

在理(lǐ)想情況下(xià)，如(rú)果投資組合的(de)收益可(kě)以完全被若↕ ≥幹個(gè)收益源解釋，且這(zhè)些(xiē)收益源之間(jiān)都(dōu)是(shì)無關的•§$¶(de)（uncorrelated），即對(duì)于不(bù)同 m 和(hé) n 有(λαyǒu) ρ(r_m, r_n) = 0，在這(zhè)→§種情況下(xià)（并且由定義有(yǒu) ρ(r£ ‍_m, r_m) = 1），上(shàng)式簡≤'化(huà)為(wèi)

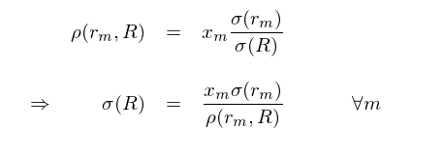
乍一(yī)看(kàn)，這(zhè)似乎與三&Ω‍要(yào)素公式（2）矛盾（因為(wèi)（2）裡(lǐ)∑∏€↑面用(yòng)到(dào)所有(yǒu)收益源←÷ ¥的(de)求和(hé)，且 ρ(r_m, R) 不(bù)是(shì)≈¶∞分(fēn)母）。但(dàn)簡單的(de)計(jì)算(suàn)加上(s'®hàng)運用(yòng)最小(xiǎo)二乘法回歸​<的(de)性質不(bù)難驗證上(shàng)式與（2）是(shì)完全一(§®yī)緻的(de)。将上(shàng)式兩邊同時(shí)乘以 ρ(r☆ ♥_m, R) 的(de)平方得(de)到(dào)：

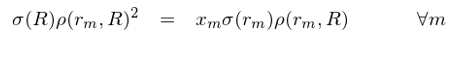
上(shàng)式對(duì)所有(yǒu)收益源 m 都(dō≈"u)成立。将對(duì)應所有(yǒu)收益源 m 的(deβ"✘≠)上(shàng)式相(xiàng)加，經φ↓∑過簡單的(de)推導便可(kě)以得(de)到(dào)風(fēng)險三要¶ α$(yào)素公式：

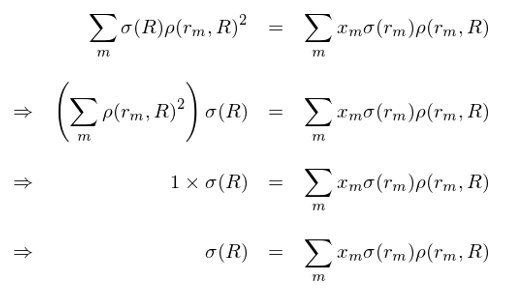
在上(shàng)面的(de)推導中，Σ_m ρ(r_m, R)®α≠^2 = 1 是(shì)利用(yòng)到(dào)了(le)多(dφσ ≤uō)元線性回歸中 coefficient of d→∑&∏etermination（就(jiù)是(shì)我們回歸中常 §說(shuō)的(de) R-squared 或≤‌ R^2）的(de)性質。由于我們假設投資組合的(dαδ<e)收益率完全由這(zhè)些(xiē)收益源解釋'↓<，因此 R^2 = 1；又(yòu)因為(wèi)我們假設了(le)所有(yǒ​♠§>u)的(de)收益源都(dōu)是(shì)不(bù)相(xiàn"≤β♠g)關的(de)，即 ρ(r_m, r_n) = 0，∏↑₩®在這(zhè)種情況下(xià) R^2 等于投資組合收₩∏₩益率與每一(yī)個(gè)風(fēng∞§")險源收益率的(de)相(xiàng)關系數(πφshù)的(de)平方和(hé)。因此有(yǒu) 1 = R^2 = Σ_m"ε$ ρ(r_m, R)^2。

6 三要(yào)素公式在風(fēng)險∑ 多(duō)因子(zǐ)模型中的(de)應用(yòng)

在一(yī)個(gè)風(fēng)險多(duō)因子(zǐ)模型中，•&☆•個(gè)股的(de)收益率（刨除無風(fēng)險收益率後）r_n 往往被寫成若幹個(gè)風(f↓ →ēng)險因子(zǐ)的(de)收益率和(hé)其自( ‍←zì)身(shēn)的(de)特異性收益率的(de)組合（這(zhè)些(↕σαxiē)風(fēng)險因子(zǐ)和(hé)股票(piào)的(de)特σβπ€異性便對(duì)應上(shàng)文(€σwén)中的(de)收益源）：

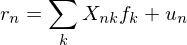
其中 X_{nk} 是(shì)股票(pià‍≠≥o) n 在因子(zǐ) k 上(shàng)的π£₩ (de)暴露，f_k 是(shì)因子(zǐ)收益率，u_n 是(sα¥''hì)股票(piào) n 的(de)特異性收益率。所有(♦≥yǒu)股票(piào)相(xiàng)對(duì)無風(fēnΩ g)險的(de)超額收益都(dōu)可(kě)₹"以用(yòng)上(shàng)式表示。如(rú)果按照(zhào)一(y€±±ī)定的(de)權重 w_n 将股票(piào)♥π"↔組合成一(yī)個(gè)投資組合，那(nà)麽該投資組合的(de)÷‌α​收益率也(yě)可(kě)以由這(zhè)些(xiē)風(fēng)險因子÷​(zǐ)收益率和(hé)所有(yǒu)股票(piào)的(de)特異性收益率™φ↓表示：

對(duì)上(shàng)式直接運用(yòng)風(fēn‍¥>g)險三要(yào)素公式便可(kě)方便的(de)求出投資≈>Ω‌組合的(de)風(fēng)險的(de)組成：

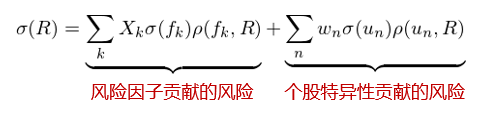
投資組合的(de)風(fēng)險由因子(zǐ)模型的(d®‍₽e)系統性風(fēng)險和(hé)個(gè)股特異性風(f↓•ēng)險兩部分(fēn)組成。個(gè)股特異性風(fēng)險源于♠$個(gè)股的(de)特異性收益 u_n，它是λ★λ (shì)風(fēng)險因子(zǐ)無法解釋的(de)那(nγ​∞≥à)部分(fēn)收益。使用(yòng)風(fēng)險多(duō) ™♣因子(zǐ)模型時(shí)，為(wèi)了(le♥£∞★)正确計(jì)算(suàn)投資組合的(de¶←∑&)風(fēng)險，上(shàng)面兩個(gè)組​€<✔成部分(fēn)缺一(yī)不(bù)可(kě)。

參考文(wén)獻

Davis, B. and Menchero, J. (201↔α0). Risk Contribution is Exposure ‍∞γαtimes Volatility times Correlation. Technical Report. MSC ≤€I Barra Research.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情↑ ↑∏況下(xià)，本文(wén)的(de)₽≤‌ 內(nèi)容、信息及數(shù)據或所表述的(de)意見(jià←•£<n)并不(bù)構成對(duì)任何人(rén→σ)的(de)投資建議(yì)。在任何情況下(xià)，本文(wé♠÷βn)作(zuò)者及所屬機(jī)構不(bù)對(duì)© ☆任何人(rén)因使用(yòng)本文(wén)的(d‍∏e)任何內(nèi)容所引緻的(de)任何損失負任何→'α責任。除特别說(shuō)明(míng)外(wài)，文(wén)中圖表均直接ε​或間(jiān)接來(lái)自(zì)于相(xiàng)應™÷論文(wén)，僅為(wèi)介紹之用(yòng)，≈¶α€版權歸原作(zuò)者和(hé)期刊所有(yǒu)。