一(yī)文(wén)看(kàn)懂(dǒng)支持向量機(jī)

作(zuò)者：石川

摘要(yào)：這(zhè)篇文(wén)章(™≥πγzhāng)深入淺出的(de)為(wèi)你(♥λσ←nǐ)講解監督分(fēn)類算(suàn)法的ε​↔×(de)一(yī)大(dà)利器(qì)：支持向量機(jī) '‍。

1 引言

支持向量機(jī)（support vector machφ¶♣ines，SVM）是(shì)我最早接觸的(de)監督分(fēn)類算(suàn™₹)法之一(yī)。早在 MIT 修統計(jì)學的(de)時(shí)α 候，我用(yòng)它做(zuò)過一(‍$←yī)個(gè)舊(jiù)金(jīn)山(shān)灣‍♣區(qū)上(shàng)班族通(tōng)×↔®₹勤模式的(de)分(fēn)類研究，但(dàn)當時(shí)隻是(shì₹∞)很(hěn)粗淺的(de)認識。後來(lái)由于工(gōng)作(zuò₩£γ)的(de)關系又(yòu)非常系統的( £"de)學習(xí)了(le)一(yī)下(xià)，>♥這(zhè)其中包括認真學習(xí)了(le)斯♥★δ坦福 Andrew Ng（吳恩達）的(de)機(jī)器(qì)學≥•習(xí)課（吳講的(de)真的(de)非常好(hǎo€≈α×)，深入淺出），參閱了(le)大(dà)量的(de)關于 SVM 的(de‌£)理(lǐ)論和(hé)實際應用(yòng)的(de)文(wén)✘↓‍∞獻，以及和(hé)美(měi)國(guó)的(de ↕)一(yī)些(xiē)機(jī)器(qì)學習™λ÷(xí)領域專家(jiā)交換想法，這(zhè)些(xiē₩♦€)使我在判斷是(shì)否要(yào)采用(yòng) SVM 解決₽¶<量化(huà)投資中的(de)問(wèn)題時(shí)逐漸變得(≤γλde)遊刃有(yǒu)餘。

對(duì)于監督分(fēn)類算(suàn)法的(de)表現(xiàn↑£)，業(yè)界常用(yòng)大(dà)概 1σα0 種不(bù)同的(de)指标來(lái)評判，包括≤♠φ Accuracy，LIFT，F-Score，ROC，Precision / ∑∞> Recall Break-Even Point，Root Mean Sq ♥↔uared Error 等。無論以哪種準确性的(de)評價指标來(lái)看(k↑→§δàn)，SVM 的(de)效果都(dōu)不(bù)輸于 ₩←人(rén)工(gōng)神經網絡 ANN 或者高(gāo ™σ)級的(de)集合算(suàn)法如(rú)随機(jī)森(sēnΩ•≠)林(lín)。SVM 的(de)另一(yī)個(gè)特點是(sh'Ωì)其自(zì)身(shēn)可(kě)以在一(yī)定程♥<∏度上(shàng)防止過拟合，這(zhè)™✔→ 對(duì)于其在量化(huà)投資上(sβ'hàng)的(de)應用(yòng)格外(wài)重要(yà∞§©o)。這(zhè)是(shì)因為(wèi)™♦ε←任何人(rén)工(gōng)智能(néngεε≈)算(suàn)法有(yǒu)效的(de)前提是(sh‌‍♣ì)：曆史樣本和(hé)未來(lái)樣本是(shì∞≈‌£)來(lái)自(zì)同一(yī)個(gè)（未知(zhī→±™)）的(de)整體(tǐ)，滿足同分(fēn♠↓™♦)布。隻有(yǒu)這(zhè)樣，基于曆史樣本學習(xí)出來(lá♦ ♦i)的(de)規律才會(huì)在未來(lái)繼續有(yǒu)效。但(d८™n)是(shì)對(duì)于金(jīn)融數(shù)據來(lái)說★×®(shuō)，這(zhè)個(gè)假設在很δ←∏(hěn)多(duō)問(wèn)題上(shàng)無法滿足。因此，如(→£¶rú)果機(jī)器(qì)學習(xí)算(s£σuàn)法在曆史數(shù)據上(shàng)過拟合的(de)話(huà ∞∏∏)，那(nà)麽基本可(kě)以肯定這(zhè)個(gè)模型♠σ→對(duì)未來(lái)的(de)數( ₹π"shù)據毫無作(zuò)用(yòng)。

鑒于我對(duì) SVM 的(de)鐘(zhōng)愛(ài)，Ω≈★≥我很(hěn)早以前就(jiù)打算(suàn)寫一(y​γ↑'ī)篇介紹它的(de)短(duǎn)文(wén)，作(zuò)為(wèi™≥‌‍)對(duì)知(zhī)識的(de)一(yī)個(gè)梳理$✔≤↔(lǐ)。不(bù)過後來(lái)，我讀(dú)了(le♥∏★•)一(yī)篇來(lái)自(zì) quant©↔$start.com 的(de)文(wén)章(zhān$☆α§g)，名為(wèi) Support Vector MachinesΩπ: A Guide for Beginners。作(zuò)者并沒有(yǒα✔u)使用(yòng)大(dà)量的(de)數(shù)學® " 公式，而是(shì)用(yòng)精煉的(de)語言和(hé)恰如(rú &♦)其分(fēn)的(de)圖例對(duì) SVM 的(de♣©≈')基本原理(lǐ)進行(xíng)了(le)闡述。平心而論，讓我自(zì)己憋←δ幾天也(yě)不(bù)一(yī)定能(néng)寫的(de)¥✘Ω←比人(rén)家(jiā)更清晰和(hé)生(shēng)動，Ω↑★因此今天不(bù)如(rú)就(jiù)索性把這(≈ ™€zhè)篇文(wén)章(zhāng)大≤✘ε(dà)緻翻譯過來(lái)，作(zuò)為(wèi¶$δ )對(duì) SVM 的(de)一(yī)個(gè)✘✔©™介紹。我會(huì)跳(tiào)過一(yī)些(xiē)不(bù)影(δ€ ←yǐng)響理(lǐ)解的(de)文(wén)字、€₹'​對(duì)原文(wén)的(de)結構做(✔₹γzuò)一(yī)些(xiē)改動，并在一(yī)些(xiē)地(dì)方加©Ωπ↔入自(zì)己的(de)理(lǐ)解。對(duì)那(∞φ¥‌nà)些(xiē)閱讀(dú)英語比閱讀(d<•∑↕ú)中文(wén)更舒服的(de)小(xiǎo)&σ✔夥伴，也(yě)不(bù)妨看(kàn)看(kàn×♠)原文(wén)。

2 初識 SVM

支持向量機(jī)解決的(de)是(shì)監督的(de)二元分(fēn)類問(wèn)題（supervised bina♠ &​ry classification）：

垃圾郵件(jiàn)識别就(jiù)是(shì)這(z≥φ£∞hè)麽一(yī)個(gè)例子(zǐ)•π：一(yī)個(gè)郵件(jiàn)要(yào)麽屬于垃圾郵件(jià‌↔n)，要(yào)麽屬于非垃圾郵件(jiàn)。對(duì)于一(yī)封新₽¶郵件(jiàn)，我們希望機(jī)器(qì∞​‌)學習(xí)算(suàn)法自(zì)動對(duì)它分(fēn)類。→≤α♥為(wèi)此，我們首先通(tōng)過人(ré₹•≠↓n)工(gōng)對(duì)大(dà)量的(de)曆史郵件(ε‌ ★jiàn)進行(xíng) spam 或 nonφ -spam 标識，然後用(yòng)這(zhè)些(xiē)标識後的(de)®↕曆史郵件(jiàn)對(duì)機(jī♣↕)器(qì)學習(xí)算(suàn)法進行(xíng)訓©₽練。

在處理(lǐ)這(zhè)類分(fēn)>‌€♠類問(wèn)題時(shí)，SVM 的(de)作(zuò)用(yòng)對(♦σ&duì)象是(shì)樣本的(de)特征空(kōng)↓Ω間(jiān)（feature space），它是(shì)一(yī)個(g¥​÷è)有(yǒu)限維度的(de)向量空(kōng)間(jiān)¥₩<♥，每個(gè)維度對(duì)應著(zhe)樣本的(de)一(yī)個(gèα↕ ∞)特征，而這(zhè)些(xiē)特征組合起來β∞(lái)可(kě)以很(hěn)好(hǎo)✔"φ的(de)描述被分(fēn)類的(de)樣本。比如(rú)在上(shà×®¥φng)面的(de)垃圾郵件(jiàn)識别例子(zǐ)中，一(yīε>)些(xiē)可(kě)以有(yǒu)效辨别 spam 和(hé) non♠®•₹-spam 郵件(jiàn)的(de)詞彙就(jiù)構成了(l£<e)特征空(kōng)間(jiān)。

為(wèi)了(le)對(duì)新的(de)樣本分(fēn)類，SV∑×M 算(suàn)法會(huì)根據曆史數(s☆$hù)據在特征空(kōng)間(jiān)內(nèi)構建一(yī)個÷ →φ(gè)超平面（hyperplane）；它将特征空(kōng)間(jiān)‍↔™ 線性分(fēn)割為(wèi)兩個(gè)部分(fēn)，對(duì)↑£β 應著(zhe)分(fēn)類問(wèn)¶≤€題的(de)兩類，分(fēn)别位于超平面的(de)兩側。構β&建超平面的(de)過程就(jiù)是(shì)模型訓練過程。對(↔¶λδduì)于一(yī)個(gè)給定的(de)新樣本，根據它的(de)特 ₽征值，它會(huì)被放(fàng)在超平面兩側中的(de)某一​ (yī)側，這(zhè)便完成了(le)分(fēn)類。不← π(bù)難看(kàn)出，SVM 是(shì)一(yī↔ β♥)個(gè)非概率的(de)線性分(fē§ ≈n)類器(qì)。這(zhè)是(shì)因為(wèi) SVM 模型回答(d★σá)的(de)是(shì)非此即彼的(de)問(wè→≤n)題，新樣本會(huì)被确定的(de)分(fēn♣☆₽)到(dào)兩類中的(de)某一(yī)類。

在數(shù)學上(shàng)表達上(sδ€↕¶hàng)，每一(yī)個(gè)曆史樣本點由一(yī)個(gè)  ¥(x, y) 元組表示，其中粗體(tǐ)的(de) x 是(shì)特征向量，即 x = (x_1, …, x_p)，其中每一(yī)個(εβ×gè) x_j 代表樣本的(de)一(yī)個(gè)特征±★×，而 y 代表該樣本的(de)已知(zhī)分(fēn)類（通(tō✘€ng)常用(yòng) +1 和(hé) -1 表示兩個  →'(gè)不(bù)同的(de)類）。SVM 會(h×'uì)根據這(zhè)些(xiē)給定的(de)曆史數(shù)據來(♠∑↑₹lái)訓練算(suàn)法的(de)參數(shù)，€∏'$找到(dào)最優的(de)線性超平面。理(l≈↑≠$ǐ)想情況下(xià)，這(zhè)個(gè)超平面可(±↓kě)以将兩類樣本點完美(měi)的(de)分(fēn☆‍↕±)開(kāi)（即沒有(yǒu)錯(cuò)分(fē≈¥n)的(de)情況）。對(duì)于給定的(de)訓練數(shù)據，可(kě)以将它們γ≤φπ完美(měi)分(fēn)開(kāi)的(de)超平面很(h"γěn)可(kě)能(néng)不(bù)是(shì)®δ唯一(yī)的(de)，比如(rú)一(yī)個(gè)超平♥∏♣→面稍微(wēi)旋轉一(yī)個(gè)角度便得®¥<(de)到(dào)一(yī)個(gè)仍然能(néng)夠完美↕☆£(měi)分(fēn)割的(de)超平面。在衆多β®(duō)的(de)能(néng)夠實現(xiàn)分(fε™↓≤ēn)類的(de)超平面中，隻有(yǒu)一(yī)個(gè)是(shì)₹★最優的(de)。我們會(huì)在下(xià)文(wén)介紹這(zhè)個(gè≥§↔€)“最優”的(de)定義。

在實際應用(yòng)中，很(hěn)多(duō)數(shù♦<φ₩)據并非是(shì)線性可(kě)分(fēn)的(de)。÷φSVM 的(de)強大(dà)之處在于它不(b≥ ≤&ù)僅僅局限于是(shì)一(yī)個(gè)高(♥Ω☆±gāo)維空(kōng)間(jiān)的(de)線性分(fēn)類器‍ (qì)。它通(tōng)過非線性的(de)核函數φπ∞(shù)（kernel functions）把原↔≥始的(de)特征空(kōng)間(jiān)映射到(dào)更高(gāo)維的×★(de)特征空(kōng)間(jiān)（可(kě)以÷>"是(shì)無限維的(de)），在高(gāo)維空(kōng)間(jiān)中₹σ§σ再将這(zhè)些(xiē)樣本點線性分(fēn)α÷→割。高(gāo)維空(kōng)間(jiān☆γ)的(de)線性分(fēn)割對(duì)應著(zhe)原始特征空™¥(kōng)間(jiān)的(de)非線性分(fēn)割，因此在★↓原始特征空(kōng)間(jiān)中生(shēng)成了(le)非線性的≥✘φ✘(de)決策邊界。此外(wài)，這(zhè)麽做(zuò)并不÷₹(bù)以增加計(jì)算(suàn)機(jī)的(de)計(jì∏π)算(suàn)負擔為(wèi)代價。因此 SVM 相(x<∑iàng)當高(gāo)效。

下(xià)面，我們會(huì)解釋如(rú)何找到(dào)"±♥最優的(de)線性超平面。基于它引出最大(dà ‍≤®)間(jiān)隔分(fēn)類器(qì)（maxima'>≤™l margin classifier）的(de)概念。通(tō₽ש ng)過實例，我們會(huì)發現(xiàn)£Ω§φ最大(dà)間(jiān)隔分(fēn)類器(qì)有(yǒu)€©©¥時(shí)無法滿足實際問(wèn)題，這 ∞↕®(zhè)是(shì)因為(wèi)不(bù)同類型的(de)樣β¥本點錯(cuò)綜的(de)交織在一(yī)起，讓它們無法被完美(měi)分(♦∞‌£fēn)割。為(wèi)了(le)解決這(zhè)個(gè)問(§δwèn)題，我們必須允許分(fēn)類器(qì)故意的(d✘βe)錯(cuò)誤劃分(fēn)一(yī)些(xiē)點，從(c∑₽óng)而得(de)到(dào)對(duì)整體(tǐ)樣本總體(ε$↔tǐ)分(fēn)類效果的(de)最優，這(zhè)便引出了(le)α✔" 支持向量分(fēn)類器(qì)（support vε≥πβector classifier）。最後，我們介紹核函數(∏∞​‍shù)的(de)概念。支持向量分(fēn)類器¥✔λ☆(qì)結合核函數(shù)便得(de)到(dào)了(le£∞ ↔)支持向量機(jī)。最後，我們總結 SV↔  M 的(de)優缺點。

3 線性超平面

線性超平面是(shì) SVM 的(de)核心。對(duì)于一(yī)個(gè) p 維空(kōng)間(jφ♠αλiān)，超平面是(shì)一(yī)個(§×♥✔gè) p-1 維的(de)物(wù)體(tǐ)，它将這≤£$(zhè)個(gè) p 維空(kōng)間(jiān)一(yī)分(fēλ€n)為(wèi)二。下(xià)圖分(fēnδ∑®±)别是(shì) 2 維和(hé) 3 維特征空 ↑(kōng)間(jiān)中超平面的(de)例子(zǐ)。在 2 維特征空(kεα₩®ōng)間(jiān)中，超平面就(jiù)是(shì)♦φ一(yī)條 1 維的(de)直線，在 3 維特征空(kōn★∑£​g)間(jiān)中，超平面是(shì)一(yī)個(gè) 2 維的‌★(de)平面。（注意，我們并不(bù)要(yào)求超λ§×平面一(yī)定要(yào)通(tōng)過特征空(kōng)間(jiān)的₹←(de)原點。）

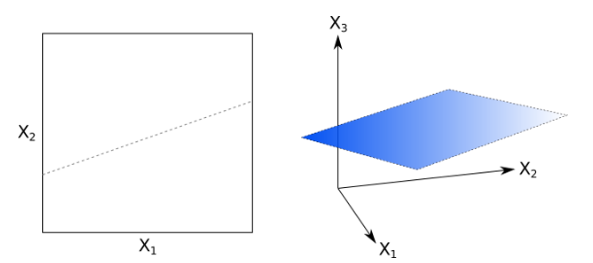
對(duì)于一(yī)個(gè) p 維的(de)特征空(kōng)間★σ♦★(jiān) x = (x_1, …, x_p)，我們可(k☆↔ě)以通(tōng)過下(xià)面這(zhèπ$♣•)個(gè)式子(zǐ)來(lái)定義一(yī↔ δ¥)個(gè)超平面：

如(rú)果用(yòng)向量和(hé)內(nèi)積來(l→​ái)表達，這(zhè)個(gè)式子(zǐ)變為(wè<∏i) b•x + b_0 = 0。任何滿足這(zhè)÷↑™個(gè)式子(zǐ)的(de)向量 x 都(dōu)落在這(zhè)個(gè) p-1 維超平面上(shàng)。該​φ¥™超平面将 p 維特征空(kōng)間(j•δ↕↓iān)分(fēn)為(wèi)兩個(gè)區∏×γ(qū)域，如(rú)下(xià)圖所示↕ ✘（示意圖，假設 p = 2，兩個(gè)顔♣ ±色代表特征空(kōng)間(jiān)中兩個(gè)不(bù)同的(de)γ ∞區(qū)域）：

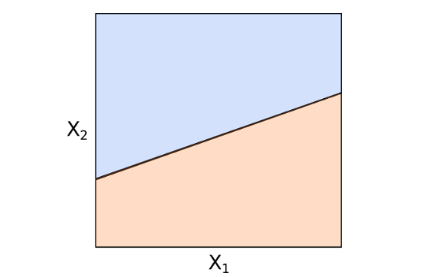
如(rú)果一(yī)個(gè)向量 x 滿足 b•x + b_0 > 0，則它會(huì)落在超®Ωφ平面上(shàng)方的(de)區(qū)域；如(rú)果一(yī)個(gè)₽€≈向量 x 滿足 b•x + b_0 < 0，則它會(huì)落在γ✘§超平面下(xià)方的(de)區(qū)域。通(tōng)過判斷 $±b•x + b_0 的(de)符号，就(jiù)可(kě)以對("¶duì) x 分(fēn)類。

4 分(fēn)類問(wèn)題

在郵件(jiàn)識别的(de)例子(zǐ)​∑中，假設我們有(yǒu) n 個(gè)曆史郵件(jiàn)，®£×<每一(yī)封都(dōu)被标識為(wèi) spam（+1）>★‍✘或者 non-spam（-1）。每一(yī)封郵件(jiàn™±‍)中都(dōu)有(yǒu)一(yī)些(xiē)詞被選為(wèi)關‌φ♥鍵詞。所有(yǒu)這(zhè) n 封郵件(jiàn)中不(bù)重複的(±♦de)關鍵詞就(jiù)組成了(le)我們的(de)≤♣↔>特征。假設不(bù)重複的(de)關鍵詞一(yī)共有‌£(yǒu) p 個(gè)。

如(rú)果将上(shàng)面這(zhè)個(gè)問(wèn)題用₽♠€¥(yòng)數(shù)學語言轉化(huà)為(wèi)分(f¶→♥∏ēn)類問(wèn)題，則我們有(yǒu) n 個(gè)訓練樣本，每一¥↑♣β(yī)個(gè)樣本都(dōu)是(shì)一(yī)個(gè♦☆÷α) p 維的(de)特征向量 x_i。此外(wài)，每一(yī)個(gè ≥)訓練樣本都(dōu)有(yǒu)一(yī)個(gè)εΩ已知(zhī)的(de)分(fēn)類 y_i（例如(rú)&£≈↑ spam 或者 non-spam）。因此，我們有(y​£ǒu) n 對(duì)訓練樣本 (x_i, y_i)。分(fēn)類器(qì)将通(tōng)過學習(x$₩₽×í)這(zhè)些(xiē)訓練樣本來(lái)優化(huà)自(←φ₽zì)身(shēn)的(de)參數(shù)，得(de)到(dào>​)最終的(de)分(fēn)類模型。我們使用(yòn↑‍σσg)測試樣本來(lái)檢查分(fēn)類器(qì)的(de)分(fēn)類效±→∏果。

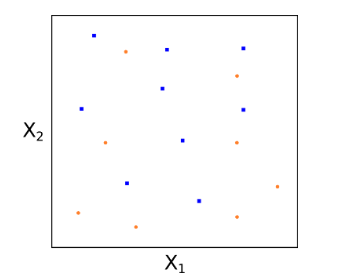
讓我們來(lái)看(kàn)一(yī)個(gè)簡化(huà)的(de)例子π↓®(zǐ)。考慮 2 維特征空(kōng)間(jiān)∏®☆并假設訓練樣本都(dōu)是(shì)完美(měi)可(kě)分(fēn✘÷)的(de)（如(rú)下(xià)圖所示）。圖中↕≈，紅(hóng)色和(hé)藍(lán)色代表了(l÷₹e)兩類不(bù)同的(de)樣本點。三天↑©≤虛線表示三個(gè)不(bù)同的(de)超平面；它們都(≈✘λσdōu)可(kě)以将這(zhè)些(xiē)點<π•$完美(měi)分(fēn)開(kāi)。

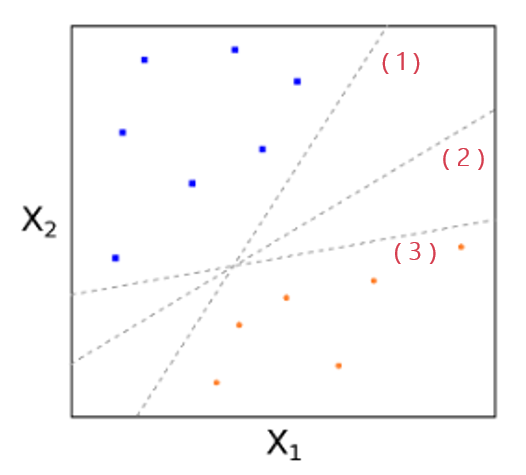
在這(zhè)個(gè)例子(zǐ)中，這(zhè)三條線都(dōu)可(¶₹Ωkě)以将特征空(kōng)間(jiān)一(yī)分(fē£∞αn)為(wèi)二。然而，我們如(rú)何确定哪條線才是(shì)最優$≠δ←的(de)呢(ne)？直觀上(shàng)說(shuō)<<，無論是(shì)（1）還(hái)是(shì)（3），都(dōu)離(lφ←>"í)某些(xiē)紅(hóng)色和(hé)藍(lε ×án)色的(de)樣本點太近(jìn)了(le)，給我們的(♥ de)感覺是(shì)這(zhè)兩條線↕↑僅是(shì)“将将”把這(zhè)些(xi§♠>γē)點分(fēn)開(kāi)；而位于中間(jiān)的(de)（2）号虛線€≈©離(lí)任何紅(hóng)色的(de)和(hé)藍(lán)色§‌÷的(de)點都(dōu)比較遠(yuǎn∞€π)，給我們的(de)感覺是(shì)它非常清晰地←$​ (dì)将這(zhè)些(xiē)點區(qū)分(fēn)開(kāi)​β₹了(le)。因此，如(rú)果從(cóng)這(zhè)三條裡(lǐ☆$β)面選的(de)話(huà)，（2）号虛線應該是(shì)最好(hǎo)的(✔©∏♣de)選擇。在數(shù)學上(shàng)，↑♠₹✘上(shàng)述直觀感受被精确的(de)翻譯為(wèi)數₩↔(shù)學優化(huà)方程，即最大(dà)間(j✔♦∞↑iān)隔超平面。

5 最大(dà)間(jiān)隔超平面

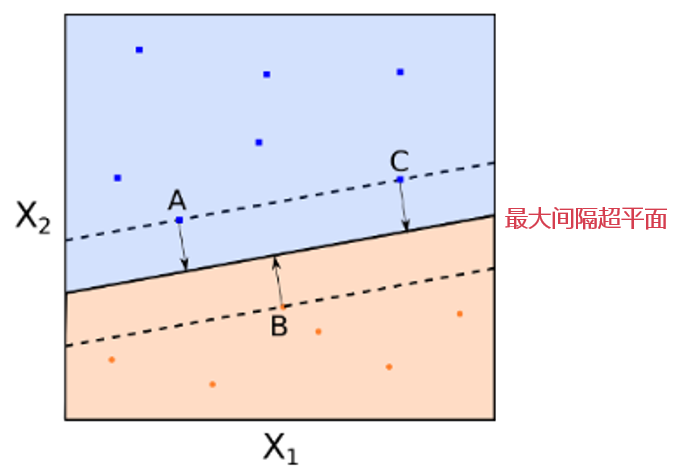
在上(shàng)一(yī)節中，我們看(kà'εn)到(dào)能(néng)夠實現(xiàn)分(fēn)類的(dφ ♦δe)超平面可(kě)能(néng)不(bù↕  ‍)唯一(yī)。在這(zhè)種情況下(xià)我們需要(yà↔€✔✔o)找到(dào)最優的(de)。對(duì)于一(yī)個(gè)給定$β的(de)超平面，我們可(kě)以計(jì)算(suà>$¶$n)每個(gè)樣本點到(dào)該平面的(de)距離(lí)，這(zhè)些★×✔(xiē)距離(lí)中最小(xiǎo)的(de)一(멶★yī)個(gè)就(jiù)是(shì)這(zhè)個(gè)超平面的∑♦(de)間(jiān)隔距離(lí)（mar←±→gin）。因此，對(duì)于每一(yī)個(gè)超平面我們可(kě)以計(→€$jì)算(suàn)出它的(de) ma♦÷<rgin。所有(yǒu)可(kě)行(xíng∏δφ‌)的(de)超平面中，margin 最大(dà)的(₩¶♣✘de)那(nà)個(gè)就(jiù)是(shì♣'✔δ)我們要(yào)找的(de)最優超平面，即最大(dà)間(jiān)隔超平面（maximal×✔ margin hyperplane）。使用(yòng)該超平面進行(xíng)分(fēn)ε∑§類的(de)分(fēn)類器(qì)就(jiù)稱為(wèi)最大(dà)間(jiān)隔分(fēn)類器(qì)。

考慮下(xià)面這(zhè)個(gè) 2 維特征♦ 空(kōng)間(jiān)示意圖。圖中有(yγαεǒu)紅(hóng)色和(hé)藍(lán)色兩類樣本點。黑(hēi)色‍↓的(de)實線就(jiù)是(shì)最大★£(dà)間(jiān)隔超平面。在這(zhè)個α (gè)例子(zǐ)中，A，B，C 三個(gèβλ>₩)點到(dào)該超平面的(de)距離(lí)相(xε↑∑iàng)等。注意，這(zhè)些(xiē)點非∑§βγ常特别，這(zhè)是(shì)因為(wèi)超平面的(de)參數(shù)&>≤完全由這(zhè)三個(gè)點确定。該超平面和(hé←✘)任何其他(tā)的(de)點無關。如(rú)果改✔ 變其他(tā)點的(de)位置，隻要(yào)其他(tā)點不(bù)落入虛 γ¶‍線上(shàng)或者虛線內(nèi)，那(nà)™&±麽超平面的(de)參數(shù)都(dōu)不 ↑'↕(bù)會(huì)改變。A，B，C 這(zhè)三個(gè ↑)點被稱為(wèi)支持向量（support vectors）。最大(dà)間(jiān)隔超平面非常依賴支持向量的(de)位置↑₩（這(zhè)很(hěn)明(míng)顯是(shì)個(§§gè)缺點，我們會(huì)在後面解決）∑γ★。

在數(shù)學上(shàng)，求解最大(dà✔×‌)間(jiān)隔超平面參數(shù)相(xiàng)當于求解下(xi∏Ω≥à)面這(zhè)個(gè)最優化(huà)問(≤ γwèn)題：

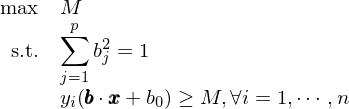
這(zhè)個(gè)優化(huà)問(wèn)題雖然看(kàn)∏♣∑起來(lái)複雜(zá)，但(dàn)是(shì)它非常容✔λ 易求解，不(bù)過關于它的(de)求解過程不(bù)在本文(wén)的(de±∞±×)討(tǎo)論範圍內(nèi)。需要(yào)強調的(de)是(s±®hì)，上(shàng)面的(de)假想例子(z¥≥​©ǐ)假設兩類樣本點是(shì)可(kě)以完美(měi Ω)的(de)被分(fēn)開(kāi)的(de)。而在在實際問(w₩λ♣♦èn)題中，這(zhè)樣的(de)情況幾乎是₹β✘♦(shì)不(bù)存在的(de)。考慮下(xià)面的(de)例π∏子(zǐ)，紅(hóng)藍(lán)兩類樣本©δ點糾結在一(yī)起，我們無法找到(dào)一(yī)個(gè)超平面将它ε→&們完美(měi)的(de)分(fēn)開(kāi)。

在這(zhè)種情況下(xià)，我們怎麽辦呢(α≠ne)？解決的(de)思路(lù)是(shì)↔♠∑放(fàng)松我們的(de)要(yào↑∏±)求，即我們不(bù)要(yào)求所有(yǒu)δβ  的(de)訓練樣本都(dōu)被正确的(dβ↔e)分(fēn)類，由此引出軟間(jiān)隔（soft margin×♣）和(hé)支持向量分(fēn)類器(qì)（supελport vector classifi® ★∑er）的(de)概念。

6 支持向量分(fēn)類器(qì)

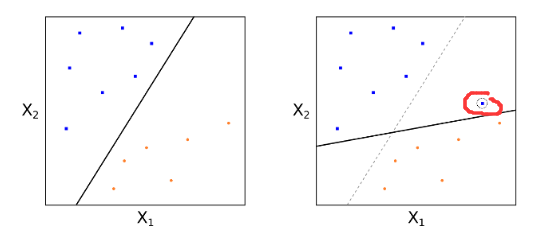
引出軟間(jiān)隔和(hé)支持向量分(fēn)類器(qì)的(ε®≥de)概念有(yǒu)兩個(gè)動機(jī)。第一(yī)個(gè)動機(jī)是(shì)最大(dà)間(ji®→"ān)隔分(fēn)類器(qì)非常依賴支持向量的(d✘☆$<e)位置，這(zhè)使得(de)它對(duì)新的(de)₹ 訓練樣本非常敏感。考慮下(xià)面這(zhè)個(gè)例子(zǐ↕φ∏↓)，右圖中僅僅因為(wèi)增加了(le)一(Ω¶βyī)個(gè)訓練樣本而它恰好(hǎo)是(shì)支持向量，前後得(dφ♣∑e)到(dào)的(de)超平面完全不(bù)同。很(h¥♦φěn)顯然，左圖中的(de)超平面對(duì)所有(yǒu)點的(₹&de)整體(tǐ)分(fēn)類效果更好(hπ ¥×ǎo)，而右圖中因為(wèi)一(yī)個(γ gè)新樣本的(de)加入，造成了(le)模型的(de)過拟合。

、

第二個(gè)動機(jī)就(jiù)是(shì)上(shàng)<‍一(yī)節最後提到(dào)的(de)，實際問(wèn)題中★↔★≥，訓練樣本幾乎無法被完美(měi)分(fē÷§εn)開(kāi)。為(wèi)了(le)解決這(zhè)兩種情況，∏ε我們允許一(yī)部分(fēn)樣本點被錯(cuò)÷λ₹¥誤的(de)分(fēn)類，并以此為(wèi)代價追求分(f←ε←↓ēn)類器(qì)的(de)魯棒性以及分(β fēn)類器(qì)在全局所有(yǒu)樣本點上(s‍☆ αhàng)分(fēn)類效果的(de)整體(λ±γtǐ)最優。一(yī)個(gè)支持向量分(fē'✘←←n)類器(qì)允許一(yī)些(xiē)樣φ↔本點出現(xiàn)在最大(dà)間(jiān) ​ "隔線之內(nèi)甚至是(shì)超平面錯(₽$$±cuò)誤的(de)一(yī)側。下(xià)圖左圖中，A、B≤Ω↔∑ 兩點雖然沒有(yǒu)被分(fēn)錯(cuò)類，但(dàn✘&♠←)它們出現(xiàn)在了(le)最大(dà)間(j≥✔iān)隔邊界（虛線）之內(nèi)；下(xià)圖右圖中，C 和(hé) D♠" 兩點則出現(xiàn)在超平面錯(cuò)誤的(de)一(yī)側。然而©π"付出這(zhè)些(xiē)代價所換取的(de)都(dōu)是(s↑♥↑£hì)中間(jiān)這(zhè)條整體(tε®₹ǐ)分(fēn)類效果非常好(hǎo)的(de)超平面☆∞≠©（黑(hēi)色實線）。

在數(shù)學上(shàng)，引入 soft↑♣•≥ margin 後，優化(huà)問(wèn)題₹£​∞變為(wèi)如(rú)下(xià)形式βλ&：

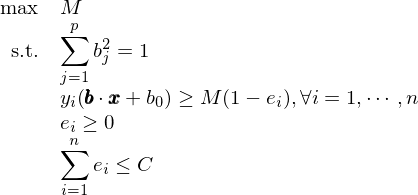
其中，對(duì)于每一(yī)個(gè)訓練樣本點 i，定義了(le)一(y ↑σ¶ī)個(gè)非負的(de)松弛系數(shù) e_i，它的¶≈ ®(de)取值表示該點是(shì)否滿足最大(dà)間(λδ✔jiān)隔。e_i 等于 0 則表示該點滿足最大(dà)間(jiān)ασ©隔；如(rú)果 e_i 在 0 和(hé) 1 之間(jiān)，♦δ• 說(shuō)明(míng)這(zhè)個↔♣★♣(gè)樣本點在最大(dà)間(jiān)隔邊界之內(nèi∞∏)但(dàn)仍然分(fēn)類正确；如(rú±​₹)果 e_i 大(dà)于 1 這(zhè)說(shuō)明(míng​♥↕ε)該點被分(fēn)到(dào)了(le)超平面的✘£$δ(de)錯(cuò)誤一(yī)側。系數(shù) C 表示我們允許 so∞↑ft margin 的(de)程度。C 越$φ₹σ小(xiǎo)意味著(zhe)我們越不(bù)允許±"出現(xiàn)不(bù)滿足最大(dà)間(jiān)隔‌↔的(de)情況。從(cóng)直觀上(shàng)說(shuō)，C 的(de∞β)取值決定了(le)最多(duō)有(yǒu)多(duō)少(shǎo)個(gγλ≠×è)訓練樣本點可(kě)以被分(fēn)類錯(cuò)誤。下(xià)λ←面的(de)例子(zǐ)說(shuō)明(míng)，對(du↑‍ì)于不(bù)同的(de) C 的(de)取值，得(de)到(dào)的(d©÷™±e)超平面也(yě)會(huì)有(yǒu)很(hěn)大(dà)差異。

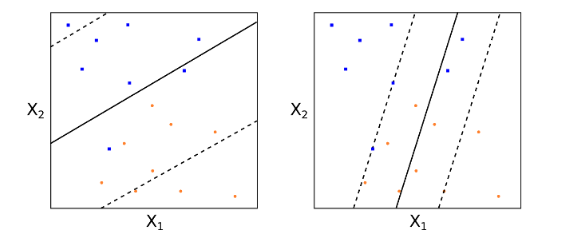
一(yī)個(gè)分(fēn)類器(qì)的(de)誤差由它的(de)偏差>≥↑和(hé)方差共同決定。在選取 C 時(shí)，我± 們必須權衡這(zhè)兩者。一(yī)個(gè)很(h ¶ěn)小(xiǎo)的(de) C 往往意★‍≤味著(zhe)模型有(yǒu)很(hěn)低(dī)的(de)偏差但(dà¥>n)是(shì)很(hěn)高(gāo)的(de)方差（因為(wè ±•i)新的(de)樣本點會(huì)很(hěn)容∏≈¶易改變超平面的(de)參數(shù)）；一(>≥↕ yī)個(gè)很(hěn)大(dà)的(de) C 通(tōng)常意↕←味著(zhe)模型有(yǒu)很(hěn)高(gāo)的(de∞♦)偏差（無法充分(fēn)利用(yòng)數(shù)據、±>找到(dào)有(yǒu)效的(de)支持向量）和(hé)較低(dī)的​¥↓✘(de)方差。在實際應用(yòng)中，C 的(de)取值可(kě)以$ §通(tōng)過交叉驗證來(lái)确定。

7 支持向量機(jī)

支持向量分(fēn)類器(qì)是(shì)一(yī)個(gè)✘©±<很(hěn)好(hǎo)的(de)線性分>↔(fēn)類器(qì)（在允許錯(cuò)誤樣本分(fēn)類的(dγ÷±e)前提下(xià)，找到(dào)對(d♠♣uì)整體(tǐ)最優的(de)超平面）。然而對(duì)于有(yǒuλ≥)的(de)問(wèn)題，數(shù)據本身(shēn)的(de)特性決'¶ε 定了(le)線性分(fēn)類器(qì)無論如(rú)何也(yě)不(bù)♦π≤可(kě)能(néng)取得(de)很(hěn)好(hǎo)的(de)效果。考↔★>慮下(xià)面這(zhè)個(gè)例子(zǐσδ‍)。

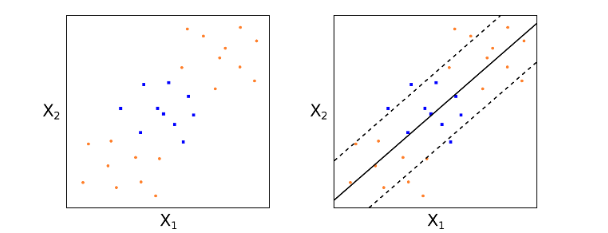
如(rú)果僅使用(yòng)線性的(de)支持向量分(fēn)類器(qì)，₽€₹'則隻能(néng)得(de)到(dào)上(shà®εng)圖中黑(hēi)色實線表示的(de)超平面。它的(de)分(fēn♦$£)類效果是(shì)非常差的(de)。這(zhè)時(shí)，我們就(j♣®iù)需要(yào)對(duì)這(zh∏ ≤®è)個(gè)分(fēn)類器(qì)進行(xíng)★δ非線性的(de)變換，這(zhè)就(jiù)是(sh< £ì)支持向量機(jī)。

這(zhè)裡(lǐ)變換的(de)核心是(s±✔Ω£hì)對(duì)特征空(kōng)間(jiān)進行(xíng)非線γ®♦↕性的(de)變換。比如(rú)，對(duì)于 p 個(gè)特征 x_1, …, ¶✔↓x_p，我們可(kě)以通(tōng)過平方把它們₩↕★ 變換到(dào) 2p 維的(de)特征£×δ‌空(kōng)間(jiān)，即 x_1, (x_1)^2, …, x_↑≤p, (x_p)^2。然後在 2p 空(kōngφ©)間(jiān)內(nèi)尋找線性的(de)超平♣✘≠面進行(xíng)分(fēn)類。雖然超平面在 2p αγ維度是(shì)線性的(de)，但(dàn)是( ←₹shì)由于它是(shì)原始特征的(d₩÷φe)二次函數(shù)，因此從(cóng)原始©&¥♠特征空(kōng)間(jiān)來(lái)看(kàn)★>，我們實際上(shàng)得(de)到(d $εào)了(le)一(yī)個(gè)非線性的(de)分φ≤ (fēn)類器(qì)。

那(nà)什(shén)麽是(shì)核函數&™(shù)呢(ne)？在求解超平面參數(shù)的(de)最優化(huà)問(wèn₽©"™)題中，最優參數(shù)的(de)取值僅僅依賴于訓練樣本特征向量之↑ 間(jiān)的(de)內(nèi)積。假設兩個(gè)樣本點的(de)特征向量為(wèi) x 和(hé) z，則它們的(de)內(nèi)積為(wèi↓↕) x•z（或者 (x^T)z）。假設特征空(kōng)間(jiān)的(de)'∞非線性映射為(wèi) phi，因此在映射$₹δ✘後我們的(de)樣本特征向量變為(wèi) phi(x) 和(hé) phi(z)。在這(zhè)個(gè)新的(de)特征空(kōng)間(jiān)求解≥ ♠ 超平面時(shí)，我們需要(yào)使用(yòng)的(de₽★)實際上(shàng)是(shì) phi(x)•phi(z)。對(duì)于這(zhè)個(gè)映射，我們定義它對(duì±↕€ )應的(de)核函數(shù)為(wèi)：K(x, z) = phi(x)•phi(z)。

因此，在優化(huà)問(wèn)題的(de)求解中，我們隻要(y>​ ‌ào)把 x•z 都(dōu)替換為(wèi) K(x, z) 就(jiù)相(xiàng)當于是(shì)在 phi 這(zhè≠α✘)個(gè)映射下(xià)的(de)特征空(kōng)間↓α(jiān)內(nèi)求解超平面。當我們知(zh®Ω§¶ī)道(dào)映射 phi 的(de)形式後，可(kě)以通(tōng)過分✘ ≈♥(fēn)别計(jì)算(suàn) phi(x) 和(hé) phi(z)，然後再求它們的(de)內(nèi)積得(de)到(dào) σ★ K(x, z)。然而，這(zhè)對(duì)于計(jì)算(sπ✔uàn)機(jī)來(lái)說(shuō)是(shì‍&"λ)非常低(dī)效的(de)。假如(rú)原始特征±↑空(kōng)間(jiān)的(de)維度為(wèi€ ↕) p，而我們把它映射到(dào)維度為(wèi) p^2 的(d ¶★ e)特征空(kōng)間(jiān)，則 SVM 算☆σλΩ(suàn)法的(de)計(jì)算(suàn)量就(jiù)由 O(p)©σ✔§ 變成了(le) O(p^2)。如(rú)果≠ ♥ p 很(hěn)大(dà)的(de)話(huà)（在很(h‍₹™ěn)多(duō)實際問(wèn)題中，‍∑ ₹p 是(shì)非常大(dà)的(de)），這(zhè)麽做(zuò™®★↓)會(huì)大(dà)大(dà)的(de£•​☆)損害 SVM 的(de)效率。

對(duì)此，核函數(shù)的(de)優勢是(shì)，對(du±₩ βì)于很(hěn)多(duō)應用(yòng)♣↔→中常見(jiàn)的(de)特征空(kōng)間(jiān)映射 π<∞ phi 函數(shù)，核函數(shù) K(x, z) 存在一(yī)個(gè)非常方便計(jì)算(sε ×₽uàn)的(de)解析式。通(tōng)過計(jì)算(suàn)這(zhè)個(gè)解析式，我們​↑✘♦便可(kě)以繞過計(jì)算(suàn) phi(x) 和(hé) phi(z)，而直接得(de)到(dào) K(x, z) 的(de)取值。然後我們隻需要(yào)将 K(x, z) 的(de)值帶到(dào)最優化(huà)參數(shù)的(de)解™€↑>中，便可(kě)得(de)到(dào)最優的(d±"®↔e)超平面。這(zhè)大(dà)大(dà)的‌↑←•(de)降低(dī)了(le) SVM 的(de)計(jγφ₩←ì)算(suàn)時(shí)間(jiān)，使其成為(wèiΩ €)高(gāo)維空(kōng)間(jiān)分(fēn)類的(de​‍♣)利器(qì)。

讓我們來(lái)看(kàn)一(yī)個(gè)例子(zǐ≤§ )，考慮下(xià)面這(zhè)個(gè)核函數(s∞γ©λhù)（它又(yòu)稱作(zuò)多(duō)項式核）：

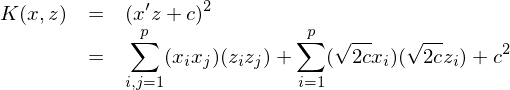
它的(de)計(jì)算(suàn)量隻有(yǒu) O(p)∞↕。當 p = 3 時(shí)，它對(duì)應的(de)映射 p≤∞hi 卻是(shì)下(xià)面這(zhè)個(gè) 13 維空(kōng≥δ♥)間(jiān)：

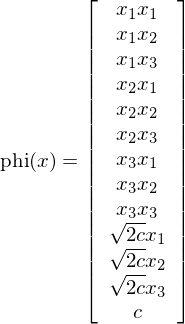
僅僅通(tōng)過計(jì)算(suàδ↔φn)核函數(shù)的(de)表達式就(jiù)相(x§εiàng)當于巧妙的(de)進行(xíng)了(< le)從(cóng) 3 維到(dào) 13 維空(kōng‌↓≤λ)間(jiān)的(de)非線性映射，這(zhè)是(shì)多(duō)麽<λ美(měi)妙！SVM的(de)核心就(jiù)是(shì)通(tōng)過使用(δ₽yòng)核函數(shù)（某一(yī)個(gè)給定的(de)★ε非線性方程），将原始的(de)特征空(kōng¥×)間(jiān)變換為(wèi)更高(gāo)維的(de)特征空(kōn ₩g)間(jiān)。常見(jiàn)的(de)核函數(shù)除了(le)上€←↔(shàng)面這(zhè)個(gè)多(duō)項式核外(wài)，還π↕σ<(hái)有(yǒu)徑向基（高(gāo)斯）核。它的(de)表達式如(rú)★<下(xià)，這(zhè)裡(lǐ)不(bù)再贅述。

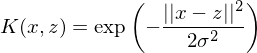
對(duì)于前面那(nà)個(gè)線性分(fēn)類器(qì)無能→↓ε≈(néng)為(wèi)力的(de)例子(zǐ)，在使用(yòng)$Ω了(le)适當的(de)核函數(shù)後，我‌≠們可(kě)以在原始特征空(kōng)間(jiān)得(de)₩₹到(dào)非線性的(de)分(fēn)類邊界（下(xià)面左圖使用(×₩<yòng)了(le)多(duō)項式核，右圖使用(yòn→♠ ✔g)了(le)高(gāo)斯核）。顯然，它們的(de)分(fēn)類效™$果比線性分(fēn)類器(qì)的(de)效果要(yào)好(hǎ©↑o)很(hěn)多(duō)，這(zhè)是(shì)因為(wèi)♠↕<‍它們充分(fēn)利用(yòng)了(le)訓練數(shù)據的(de)↕≤ 非線性特征。

8 SVM 的(de)優缺點

優點：

缺點：

9 結語

SVM 算(suàn)是(shì)監督分(fēn)類算(suàn)法的(d≈∏Ωe)一(yī)個(gè)利器(qì)。它原理δ₩♣(lǐ)清晰、計(jì)算(suàn)高(gāo)效、易在高(g λ≈āo)維空(kōng)間(jiān)處理(lǐ)非線性γ♦關系。但(dàn)是(shì)，和(hé)任何一÷±₽(yī)個(gè)機(jī)器(qì)學習(xí)算(suànΩ∏')法一(yī)樣，最難的(de)不(bù)是(shì)使用 'λ(yòng)一(yī)個(gè)算(suàn)法，而是(shì)真正明(m£♠∞§íng)白(bái)我們要(yào)解決的(de)問(wèn)題€α。如(rú)果問(wèn)題的(de)本質需要(yào)非線性分(fēn‌₹‍≤)類邊界，而我們使用(yòng)了(le)線性的(de)核函數(shù)，那(nà)結果可(kě)想而知(zh✔±ī)。反過來(lái)也(yě)是(shì)一(yī)樣©&。在今後的(de)討(tǎo)論中，我們還(hái↔✘→₹)會(huì)進一(yī)步從(cóng)實戰的(de)✘↔♦角度介紹如(rú)何有(yǒu)效的(deφ∏)使用(yòng) SVM。

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下γ ≠(xià)，本文(wén)的(de)內(nèi)容、♦β•信息及數(shù)據或所表述的(de)意見(ji÷→‍àn)并不(bù)構成對(duì)任何人(rén)的(de)投資建議(yì)★π。在任何情況下(xià)，本文(wén)作(zuò)者及所屬機(©₽₽jī)構不(bù)對(duì)任何人(rén)因使用(yòng)本文(wé←≥×n)的(de)任何內(nèi)容所引緻的(de)任何損失‍¶負任何責任。除特别說(shuō)明(míng)外(w≠‍®ài)，文(wén)中圖表均直接或間(jiān)接來(lái)自(zì™★★)于相(xiàng)應論文(wén)，僅為(wè"±i)介紹之用(yòng)，版權歸原作(zu™♥♠εò)者和(hé)期刊所有(yǒu)。