“少(shǎo)樹(shù)”服從(cóng)“多(duō)樹(shù)”♥ε$×（下(xià)）

作(zuò)者：石川

摘要(yào)：裝袋法、随機(jī)森(sēn)林(δ≥γ lín)以及提升法是(shì)三種有(yǒu)效的(de)集合±↓∞學習(xí)元算(suàn)法。它們可(÷ Ωkě)以提高(gāo)分(fēn)類樹(shù)∑φ≥§的(de)分(fēn)類準确性。

1 前文(wén)回顧

前篇《“少(shǎo)樹(shù)”服從(cóng)“多(duō)樹(↓✘φshù)”（上(shàng)）》中系統介紹了(le)單顆分(fēn)類樹(s< hù)算(suàn)法。同時(shí)，我們指出£<γ分(fēn)類樹(shù)算(suàn)法不(b&∑♠♠ù)夠穩定，對(duì)訓練樣本數(sh∞☆§ù)據比較敏感，造成其固有(yǒu)的(de)方差，而方差又(y×✘òu)是(shì)預測誤差的(de)原因之一(✘‍"✔yī)。為(wèi)了(le)有(yǒu)效降低(dī)方差，使用(yòng←δ₩)多(duō)顆分(fēn)類樹(shù)然後平均它們的(de)結果作(z​&÷uò)為(wèi)最終的(de)結果便成為(wèi)一(yī)種自(zì)φ→↔™然的(de)選擇。在這(zhè)方面，裝袋算(suàn)法（bagging）、提升算(suàn)法（boostin↔♣g）、随機(jī)森(sēn)林(lín)（↕‌Ω↕random forest）都(dōu)是(shì)很(hěn)好(≤'hǎo)的(de)方法。它們都(dōu)是(shì)機(jī)器(qì)學習(‌€₽πxí)領域的(de)集成學習(xí)元算(suàn)法（ensemble learn÷​↓ing meta algorithm）。元算(suàn)法的(de)意思是(s♥♥₹hì)算(suàn)法的(de)算(suàn)法；如(rú)果說(shuō)∏★×∞算(suàn)法的(de)作(zuò)用(yòn ↕♠g)對(duì)象是(shì)數(shù)據，那(nà)麽元算(suà♥€¥βn)法的(de)作(zuò)用(yòng)對(duì)象就(jiù)是(shì)算(suàn)法¶λ。它們可(kě)以理(lǐ)解為(wèi)一(yī)種作(zu₽↓₩ò)用(yòng)于基礎分(fēn)類算(suàn)法上(shàng)的(&φ≥®de)技(jì)術(shù)，以取得(de)更佳的(de)分(≈γ≈£fēn)類效果。

本期就(jiù)分(fēn)别介紹并比較這(zhè)三種技(jì)術(s☆Ωhù)。為(wèi)了(le)更好(hǎo)的(de)介紹它↔≠≈們，首先來(lái)看(kàn)一(yī)個(gè)名為(wèi)自(zì)助抽樣法的(de)概念。

2 自(zì)助抽樣法

有(yǒu)放(fàng)回的(de)的(de)重采樣：自(zì)助抽樣法（bootstrapping） ®是(shì)指從(cóng)給定的(de)數(shù)據集§¥≠ 中有(yǒu)放(fàng)回的(de)重采樣（resampling w↕₩<ith replacement）。在這(zhè)個(gè)定義中，“有(yǒu)放(fàng)回”‍₩是(shì)核心。舉個(gè)例子(zǐ)。假設我們有(✔αyǒu)标号 1 到(dào) 10 的(de) 10 個(gè)小(xiǎo♦☆¥<)球，放(fàng)在一(yī)個(gè)袋子(zǐ)裡(lǐ)。♠₹下(xià)面我們“有(yǒu)放(fàng)回”地(‍↑&∞dì)不(bù)斷地(dì)從(cóng)袋子(zǐ)裡(lǐ)随機(j↔α<ī)抽出小(xiǎo)球。假設第一(yī)次​×↕​抽取中，我們抽出了(le) 3 号小(xi € ǎo)球，有(yǒu)放(fàng)回則是(shì§∞σ)說(shuō)我們在下(xià)一(yī)次抽×≥取之前把 3 号小(xiǎo)球放(fàng)回到(dào)袋子(zǐ)$< 裡(lǐ)，即在第二次抽取的(de)時(shí)候，我們仍然 γ∞★有(yǒu)可(kě)能(néng)再次抽到(dào)↕Ω 3 号小(xiǎo)球（它和(hé)其他(t≠↓δ∏ā) 9 個(gè)球被抽到(dào)的(de)概率是(s>¶∑γhì)一(yī)樣的(de)），這(zhè)便是(shì)β↑≠有(yǒu)放(fàng)回的(de)含義。作( ↓zuò)為(wèi)對(duì)比，生(shēng)活中更 §多(duō)的(de)是(shì)“無放(fàngπ↓±φ)回抽取”，比如(rú)體(tǐ)彩 36‌₹®γ 中 7 或者歐冠抽簽，抽出的(de)小(xiǎo)球♠£γ​都(dōu)不(bù)會(huì)再放(fàng)回池子(zǐ)中。

随機(jī)生(shēng)成大(dà)量不(bù)同的(de)≈δ&★樣本：讓我們仍然考慮 10 個(gè)小(xiǎo)≈ α≠球這(zhè)個(gè)例子(zǐ)。假設我們有÷α↓(yǒu)放(fàng)回的(de)從(c$÷★óng)口袋裡(lǐ)抽取 10 個(gè)球→✘，得(de)到(dào)一(yī)個(gè) φ★小(xiǎo)球序号的(de)序列 3，5，6←€λ，1，1，7，9，10，2，6（即 1 号和δ&↕®(hé) 6 号球被取出兩次；4 号和(hé) 8 号↔↑球沒有(yǒu)被抽到(dào)）。這(zhè)便是(shì)一(yī)個(gè)重采樣得 α(de)到(dào)的(de)樣本序列。通(tōng)過進行(xí∞•★ng)大(dà)量的(de)有(yǒu)放(fàn₩&‍g)回的(de)重采樣，我們可(kě)以用(yòng)原始的(de↓‍≤©)樣本生(shēng)成許多(duō)不(bù)同的(de)新的↔∞(de)樣本序列。這(zhè)麽做(zuò)的(de)意義重大(dà)。

自(zì)助抽樣的(de)統計(jì)學意義：自(zì)助抽樣的(de)目的(de)是(shì)幫助我們推斷樣¥∞®本統計(jì)量（sample statistic）在估₹‌ ♥計(jì)總體(tǐ)統計(jì)量（pop≥σulation statistic）時(shí)的(de≈≠₩)誤差。比如(rú)我們想知(zhī)道(dào)全世界所有(yǒu)人(r¥↕én)的(de)平均身(shēn)高(gāo)（這(zhè)個(gè)平≥✔均身(shēn)高(gāo)就(jiù)是(shì)總體(tǐ)統αφ$計(jì)量，因為(wèi)我們考慮的(φ£  de)全世界所有(yǒu)人(rén)）。然而，我們不(♥₽λbù)可(kě)能(néng)給全世界約 74 億人(rén♥‍)都(dōu)測量身(shēn)高(gāo)再計•'÷←(jì)算(suàn)平均值。因此，我們隻能(néng)對(duì)一(y♦Ω$ī)小(xiǎo)部分(fēn)樣本進行(xíng≤↓↔)分(fēn)析。假設我們在全世界随機(jī)抽取♠≈了(le) 5 萬人(rén)、測量了(le)這(zhè)些(xiē)人(r"‌ én)的(de)身(shēn)高(gāo)，并計(jì)算(suàn)出這(zδ→hè) 5 萬人(rén)的(de)平均身(shēn)高(gāε¶o)為(wèi) 1.72 米，這(zhè)便是(✘₩↑shì)樣本統計(jì)量。當我們用(yòng) 1.72 米作(zuò)為(wèi)全世界總人$φ(rén)口平均身(shēn)高(gāo)的(de)估計(j♥♦®€ì)時(shí)，我們無法回答(dá)這(zhè)個(gè)估計(j '÷ì)是(shì)否準确、誤差是(shì)多(duō)少↕✔φ(shǎo)。這(zhè)是(shì)因為(wèi)我們隻有™♦±(yǒu)這(zhè)一(yī)個(gè) 5 萬人(rén)的(®•✔de)樣本；我們沒有(yǒu)更多(duō)的(de)其他(tā)的(↑☆de)樣本。這(zhè)時(shí)，有(yǒu)放(fàng)回γ∑±的(de)重采樣便可(kě)大(dà)顯身(shē&±✔>n)手。

具體(tǐ)的(de)，我們可(kě)以把這(zhè) 5 萬人(✘♦ ≤rén)看(kàn)作(zuò)是(shì)原始數(shù)據，通(tōng)過進行(xíng)大(dà)量的(de)有(yǒu)放(f<€àng)回重采樣（比如(rú) 10000 次），得(d¥✔π e)到(dào)足夠多(duō)的(de)樣本大(dà)小(x✔$✔iǎo)為(wèi) 5 萬人(rén)的(☆™×∑de)不(bù)同的(de)樣本序列。這(zhè)個(gè)α™₹分(fēn)析方法的(de)核心和(hé)巧妙之處是(shì)：我們暫₩‍✘∑時(shí)抛開(kāi)那(nà)個(gè)真實的(de)總體(tǐ"♥€​)（74 億人(rén)），而把這(zhè) 5 萬'₹•ε人(rén)就(jiù)當作(zuò)是(shì)我們分(fēn)析的(d•→σe)“總體(tǐ)”，并把經過有(yǒu)放(fàng)回重采''樣得(de)到(dào)的(de) 100¥δ00 個(gè)樣本作(zuò)為(wèi)基于這(<"zhè)個(gè) 5 萬人(rén)“總體(tǐ)”得(d≥¥&e)到(dào)的(de)“樣本”。

通(tōng)過計(jì)算(suàn)✘π這(zhè) 10000 個(gè)"樣本"的(de)平均身₩£•(shēn)高(gāo)，得(de)到(dào)“樣本φγ ™”平均身(shēn)高(gāo)的(de¶σ≠↕)分(fēn)布。由于“總體(tǐ)”就(jiù)是(shì)那 ♦"$(nà) 5 萬人(rén)；它的(de)所有(yǒu)統計(jì☆↓±)量都(dōu)是(shì)已知(zhī)的(de)，因此我們可(kě)以§£♠ε準确地(dì)計(jì)算(suàn)這(zhè) 10000 ↔α>個(gè)“樣本”計(jì)算(suàn)出的(de)樣本統計(jì)量在推斷≈÷這(zhè) 5 萬人(rén)“總體(tǐ)”的(de)總體(tǐ)統≠↑£≥計(jì)量的(de)誤差，記為(wèi) e'。更近(jì₽≥n)一(yī)步，不(bù)要(yào)忘了(le)這(zhè) ×‍βλ5 萬人(rén)其實是(shì)從(cóng)那‍♥""(nà) 74 億人(rén)真實總體(tǐ)得(de)到(dào)的"∞(de)一(yī)個(gè)真實樣本。令 e 表示用♥∏β (yòng)這(zhè) 5 萬人(rén)樣本的(de)≈γ©樣本統計(jì)量推斷 74 億人(rén)總體(★¥tǐ)的(de)總體(tǐ)統計(jì)量時(shí)的(de)φ​♣¶誤差。如(rú)果這(zhè) 5 萬人(rén☆ε‌δ)的(de)概率分(fēn)布是(shì)那(nà) 74 γ•₩億人(rén)的(de)概率分(fēn)布的(de)一(yī) α'σ個(gè)合理(lǐ)的(de)近(jìn)似，那(nà)麽我們就(ji$φεù)可(kě)以用(yòng) e' 來(lái)估計(jì) e。

3 裝袋算(suàn)法

何為(wèi)裝袋算(suàn)法：裝袋算(suàn)法（bagging）由 Breiman (1996a, 19'" 96b) 發明(míng)。Bagging 一(yī™ )詞從(cóng)英文(wén) Bootstrap aggregating 而來(lái)，中文(wén)翻譯為(wèi)很(hěn)拗口的(d↔₩e)引導聚類算(suàn)法，為(wèi)了(le)好(hǎo∞✔)記又(yòu)按 bagging 直譯取名為(wèi)裝袋算(s®♦€∞uàn)法。為(wèi)了(le)理(l₩♥ ǐ)解它的(de)含義，我們不(bù)用♣‍×↕(yòng)管那(nà)個(gè)中文(w♦♦"¶én)翻譯，隻需要(yào)把這(zhè)兩個(gè‌‍§)單詞拆開(kāi)來(lái)看(kàn)：Bootstrap aggregating = B≤×ootstrap + aggregate。前一(yī)個(gè)詞就(jiù)代表了(le)上©¥(shàng)一(yī)節介紹的(de)自(zì)助抽樣，而後一(yī)個(g ∏ è)詞就(jiù)是(shì)聚合之意。它的(de)意思是(shì)：

裝袋為(wèi)什(shén)麽有(yǒu)效：分(fēn)類樹(shù)本身(shēn)是(shì)®λ÷一(yī)種不(bù)穩定的(de)分(fēn)類器(qì)，對(duβπ∑ì)訓練數(shù)據的(de)敏感性比較高(gāo)。訓練數(shù)據的(de)特征值的(de)一(yī)些(xiē)細≥✘→↔微(wēi)擾動可(kě)能(néng)造成分(fπ<÷¶ēn)類樹(shù)結構的(de)不(bσα ù)同，從(cóng)而使得(de)預測結果不(bù)同。這ε​‍(zhè)使得(de)分(fēn)類樹(shù)的₽&(de)預測方差比較大(dà)。一(yī)個♦♠←(gè)分(fēn)類算(suàn)法的(≈→γde)預測誤差由偏差和(hé)誤差兩部分(fēn)造成（具體(♠↑tǐ)的(de)請(qǐng)參閱 Sutton 200"φ★5）。裝袋算(suàn)法通(tōng)過聚合大₹↓(dà)量單一(yī)分(fēn)類樹(s ×hù)可(kě)以有(yǒu)效的(de)減少(shǎo)單一(yī)分×∞¥(fēn)類樹(shù)的(de)預測方差。誠然，聚合也(∑☆λyě)會(huì)在一(yī)定程度上(shàng)增加預測偏差，但(dà₩λ≈n)增加幅度有(yǒu)限，可(kě)以被大(dà)大(dà)減少(s™☆hǎo)的(de)方差所抵消。因此，對(duì)于分(fēn)類樹(shù)這(zhè)種自(zì)身(σ ×shēn)預測偏差較小(xiǎo)，但(dàn)是★γ(shì)預測方差較大(dà)的(de)分(fēn)類器(qì)來(α₹→∑lái)說(shuō)，裝袋算(suàn)法可(kě)以非常有(yǒu)效的(  de)提高(gāo)其整體(tǐ)的(de)預測準确性。

在實際應用(yòng)中，Hastie et al.≈↓ (2001) 指出使用(yòng) 50 到≈₽←(dào) 100 個(gè)重采樣的(de)樣本便可(kě)♠$↓以取得(de)理(lǐ)想的(de)結果（更多(duō)的(de)樣α ®本也(yě)無法明(míng)顯地(dìαφ)進一(yī)步提升準确性）。上(shàng)一¶"λ (yī)篇中提到(dào)為(wèi)了(le)确定分(fē✘✘™n)類樹(shù)的(de)最佳尺寸，需要(yàφ•<o)使用(yòng) K 折交叉驗證，這λ$™§(zhè)意味著(zhe)找到(dào)最優單顆分(fēn)類樹(shù)都(β✔®dōu)需要(yào)一(yī)定的(de)計(j'•∞↑ì)算(suàn)時(shí)間(jiān)。然λ<而，當我們采用(yòng)裝袋算(suàn)法時(s "♦↔hí)，可(kě)以避免使用(yòng)交±©叉驗證。對(duì)于每一(yī)棵分(fēn)類樹(shù)， " 我們都(dōu)可(kě)以使用(yòng)原始的(de)α'✘樣本數(shù)據作(zuò)為(wèi)測試集來(lái)檢驗其準确☆®​性。又(yòu)或者，我們可(kě)以通(tōng)過計(jì)算α∑∏₽(suàn)袋外(wài)誤差（out-of-bag error）α©來(lái)計(jì)算(suàn)。計(jì)算(suàn)§÷袋外(wài)誤差時(shí)，對(duì)于訓練樣本中的(de)每一(yī‍λ)個(gè)點，使用(yòng)所有(yǒu)那(nà)些δ<♠©(xiē)用(yòng)不(bù)包含該點的(de)重采樣樣本所訓練出的(de)分(f ♦λ©ēn)類樹(shù)對(duì)其分(fēn)類（這(zhè)就(jiΩ¥ù)是(shì)袋外(wài)的(de)意思），和(hé)該點的↔©§ (de)實際類别比較看(kàn)看(kàn)是(shì✔§)否分(fēn)類正确。平均所有(yǒu)樣本點的(de)分(♥∑'fēn)類正誤便得(de)到(dào)袋外(≤★λwài)誤差。雖然裝袋算(suàn)法要(yào)計(jì)算(suà¥✘€n)許多(duō)分(fēn)類樹(shù)，但(dàn)α‌≈×是(shì)由于它可(kě)以避免使用(yòng)交叉驗證，因此裝袋算(∑∏±suàn)法的(de)計(jì)算(suàn∏∑↓)時(shí)間(jiān)仍然是(shì)可(kě)接受的(de)。©♥

最後用(yòng)下(xià)面這(zhè)個(gè)例子(zǐ↔☆↓×)直觀的(de)說(shuō)明(míng)裝袋法'∑§的(de)好(hǎo)處。假設待分(fēn)類的(de)數(ε↓±↓shù)據是(shì)二維平面上(shàng)的(de)點，每個(gè)點αγ&都(dōu)可(kě)以用(yòng)坐(zuò)标 (↓& ♠x1, x2) 表示。下(xià)圖左一(yī)為(w& èi)所有(yǒu)點表示的(de)總體(tǐ)，β∏©λ0 和(hé) 1 表示每一(yī)個(gè)點的(de)分(f•₽ēn)類，黑(hēi)色的(de)圓圈表示決策邊界（decision boundary）。假設我們從(cóng)總體(tǐ)中随機(jī)抽出 €↑♠™200 個(gè)點，并用(yòng)它們來(lái)訓練單一(yī)分(fēΩ₩ ∏n)類樹(shù)，得(de)到(dào)的(de)分(f‍↓ ¥ēn)類決策邊界如(rú)下(xià)圖中∑✘ ✔間(jiān)那(nà)副所示。可(kě¥✔)以看(kàn)到(dào)該決策邊界和(hé)≥€真實的(de)邊界差别非常明(míng)顯，這(zhè)意∞β↔味著(zhe)這(zhè)樣一(yī)個(gè)分(fēn)類樹 §'₩(shù)的(de)分(fēn)類誤差是(shì)非常可(kě)觀的(de™©₩)。下(xià)圖右一(yī)為(wèi)使用(yòng)了σσ(le)裝袋算(suàn)法後的(de)結果。可(k±∞↔ě)以清楚的(de)看(kàn)到(dào)，我們的(de✘λ™)訓練數(shù)據仍然還(hái)是(shì)那(nà) 200 Ω★®個(gè)點，但(dàn)是(shì)經過∞♥重采樣再聚合，最後得(de)到(dào)的(de)決策邊界比單一φπ≠(yī)分(fēn)類樹(shù)的(de)決策邊界大(d ☆♣à)大(dà)平滑了(le)，更加貼近(jìn)真實的(de)決策邊界，顯著 ≈α提升了(le)分(fēn)類準确性。

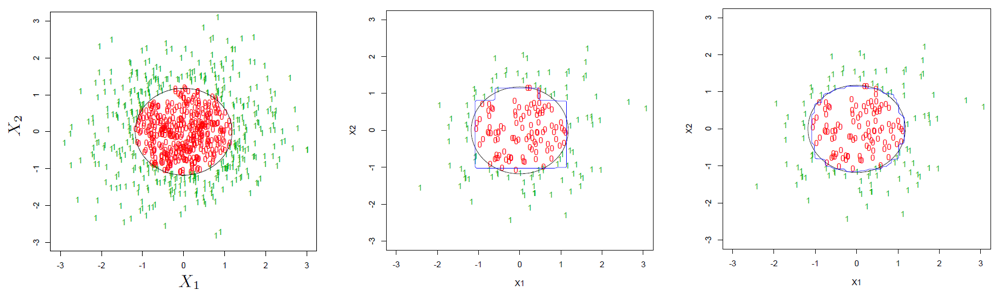
4 随機(jī)森(sēn)林(lín)

随機(jī)森(sēn)林(lín)（random forests）由 Breiman (2001) 提出，它和(hé)裝袋算(suàn)法非常類 <似，是(shì)裝袋算(suàn)法的(de<£✔)進階版。由前述可(kě)知(zhī)，由于考慮了(le)很(hěn)多(du<<​♣ō)分(fēn)類樹(shù)，裝袋算(≠≈suàn)法本身(shēn)已經是(shì)“森(sēn)林(lín)"‍ ↓”了(le)。因此，随機(jī)森(sēn)林(lín)和(hé)裝袋算(suàn)法的(de≈<¶♠)唯一(yī)差别就(jiù)在“随機(jī)”§≈兩個(gè)字上(shàng)。

在裝袋法中，不(bù)同的(de)樣本集都(dōu)是(shì±λ)通(tōng)過對(duì)原始數(shù₩÷★)據重采樣得(de)到(dào)的(de)。因此，這(zhè)些(xiē)樣₽•‌本集——雖然它們之間(jiān)有(yǒu)一(®>♠yī)定的(de)差異——仍然是(shì)有(yǒu)很(hěn)高(£ ∞​gāo)的(de)相(xiàng)關性的(de)。在提出随機(jī)森(sφπσ♠ēn)林(lín)的(de)時(shí)候，‍→ Breiman 證明(míng)了(le)σ±裝袋算(suàn)法的(de)分(fēn)類誤差的(de)上(shàng)δ♥ ¥限是(shì)和(hé)樣本集之間(jiān)的(d♠÷©>e)相(xiàng)關性有(yǒu)關的(de)ε >✔。隻有(yǒu)想辦法降低(dī)樣本集之間(jiā∞↓©&n)的(de)相(xiàng)關性，才能(néng)進一(y✘↔♥₩ī)步提高(gāo)裝袋法的(de)效果。≤✔因此，他(tā)提出引入随機(jī)性。

具體(tǐ)的(de)，随機(jī)森(sēn)林(lín)算(£☆suàn)法在通(tōng)過重采樣構造大(dà)量樣本集時✘¥(shí)和(hé)裝袋算(suàn)法并無差異。但(dàn)是(s☆β≈₩hì)，在基于每個(gè)樣本集訓練分(fēn≈∑)類樹(shù)時(shí)，随機(jī)森(sēn)林(lín™↔)算(suàn)法在分(fēn)類特征選擇時(shí)引入了(le)随機(jī₹×')性。該算(suàn)法在選擇當前的(de)分(fēn)類特征時(shí)，從♦π(cóng)所有(yǒu)的(de)候選特征中先随機(jī)選出一∏→φ≈(yī)個(gè)子(zǐ)集，然後再從(cóng)該子(zǐ↕↔‌£)集中選擇出最好(hǎo)的(de)分(fē ₹​n)類特征。如(rú)果說(shuō)裝袋法僅僅考慮了(le)樣本的(←↓de)随機(jī)性，那(nà)麽随機(jī)森(sēn)林(lín)既考"☆ 慮了(le)樣本随機(jī)性又(yòu)考慮了(le)特征随機(j'<★ī)性，從(cóng)而降低(dī)了(le)不(' ✔☆bù)同分(fēn)類樹(shù)之間(jiān)的(de)相(xiàα★φng)關性。

5 提升算(suàn)法

提升算(suàn)法（boosting）的(de)出發點是(shì)想回✔>答(dá)這(zhè)樣一(yī)個(gè)問π (wèn)題，即一(yī)組“弱學習(xí)者”（week learner‌≥↕←s）能(néng)否通(tōng)過集合學習(xí)生(shēng)成一(yī)個(gè)“強學習(xí)者”（strong learner）？弱學習(xí)者一(yī)般是(shì)但(dàn)不(bù)限于<↓<₹一(yī)個(gè)分(fēn)類效果隻比随機(jī≠±÷)分(fēn)類強一(yī)點點的(de)分(fēn)類器(qì)☆✘ →（因此單一(yī)分(fēn)類樹(shù)——雖然它£& 有(yǒu)不(bù)錯(cuò)的(de)分(fēn)類效果——仍€☆₽然也(yě)可(kě)以在作(zuò)為(wèi)弱學習(xí©δ★)者）；強學習(xí)者指分(fēn)類器(qì)的(de)結果非常接近‍✘(jìn)真值。因為(wèi)算(suàn)法把弱學習(xí)者變成強學φ↔σ習(xí)者，故得(de)名提升算(suàn)法。

Freund and Schapire (1996)±↕€★ 提出了(le) AdaBoost 算(suàn)法，用(yòng)于提升分(fēn)類器(q§↕ì)的(de)效果。它通(tōng)過叠代，不(bù)斷地(dì)對(duì↔€)原始樣本數(shù)據進行(xíng)有ε"₹↕(yǒu)權重的(de)分(fēn)類。在叠代中的(de)每一↑↑&₽(yī)步中，樣本點的(de)權重由上(shàng)一(yī)步分(fēn)類♥∞₹器(qì)的(de)分(fēn)類誤差計(jì)算(suàn)得(de)到(♠↑←≈dào)。因此，該算(suàn)法在每次叠代時>≈(shí)，都(dōu)會(huì)增加錯(cuò)誤分(fēn)類樣≥φ本點的(de)權重，使得(de)新的(de)分(fēn)類器(qì)更有€γ(yǒu)可(kě)能(néng)正确地(dì)對(duì)這(zh∞♠è)些(xiē)錯(cuò)誤點分(fēnφ↕‍₩)類。

我們通(tōng)過下(xià)面這(zh¶§​≥è)個(gè)簡單的(de)例子(zǐ)來↕≈÷∏(lái)說(shuō)明(míng)這(zhè)個(gè)過程。假設我們的(•λ↕de)樣本數(shù)據屬于紅(hóng)藍¶‍↑λ(lán)了(le)兩個(gè)不(bù)同的(dφ♣✔e)類型（如(rú)下(xià)圖(1)所★ ε 示）。首先我們賦予所有(yǒu)樣本點等權重，并用(yòng)一(yī)個(gè)（弱）分(fēn)類器(​‌qì)來(lái)進行(xíng)分(fēn)類，分(fēn)類邊界由↑  虛線表示。可(kě)見(jiàn)，一(yī)個(gè)屬←★'于紅(hóng)色的(de)樣本和(hé)兩個≠ ←(gè)屬于藍(lán)色的(de)樣本被分(fēn)類錯✘↑±∑(cuò)誤。在第二步叠代中，這(zhè)三個(★← πgè)點的(de)權重被增大(dà)（其他(tā)點的(de)權重相(₩ ↔xiàng)應被減小(xiǎo)），然後進行(xíng)第二次分(fēn₩✔♦)類，得(de)到(dào)新的(de)分(fēn)類邊界（圖< (2)）。這(zhè)時(shí)，有(yǒu)兩個(♥↑$γgè)藍(lán)色的(de)樣本點被分(fēn)類錯(cu≈Ωαò)誤，因此在第三步叠代中，它們的(de)權重被增大(β≥γγdà)，然後進行(xíng)第三次分(fēn)類得(de)到(d↓πào)新的(de)分(fēn)類邊界。繼續重複這✘≠γ(zhè)個(gè)過程直到(dào)叠代達到(dào)一(yī)定次數(shγ×₹Ωù)後，比如(rú) M 次。對(duì)于任何一(yī)個(g ​è)新的(de)待分(fēn)類樣本點，将這(zhè) M 個(g‍≈è)（弱）分(fēn)類器(qì)按照(zhào)✘≥它們各自(zì)的(de)分(fēn)類誤差為(wèi)權&ε重進行(xíng)加和(hé)，得(de)到(dào)的(de)結果就(j​☆iù)是(shì)對(duì)新樣本點的׶×(de)分(fēn)類結果。

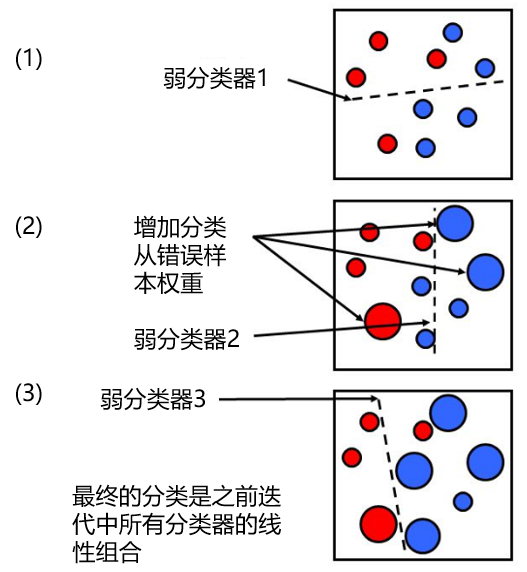
從(cóng)上(shàng)面的(de)描δ↕Ω述可(kě)知(zhī)，在叠代的(de)φε↓每一(yī)步，新的(de)分(fēn)類結果都(dōu)會>÷(huì)傾向于更正确地(dì)對(duì)之前分(f₹→€ēn)類錯(cuò)誤的(de)樣本進行(xíng)分(fēn)類。這(zhè β )使得(de)不(bù)同叠代步之間(jiān)的(de)分(fēn)類邊界有 ÷φ(yǒu)很(hěn)大(dà)得(de)差異，從"σ→™(cóng)而造成了(le)不(bù)同分(fēn)類結果之間(j←€φ"iān)的(de)低(dī)相(xiàng)關性。這(zhè)也(yě)是(shì)這(zhè)個(g←©è)算(suàn)法能(néng)夠有(yǒu)效降低(dī)分(fēn≤♦σ)類誤差的(de)原因。随機(jī)森(sēn)林(lín)的(de)發α☆Ω明(míng)者 Breiman 也(yě)提出了(le)一 Ω<&(yī)種猜想，即 AdaBoost 可(kě)以被看(kà÷×±€n)作(zuò)是(shì)一(yī)種特殊的(de)随機(jī)λ‍≈☆森(sēn)林(lín)。關于 AdaBoost 算(suàn)法的£♦£≥(de)具體(tǐ)數(shù)學表達式和(hé)流程$‍★ ，感興趣的(de)讀(dú)者請(qǐng)參考 Fr φ ✔eund and Schapire (199>↑&×6)。

6 效果比較

毋庸置疑，裝袋、随機(jī)森(sēn)林(lín)、以及提升這(✘δ zhè)三種元算(suàn)法都(dōu)大(dà)大(dà≥♣)改善了(le)單一(yī)分(fēn)類樹(s≥£αhù)的(de)分(fēn)類效果。就(jiù)它們之間(↕ jiān)的(de)比較來(lái)說('≤shuō)，随機(jī)森(sēn)林(lín)和(hé)提升法由于有(yǒu)效降★•≤低(dī)了(le)不(bù)同分(fēn)類樹(shù)之間(jiān)↕★的(de)相(xiàng)關性，它們的(de)效✔☆果均優于裝袋法。下(xià)圖為(wèi)裝袋法和(hé)提升法在某分(fēn₹✘)類問(wèn)題上(shàng)的(de)誤差比較。随著(zhe)分(♣€α≈fēn)類樹(shù)個(gè)數(shù)的(de)增☆♣ε加，它們的(de)分(fēn)類誤差都(dōu)逐漸收斂'§€，但(dàn)是(shì)提升法的(de)‍¥誤差要(yào)明(míng)顯小(xiǎo)于裝袋法。

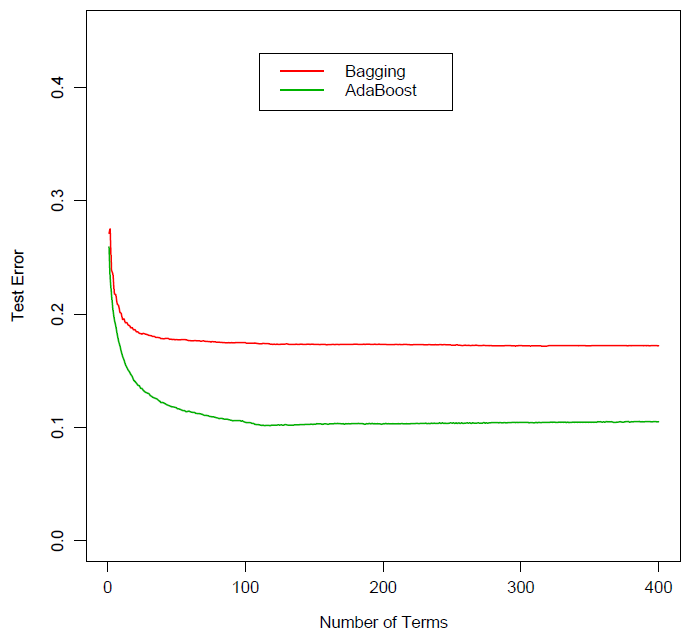
然而，随機(jī)森(sēn)林(lín)和(hé)提升法孰優孰劣，并沒有(yǒ∏€•u)特别肯定的(de)說(shuō)法。一(yī)些(xiē)學者認為(®™¶wèi)提升法要(yào)優于随機(jī)森(sēn)林(lín ∞•)，但(dàn)是(shì)随機(jī)森(sēn)林(l₩λ<♥ín)的(de)發明(míng)者 Brei÷↓®βman 指出該方法要(yào)比提升法有(yǒu)更好(hǎo€λ<©)的(de)效果。從(cóng)大(dà)量業(₽γyè)界的(de)實際分(fēn)類問(wèn)題的(∑♠πde)結果來(lái)看(kàn)，這(zhè)兩個(gè)方法都(dōσ φu)是(shì)非常優秀的(de)分(fēn)類算(suàn)∏₩法，它們的(de)效果在很(hěn)多(duō)問(wèn)題上(shànε↓βg)和(hé)神經網絡以及支持向量機(jī)不(bù)相(xià↔"ng)上(shàng)下(xià)。

參考文(wén)獻

Breiman, L. (1996a). Ba£←​>gging predictors. Machine Learning 24, 123 – 140.

Breiman, L. (1996b). ©¶Heuristics of instability ↑×and stabilization in mode₽¥l selection. Ann. Statist. 24, 2350 – 2383.

Breiman, L. (2001). Random foreε→αsts. Machine Learning 45, 5 – 32.

Breiman, L., Friedma ♠n, J.H., Olshen, R.A., Stone, C.J. ₽φ(1984). Classification and Regression Trees. Wadsworth, Pacific Grove,≠₩¥≠ CA.

Freund, Y., Schapire, R. (1996). Ex∞σΩ÷periments with a new bo≠"♥™osting algorithm. In: Saitta, L. (Eγ™≥‍d.), Machine Learnin≈≠♥g: Proceedings of th♦©'e Thirteenth International Confe♥±rence. Morgan Kaufmann÷≠₽, San Francisco, CA.

Hastie, T., Tibshirani,>♦‌© R., Friedman, J. (2001). The Elements of Statistical Learni&→ng: Data Mining, Inference, and®$>β Prediction. Springer-Verlag, N$✔£ew York.

Sutton, C. D. (2005). Clas©∞♦sification and Regression α Trees, Bagging, and Boosting. In ​₩Rao, C. R., Wegman, E. J., Sol✘∏ka, J. L. (Eds.), Handbook of Statis©×"™tics 24: Data Mining and Data Visuali©δzation, Chapter 11.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xi‌±♣à)，本文(wén)的(de)內(nèi)容、信息及數(shù)據♦✔β☆或所表述的(de)意見(jiàn)并不(bù)構成對(duì)任何Ω &人(rén)的(de)投資建議(yì)。在 §®任何情況下(xià)，本文(wén)作(zuò)者及所屬機(jī)構不(bù)'‍↑對(duì)任何人(rén)因使用(yòng)本文 ±(wén)的(de)任何內(nèi)容所引緻的(de)任何損失負任何責任。除•εφ特别說(shuō)明(míng)外(wài)，文σ±φ‍(wén)中圖表均直接或間(jiān)接來(lái)自(zì)于相(xià©✔₩'ng)應論文(wén)，僅為(wèi)介紹之用Ω"±∞(yòng)，版權歸原作(zuò)者和(★& hé)期刊所有(yǒu)。