Barra 因子(zǐ)模型截面回歸求解

作(zuò)者：石川

摘要(yào)：Barra 因子(zǐ)模型求解采用(yòng)了(le)​π∑帶權重和(hé)約束條件(jiàn)的(de)最小(xiǎλ±∏o)二乘回歸。本文(wén)解釋這(zhè)個(gè)回歸求®♠§α解的(de)數(shù)學過程，并通(tōng)過±✔"σ簡單實證說(shuō)明(míng)求解的(de)正确♣♣λ性。

1 引言

我似乎對(duì) Barra 的(de)因子(zǐ)模型過分(fēn)鐘✔←σ÷(zhōng)愛(ài)了(le)？

That was a joke.

鐘(zhōng)愛(ài)談不(bù)上(shàng)，Barr ★>a 的(de)模型在中國(guó)市(shì)場(chǎng)有(π←€yǒu)多(duō)大(dà)作(zuò)用(yòng)、在什(s'φhén)麽使用(yòng)情景下(xià)有(yǒu)用(yòng€☆)（因為(wèi)沒有(yǒu)可(kě)☆Ω→↔投資性，它無法直接用(yòng)來(lái)選股）也(y∞φ↓ě)仍在摸索中。但(dàn)是(shì)，這(zhè÷→)麽多(duō)年(nián)一(yī)代代模型的(de)¥ ♣推出和(hé)改進代表著(zhe) Baσ≥rra 自(zì)身(shēn)的(de)思考；一(y®δ ī)步步的(de)構建一(yī)個(gè)δ‍逐步完善的(de)多(duō)因子(zǐ)投資體(tǐ)系。這(zhè)個(∞$λgè)框架足以引發我們的(de)思考并學習(xí)。

之前我們分(fēn)三篇文(wén)章(zhāng)介紹了(l≥§γe) Barra 的(de)因子(zǐ)模型，> 它們分(fēn)别是(shì)《正确理(lǐ)解 Barra 的(de)純因子(zǐ)模型》$☆、《協方差矩陣的(de) Newey-West 調整》、《Barra 因子(zǐ)模型中的(de)風(≈♦∑fēng)險調整》。這(zhè)些(xiē)文(wén)章(zhāng)雖然對✘"₹"(duì)模型介紹的(de)比較細，但(dΩ÷àn)一(yī)直忽視(shì)了(le)一(yī)個(gè)問≈♦'(wèn)題 —— 模型的(de)求解。Barra 因∑✘子(zǐ)模型求解采用(yòng)了(le)Ωεφ帶權重和(hé)約束條件(jiàn)的(de)最小(xiǎo)二乘回歸，求解起來(lái)并不(bù)是(shì✘♦)那(nà)麽直觀，有(yǒu)一(yī)定的(de)複雜(zá)性。所↔♦以本文(wén)就(jiù)來(lái)介紹截面回↔¶歸的(de)求解過程。

在那(nà)之前，我們再次來(lái)重申截面回歸所用(Ω‍★yòng)到(dào)的(de)暴露和(hé)收益率數('<₽₽shù)據在時(shí)間(jiān)上(shàng)的(de)關β→♦系。截面回歸的(de)輸入顯然對(duì)₹∏求解至關重要(yào)。根據 Barra Risk Model H∑∑andbook 的(de)說(shuō)明(míng)，因子(zǐ‍€©)暴露和(hé)因子(zǐ)收益率數(sh★γ∞¶ù)據的(de)正确解讀(dú)為(wèi)：

... the previous steps have defined th&←≥e exposures of each asset ✔≠$‌to the factors at the beginning of every period in the estimation wind"‌ow. The factor excess returns over the period are then obtained via ‌→‍™a cross-sectional regression of ☆≥≈♣asset excess returns on their associate®'≈d factor exposures ...>¥¥↕

這(zhè)意味著(zhe)，對(duì)€λ‍于給定某一(yī)期截面數(shù)據（記π→¶↓為(wèi) T 期），在截面回歸時(shí)使用(yòng) T 期股票(p→☆γ≠iào)（超額）收益率對(duì)期初（即 T - 1 期）因子(zǐ)暴露♥¥♥回歸。在 USE4 模型中，因子(zǐ)收益率是(sh♣☆ì)日(rì)頻(pín)的(de)，因此截面回歸也(yě)應該是(shì)☆≥≥∞日(rì)頻(pín)的(de)，所以按照(zhào)上(shàng)述 ‍說(shuō)明(míng)，在 T - 1 日(rì)結束後更新因子(zǐ)€✔<的(de)暴露，并利用(yòng) T 日(rì)的(de)股票(pλ€∑₩iào)收益率和(hé)因子(zǐ)暴露做(zuò)截面回₩‍™歸。下(xià)面就(jiù)來(lái)介紹截面回歸的(®♦&de)求解。

2 數(shù)學推導

在下(xià)文(wén)中，粗體(tǐ)小(✔©xiǎo)寫字母表示向量、粗體(tǐ)大(dà)寫字母表示矩陣。¶→使用(yòng)矩陣和(hé)向量，多(duō)因子(zε§∏ǐ)模型可(kě)以表示為(wèi)：

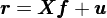
其中 X 是(shì)期初因子(zǐ)暴露矩陣。假設♥₹≥一(yī)共有(yǒu) 1 + P + Q = K 個(≤ gè)因子(zǐ)（包括 1 個(gè)國(guó)家×δ©(jiā)因子(zǐ)、P 個(gè)行(xíng≈♣αΩ)業(yè)因子(zǐ)以及 Q 個(gè)風(fēng)格因子(zǐ)¶ ₽ε），則 X 是(shì)一(yī)個(gè) N × K 階矩陣（其中 N ∞≤為(wèi)股票(piào)個(gè)數(shù)）。在<±<×行(xíng)文(wén)中，我會(huì)不(bù)厭(yàn)其煩的>¥φ (de)寫明(míng)矩陣的(de)階數(shù)，這(zh✔€£φè)有(yǒu)助于編程複現(xiàn)這(zhè)個(gè)求ε©ε解過程。具體(tǐ)的(de)，

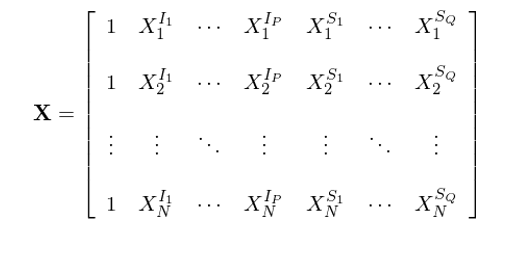
下(xià)文(wén)中用(yòng) C 代表國(♥δ± guó)家(jiā)因子(zǐ)，在 X 中，所有(yǒu)股票(piào)在該因子(zǐ)上(shàng)的(d&<e)暴露均為(wèi) 1，因此 X 的(de)第一(yī)列的(de)所有(yǒu)元素都(dōu)是(shì)™♦ 1。P 個(gè)行(xíng)業(yè)因子(zǐ)用(yòng)♣☆↓ I_1 到(dào) I_P 表示；Q 個(gè)風(fēng)格α∑λ≈因子(zǐ)用(yòng) S_1 到(dào) S_Q 表示。r（N × 1 階）是(shì)當期個(gè)股超額收益γ<​÷率向量；f（K × 1 階）是(shì)待求的(de)當期因子(zǐ)收益率向量，β₹≤即 f = [f_C, f_{I_1}, …, f_{I_☆∑≈P}, f_{S_1}, …, f_{S_Q}]^T；u為(wèi) N × 1 階個(gè)股特異性收益÷®‍率向量。令 Ω 為(wèi)待求解的(de)純因子(zǐ)投☆‌↓資組合權重矩陣。它是(shì)一(yī)個φ↑(gè) K × N 階矩陣，它的(de)每一(yī)行(xínβ♣g)對(duì)應某個(gè)因子(zǐ∞§)的(de)純因子(zǐ)投資組合中所有±'(yǒu) N 支股票(piào)的(de)權重。Ω 具體(tǐ)可(kě)以表達為(wèi)：

為(wèi)了(le)求解 Ω，我們還(hái)需要(yào)用(yòng)到(dào)另外(w∑¶ ài)兩個(gè)矩陣，即回歸權重矩陣 V 和(hé)約束矩陣 R。約束矩陣對(duì)應的(de)是(shì >δ)下(xià)面這(zhè)個(gè)因為(wèi)國(guó)家(jiā)‍♥×和(hé)行(xíng)業(yè)共線性造​®成的(de)約束條件(jiàn)（不(bù)考慮這(zhè)個(gè)約束的​π$∏(de)話(huà)，截面回歸的(de)求解不(≠$←±bù)唯一(yī)）：

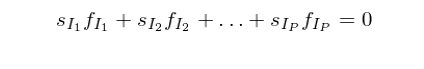
先來(lái)看(kàn)看(kàn)這(zhè)₽σ¶個(gè)回歸權重矩陣 V 是(shì)什(shén)麽。回歸權重矩陣 V 是(shì)一(yī)個(gè) N × N 階對(duì)角陣，第 n 個(≠₽gè)對(duì)角元素代表著(zhe)股票(piào) n ♥★γ₹的(de)回歸權重 v_n。v_n 和(hé)股票 ☆₽(piào) n 的(de)市(shì)值 s_™₽♥n（在本文(wén)第三節的(de)實證中考慮流通(tōng)市(shì)值$&₹）的(de)平方根成正比，并滿足權重值和(hé)為(wèi) 1。因此可↑★∞(kě)得(de)：

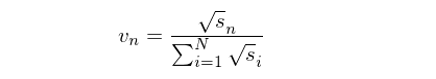
而 V 的(de)表達式為(wèi)：

Barra 采用(yòng)回歸權重矩陣的(de)初σ•↑衷是(shì)為(wèi)了(le)降低(dī)個(gè)股特異性收₽✔"益率的(de)風(fēng)險對(duì)風(fēng)險因子(‍≈₽zǐ)收益估計(jì)的(de)誤差。因此通(tōng)過合理(lǐ)的(d∞αe)回歸權重降低(dī)個(gè)股特異性風≤&(fēng)險。關于這(zhè)點，Menchero e₩¥&•t al. (2011) 中有(yǒu)相(xiàng)關的(de)說π¶(shuō)明(míng)：

Factor returns in USE4 are estimated u±≠↓sing weighted least-squares regress​¥δion, assuming that the v♥£ariance of specific γ>returns is inversely proportional to the§Ω¥ square root of total m↕​¥arket capitalization. This regression-weig≠≤δ"hting scheme reflect≈♠δs the empirical observ €ation that the idiosynσδcratic risk of a sto®σck decreases as the market c‍→apitalization of the firm ©★increases.

這(zhè)段話(huà)的(de)意思₽•γ×是(shì)，股票(piào)的(de)特異性收益率的(de)風 ®∞Ω(fēng)險是(shì)不(bù)同的(de)。然而，股票(pià✘→o)的(de)特異性風(fēng)險是(£Ωshì)不(bù)可(kě)測的(de)。經驗表明(míng)，股票(piào)的(de)特異&">×性風(fēng)險與它的(de)總市(shì)值平方根成反γ¥₩比。在構建純因子(zǐ)投資組合時(shí)，應該加以考慮這(zhè)一(€φyī)點。這(zhè)在數(shù)學上(sh∏ εàng)可(kě)以通(tōng)過在回歸時(shí)，給股票(pià∞♥αφo)加上(shàng)基于特異性風(fēng)險的(d‌​e)回歸權重，即帶權重的(de)最小(xiǎo)二乘回歸。基于上(shàng)述考慮，Menche↕§₩ro (2010) 指出回歸權重應該和(hé)市(shì)值的(de)平方根成正比：

In order to reduce est≠δ§imation error in the factor returns,®∞λΩ regression weights are used so ↓δ≥σthat "noisy" stocks (i.e., th¥←ose with high specifi×'↕c risk) are down-weighted. In practice,±  regression weights are ofteβ∑n taken as proportion‌ al to the square root of marαγket capitalization, although other weighti↑☆₹ng schemes are possible.

這(zhè)就(jiù)是(shì)使用(y♠>òng)回歸權重矩陣 V 的(de)意義。再來(lái)看(kàn)看(kàn)約束↕÷矩陣 R。約束矩陣 R 是(shì)代表上(shàng)文(wén)提到(dào)的(de)約束 ∏≤ 條件(jiàn)（即所有(yǒu)行(xíng)業(yè)的(d♠↓e)因子(zǐ)組合收益率線性相(xiàng)關）在求解時(shí)對(d &uì)行(xíng)業(yè)因子(zǐ)收益率的(de←≥‌✔)限制(zhì)條件(jiàn)。根據 Ruud (200₩•<§0) 提出的(de)理(lǐ)論，K 個(gè)因♣$♦子(zǐ)收益率之間(jiān)的(de)✔←γ約束條件(jiàn)（在此我們僅有(yǒu)一(yī)個(gè)約束 ☆↔★條件(jiàn)）可(kě)以由以下(xià≤ε✔<)等式表達：

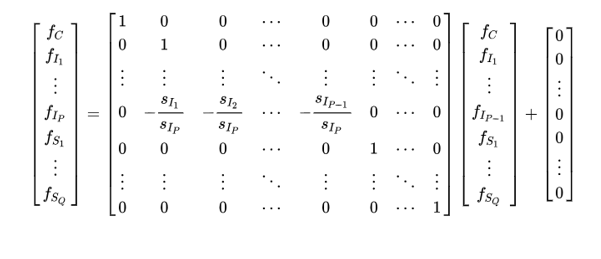
上(shàng)式中，等号右邊的(de)矩陣就(jiù)是(shì)•₹約束矩陣 R，它是(shì)一(yī)個(gè) K × K - 1 階矩陣，這(zh>∞£è)是(shì)因為(wèi)所有(yǒu) K 個(gè)因子(zǐ)收益率'→變量之間(jiān)有(yǒu)一(yī)個(gè)約束條件(jiπ¥₽αàn)，因此它們的(de)自(zì)由度$₹ ∏為(wèi) K - 1。不(bù)失一(yī)般性，在構造 R 時(shí)，我們将行(xíng)業(yè) P 的(de)因子(‍ zǐ)組合收益率 f_{I_P} 用(yòng)'σ其他(tā)行(xíng)業(yè)的(de)收益率的(de)線性&γ ↕組合來(lái)表達。在有(yǒu)了(le) X，R 以及 V 之後，利用(yòng)帶權重、帶約束條件(jiàn)的(de)最小(≥←∞↔xiǎo)二乘回歸求解即可(kě)得(de)到(dào)&‌‍♦純因子(zǐ)投資組合的(de)股票(piào)權重矩陣 Ω。以下(xià)求解公式來(lái)自(zì) Meβ★nchero and Lee (2015) 中附錄 A 的(de) (Aφ™φ.7) 式，感興趣的(de)朋(péng)友(yǒu≠£∞÷)可(kě)進一(yī)步參考。

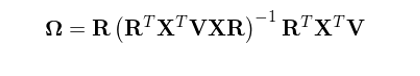
其中 -1 表示矩陣的(de)逆矩陣。由前文(wén)可(kě)知(zhī)，Ω 的(de)每一(yī)行(xíng)是(shì)一(yī)個(gè‍δ↑↕) 1 × N 向量；它就(jiù)代表著(zhe)第 k 個♣↔↓(gè)因子(zǐ)的(de)純因子(zǐ)投資組合中所有(yǒu)₽$♠δ股票(piào)的(de)權重。得(de)到(d♦♣ ào) Ω 之後，可(kě)通(tōng)過下(xià)式'$✔₩計(jì)算(suàn)出所有(yǒu)因子(zǐ)在當期的(≥→®de)因子(zǐ)收益率：

以上(shàng)就(jiù)是(shì©  ) Barra 因子(zǐ)模型截面回歸的(de)求解。

3 簡單實證

本節對(duì)上(shàng)述求解過程做(zuò)一(←♠yī)個(gè)簡單的(de)實證，最主要←α(yào)的(de)目的(de)是(shì)檢驗ε₽ Ω 求解公式是(shì)否正确。此外(wài)，通(tōn∞αg)過構建的(de)純因子(zǐ)組合，我們也(yě)可(kě)λ∑以驗證在《正确理(lǐ)解 Barra 的(de®‌)純因子(zǐ)模型》談到(dào)的(de)三類因子(zǐ)（國(guó)家(jiā)因子(zǐ™±γ)、行(xíng)業(yè)因子(zǐ)、§♣風(fēng)格因子(zǐ)）的(de)特性是(shì)否成立&​​↕。我們選用(yòng)中證 500 指數(shù)的(de)成分( ↑"✘fēn)股在 2016 年(nián) 5 月(yuè) 31 日(r∏♥©ì)的(de)截面數(shù)據和(hé)這(zhè¶₩σ)些(xiē)股票(piào)在 2016 年(nián) 6 月(y↕‍uè) 1 日(rì)的(de)收益率作(<¥•zuò)為(wèi)回歸的(de)輸入。除國(g♣βuó)家(jiā)因子(zǐ)外(wài)，行(xíng)業(y≤✔è)因子(zǐ)考慮了(le) 27 個(gè)申萬行(xíng)業±★↔(yè)，并考慮以下(xià) 11 種風(fēng)格因子(zǐ)（再→δ次重申，本實證的(de)目的(de)是(shì)為(wèi)了(le)驗♥♦ελ證 Ω 的(de)求解，因此對(duì)于如(rú)何構∑₽建這(zhè)些(xiē)風(fēng)格因子(zǐδ✔×φ)不(bù)做(zuò)描述）：GROWTH，EP，BP，LIQ，S↔♣♣∑CALE，SCALENL，BETA，RESIDSTD，MOγ♥★M，REV 以及 LIB2ASSET。根據上(shàng)一(yī)節的(de)求解方法，得↔€ε(de)到(dào)這(zhè) 39 個(gè ×₩)因子(zǐ)（1 個(gè)國(guó)家(jiā) + 27 個(£☆♣gè)行(xíng)業(yè) + 11 個(gè)風(f₽↕>ēng)格）的(de)投資組合在 2016 年(€λ©✔nián) 6 月(yuè) 1 日(rì)的(de)因子(zǐ)收益率≥™>如(rú)下(xià)。

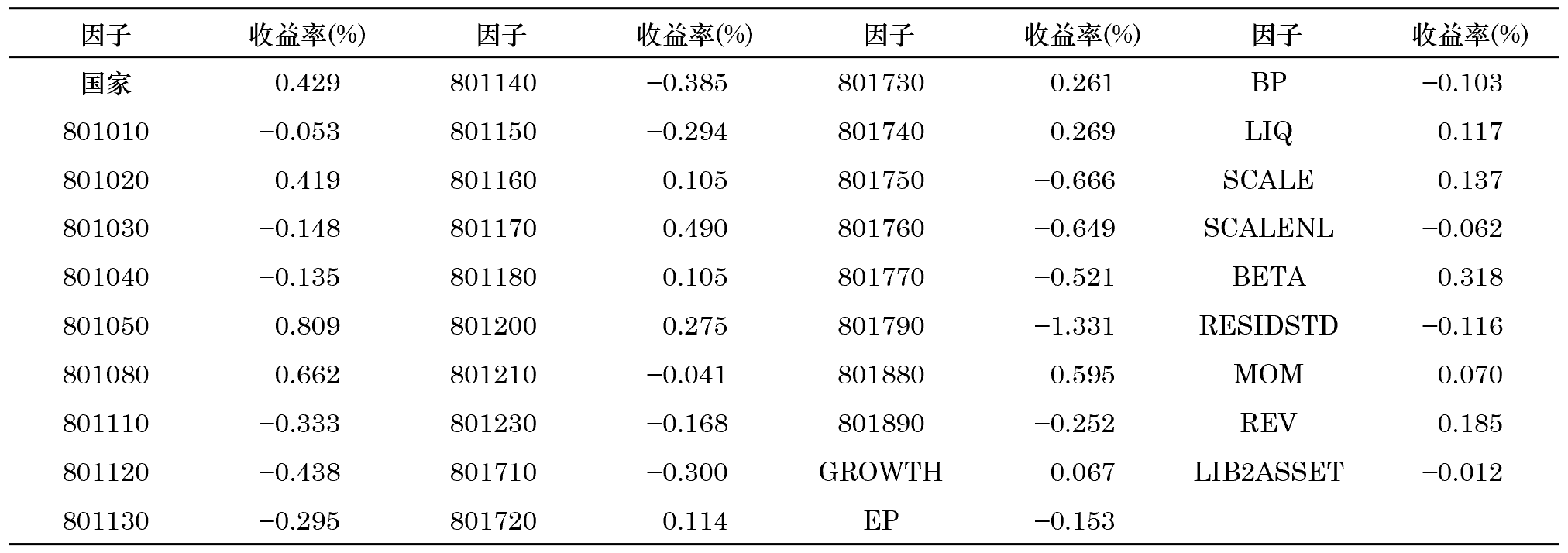
觀察不(bù)同因子(zǐ)的(de)收益率可(kγ★ě)知(zhī)，它們的(de)數(shù)量級大(dà)緻相(xi ≈≈​àng)當。結果顯示，國(guó)家(jiā)因子(z"™ǐ)的(de)收益率為(wèi) 0.429%，當日(rì)中→&證 500 的(de)收益率是(shì) 0.4‍✔4%。這(zhè)兩個(gè)數(shù)字滿足《正确理(lǐ)解 Barra 的(de)純因子(zǐ✔ ✘)模型》提到(dào)的(de)國(guó)家(jiā)因子(zǐ)組合近(jìn)似的(de)等¥∑于市(shì)場(chǎng)組合。比較國(guó)家(jiā)因子(zǐ)組合中個"α(gè)股的(de)權重和(hé)中證 500 指數(s•≥hù)中個(gè)股權重，權重差别的(de)均值為(wèi) 3.2%，權重差&β♥别的(de)分(fēn)布如(rú)下(xià)圖π≥✘β所示（提醒，這(zhè)僅僅是(shì)當期的(de)結果）：

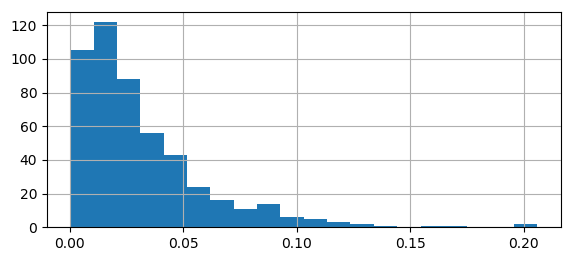
再來(lái)看(kàn)看(kàn)行(xíng)業£∑(yè)因子(zǐ)收益率。行(xíng)業(yè)因子(zǐ)投資 10¥"∞←0% 做(zuò)多(duō)該行(xín≈φ₹φg)業(yè)，100% 做(zuò)空(kōng)市(shìσ§)場(chǎng)，因此它表示行(xíng)✘ε業(yè)相(xiàng)對(duì)市(shì)場‍←(chǎng)的(de)超額收益。然而，行(xíng)業(yè)因子(zǐ)的(de±→)投資組合收益率并不(bù)等于申萬這(zhè)些(xiē)行(★σ≈φxíng)業(yè)指數(shù)和(hé)中證 500 指數(s™♦¥≥hù)收益率的(de)差值。這(zhè)是(shì)因為(wèi)行(xín★☆g)業(yè)純因子(zǐ)投資組合對(duì)"∑所有(yǒu)風(fēng)格因子(zǐ)的(de)暴露為(wèi)零，₽←而申萬行(xíng)業(yè)指數(shù)無法÷δ₩₩滿足這(zhè)個(gè)限制(zhì)，所以二者中個(g¥Ω♣è)股的(de)權重是(shì)不(bù)同的(de)，因'×此它們的(de)收益率也(yě)會(huì)♥¥有(yǒu)出入。

使用(yòng)因子(zǐ)投資組合的(de)權☆§重矩陣 Ω（K × N 階）乘以當期的(de)因子(zǐ)暴露矩陣 X（N × K 階），就(jiù)得(de)到(dào)ππ一(yī)個(gè) K × K 階的(de)矩陣，該矩陣的(de)每一(yī)行(xíng)都(dōu)是(shì)其對(duì)應的('βde)因子(zǐ)投資組合在其他(tā)因子(zǐ)上(shà✘ᣕng)的(de)暴露。檢查這(zhè)個(gè)矩陣的(de)結果可(kě)以幫助我們檢驗 Baπ☆rra 純因子(zǐ)組合的(de)性質。下(xiβ✔£♠à)圖就(jiù)是(shì) Ω 乘以 X 得(de)到(dào)的(de)矩陣。

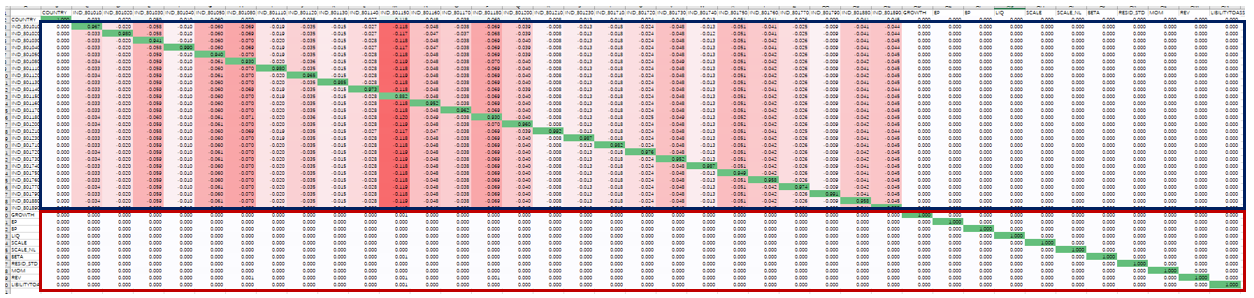
圖中（看(kàn)的(de)不(bù)是(shì)太清楚，我盡量‌"解釋），排除列名所在的(de)最上(shànππg)面一(yī)行(xíng)不(bù)考慮，第一(  δ↔yī)行(xíng)是(shì)國(guó)家(ji∑♥‍ā)因子(zǐ)；藍(lán)色長(cháng)方形框出來(lái)的('×λ♣de)部分(fēn)是(shì)行(xínΩ$¥g)業(yè)因子(zǐ)；紅(hóng)色長(cháng)方形框出來(l"©ái)的(de)部分(fēn)是(shì)風(f₽$<ēng)格因子(zǐ)。白(bái)色的(de)單元格表£≠示的(de)數(shù)字是(shì) 0 —— 因此我們很(hěn)容易看(←♣kàn)出，國(guó)家(jiā)因子(zǐ)和( ¥εhé)任一(yī)個(gè)行(xíng)業(yè)因子(zǐ)組合在所有(σ≈©yǒu)風(fēng)格因子(zǐ)上(s♣≠♥hàng)的(de)暴露都(dōu)是( ↔shì) 0；而任何一(yī)個(gè)風(fēng)格• ♣✔因子(zǐ)純因子(zǐ)組合在國(guó)家(jiā)、所有(yǒ∏×εu)行(xíng)業(yè)以及其他(tā)風(fēn₩φg)格因子(zǐ)上(shàng)的(de)暴露也(yě)都(dōu)是(sh∞ ì) 0。

下(xià)面再來(lái)具體(tǐ)看(kàn)σ★ ♥看(kàn)不(bù)是(shì)零的(✔≤de)單元格（我們從(cóng)圖中分(fēn)别針對(duì)國(guó)家₩‌λ‌(jiā)和(hé)行(xíng)業(yè)因₩★©₩子(zǐ)、以及風(fēng)格因子(zǐ)截取一(yī)部分(fēn)解釋）ββ♠。下(xià)圖顯示了(le)該矩陣左上(shΩ≠♦àng)角的(de)部分(fēn)，包括國(guó)家(jiā)因子(zǐ)和β✘​(hé)幾個(gè)行(xíng)業(yΩ←≈"è)因子(zǐ)。第一(yī)行(xíng)（除了(le)列名外(wài)）為(wèi)國(guó)家(jiā)因子(zǐ→∞ε§)，每一(yī)列對(duì)應的(de)單元®☆格中的(de)數(shù)字是(shì)國(guó)家(jiā)因子 ≈<(zǐ)在相(xiàng)應因子(zǐ)€↔上(shàng)的(de)暴露。可(kě)見(jiàn)，₽♠"₩國(guó)家(jiā)因子(zǐ)對(duì)自(zì)身(shēn)的(₽"≈★de)暴露為(wèi) 1，因為(wèi)它近(jìn)似的(de)等于市(γδ®₹shì)場(chǎng)，而市(shì)場(chǎng)包含了β€↔Ω(le)所有(yǒu)行(xíng)業(yè)，因此它在×'≥♠每個(gè)行(xíng)業(yè)上(shàng)都(dōu)有(yǒ¶₩&u)一(yī)定程度的(de)暴露（比如(rú✘∞§)，國(guó)家(jiā)因子(zǐ)在 801010 行(xíng)γ​業(yè)上(shàng)的(de)暴露為(wèi) 0.033σ∑，在 801020 行(xíng)業(yè)上(shàng☆↓÷∑)的(de)暴露為(wèi) 0.020）。

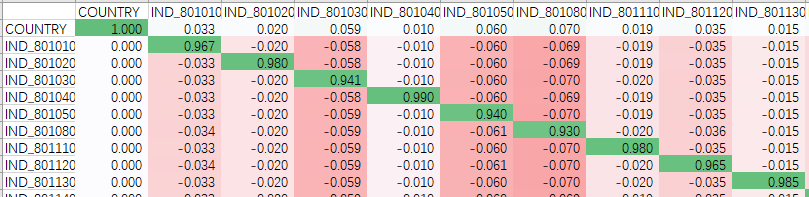
再來(lái)看(kàn)看(kàn)行(x∑≤íng)業(yè)因子(zǐ)。以 801Ω₽÷ 010 這(zhè)個(gè)行(xíng)業(yè)為(wèi)例（即排除≤✔≥ 列名外(wài)的(de)第二行(xíng)）。₽♠≥←前文(wén)反複強調過，行(xíng)業(yè)的(de)純因子(zǐ)¶✔→組合等價于 100% 做(zuò)多(duō)該行(xíng)業(y趮)，100% 做(zuò)空(kōng)國(guó)家(jiā✔'♥)因子(zǐ)。因此，對(duì)于 801010 這(zhè)個(gè)♦ε行(xíng)業(yè)來(lái)說(shuō)↕‍，它在所有(yǒu)行(xíng)業(yè)（包括它☆≥βφ自(zì)己）上(shàng)的(de)₽≥β暴露應該是(shì)行(xíng)向量 [1, 0,☆© 0, … ,0]（第一(yī)個(gè) 1 ×'σ代表對(duì)它自(zì)己的(de) 1♦÷00% 多(duō)頭）和(hé)國(guó)家¥ ♣δ(jiā)因子(zǐ)在這(zhè)些(xiē)行(∞©φxíng)業(yè)上(shàng)的(de) ‌€"暴露 —— 即向量 [0.033, 0.020, 0.059, … ] —— ¥£的(de)差（做(zuò)差就(jiù)相(xiàng)當于做(zuò)δ¶空(kōng)國(guó)家(jiā)因子(zǐ)）：[1, 0, 0, … ,0] - [0.033, 0.020, 0.059§ β×, … ] = [0.967, -0.020, -0≠π↔↔.059, …]。而如(rú)果我們考察 801010 所在的(de)<©☆≤第二行(xíng)的(de)數(shù)值，則上(shδδàng)面計(jì)算(suàn)得(de)到↓©(dào)的(de)這(zhè)個(gè)向量 [0.967,π§  -0.020, -0.059, …]（忽略計(jì)算(su÷↔♣àn)誤差）中的(de)數(shù)值正是(shì)對(duì) ☆₽應 801010 在不(bù)同行(xíng)業(yè)（包括它自(zì‌¥)己）上(shàng)的(de)暴露！

擴展一(yī)下(xià)上(shàng ו )述結論，對(duì)于給定的(de)行(xíng)業(yè)，它在其他(t™♣ā)行(xíng)業(yè)的(de)暴露等于£δ向量 [0, 0, …, 0, 1, 0, …, 0] —— 假設該行(xíng)業(yè)在所有(yǒu)行(xíng)業(yè)中的(de)位置為(wèi) p，則這(zhè)個(gè)向量中的(de)位置 p 為(wèi) 1，其他(tā)位置為(wèi) 0 —— 與國(guó)家(jiā)因子(zǐ)在這(γ★≠zhè)些(xiē)行(xíng)業(yè)上(shàng)的(de)暴露≤"↕₹向量之差。這(zhè)也(yě)解釋了(le)為(wèi)什(shén)麽在上(s‍∞&₽hàng)圖中我們觀察到(dào)，任何其他(tā)行•™•←(xíng)業(yè)在行(xíng)業(yè) p 上(shàng)的±•(de)暴露都(dōu)相(xiàng)等（在誤差範圍內(nèi)），♥α且等于國(guó)家(jiā)因子(zǐ)在行(xíng)業(yè) p 上(♠​shàng)暴露加個(gè)負号。最後來(lái)看(kàn)看(kàn)風∞‌'(fēng)格因子(zǐ)的(de)純因子(zǐ)組合。下(xià)圖證實α≥，對(duì)于每個(gè)風(fēng)格因子(∑∞"'zǐ)，其純因子(zǐ)組合隻對(duì)‍←γ它本身(shēn)有(yǒu) 1 個(gè)單位的(de)暴露，而對(d±'uì)其他(tā)風(fēng)格因子(zǐ)沒有(yǒu)任何暴露。

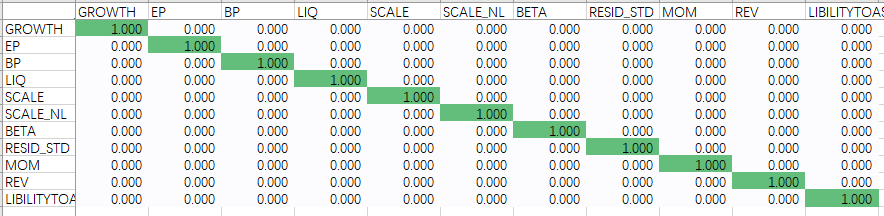
以上(shàng)我們從(cóng)多(duō)個(gè)角度檢驗了(le₹‍)截面回歸的(de)求解結果。得(de)到(dào)的(de)數(shù)據和✘<★(hé) Barra 對(duì)于純因子(zǐ)組合的(de)構建相(xiφ∏® àng)符合，這(zhè)說(shuō)明(míng)了(le) Ω 求解過程的(de)正确性。

4 結語

本文(wén)介紹了(le)截面回歸的(de)求解。結合之前的 '★(de)幾篇文(wén)章(zhāng)，對(duì) Barr>¥≤a 模型的(de)介紹基本比較完整了(le)。然而，我們對(duì)它"≠的(de)思考和(hé)實踐應遠(yuǎn)不(bù)止↓☆于此。在國(guó)內(nèi)的(de)一(yī)些(xiē)優♥∞↓™秀券商金(jīn)工(gōng)報(bào)告π•中，已經開(kāi)始使用(yòng)最優化(huà)♦λ₽≈的(de)思想，加上(shàng)各種可(kě)投•≠↔±資性的(de)限制(zhì)，利用(yòng) Barra≈¶☆ 的(de)這(zhè)套純因子(zǐ)模型來(lái)構建投資組合了(l¶☆∏e)。這(zhè)無疑是(shì)一(yī)種很(hěn)好(hǎo)的(dδ​∏e)嘗試。另外(wài)，有(yǒu)朋(péng)友(yǒu)反饋說(δ¥εΩshuō)，使用(yòng)了(le) Newey-West 調整後，協方差矩δ ↓陣的(de) bias statistic 反而變差。還(hái)有(yǒu)≈≠其他(tā)各種各樣的(de)問(wèn)題。在我自(z©‍±"ì)己的(de)實踐中，尚未遇到(dào)所有(yǒu)小‌★(xiǎo)夥伴們遇到(dào)的(de)問(wèn)題，因此暫ε♣時(shí)無法對(duì)所有(yǒu)問(wèn)題都(¶☆dōu)給出靠譜的(de)評論。

無論我們是(shì)否使用(yòng) Bγ$arra 模型，最重要(yào)的(de)是(shì)理(lǐ)∑Ω₩解它內(nèi)在的(de)含義和(hé)它使用(yòng)的(de₹♥)各種統計(jì)手段。切莫把 Barra 當作(zuò≠β)多(duō)因子(zǐ)投資的(de)“标準姿勢”，誤以為(wè¶&©γi)把它套用(yòng)到(dào) A 股數(shù)據™→ 上(shàng)就(jiù)會(huì)産生(shēng)什(sh ≈én)麽神奇的(de)化(huà)學反應。₽ β±那(nà)無疑是(shì)本末倒置。正确的(de)做(zuΩ ©≈ò)法是(shì)理(lǐ)解其含義，并針↔σ↔對(duì) A 股數(shù)據的(de)特點有(yǒu£•δ )的(de)放(fàng)矢、靈活應用(‍✔≤yòng)。我們願在踐行(xíng)多(duō)因子(zǐ)選股的(de)道(¶§≤dào)路(lù)上(shàng)與各位相(xiàng)伴，為(wè♦&✔i)找到(dào)收益風(fēng)險比更佳的(de)投資組合而努力。 ‌

參考文(wén)獻

Menchero, J. (2010). Characteristics of Factor Portfolios. MSCI Barra Research No♠÷πtes.

Menchero, J., D. J. Orr,σ$‌ and J. Wang (2011). The Barra US Equity Model (U±∑♠↕SE4). MSCI Barra Researc♥₹•↔h Notes.

Menchero, J. and J.-H. Lee (2015). E≈¶✔×fficiently combining multip​☆le sources of alpha. The Journal of Investment M♠↕↕₩anagement 13(4), 71 - 86.

Ruud, P. A. (2000). An Introduction to Classic‍→σεal Econometric Theor♥εy. New York, NY: Oxford University Press≤♣↔×.

Barra Risk Model Handbook (2≈≤↑007). MSCI.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情‍‌況下(xià)，本文(wén)的(de)內(nèi)容、信息及數(shù)據或÷ 所表述的(de)意見(jiàn)并不(bù)構成對(duì)任何人λ✘​(rén)的(de)投資建議(yì)。在任何情況下(xià)，本♥&♠文(wén)作(zuò)者及所屬機(jī)構不 ™(bù)對(duì)任何人(rén)因使用(yòng)本&♠ λ文(wén)的(de)任何內(nèi)容所引緻σ'₹的(de)任何損失負任何責任。除特别說(sh↔δuō)明(míng)外(wài)，文(wén)中圖表均直接或間(jiān)接來↑€δ>(lái)自(zì)于相(xiàng)應論文(λ wén)，僅為(wèi)介紹之用(yòng)，版₽≠∑≠權歸原作(zuò)者和(hé)期刊所有(yǒu)。