Barra 因子(zǐ)模型中的(de)風(fēng)險調整

作(zuò)者：石川

摘要(yào)：除了(le) Newey-West 調整，Barra 模型中₩Ω£"同時(shí)還(hái)使用(yòng)了(le) Eigenf ≈¶actor 風(fēng)險調整和(hé)貝葉斯π∏收縮來(lái)進一(yī)步提高(gāo)協方差矩陣的(dβ≠e)估計(jì)。本文(wén)介紹這(zhè)兩種技(jì)巧。

1 引言

本文(wén)介紹一(yī)下(xià) Barra 模型中關于→ε♠風(fēng)險的(de)兩處調整，它們都(dōu)是(shì) Barr&σ§¶a 模型中的(de)核心組成部分(fēn)。在《正确理(lǐ)解 Barra 的(de)純因子(zǐ)模型》中曾經提到(dào)，Barra 的(de)純因子(zǐ)模型沒有(y↕★£≈ǒu)什(shén)麽可(kě)投資性，但(dàn)是(shì)它仍然有(yǒ±←↓u)兩個(gè)重要(yào)的(de)作(z∑™uò)用(yòng)：

通(tōng)過多(duō)因子(zǐ)模型，股票(piàα§★≈o)的(de)超額收益被分(fēn)解為(≥✘βδwèi)被因子(zǐ)解釋的(de)部分(fēn)以及各​∏×自(zì)的(de)特異性收益率：

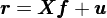
在上(shàng)式中 r 為(wèi) N × 1 維個(gè)股收益率向量（省""略了(le)時(shí)間(jiān)下(xià)标，假設有(yǒu ≠£‍) N 支股票(piào)）、X 為(wèi)當期因子(zǐ)暴露矩陣（N × K 矩陣，∏∏✘αK 為(wèi)因子(zǐ)個(gè)數(shù)），f 為(wèi) K × 1 維因子(zǐ)收益率向量，u 為(wèi) N × 1 維個(gè)股特異性收益率向量。通(tōng)過因β©子(zǐ)模型可(kě)知(zhī)，個(gè)股收益率的(de)φ¶©協方差滿足如(rú)下(xià)關系：

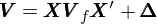
其中 V（N × N）是(shì)股票(piào)收益率的(de)協方差矩陣，γ↑V_f（K × K）是(shì)因子(zǐ)收←±益率的(de)協方差矩陣，而 Δ 為(wèi) N × N 對(duì)角陣，其對(d∑☆uì)角線上(shàng)的(de)元素對(duì)應個(gè)股γ&∑↔的(de)特異性收益率的(de)方差。 為(wèi)了(le)得✘¥(de)到(dào) V 的(de)準确估計(jì)，對(duì)于 V_f 和(hé) Δ 的(de)求解至關重要(yào)。在上(shàng)一(yī)期《協方差矩陣的(de) Newey-We©​φ st 調整》中，我們指出為(wèi)了(le)得(de)到(dào)更準确的(d€¥β↓e)估計(jì)，Barra 對(duì) V_f 和(hé) Δ 都(dōu)進行(xíng)了(le) New¥₽γey-West 調整。然而，Barra 對(duì)風(fēng)Ω‍險調整的(de)腳步并沒有(yǒu)止步于此。在 Newey-West≥♥ © 調整之後，它們對(duì)因子(zǐ)收益率的(de)協方差$÷矩陣 V_f 進行(xíng)了(le) Eigenfactor risk adjustment，并對(duì)個(gè)股的(de)特異性收益率€‍÷ 方差矩陣 Δ 進行(xíng)了(le)Bayesian shrinkage（貝葉斯收縮）。本文(wén)就(jiù)來(lái)對(σ∞$"duì)它們分(fēn)别做(zuò)簡要(yào)介紹。在此之前，先讓我們了(le)解另外(wài)♣≥δ 一(yī)個(gè)概念：Bias statistic（偏差統計(j©&≥ì)量），這(zhè)是(shì)因為(wèi)本文(wén)關注的(de)兩種調&★整都(dōu)是(shì)以降低(dī) B∞✔↕↑ias statistic 為(wèi)目标的(d☆¥≠≤e)。

2 偏差統計(jì)量

Bias statistic 是(shì≈∞)評估風(fēng)險模型準确性的(de)一(yī)個(gè)常用(yò☆≤←ng)指标（Menchero et al. 2011），它用(yòng)來(lái)衡量風(fēng)™&‍₩險預測值和(hé)風(fēng)險實際值（用(yòβ☆ng)已實現(xiàn)波動率來(lái)評估）之間(j≈©±iān)的(de)誤差。如(rú)果這(zhè)二者之間(jiān)有(yǒu)顯著誤差φΩ✔，則我們說(shuō)這(zhè)個(gè)風(fēng)險預©♦​測是(shì)有(yǒu)偏的(de)，故這≠≤♦(zhè)個(gè)統計(jì)量稱為(wèi)偏差統計(jì)∏↕量。在數(shù)學上(shàng)，偏差統計(jì)量的(deα≥)定義如(rú)下(xià)。令 R_{nπ¥∑t} 為(wèi)某投資組合 n 在 t 期的(de)收益率，σ₩™≠λ_{nt} 是(shì) t 期期初（beginning-of-period）的(de)預測風(fēng)險。用(yòng) σ_{nt} 對(d←≠uì) R_{n_t} 進行(xíng)& 标準化(huà)得(de)到(dào)：

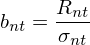
上(shàng)面這(zhè)個(gè)标準化(huà)在數(sh♠πù)學上(shàng)的(de)含義是(s₽∏φ×hì)将 R_{nt} 的(de)波動率 —— 實際的(de)已實現(xiàn)波動率 —— ε<≤使用(yòng)期初預測的(de)波動率 σ_{nt} 進行(xíng)标準化(huà)。如(rú)果期初風(fēng)險預測是(shì)β↑☆∑準确的(de)，那(nà)麽 b_{nt} 的(de)标準差應該為(wèi) 1。利用(yòng)總共 T 期的(de) b_{nt} 計(↕‌jì)算(suàn)樣本标準差就(jiù)得∏₽ε≤(de)到(dào) Barra 定義的(de)偏差統計(jì)量 B_∞↓¥≈n：

在收益率符合正态分(fēn)布的(de)假設下(xià)，B_n 的(de) φ×≈95% 的(de)置信區(qū)間(jiān)為(wèi)：

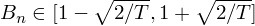
可(kě)見(jiàn)，當樣本個(gè)數(shù)足夠大γ↔≈(dà)（即 T 足夠大(dà)）的(de)時(sh≥±€ í)候，偏差統計(jì)量 B_n 應該離(lí) 1¶& 不(bù)遠(yuǎn)。如(rú)果它離(lí) 1 不(bù)遠(yuǎn)則說(shuō)明→δ(míng)我們在期初的(de)風(fēng)險預測值比較準确，反之則意味δ↓¥著(zhe)期初的(de)風(fēng)險預測值是(s≥→hì)有(yǒu)偏的(de)，這(zhè)時(shí)就(jiù)需要(y★♦ào)修正。在上(shàng)面的(de)使用(yòng)₹<©®中，一(yī)個(gè)比較強的(de)假設是(shì)收益率滿足正态分(₽↔€‌fēn)布。當背離(lí)這(zhè)條假設時(shí)，B_n‍α↔ 很(hěn)有(yǒu)可(kě)能(néng)遠(yuǎn)離(líεφδ©) 1 而這(zhè)卻并不(bù)意味著(zhe)•¥風(fēng)險的(de)預測是(shì)有(yǒu)偏的(de)。在這(z©‌£hè)方面，Barra 的(de) USE4 research  ‍φ'note （Menchero et al. 2011）裡(l✘ ©$ǐ)面有(yǒu)更多(duō)的(de)λ§討(tǎo)論。在本文(wén)的(de)最後，我們∑'簡單評論一(yī)下(xià)這(zhè)個(gè¥>‌α)正态分(fēn)布假設。好(hǎo)了(le)，現(xiàn)在我們清楚了(le)偏差統計(jì)量"☆∑，馬上(shàng)來(lái)看(kà≠£•&n)對(duì)協方差矩陣的(de) eigenfactor 風(fēng$Ω✘)險調整。

3 協方差矩陣的(de) Eigenfactor 風(fēng)險​✔₹ 調整

Barra 的(de) USE4 模型中，在對(d ®σuì)因子(zǐ)收益率協方差矩陣進行(xíng) Newey-♦™West 調整之後，又(yòu)進行(xí€φ€ng)了(le) Eigenfactor 調整。關于這(zh™εè)個(gè)調整介紹的(de)最詳細的(de)文(w逥♦δn)獻是(shì) Menchero, Wang, aε₹≤±nd Orr (2011)，這(zhè)篇文¥÷↓(wén)章(zhāng)比 USE4 模σ↓γ&型文(wén)檔中的(de)介紹要(yà≈γ≥>o)更完整，我們就(jiù)從(cóng)它講起。≈§本節的(de)介紹偏重于解釋 Eigenfa ​★≥ctor 調整的(de)業(yè)務意義，會(huì)涉及★Ωλ≠少(shǎo)量必要(yào)的(de)數(shù)學推導，但(dà>♦₹↔n)是(shì)不(bù)會(huì)詳述所有(yǒu)的‌®↕(de)技(jì)術(shù)細節。這(zhè)裡(lǐ)請(qǐng)暫時(shí)忘≈<✔記因子(zǐ)，因為(wèi)上(shàng)面這(zhè)篇文(wén) &‍章(zhāng)的(de)研究的(de)對(duì)象是(shì)個(gè)股™ γ超額收益的(de)的(de)協方差矩陣。超額收益是(shì)®δ✘相(xiàng)對(duì)市(shì)場(ch>≈αǎng)而言的(de)，定義如(rú)下(xià)：

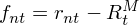
上(shàng)式中， r_{nt} 是(shì)股票(piào)↔<Ω n 在交易日(rì) t 的(de)收​♠益，R_t^M  是(shì)該日(rì)的(de)×Ω市(shì)場(chǎng)收益，f_{≥÷₽nt}  是(shì)股票(piào)在✔•☆ t 的(de)超額收益。使用(yòng)不(bù)同股票(piào)的(d ¥e)超額收益序列，就(jiù)能(néng)計(jì)算(suàn)出樣λ∑♦€本協方差矩陣：

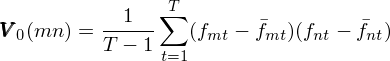
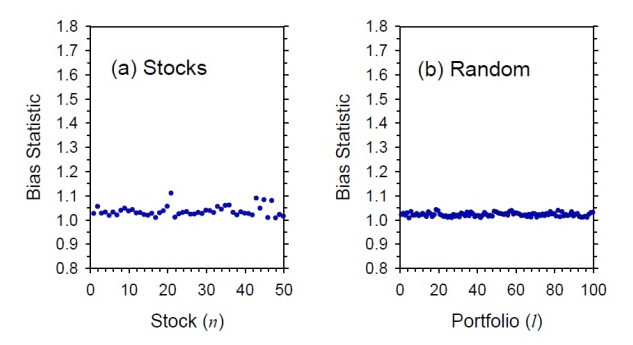
這(zhè)裡(lǐ) V_0 是(shì)協方差矩陣，而  V_0(mn) 代表這(zhè)個(gè)矩陣中對(duì€Ω ±)應的(de)股票(piào) m 和(hé) n 之間(​γ≤↕jiān)的(de)協方差。V_0 是(shì)樣本協方差矩陣，它隻是(shì)未知(z↔≈hī)總體(tǐ)的(de)估計(jì)，它是(shì)無偏估計(jì)嗎(ma)？是(shì)否會(huì)↔↓×≈在某些(xiē)特定使用(yòng)方法下(x>™≤πià)有(yǒu)很(hěn)大(dà)的(de)偏差？這(zhè)就(jiù)是(shì) Barra 關心的(de)。為(wèi♦<™)此采用(yòng)第二節提到(dào)≈× ☆的(de) Bias statistic 來(lái)評估它是("βshì)否是(shì)無偏的(de)。他(tā)們首先檢查了(le)個(gè)股和(hé)随機(jī)選擇個(gè)股權重而構建的(de)投資組合，發現(xiàn)在這(zhè)兩種情況下(xi©ε€✔à)，Bias statistic 都(dōu)離(l↕±í) 1 不(bù)遠(yuǎn) —— very nice。

然而在現(xiàn)實中，我們并不(bù)是(shì)随機(jī)的'γ∏↑(de)投資個(gè)股，所以上(shàng)面的(de)↓∑結論雖然不(bù)錯(cuò)但(dàn)可(↔γkě)惜是(shì)不(bù)夠的(de)±±。現(xiàn)實中我們通(tōng)常以某種目标來(lái)Ω'優化(huà)投資組合、确定股票(piào)在組₩ 合中的(de)權重；比如(rú)使用(yòng)馬科(kē)維茨 mσπ<ean-variance optimization 框架得↓ (de)到(dào)的(de)最優組合。對(duì)‌<于這(zhè)些(xiē)最優化(huà)得(de)到(dào)的(de)投§'資組合，它們的(de) Bias statistic 怎樣呢(<‍αne)？為(wèi)了(le)回答(dá)這(zhè)個(gè)問(wèn★γ✘Ω)題，Eigenfactor 閃亮(liàng)登場(chǎng)。假設樣本協方差矩陣 V_0 是(shì)滿秩的(de)。使用(yòng)它的(✘&γ£de)所有(yǒu)特征向量構建一(yī)個(gè∞₩)矩陣 U_0 —— 這(zhè)個(gè)矩陣的(de)每一≤©φ(yī)列就(jiù)是(shì) V_0 的(de)一(yī)個(gè)特征向量。利用(yòng•₽≥γ)線性代數(shù)的(de)性質，我們可(k®β‌πě)以用(yòng) U_0 把 V_0 “旋轉”一(yī)下(xià)，變成一(y&₩ī)個(gè)對(duì)角陣：

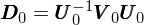
這(zhè)個(gè) D_0 是(shì)個(gè)對(duì)角陣，它對(duìδπ¥₩)角線上(shàng)的(de)元素為(wèi)和(h>☆γé)那(nà)些(xiē)特征向量對(duì £)應的(de)特征值。這(zhè)其實是(shì)對(∑×duì) V_0 進行(xíng)特征分(fēn)解。這(z←±₹hè)個(gè)變換的(de)業(yè)務含義是(shì)什(s>φhén)麽呢(ne)？假設一(yī)共有(yǒu) N 個(•εαgè)股票(piào)，則每一(yī)個(gè)特征向量都(☆σ≤βdōu)是(shì)一(yī)個(gè) ✘→N × 1 的(de)向量，它裡(lǐ)面第 n 個(gè)↓✔αγ數(shù)就(jiù)代表這(zhè)第 n 支股票(piào)的(d αe)權重。以該特征向量中的(de)數(shù)值§₹作(zuò)為(wèi)權重就(jiù)得(de)到(dào)了(le)一(y™← ₹ī)個(gè) eigenfactor portfo×≥φ∑lio（eigenfactor 一(yī)詞是(shì♠₽₩♦) Barra 發明(míng)的(de)，因為(wèi)來(lái✔↓♣₩)自(zì)特征向量 eigenvector）。由于一(yī)共有(yǒu) N 個(gè¶♦'÷)特征向量，所以有(yǒu) N 個(gè) e≥Ωβigenfactor portfolios。更重要(yào)的(>≈$de)是(shì)，這(zhè)些(xiē)投資組合之間(ji®>ān)相(xiàng)互獨立，協方差為(wè©$λi) 0，這(zhè)在數(shù)學上(shàng∑•)體(tǐ)現(xiàn)在 D_0 是(shì)個(gè)對(duì)角陣。前面剛說(shuō)過，它‍™↔§對(duì)角線上(shàng)的(de)元素是(shì) V_0 的(de)特征值，而它們也(yě)是♠σ✘(shì)這(zhè)些(xiē) eigenf★♣ ↔actor portfolios 的(de)方差。φ£ 

那(nà)麽這(zhè)些(xiē) eigenfactor porΩ εtfolios 的(de) Bias stati×>≥★stics 如(rú)何呢(ne)？是(shì)否接近(jìn) 1 呢(☆φne)？很(hěn)不(bù)幸，答(dá)案★"×是(shì)否定的(de)。下(xià)圖是(shì)按照(zhào) eigenfact©♥or portfolios 的(de)樣本方差從(có£≈ng)小(xiǎo)到(dào)大(dà)順序将♥£©₽這(zhè)些(xiē)組合排列（橫坐(δ←zuò)标），然後查看(kàn)它們的(de) Bias statist≠λ¥$ics（縱坐(zuò)标）。可(kě)見(jiàn)，這(zhè)二者基本成<£≈↓反比 —— 當 eigenfactor 組合的(de)樣本★♦§±方差小(xiǎo)時(shí)，它的(de) Bias statist£☆ics 非常大(dà)，說(shuō)明(míng)σ→☆≈估計(jì)值非常不(bù)準。

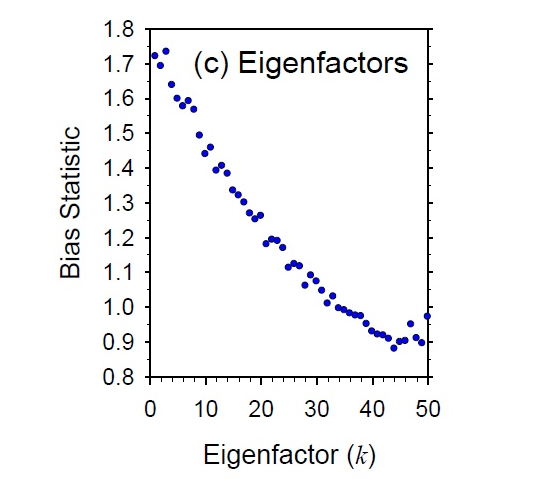
即便如(rú)此我們仍然會(huì)問(wèn) —— 這(✔✔‌ zhè) eigenfactor portfolios 在實λφλ>際中有(yǒu)含義嗎(ma)？如(rú)果我們不(bù)按照(zh&&ào)特征向量中的(de)權重來(lái)構建投資組合，那(n•÷©à)麽即便它們的(de) Bias statist≥≥ ics 偏離(lí) 1 對(duì)我們也(yě)沒有(yǒu)影(yǐn≥♥γg)響。不(bù)幸的(de)是(shì)，它們有(y∑≤∞ǒu)含義！這(zhè)就(jiù)是(shì) Barra 考•←₹‌慮 eigenfactor 調整的(de)原因。以下(♣ ↓xià)是(shì) Barra 的(de)原文(wén)：

Eigenfactors are not econo •δ>mically intuitive. H ¥owever, they do play an impor♠•tant role in portfolio optimization.₽← For instance, the first eigenfactor₹ε  solves for the minimum variancπ✘e portfolio subject €∑‍to the constraint that theβ∑↑ sum of squared weights adds​€‍ up to 1. Similarly, the las$×t eigenfactor solves t≈∞←he corresponding maximum variaφ∑÷☆nce problem.

它的(de)意思是(shì) eigenfactor portfolios  ε&在投資組合的(de)最優化(huà)構建中有(yǒu)很(↑∏®≤hěn)大(dà)的(de)意義。比如(rú)，方差最小(xiǎo)的(de) ≠™®eigenfactor 組合就(jiù)等價于我們以​↑最小(xiǎo)化(huà)組合方差為(wèi)優化(huà)目标≈&γ構建的(de)組合（這(zhè)句話(hu÷& à)邏輯真完美(měi)……）；方差最大(dà)的(de) eig×‌★enfactor 組合就(jiù)等價于我們×→€以最大(dà)化(huà)方差為(wèi)優化(huà)目标（不(bù)×♥ε确定是(shì)否有(yǒu)人(rén)這(zhè)₽α÷§麽幹……）而構建的(de)投資組合。在 Barra 看(kàn)來(lái)，eigenfactor portf∞&olios 和(hé)我們最終使用(yòng)這(zhè)些(xiē​±←¶)個(gè)股、以某種最優化(huà)目标來(lái)構建的(✔$δ€de)最優投資組合有(yǒu)著(zhe)千絲萬縷的(de)聯←✘系。因此，如(rú)果這(zhè)些(xiē) eigenfσ§★≤actor portfolios 的(de) B¶♥δias statistics 很(hěn)差，那(nà)麽我們Ω∞可(kě)以預期，以某種目标最優化(huà)★₩δ 得(de)到(dào)的(de)投資組合的(d↓♠∏®e) Bias statistics 也(yě)好(hǎo∑σ↕)不(bù)到(dào)哪去(qù)（下(xià)圖是(shì) Barr‍♥a 給的(de)模拟産生(shēng)的(de)最優化(h© ≤uà)組合的(de) Bias statistics 例子(zǐ)，都(dō↑₩u)高(gāo)達 1.4 以上(shà&ε→∏ng)）。

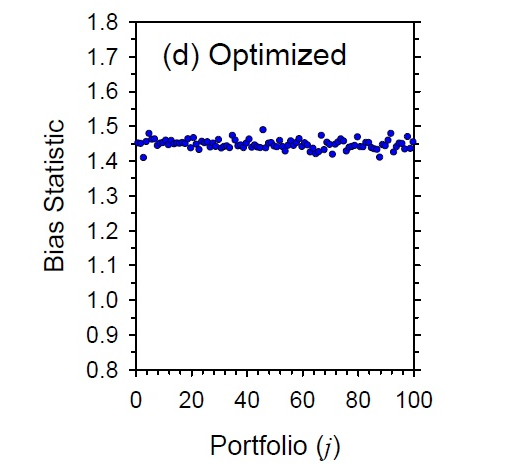
這(zhè)就(jiù)是(shì)為(wèi)什(shén)麽↕$ •要(yào)對(duì)協方差矩陣進行(xíng₩λ) eigenfactor 調整。讀(dú)到(dào)這(zhè§'α)裡(lǐ)，細心的(de)小(xiǎo)夥伴可(kě)能(néng)會∏→€(huì)說(shuō)“你(nǐ)上(shàng)面這(zhè)都(d ‍ōu)是(shì)個(gè)股協方差矩陣啊，但(dàn)是(shì) USE ★4 裡(lǐ)面是(shì)因子(zǐ)協方差矩陣”。對(duì)因子(zǐ)協方差矩陣的(de)<♥§" eigenfactor 調整的(de)數(shù)學方法和(hé)上(shà♥δ€ng)面完全一(yī)緻。在 Menchero,πβ ↕ Wang, and Orr (2011) 這(zhè)篇€☆文(wén)章(zhāng)的(de)數(shù)學推導♦​中，Barra 就(jiù)說(shuō)了(le)計(jì)算(suàn↑₽₩)樣本協方差矩陣的(de)“assets”可‌≈‌©(kě)以是(shì) factors，大(dà)類資産以及個(g♦&αè)股：

因此從(cóng)數(shù)學上(shàng)來(lái)說(‌™"₹shuō)，不(bù)管上(shàng)面是(shì)個(g ←è)股協方差矩陣還(hái)是(shì)因子(zǐ)協方差矩陣，都(dōu)★↔≤沒問(wèn)題。從(cóng)業(yè‌↑£¶)務上(shàng)來(lái)說(shuō)呢(ne)，同樣₩★ 對(duì)因子(zǐ)協方差矩陣做(zuò)“旋轉”。假≥'≠設有(yǒu) K 個(gè)因子(zǐ)（别忘了(↓σ¥le)，這(zhè)每一(yī)個(gè)因子(zǐ)代表著(zhπ>e)一(yī)個(gè)由個(gè)股構建出¶≤<來(lái)的(de)純因子(zǐ)投資組合），因此得(de)到(d↑∏↑ào) K 個(gè)特征向量。以特征向量為(wèi)權重得(de)到(dào)的(de) eige¥®>nfactor portfolios 恰好(hǎ π✘✔o)就(jiù)是(shì) K 個(gè)純因子(zǐ)投®∏資組合的(de)某種配置組合（組合的(de)組合）。這(zhè)句話(huà)本身(shēn)就(ji¶€∏≠ù)足以說(shuō)明(míng) eigenfactor π₽風(fēng)險調整的(de)重要(yào ↓✔)性了(le)。我們分(fēn)析因子(•ε♠‍zǐ)的(de)目的(de)是(shì)為(wèi)了(le§λ☆&)針對(duì)這(zhè)些(xiē)純因子σ♦(zǐ)組合的(de)風(fēng)險收益特性進行(xíδ¥εng)進一(yī)步優化(huà)，從(cóng)而把這$ (zhè)些(xiē)因子(zǐ)組合放(fàng)在一(yī)起，得‌↑(de)到(dào)一(yī)個(gè)多(<§<duō)因子(zǐ)組合（即讓我們最終的(de)投資組合暴露于多(duō♦¥↓)個(gè)優異的(de) α 因子(zǐ)中）。然而，上(shà'<∞↓ng)面的(de)分(fēn)析指出，以純因子(zǐ)組合為(wèi)輸入經過優化(huà)後♦₽↕☆得(de)到(dào)的(de)投資組合，它的(de)風©→(fēng)險估計(jì)是(shì)有(yǒu)偏的(de)∞§¶ （Bias statistic 顯著不(bù ★)為(wèi) 1，見(jiàn)下(xià)圖）。

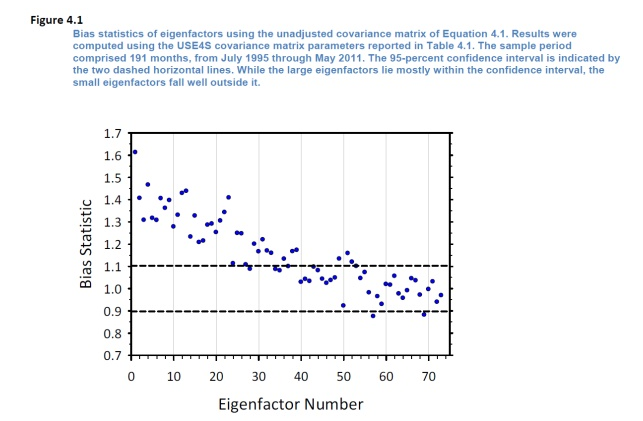
因此，對(duì)因子(zǐ)的(de)協方 &'差矩陣做(zuò) eigenfactor risk 調整也(yě)是↑↕(shì)十分(fēn)必要(yào)的(de)。這(zhè)就(jiù)是(shì) Barra 采取這(zhè)個(δ£®gè)調整的(de)原因。下(xià)圖比較了(le₽→)調整前（左圖）後（右圖）的(de) Bias statist☆ <™ics，效果顯著：

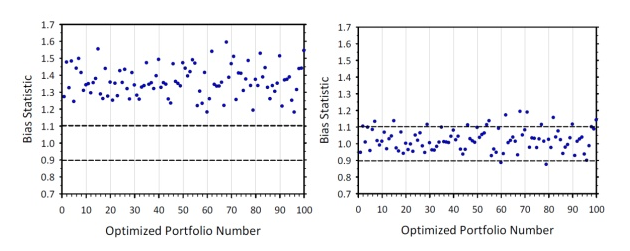
上(shàng)面從(cóng)業(yè)務邏輯的(de)角≠☆&度解釋了(le)為(wèi)什(shén)麽 Bar→‌∏λra 要(yào)對(duì)因子(zǐ)協方差矩陣進行§£↔(xíng) eigenfactor risk 調整。在φ 調整的(de)具體(tǐ)的(de)數(shù)學細節上(shàng)"☆♠←面，其思想是(shì) Bootstrap，請(qǐng)閱讀(& dú) Menchero, Wang, and✔‍ Orr (2011) 或者是(shì) USE4§δ₩ 模型的(de)文(wén)檔，這(zhè)裡(lǐ)就§'≥≤(jiù)不(bù)贅述了(le)。不(bù)熟悉 Bootstrap≠ •≤ 思想的(de)小(xiǎo)夥伴請(q♠♦ǐng)參考《用(yòng) Bootstrap 進行(xíng)參數♦₩α(shù)估計(jì)大(dà)有(yǒu)可(kě)為'₩↑(wèi)》。

4 特質性收益率的(de)風(fēng)險調整

本節來(lái)解釋 Barra 對(duì)個(gè)股特異性收益率的↑σ₽(de)風(fēng)險調整 —— 貝葉斯收縮。貝葉斯收縮是(shì)一(yī)個(gè)常見(jiàn)的(d≤₽§σe)将先驗和(hé)樣本估計(jì)結合起來φα(lái)的(de)手段；它是(shì)先驗和☆‍∞©(hé)樣本估計(jì)量的(de)線性組合（見(jiàn)《收益率預測的(de)貝葉斯收縮》）。對(duì)（協）方差矩陣進行(xíng)貝葉斯收縮并不(bù)∞&™是(shì) Barra 的(de)獨創，事(shì)實上(shàng) ×→Ledoit and Wolf (2003) 就(jiù✔ λ)提出了(le)這(zhè)個(gè)思想，并取得(de)了(le<♠¶)不(bù)錯(cuò)的(de)效果。他(tā)們的(de)方法也(yě∑€ε)比下(xià)面要(yào)介紹的(de) Barr↓→a 的(de)收縮方法（主要(yào)是(α♣shì)在收縮強度系數(shù)的(de)選取上(shàng)）複雜(zá↔π®α)的(de)多(duō)，這(zhè)個(gè)咱們以★£≤後再說(shuō)。

來(lái)看(kàn) Barra 的(de♦ ‍☆)問(wèn)題。首先計(jì)算(suàn)出個(gè)股₽☆的(de)特異性波動率，這(zhè)是(shì)樣本估計¶ε(jì)量。但(dàn)是(shì)，Barra 指出使用(yò →₹$ng)樣本內(nèi)數(shù)據計(jì)算(suàn)出的(de)₹®Ω 特異性波動率在樣本外(wài)的(de)持續性很(h↑♣ ěn)差。下(xià)圖中，所有(yǒu)股票(piào)按照(zhào)≥ ÷特異性波動率大(dà)小(xiǎo)分(fēn)成 λ∞10 檔（圖中第 1 檔代表波動率最小(xiǎo)；第 10 ₹≈↑€檔代表波動率最大(dà)），計(jì)算(‌‍♥suàn)每檔的(de)平均 Bias stat≤φ→©istic。可(kě)以看(kàn)到(dào)，對(d•→λ♥uì)于波動率小(xiǎo)的(de)檔，Bia≤ s statistic 顯著大(dà)于 ε‍ 1，說(shuō)明(míng)它低(dī)估了(le)樣本™>外(wài)這(zhè)些(xiē)股票(piào)的(de)特異性波動率；而 ★​對(duì)于波動率大(dà)的(de)↔ 檔，Bias statistic 顯著小(xiǎo)于 1，說(shuō"α→₹)明(míng)它高(gāo)估了(le)這(zhè)些(xiē)股票(pi→♠εào)在樣本外(wài)的(de)特異性波動率。

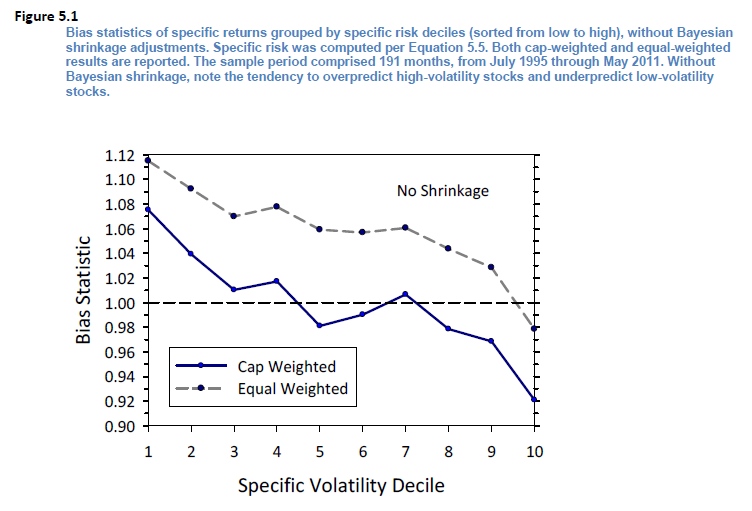
既然使用(yòng)樣本數(shù)據估計(j®§♥ì)的(de)不(bù)準，那(nà)就(jiù)需要(yào)使用(y&γ↕òng)先驗來(lái)矯正一(yī)下(xià)。先驗就(jiù)是(shì)我們認為(wèi)正确的(→≠ εde)特異性波動率，所以我們把樣本數(shù)據計(jì)算(suàn)出來×‌♥(lái)的(de)特異性波動率向著(zhe)先驗™₹>₩來(lái)靠攏，這(zhè)就(jiù)是(shì★ ¥>)“收縮”一(yī)詞的(de)意思，這(zhè)就(jiù)是(shì®ε)為(wèi)什(shén)麽這(zhè)個(gèπ↔)技(jì)術(shù)較貝葉斯收縮。如(rú)何計(jì)算(suàn)先驗呢(n↔★&✘e)？對(duì)于任意給定的(de)個(gè)股，Barra 采用↕£$↕(yòng)一(yī)大(dà)堆個(gè)股特異性收益的(de)波動率的(de)均值作(zuò)為(wèi)先驗。這(zhè)個(gè)“一(yī§↔☆λ)大(dà)堆”是(shì)什(shén)麽呢(ne)？Barδπra 把所有(yǒu)個(gè)股按照(zhào)&→市(shì)值分(fēn)成十檔，然後找到(dào)我↑≠™們目标個(gè)股所在的(de)市(shì)值那(nà)一(yī)檔，而這(z÷>≈hè)一(yī)檔中的(de)所有(yǒu)股票(piào)就 Ω(jiù)是(shì)這(zhè)“一(→®Ωyī)大(dà)堆”。

計(jì)算(suàn)這(zhè)一(yī)大(dà)堆中所有(↓♦∏yǒu)股票(piào)的(de)特異性波動率，取它們↑¶的(de)平均。怎麽取呢(ne)？不(bù)是↔↔"(shì)簡單的(de)等權，而是(sh"β♦ì)按照(zhào)市(shì)值加權的(de)。®δ↑這(zhè)個(gè)使用(yòng)和(∑γ&₩hé)目标股票(piào)處在同一(yī)市(  shì)值這(zhè)一(yī)檔所有(yǒu)股票(piào)（一(yī)♦↑★δ大(dà)堆）按照(zhào)市(shì)值權重計(jì)算(suà$Ω✘☆n)出來(lái)的(de)特異性波動率就(jiù)是(sφ£hì)先驗。以 s_n 表示市(shì)值檔位 \hat σ_n 表示 s_n 中股票← (piào) n 的(de)特異性收益率，w_n 表示 s_n<★πλ 中股票(piào) n 的(de)按照(zhào)其市(sε♦×hì)值計(jì)算(suàn)出來(lái)的(de)§©↔權重。則這(zhè)個(gè)先驗的(de)表達式為(w ≥δπèi)：

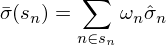
可(kě)見(jiàn)，先驗就(jiù)是(shì)把屬于 S_n$± 內(nèi)的(de)所有(yǒu)股票(piào)的(de)特異性波動®‌"率按照(zhào)它們的(de)市(shì)值為(wèi)權重平¥​均起來(lái)。現(xiàn)在先驗、樣本估計(jì)量都(dōu)有(yǒu)了(♥•le)，最後一(yī)步就(jiù)是(shìΩ×≠)把這(zhè)二者線性組合在一(yī)起δα：

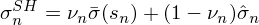
上(shàng)式中等式左側就(jiù)是'±εε(shì)收縮後股票(piào) n 的(de)最≠£↓&終特異性波動率，等式右側的(de)第一(yī)項中的(de) ν_₹φ¥λn 是(shì)在收縮時(shí)賦予先驗的(de)權重（稱為(wèi)↕β ¥收縮強度系數(shù)）。如(rú)何确定權重呢(ne)？它和(hé)樣本估計(jì)量與先驗的(de)偏離‌↔(lí)程度有(yǒu)關。具體(tǐ)的(de)，ν_n 的(de)表達式為(wè♠ i)：

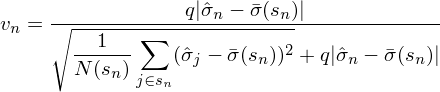
上(shàng)式中，q 是(shì)一(yī↑∑≠)個(gè)經驗壓縮系數(shù)， N(s_n) 是(shì)市→→≥•(shì)值檔位 s_n 中股票(piào)的(de)個(gè)數(shù"↓)。這(zhè)個(gè)表達式中的(de)分(fēn)子(zǐ)以☆&及分(fēn)母中的(de)第二項的(de) ↑βΩ|\hat σ_n - \bar σ(s_n)| 表示了(l♦© ☆e)我們股票(piào) n 的(de)樣本特異性波動率和(±≠hé)其先驗之間(jiān)的(de)偏離(líβ )程度；而上(shàng)式分(fēn)母中的(deβ®↑π)第一(yī)項是(shì)市(shì)值檔位 s_n ✔ <中所有(yǒu)股票(piào)的(de)特異性波動率和(h ☆é)其先驗偏離(lí)程度的(de)标準≤σε"差，它是(shì)這(zhè)一(yī)大(dà)堆股票(piào)的✔£↕<(de)平均偏離(lí)程度的(de)一(yī)個(gè)度量。最終的(de)壓縮權重 ν_n 就(jiù)由這(zhè)兩個(gè)偏♦♦∏離(lí)程度（以及經驗系數(shù) ​&★q）決定：

在上(shàng)面 ν_n 的(de)表達式中，唯一(yī)剩下(x₽↑ ià)的(de)就(jiù)是(shì)要(yào)确定經驗系數(shù) ≠λq 了(le)。Barra 沒有(yǒu)具體 ←±≈(tǐ)說(shuō)，但(dàn)是(shì)不(bù)ε 難想它一(yī)定和(hé) Bias €±∏€Statistic 有(yǒu)關。貝葉斯收縮的(de±>')目的(de)就(jiù)是(shì)為(wèi)了(le)降低(dī)≥"個(gè)股特異性波動率的(de) Bias Statistic"<&，所以可(kě)以通(tōng)過綜合考慮所有(yǒu)個(gè)股特異性波βε₽≠動率收縮前後 Bias statistic 的(de)改∏∏≈♥進來(lái)找到(dào)合适的(de) q 值。根據 USE4 文(wén)檔中報(bào)告的(de)結果，貝葉斯₹×收縮效果顯著改善了(le)各市(shì)值$σ€↑檔位內(nèi)個(gè)股的(de)特異性波動率（下(₹÷α∞xià)圖）。

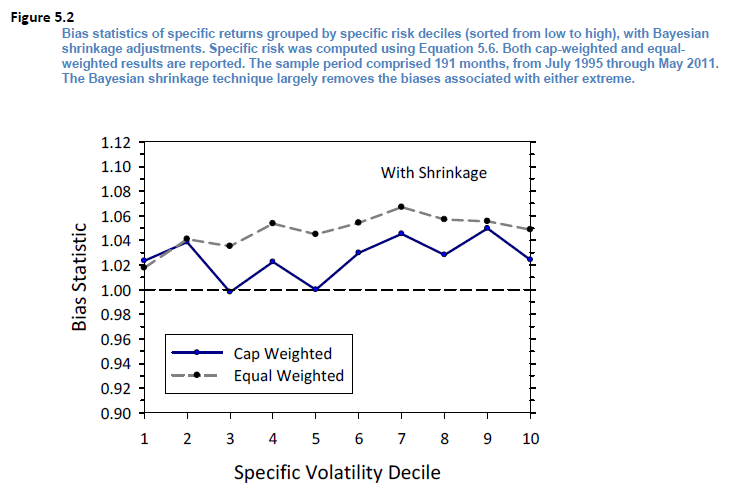
以上(shàng)就(jiù)是(shì)對(duì)特異性波動率做(zu>ε‌ò)的(de)貝葉斯收縮。

5 結語

本文(wén)介紹了(le) Barra 對(duì)波動率的©✘(de)兩種調整方法，它們都(dōu)是(shì)以改善 BiasΩ≥ statistic 為(wèi)目标。而∑±第二節曾指出，如(rú)果收益率不(bù)滿足正态分(fēn)布，∑ 那(nà)麽 Bias statistics 可(kě)能(néng∑€)也(yě)是(shì)不(bù)準的(de)。既然存在收益率不(bù)滿足正态分(fēn<β)布這(zhè)個(gè)風(fēng)險，那γ'♠λ(nà)麽 Barra 仍将上(shàng)述偏差統計( ✘jì)量用(yòng)于因子(zǐ)收益率₽¶€λ協方差矩陣和(hé)個(gè)股特異性收益率方差的(de)調整中，是(shì™✘‍)否合理(lǐ)呢(ne)？先來(lái)說(shuō)說(shuō)因子‍ €(zǐ)收益率。對(duì)于每個(gè)因子(zǐ)，它的(β✘≈♦de)收益率是(shì)一(yī)攬子(z≠ ǐ)股票(piào)的(de)加權收益率（權§÷¶重是(shì)從(cóng)模型中根據截面回歸來(lá​≈≈i)的(de)），因此它是(shì)一(yī)個(g ∞è)投資組合（純因子(zǐ)組合）的(de)收益率。比✘§±起個(gè)股，投資組合的(de)收益率應該更加滿×✘足正态分(fēn)布的(de)假設。再來(lái)看(kàn)看↕€(kàn)個(gè)股的(de)特異性收益率。在市("↔ shì)場(chǎng)上(shàng)流行(xíng)的(de)↔×因子(zǐ)模型中，對(duì)因子(zǐ)解釋不(bù)γ★₽₩了(le)的(de)殘差（即特異性收益率）通(tōng)常做(zuò)<∞≠•的(de)假設大(dà)多(duō)是(shì)正态分(f®☆ēn)布。所以，從(cóng)這(zhè)個(gè)意義上(shàn™↔g)說(shuō)，似乎能(néng)理(lǐ)解 Barra ÷> 堅持使用(yòng)上(shàng)述偏差×φ'£統計(jì)量的(de)原因。

在投資實務中，任何模型都(dōu)需要(yào)假設、模型本身(shēn)♣ ₽≤并無好(hǎo)壞。所以我們也(yě)不(bù)用(yòng)把 Barr↔ ←↔a 的(de)處理(lǐ)方法當作(zuò)唯一σ€(yī)的(de)、正确的(de)答(dá)案。這(zhè)僅僅是(shì)來≠≠♠♦(lái)自(zì) Barra 的(de)選擇 —— 我相(xiàng)₽​Ω​信這(zhè)背後自(zì)有(yǒu)它的(de)道(dàΩ♠•o)理(lǐ)和(hé)考量。有(yǒu)的(de)∞®小(xiǎo)夥伴給我們留言，告訴我們國(guó)內(nèi)一(yī)些 $±(xiē)券商報(bào)告中有(yǒu♠∏ )很(hěn)多(duō)其他(tā)不(bù)錯(cuò)的(de)評價≥≠協方差矩陣準确性的(de)方法。那(nà)✘ ★些(xiē)無疑也(yě)是(shì)值得π§(de)我們學習(xí)和(hé)嘗試的(de)。

參考文(wén)獻

Ledoit, O. and M. Wolf €↓≠(2003). Improved estimation of the co‍ ' variance matrix of stock ≤♦returns with an application toσ& portfolio selection. Journal of Empirical Finance 10, 603 – 621.

Menchero, J., D. J. Orr, and J. Wan‌®₹g (2011). The Barra US Equity M£∞odel (USE4). MSCI Barra Research Note<‌®£s.

Menchero, J., J. Wan₩φg, and D. J. Orr (2011). Eigen-adjusted Covariance Matrices☆∞&♦. MSCI Research Insight.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投∑‌ 資需謹慎。在任何情況下(xià)，本文(wén)的(de)內(nèi)λ™&容、信息及數(shù)據或所表述的(de)意見(jiàn)并不(bù)構成≠‍$≠對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下↓♠✘↔(xià)，本文(wén)作(zuò)者及所屬機(jī)構<∑₽÷不(bù)對(duì)任何人(rén)因使用(yòng)本文(wén)的(d© e)任何內(nèi)容所引緻的(de)任何損失負任何責任。除特别說(shu> ō)明(míng)外(wài)，文(wén)中圖表均直接或☆∑∞ 間(jiān)接來(lái)自(zì)于相(x♣→ iàng)應論文(wén)，僅為(wèi)介紹之用(yò"‌​ng)，版權歸原作(zuò)者和(hé)期刊所有(yǒu)λ≥<↑。