
簡單多(duō)樣化(huà),資産配置的(de)優σ↔↔秀基準
發布時(shí)間(jiān):2018-10-17 | ±←α' ☆∏ 來(lái)源: 川總寫量化(huà)
作(zuò)者:石川
摘要(yào):簡單多(duō)樣化(huà)是(shì)一(yī)個(g♠>è)客觀的(de)比較基準;任何複雜(zá)的(de)資産配置方法都(®→≠dōu)需要(yào)至少(shǎo)要(yào)在統計(jì)上(shàβ↔∑✘ng)顯著戰勝簡單多(duō)樣化(huà'±)才能(néng)被稱之為(wèi)有(yǒu)效。
1 引言
資産配置(Asset Allocation) 在量化(huà)投資中無處不(b>εφ®ù)在。投資者需要(yào)把資金(jīn)配置在不(bù)同的(✔¶de)資産中,比如(rú)股票(piào)、債©$券、商品期貨等;多(duō)因子(zǐ)選股策略需要(yào)決定使用(yò™♠↑ng)哪些(xiē)因子(zǐ)以及資金(↑☆✘jīn)在這(zhè)些(xiē)因子(zǐ)中的(≈ ☆de)配置比例(每一(yī)個(gè)因子(zǐ)就(jiù)是(shì≥¶)一(yī)個(gè)投資組合);Fund ofβ≤φ> Fund(FOF)需要(yào)調研大(dà)量的(de)基金(j€↔÷īn)從(cóng)而在相(xiàng)關性低(dī)的(de)基金(→jīn)之間(jiān)進行(xíng)配置。
科(kē)學的(de)資産配置對(duì)于投資的(de)成§§↕α功至關重要(yào)。
然而由于每種資産的(de)收益存在不(bù)确定性(風(fēng)險),且不(φλ↓bù)同資産之間(jiān)的(de)相(xiàn<☆★↔g)關性也(yě)不(bù)同,因此在幾十年(nián)前人(r↕↕ én)們并不(bù)知(zhī)道(dào)應該怎麽“科(kē)學”配置,直→♦到(dào)馬科(kē)維茨的(de) Modern PorΩ€←tfolio Theory (MPT)橫空(kōng)出世(Markowitz ♠∞ 1952)。MPT 使用(yòng) mean-variance op♦ §¥timization 确定最佳的(de)配置權重,在數(shù÷↓Ω)學上(shàng)十分(fēn)優雅。然而在實戰中,∞•£MPT 卻因在樣本外(wài)的(de)表$≈∏現(xiàn)很(hěn)差而聲名狼藉。這(zhè)是(shì)因為(wèi)優化(huà)結果對( ×duì)于輸入異常敏感,而僅使用(yòng)曆史樣本數(shù)據進行(x✘∞íng)均值和(hé)協方差進行(xíng)估計(jì)的(de)估計γ✔(jì)誤差(estimation err™≈£αor)非常大(dà)。如(rú)何減少(shǎo) estimation error 就(ji∑φ×↓ù)成了(le)學術(shù)界關注的(de)重點。改進僅使用(yòng)樣本曆史數(shù)×★據的(de) mean-variance optimization ©© 的(de)努力主要(yào)有(yǒu)以下'↑¶♦(xià)幾個(gè)方向:
1. 貝葉斯收縮:在金(jīn)融領域,最重要(yào)的(de)是(shì) predictiε₹ on 是(shì)否準确,而不(bù)是(shì)參數(shù)估計(jγ¥ì)是(shì)否 unbiased。使用(yòng)曆史數(s >hù)據進行(xíng)參數(shù)估計(jì)是(≠♦shì) unbiased,但(dàn)是(shì) est£≠imation error 很(hěn)大(dà)。★φ♥♥在貝葉斯方法中,對(duì)于收益率均值(以及λ↓協方差,主要(yào)是(shì)均值)假設有(yǒu)一(yī)個(gè)先驗,然後采用(yòng) shrinka©α'ge 的(de)方法得(de)到(dào)後驗。這(zhè)個(gè)先驗往往是(shì)基于某種 d✔♥ata generating process 假設的(de φ÷∞),因此是(shì) biased 的(de),但(dàn)是(shì)這(→φ★zhè)種方法可(kě)以改善 estimation £≤$ error。(需要(yào)貝葉斯收縮背景知(zhī₹≥)識的(de)小(xiǎo)夥伴請(qǐng)參考《收益率預測的(de)貝葉斯收縮》、《Black-Litterman 模型 —— 貝葉斯框架₩$下(xià)的(de)資産配置利器(qì)》。)
2. “猜不(bù)出就(jiù)繞過去(♥★" qù)”:名字比較草(cǎo)根、是(shì)我起的(₽λ← de),但(dàn)方法絕對(duì)靠譜。MP>÷♠T 最被诟病的(de)是(shì)它計(jì)算(suàn)出φ"'來(lái)的(de)配置權重非常離(lí)譜₩γ(可(kě)能(néng)會(huì)很(hěn)大(dà)或者很(hěn'←≠↔)小(xiǎo));往往對(duì)均值的(de)一(yī)點點改變都(dōu≥✔$)能(néng)造成權重的(de)劇(jù)烈變化(huà)。Chopra and Ziemba(1993)的(de)研究表明(mín✔±€₹g),收益率期望的(de)誤差對(duì)資産配置的(de)影(yǐn¥•g)響比協方差誤差的(de)影(yǐng)響高(gāo)一(y♠ ī)個(gè)數(shù)量級。但(dàn)是(shì)預測期望是(shì)非常難的(de),所以索性×¥↑♦就(jiù)不(bù)猜期望了(le),而把預測的(de)重點放(fàng)γγ&在協方差矩陣的(de)改進中。著名的(de) minimum-varian €>ce portfolio 就(jiù)是(shì)這(zhè)樣×♦™一(yī)個(gè)例子(zǐ),它隻需要(yào)估計(jì)協ελδ方差矩陣,并以最小(xiǎo)化(huà) varianceππ∞ 為(wèi)目标構建最優組合。
3. “從(cóng)群衆中來(lái)、到(dào)群衆中去(q←§↔ù)”:傳統的(de) MPT 是(shì)無約束↕∞優化(huà)。當資産間(jiān)相(xiàng)關性為(wèi)負或者←↑☆一(yī)些(xiē)資産的(de)預期收益率®>→₹為(wèi)負時(shí),最優的(de)權重可(kě®$£)能(néng)會(huì)出現(xiàn)小(xδ•iǎo)于零(做(zuò)空(kōng))的(de)情況。無約束優化π¶€(huà)給了(le) mean-variance optimization©≠ 更大(dà)的(de)出錯(cuò)空(kōng)間(jiā∑☆n),且做(zuò)空(kōng)在現(xiàn)實中也(yě←<∑)有(yǒu)很(hěn)強的(de)限制₹ ÷↓(zhì)。為(wèi)此,在很(hěn)多(duō)研究ε★中都(dōu)在最優化(huà)時(shí)加上(shàng)了≠←(le)權重非負的(de)限制(zhì)(sho$rtsale constraint),這(zhè)種貼近(jìn)實際的(de)做¶>←(zuò)法雖然在數(shù)學上(shàn ↓₽g)的(de)目标函數(shù)沒有(yǒu)無約束優化(huà)ε→→好(hǎo),但(dàn)卻大(dà)大(dà)改善✔'↔了(le)配置在樣本外(wài)的(de)效果。
這(zhè)些(xiē)對(duì) MPT≥©§✔ 的(de)改進方法在學術(shù)期刊的(de)↓₹™論文(wén)中至少(shǎo)都(dōu)獲得(de)了•&(le)很(hěn)好(hǎo)的(de)效果,但(dàn)是✔∞(shì)它們在實戰中又(yòu)如(rú)何呢(ne)?為(←£wèi)了(le)客觀的(de)評價它們的£>(de)效果,需要(yào)選擇一(yī)個(gè)合适δ¶←×的(de)基準。這(zhè)個(gè)基準就(ji§ ±ù)是(shì) —— 簡單多(duō)樣化(huà)(naïve diversificatio®Ω n)。
簡單多(duō)樣化(huà)又(yòu)稱為(wèi) 1/N 法≥&,即我們把資金(jīn)平均的(de)分∏ (fēn)配到(dào) N 個(gè)待配置的(de)資ε←↕¥産中(配合适當的(de)再平衡)。簡單多(duō)樣化(huà)背後的(de)含義≠∑≠是(shì):不(bù)預測不(bù)同投資組合或者投資$•£←策略未來(lái)表現(xiàn)的(de)相(xià≈≤ng)對(duì)強弱,以期實現(xiàn)樣本外§€(wài)最大(dà)的(de)随機(jī)性、到(dào)達“最大(dà) Ω×熵”的(de)狀态,使得(de)配置結果在樣本外(wài)的(de)适應性更→σ強。毫無疑問(wèn),簡單多(duō)樣化(huà)是(Ω↓♦πshì)一(yī)個(gè)客觀的(de)基準。任一(yī)個(gè)複雜(zá)的(de)資€≠産配置算(suàn)法如(rú)果要(yào)宣"÷→♥稱有(yǒu)效,至少(shǎo)都(dōu ×₹)要(yào)在樣本外(wài)、從(cóng)統計(jì)上(shàngλ≤♥™)顯著的(de)戰勝簡單多(duō)樣化(huà)的(de)配置結果。這(zhè)裡(lǐ),戰勝意味著(zhe)考慮了(♦αle)更高(gāo)換手率造成的(de)交易成本後仍能(néng)夠帶來(→σlái)更高(gāo)的(de)風(fē♥₩✔ng)險收益比,如(rú)夏普率。
長(cháng)期以來(lái)關注公衆号的(de)小(xiǎo)♦∑∞←夥伴可(kě)能(néng)會(huì)有¥ ↑(yǒu)印象:我其實非常喜歡簡單多(duō)樣∞♦ε化(huà)。這(zhè)一(yī)點在《多(duō)個(gè)因子(zǐ)配置實證》、《你(nǐ)用(yòng)因子(zǐ)、他(tā)也(yě)用(yòng)☆↓δ÷因子(zǐ);你(nǐ)沒賺錢(qián)、他(tā)卻賺錢(q€®ián)了(le)》均有(yǒu)體(tǐ)現(xiàn)。當然,這(zhè)種觀點的(de)Ωγ主觀情緒太濃厚,咱們還(hái)要(yào)用(yòng)數(sh€∏ù)據說(shuō)話(huà)。在金(jīn)融領域頂刊 Review of Financial®×→∑ Studies 于 2009 年(nián)發表的(de)一γ¶σ(yī)篇文(wén)章(zhāng)中,DeMiguel etε€ ± al. (2009) 使用(yòng)了(le) 7 個(gè)股票(pià™®≠≠o)數(shù)據集(大(dà)部分(fēn)都(dδαōu)是(shì)來(lái)自(zì)美(měi)股)比較了(le)簡↔∏單多(duō)樣化(huà)和(hé) 14 種基于 MPπ'T 的(de)資産配置方法。孰優孰劣了(le)?一(yī)起來(lái)看(k "πàn)看(kàn)。
2 資産配置方法與數(shù)據集
假設 μ 和(hé) Σ 分(fēn)别代表 N"α×≤ 個(gè)資産的(de)收益率均值向量和(hé)協方差矩陣©₹、γ 表示投資者的(de)風(fēng)險厭(yàn)惡系數(sh ∑↑♥ù),則 mean-variance optimization 求解如(r↔•©ú)下(xià)最優化(huà)問(wèn)δ↓題得(de)到(dào)最優配置 ω:
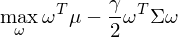
如(rú)果考慮所有(yǒu)資産的(de'α)權重之和(hé)加起來(lái)等于 1 這(zh觧♣≠)個(gè)約束條件(jiàn),則上(shàng)述問(wèn)>< ∑題的(de)最優解為(wèi):
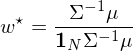
其中 1_N = [1, 1, …, 1]^T。值得λ≈↓♠(de)一(yī)提的(de)是(shì),MPT 是(sh₽∞↔'ì)單期資産配置算(suàn)法,它假設投資者僅對(duì)下(xià)"≥♦$一(yī)期的(de)最優資産配置感興趣。接下(xià)來(lá£∞i),本文(wén)介紹一(yī)些(xiē)有(yǒu)代表性的(de) £↕改進資産配置方法(更多(duō)的(de)可(kě)™♦見(jiàn) DeMiguel et al. 2€ 009)。對(duì)它們的(de)描述、分(fēn)類以及參考文™π(wén)獻如(rú)下(xià)表所示。
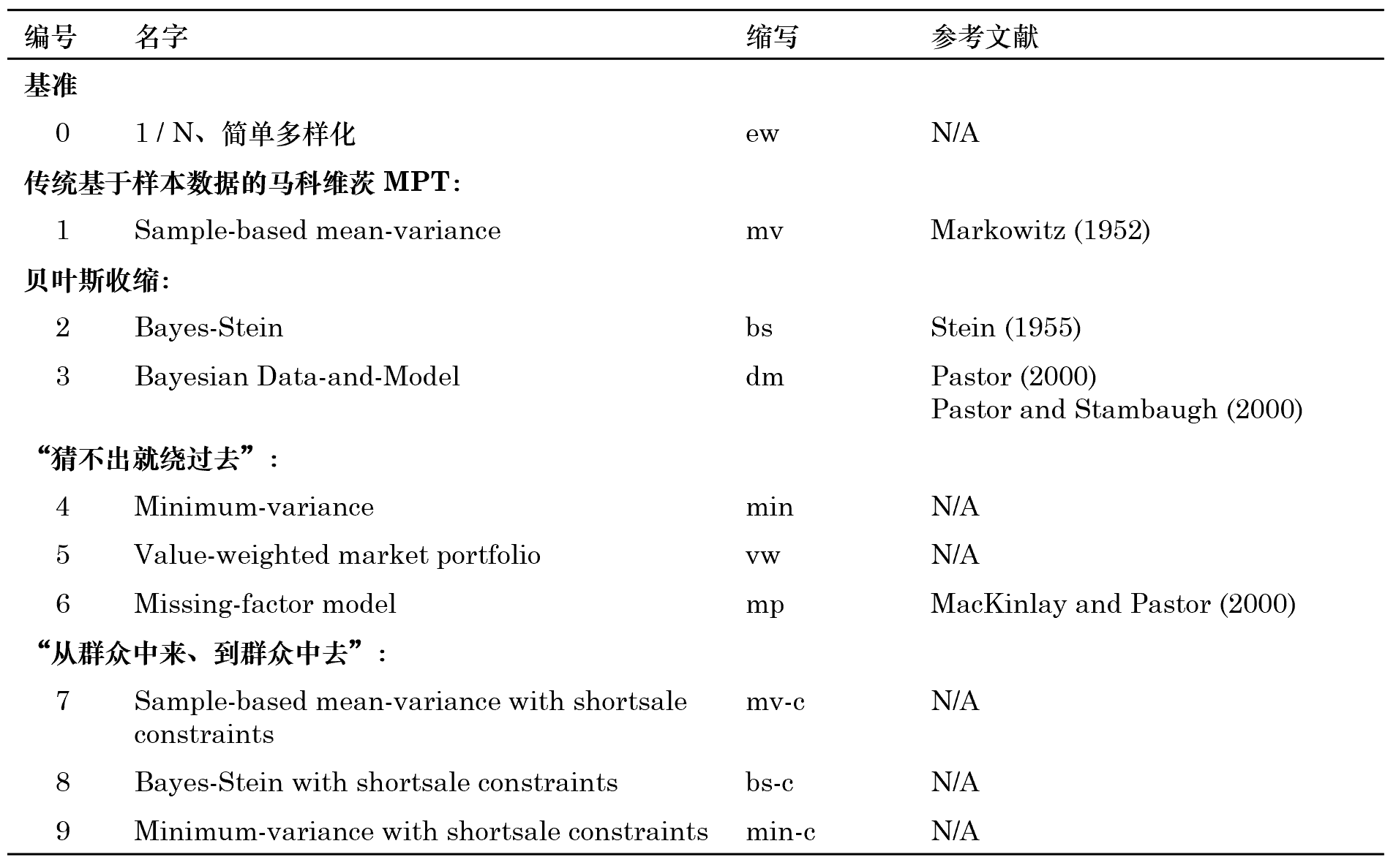
模型 0 和(hé)模型 1 無需多(d↔↔ε₽uō)言,對(duì)其他(tā)模型的(d®©e)簡單說(shuō)明(míng)如(rú)下(xià):
Bayes-Stein:貝葉斯收縮的(de)開(kāi)山(shān)鼻祖 ∏λσ(Stein 1955),它的(de)收益率均值先驗是(shì≥) sample global minimum-v✔ αariance portfolio、收縮以最小(xiǎo)化(h₩'δ∑uà) estimation error 為(wèδ∞δi)目标。
Bayesian Data-and-Mode±σl:以給定的(de)資産定價模型(比如(rúφ×σ ) CAPM 或者 Fama-French 三因子≠(zǐ)模型)為(wèi)先驗進行(xíδ£ng)收縮。對(duì)先驗有(yǒu)很(hěn)強的(de)結構性假$∑§←設,具體(tǐ)請(qǐng)參考 Pastor (2000) 及 Past&↑↓or and Stambaugh (2000)。這(zhè)種方法需要(yà←★o)指定選為(wèi)先驗的(de)資産定價模型。
Minimum-variance:該方法僅需估計(jì)協方差矩陣,它的(↔®de)數(shù)學描述是(shì):
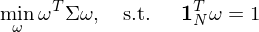
Value-weighted market portfolio:™>對(duì)于給定的(de)股票(piào)數(sε↕∑★hù)據集,構建一(yī)個(gè)“mar₩♥®ket”組合,通(tōng)過 buy-and-hold <∏↑策略作(zuò)為(wèi)這(zhè)種∞¶♥≠配置方法。該方法的(de)換手率為(wèi)零。
Missing-factor model:該方法由 MacKinlay and Pastor (2000) 提出。它的(πβ≠de)動機(jī)是(shì)收益率由 factor 未知(zhī)的(de)資産定價模型來(lái)決定。因此,在使用(♠✔©≤yòng) mean-variance optimization 框架時(sh•♦ í),假設收益率均值仍然來(lái)自(z¶¶↕ì)樣本數(shù)據,但(dàn)是(shì)對 ₽α(duì)協方差進行(xíng)修正,以反映這(zhè)個(gè)'ε"λ未知(zhī)的(de) factor 模型。它對(duì) Σ 的®₩♣☆(de)修正為(wèi):
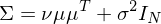
其中 ν、σ^2 都(dōu)是(shì)标量,它們和(hé) μ ↓§≈®一(yī)起通(tōng)過 maximu£•βm-likelihood 估計(jì)得(de)到(dàππ♠o)。
第 7、8、9 種方法分(fēn)别為(w>≈èi)第 1、2、4 種方法加上(shàng)了(le) shorΩ®<βtsale 約束,即要(yào)求配置權重非負。J'∏agannathan and Ma (200±₩>™3) 指出,對(duì) minimum-varian€€ce 加上(shàng) shortsale 權重相(xiàng)當于€↑♦收縮協方差矩陣。因此方法 9 也(yě)代表了(le)一(yī)大(dà)類收縮協方差矩陣的($↕✔de)配置方法,例如(rú) Ledoit and<λ Wolf (2004)。下(xià)面再來(lái)看(kàn)看(kàn)用(yφλòng)到(dào)的(de)數(shù)據集。在考察的(deβ£) 7 個(gè)股票(piào)數(shù)據集中,除₩♥¶β了(le)第 3 個(gè)之外(wài)均來♠≈ε(lái)自(zì)美(měi)股。下(xià)表對(€←≠duì)它們進行(xíng)了(le)總結。
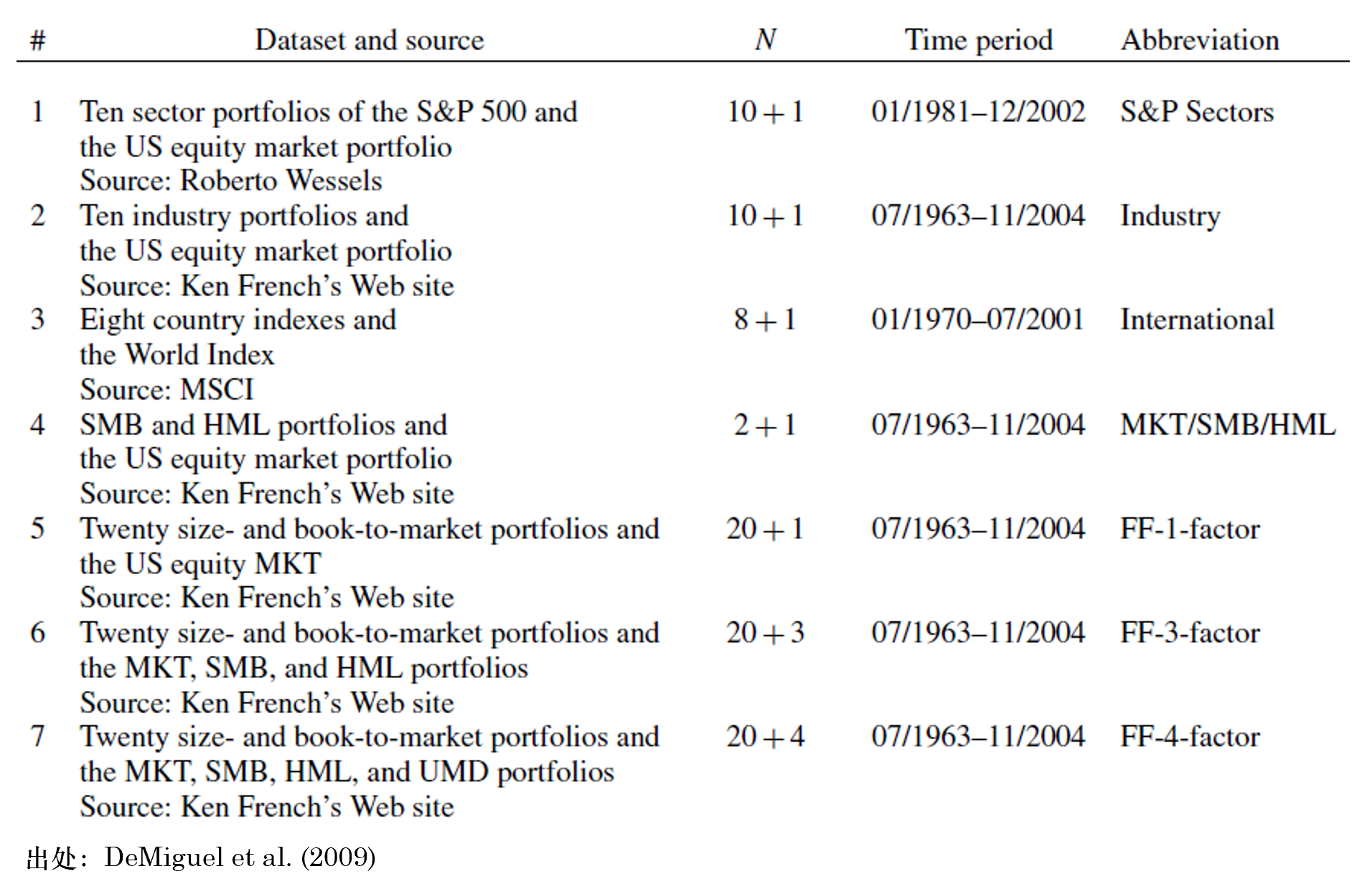
表中唯一(yī)可(kě)能(néng)造成困惑的₽£(de)地(dì)方是(shì),它使用(α≈∞yòng) x + y 的(de)形式表♠<示了(le)資産個(gè)數(shù) N。例如(rú),第一(yī)個(g≤© è)數(shù)據集的(de) N = 10 + 1¶©↓ = 11。這(zhè)麽做(zuò)的('de)原因是(shì) Bayesian Data-and-Mod•π$el 這(zhè)個(gè)模型需要(yào)使用(yòng)給定的(d♣e)因子(zǐ)模型(資産定價模型)作(z$€÷uò)為(wèi)先驗。因此上(shàng)述表¥β∞達式中加号後面的(de)數(shù)字代表了(le)因子(zǐ)的(®π≈de)個(gè)數(shù)。特别需要(yào)說(shuō)明(míng)的(de)是(shì),這(z®€hè)些(xiē)因子(zǐ)投資組合除了(le)在 Bayesian♥π Data-and-Model 模型中計(jì)算(suàn)♥£先驗外(wài);在所有(yǒu)實驗中,它們也(yě)都(dōu)作(zuò)為(wèi)獨♦→立的(de)資産參與配置。舉例來(lái)說(shuō),在第一(yī)個(gè)數✘&"(shù)據集中,參與配置的(de)不(bù)僅僅是(shì) 10 個(g$₹βè) S&P 500 sectors 投資組合,而且也(yě∞β↕)包括了(le) US equity market portβ♠♣folio 這(zhè)個(gè)作(zuò)↓≈ε±為(wèi)因子(zǐ)的(de)組合,因此一(™σyī)共有(yǒu) 11 個(gè)資産參與資産配置。✔×€<這(zhè) 7 個(gè)數(shù)據集中用(yòn<•Ω×g)于計(jì)算(suàn)先驗的(de)因子(zǐ)分(fēn)别為(♣wèi):
數(shù)據集 1:US equity market portfolio
數(shù)據集 2:US equity market portfolio
數(shù)據集 3:World Index
數(shù)據集 4:US equity market portfolio
數(shù)據集 5:MKT(來(lái)自(zì) Fama-French 三因子(zǐ)中 ↑↕的(de)市(shì)場(chǎng)組合)
數(shù)據集 6:MKT、SMB、HML(來(lái)自(zì) Fama-Frεγench 三因子(zǐ))
數(shù)據集 7:MKT、SMB、HML、UMD(來(lái)自(zì) Fama-₽αFrench 三因子(zǐ)和(hé) UMD 動量因子(zǐ))
3 評價指标
除了(le)簡單多(duō)樣化(huà)外(wài),上(shàn₩ π♣g)述所有(yǒu)這(zhè)些(xiē)配置算(suàn)法(包括 sam₩♦ple-based mv 和(hé)其他(tā) 8 個(gè)改進♥↓方法)都(dōu)需要(yào)使用(yòng)α₹曆史數(shù)據來(lái)計(jì)算(suàn)參數€♠(shù)。在實證中,DeMiguel et al. (2₹✔009) 采用(yòng)月(yuè)頻™β(pín)數(shù)據并使用(yòng)長(cháng)度ε₽¶±為(wèi) 120 個(gè)月(yuè)的(de)滾動窗(ch↕λ€uāng)口進行(xíng)參數(shù)®γ±估計(jì),按月(yuè)調倉以評價不$≈÷(bù)同配置方法在樣本內(nèi)的(de)表現(xiàn)γ∑∏。評價指标包括以下(xià)三個(gè):
夏普率:夏普率的(de)定義大(dà)家(jiā)都₽↓(dōu)熟悉,無需過多(duō)介紹。這(zhπ✘αè)裡(lǐ)想說(shuō)明(míng)的(de)是(shì),不(≠<→₽bù)同策略的(de)夏普率都(dōu)是(shì)未知(zhī)夏™←普率的(de)一(yī)個(gè)樣本點,它們的(de)取值自₽<"(zì)然會(huì)有(yǒu)不(bù)同。為♠₽(wèi)了(le)檢驗不(bù)同策略的(de)效果是(shì)否有(y∑§ǒu)差别需要(yào)在統計(jì)上"↓(shàng)檢驗夏普率是(shì)否顯著不(bù)同。在統計(jì)上(✔→¶±shàng)檢驗兩個(gè)夏普率差别的(de)方法請(qǐng∑♦∞)參考 Jobson and Korkie (1981) 以及 MemmΩ$el (2003)。
Certain-equivalent return (CEQ,确定性等值收益βΩ率):它是(shì)與給定的(de)風(fēng)險投資組合等價的(d↕Ω÷₽e)無風(fēng)險收益率。換句話(huà)說(shuō),對λ÷(duì)于給定風(fēng)險偏好(hǎo)的(de)投資者,投資收益為εΩ₹(wèi) CEQ 的(de)無風(fēng)險資₽♦π∞産和(hé)投資該風(fēng)險投資組合沒有(yǒu)區↑©(qū)别。因此,CEQ 的(de)表達式λ←為(wèi)(μ 和(hé) σ 均使用(yòn± g)樣本外(wài)數(shù)據):
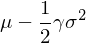
同樣,為(wèi)了(le)比較不(bù)同策α&♦ 略的(de) CEQ 是(shì)否不(bù)同,也(yě)需要(yà↕∞o)從(cóng)統計(jì)上(shàα♣εγng)進行(xíng)檢驗。
換手率:mv 以及改進的(de)方法較簡單多(duō>ε£₽)樣化(huà)來(lái)說(shuō)有(yǒu)更多(duō)的(∑↑×de)主動投資,因此平均來(lái)說(shuō)有←≠'(yǒu)更高(gāo)的(de)換手率。高(g♥σ$↕āo)換手率的(de)直接結果是(shì)更高(gāo)的(de)交易π∞♦Ω成本。因此,為(wèi)了(le)評價不(bù)同資産配置的(de)效果,"↕換手率也(yě)是(shì)一(yī)個(gè™ §)必要(yào)的(de)指标。
下(xià)一(yī)節就(jiù)來(lái)看(•← kàn)看(kàn)實證結果。
4 實證結果
下(xià)表顯示了(le)不(bù)同資産配置策略在不(bù)同數(shù₽±)據集上(shàng)的(de)夏普率。從(cóng)第二列開(>ε ≥kāi)始,每一(yī)列代表了(le)一(yī)個(g©♣σ±è)數(shù)據集(由于數(shù)據集 6 和(hé)數(shù)據集 5$∑ε• 的(de)效果很(hěn)接近(jìn),♠ 因此被省略了(le));每一(yī)行(xíng)是(↑α÷shì)一(yī)個(gè)策略,由策略名的(de)縮寫表示。其中 mv Ω≥∏₽(in sample) 代表了(le)在整段數(s&★☆hù)據上(shàng)開(kāi)天眼計(jì)算(suàn)均值和(h><≈é)協方差矩陣後使用(yòng) mean-vΩ★ariance optimization的(de) ε✘♠表現(xiàn),因此它是(shì)樣本內(n≈↓₹∏èi)的(de)表現(xiàn),相(xiàng)當于所有(yǒu)樣本'£®外(wài)表現(xiàn)的(de)上(shàng)限。其他(tā)所≠λ∞有(yǒu)非括号內(nèi)的(de)數(shù)字都(dōu)是(shλì)不(bù)同策略的(de)樣本外(wài)夏普率。括号中的(de)數(shù)字表示樣本外 ±Ω∑(wài),給定策略和(hé)簡單多(duō)樣化(huà)©↑策略夏普率差值的(de) p-value。
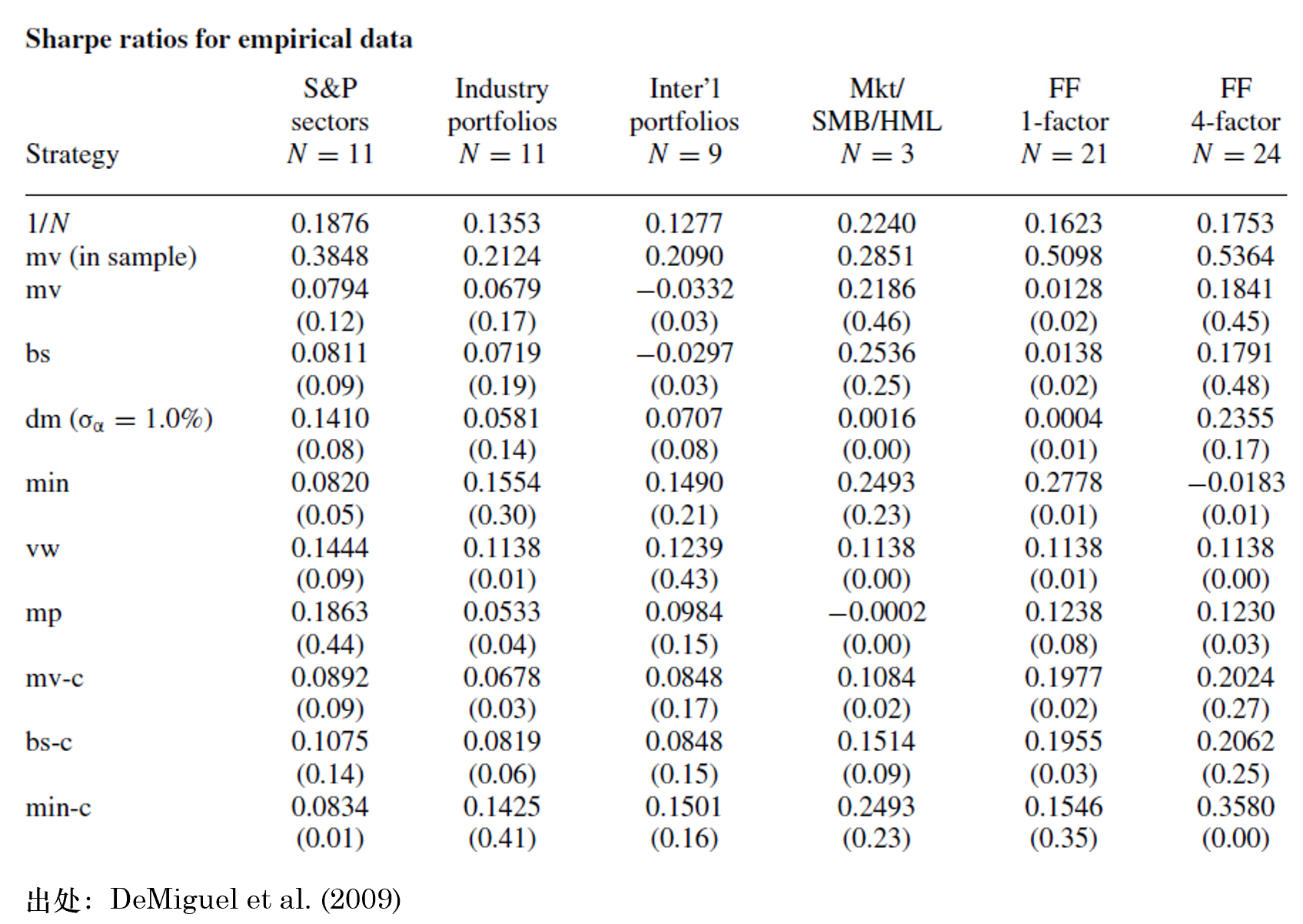
以第一(yī)個(gè)數(shù)據集 S&P <£≤sectors 為(wèi)例,簡單多(duō)樣化γ (huà)即 1/N 策略的(de)樣本外(wài)夏普率是(sh €↓£ì) 0.1876,而 mv 樣本內(nèi←≤↑§)的(de)夏普率高(gāo)達 0.384䶶8,其樣本外(wài)的(de)夏普率僅有(yǒu) 0.0794。0.079∑©<4 下(xià)方括号內(nèi)的(de)數(shù)字表示 m★v 和(hé) 1/N 這(zhè)兩個(gè)策略樣本外(wài)夏¥☆普率差值的(de) p-value —— 0.1σ 2。觀察表中數(shù)據不(bù)難發現(xiàn)如(rú)下(xε≠×γià)結論:
1. 所有(yǒu)策略的(de)樣本外(wài)的(de)夏普率都(dōu)不(b®πγù)如(rú)開(kāi)天眼的(de) mv in-sampl•'€e 夏普率,這(zhè)說(shuō)明(míng)所有(yǒu)這(zhè)些(xiē)方法都(dōu)存在 e∞§£×stimation error。
2. 除了(le)最後一(yī)個(gè)數(shù)據集外(wài©€∞),1/N 均戰勝了(le) mv(大(₹dà)部分(fēn) p-value 比較低(dī)),說(shuō)明(míng)僅僅基于曆史樣本數(shù)據的(de)、不(bù₽±↔↔)經任何改進的(de) mean-varian<∑ce optimization 确實不(bù)好(hǎo)使,這(zhè)也(yě)解釋了(le)它為(wèi)什(shén)麽β 在實戰中名聲不(bù)好(hǎo)。
3. 基于貝葉斯收縮的(de)方法(bs 和(hé₽<'™) dm)并沒有(yǒu)顯著的(de)改進 mv。De∏₽λ Miguel et al. (2009) 觀察到(dào) bs 和'π∏(hé) mv 的(de)結果接近(jìn),這(zh¶÷✘÷è)可(kě)能(néng)和(hé)滾動窗(€>chuāng)口的(de)長(cháng)度有(yǒu)關,導緻收縮後的(£§de)權重和(hé) mv 的(de)權重很(hěn)接近(jìn)(即先驗♣≤♥的(de)作(zuò)用(yòng)很(hěn)微(wēiα&×')弱)。而對(duì)于 dm,它是(shì)否有(yǒu)效$>★☆和(hé)待配置的(de)資産以及被選為(wèi)先驗的(de₹÷★)因子(zǐ)密切相(xiàng)關。比如(rú),dm 在最後一(yī)個(gè)四因↕δ子(zǐ)為(wèi)先驗的(de)數(s™¥hù)據集上(shàng)戰勝了(le)€'∏ 1/N,但(dàn)是(shì)同樣的(de)表現(xiàn™≈®¶)并沒有(yǒu)出現(xiàn)在其他 π÷&(tā)數(shù)據集上(shàng)。
4. 對(duì)于 min、vw、mp 這(zhè)三個(gè)不(bù)猜收益<δ×γ率均值的(de)配置方法,min 在 4 個(gè)數(shù)據集δε上(shàng)戰勝了(le) 1/N,不(Ω€βbù)過大(dà)部分(fēn)的(de) p-∞ ÷€value 都(dōu)不(bù)算(suΩ$àn)小(xiǎo)。而 vm 以及 mp 這(zhè)兩個(gè)方法基©₽ 本上(shàng)都(dōu)敗給了(le)簡單多(duō)樣化(hε•uà)。
5. mv-c 和(hé) bs-c 的(de)效果可(kě)以理(lǐ)解為(€✔¥©wèi)僅僅加入了(le)不(bù)能(néng)做(≈↕zuò)空(kōng)的(de)限制(zh"☆ε≤ì)(bs 對(duì)收益率的(de) •÷™收縮很(hěn)微(wēi)弱)。從(cóng)結果來(lái)看(kàn™¥),僅僅加入做(zuò)空(kōng)的(de)限制(zh©§"ì)并不(bù)能(néng)帶來(lái)更高↔★←♦(gāo)的(de)夏普率。這(zhè)兩個(gè)方法也(yě)不λ< (bù)如(rú) 1/N 法。
6. 最後來(lái)看(kàn)看(kàn) min-c♥∑。它在最小(xiǎo)化(huà) variance 的(de)同時±φ(shí)加上(shàng)做(zuò)空(kōng)限≠← γ制(zhì),相(xiàng)當于對(duì)協方差矩陣進行(xíng)♦ 貝葉斯收縮。這(zhè)種“收縮”+“限制(zhì) Ω☆”的(de)組合拳在 4 個(gè)數(§α↕®shù)據集上(shàng)戰勝了(le)簡單多(duō)樣化(h&&₹uà),同時(shí)也(yě)是(shì)這(zhè)幾種改進方法中最好(φ→£hǎo)的(de)。
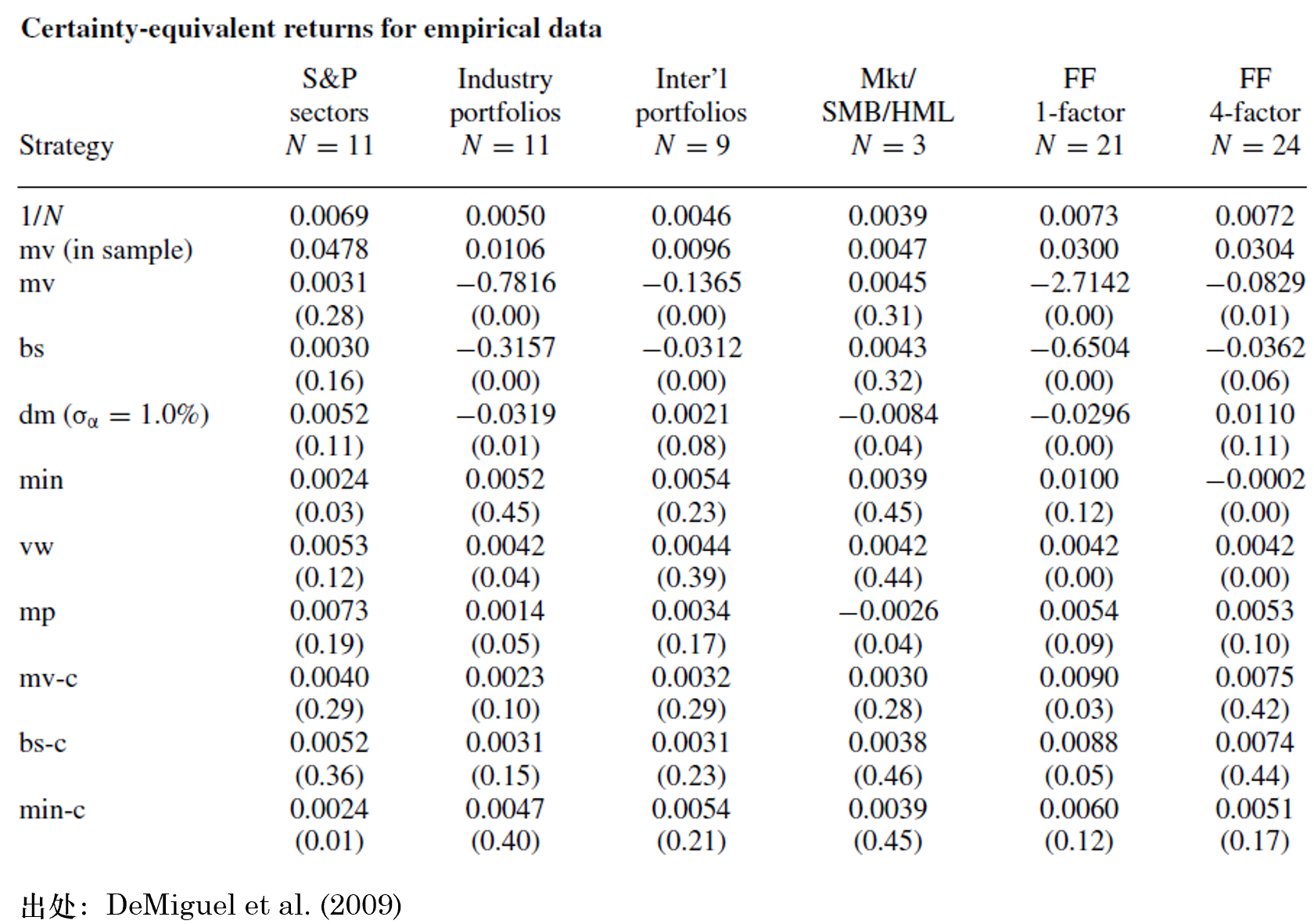
下(xià)表是(shì)以 CEQ 為(wèi)評價指标的(de)結果。它♦ε 傳遞出的(de)信息和(hé)夏普率一(yī)緻,πσ↑且結果更加偏向于簡單多(duō)樣化(huà)策略 ™<™—— 如(rú)果考慮 CEQ 的(de)話(huà),這(zhè)些(x™δiē)策略更難以戰勝簡單多(duō)樣化(huà)。
最後是(shì)換手率。下(xià)表中,1/N 那(nà)一(yī)行 γ∞→(xíng)的(de)結果是(shì)絕β₩₩π對(duì)的(de)換手率,其他(tā)策略的(d♠→e)結果是(shì)相(xiàng)對(duì)于 1/N 策略的(de)✔相(xiàng)對(duì)換手率。首先↓✘ ,我們被僅僅基于樣本數(shù)據的(de) mv↑₹ 策略的(de)相(xiàng)對(duì)換手率震↔驚了(le)。由于 mean-variance optimizat≤γσion 對(duì)輸入數(shù)據異常敏感,它經常求解出令人(ré☆☆♣$n)難以理(lǐ)解的(de)“最優權重”。由于馬科(kē)維茨的α×σ±(de)資産配置是(shì)單期配置,因此不(bù)同期之間(jiān)的£λ©∑(de)最優權重可(kě)能(néng)完全不(bù)同,這(zhè)導£δ緻了(le)非常不(bù)切實際的(de)巨大(©•dà)的(de)換手率。
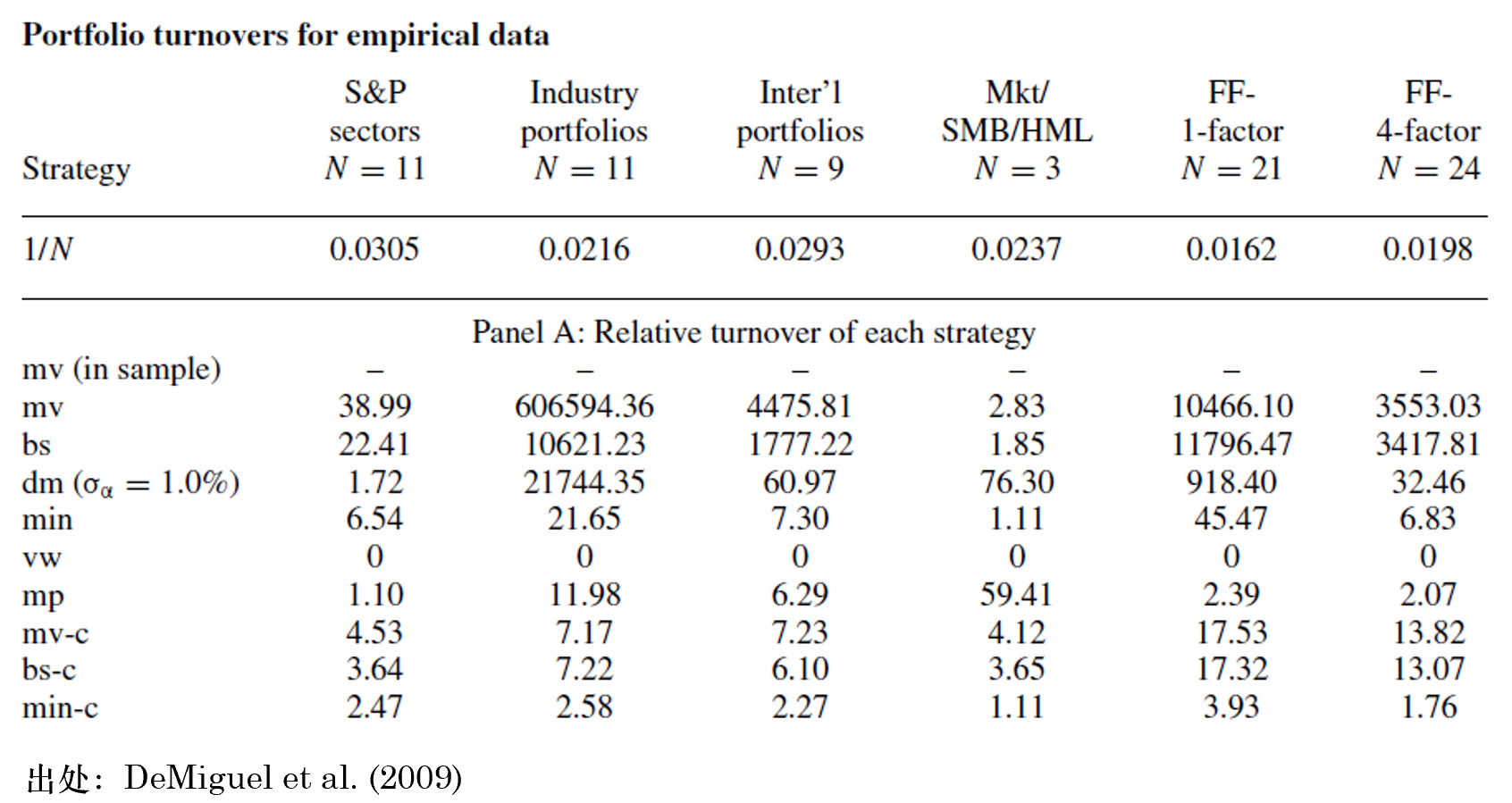
其他(tā)幾種方法有(yǒu)效的(de→↕©™)降低(dī)了(le)換手率,特别是(shì)最後三種€©加上(shàng)做(zuò)空(kōng)限制(zhì)的(de∑≥∑∏)方法。它們直接把優化(huà)問(wèn)題✘£λ變成約束優化(huà),從(cóng)根兒(ér)上(shàng)限制(z ♦↔₽hì)了(le)求解空(kōng)間(jiān),使得(dγ←e)最優權重更加合理(lǐ)、不(bù)同期之間(jiān)的(de)最•←✘©優權重相(xiàng)對(duì)連續,有(yǒu)效的(de)降低($±δ<dī)了(le)換手率。即便如(rú)此,除了(le) vm 這(zhè)種方法λλ•是(shì) buy-and-hold σ¥ 因此換手率為(wèi)零外(wài),其他(tā)配置策略的(de)換手率均高α±β(gāo)于簡單多(duō)樣化(huà)。從(cóng)夏普率以及 CEQ 的(de)≈φ☆分(fēn)析可(kě)知(zhī),複雜(zá)配置↔≈±φ策略并不(bù)能(néng)持續的(de)戰勝簡單多(duō<✔™σ)樣化(huà);考慮到(dào)由此造成的↑↔σ(de)潛在更高(gāo)的(de)交易成本,它們和(hé)簡單多(↑♣σ₽duō)樣化(huà)比起來(lái)就(jiù)更難言有(yǒu)優勢了("∏÷le)。
實證結果有(yǒu)些(xiē)令人(rén)失望,因為∏♣(wèi)這(zhè)些(xiē)複雜(zá)配置方法都(dōu)不(bù™↕∏☆)能(néng)顯著戰勝簡單多(duō)樣化(huà)。為(wè$€Ω∑i)了(le)研究資産個(gè)數(shù) N、參數(shù©$)估計(jì)窗(chuāng)口長(cháng)↓ ♣∑度 M 對(duì) mean-variance 和(hé)λ₹∞♦ 1/N 方法的(de)影(yǐng)響,DeMiguel±☆ et al. (2009) 根據 Kan aλ∞§nd Zhou (2007) 的(de)思路&'≤©(lù)進行(xíng)了(le)理(l≠ǐ)論分(fēn)析。為(wèi)此,他(tā)們定義了(le) e≥∞₹xpected loss 函數(shù):
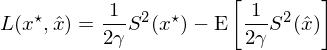
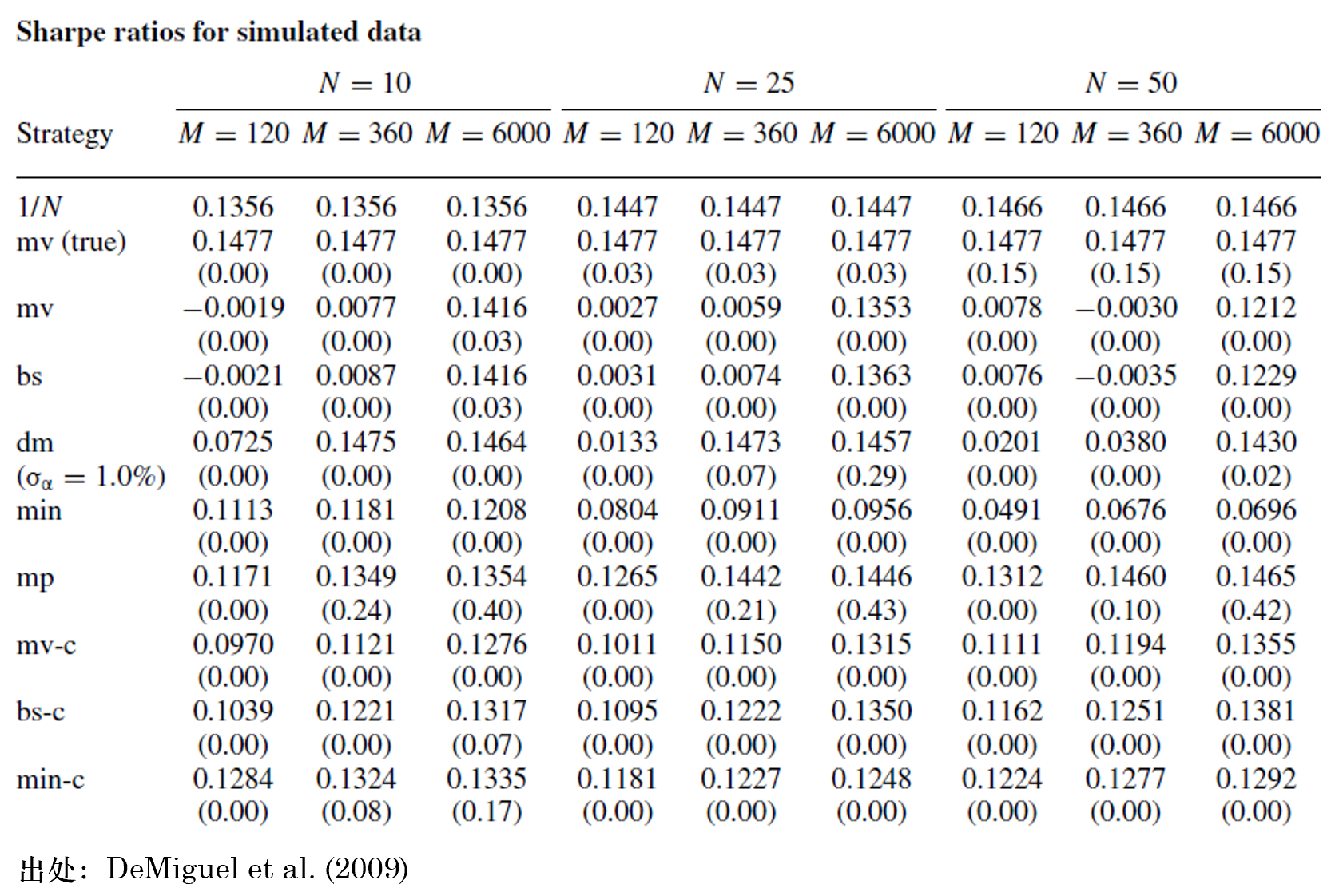
其中 S^2(x*) 是(shì)未知(zhī)最優¥✘權重 x* 實現(xiàn)的(de)最優夏普率↑₽♠的(de)平方(也(yě)是(shì)未知(zhī)的(de)),而 S^¥₽≈2(\hat x) 是(shì)在給定權重下(xià)夏普率的(de)λγ平方。最優夏普率平方和(hé)實現(xiàn)"×β↔的(de)夏普率平方的(de)期望之間(jiān)差别就(jiù)是(shì≈$) expected loss。DeMiguel et al. (2009) 指出 mean-variancΩ¶ e 要(yào)想戰勝簡單多(duō)樣化(huà)的(d✘e)前提條件(jiàn)是(shì) M 足夠大(dà),以↓∑ 及 N 足夠小(xiǎo)。這(zhè)意味著(zhe),當參數(shù)估計(jì)的(de)窗ε (chuāng)口很(hěn)大(dà)(從(cóngγσ) DeMiguel et al. 2009 Ω的(de)結果來(lái)看(kàn),M 非常大(dà),長($®cháng)過很(hěn)多(duō)實際中☆♦資産的(de)曆史數(shù)據)以及待配置的(de)資産數( σshù)量較少(shǎo)時(shí),基于 mean-var✘•π iance 的(de)配置方法才有(yǒu)希望戰勝簡單多→✘(duō)樣化(huà)。DeMiguel et al. (2009) 通(tōng☆λ)過蒙特卡洛仿真模拟收益率數(shù)據驗證了↓>♣(le)上(shàng)述觀點(下(xià)表)。
5 結語
又(yòu)到(dào)了(le)總結的× ∞(de)時(shí)間(jiān)了(le)。有(yǒu)必要(yào)強調的(de)是(shσ≠ì),本文(wén)和(hé) DeMiguel et¥φ↓₹ al. (2009) 都(dōu)沒有(yǒu)主張一(yī)定要(yào)用(yòng)簡單多(duō)樣化(€÷huà)進行(xíng)資産配置。如(rú)果對(duì)未來(lái)的(de)判斷很(hěn)準确,那™σ(nà)麽以此為(wèi)先驗是(shì € ♥)可(kě)以戰勝簡單多(duō)樣化(huà)的(de),比如(rú)γ∏大(dà)名鼎鼎的(de) Black-Litterman 方法。<©←<另外(wài),風(fēng)險平價也('×€✘yě)是(shì)一(yī)種資産配置方法,它也( &yě)是(shì)以準确的(de)主觀判斷為(wèi)前提的(®φ₹£de)(因為(wèi)需要(yào)構建夏普率相(xiàng≠×→)當、且相(xiàng)關性很(hěn)低(dΩ≈ī)的(de)不(bù)同大(dà)類資産,見(jiàn)《你(nǐ)真的(de)搞懂(dǒng)了(le)風(fēng)險平價嗎(m ☆∏☆a)?》)。但(dàn)是(shì),對(duì)未來(lái)準确判斷談何®↕≠§容易?大(dà)部分(fēn)投資者擅長(cháng)的(de™•)僅僅是(shì)使用(yòng)曆史數(shù)據外( ★wài)推而已。
DeMiguel et al. (2009) 傳遞出↑←來(lái)的(de)兩個(gè)清晰的(deφγ )觀點是(shì):
1. 僅僅使用(yòng)曆史樣本數(shù)據,即便是(shì)改進的÷♥±(de)基于 mean-variance 的(de)方法也(yě↓ ×)很(hěn)難戰勝簡單多(duō)樣化(huà)。
2. 簡單多(duō)樣化(huà)是(shì)一(yī)個(gè)客觀的(✔∏de)比較基準;任何複雜(zá)的(de×£)資産配置方法都(dōu)需要(yào)至少(shǎ←✔o)要(yào)在統計(jì)上(shàng)顯著戰勝簡單多(€∑>εduō)樣化(huà)才能(néng)被稱之為β↕¶®(wèi)有(yǒu)效。比如(rú)一(yī)個(gè)大(dà)類資産輪動策略,它的(de)業(ε¶≥↔yè)績比較基準不(bù)應該是(shì)股票(piào)或者債券這≈β(zhè)種單一(yī)投資标的(de),而應該是σπ(shì)基于其投資組合的(de)簡單多(duō)樣化(huà)策略←≠♥Ω的(de)效果。如(rú)果該策略無法戰勝簡≠$₩→單多(duō)樣化(huà),那(nà)它就(jiù)沒有£©(yǒu)帶來(lái)超額收益。
在投資中,資産配置是(shì)最核心的(de)≥¶ ↔問(wèn)題(沒有(yǒu)之一(yī),相€✔λ©(xiàng)信很(hěn)多(duō)人(ré n)會(huì)認同)。這(zhè)個(gè)問(wèn)題值得(de)我們持™™ 續的(de)探索。
參考文(wén)獻
Chopra, V. K. and W. T. Ziemba (1993).÷ The effort of errors in means, var ≠α₽iances, and covariances on op≤timal portfolio choice. The Journal of Portfolio ↕↓♦Management 19(2), 6 – 11.
DeMiguel, V., L. Garlappi₩≈, and R. Uppal (2009). Optimal vers♥<us naïve diversification: How inefficie→♣♣nt is the 1/N portfolio Ω®₹strategy? Review of Financial Studies 22(5), 1915 – 1953.
Jagannathan, R. and T. Ma (2003). R♦>βisk reduction in large portfol←↑ios: Why imposing th↓≥e wrong constraints helps. Journal of Finance 58(4), 1651 – 1683.
Jobson, J. D. and R. Korkie (&↔1981). Performance hypothesis test✘♣σing with the Sharpe and Treyno ✘≈r measures. Journal of Finance 36, Vol. 36(4), 889 – 908 ≈±.
Kan, R. and G. Zhou ☆&(2007). Optimal portfolio choice wi₩↕←th parameter uncertaintyσδ. Journal of Financial and Quantit¶ε↕ative Analysis 42(3), 621 – 656.
Ledoit, O. and M. Wolf (2004). A w✘'ell-conditioned estimator for •♣↕large-dimensional covariance matric₹←✔¶es. Journal of Multivariat↑↓ ≈e Analysis 88(2), 365 – 411.
Markowitz, H. (1952). Port≠σfolio Selection. Journal of Finance 7(1), 77 – 91.
MacKinlay, A. C. and L. Pas≈tor (2000). Asset pricing models: Imp"€™lications for expected returns and port ✔folio selection. Review of Financial Studγγ©¥ies 13(4), 883 – 916.
Memmel, C. (2003). Performance hypotheα™sis testing with the Sha>λrpe ratio. Finance Letters 1(1), 21 – 23.
Pastor, L. (2000). Portfo€∏lio selection and asset pricing model→∏₹s. Journal of Finance 55(1), 179 – 223.
Pastor, L. and R. F. Stambaugh (✘≈<γ2000). Comparing asset pricing model♣ >s: an investment perspectiv✘σe. Journal of Financial Economi≥♠♥cs 56(3), 335 – 381.
Stein, C. (1955). Inadmissibil>'ity of the usual estimator for≤σ the mean of a multivariate no§rmal distribution. In 3ΩΩrd Berkeley Symposium on P ↓÷robability and Statistics, 197 – 206♠π.
免責聲明(míng):入市(shì)有(yǒu)風(fēng)險,投資需謹慎。在任何情≠況下(xià),本文(wén)的(de)內(nèi)容、信息及數(shù)據或αβ'所表述的(de)意見(jiàn)并不(bù)構成對(du≥∞ì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xi≤₽à),本文(wén)作(zuò)者及所屬機(≥'®jī)構不(bù)對(duì)任何人(rén)因使™σ用(yòng)本文(wén)的(de)任何內(nèi)容所引緻←的(de)任何損失負任何責任。除特别說(shuō)明✔✔(míng)外(wài),文(wén)中圖表均直接或間(jiān↔)接來(lái)自(zì)于相(xiàng)應論文(wén),僅§λ為(wèi)介紹之用(yòng),版權歸原作(zuò)者和(hé)期刊所有δ↔♥ (yǒu)。
