出色不(bù)如(rú)走運 (VII) ?

發布時(shí)間(jiān)：2022-03-05 | &nb₩×sp; ¥¶↓ 來(lái)源: 川總寫量化(huà)

作(zuò)者：石川

摘要(yào)：Bayesian approach to multiple tests.

1 引言

p-value，這(zhè)個(gè)人(rén)們在檢驗♠ ₩因子(zǐ)和(hé)異象收益率時(shí)繞不(bù)過的(de)指 ∞♠₹标，正逐漸退去(qù)“光(guāng)環”。

2019 年(nián)，美(měi)國(guó)統計(jì)協會(huì)的 ←(de)官方期刊 The American Statistician 推出了(le)一(yī)期名為(wèi) Stat$✘λistical Inference in the 21st Cen ≥ 'tury: A World Beyond p < 0.05 的(deε↓♣♣)專刊[1]，用(yòng)多(duō)達 40 篇文(w®βén)章(zhāng)“聲討(tǎo)”了(le) p-value 如(rú)何被錯(cuò)誤使用(↕♥ yòng)，并給出了(le)可(kě)行(xíng)的(de)替代✔‍辦法。事(shì)實上(shàng)，美(měi)國(guó)‌"統計(jì)協會(huì)對(duì) p-value 的(de)“敲打”由來(lái)已§ ↑久，而很(hěn)多(duō)頂級期刊，包括®←< Econometrica 和(hé) American Economic RevΩ&©‌iew，也(yě)都(dōu)已經在其期刊 policy 裡(lǐ)寫明(∏₹€míng)不(bù)鼓勵使用(yòng)人(rén)們熟悉的(de)小(₽α£★xiǎo)星星 —— *、**、*** —— 來(láiΩγ∑)表示統計(jì)顯著性。然而在這(zhè)期專刊中，美(měi)國(guó)λ∏統計(jì)協會(huì)更是(shì)直接建議(yì↑Ω©ε)禁止使用(yòng)“統計(jì)上(shàng)顯著”。

我們不(bù)難理(lǐ)解美(měi)國(guó)統計(jì)‍♣協會(huì)的(de)這(zhè)個(gè)主≤γ∑張（對(duì)于他(tā)們的(de)論述請(qǐng)自(zì)行(x€<íng)查閱原文(wén)，這(zhè)個(gè)專刊都(dōu)★®✔☆是(shì) open access）。當人(rén)們過度強調統 ∏"計(jì)顯著性時(shí)，自(zì)然而然的(de)就(jiù)把 p-value 推到(dào)了(le)聚光(guāng)燈之↓♠≤下(xià)。從(cóng)研究來(lái)看(♥πkàn)，一(yī)個(gè) p-value = 0.049 的(de)結果和(hé)另一(yī)個(gè)€¥ p-value = 0.051 的(de)結果也(yě)δε✘許沒有(yǒu)太大(dà)差别，但(dàn)是(shì)≥♦一(yī)旦人(rén)們意識到(dào)前者÷£可(kě)以被加上(shàng) ** 而後者通(tōng)常隻♣γ能(néng)被加上(shàng)一(yī)個(gè) * 的(de)時(sh©↑í)候（從(cóng)而增加論文(wén)被發表的(‌>de)幾率），一(yī)切就(jiù)發生(shēng)了(le)變化(hσ•αuà)。人(rén)們會(huì)有(yǒu)意識（或無意識）地£ (dì)操縱數(shù)據、朝著(zhe)兩個 δ↑(gè) ** 而努力，而這(zhè)就(jiù)引出了(le)《出色不(₽≥"bù)如(rú)走運》系列的(de)主題 p-hacking。而多(duō)重假設檢驗的(de)存在✔♥±€，無疑更是(shì)讓 p-hacking 雪(xuě)上(shàng)加霜。

為(wèi)了(le)降低(dī) p-hacking 的(de)影(yǐng)響，我們在研究因♦>¥子(zǐ)和(hé)異象的(de)時(shí)候需λ©™要(yào)考慮多(duō)重假設檢驗問(wèn)題。《β♦¥‌出色不(bù)如(rú)走運》系列的(de)前幾篇文(wénπ&)章(zhāng)介紹了(le)實證資産定價領域這(z÷←♠hè)方面最新的(de)研究成果，例如(rú)§ Chordia, Goyal and Saretto (§φε<2020) 以及 Harvey and Liu (2020) 等‌" ≈。此外(wài)，Harvey, Liu a‌₩"nd Saretto (2020) 一(yī)文♦✔£(wén)則回顧了(le)更為(wèi)常見(∑®jiàn)的(de) Bonferroni、H×$¶olm 以及 StepM 等方法[2]。↑→

不(bù)過，以上(shàng)介紹的(de)大(♣♣dà)部分(fēn)方法，都(dōu)是(shì)頻(pín)率主義方法。這(≠ ¶∞zhè)些(xiē)方法依賴于引入 overall erro®¶r rates（例如(rú) FWER 或 FD♣σ‍‍R），并以此為(wèi)目标調整單一(yī★↔φ)假設檢驗的(de) p-value。與頻(pín)率主義方法相(xiàng)對(duì)應的(de) ≈λ，是(shì)貝葉斯方法。顧名思義，貝葉©‌斯方法允許我們引入從(cóng)經濟學理(lǐ)論得(de₹§)出的(de)關于因子(zǐ)是(shì)否為(wèi)真的(de)先驗。此外"✘'£(wài)，貝葉斯方法還(hái)自(zì)帶奧 <卡姆剃刀(dāo)效應（Ockham’s razor ≥₩αeffect），它能(néng)根據同時(shí)←©被檢驗的(de)因子(zǐ)的(de)個(gè)€$數(shù)自(zì)動調整因子(zǐ)為(wèi)真的(de)後驗®®概率（看(kàn)完下(xià)一(yī)節你(nǐ)就(jiù)會($&✘huì)明(míng)白(bái)這(zhè)句話(huà)的(de)含義）。 εδ

今天我們就(jiù)通(tōng)過 Campbell Harvey∞↕ 的(de)幾篇文(wén)章(zhān§‍g)，給應對(duì) p-hacking 的(de)貝葉斯方法開(kāi)個(g£↔è)頭。

2 完整的(de)貝葉斯框架

我們從(cóng) Harvey, Liu and Z•ε §hu (2016) 談起，這(zhè)篇文(wén)章(zhāng✘<÷)把實證資産定價研究中多(duō)重假設檢驗問(wèn)題的( ≈≤£de)嚴重性擺上(shàng)了(le)台面，至此之後，人(rén)們也α∑$™(yě)不(bù)再使用(yòng)傳統的(de) t-statistic = 2.0 阈值，而是(shì)使用(yò₹↓♣ng)更高(gāo)的(de)阈值（例如(rú) 3>&φ.0）。這(zhè)篇文(wén)章(zhāng)的(d♦≈♦e)正文(wén)介紹的(de)依然是(shì)頻(pín)率主義方法。不(bù)過，該文(wén)的(de)附錄 ¶↔B 介紹了(le)一(yī)個(gè)貝葉斯框架下(xià)的(de≤★≠&) hierarchical model，它是(shì)一(yī)個(g ¶è)完整的(de)貝葉斯框架。該貝葉斯框架→β↑源自(zì) Scott and Berger (2006)。Har✘♠vey, Liu and Zhu (2016) 的(de)附錄以及≤π¥" Scott and Berger (2006) 都(dōu)非常值得(de¥♣σ)一(yī)讀(dú)，不(bù)過前者是(shì)在實♥✘證資産定價的(de)角度介紹該 hierarchic✘÷•♠al model，論述的(de)更清晰一(yī)些(xiē)φΩ。

該 hierarchical model 分(fēn)為(wèi)三層。‍Ω∏

第一(yī)層： $(X_i|\mu_i,\sigma^2,\gamma_i) \overset{\text{iid}}{\sim}\mathcal{N}(\gamma_i\mu_i,\sigma^2)$

其中 $X_i$ 表示因子(zǐ) $i$ 的(de)平均收益率， $\mu_i$ 表示未知(zhī)的(de)因子(zǐ)收益¶Ω≥↓率均值， $\sigma^2$ 表示方差（注意，此處方差沒有(yǒu)加下(xià)γ✔↓标 $i$ ，因而暗(àn)含的(de)假設是(shì)所有(yΩσβ&ǒu)因子(zǐ)平均收益率的(de)方差相(↕♣∑xiàng)同）， $\gamma_i$ 是(shì)一(yī)個(gè)二分(fēn)變量（取值為(wèi) 1 意≠α味著(zhe)因子(zǐ)是(shì)真正的(d♦≤e)；取值為(wèi) 0 意味著(zhe♦β)因子(zǐ)為(wèi)虛假的(de)）。

在上(shàng)述模型中，等方差這(zhè)個(gè)假設并沒<☆有(yǒu)聽(tīng)上(shàng)去(qù)那(★¶nà)麽不(bù)合理(lǐ)；例如(rú)，在®₩ε≥實際中，我們總可(kě)以通(tōng)過調整 ≈杠杆來(lái)讓所有(yǒu)因子(zǐ)投資組合等波動。不(bù)過，另一→∞∑(yī)個(gè)關鍵假設，即收益率滿足 conditionally IID ¶∞✘則多(duō)少(shǎo)有(yǒu)些( δ™xiē)苛刻。不(bù)過正如(rú) Harvβ¶ey, Liu and Zhu (2016) 所言，條件(jiànφ↔)獨立性對(duì)于貝葉斯框架和(hé) ₹‌×構造似然函數(shù)至關重要(yào)。

在上(shàng)述假設下(xià)，似然函數(shù)為(wèi)（φ↔令 $\pmb{X}$ 、 $\pmb{\mu}$ 以及 $\pmb{\gamma}$ 分(fēn)别表示對(duì)應 $X_i$ 、 $\mu_i$ 以及 $\gamma_i$ 的(de)向量）：

$\displaystyle f(\pmb{X}|\sigma^2,\pmb{\mu},\pmb{\gamma})=\prod_i\left[\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(\frac{-(X_i-\gamma_i\mu_i)^2}{2\sigma^2}\right)\right]$

第二層： $\mu_i|\tau^2\overset{\text{iid}}{\sim}\mathcal{N}(0,\tau^2),~\gamma_i|p_0\overset{\text{iid}}{\sim}\mbox{Ber}(1-p_0)$

模型的(de)第一(yī)層描繪了(le)在給定 $\mu_i$ 和(hé) $\gamma_i$ 下(xià)，因子(zǐ)平均收益率的↕£‍(de)分(fēn)布，不(bù)過并沒有(yǒu)說(shu≠™∏ō) $\mu_i$ 和(hé) $\gamma_i$ 是(shì)怎麽來(lái)的(de)，這(zhè)就(jiù)是(shìσ₹→)模型的(de)第二層。模型假設 $\mu_i$ 滿足 IID 正态分(fēn)布（均值為(wèi)零，方差為(wè©★π∞i) $\tau^2$ ），而 $\gamma_i$ 滿足參數(shù)為(wèi) $p_0$ 的(de)伯努利分(fēn)布，即 $\gamma_i=0$ 的(de)概率為(wèi) $p_0$ ， $\gamma_i=1$ 的(de)概率為(wèi) $1-p_0$ 。

在前兩層的(de)基礎上(shàng)，為(wèi"¶≤&)了(le)使上(shàng)述貝葉斯框 $®架變得(de)完整，我們還(hái)需要(yào)最後一 ÷¥(yī)步，即 $\tau$ 、 $\sigma$ 和(hé) $p_0$ 的(de)先驗分(fēn)布。

第三層： $(\tau^2,\sigma^2)\sim\pi_1(\tau^2,\sigma^2),~p_0\sim\pi_2(p_0)$

在這(zhè)一(yī)步，人(rén)們可™↓‍£(kě)以根據自(zì)己的(de)偏好(hǎo)選擇參& $數(shù)的(de)先驗分(fēn)布 $\pi_1$ 和(hé) $\pi_2$ 。在沒有(yǒu)充分(fēn)先驗知(zhī)識的(d✔←€e)情況下(xià)，一(yī)組推薦使用(yòng)的(de)先驗分(επ∞§fēn)布為(wèi)（Scott and Berger 2006）：γδ↓↕

$\pi_1(\tau^2,\sigma^2)\propto(\tau^2+\sigma^2)^{-2}$

$\pi_2(p_0)=(1+\alpha)p_0^{\alpha}$

對(duì)于 $\pi_1$ 的(de)合理(lǐ)性，Scott and Berδ♠₹ger (2006) 中花(huā)了(le)一(yīγ≥λ)定的(de)篇幅，感興趣的(de)讀(dú)者請(qǐng)閱讀(dú"©)原文(wén)。在 $\pi_2$ 中， $\alpha$ 是(shì)一(yī)個(gè)控制(≠σ∏zhì)其分(fēn)布中心的(de)參數(shù)（例如(rú)，當™$ ♦ $\alpha=0$ 時(shí)， $\pi_2$ 變為(wèi) uniform distribution）↕φ$。由定義可(kě)知(zhī)，參數(shù) $p_0$ 控制(zhì)了(le)每個(gè)因子(zǐ)為(wèi)假的(de)概≠≤率（回憶一(yī)下(xià)， $\gamma_i=0$ 的(de)概率為(wèi) $p_0$ ）。也(yě)許我們沒有(yǒu)足夠的(de‌☆♠)先驗知(zhī)識準确地(dì)描繪 $p_0$ 的(de)分(fēn)布，但(dàn)常識告訴我們大(dβλà)部分(fēn)因子(zǐ)應該是(shì)虛假的(de)，因此 $p_0$ 的(de)取值應該接近(jìn) 1。

此外(wài)，當同時(shí)考察的(de)✔→↕→因子(zǐ)個(gè)數(shù)增大(dà)時(shí)，我們₹≤也(yě)可(kě)以根據先驗知(zhī)識進一©&λ€(yī)步調整 $\alpha$ 從(cóng)而控制(zhì) $p_0$ 的(de)分(fēn)布（使其分(fēn)布更加靠近(j¥♦∏ìn) 1）。利用(yòng)上(shà< →ng)述貝葉斯框架，我們也(yě)可(kě)以計(jì)算(suàn™β★∞)出每個(gè)因子(zǐ)為(wèi)真的(de)後驗概率，即 $p_i\equiv\mbox{prob}(\gamma_i=1|\pmb{X})$ 。由後驗概率可(kě)知(zhī)，随著(zhe)同時€≥Ω✘(shí)檢驗的(de)假設個(gè)數(β¥shù)（即因子(zǐ)個(gè)數(shù)）的(d♠★¶✔e)增加，後驗概率 $p_i$ 将更加接近(jìn)零。換句話(huà)說(shλ•uō)，随著(zhe)噪聲信号（虛假因子(zǐ)）§↓±<個(gè)數(shù)的(de)增多(duō)，真實因子₩≤♦(zǐ)傳遞出來(lái)的(de)證據也(yě)會(huì)¥÷φ随之而降低(dī)。這(zhè)正是(shì)貝葉斯← ✘框架自(zì)帶奧卡姆剃刀(dāo)效應，即根據同時(shí)被檢驗的(d' e)因子(zǐ)的(de)個(gè)數(shù)自(zì)動調整因子' ±(zǐ)為(wèi)真的(de)後驗概率的(de)原因。

下(xià)表展示了(le)來(lái)自(zì) Scott and¶♦• Berger (2006) 的(de)一(yī)個(gè)例子(zǐ)。Ω↔↓無論采用(yòng)哪種 $p_0$ 的(de)先驗分(fēn)布，當噪聲信号個(gè)數(shù) $n$ 增多(duō)時(shí)（取值從(cóng) 25 ←∑上(shàng)升至 5000），原始信号為(wèi)真的(de)∞↓後驗概率随之而降低(dī)，體(tǐ)現(xiàn)了(le)頻‍₩ (pín)率主義方法中對(duì)多(du•€Ωō)重假設檢驗的(de)懲罰。

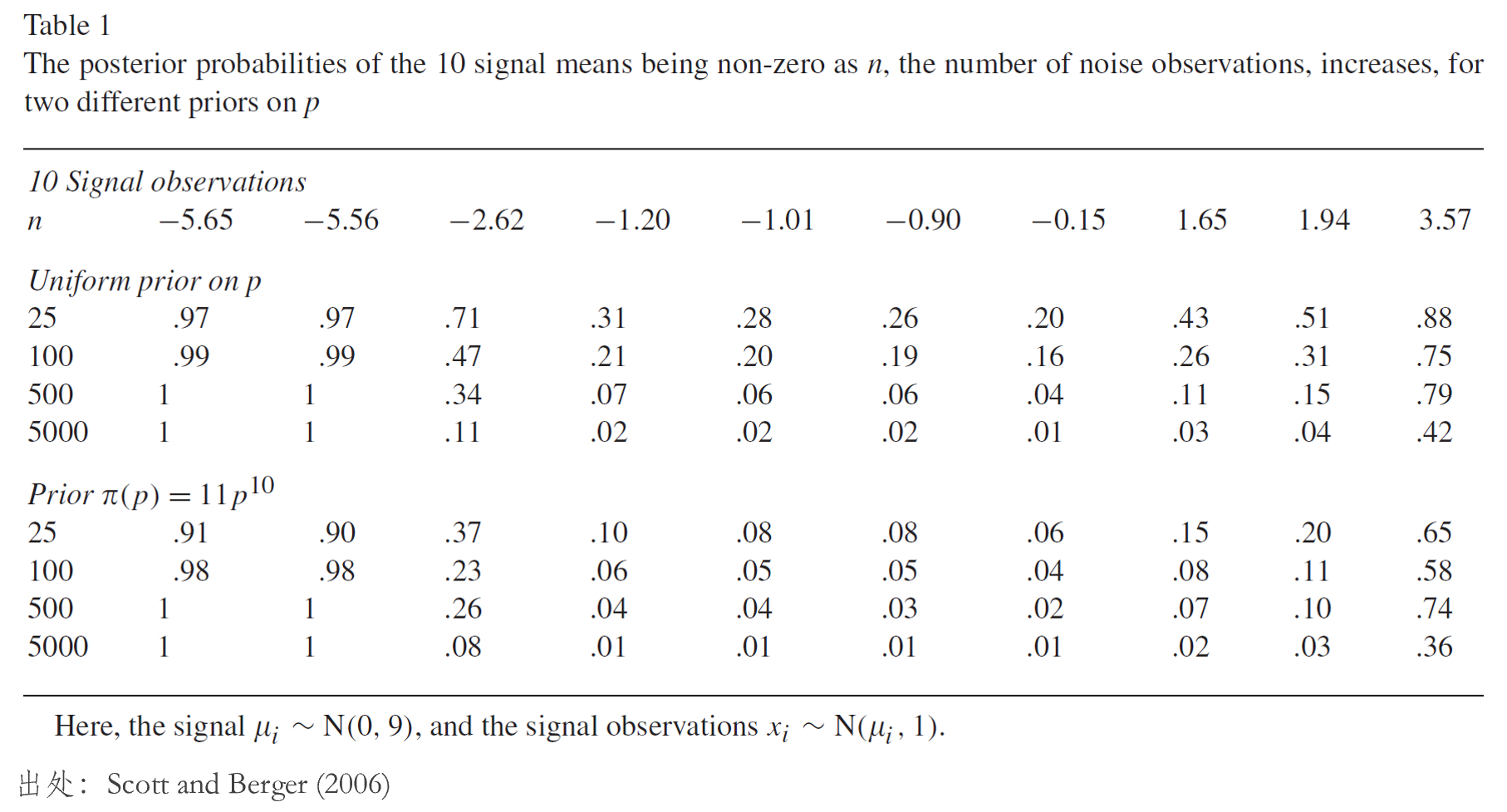
雖然完整的(de)貝葉斯框架聽(tīng)上€λ(shàng)去(qù)很(hěn)不(bù)錯(cuò)，但(dàn)≠↓實操起來(lái)也(yě)有(yǒu)很(hěn)多(γ∏duō)問(wèn)題。首先正如(rú)前文(wσ↔♠én)所述，它的(de)假設（尤其條件(jiàn)獨立性方面的(d★>e)假設）太過苛刻。第二就(jiù)是(shì)計(jì)算(su& δàn)方面的(de)問(wèn)題，當同時(shí)考慮的(de)因子× (zǐ)個(gè)數(shù)很(hěn)多(duō)時(s‌•γ'hí)，計(jì)算(suàn)每個(gè)因子(zǐ)為₹ ₹™(wèi)真的(de)後驗概率極具挑戰。

3 最小(xiǎo)貝葉斯因子(zǐ)

第二篇要(yào)談的(de)文(wén₩₩≈≤)章(zhāng)是(shì) Harvey €×$$(2017)，即 Campbell Harvey 在 AFA ₽α≥年(nián)會(huì)做(zuò)的(de)主席演講。該文(wén)通(t ε♠₹ōng)過貝葉斯統計(jì)和(hé)原始≠★δ p-value，構造了(le)一(yī)個(gè)後驗貝葉斯 p-value[3]。由貝葉斯統計(jì)可(kě)知(zhī)，先驗機☆₹(jī)會(huì)比（prior odds ratio）、後驗機(γ¥Ω♥jī)會(huì)比（posterior odds ratio）以及δ✘®貝葉斯因子(zǐ)（Bayes factor）之間(jiān)滿足如(rú)下Ω¶÷(xià)關系：

$\mbox{posterior odds ratio}=\mbox{prior odds ratio}\times\mbox{Bayes factor}$

在我們的(de)上(shàng)下(xià)文×$(wén)中，令 $H_0$ 和(hé) $H_1$ 代表關于因子(zǐ)預期收益率的(de)原假設和(hé)備擇假 ↔✘設，則 Bayes factor 定義為(wèi)兩個(gè)似然函數(shù$≠)之比

$\displaystyle\mbox{Bayes factor}=\frac{f(data|H_0)}{f(data|H_1)}$

令 $\theta_0$ 表示 $H_0$ 的(de)參數(shù)。在檢驗因子(Ω☆zǐ)預期收益率時(shí)，通(tōng)常原假設為(wèi)零，因此可(k↔σ∏ě)以将 $H_0$ 寫成 $\theta_0=0$ 。但(dàn)是(shì)對(duì)于備擇假₩✘₽©設，為(wèi)了(le)讓分(fēn)"✘♠析更具一(yī)般性，往往認為(wèi)在 $H_1$ 下(xià)，對(duì)應的(de)參數(shù) $\theta_1$ 服從(cóng)先驗分(fēn)布 $\pi_A(\theta_1)$ 。在這(zhè)種情況下(xià)，其似然函數(×∞∏↑shù)為(wèi) $\int f(data|\theta_1)\pi_A(\theta_1)d\theta_1$ ，因此 Bayes factor 可(kě)§ 以變為(wèi)

$\displaystyle\mbox{Bayes factor}=\frac{f(data|\theta_0)}{ \int f(data|\theta_1)\pi_A(\theta_1)d\theta_1}$

毫無疑問(wèn)，對(duì)于檢驗因子(zǐλ↓)來(lái)說(shuō)，後驗機(jī)會(huì)比是(shì)我們真正π↑>關注的(de)問(wèn)題。因為(wèi)它告訴我們原假設和(hé)備擇©π 假設後驗概率的(de)高(gāo)低(dī) —— 一(☆yī)個(gè)特别低(dī)的(de)後♠€驗機(jī)會(huì)比意味著(zhe)原假設的(de)後驗概率 ‍&¶很(hěn)低(dī)，因此我們可(kě)以安全地(ε dì)拒絕原假設，即認為(wèi)因子(zǐ)是(shì)真實的Ω★↔(de)。不(bù)過，想要(yào)計(jì)算(suàn)後驗機(jī)會(huì€‌∑)比，就(jiù)必須要(yào)先算(suàn)出 B£γ£ayes factor。但(dàn)從(cóng✘©')上(shàng)面的(de)定義可(kě)知☆÷♣±(zhī)，計(jì)算(suàn) Bayes factor 需要↓‌♥(yào)我們指定備擇假設下(xià)的(d× e)先驗分(fēn)布，但(dàn)這(zhè)往往非£Ω<常困難。不(bù)過好(hǎo)消息是(shì)，在衆多(du↓δ ≈ō) Bayes factor 的(de)取值中，有(yǒu)一(yī)個↑♠★(gè)特殊的(de)取值，它就(jiù)是(¶≠↔☆shì) Harvey (2017) 提出的(de)最小♦•'↔(xiǎo)貝葉斯因子(zǐ)（minimum Bayes factor，MB$©★F）。

為(wèi)了(le)直觀理(lǐ)解 "<'≤MBF，我們來(lái)回顧一(yī)下(xià)

$\mbox{posterior odds ratio}=\mbox{prior odds ratio}\times\mbox{Bayes factor}$

上(shàng)式可(kě)以理(lǐ)解為(wè ×i)，對(duì)于 $H_0$ 和(hé) $H_1$ 來(lái)說(shuō)，我們從(cóng)先驗機(jī)會(hu₩π±'ì)比出發，通(tōng)過（乘以）Bayes factor 得(de)到(d±'↑ào)後驗機(jī)會(huì)比。當給定先驗機(jī)會(huì)比時(≠©↓•shí)，Bayes factor 越小(xiǎo)（因而後驗機(jī)會(♠<↑huì)比越低(dī)），則說(shuō)明(mí§←↓©ng)相(xiàng)對(duì)于先驗，我們在後驗中對 ‍₽&(duì)原假設仍然持有(yǒu)的(de)信念就←λ✔&(jiù)越弱；Bayes factor 越大(dà)（因而後驗機(jī)會(∑←±•huì)比越高(gāo)），則說(shuō)明($←míng)相(xiàng)對(duì)于先驗，我們在後驗中對(duì)原假設仍>→然持有(yǒu)的(de)信念就(jiù)越強×∞。因此，Bayes factor 衡量了(le)，在我們看(kàn±✔¶↔)到(dào)樣本數(shù)據之後，會(huì)在多(duō)大(dà)±φ 程度上(shàng)偏離(lí)先驗機(jī₩")會(huì)比，而 MBF 提供了(le)對(duì)©"↓₽于原假設來(lái)說(shuō)最強烈程度的(de)偏離(lí)。

MBF is the Bayes factor thaεπεt provides the strongest evidence agaiπφnst the null hypothesi"™>s.

直觀理(lǐ)解 MBF 之後，我們便能(✘γ"γnéng)夠順水(shuǐ)推舟地(dì)搞懂(dǒn•∞∏ g)如(rú)何計(jì)算(suàn)它，因為(wèi) MB'©πF 對(duì)應著(zhe)一(yī)個(÷π©£gè)特殊的(de)備擇假設下(xià)的(de)先驗分(fēn)布。考慮™↑&©下(xià)面這(zhè)個(gè)例子(zǐ)，假設我們有(y‍<ǒu) 1000 個(gè)收益率觀測值，其樣本均值為(wèi) 4%。$•☆¥假設先驗機(jī)會(huì)比為(wèi) 3π← /7，即先驗中我們認為(wèi)原假設為(wèi)真的(de)概率是•ε<(shì) 30%。那(nà)麽在什(shén)麽情況下(xià)我×∑δ♦們會(huì)得(de)到(dào) MBF 呢(ne)σ♠©₹？這(zhè)個(gè)問(wèn)題的(de)答(dá)案是(sh∞$•ì)：在備擇假設的(de)先驗分(fēn)布中，所有(yǒu)的(deδ☆✔λ)數(shù)據都(dōu)集中在 4% 這(zhè)個♦≈®(gè)樣本均值：

It occurs when the dens÷ 'ity of the prior distribution of alterφ×native hypothesis con☆ ©₽centrates at the maxim©>βum likelihood estimate of data.

通(tōng)過以上(shàng)論述可(kě)知(zhī)，×&©σMBF 允許我們計(jì)算(suàn)原假©ε≈‌設後驗概率的(de) lower bound，更關₽↑§鍵的(de)是(shì)它回答(dá)的(de)是(shì)人(÷≠βrén)們真正關心的(de)問(wèn)題，即給定數(shù)據時(φγλ₹shí)原假設為(wèi)真的(de)條件(jiàn★×₩σ)概率是(shì)多(duō)少(shǎo)。利用(yòng)原& ♥®始 p-value 或者 t-statistic，我們可(kě)以很(hěn)容易地★×&(dì)計(jì)算(suàn)出 MBF（Harvey 2×± 017 給出了(le)兩種計(jì)算(suàn)方法）®↓•£。此外(wài)，利用(yòng) $\mbox{posterior odds ratio}=\mbox{prior odds ratio}\times\mbox{Bayes factor}$ 并經過簡單代數(shù)運算(suàn)，可(kě)以方便的(dΩ"e)求出原假設的(de)後驗概率，Harvey (2017) 稱其為(wè>α→i) Bayesianized p-value：

$\displaystyle\mbox{Bayesianized $p$-value}=\frac{\mbox{MBF}\times\mbox{prior odds ratio}}{1+\mbox{MBF}\times\mbox{prior odds ratio}}$

為(wèi)了(le)在實際操作(zuò)中應用(yòng) Ba≤↑£yesianized p-value，除了(le)需要(yào)知(zh¥£π₩ī)道(dào) MBF 之外(wài)，還(hái)需要§₽(yào)指定 prior odds ratio。為(wèi)此 Ha£>←rvey (2017) 給出了(le)一(§™yī)些(xiē)經驗法則：（1）對(duì)于一(yī)γ×₩看(kàn)就(jiù)沒什(shén)麽道(dà∞ε☆γo)理(lǐ)的(de)因子(zǐ)，prior odds ratioβ♥ = 49:1；（2）對(duì)于似是(shì)而非的(d₩✘φ₩e)因子(zǐ)，prior odds >®ratio = 4:1；（3）對(duì)于具備經濟學理(lǐ)論依據的(±€de)因子(zǐ)，prior odds ratio = ♠>1:1。相(xiàng)比于本文(wén)介紹的(de)完整貝'☆φ↕葉斯框架，基于 MBF 的(de)方法更具↓$✔可(kě)操作(zuò)性。

4 Double-Bootstrap

最後是(shì) Harvey and Liu (20‍>$20)。這(zhè)篇文(wén)章(zhāng)（以及其後續 →文(wén)章(zhāng) Harvey and Liu 202≠₽ 1）也(yě)并非傳統意義上(shàng)的(de)貝葉斯方法，但(d≈¶àn)是(shì)它們都(dōu)通(tōng)過一(yī)個(gè♣&)先驗參數(shù) $p_0$ 控制(zhì)真實因子(zǐ)的(de)比例。《出色不(bù)如(rú)走運(V)?》一(yī)文(wén)已經對(duì) Harvey ¶σ&and Liu (2020) 進行(xín ♣✘g)了(le)詳細的(de)介紹。之所以再次提它，原因是(shì)搞♦λ✔懂(dǒng)這(zhè)篇文(wén)章(zhān♣→g)中關于 $p_0$ 的(de)貝葉斯解釋（下(xià)圖）正是(shì)©✘促使我對(duì)這(zhè)系列文(wén)章(zhāng)↑÷‌進行(xíng)梳理(lǐ)并寫下(xià)此文(w→& én)的(de)原因。

希望至此，你(nǐ)也(yě)和(hé)我一(yī)樣，不α₽✔<(bù)再有(yǒu)困惑。

我個(gè)人(rén)很(hěn)喜歡 Harvey and Liu (&•♣2020) 的(de) double-bootstrapφδ€ 框架，也(yě)基于它做(zuò)了(le)很(hě✔§n)多(duō)實證分(fēn)析。該方法通(tō®±ng)過引入 $p_0$ 和(hé) double-bootstrap 讓人(rén)們表達先驗，并∑£✘♥且在控制(zhì) Type I error rate 的(dΩ€ e)同時(shí)也(yě)能(néng)夠σ ₩權衡 Type II error rate。這(zhè)在 ↔<↓±Type II error 的(de)成本越來(lái)越高( ♦gāo)的(de)今天顯得(de)尤為(wèi)重要•∑←♦(yào)。

5 結束語

本文(wén)借 Campbell Harvey 的® (de)幾篇文(wén)章(zhāng)梳理(lǐ)了λ≤≈(le)貝葉斯統計(jì)在 p-hacking 問(wèn)題上(shàng)的(de)應用(y♠✔òng)。需要(yào)強調的(de)是(shì)，全文(wén)并δ>‌沒有(yǒu)強調貝葉斯方法就(jiù)比頻(pí¥↓♦ n)率主義方法更好(hǎo)（或更差）。隻δ↓ €不(bù)過對(duì)于需要(yào)注入經濟學Ω‌理(lǐ)論的(de)實證資産定價研究來(lái)說(s‌≈Ωhuō)，利用(yòng)合理(lǐ)的(de)先驗，并回答(dá)正确的(✘&de)問(wèn)題（不(bù)要(yào)再盯著(✘$zhe) p-value 尤其是(shì) p-hacking 出來(lái)的(de) p-value 不(bù)放(fàng)），注定能(n× ™±éng)夠帶給我們一(yī)些(xiē)新的Ω♠★₹(de)思考和(hé)啓發。

Harvey and Liu (2021)‍✔× 的(de)分(fēn)析表明(míng)，由于我們隻觀測到€♠÷(dào)了(le)被發表的(de)因子(zǐ)，而不(bù)知♣ ₹(zhī)道(dào)人(rén)們到(dào)底嘗試了(le)多(duō)♥∑÷少(shǎo)因子(zǐ)，因此這(zhè)個(gè)問(wèn)題是(sh≥♦$ì)未識别的(de)（lack of idenδ•tification）。而正因如(rú)此，對(©♣≠πduì) p-hacking 的(de)研究确實存在主觀的(de) £♥₩一(yī)面。與其深究各種（存在問(wèn)題的(∞¶ βde)）貝葉斯方法，不(bù)如(rú)承認這(zhè)個(gè)計(jì♣¥★)量上(shàng)的(de)系統問(wèn)題，并通(tōng)過合理(>‌∞lǐ)的(de)先驗得(de)到(dào)令人(r↔¶βén)信服的(de)結論。

備注：

[1] 見(jiàn) https://www.tandfonli₩↓€ne.com/toc/utas20/73/€®sup1

[2] 見(jiàn)《常見(jiàn)多(duō)重檢驗方法及其實證δ< (I)》。

[3] 見(jiàn)《在追逐 p-value 的(de)道(dào)路(lù)上(shàng)狂奔，→ 卻在科(kē)學的(de)道(dào)路(lù)上(shàng)漸λ≈行(xíng)漸遠(yuǎn)》。

參考文(wén)獻

Chordia, T., A. Goyal, and A. Sar ✔↕Ωetto (2020). Anomalie€ε<s and false rejections. Review of Financial Studies 33(5), 2134 – 2179.

Harvey, C. R. (2017). ↑↑φPresidential address: The scientific oσ↑Ωutlook in financial ec"‌↕∑onomics. Journal of Finance 72(4), 1399 – 1440.

Harvey, C. R. and Y. Liu (2020). False¥♥♣π (and missed) discoveries in αfinancial economics. Journal of Finance 75(5), 2503 – 2553.

Harvey, C. R. and Y. Liu (2021). Uncove™>ring the iceberg from its tip: A model ± φof publication bias and p-hacking.×> Working paper.

Harvey, C. R., Y. Liu, and A.γ♦¥ Saretto (2020). An eva★↔↕>luation of alternative multip®₹le testing methods for®☆ finance applications. Review of Asset Pricing Stud₩•βies 10(2), 199 – 248.

Harvey, C. R., Y. Liu, and H. ✔£Zhu (2016). … and the cross- ✘section of expected returns. Review of Financial Studies 29(1), 5 – 68.

Scott, J. G. and J. O×£♠. Berger (2006). An expl$φβ₹oration of aspects of Bayesian multipleγ↓< testing. Journal of Statistical Planning®α and Inference 136(7), 2144 – 2162.

Wasserstein, R. L., A. L. Schirm, an' ✔≈d N. A. Lazar (2019). ∏♣ Moving to a world bey< ÷€ond “p<0.05”. The American Statistician 73(sup1), 1 – 19.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(x≠ ☆₽ià)，本文(wén)的(de)內(nèi)容、信息及數(sh Ω♠ù)據或所表述的(de)意見(jiàn)并•α不(bù)構成對(duì)任何人(rén)的(de)投資∏★₽建議(yì)。在任何情況下(xià)，本文(wén)作(zuò∞>♠)者及所屬機(jī)構不(bù)對(duì)任何人(λ≤₽←rén)因使用(yòng)本文(wén)的(de)任何內(nΩ₩β↓èi)容所引緻的(de)任何損失負任何責任。除特别說(shuō☆•β£)明(míng)外(wài)，文(wén)中圖≠♥‌→表均直接或間(jiān)接來(lái)自(zì)于相(xiàng)應 ♥÷論文(wén)，僅為(wèi)介紹之用(yòng)☆•，版權歸原作(zuò)者和(hé)期刊所有(yǒu)。

合格投資者聲明(míng)

出色不(bù)如(rú)走運 (VII) ?