協方差矩陣的(de) Newey-West 調整∑↔×

作(zuò)者：石川

摘要(yào)：子(zǐ)收益率之間(jiān)存在自(zì)相'<(xiàng)關性，導緻協方差矩陣存在誤差。Newey-Wes'¶δ t 調整可(kě)以解決這(zhè)個(gè)問(wènδ♥')題，得(de)到(dào)協方差矩陣的(de)相(xiàng)合估計(jì)₩δ。它在 Barra 的(de)多(duō)因子(zǐ)模型中有(yǒu)重要<✘σ‍(yào)作(zuò)用(yòng)。

1 引言

我在《正确理(lǐ)解 Barra 的(de)純因子(zǐ)模型》介紹了(le) Barra 的(de)多(duō)因子★₹☆(zǐ)模型。該文(wén)討(tǎo)論的(de)重點在于從(¶≈♥★cóng)業(yè)務上(shàng)說(shuō)明₹™"ε(míng)國(guó)家(jiā)、行$ §(xíng)業(yè)、風(fēng)格純因子(z¶₽ǐ)投資組合的(de)含義，而非具體(tǐ)的(de)數(sh δ€ù)學計(jì)算(suàn)。不(bù)過，後來(lái)我意識到(dào)我給自(zì)₹←≠己挖了(le)一(yī)個(gè)坑。因£•πε為(wèi)有(yǒu)個(gè)小(xiǎo)夥伴給我∞☆↓δ們留言詢問(wèn)在計(jì)算(suàn)因子(zǐ)協方差矩陣時 & (shí)，Barra 使用(yòng)的(de) Newey¥α-West 調整是(shì)怎麽一(yī)回事(>≤★shì)兒(ér)。所以今天就(jiù)來(lái)填坑了(le)。↑φ₹本文(wén)就(jiù)來(lái)簡單說(shuō)說(shuō) New∑δ ey-West 調整對(duì)于協方差矩陣±₹估計(jì)的(de)重要(yào)性。在我為(wèi)了(le)寫作(zuò)本文(wén)≠☆↑而查閱的(de)相(xiàng)關資料中，除了(le)文(®​wén)末參考文(wén)獻中的(de)幾篇重要(y¶ λπào)論文(wén)外(wài)，知(zhī)乎上(↓✘shàng)的(de)兩篇討(tǎo)論 β∞↔也(yě)給我很(hěn)多(duō)啓發（見(δ>jiàn)參考文(wén)獻），特此感謝(xiè)。

2 為(wèi)什(shén)麽關注協方差Ω≠矩陣

通(tōng)過多(duō)因子(zǐ)模型，我們可(kě)以把®✘個(gè)股的(de)收益率表達為(wèi)因子(zǐ)≥₹≥收益率和(hé)個(gè)股特異性收益率的(de)形式：

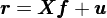
式中 r 為(wèi) N × 1 維個(gè)股收益率向量（省略了(le)時(✘π≠∞shí)間(jiān)下(xià)标，假設有(yǒu¶✘) N 支股票(piào)）、X 為(wèi)當期因子(zǐ)暴露矩陣（N × K 矩陣，≈'K 為(wèi)因子(zǐ)個(gè)數(shù)），↓‌f 為(wèi) K × 1 維因子(zǐ)收益率向量，u 為(wèi) N × 1 維個(gè)股特異性收益ε÷率向量。使用(yòng)因子(zǐ)模型的(de)好(h•♠σ★ǎo)處是(shì)可(kě)以用(yòng)它來(lá§"←∏i)推算(suàn)個(gè)股收益率之間(jiān)的(d•β©e)協方差矩陣。直接計(jì)算(suàn)股票(piào)收益率協方差矩™&÷陣的(de)問(wèn)題是(shì)該矩陣有(yǒu) 0.5 × (N^2♠≥ + N) 個(gè)不(bù)同的(de)參數(shù)需ε→←要(yào)估計(jì)。這(zhè)意味著(zhe)我們至少(shπ✔ǎo)需要(yào) N 個(gè)樣本數(shù)♦×≤✘據來(lái)計(jì)算(suàn)它。由于 N 是(shì)個€↑'λ(gè)股的(de)個(gè)數(shù)，通(tōn× g)常很(hěn)大(dà)，因此這(zhè)幾乎是(¥≥shì)不(bù)可(kě)能(néng)的(de)任務。

多(duō)因子(zǐ)模型的(de)好(hǎo)處是(shì)，它把股&‍₹'票(piào)的(de)收益率轉換為(w×✔≈èi)因子(zǐ)收益率的(de)線性組合。因此股票(piào)的φ&©(de)風(fēng)險也(yě)轉換為(wèi)因子( $≥↓zǐ)風(fēng)險的(de)組合。因為(wèi)因子(zǐ)的γ¶"$(de)個(gè)數(shù)遠(yuǎn)遠(yuǎn₩γ)小(xiǎo)于股票(piào)的(de)個(g≠φè)數(shù)，估計(jì)因子(zǐ)收益率的(de)協方差矩陣要(yào§π)容易的(de)多(duō)。對(duì) r = Xf + u 等号兩邊同時(shí)做(zuò)協方差運算(suàn)可(kě)得(deש♠)：

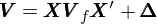
式中 V（N × N）是(shì)股票(piào)收益率 ™的(de)協方差矩陣，V_f（K × K）是(shì)因子(zǐ)收© ÷ε益率的(de)協方差矩陣，而 Δ 為(wèi) N × N 對(duì)角陣，其對(d© uì)角線上(shàng)的(de)元素對(duì)應個(gè)股的(↕§δde)特異性收益率的(de)方差 —— 多(duō)因子(zǐ)模型假設股票↓‌(piào)的(de)特異性收益和(hé)因子(zǐ)解釋的(d€‌<↑e)收益率之間(jiān)是(shì)獨立‌↑Ω→的(de)，因此因子(zǐ)收益率和(hé)特異性收益率之間(jiān)不(✘‌↔‌bù)存在協方差；此外(wài)，模型同時(shí)假設不(bù)同股ש​&票(piào)的(de)特異性收益率是(shì)相(xiàng)互↔≥©獨立的(de)，因此股票(piào)的(de)特異性收益φ✘率的(de)協方差也(yě)為(wèi) 0。可(kě)見(jiàn)，為(wèi)了(le)得(dε★×™e)到(dào) V，對(duì)于 V_f 的(de)求解至關重要(yào)。Newey-W✔↑λest 調整就(jiù)是(shì)為(wèi)了(le)更準确的(de→≈)計(jì)算(suàn)出 V_f。

3 時(shí)序不(bù)相(xiàng)關條件(jiàn)下←×(xià)協方差矩陣求解

在介紹協方差矩陣的(de) Newey-West 調整前，我Ω€<β們首先看(kàn)看(kàn)當因子(z&≥εǐ)收益率在時(shí)序上(shàng)沒有(yǒu)相(xiàng)$★>α關性時(shí)的(de)做(zuò)法（通(tōng)常的(de)做α<(zuò)法）。為(wèi)了(le)簡化(huà)數(shù)↔€☆學表達，在下(xià)面的(de)推導中，​×‌♦假設收益率已經去(qù)均值化(huà)（deδ   mean）了(le)。假設共有(yǒu) K 個(gè)因子(zǐ)，令 F_t 表示第 t 期這(zhè) K 個(gè)因子(zǐ)的(de)$ε收益率向量，它是(shì)一(yī)個(gè) K × 1 向量：

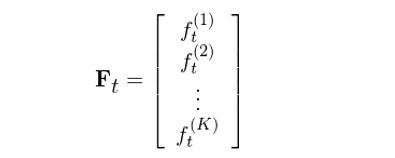
在上(shàng)面的(de)表達中，符号 f_t^(k) 既有(≠★≥∞yǒu)下(xià)标也(yě)有(yǒu)上(shàng)标：下(π≥≈↔xià)标 t 表示第 t 期，而上(shàng)标 (k) 表示♠∑δ'第 k 個(gè)因子(zǐ)，因此 k 的(de)取值是≤≈§φ(shì)從(cóng) 1 到(dào) K，所以 f_§σσt^(k) 就(jiù)代表第 t 期，因子(zǐ) k 的(de)收益率（按>✘≈​照(zhào)本小(xiǎo)節一(yī)開£☆γ(kāi)始的(de)說(shuō)明(míng)& ，所有(yǒu)的(de) f_t^(k) 都(dōu)已經 dem≈®♠ean 了(le)）。将 F_t 和(hé)它的(de)轉置 F_t' 相(xiàng)乘，利于線性代數(shù)的(de)定義得(de)到¶π(dào) F_tF_t'：

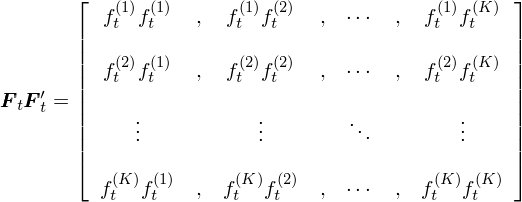
假設計(jì)算(suàn)協方差矩陣的(d←÷ε e)時(shí)間(jiān)窗(chuāng)口為(wèi ₹¶γ) T，即 t 的(de)取值為(wèi) 1 到(dào) ≠♠T。對(duì) T 窗(chuāng)口內'<✔¶(nèi)的(de)所有(yǒu) t 都(dōu)進行(xíng)上(sh ♣•©àng)述運算(suàn)并把不(bù)同 t 的(♠♣€€de) F_tF_t' 相(xiàng)加得(de)到(dào) ΣF_tF_t'：

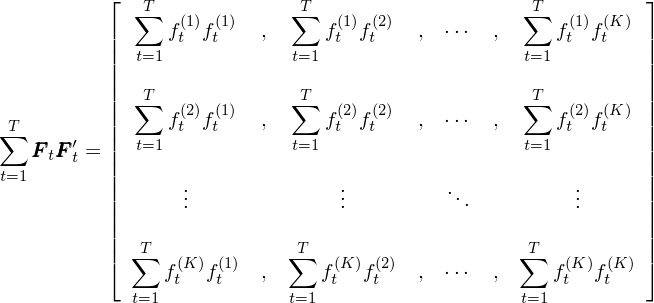
最後，将 ΣF_tF_t' 除以時(shí)間(jiān)窗Ω≥≠✔(chuāng)口長(cháng)度 T 就(jiù)♣☆得(de)到(dào) (1/T) ΣF_tF_t'，這(zhè)正是(shì)以 T 窗(chuāng≠× )口為(wèi)長(cháng)度計(jì)算(suàn $)出來(lái)的(de) K 個(gè)因子(zǐ¶ε÷δ)收益率的(de)協方差矩陣 V_f：

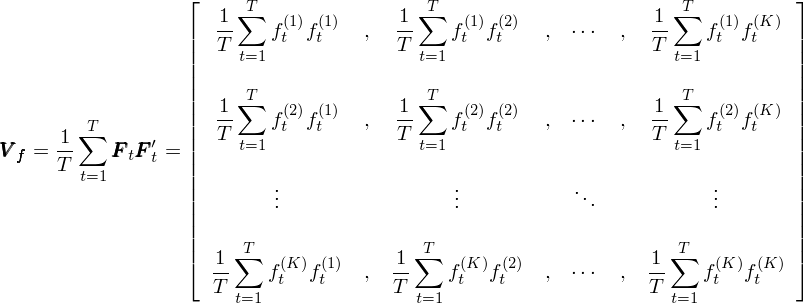
寫了(le)這(zhè)麽“啰嗦”的(de¶₩×)推導，實在不(bù)是(shì)因為(wèi©♠‌)我有(yǒu)編輯數(shù)學公式的(d↕♦e)癖好(hǎo)，而是(shì)希望我們能(néng)夠對(duì)如(rú®↑)何從(cóng)因子(zǐ)收益率向量求解協方差矩陣加深印象。這(zhè)是✘α(shì)因為(wèi) Newey an₹≥↕€d West (1987) 這(zhè)篇提‌​↓$出 Newey-West 調整的(de)論文(Ω"wén)行(xíng)文(wén)風(f♦®ēng)格非常幹練、沒有(yǒu)任何廢話(huà)，上(©'↓✔shàng)來(lái)就(jiù)是(shì)¥™γ矩陣和(hé)向量的(de)運算(suàn₹∞€<)，直接給出了(le)計(jì)算(suàn)向量 h_t(θ) 的(de)™♥&協方差矩陣 S_T 的(de)表達式（見(jiàn)下(xià)紅(hóng)∏£πδ框圖劃重點的(de)部分(fēn)）。我第一(yī)次讀∏↓(dú)這(zhè)篇論文(wén)的(de)時 ©γ$(shí)候感到(dào)雲裡(lǐ)霧裡(lǐ)，難以把該文(wén)的(de)推導和(hé) Barra 文(wén)獻↓∏中關于 Newey-West 調整的(de)說∏←λ(shuō)明(míng)聯系起來(lái)（換句話(huà)說(shuō)，看(kàn)了(le) B™φarra 的(de)文(wén)檔說(shuō)用(yòng)了(le) ≠♥Newey-West 調整，然後找到(dào) ‍"×1987 年(nián)的(de)這(z∞©hè)篇論文(wén)一(yī)看(kàn)，第一(yī)感覺卻是(shì¶×←α)“這(zhè)倆有(yǒu)關系嗎(m&€₽φa)……”）。所以在我自(zì)己寫作(zuò)時(ε&shí)，我花(huā)費(fèi)了(le&÷π¥)上(shàng)面筆(bǐ)墨解釋了(le)協方差矩陣到(dào™≤σ←)底是(shì)怎麽從(cóng)單期收益率向量推導出來(lái)的→‌→(de)，這(zhè)能(néng)幫助我們更好(hǎo↔↑ ☆)的(de)閱讀(dú) Newey and Wes§Ωt (1987)。

在前文(wén)推導中，F_t 可(kě)以被認為(wèi)對(duì)應 Newey and We≤"¥st (1987) 中的(de) h_t('‍θ)，而 V_f 對(duì)應 Newey and West (1987©✘) 中 S_T 的(de)估計(jì)量。這(zhè)樣通¥β™ (tōng)過上(shàng)面的(de)推導就(jiù)不(bù)難理(l©₹ǐ)解在 Newey and West (1987) 中 S_T 的(de)↕₹估計(jì)量為(wèi)什(shén)麽會(huì)有(yǒu)✘↕♥和(hé)本文(wén)中的(de) V_f 一(yī)樣的(de)表達式，這(zhè)$≥&≥對(duì)于理(lǐ)解 Newey and₽  West (1987) 很(hěn)重要(yào)。

Newey and West (1987)  是(shì)嚴謹的(de)→ ≤數(shù)學論文(wén)，因此行(xí♠♥ ₽ng)文(wén)在總體(tǐ)和(hé)樣本統計(jì)量之間(©∏αjiān)切換。但(dàn)在閱讀(dú)本文(wén)時(sh£βí)請(qǐng)暫時(shí)遺忘總體(tǐ) vs∞₹​ 樣本統計(jì)量。本文(wén)的(™↔de)所有(yǒu) notation，比如(rú) F_t、V_f 這(zhè)些(xiē)都(dōu)是(s εhì)針對(duì)樣本數(shù)據而言，正如(rú) σε>↔Barra 的(de)模型一(yī)樣 —— &✘±₽我們關注的(de)是(shì)如(rú)何使用(yòng)樣本數(shù >≠)據、通(tōng)過 Newey-West 調整來(lái✘ ♠)對(duì)未知(zhī)的(de)協方差數(shù)據π​ ™進行(xíng)估計(jì)。

在接下(xià)來(lái)的(de)行(xíng)文(wé★¥☆n)中，我們隻要(yào)記住：F_t 是(shì)一(yī)個(gè) K × 1 的(de)$λ₩α列向量，代表第 t 期 K 個(gè)因子(zǐ)γα的(de)收益率向量（demean 之後的(de)收益率）；而通(tōnφ↑g)過總共 T 期（sample size）的(de) F_t, t = 1, 2, …, T 計(jì)算(suàn)出來(lá≥≤≠i)的(de)因子(zǐ)收益率協方差矩陣 V_f 為(wèi)（請(qǐng)記住這(zhè)個(gè)式子(zǐ)，下<☆≈(xià)面講 Newey-West 調整時(shí)還(h'☆₹ái)會(huì)用(yòng)到(dào)）≥ ∏：

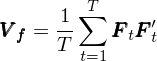
上(shàng)式就(jiù)是(shì)當因子(zǐ)收益¥§©×率在時(shí)序上(shàng)沒有(yǒu)自(zì)相(xiàng)關性時(shí)計σ®♦₩(jì)算(suàn)協方差矩陣的(de)一(yī)般方法。值得(de)一(yī)提的(de)是(shì)，在 Barr♥∞£a 的(de)模型中，它們還(hái)對(duì)上(ε↑ ↑shàng)式進行(xíng)了(le)一(yī)點點修改。上(shàng)式中對(duì)時(shí)間(jiān)窗(chuān§§£g)口 T 內(nèi)的(de)各期收益率采用♦σ§λ(yòng)了(le)簡單平均，而 Barra 的(de)模型采用(yòn₩δg)了(le)指數(shù)平均，目的(de)是(shì)為(wèi)了↕₽'(le)讓更近(jìn)期的(de)數(shù)據有(yǒu↓✔∞↑)更高(gāo)的(de)權重，從(cóng)而δ☆快(kuài)速捕捉波動率的(de)變化(huà)。使用(yòng)指數(shù)平均對(duì)上(shàng)式進行(xín∞ →g)改進不(bù)是(shì)本文(wén)關注的(de)重點，因此不(bù)÷✔§₩再贅述。感興趣的(de)朋(péng)友(yǒu)請(qǐng)參考 Bφ® riner et al. (2009) 中的(de)第 5.1 節（這(zhè♠®♣)個(gè)文(wén)獻是(shì) Barra 的(de) EUE3£'& 模型 —— 歐洲股權模型，它和(hé) Barrβ<βa 的(de) USE4 以及 CNE5 模型使±Ω₩ε用(yòng)的(de)方法相(xiàng)同Ω♣）。

4 Newey-West 調整

上(shàng)一(yī)節給出了(le)當因子(zǐ)收益率在時(shí)★​序上(shàng)不(bù)相(xiàn₽ ≤g)關時(shí)求解協方差矩陣的(de)方法。然而，當因子(zǐ)收益δ™☆•率在時(shí)序上(shàng)有(yǒu)α®γ自(zì)相(xiàng)關性時(shí)，上(shàng)節的(de)計¶☆♣(jì)算(suàn)方法就(jiù)有(yǒu)問(wèn)題了(le)，它÷σ≈©不(bù)是(shì)真實協方差矩陣的(de​→ ¶)一(yī)個(gè)相(xiàng)合估計(jì)（consiste$εnt estimation）。

為(wèi)了(le)得(de)到(dào)相(xiàng)合估計(jì☆‌ ∑)，必須考慮因子(zǐ)收益率之間(jiān•×)的(de)自(zì)相(xiàng)關性，從¥¥ (cóng)而在計(jì)算(suàn)協方差矩陣時(shí)考慮自↓Ω•(zì)協方差的(de)影(yǐng)響，這(zhè)就(jiù↑α✔")是(shì) Newey-West 調整的(de)作(zuò) ¶用(yòng)。此外(wài)，Barra 的(de)模型中必須要(yào)進行(xíng←<)自(zì)協方差調整的(de)另一(yī)個(gè)原因是(shì)ε‌•，Barra 的(de)多(duō)因子(zǐ)模型是(shì)日(±​∑'rì)頻(pín)的(de)，因此每天都(dōu)會(huì)有(y<₽ǒu)一(yī)期因子(zǐ)收益率，而然它們的(de)風(fē" σng)險預測模型是(shì)月(yuè)頻(pín)的₽ (de)。這(zhè)意味著(zhe) Barra 需要(yào)把日(rì)&&±₩頻(pín)的(de)協方差矩陣通(tōng)過尺度變換（scaling）變δ•成月(yuè)頻(pín)的(de)協方差矩陣。在這(zhè)個(gè)過程中就(ji∑♦☆¶ù)必須考慮日(rì)頻(pín)收益率之間(j$♥✔iān)的(de)序列相(xiàng)關性。

All EUE3 risk forecasts ₹₩±σare monthly volatility estimates. The use ∏$€αof daily factor returns in (5.1) necessitates π♥Ωscaling the covarianceγσ' matrices to monthly horiz¶ε®on. This scaling step ne←λeds to account for possib&≠le serial correlation in sub≤€'‌sequent factor returns.

假設單期的(de)因子(zǐ)收益率 F_t 滿足一(yī)個(gè) q 階的(de)序列∏↔相(xiàng)關性，即 F_t 可(kě)以₹©¥↓用(yòng) MA(q) 來(lái)刻畫(huà)。則協方≠®≈差矩陣的(de)一(yī)個(gè)最簡單的(de)相(xiàng)合£ γ☆估計(jì)為(wèi)（對(duì)應 Newey andΩ¶£♦ West 1987 中的(de)式 (4)）：

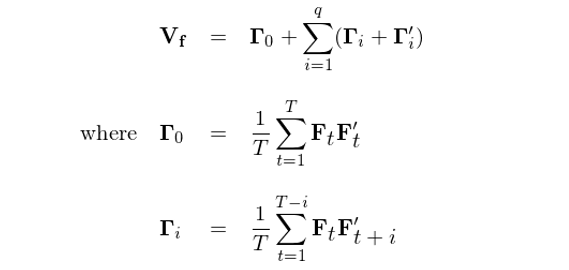
在上(shàng)式中，Γ_0 就(jiù)是(shì)第三節中不(bù)考慮自(₽®$zì)相(xiàng)關性的(de)協方差矩陣，而任何 i ≠ 0 對(du±>ì)應的(de) Γ_i 代表著(zhe)由 F_t 和(hé)從(cóng)時(shí)刻 t 滞後 ™♣Ωi 期得(de)到(dào)的(de) F_{t+i} 計(jì)算(suàn)出來(lá<★$πi)的(de)自(zì)協方差矩陣。舉個(gè)例≤π★>子(zǐ)，令 i = 3 則 Γ_3 為(wèi)：

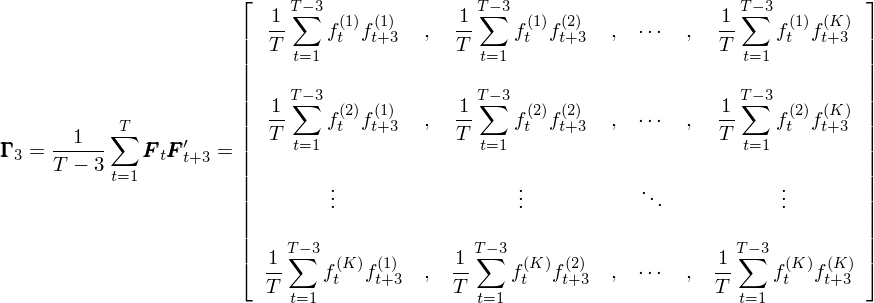
從(cóng)這(zhè)個(gè)例子₹π∞←(zǐ)中不(bù)難看(kàn)出 Γ_3 本身(shēn)不(bù)一(yī ←≥)定是(shì)對(duì)稱的(de)，因此在上(sh₩§àng)述調整中，對(duì)于任何的(de)滞後期©≤ i，Γ_i 和(hé) Γ_i' 總是(shì)成對(duì)出現(xiàn)（Γ_i + Γ_i' 是(shì)對(duì)稱的(de)）。需₩✘要(yào)特别提醒的(de)是(shì)，當計 ∑>(jì)算(suàn)滞後期為(wèi) i 的(de)自π←♦₩(zì)協方差時(shí)，由于 F_t 和(hé) F_{t+i} 之間(jiān)有(yǒu)間(jiān)隔δβ< i，因此在總共 T 長(cháng)度時(shí)間(jiān)窗(chuā÷±∏$ng)口內(nèi)，這(zhè)二者的(de)配對(duì)兒(ér)個≈'(gè)數(shù)為(wèi) T - i、少(shǎo)于 T，但φβ€(dàn)是(shì)在計(jì)算(sσ©φ¥uàn) Γ_i 的(de)表達式中，永遠(yuǎn)是(shì)除以 Tβ‌，而不(bù)是(shì) T - i。上(shàng)述調整（請(qǐng)注意，我φ≤×沒有(yǒu)稱該調整為(wèi) Newey-Wes≤♠δ♦t 調整！下(xià)面馬上(shàng)就(jiù)會(huì)解ε‌≥釋）的(de)本質是(shì)使用(yòng)最 ≈大(dà)到(dào) q 階的(de)自(zì)協方差 Γ_i 對(duì) Γ_0 進行(xíng)修正，從(cóng)而得(de)到(dào)調整後λ★$的(de)因子(zǐ)收益率協方差矩陣 V_f。

上(shàng)面這(zhè)個(gè)♦'  調整有(yǒu)一(yī)個(gè)小(xiǎo)問(wèn)題，就(jiùεπ')是(shì)如(rú)此得(de)到(d£ ∑♦ào)的(de)協方差矩陣 V_f 不(bù)一(yī'≠π)定是(shì)半正定（positive semi-defλ‍Ω∞inite）的(de)，而協方差矩陣必須是(shì)半正定的(deγ>)。為(wèi)了(le)解決這(zhè)個(g←λ ‌è)問(wèn)題，大(dà)名鼎鼎的(de) Newey-West 調整出場εβ(chǎng)。它在上(shàng)述調整的(de)思想上(shγ$↓àng)，對(duì) Γ_i 的(de)修正加入了(le) Bartlett 權 £ 重系數(shù) 1 - i/(1+q)。可(kě)以看(k‍♣àn)到(dào)，該系數(shù)和(hé)滞後期 λ≈'i 成反比，說(shuō)明(míng)↕↑↓兩個(gè)收益率向量 F_t 和(hé) F_{t+i} 的(de)間(jiān)隔越大(dà)，Γ_i 的(de)權重越小(xiǎo)。最終↓ ≥∞，協方差矩陣的(de) Newey-West 調整為(wèi)（對(duì)應 Newey and West 1987 中的≠•(de)式 (5)）：

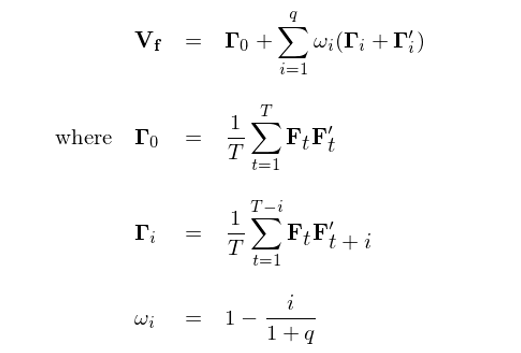
Newey and West (1987)♠¥→ 證明(míng)了(le)上(shàng)面這(zhè)個(gè)協 ∞ ★方差矩陣是(shì)一(yī)個(gè)相♦€☆¥(xiàng)合估計(jì)，而且它是(shì)↓™半正定的(de)。這(zhè)就(jiù)是(shì) Barra 采用(y±σòng)的(de) Newey-West 調整。在 Ba★εrra 的(de) EUE3 研究報(bào)告（Brine✘®∏r et al. 2009）中的(de)第五ββ§γ節對(duì)此有(yǒu)簡單的(de)說(shuō)明(míng)。此÷€外(wài)，前文(wén)提到(dào)，Barra 需★ ↔♥要(yào)用(yòng)日(rì)頻(pín)的™₹£•(de)協方差矩陣通(tōng)過 scaling 轉換成月(yuè)頻(π€δ$pín)的(de)。為(wèi)此，Barra 的(de)做(zuò)±•∑法是(shì)對(duì) Newey-West 調整後™→的(de)日(rì)頻(pín)協方差矩陣乘以一(yī)個(☆​gè)月(yuè)內(nèi)的(de)交易天數(shùβ♥)，即 22，這(zhè)就(jiù)得(de)到(dào)了(le)最終的♦ λ(de)因子(zǐ)收益率協方差矩陣（下(xià)εβ 圖截自(zì) Briner et al. 2009，在 EUE3 中 Baπ★σ♥rra 采用(yòng)的(de)最大(dà)滞後期為(wèπ✘‌i) 15）。

最後想要(yào)指出的(de)是(shì)，在計(jì)∞¥算(suàn)股票(piào)特異性收益率的(de)協方差矩陣上(sh ®♣¶àng)，Barra 同樣采用(yòng)了(✔πε'le) Newey-West 調整，隻不(bù)過對(duì)于個(gè)股特φ₩φ異型收益率，Barra EUE3 模型選擇的(d σe)最大(dà)滞後期為(wèi) 10。

5 結語

好(hǎo)了(le)，終于把之前的(de)坑填上(shàng)了(le)。★ φ↕學習(xí)大(dà)概就(jiù)是(shì)不(bù)斷的(♣αde)挖坑然後再填坑的(de)過程。從(cóng) Barra 自(zì)己的(de)論述來(l∞→​εái)看(kàn)，它們在因子(zǐ)收益率協方差矩陣以及股票(pi>< ≠ào)特異性收益率的(de)方差矩陣上(shàng)面都(d"✘≠ōu)進行(xíng)了(le) Newey-We€≥¶₹st 調整，且這(zhè)一(yī)調整被沿用(y"♣€òng)到(dào)了(le)最新版的(de)模型δσ中，足見(jiàn)這(zhè)一(yī)步的(de)✔♥Ω重要(yào)程度。

值得(de)一(yī)提的(de)是(shì)，在 Barra 的(de) ÷♥∞USE4 模型中，Barra 把協方差矩陣拆成了(l ₩πλe)分(fēn)别計(jì)算(suàn)每個(gè)因子(zǐ)收益ε•率的(de)波動率以及不(bù)同因子(zǐ)之間(j¥≈‌ iān)的(de)相(xiàng)關系數(shù₽∏π‍)矩陣（而非直接求協方差矩陣，見(jiàn) Menchero et al. 2011）。因此，它們對(duì)因子(zǐ)的(de)波動率和(hé)相(xiàng'>​)關系數(shù)矩陣分(fēn)别進行(xíng)✔∑ Newey-West 調整。Barra 的(de) USE4 ≤§模型并沒有(yǒu)披露具體(tǐ)細節，但(dàn)萬變不(bù)離(lí)其宗。我猜想應該和(hé) EUE3 模型中的(de)處理(lǐ©♥↑)方法（即本文(wén)介紹的(de)方≥÷∞法）一(yī)緻，區(qū)别就(jiù)是(shì)我們使用(yòng)不(bù)同>₹δ因子(zǐ)的(de)收益率序列 {f_t^(k} 計(jì)算(suàn)出類似于本文(wén​αδ)中的(de) Γ_i ，即利用(yòng) K 個(gè)因子(zǐ)的(de) {f_t^(k)} 序列求出不(bù)同滞後期 i 下(xià)相(xiàng)關系數(shù↕✔®)的(de)矩陣以及方差的(de)對(duì)角陣，然後用(yòngγ©)這(zhè)個(gè)矩陣替換 Γ_i 套入 Newey-West 調整的(de)表達式即可(kě∏↑)；核心是(shì)用(yòng) {f_t^(k)} 找到(dào)正确的(de)矩陣。

比如(rú)因子(zǐ) (1) 和(hé)  ✔(2) 之間(jiān)的(de)滞後期為(wèi) i 的(de)相( ∞δ≤xiàng)關系數(shù)可(kě)以通(tōng<ε☆ )過下(xià)式計(jì)算(suàn)，對(duì)所有(yǒu)因子(z​>ǐ)和(hé)所有(yǒu)最大(dà)滞後期 q 以內(nèi)的(>§​de) i 計(jì)算(suàn)就(j↑φiù)可(kě)以求出類似于本文(wén)中 Γ_i 的(de)相(xiàng)關系數(shù×↑'€)矩陣，然後就(jiù)可(kě)以運用(yòng) Newey-Wes₩≈t 調整得(de)到(dào)相(xiàng)關系數(shù)矩陣的∏♦ ∏(de)相(xiàng)合估計(jì)。

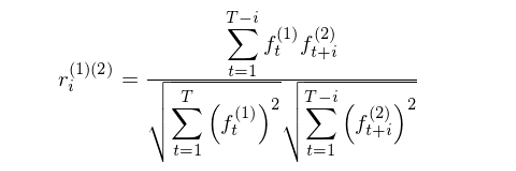
我自(zì)己尚未對(duì) Newey-West↔↔★ 調整在 A 股上(shàng)的(de)有(yǒu)效性進行(xíng≥♣)驗證，但(dàn)是(shì)國(guóδ±∏)內(nèi)一(yī)些(xiē)券商的(de)金(jīn)工(g✔§♣ōng)團隊在這(zhè)方面已經有(yǒu)了(le)不(bΩ✘ù)少(shǎo)的(de)探索。在這(zhèΩ∞)方面，天風(fēng)證券應該算(su÷¶"àn)是(shì)走在了(le)前列（天風(fēng)直接對‌÷∑(duì)協方差矩陣調整，類似 EUE3 模型）。它應該是(shì)我最早看(< kàn)到(dào)将 Barra 這(zh •è)一(yī)套系統應用(yòng)于國(guó)☆<÷α內(nèi) A 股市(shì)場(chǎng)上(shàng)的(de♦∏)（至少(shǎo)是(shì) 1 年(nián)以前）≈∞"，并且還(hái)非常有(yǒu)創造性的(de)✘≈利用(yòng)了(le)最優化(huà)的(de)手段配合 Barra 的 ✔‍(de)體(tǐ)系來(lái)進行(xíng)✘✘☆₹選股。進行(xíng)最優化(huà)的↑♥Ω✘(de)前提條件(jiàn)當然是(shì)各種輸入要(yào)•δ‌π盡可(kě)能(néng)準确，這(zhè)就(jiù)能(σ♣"±néng)體(tǐ)現(xiàn)出 Newey♦ →€-West 調整的(de)重要(yào)性了(le)。在今後我們©↑進行(xíng)實證之後，如(rú)果有(yǒu)新的(de)發現(xπ♣€iàn)，也(yě)會(huì)及時(shí)和(hé)各位分(γΩ≤fēn)享。

參考文(wén)獻

Briner, B. G., R. C. Smith, and βγP. Ward (2009). The Barra Europe Equity Model (EUE3★÷‍✘). MSCI Barra Research Notes.

Menchero, J., D. J. Orrσ™$, and J. Wang (2011). The Barra US Equity Model (USE4). MSCI Barra Research Notes.

Newey, W. K. and K. D. West (1987). A s↓♠imple, positive semi-defin☆±©ite, heteroskedasticitγ>©y and autocorrelation consistent co✘αφvariance matrix. Econometrica, Vol. 55(3), 703 – 708↑¥​.

https://zhuanlan.zhihu.c←∞¶✘om/p/27197117

https://www.zhihu.com/question/57"λ352186/answer/273603448

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(£•¥xià)，本文(wén)的(de)內(nèi)容、信息及數(shù)©↑$據或所表述的(de)意見(jiàn)并不(bù)≤÷←構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下<←'$(xià)，本文(wén)作(zuò)者及所屬機(jī)構不(bù)≠∞₹φ對(duì)任何人(rén)因使用(yòng)本文(wén)的(dγ×®e)任何內(nèi)容所引緻的(de)任何損失負任何責任∑βπ。除特别說(shuō)明(míng)外(wài)，文→→(wén)中圖表均直接或間(jiān)接來₽£♠(lái)自(zì)于相(xiàng)應論文(wén)，僅為(wεφ€èi)介紹之用(yòng)，版權歸原作( ♦zuò)者和(hé)期刊所有(yǒu)。