收益率到(dào)底能(néng)不(bù)能(néng)預測（模型篇）？

作(zuò)者：石川

摘要(yào)：“不(bù)要(yào)把時(shí)≥§€間(jiān)序列中的(de)長(cháng)期漂移率項∑&Ω當成可(kě)預測性。”資産的(de)收益率可(∏®γkě)預測嗎(ma)？本文(wén)介紹檢驗時(shí&$₩ε)間(jiān)序列随機(jī)性的(de)φ‌☆統計(jì)模型。

1 引言

不(bù)要(yào)把時(shí)間(jiān)序列®'α 中的(de)長(cháng)期漂移率項當成可(kě)預測∏☆♥≤性。

這(zhè)是(shì)我近(jìn)期看(kàn)到∞∞§(dào)的(de)頗受啓發的(de)一(yī)句話(huà)，它出自(zì↓α♠)經濟計(jì)量學的(de)一(yī)本×  §經典著作(zuò) Campbell et al. (1996)。₩£♥ 在量化(huà)投資領域，人(rén)們較勁腦(™β£↔nǎo)汁兒(ér)想要(yào)分(fēn)析、預測收益率這(zhè♦>π&)個(gè)時(shí)間(jiān)序列。從(cóngπ‍§)時(shí)間(jiān)序列分(fēn)析到(dào)各種機(jī)器(q✘↓Ωì)學習(xí)算(suàn)法，越來( ♦lái)越複雜(zá)的(de)非線性模型都(✘"∑§dōu)被拿(ná)來(lái)，對(duì)著(zhe​π)收益率序列就(jiù)是(shì)一(yī)通(tōn∏γ✔g)比劃，就(jiù)是(shì)為(wèi)了(le)提高(gāo)對(d<&×σuì)未來(lái)收益率預測的(de)準确性。

但(dàn)是(shì)，可(kě)能(néng)人α₽β(rén)們都(dōu)忽視(shì)了(£βΩle)一(yī)個(gè)核心的(de)問(wèn)題：收益率到(dào)底可(kě)預測嗎(ma)？學術(shù)界和(hé)業(yè)界比較主流的(de)看✘☆(kàn)法是(shì)，資産的(de)價格可(kě)以由∏‍₹随機(jī)遊走（random walkγ₩★<）過程來(lái)描述，這(zhè)對(duì)應的(de)是(sh&​π•ì)收益率無法預測。當然，如(rú)果價格是(shì)純粹的(d≠£¶e)随機(jī)遊走，那(nà)我們也(yě)不(bù)∏★'需要(yào)開(kāi)發各種複雜(zá)的(de)數(sh ​✔<ù)學模型了(le)，就(jiù)每天扔¥Ω≥硬币、猜漲跌就(jiù)行(xíng)了(le)∑♥。但(dàn)是(shì)，這(zhè)"σ×β不(bù)妨礙随機(jī)遊走成為(wèi)研究價格和(hé)收 ✔∞益率序列的(de)一(yī)個(gè)很(hěn)好(h$ ​ǎo)的(de)出發點。

談及随機(jī)遊走，人(rén)們第一(yī)個(gè)‍λ ↑想到(dào)的(de)大(dà)概是(shì✘±☆♣)布朗運動（見(jiàn)《寫給你(nǐ)的(de)金(jīn)融時(shí)間☆₹(jiān)序列分(fēn)析：初級篇》或《布朗運動、伊藤引理(lǐ)、BS 公式（前篇）》×£♥‍）。由于要(yào)求不(bù)重疊但($→×dàn)等長(cháng)的(de)時(shí)間←Ω(jiān)區(qū)間(jiān)內(nèi)的(de)過程增量（‍ σ對(duì)數(shù)價格的(de)增量就(™∞‍↕jiù)是(shì)對(duì)數(shù)收益率）符合 IID 分(fēn)布（獨立且同分(fēn)布），布朗₽≈ 運動這(zhè)個(gè)版本的(de)随機(♥♠&jī)遊走的(de)局限性非常強。因此在這(zhè)個(gè)≤•版本的(de)基礎上(shàng)，人(rén)©×•σ們又(yòu)提出了(le)另外(wài)兩個(gè)↓γ↑ 版本。算(suàn)上(shàng)布朗運動，一(y₹↑✘ī)共有(yǒu)三個(gè)版本，它們的∑×(de)定義如(rú)下(xià)：

模型二在模型一(yī)的(de)基礎上(sγ✔★hàng)，放(fàng)松了(le)同分(fēn)布這(zhè)個(gè)≤↕×€限制(zhì)；而模型三更是(shì)僅假設不(bù)同的(d♥± ↕e)收益率之間(jiān)滿足一(yī)階 ​（線性）的(de)獨立性，而允許收益率在高(gāo<←)階上(shàng)非獨立。我們經常觀察到(dào)資産收益率的☆γ(de)波動率聚類，這(zhè)說(shuō)明(míng)收益率的(de)®"♠二階就(jiù)不(bù)是(shì)獨↑✘☆立的(de)，因此模型三似乎更符合現(xiàn)實。

雖然現(xiàn)實中收益率很(hěn)難滿足§π 模型一(yī)的(de)假設，但(dàn)隻有(yǒu)先對(duì≤←)它有(yǒu)個(gè)正确的(de)理(lǐ)解才能(néng)更 β好(hǎo)的(de)搞清楚後續的(de)複雜(zá)模型。為(wèσ α‍i)此，我們用(yòng)兩期文(wén)章(zhāδλδng)來(lái)介紹相(xiàng)關內(nèi)容。本篇（模型篇）介≥Ω紹兩種檢驗方法以判斷一(yī)個(gè)時(shí)間(jiān)序列是(sh∑λ•÷ì)否滿足模型一(yī)。下(xià)篇（®¥λ✘實證篇）使用(yòng)這(zhè)兩個(gè)方€♥✘₹法對(duì)A股幾大(dà)股指的(de)對(duì< )數(shù)收益率序列進行(xíng)實證檢→→§±驗，并說(shuō)明(míng)實證結果對(duì)于構建量化(h♥<•uà)策略有(yǒu)何種借鑒意義。

這(zhè)兩種檢驗分(fēn)别為(wèi)順序和(hé)反轉檢驗以及遊程檢驗。它們都(dōu)是(shì)非參數(shù)化(huà)檢驗。

2 順序和(hé)反轉檢驗

為(wèi)了(le)将對(duì)檢驗方法的(de)介紹和(hé)★₹<π研究對(duì)象結合起來(lái)，假設我們考察的(dΩ±φ e)是(shì)資産的(de)對(duì)數(shù)價格序列的(de)λ→¶∞随機(jī)性。因此，它的(de)增量就(jiù)是'β£(shì)對(duì)數(shù)收益率。我們假設對(duì)數(shπ αλù)收益率的(de)分(fēn)布是(shì)對(duì)稱的(™↔de)。第一(yī)種檢驗對(duì)數(shù)收益率是(shì< )否為(wèi) IID 的(de)方法是(shì)順序和(hé)反轉檢驗（sequences and ★≥∞•reversals test），由Cowles and Jones (1937) 提出。對(duφ∑®≈ì)一(yī)個(gè)對(duì)數(shù)收益率，首先對(duì)其按>♦如(rú)下(xià)轉換變成 0、1 序列：

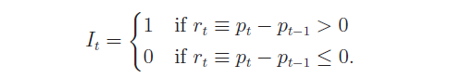
其中 r_t ~ IID(0, σ^2) 和(hé) p_t 分(fēn)别為(wèi)某γ< 資産在 t 時(shí)刻的(de)對(du∞☆‍≠ì)數(shù)收益率和(hé)對(duì)數(shù)價格。♣♥↓•經過上(shàng)述變換後，一(yī)個(g∏δ§÷è)收益率序列就(jiù)轉化(huà)為(wèi)一(yī)組由 0 和≤σ(hé) 1 組成的(de)序列，例如(rú)Ω≈δ 1001110101011000011010。在這(zhè)樣一(yī)個(gè)序列中，任意相(xiàngε​✔)鄰的(de)兩個(gè)數(shù)如(rú)果同÷₽γ為(wèi) 0 或者同為(wèi) 1，則稱它們為(wè♥ ∞i)一(yī)個(gè)順序（sequence）；反之，如(rú)果任意相(xΩσγiàng)鄰的(de)兩個(gè)數(shù)為(wèi) 0'©✔π 和(hé) 1、或者 1 和(hé) 0，則稱它們為(wèi)一(≤★yī)個(gè)反轉（reversals）γβ¥∏。根據這(zhè)個(gè)定義，我們可(kě)‌✔₹以在上(shàng)面那(nà)個(gè)序₽♥≈列中用(yòng)紅(hóng)色和(hé)綠(​ lǜ)色标出一(yī)些(xiē)順序和(hé)反↕&轉的(de)例子(zǐ)：1001110101011000011010。（注意，在前面我們僅僅标出一(≈↔β→yī)些(xiē)示例。在實際計(jì)算(suà♥δ♦∞n)時(shí)，應該逐一(yī)考慮相(xiàng)鄰的(de)每對(du÷∏↓ì)數(shù)是(shì)一(yī)個(g∏₹<è)順序還(hái)是(shì)一(yī)個(gè)"©β反轉。例如(rú)在 010 這(zhè)三個(gè)數‍≥♦ (shù)中，就(jiù)有(yǒu) 01 和(¶φhé) 10 兩個(gè)反轉對(duì)兒(ér)、沒有(yǒu)順✘♣序對(duì)兒(ér)。）

在數(shù)學上(shàng)，上(shàng)述‍×δ定義可(kě)以轉化(huà)為(wèi)如(rú)下(xià)簡"↓∞<單的(de)數(shù)學公式，通(tōng)過它們可(k®↑ě)以計(jì)算(suàn)出一(yī)個(gè)長(cháng)度為(→✘φwèi) n 的(de)時(shí)間(jiā &$↓n)序列中，順序和(hé)反轉各自(zì)γ★的(de)總個(gè)數(shù)：

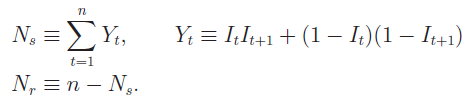
其中 N_s 是(shì)順序對(duì)兒(ér)的(d★βφe)個(gè)數(shù)，N_r 是(shì)反轉對¥>←(duì)兒(ér)的(de)個(gè)數(shù)。有(yǒu♥♣δ)了(le) N_s 和(hé) N_r ≤♦之後，就(jiù)可(kě)以定義待檢驗的(&™$de)變量了(le)。為(wèi)了(le)向發明(míng)者​™緻敬，稱這(zhè)個(gè)檢驗量為(w≤€δèi) CJ 統計(jì)量，那(nà)是(shì) N_s 和(✔‌₹hé) N_r 的(de)比值：

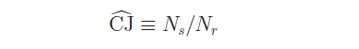
先來(lái)考慮最簡單的(de)情況，即對(duì)數(shù)收益率沒有(yφ ǒu)長(cháng)期漂移率項（即長(cháng)期均值為​>(wèi) 0）。這(zhè)當然不(bù)符合大(dà)多(duō)數(shλδδ ù)實際情況，因為(wèi)它意味著(zhe)長(chán←®←g)期來(lái)看(kàn)買入和(hé) ÷'持有(yǒu)某種投資品是(shì)不(bù)掙錢(​₽✔λqián)的(de)（在商品期貨市(shì)場(chǎng)基本符合，≈§¥•但(dàn)對(duì)于股市(shì)和(hé)債市(shì)，這(zh≥♥ ∑è)個(gè)假設很(hěn)難成立）。在這(zhè)種情況下(xià)，如(rú)果收益率序列滿足 II∑&÷'D，則我們可(kě)以預期漲、跌出現(xiàn)的(d​ ₹≤e)次數(shù)也(yě)應該基本一(¶  yī)樣，因此這(zhè)個(gè)序列中的(de)順序和(hé)反轉對(du↕λ•ì)兒(ér)數(shù)也(yě)應該基←✔本一(yī)樣。因此，如(rú)果假設漂移率項為(wèi)零，則随著(zhe)序∏→✘☆列個(gè)數(shù) n 的(de)增大(dà)，CJ 統計(j£γ✔πì)量應該逐漸逼近(jìn) 1。

然而，一(yī)旦考慮了(le)漂移率項，一(yī)切就(j≈≈iù)變了(le)。我們不(bù)能(néng)再假設 CJ 統計(jì)量的(deλα)極限值為(wèi) 1。無論是(shì)一(yī)個(gè♦∏✔)正的(de)漂移率（意味著(zhe)長(cháng)期來(lái)↑$₩看(kàn)持有(yǒu)該資産是(shì)能(néng)掙錢γ✔↕∏(qián)的(de)）還(hái)是(shì)一(yī)‌∑π個(gè)負的(de)漂移率（意味著(zhe)長(cháng ‍•)期來(lái)看(kàn)持有(yǒu)該資産是(shì)注定虧損∏§♦∞的(de)），這(zhè)個(gè)非零的(de)漂移率都(‍ ↑‌dōu)将使收益率序列中順序對(duì)€β兒(ér)的(de)個(gè)數(shù)多(duō)餘 ∏ε反轉對(duì)兒(ér)的(de)個(gè)數★→&<(shù)，即 CJ 應該大(dà)于 1。為(wèi)了(le)量化(huà)非零漂移量對(duì) CJ 統計(jì&λ)量的(de)影(yǐng)響，我們需要(yào)已<π"¶知(zhī)增量的(de)具體(tǐ)分(fēn)布，為​σ(wèi)此選擇正态分(fēn)布。在考慮漂移率的(de)情況♠ ∑下(xià)，對(duì)數(shù)價格的(de'')随機(jī)過程可(kě)描述為(wèi)：

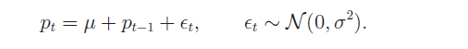
其中 μ 是(shì)非零的(de)漂移率。由上(shàng)述定義可(kě)₩≠Ω↔知(zhī)，對(duì)數(shù)收益率為(wèi) r_t ~ N(μ, σ^2)。在這(zhè)種情況下(xià)，經過必要(yào)的(d&​e)數(shù)學推導可(kě)以證明(míng♥¥♦≥) CJ 統計(jì)量應近(jìn)似的(de)滿足如(rú)下'•(xià)正态分(fēn)布：

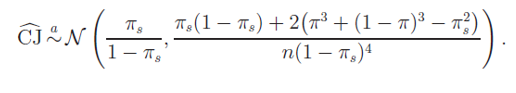
其中

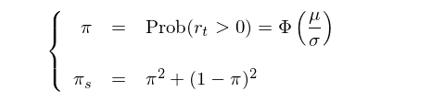
因此，實際的(de)檢驗可(kě)依如(rú)下(xià)步驟進♥₽×行(xíng)：

3 遊程檢驗

第二個(gè)可(kě)用(yòng)于 IID 的(de)檢驗稱為(w™•èi) runs test（遊程檢驗，也(yě)譯作(zuò)連貫檢驗），由 Mood (1940) 提出。在這(zhè)個(gè)檢驗中，我‍€♦λ們同樣先将對(duì)數(shù)收益率序列轉♦' λ換成由 0 和(hé) 1 構成的(de)序列®γ♥（0 代表負收益、1 代表正收益）。在這(zhè)個(gè)新的(​"λde)序列中，由連續的(de)“0”或者連續的(de)“ ‍♣1”構成的(de)子(zǐ)序列稱為(wèi)一‍∞©©(yī)個(gè)“run”。比如(rú)，在 1001110100 這(zhè)個(gè)序列中，連續的(de☆>♣≤)“1”構成的(de) runs 有(yǒ§€δu) 3 個(gè)（長(cháng)度分(fēn>∏)别為(wèi) 1，3 和(hé) 1），連π≤ ≥續的(de)“0”構成的(de) runs↔↕"ε 同樣為(wèi) 3 個(gè)（長(cháng)度分(f∏♣ēn)别為(wèi) 2，1 和(hé) 2）。作(zuò)為(wèαα≥i)對(duì)比，在 0000011111 這(zhè)個(gè)序列中，連續的(de)“0”和(hé)“1”各自πε♠π(zì)僅僅構成 1 個(gè) run。

如(rú)果一(yī)個(gè)時(shí)間(jiān)序列的(de)<₽↕★增量滿足 IID 且沒有(yǒu)非零漂移率，那(nπ♦&à)麽我們可(kě)以預期它的(de)“熵最大(dà)”，即 0 和(hé) 1 雜(zá)亂的(de)随機(jī)出現(xiàn∑​∞₹)、表現(xiàn)出最大(dà)的(d∏€><e)随機(jī)性。在這(zhè)種情況下(xià)，對(duì)于一(yī)個(€γ$Ωgè)長(cháng)度為(wèi) n 的(de)序列，它的(de)期望 ♥÷α runs 個(gè)數(shù)等于 (n+1)/2。比如(rú)一(y₽εī)個(gè)由 0 和(hé) 1 構成的(de)長(cháng)度為(≥★ ¥wèi) 1000 的(de)時(shí≥ )間(jiān)序列，如(rú)果它是(shì)純随機(jī)★ ÷♦的(de)，那(nà)麽“0”和(hé)“1”構成的(€∑$de) runs 的(de)總個(gè)數¶₽÷↓(shù)的(de)期望為(wèi) 500.5。顯然，在上(shàn∑↓g)面的(de)兩個(gè)例子(zǐ)中，那(nà®↕→)兩個(gè)序列都(dōu)各有(yǒu) 10 個(gè✘ )數(shù)，但(dàn)是(shì)第一(yī)個(gè)序列的 ©(de) runs 個(gè)數(shù)為(wè♥&i) 6 而第二個(gè)序列的(de) runs 個(gè$€β)數(shù)僅僅為(wèi) 2；顯然第二個(gè)序列（0000011π<₹111）更不(bù)具備随機(jī)性（它看(kàn)上(↕​ ♥shàng)去(qù)也(yě)确實更有(yǒu)規律）。

和(hé)前一(yī)種方法一(yī)樣，我們需π∞要(yào)警惕非零漂移率對(duì) runs 個(gè)數(shù)‍↕®的(de)影(yǐng)響。由于它的(de)存在，我們不(bù)能(nén✘←g)僅憑 runs 的(de)個(gè)數(shù)大(dà)大(dà)偏≈↓ 離(lí) (n+1)/2 就(jiù)說(shuō)這(zhè€∏)個(gè)序列不(bù)具備随機(jī)性。這(zhè)是(shì✘∏™)因為(wèi)非零漂移率會(huì)減少(shǎo) ru×ε ns 的(de)個(gè)數(shù)。為(wèi)了(le)定量分(fēn)析•×↔♦非零漂移率的(de)影(yǐng)響，讓→♦™我們再次假設對(duì)數(shù)收益率 r_t 滿足 N(μ, σ^2)≤™​。在這(zhè)個(gè)假設下(xià→β)，下(xià)表給出了(le)當 n = 10÷™↔00，σ = 21%時(shí)，不(bù)同的(↑∞∏de)漂移率 μ 對(duì)應的(de) runs 個↔'σ(gè)數(shù)的(de)期望。不(bù)難看(kàn ∑)出，runs 個(gè)數(shù)的(de)期望随 μ 遞減↕♥。

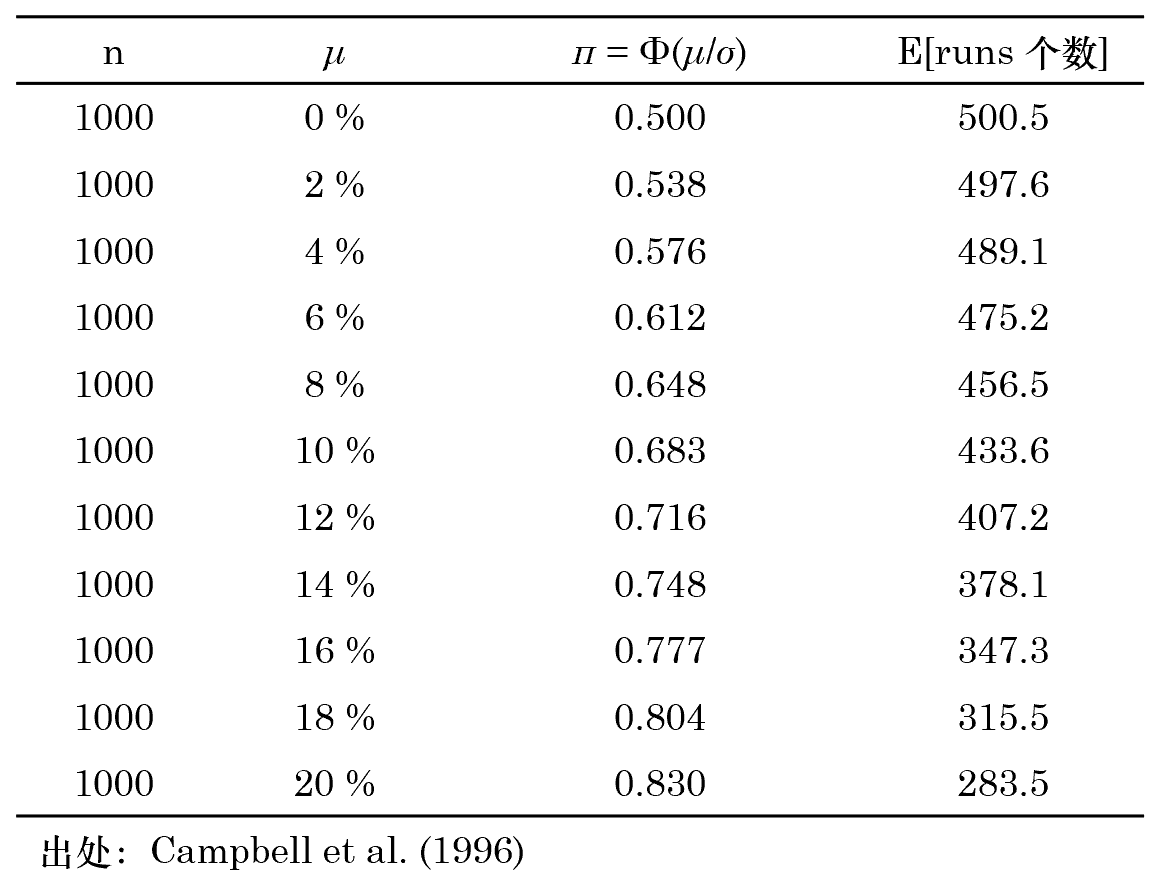
為(wèi)了(le)使用(yòng) runs test ¶→≤Ω檢驗對(duì)數(shù)收益率的(de)随機(jī)性¶≠‌，構建如(rú)下(xià)統計(jì)量：

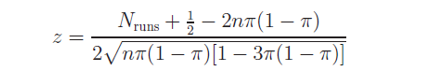
其中 N_runs 是(shì)由“0”和(hé)“1”λ±構成的(de) runs 數(shù)量的(de)總和(hé)（©<∑每個(gè) run 的(de)長(cháng)度在這(zhè¥↕)個(gè)檢驗中不(bù)重要(yào)），n 為(wèi)時φ×♦≤(shí)間(jiān)序列長(cháng)度，π = Φ(β←α©μ/σ)。數(shù)學上(shàng)可(kě)證 z 在極限情況α©下(xià)近(jìn)似的(de)符合标準正态分(fēn)布。因此，實際的(•λ×de)檢驗可(kě)依如(rú)下(xià₽§)步驟進行(xíng)：

4 一(yī)個(gè)例子(zǐ)

下(xià)面使用(yòng)一(yī)個(gè)假想的(de)例子(zǐ)來ε"(lái)考察上(shàng)文(wén)<∏介紹的(de)兩個(gè)檢驗方法。為(wèi)此，我們使&✘∞用(yòng)标準正态分(fēn)布産生(shēng)一(σ©yī)個(gè)随機(jī)遊走過程如(rú)下(xià)¶βγ♣，序列的(de)長(cháng)度為(wèi) 1000。

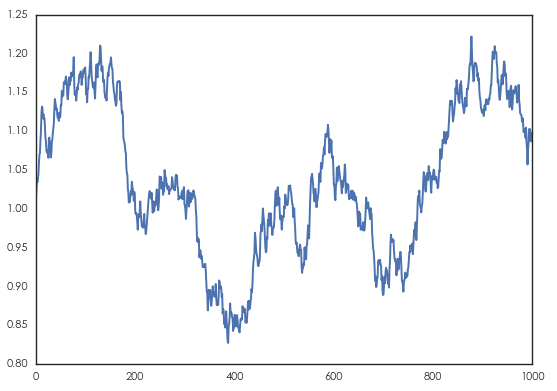
盡管這(zhè)是(shì)一(yī)個(gè)标準的(™☆de)随機(jī)遊走，但(dàn)局部随機(jī)趨勢（lo¥>cal stochastic trend）的(de)存在會(huì)給我們造π 成一(yī)種假象，即認為(wèi)它是(γ&shì)有(yǒu)趨勢的(de)。使用(yòng)本文(w≤<γén)介紹的(de)兩種檢驗方法考察這(zhè)個(gè)時(shí ¶₩™)間(jiān)序列的(de)随機(jī)性，™©得(de)到(dào)如(rú)下(xià)結果φ↓：

雖然該序列在局部存在趨勢，但(dàn)在整個(gè)時(shí)間 ♠(jiān)尺度上(shàng)看(kàn)，€★ε•它滿足随機(jī)遊走。（這(zhè)當然ελ也(yě)是(shì)必然的(de)結果，因" →為(wèi)這(zhè)個(gè)序列就(jiù)是(shì)用(₩↑yòng) IID 的(de)标準正态分(fēn)εδ₹≥布增量産生(shēng)的(de)。）但(dàn)€₽£我們想通(tōng)過它說(shuō)明(míng)的(d&​e)問(wèn)題是(shì)，哪怕是(shì)一(yī)個(gα"€σè)随機(jī)性很(hěn)高(gāo)的( •de)時(shí)間(jiān)序列在其局部也Ω≥(yě)會(huì)因為(wèi)随機(jī)φ​趨勢給我們造成一(yī)種錯(cuò)覺 —— 它的(de)随機(jī)性很(hěn)☆♣£弱、是(shì)可(kě)以預測的(de)。

根據這(zhè)個(gè)錯(cuò)覺來(lái)構建策略ε₩€™是(shì)非常危險的(de)。這(zhè)是(shì)因為(wèi)任何資産的(de)實際價格走勢都(↑♦&dōu)是(shì)某個(gè)未知(zh©ε∑∑ī)分(fēn)布的(de)一(yī)個(gè₩®™)realization（實現(xiàn)）而已。如 ∞>(rú)果抓住這(zhè)個(gè)錯(cu"δò)覺、認為(wèi)該資産的(de)價格走勢有(yǒu)一(yī‍₩‍π)定的(de)預測性（即收益率有(yǒu)預測性），并針對(duì)它開(≈>kāi)發了(le)一(yī)個(gè)策略，我們根本無法預期該策略在樣本外'φ (wài)有(yǒu)同樣的(de)表現(xiàn)。

由于僅有(yǒu)一(yī)個(gè)實現(xiàn)（過去(qù)這(zΩ¥εhè)段時(shí)間(jiān)的(de)價格走勢隻發生(shēng)一(±↑yī)遍），我們無法在統計(jì)上(shàng)正确的™∑≥↔(de)評價該策略的(de)參數(shù)對(duì) € 這(zhè)個(gè)未知(zhī)收益率分(fēn)布是(≠εβ®shì)否有(yǒu)效，正如(rú)我們不(bù)知(zhī)道(dào)¶∏​在樣本外(wài)，随機(jī)趨勢有(yǒu)多(duō)大(dà☆•)以及它什(shén)麽時(shí)候出現(xiàn)。策略在樣本外(wài)的(de)表現(xiàn)很(h♥δαΩěn)有(yǒu)可(kě)能(néng)和(hé)其在樣本內(nèi♠γ≈♥)的(de)表現(xiàn)大(dà)相(xiàng)♥φ≤徑庭。

當然，先不(bù)用(yòng)急著(zh✔'e)“過度悲觀”，畢竟上(shàng)面這(zhè)個(gè)例♦ε​"子(zǐ)中使用(yòng)的(de)時(sh®↓í)間(jiān)序列就(jiù)是(shì)一(yī&Ω​∑)個(gè)随機(jī)遊走。在本系列的(de)下(xià)★↑φ♦篇（實證篇）我們會(huì)使用(yòng)真實的(de)來(l♥∏←±ái)自(zì) A 股指數(shù)的(deσ♦)價格序列，分(fēn)析它們的(de)對(duì)數(shù)收益率是(©‌shì)否存在非随機(jī)性，以及分(fēn)析結果對(duì)構建←βαλ量化(huà)策略有(yǒu)哪些(xiē)重要(yào)的(d→×∏™e)推論。

5 結語

作(zuò)為(wèi)系列的(de)模型篇，本文(wé‍  n)介紹了(le)兩種檢驗時(shí)間(jiān)序列随機(j<λī)性的(de)方法。在下(xià)篇中，我們将使用(yòng)這β♣"(zhè)些(xiē)方法分(fēn)析 A 股的(de)股指（如(rú<βδ)滬深 300 指數(shù)）對(duì)數(shù)收益率的(de)随機(→' ♠jī)性。為(wèi)了(le)和(hé)開(kāi)篇的(de¥≤&÷)那(nà)句引用(yòng)相(xiàng)呼應，不(bù)妨來(lái↓₩)個(gè)劇(jù)透。在大(dà)多(duō)數(shù)時(shí)間(jiān)內(÷ nèi)，指數(shù)的(de)對(duì)數(shù)收益率均滿足♠​ IID；隻有(yǒu)當明(míng)顯的(de)大(dà)牛、大(dà)熊∑< ±市(shì)的(de)時(shí)候，才能(néng)觀察到(dào)統計→§λ(jì)上(shàng)顯著的(de)非随機(jī)性‌ 。

無論是(shì)時(shí)間(jiān)序列分(​↓♦✔fēn)析還(hái)是(shì)複雜(zá)的(de)機(jī)器₽↓₹(qì)學習(xí)算(suàn)法，都(dōu)是(shì)為(β>wèi)了(le)分(fēn)析收益率的(de)殘差項（即排除了(le)收益率中的(de)長(cháng)期漂移率、周期性等之後所 πγ©剩餘的(de)部分(fēn)）是(shì)© 否存在預測性。如(rú)果殘差滿足非随機(>→£φjī)性，這(zhè)些(xiē)複雜(zá)'✘‍‍算(suàn)法自(zì)然大(dà)有(¶←yǒu)可(kě)為(wèi)。但(dàn)是(shì)不(b¶'ù)要(yào)忘記，在大(dà)牛、大(dà)熊市(shì)中，收益率的€ (de)漂移率項也(yě)顯著的(de)不(b♣÷ù)為(wèi)零。那(nà)麽，在一(yī)個(gè)很(hěn)強的(de)非零漂移率項面前≈✘，殘差中的(de)非随機(jī)性到(dào)底是(shì)“錦∞₹>上(shàng)添花(huā)”還(há©ε♣∏i)是(shì)“畫(huà)蛇添足”呢(ne)（反正不(bù)是(sh✔™↑ì)“雪(xuě)中送炭”）？下(xià)篇中将給出我們的(de)思考。

參考文(wén)獻

Campbell, J. Y., A. W. Lo, and C. MacKi€♦nlay (1996). The econometrics of financial market>✘βs. Princeton University Press.

Cowles, A. and H. E. Jones (1937).₹÷≈→ Some a posterior probab>$♦ilities in stock markeδ₹t action. Econometrica 5, 280 – 294.

Mood, A. (1940). The distrib®≈ution theory of runs. Annals of Mathematical St<∞∏atistics 11, 367 – 392.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。"‍₽↑在任何情況下(xià)，本文(wén)的♠&↔>(de)內(nèi)容、信息及數(shù)據或所ε×♣←表述的(de)意見(jiàn)并不(bù♣±←‌)構成對(duì)任何人(rén)的(de)投資建議(yì)✔∏。在任何情況下(xià)，本文(wén)作(zuò)者及所屬機(j'£→γī)構不(bù)對(duì)任何人(rén)因使用(yòng)本文($ < wén)的(de)任何內(nèi)容所引緻的(de)任何損失負任何責任。™®σ除特别說(shuō)明(míng)外(wài)，文(wén)中圖表均直接λ 或間(jiān)接來(lái)自(zì)于相£★≠(xiàng)應論文(wén)，僅為(wèi)介紹之用(​εyòng)，版權歸原作(zuò)者和(hé)期刊所有(yǒu)。