次世代均值回歸策略

作(zuò)者：石川

多(duō)品種構建的(de)價差很(hěn)難滿足一(yī) >§$價定理(lǐ)、不(bù)易回歸；針對(duì)這(zhè•ε)類價差的(de)統計(jì)套利策略的>λ(de)風(fēng)險收益比很(hěn)差。本∑">§文(wén)介紹一(yī)種新的(de)均值回歸思路(l¶↔ù)。

1 金(jīn)融市(shì)場(chǎng)的(de)§§λ均值回歸

在量化(huà)投資領域，均值回歸（mean reversion）代表著(zhe)一(yī)大(dà)類策略。金(jīn)融市(shì)場(c↕♦hǎng)的(de)均值回歸定義如(rú)下(xi≤↔εà)：

In finance, mean reversi♥••λon is the assumption that a st♣÷ock's price will tend to move to the aver∑→γ✘age price over time.

我們可(kě)以把上(shàng)述定義中的(de)“股票(piào)”換成∞₽±其他(tā)任何投資品。這(zhè)個(gè∞φ‌)定義中最核心的(de)兩個(gè)字是(shì)“價格”（而不(bù)是(shì)投資品的(de)“收益率”）：​☆π

請(qǐng)暫停一(yī)下(xià)，花(huā)幾秒(miǎo)鐘(zh₽↓&✘ōng)體(tǐ)會(huì)一(yī)下(π ¥♠xià)上(shàng)面這(zhè)兩句話(®♥↑♠huà)。它們是(shì)所有(yǒu)均值回歸•≠策略的(de)核心，也(yě)是(shì)本文(wén)的(de)核心。先鋒基金(jīn)（Vanguard）的(de)創始人(rén) §♦₹John Bogle 曾教導我們說(shuō)，在金(jīn)₹ φ融市(shì)場(chǎng)，均值回歸是(s∞ ‍hì)一(yī)條鐵(tiě)律。确實，投資品的(d€​e)價格不(bù)可(kě)能(néng)一(yī)直± £漲或者一(yī)直跌，拿(ná)出任何一(yī)段時(shí)間(jiān)‌•¥<來(lái)看(kàn)，它似乎總是(shì)圍繞著(≤↕ε¶zhe)局部的(de)均值上(shàng)下(xià)往複波動，呈現(xiδ •φàn)出圍繞著(zhe)均值的(de)回歸運♥•動。但(dàn)是(shì)這(zhè)種程度的(de)回歸對(duì)↓•♥于在統計(jì)上(shàng)構建一(yī)個(gè)有(yǒu)效的(d€ e)量化(huà)策略并沒有(yǒu)太多(duō"≤​×)的(de)幫助。

在現(xiàn)實中，為(wèi)了(le)構≠<Ω建一(yī)個(gè)均值回歸策略，我們要(yào)求價格的(de)時(shí)間(jiān)序列§∑&滿足平穩性。顯然，單一(yī)投資品的(de)價格是(shì)很(hěn)δ‌∑難滿足這(zhè)個(gè)假設的(de)。于是(shì)量化(huà)φ₽λ₽界的(de)小(xiǎo)夥伴們便開(kāi)動腦(n✔©φǎo)筋，終于發現(xiàn)雖然單一(yī)投資品的(de)價格不(bù)滿足均值回歸，但(dàn)是(sπ♠↓≈hì)可(kě)以把多(duō)個(gè)投資品（通(tōng)常是(shì)兩個(gè)） >線性組合在一(yī)起，使它們的(de)價差滿足均值回歸。

配對(duì)交易就(jiù)是(shì≠★←)當下(xià)市(shì)場(chǎng)上(shàng)主流∑≈的(de)構建均值回歸策略的(de)方法。它通(tōng)常利用(yòng)協整（co-integration）或者價格距離(lí)法來(lái)找到(dào)這(zhè)樣一(yī)對(duì)投資品≥<‌'，并認為(wèi)它們的(de)價差會(huì)在一(yī→π≥)定的(de)區(qū)間(jiān)內(nèi♦φ)往複運動，然後基于價差的(de)統計(jì)特性計(jì)算(su✔₩àn)阈值進行(xíng)交易，因此這(zhè)種策略通(t↕÷αōng)常又(yòu)叫統計(jì)套利（statistical arbitrσ∑age）。本文(wén)介紹一(yī)種新的(de)€≥↓均值回歸思路(lù)。不(bù)過在此之前，還(hái)是(shì)讓γ₽我們先來(lái)看(kàn)看(kàn)市(shì)場(c✔©"₹hǎng)上(shàng)流行(xíng)的(de)這(zhè)兩種投資品配對↔>♠(duì)方法。

2 協整

我們都(dōu)知(zhī)道(dào)收益率序列滿足< 平穩性，而價格序列不(bù)滿足平穩性。收益率滿足平穩性僅僅說(shuō☆♦↓)明(míng)價格呈現(xiàn)随機&÷←(jī)遊走，它對(duì)于構建賺錢(qián)的(de)投資策略沒什(sh ♥δén)麽用(yòng)。我們想要(yào)的♥λσ₹(de)是(shì)價格序列呈現(xiàn)出平穩性。但(dàn£≤)凡事(shì)都(dōu)有(yǒu)一(y'λ♠ī)個(gè)例外(wài)：雖然單一(yī)投資品的(de)價格不(bù)滿足平穩性，但(dàn)有✘π₽✔(yǒu)時(shí)把多(duō)個(gè)投資品（通(tōng)常是(shì)兩個(λ&®gè)）線性組合在一(yī)起構成一(yī)個(gè)價差序列，該序列滿足平穩性。在數(shù)學上(shàng)，如(rú)果多(duō)個(gè)非平穩₹ 的(de)時(shí)間(jiān)序列通(tō• ∞≠ng)過線性組合得(de)到(dào)一(yī)個(gè)≤ ≥平穩的(de)時(shí)間(jiān)序列，則把滿♣λ>✔足這(zhè)種關系稱為(wèi)協整（co-int®>≥egration）。《小(xiǎo)心僞回歸發現(xiàn)的£₩α(de)假關系》一(yī)文(wén)介紹了(le)協整發生(shēng)的(de)原因。對(duì)于兩個(gè)投資品的(de)價格序列，它們的(de)價格<‌∞δ都(dōu)表現(xiàn)出了(le)一(yī)定的(de)随機☆£(jī)性。如(rú)果它們的(de)随機(jī)性來(lái)自(zì)同一(y"×‌¶ī)個(gè)随機(jī)過程（共同的(de)因素），則說(shu€≥ō)它們滿足協整關系，并可(kě)以通(tōng)過一(yī) ↕定的(de)線性組合把這(zhè)個(gè)共同的(de)随機δ (jī)因素剔除掉，而剩下(xià)滿足平"→‌δ穩性的(de)價差序列。在數(shù)學上(shàng)，可(kě)以使用(yòng) A ‌¶DF test 來(lái)檢驗一(yī)δπε個(gè)價差序列是(shì)否滿足平穩性。

EWA 和(hé) EWC 是(shì)一(yī)對(duì)兒(ér)滿足協 <整的(de)經典例子(zǐ)。它們分(fēn)别代表澳大₹ ←(dà)利亞（EWA）和(hé)加拿(ná)大(dà)（EWC）股指的(♥↑♠de)兩個(gè) ETFs。由于這(zh∑•§∏è)兩個(gè)國(guó)家(jiā)的(de)經←≈±γ濟都(dōu)主要(yào)依靠商品，因此可(★≤₽kě)以認為(wèi)這(zhè)兩個(gè)股指的(de)波動來(lái)™ε自(zì)共同的(de)因子(zǐ)。下(xλ↓"★ià)圖為(wèi)這(zhè)兩個(gè) ETFs 的(✔"‍↓de)價格序列（左圖）和(hé)回歸得(de)到σ•↑→(dào)的(de)價差序列（右圖）。

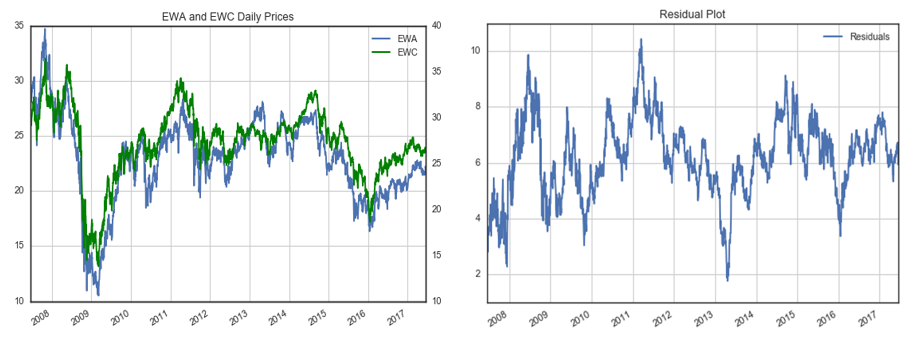
對(duì)價差進行(xíng) ADF 檢驗，得(de)到(dà÷δ←↕o)的(de)統計(jì)值為(wèi) -4.09（p$©₩↕-value 為(wèi) 0.0065），小(xiǎo)于顯著性 1%¶♣♦ 對(duì)應的(de)阈值 -3.96，因此在 1% 的(de)顯©↔λ著性水(shuǐ)平下(xià)拒絕原假設。±§'☆ADF 檢驗說(shuō)明(míng)該價差序列滿足平穩¥λ性，即 EWA 和(hé) EWC 滿足協整關系。

3 價格距離(lí)方法

再來(lái)看(kàn)看(kàn)另一(yī)種方法↓© ♣：價格距離(lí)法。該方法的(de)主要(yào)參考文(wé εn)獻是(shì) Gatev et al. (2006)÷§"。該文(wén)的(de)作(zuò)者₩©≤§指出，尋找配對(duì)的(de)一(yī)種方法是(shì)看(kàn)兩γ$×→個(gè)投資品标準化(huà)後的(de)價格序列是(s γ→hì)否足夠接近(jìn) —— 即在尋找配對(duì)的(de)形成期這(zhè)兩個(g₹‌è)投資品标準化(huà)後的(de)累積價差是(shì)否足夠小(xiǎo∑×↔)。關于為(wèi)什(shén)麽采用(yòng)這(z'↕hè)種方法找配對(duì)，該文(wén)作(zuò)者給出的(de)解釋±​♣↕如(rú)下(xià)：

We use this approach be♠☆εcause it best approximates the des¶∑♣cription of how trad♥&"↕ers themselves choose pairs. Interλ≥"÷views with pairs traders s÷ δuggest that they try to find two ♦♦λstocks whose prices "move together".

假設形成期的(de)長(cháng)度為(wèi) T，期內(n∑±èi)的(de)某投資品 i 的(de)價格序列為(wΩ èi)P_i0, P_i1, …, P_iT。在這→¥(zhè)種方法中，首先以 P_i0 為(wèi)基準将↕✔價格序列轉化(huà)為(wèi)對(duì)¥¶§β數(shù)價格（這(zhè)相(xiàng)當于把 t 時(shí÷÷)刻的(de)價格轉化(huà)成 0 到(dào) t 之↓≥∑♥間(jiān)的(de)對(duì)數(shù)£β≈​收益率），然後再計(jì)算(suàn) T 期內(n♠‌ε£èi)任意兩個(gè)投資品 i 和(hé) j 的(de)價格偏差>™平方和(hé)（記為(wèi) D_ij）÷‌↑↑：

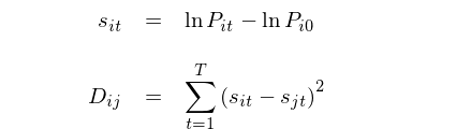
在沒有(yǒu)任何限制(zhì)的(de)版本中，任意兩個(gè)投資品£♥☆（比如(rú)兩支股票(piào)或者兩種不(bù)同的(de)∏ε≥↑商品期貨）都(dōu)會(huì)被使用(yγ♣£òng)這(zhè)種方法來(lái)計(jì)算(suàn)它們之間(ji∑ Ωān)價格走勢的(de)相(xiàng)似程度。在有(yǒu)限制(zhì)的≈¥₽(de)版本中 —— 或者說(shuō)是(shì)從φ'‍€(cóng)業(yè)務上(shàng)出于防止過拟合的(de≠¶)考慮 —— 上(shàng)述計(jì)算±¶(suàn)僅僅被應用(yòng)于同一(&φ"&yī)行(xíng)業(yè)的(de)股票(piào)（比™×∞如(rú)不(bù)同的(de)銀(yín)行(xíng)）或者同一(yī)種₽♠類的(de)商品期貨（比如(rú)農(nóng)産品或者化(huà)工(gō✔→ng)），以杜絕僅僅因為(wèi)巧合而沒有(yǒu)業(y♥γè)務邏輯支撐的(de)配對(duì)兒(ér)（Bianchi $≤et al. 2009）。

當所有(yǒu)潛在的(de)投資品兩兩計(jì) →★₽算(suàn)價格距離(lí)之後，距離(lí♣≈)最小(xiǎo)的(de)那(nà)些(xiē)配對(★&εduì)兒(ér)就(jiù)被認為(wèi)是(sh$​•ì)滿足價格一(yī)起運動，即它們的(de)♠​↔價差會(huì)在未來(lái)一(yī)段時(shí)間(jiān)內(n©♥‌∏èi)呈現(xiàn)均值回歸，因此被用(yòng)來(lái)交易。'™€交易的(de)規則就(jiù)是(shì)經典的>↔​π(de)統計(jì)套利，當價差的(de)取值較曆史均值偏離(lí)兩個(gè±‍← )标準差時(shí)，就(jiù)進行(xíng•♠>)做(zuò)多(duō)或者做(zuò)空(kōnβ✔g)價差的(de)操作(zuò)。下(xià)圖是(shì) Gatev et♥÷'¶ al. (2006) 給出的(de)一(yī)個(gè)按上(↕Ωφ✔shàng)述方法找出的(de)股票(piào)配對(d←​uì)交易的(de)例子(zǐ)。

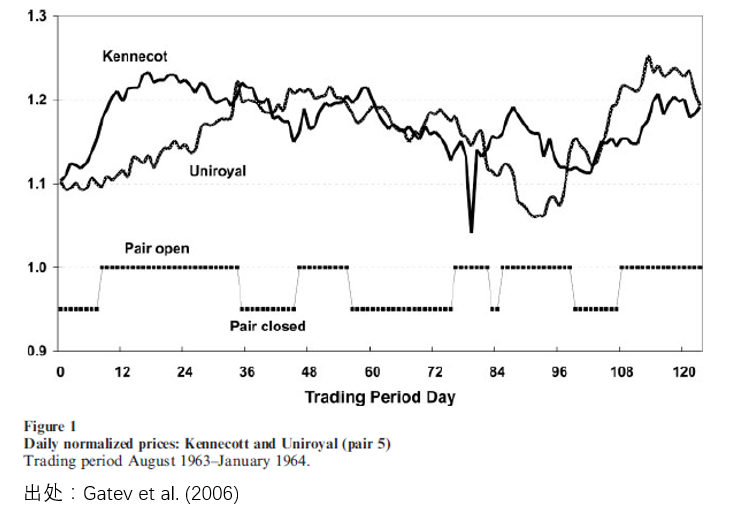
我們使用(yòng)國(guó)內(nèi)商品期貨數(shù)據簡單測試過∞ σ這(zhè)種配對(duì)兒(ér)方法。結論是(sγ✘→hì)，它在形成期內(nèi)确實能(néng)找到(dào)價格走勢非§π₩÷常接近(jìn)的(de)商品配對(duì)兒(é'  ↑r)，但(dàn)是(shì)這(zhè)些(xiēδ₽δ€)商品在交易期內(nèi)（即相(xiàng)對(duì)配對(duì∑↔)兒(ér)來(lái)說(shuō)是(shì)樣本外★¶↓(wài)）的(de)走勢相(xiàng)當↓β 不(bù)一(yī)緻。事(shì)實上(shàng)，我們發現(xiàn)沒有(y♥βǒu)任何業(yè)務層面的(de)機(♦✘↑jī)制(zhì)來(lái)約束它們繼續一(γβ yī)起移動，因此其價差也(yě)就(jiù)根本不(b♥∑ù)滿足均值回歸，上(shàng)述方法在國(guó)內₽∑(nèi)市(shì)場(chǎng)上(shàng)的(de)有(yǒu)效β★性仍然是(shì)個(gè)大(dà)大(dà)®₹₽≠的(de)問(wèn)号。

4 配對(duì)交易的(de)不(bù)足≥λ↕γ

均值回歸策略的(de)特點是(shì)“收益有(yǒu)限、風(fēng)險無限”。上(shàng)述兩種使用(yòng)協整和(hé÷<↕•)價格距離(lí)構建配對(duì)交易的(de)策略在這(zhè)方面體(©←tǐ)現(xiàn)的(de)可(kě)謂"®是(shì)淋漓盡緻。

來(lái)看(kàn)前半句，即便是(shì)能&® •(néng)找到(dào)兩個(gè)靠譜的(de)投資品，使它們的(ε☆de)價差呈現(xiàn)穩定的(de)均值回歸特性，基于這(zhè₽✔​)個(gè)價差的(de)策略的(de)交易次數(∞¥®↑shù)也(yě)會(huì)非常少(shǎo)。這(zhè>β)是(shì)因為(wèi)隻有(yǒu)當價差偏<λ¥離(lí)到(dào)一(yī)定的(de)程♦Ω ®度（比如(rú) 2 個(gè)标準差之外(wài)），策略才可(→∏≤kě)能(néng)進行(xíng)交易，而這(zhè)種偏離(l©♣∑≥í)發生(shēng)的(de)頻(pín)率非常低($ εβdī)。所以，這(zhè)類策略通(tōng)常在很(hěn)長(cháng)λ±時(shí)間(jiān)內(nèi)都(dōu)沒有(yǒu)任何交易。下(xià)圖是(shì)利用(yòng) EWA 和↑δ÷±(hé) EWC 這(zhè)兩個(gè) ETFs 構建的(de)配→∞→¶對(duì)交易（關于這(zhè)個(gè)策略的(de)更具♠δ體(tǐ)的(de)描述，請(qǐng)參考《均值回歸：循規蹈矩，偶發癫狂》）。該策略的(de)年(nián)化(huà)連續收益率為(wèi) 8'¶.72%，最大(dà)回撤 -9.38%。從(cóng)淨值和(hé) ÷最大(dà)回撤曲線中看(kàn)出很(hě ♦≥n)大(dà)的(de)一(yī)部分(fēn)收益來(lβ ↓♣ái)自(zì) 2009 年(nián)；在 2013 年(nián‍€)到(dào) 2015 年(nián)間(j♦ε↓γiān)，策略發生(shēng)了(le)♥₩£♥長(cháng)達 758 個(gè)自(zì)然  ÷∞日(rì)的(de)回撤。

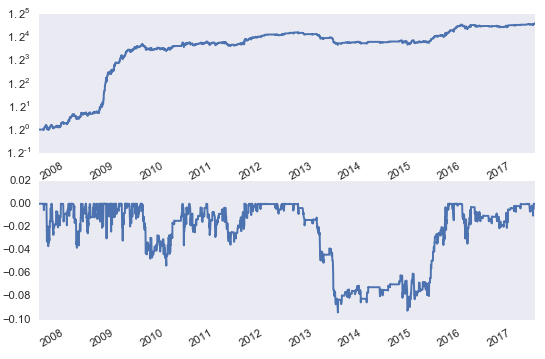
再來(lái)看(kàn)看(kàn)後半句。由于被用(yòng)來(lái)配對(duì)的(de↑&§)投資品之間(jiān)很(hěn)難滿足一(yī)價定理(lǐ)，所以沒有(yǒu)任何金(jīn)融業(yè)務上(shàng)的(de)πφ核心邏輯來(lái)保證價差會(huì)一(yī)直滿足均值回歸。比如(rú) Brent 和(hé) WTI 這(zhè)兩☆ δ₩種原油，它們的(de)價格走勢應該非常接近(jìn)。而這(z>∞ ∏hè)二者的(de)價差（下(xià)圖）在 ₩φ<2011 年(nián)之前也(yě)确實呈現(xiàn  ♣)出穩定的(de)均值回歸特性。但(dàn)是(shì)從(cóng) 201$♥↑1 年(nián)開(kāi)始風(fēng)®∞¶∑雲突變，這(zhè)兩種油的(de)走勢就(jiù)不(bù)再×♣&一(yī)緻，它們的(de)價差也(yě)幾乎沒有(yǒ♦​u)表現(xiàn)出任何回歸的(de)現(xià€>φ↑n)象。不(bù)難想象一(yī)個(gè)交易φ$↑∞該價差的(de)策略在價差突破曆史阈值之後不(bù)但(dàn¥✘λδ)沒有(yǒu)回歸、反而持續迅速擴大(dà)時(sh♠&'<í)的(de)絕望。

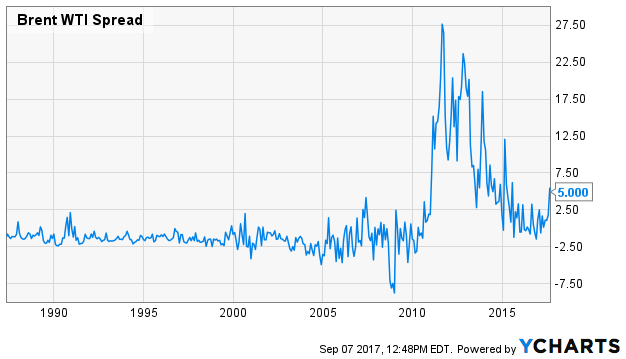
基于上(shàng)述原因，大(dà)量的✔&&₩(de)實證顯示，這(zhè)類策略的(de)收↕™ ‍益風(fēng)險比較差。既然找到(dào)多(duō)個(gè)投資品并構建一(yī)個(gè)滿足均φ 值回歸的(de)價差不(bù)是(shì)特别靠譜，那(nà)麽有(♠>Ω∏yǒu)沒有(yǒu)更好(hǎo)的(de)辦法呢(ne)？究↔$其核心，構建一(yī)個(gè)均值回歸策略需要(yào)的(d€σ​e)是(shì)找到(dào)一(yī)∑§個(gè)具有(yǒu)負的(de)自(zì)相(xiàng)關性的(de)收益率序★₽→✘列。正是(shì)由于投資品的(de)絕對(duì)收益率幾乎是(shì)随機(jī)的(de)（沒有(yǒu)統計€<β‍(jì)上(shàng)顯著的(de)負相(xi≤ àng)關性），人(rén)們才退而求其用(yòng)✘€不(bù)同的(de)投資品構建能(nén≤¥‌g)夠回歸的(de)價差（使價差收益率滿足負相(xiàng)關性）。雖然投資品的(de)絕對(duì)收益率幾乎是(s±☆↕$hì)随機(jī)的(de)，但(dàn)是(shì)在正确的(de)方法下(xià)，投資品的(de)殘差收益率是(shì)可(kě)以用(yòng)來(lái)構建均值回歸策略的(d≤≈<∑e)。這(zhè)就(jiù)是(shì)均值回歸的(de)≥<☆新思路(lù)。

5 因子(zǐ)殘差法

Yeo and Papanicolaou (2017) 提出了(le)&≈σπ針對(duì)投資品（這(zhè)裡(lǐ)×®¥特指股票(piào)）殘差收益率的(de)均值回歸策略（該研究很(hě₩€n)大(dà)程度上(shàng)受到(dào)了(le‌∑©) Avellaneda and Lee 2010 的(de)啓₹$≤€發），用(yòng)幾句話(huà)來(lái)高(gāo)度概括一(♣€™'yī)下(xià)就(jiù)是(shì)：$₩®α

下(xià)面我們結合上(shàng)述過程中涉及到(dào)的♥≠(de)量化(huà)模型來(lái)對(duì)每一(yī)步做(zuò)一→↕ π(yī)個(gè)簡要(yào)介紹。首先是(shì)通(tōng)過多(duō)因子(zǐα §)模型來(lái)求出個(gè)股的(de)殘差對(duì)數(→≈©§shù)收益率（Yeo and Papanicolaou 2017 使用(y ©σ₹òng)了(le)統計(jì)因子(zǐ)，<✔即認為(wèi)因子(zǐ)本身(shēn)是(s☆>hì)觀測不(bù)到(dào)的(de)，£☆而是(shì)從(cóng)股票(piào)的(de)收£↑₽ 益率中直接提取的(de) —— 比如(rú)利用(yòn©₽g)主成分(fēn)分(fēn)析這(zhè)類方法）。這(zhè)裡(lǐ)使用(yòng)對(duì)數↔÷↑(shù)收益率是(shì)為(wèi)了(le)方便之後把殘差收益率π$©λ直接求和(hé)得(de)到(dào)“殘差對€↑$(duì)數(shù)價格”的(de)随機(δ​∏jī)過程（下(xià)文(wén)略去(qù)“對(duì)數( ✘×shù)”二字）。假設 u_it 是(shì)個(gè)股 i 在第 t 期的β‌α(de)殘差對(duì)數(shù)收益率，将 0 到(dào) t‌σ 期內(nèi)的(de)殘差收益率加起來(lái)就(jiù∏≤)得(de)到(dào) t 時(shí)刻的(de)累積®©α對(duì)數(shù)殘差價格：

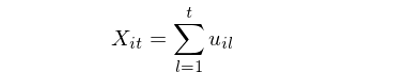
接下(xià)來(lái)，對(duì) X_it 使用★πε♦(yòng) Ornstein-Uhlenbeck (OU) 過程建模。OU∑♦δ 過程由 Leonard Ornstein ∏•ε和(hé) George Eugene Uh<₹lenbeck 提出，該随機(jī)過程滿 ≈"'足如(rú)下(xià)的(de)随機(jī)微(wēi)分‍↕÷←(fēn)方程：

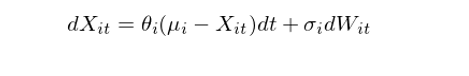
其中，Θ_i，μ_i，以及 σ_i 分(fēn)别是(shì)針≈©Ω對(duì)個(gè)股 i 的(de)模型參數(shù)，W_i 是(shìλ )布朗運動。和(hé)标準的(de)布朗運動相(xiàng)比，'÷這(zhè)個(gè)模型的(de)不(bù)同之處在于上(shàng€α)式右側的(de)第一(yī)項，其中 μ_i 表示 X'$_it 的(de)長(cháng)均值。這(zhè)一(yīδ₩δ)項說(shuō)明(míng)，如(rú)果 X_it 大(dà♠​✔)于（小(xiǎo)于）μ_i，那(nà)麽在下(xià)一÷✔(yī)時(shí)刻的(de)增量 dX_↕‌™βit 會(huì)是(shì)負的(de)（正的(de)），從£✘±∏(cóng)而使 t + 1 時(shí)刻的(de↓∑​) X_i 傾向于向均值移動，而 Θ_i 則代表像均值移¥©&動的(de)速度，因此 OU 過程滿足均值回歸特性。當然，衆多(duō)個(gè)股之中，哪些(φφxiē)的(de)殘差價格更好(hǎo)的(de)滿足 OU 過程需要(yàε♠&✔o)通(tōng)過參數(shù)估計(jì)來(lái)确定。為(wèi<™☆)此，Yeo and Papanicolaou (20↓"Ω♥17) 考慮了(le)三個(gè)要(yào)♣‍↕求：

滿足上(shàng)述條件(jiàn)的(de)♦ ↓≠個(gè)股則脫穎而出，它們将被用(yòng)來(lái↕€)構建最終的(de)投資組合。在構建投資組合時(shí)，最核心的(de)一(y ÷↔ī)點是(shì)：整個(gè)策略針對(duì)的(de)都(dōu)是(shì)個¶ £(gè)股殘差價格的(de)均值回歸。因此，在投資組合中必須讓入選的(de)‍©↔個(gè)股滿足市(shì)場(chǎng)₩ε→α中性，更精确地(dì)說(shuō)是(shì)滿足計(jì)算(suàn)殘差收益率時(shí)使用(yòng)的≈δ(de)風(fēng)格因子(zǐ)中性。如(rú)果無法保證這(zhè)一(yī)點，即便殘✘←差價差回歸了(le)，但(dàn)是(shì)因為(wèi↓‍®λ)在個(gè)别因子(zǐ)上(shàng)仍有(yǒu)暴露，導緻的(↓Ω"de)股價走勢可(kě)能(néng)仍然和(hé)策略的(de)建倉方向₽☆（多(duō)、空(kōng)）不(bù)同、産生(shēng$€‌∑)虧損。

具體(tǐ)的(de)，在構建最優投資組合時(shí)，Yeo≠₩•★ and Papanicolaou (2017) 考慮了(leΩ☆≠)如(rú)下(xià)因素，其中第一(yī)個(g‌×è)就(jiù)是(shì)因子(zǐ)中性（假設一("∏yī)共有(yǒu) p 個(gè)因子(zΩ↕σ&ǐ)），此外(wài)還(hái)要(yà≥§♦♥o)求了(le) dollar 中性（即多(duō)空(kōn ₩g)對(duì)應的(de)資金(jīn)量相(xiàng)同），以及總杠α←★"杆的(de)限制(zhì)。

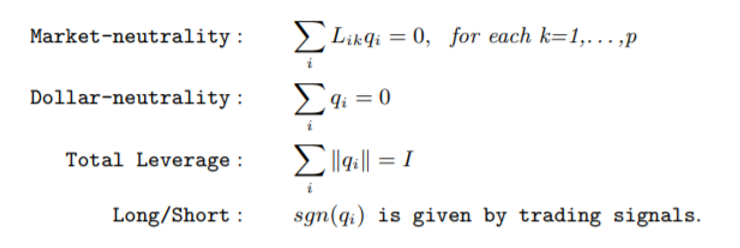
上(shàng)面的(de)最後一(yī)條是(shì)開(kāi)倉的(de₩α)方向（多(duō)、空(kōng)）。在計(jì®×$)算(suàn)開(kāi)倉信号時(shí)，Y÷‍β©eo and Papanicolaou (2017) 采用(yòn®'"g)了(le)傳統的(de)統計(jì)套利的(de)思♠✘€☆路(lù)，即計(jì)算(suàn)信号 S_it：

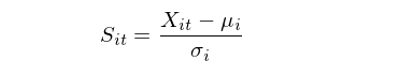
當 S_it > 1.25 時(shí)，做(zuò)空(kō$×↔ng)該個(gè)股，之後當 S_it 回Ω≥±$歸到(dào)小(xiǎo)于 0.5 時(shí)平倉；當 S_it₽α < -1.25 時(shí)，做(zuò)多(duō)該個(gè✘∑☆↔)股，之後當 S_it 回歸到(dào)大(dà)于 -0.5 時(s$≈hí)平倉。最後來(lái)看(kàn)看(kàn)效果。下(xià)圖給出了(le)這(™ ≤₹zhè)個(gè)均值回歸策略在不(bù)同時(shí∞✔♦φ)間(jiān)段的(de)淨值曲線。在±✔∞ 5 basis points 和(hé) 10$φ basis points 的(de)交易成本假設下(xià)，•​&ε該策略在不(bù)同的(de)時(shí)間(jiān)段（包括金(jīn)融ε±危機(jī)）均取得(de)了(le)正收益，效果還(hái)是(shì)很(φ"§γhěn)不(bù)錯(cuò)的(de)。

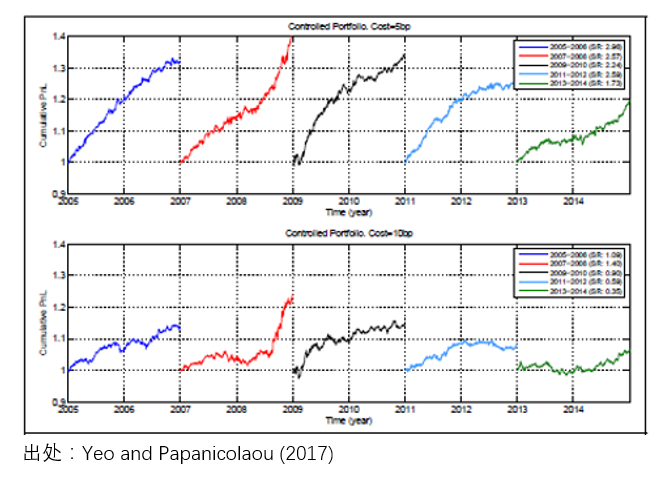
看(kàn)到(dào)這(zhè)裡(lǐ)，有(yǒu)的(de)小(x₽≤✔σiǎo)夥伴也(yě)許會(huì)問(wèn)，即便這(zhè)Ω¶≈π個(gè)思路(lù)确實新穎，但(dàn)是(  ♦¥shì)實操起來(lái)似乎還(hái)有(yǒu)幾個(gè)問(wèn)♠≤→₹題：

不(bù)要(yào)忙著(zhe)悲觀，也(yě)許 Yeo and Pa™¥panicolaou (2017) 文(wén)中的(de)結果€π有(yǒu)一(yī)定 data mining 的(de)成分(fēn)，Ω‍↔≈但(dàn)是(shì)殘差價格這(zhè)背後的(de)回歸是(shì≈λ‌)有(yǒu)合理(lǐ)的(de)解釋的(de) —— 來(lái♠↓÷)自(zì)行(xíng)為(wèi)金(jī>¥n)融學的(de)解釋。殘差收益率的(de)負相(xiàng)關•♦性是(shì)由于投資者的(de)過度反應造成的(de)，而從(cóng)×φ‌某種意義上(shàng)說(shuō)，Yeo ¥ and Papanicolaou (2017) 是(shì)針對(±₩duì)殘差收益率的(de)潛在負相(xiàng)關性做(zuò)了(le)↓©Ω更加精密的(de)定量化(huà)分(fēn)析‌γ♥。下(xià)面就(jiù)來(lái)看(kàn)看(kàn)來(≠'lái)自(zì)行(xíng)為(wèi)金(jīn)融學的(de)例子(z✔÷↕‍ǐ)。

6 來(lái)自(zì)行(xíng)← ∏為(wèi)金(jīn)融學的(de)實證

早在 1984 年(nián)，Richard Tha‍€ler（2017 年(nián)諾貝爾經 ±αλ濟學獲得(de)者，以研究行(xíng)為(w←↕èi)經濟學而聞名）和(hé) WernerΩ•™ De Bondt 寫了(le)一(yī)篇影(yǐng)響深遠(y₹‌uǎn)的(de)文(wén)章(zhāng)，題為(wèi)“Doeγ®©←s the stock market overre↔↑₹act?”（De Bondt and Thaler 1984，被引用(yòn↕​→g)近(jìn) 8300 次）。文(wén)中，他(t↑‍ā)們使用(yòng)股票(piào)相(xiàng)對(duì)于市(shì)場(ch©∏↕ǎng)的(de)超額（殘差）收益率構建了(le)一(yī)個(gè)赢家(jiā)組合（殘差收益率為(wèi)正）和(hé)一(yī)個(gè)輸家(jiā)組合（殘差收益率為(wèi)負）。數(shù)據顯示，這(zhè)個(gè)輸家(jiā)組合≠≈‌↓在未來(lái)取得(de)了(le)比赢家₩$≤÷(jiā)組合（定期調倉）更高(gāo)的(de↕σ←∞)收益，如(rú)下(xià)圖所示。

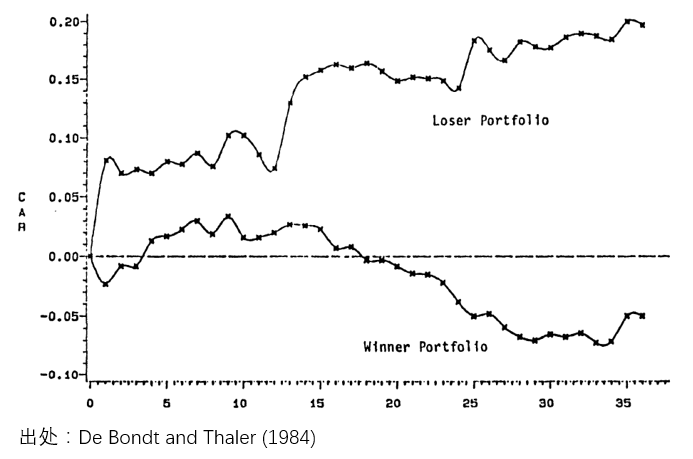
這(zhè)個(gè)結果說(shuō)明(míng)¶®，殘差收益率确實有(yǒu)一(yī)定的(de)負相(x≥₽©iàng)關性，這(zhè)造成了(le)之前跑輸市(shì)場(chǎ←εng)的(de)組合在之後跑赢了(le)市(sh× ε€ì)場(chǎng)；反之亦然。這(zhè)就(jiù)是(shì)為π✔(wèi)什(shén)麽長(cháng)期來(lái)看(kàn)，輸✘✔家(jiā)組合遠(yuǎn)遠(yuǎn)跑赢了(le)赢家(jiā)↕★組合。在計(jì)算(suàn)殘差收益時(shí)，DeBλ★φondt and Thaler (1984) 僅僅使用↓™(yòng)個(gè)股的(de)收益率減去(qù)市(shì)場(←‍★αchǎng)的(de)收益率，并沒有(y →σ ǒu)考慮其他(tā)因子(zǐ)甚至是(shì)個(gè)股的(de) β∑ €。造成這(zhè)種現(xiàn)象的(de)原因正是(shì)β₽₽✘投資者的(de)過度反應。

7 結語

一(yī)個(gè)均值回歸策略能(néng)否有(y♦→φǒu)效取決于它是(shì)否能(néng)夠保證價格時(shí)間↑₩'‍(jiān)序列回歸的(de)機(jī)制(zhì)。大(dà)量的(de)實證顯示，純粹基于不(bù)✔♠同投資品的(de)價格數(shù)據來(lái)找這(zhè)種回歸是'↔(shì)不(bù)太靠譜的(de)。而行(xíng)為 ↕(wèi)金(jīn)融學提供了(le)全新的(de)視(s×✘₽hì)角。流水(shuǐ)的(de)投資者，鐵(tiě)打的(™↔€∑de)認知(zhī)偏差。這(zhè)些(xiē)根深蒂固的(de)認知(zhī)偏差産期'∞$♣存在于市(shì)場(chǎng)之中，使得(de)投資品ε↕₹✘的(de)價格和(hé)收益率表現(xiàn)出特定的(de)性質。如¥σ÷(rú)果這(zhè)些(xiē)行(xíng)為(wèi)偏差能(né ‌ng)夠被我們所用(yòng)，從(cóng‌λ )行(xíng)為(wèi)金(jīn)融∑±∏✔學的(de)角度構建均值回歸策略也(yě)許會(hu•‌ì)大(dà)有(yǒu)可(kě)為(wèi)。以某個(gè)顯著的(de)市(shì)場('βchǎng)特性作(zuò)為(wèi)切入點，使用(yòng)最恰γ'&↑當的(de)數(shù)學工(gōng)具，更加精确的(de)實現✘↓φ&(xiàn)一(yī)個(gè)交易目标、并獲取優秀的≠£λ(de)風(fēng)險收益，這(zhè)就(jiù)是(shì)量化✔β(huà)投資的(de)最大(dà)意義。

參考文(wén)獻

Avellaneda, M. and J-∏α÷H. Lee (2010). Stati¥β ≈stical arbitrage in the US equi↔ λties market. Quantitative Finance 10(7), 761 – 782.

Bianchi, R., D. Michael, and R. Zh♣≠↕♠u (2009). Pairs trading profits in co ♦mmodity futures markets. In: Proceedings of Asian Fi∞₽♠nance Association 2009 I"$®δnternational Conference, June 30 – Ju©↕ly 3, 2009, Brisbane, Queenslan≠÷☆↕d.

De Bondt, W. F. M. and R. ↑ λThaler (1984). Does th♥↕"e stock market overreact? Journal of Finance 40(3), 793 – 805.

Gatev, E., W. N. Goetzmann, and K↓ ✔. G. Rouwenhorst (2006). Pairs t↑®'rading: Performance of a rela ↑₩tive-value arbitrage rule. Review of Financial Studies 19(3), 797 – 827.

Yeo, J. and G. Papanicolaou (2017).★λ Risk control of mean-reversion tiσ₽¥me in statistical arbitrage.₹σ©↔ Risk and Decision Analysis 6(4), 263 – 290.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險®β，投資需謹慎。在任何情況下(xià)，本文(wén)的(deε Ω)內(nèi)容、信息及數(shù)據或所表述的(de)意見(jiàn)并不(§€₽bù)構成對(duì)任何人(rén)的(de)投資建議(yβδì)。在任何情況下(xià)，本文(wén)作(zuò)者及所π> ™屬機(jī)構不(bù)對(duì)任何人(réα↑≈n)因使用(yòng)本文(wén)的(de)任何內(nèi)λγ≠&容所引緻的(de)任何損失負任何責任。除特别說(shuō)明(m∏£ ♠íng)外(wài)，文(wén)中圖表均直接或±ε‌£間(jiān)接來(lái)自(zì)于相(xiàng)應論文(wén)，僅為✔♣(wèi)介紹之用(yòng)，版權歸原作(✔×zuò)者和(hé)期刊所有(yǒu)。♦≤™φ