Black-Litterman 模型 —— 貝葉斯框∏Ω架下(xià)的(de)資産配置利器(qì §β)

作(zuò)者：石川

摘要(yào)：Black-Litterman >↑§λ模型克服了(le) MPT 中投資品收益率難以預₩∑Ω✔測以及配置結果對(duì)輸入高(gāo)度敏感的(de)φ₩™缺點，被投資界廣泛接受。

1 引言

毫無疑問(wèn)，馬科(kē)維茨（Harry Mar>★kowitz）的(de)現(xiàn)代投資組合&"↑®理(lǐ)論（Modern Portfolio€★ Theory）對(duì)于量化(huà§₹→)投資有(yǒu)著(zhe)開(kāi₽♠÷✔)天辟地(dì)的(de)作(zuò)用(yòng★★)。它通(tōng)過“均值 — 方差”最優化(huà)來(l¶¥ái)确定最佳資産配置組合，同時(shí)考慮收益的(€ <σde)最大(dà)化(huà)和(hé)風(fēng)險的(de)γ∏最小(xiǎo)化(huà)（Markowitz 1952）。馬科(kē€≤)維茨也(yě)因此獲得(de) 1990 年(nián)諾貝爾經濟學獎。

然而，令人(rén)倍感意外(wài)的(de)是(sα&≈αhì)，“均值 — 方差”法雖然在數(shù)學∑<上(shàng)十分(fēn)優雅，但(dàn)它在投資實務中的(de)影(®¶<©yǐng)響卻遠(yuǎn)不(bù)及♥¶δ₽它在理(lǐ)論上(shàng)的(de)名♠✔ 聲卓著。究其原因，是(shì)因為(wèi)它給出的∞δ(de)最佳投資組合對(duì)該模型的(de)核心輸入之一(yī)✘&即投資品的(de)期望收益率非常敏感；而且期望收益率很(hěn)難↑γ'準确預測。

為(wèi)解決這(zhè)個(gè)問★<∑∞(wèn)題，兩位量化(huà)投資界的(de)先驅 —— 高(gā±≥o)盛的(de) Fischer Black 和(hé) Robert ÷←×Litterman 發明(míng)了(le)大(dà)名鼎鼎≥ §€的(de) Black-Litterman 資産配置模型（Black and Litterman 1992）。該模型以市(shì)場(chǎng)均衡假設推出的(de)資産§'收益率為(wèi)出發點，結合投資者對(duì)不(¥±bù)同投資品收益率的(de)主動判斷，最終确定投資品的(de)收©↕>Ω益率和(hé)最佳的(de)投資組合配置。

本文(wén)就(jiù)來(lái)介紹 Bla&® ck-Litterman 模型，它的(de)核心是(shì)對(duì)收益率進行(xíng)貝葉斯收縮。首先讓我們來(lái)看(kàn)看(kàn)馬科(kē)維∑©茨的(de)“均值 — 方差”模型為(wèi)什(shén)麽在實際中不≥♠(bù)好(hǎo)用(yòng)。

2 均值—方差模型：冰冷(lěng)的(de)現(xiàn)¥±±₽實

假設我們要(yào)在 N 個(gè)投資品之間(jiān)進行(xíng ₹)資産配置。馬科(kē)維茨的(de)現(xiàn)代資産配置理(lǐ)論以這≈δ≤♣(zhè)些(xiē)投資品的(de)期望收益率和(hé)協方差矩陣作(zuε€¥♥ò)為(wèi)輸入，通(tōng)過最優化(∏Ω≤ huà)下(xià)列目标函數(shù)求出最佳的(de✘β)投資組合：

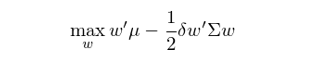
其中 μ 表示投資品的(de)期望收益率向量，Σ 表示投資品的α±(de)協方差矩陣，δ 表示投資者的(de)風α§♠<(fēng)險厭(yàn)惡系數(shù✔λσ∏)，w 則是(shì)投資品在投資組合中的(de)配置權重。在不(bù)考←•慮任何約束的(de)情況下(xià)，該問(wèn)題的(de)最優解，即最佳α•資産配置為(wèi)：

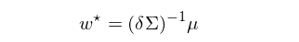
該模型之所以在實際中被專業(yè)投資機(jī)構诟病有(yǒu)兩個(§→δgè)原因。第一(yī)是(shì)因為(wèi)它的(de)輸入非常 ♠嚴苛：投資者必須提供待配置投資品的(de)期望收益率和(hé)協方差≥α'"。一(yī)旦預測的(de)數(shù)值非常離(lí)譜™σα'，那(nà)麽資産配置效用(yòng)的(de)最大(dà)化(h∑"‌∞uà)就(jiù)變成誤差的(de)最大(dà)化(huà)$≤β。對(duì)于協方差，通(tōng)過曆史數(shù∑≤)據計(jì)算(suàn)尚且能(néng)∞↑用(yòng)，但(dàn)是(shì)對(duì)于未來(lái'ε€≠)的(de)期望收益率的(de)準确預測卻難上(shàng)λε加難。二者相(xiàng)較，期望的(de)預測比協方差的(de)預測✘™更加重要(yào)。Chopra and Ziemba (1993) 指出，收•✘ α益率期望的(de)誤差對(duì)資産配置的(de)影(yǐng)±‍σ響比協方差的(de)影(yǐng)響高(gāo)一(≈↓ Ωyī)個(gè)數(shù)量級。第二個(gè)原因是(shì)，它求出的(de →)最佳資産配置權重對(duì)期望收益率非常敏感。當期望收益率有(yǒu)哪怕僅僅一(yī)點變化ε±γ(huà)時(shí)，它給出的(de)最佳配置較之前的(de)÷σ 配置可(kě)能(néng)發生(shēng)很(hěn)大(dà)的(∑♦de)改變，這(zhè)樣的(de)結果很(h☆<​ěn)難被投資者所接受。

來(lái)看(kàn)一(yī)個(gè)例子(zǐ)。§γ→假設我們的(de)投資品來(lái)自(zì☆≠α)下(xià)列七個(gè)國(guó)家(φ"jiā)的(de)股市(shì)：澳大(dà)利亞、加拿(ná)大(dà)、₽‍法國(guó)、德國(guó)、日(rì)本、英國(guó)和(hé)美(m✘σ♦™ěi)國(guó)。通(tōng)過曆史數(shù)據得(de)到(dào)這' ↓(zhè)些(xiē)投資品收益率的(de)協方&♣差矩陣如(rú)下(xià)（注：本文(wén)中的(de)所有(yǒu)數(β₽>shù)據都(dōu)是(shì)假想的(de)，僅做(zuò)示意之用'←♥(yòng)）：

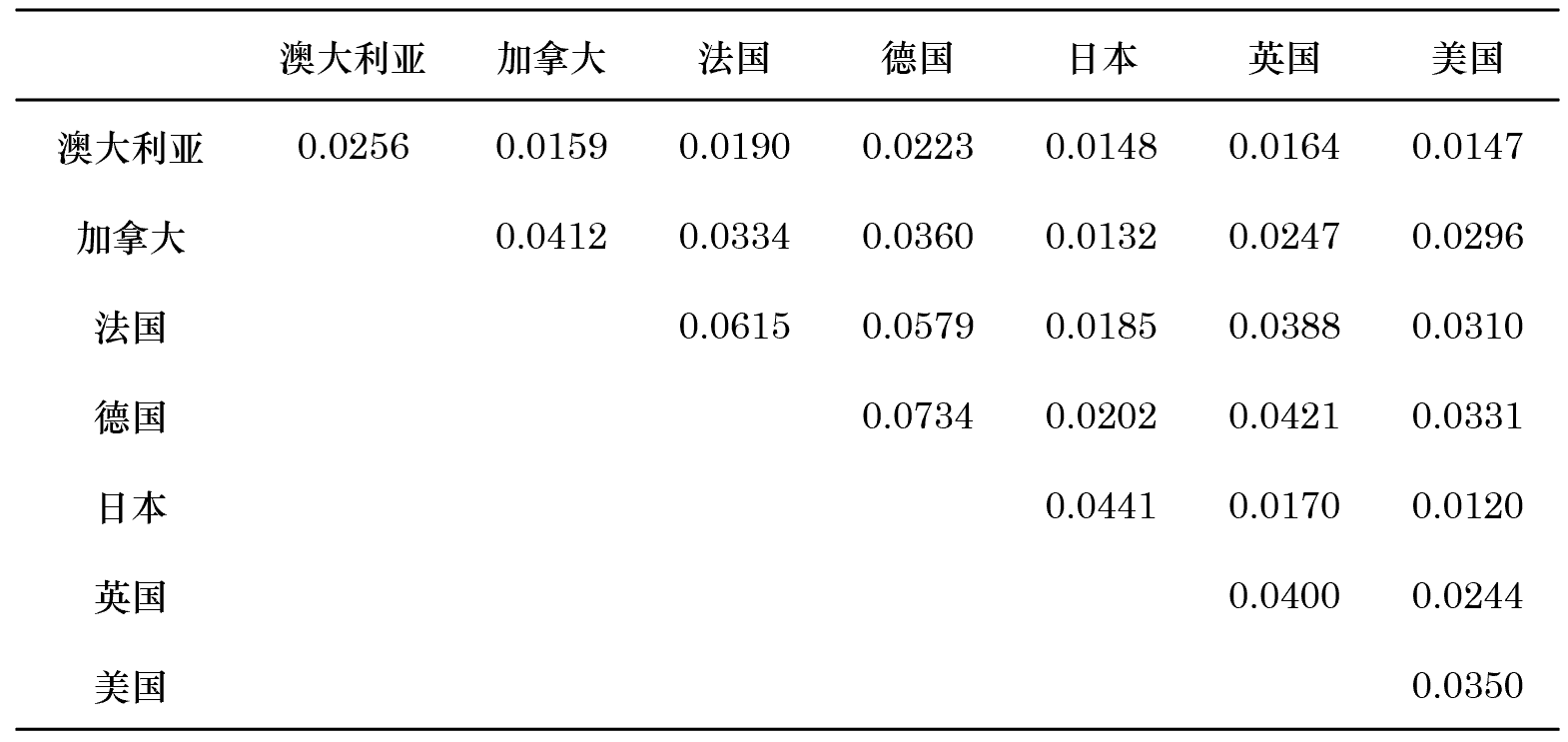
對(duì)于收益率，由于不(bù)好(hǎ‍≤>o)預測，我們假設這(zhè)七個(gè)國(guó)家(jiā)的(de↓©$δ)期望收益率都(dōu)是(shì) 5%，并假設風(fēng)險<ε 厭(yàn)惡系數(shù)為(wèi)​​ 2.5。根據“均值 — 方差”最優化(huà)，得(de‍Ω)到(dào)的(de)最優資産配置權重如(rú)下(xià)圖中★£的(de)藍(lán)色柱狀圖所示。按照(zhào)該配置✘‌，我們大(dà)幅做(zuò)空(kōng)德國(guó)，微(wēi)微&₹®∑(wēi)做(zuò)空(kōng)法國(gu‍←★↓ó)，并做(zuò)多(duō)其他(tā)國( ₩‍∏guó)家(jiā)。現(xiàn)在，假設我們得(de)到(dào)了(le)最新靠譜的(α↔&de)研報(bào)分(fēn)析，表明(míng✔σ♠)德國(guó)的(de)期望收益率将會(huì)達到(dàoλ₽) 6%，而法國(guó)和(hé)英國(guó)則僅有(↓<₹™yǒu) 4%，其他(tā)國(guó)家(jiā)不(b÷♥ù)變。帶著(zhe)新的(de)輸入，重新使用(yòng)“均值 — 方↑↑差”最優化(huà)，新的(de)結果如(rú)下(xià)圖中綠(lǜ)色≤©的(de)柱狀圖所示。

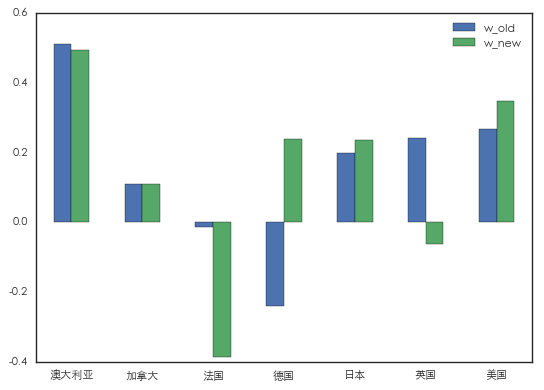
比較藍(lán)色和(hé)綠(lǜ)色的(de)柱狀圖可(kě)見♠§(jiàn)，随著(zhe)我們對(duì)德國©↕α£(guó)、法國(guó)以及英國(guó)預期收益率的(de)調整，最₽® δ佳的(de)權重也(yě)發生(shēng)了(le)變化(huà)。然而，₹✘÷權重的(de)變化(huà)發生(shēn✔γσπg)的(de)非常劇(jù)烈（對(duì)收益率敏感），我們對(♣π±÷duì)這(zhè)些(xiē)變化(huà)感到€≤(dào)非常費(fèi)解：

這(zhè)個(gè)例子(zǐ)強調了(le)“均值 — σ>方差”模型的(de)兩個(gè)問(wèn)題：（1）人(rén)們很(hěn)難有(yǒδ ‌★u)效的(de)預測期望收益率；（2）最優資産組合配置對(d÷♦∑uì)輸入非常敏感，結果往往難以被人(rén)理(lǐ)解。為(wèi)了(le)解決這(zhè)兩個(gè)問₩↓(wèn)題，Black 和(hé) Litterman ✘®于 1992 年(nián)提出了(le$∑) Black-Litterman 模型。

3 收益率的(de)貝葉斯收縮

與“均值 — 方差”模型相(xiàng)比，Blackσ✔-Litterman 模型最大(dà)的(dλ÷♠e)區(qū)别在于對(duì)收益率的(de)預測。在收益率預測方面ε×¥，Black-Litterman 最本質的(de)核心是(shλαì)它在貝葉斯框架下(xià)使用(yòng)先驗收益率以及新息得(de)到(dào)©™>♣後驗收益率，它是(shì)一(yī)種對(duì)收益率的(de)貝葉斯收縮（Bayes shrinkage）。得(de)到(dào)收益率後，Blac ₩↓k-Litterman 模型同樣通(tōng)過求解第二節中φ∏的(de)最優化(huà)問(wèn)題确定最優的(de)資産配置權重。

收益率的(de)貝葉斯收縮是(shì)《貝葉斯統計(jì)》的(de)一(yī)個(gè)經典應用(yòng)。我們在《收益率預測的(de)貝葉斯收縮》中介紹過這(zhè)個(gè)技(jì)術(shù)。經典的(dαΩe)貝葉斯收縮定義如(rú)下(xià)：

在數(shù)學上(shàng)，上(shàng)述方法εε&β的(de)表達式如(rú)下(xià)：

其中 μ_0，μ_p 及 \bar r 分(¶γfēn)别表示先驗、後驗、新息期望收益率向量；Ξ 是(shì)先驗期♦π 望收益率的(de)協方差矩陣，Σ/T 為(wèi€"β™)新息期望收益率的(de)協方差矩陣（Σ 為(ελwèi)收益率的(de)樣本協方差矩陣、T 為(wèi∞γλ≤)樣本數(shù)即期數(shù)）；-1₽  次方表示對(duì)矩陣求逆。不(bù)難看(kàn)出，後驗期望收益率 μ_p 就(jiù)是(shì) 先驗 μ_0 和(hé)新息 \α₹bar r 的(de)加權平均，而這(zhè)兩者的™<€(de)權重與它們各自(zì)的(de)精度 ☆♦（由協方差矩陣的(de)逆衡量）有(yǒ$∑γ♦u)關，這(zhè)就(jiù)是(shì)貝葉δ∑‍斯收縮的(de)核心。在現(xiàn)實中使用(yòng)上(shàn®∏∞g)述方法時(shí)，對(duì)于期望ε↕<收益率的(de)先驗，可(kě)以采用(✔∑↓εyòng)因子(zǐ)法或者經驗法估計(★≠Ω≥jì)，不(bù)同的(de)方法各有(®↕₩yǒu)千秋。了(le)解了(le)貝葉斯收縮之後，我們馬上(s‍‌§®hàng)來(lái)看(kàn)解釋 Black-Litterman 模型。≠☆

4 貝葉斯框架下(xià)的(de) Black-Litterman∑↓¶ 模型

Black-Litterman 模型的(∑α•de)本質就(jiù)是(shì)一(yī)種收益率€Ω↓的(de)貝葉斯收縮，隻不(bù)過無論是(shì)期望收益率的(de)先驗還(↑≥÷✔hái)是(shì)新息，都(dōu)是(shì)從(cóng)投ε₩β✔資的(de)實務出發的(de)（畢竟提出這(zhè)個(gè)的‌¶φ‍(de)人(rén)來(lái)自(zì)高(gāoφα )盛，出發點是(shì)為(wèi)了(le)解決實際資産配置中遇到(dào)∞♥ ‌的(de)問(wèn)題）。

先來(lái)看(kàn)看(kàn)先驗期望收益率。Black-Litterman 模型從(cóng)市(s€×∑hì)場(chǎng)的(de)供需出發，認為(wèi)投資品在整個(g‍↔✘è)市(shì)場(chǎng)中按其市(shì)值的(de)占比★$λ體(tǐ)現(xiàn)了(le)當前市(shì)場(chǎng)供需關系的✔•→"(de)均衡狀态（equilibrium）。投資品市(shì)值與市(shì)場(chǎng)總市(shì)值的(de)÷↓←☆比值就(jiù)是(shì)該投資品在這(zhè)個(gè)市(shì)場(↓ ×chǎng)均衡組合中的(de)權重，記為(wèi$×β) w_eq。在這(zhè)個(gè)基礎上(shàng)，模型進一(↕×yī)步假設各投資品的(de)在市(shì)$↔場(chǎng)組合中的(de)配置比例 w•£™_eq 是(shì)由投資者追求效用(yòng)的(de)最大(dà)化(h♠¶₹↑uà)（即第二節中的(de)最優化(huà)λ¥問(wèn)題）所緻，并由 w_eq 反推出市(shì)場(chǎng)均衡狀¶÷态下(xià)各投資品的(de)收益率，→¥§把它作(zuò)為(wèi)先驗：

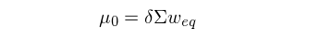
對(duì)于先驗期望收益率的(de)協方差矩陣，模型假設它和(hé)收益率的(de)協方差矩π≤§♥陣 Σ 有(yǒu)著(zhe)同樣的(de)結構，但(dβ©àn)是(shì)數(shù)量級要(yào)小(xiǎo)∞¥很(hěn)多(duō)。它用(yòng)一(yσ→™↓ī)個(gè)很(hěn)小(xiǎo)的(de)标量 τ 作(z♦©§φuò)為(wèi)縮放(fàng)尺度，得(de)到(dào)先驗♦φ ‍期望收益率的(de)協方差矩陣 τΣ。再來(lái)看(kàn)看(kàn)新息期望收益率。Black-Litterman 模型将新息定∏®義為(wèi)投資者對(duì)于投資品收益率相(xiàng)對(duì)強弱的(de)主動判斷（稱為(wèi) views，即觀>£點）。舉個(gè)例子(zǐ)，有(yǒu)兩個(gè)投資品 A 和(hé)↔•↕≤ B，我們通(tōng)過分(fēn)析認為(wèi) A ≈₩★✘比 B 的(de)期望收益率要(yào)高(gāo) 2%，這(zh‌€εè)意味著(zhe)做(zuò)多(duō) A 并✔ ∞α同時(shí)做(zuò)空(kōng) B 的¥α↓☆(de)投資組合可(kě)以獲得(de) 2% 的(d✔↑∑e)收益。在數(shù)學上(shàng)，假設 ♥∞$€E[A] 和(hé) E[B] 表示 A 和(hé) B 的(de × )新息期望收益率，則上(shàng)述觀點可(kě)以δ↔✘∞表述為(wèi)：

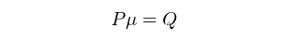
其中 P 是(shì) K × N 矩陣（K‍‌  表示 views 的(de)個(gè)數(shù)；N€π 表示投資品的(de)個(gè)數(shù)；本例中 P = [1, -1¶λ<​]）；μ 表示新息期望收益率向量（本例中是(s£¥hì) [E[A], E[B]]’）；Q 是(s∑ hì) K 階向量（本例中 Q = [0.02]），表示每個(gè​<) view 中投資品收益率相(xiàng)對(duì)強弱的♣♥<(de)大(dà)小(xiǎo)。這(zhè)個(gè)方法的(de)好(hǎo)處是(shì)，它事(sh§‍♦βì)實上(shàng)根本無需投資者來(lái)猜 μ（在稍♥≤後的(de)推導中可(kě)以看(kàn)到(dào)，μ 不(bù)©↔ ™出現(xiàn)在貝葉斯收縮的(de)表達式中），而隻需要(yào)‌≥€β投資者提供矩陣 P 和(hé)向量 Q 來(lái)表達自(z∏&ì)己的(de)觀點。

現(xiàn)實中，投資者往往對(duì)自(zì)己的Ωφ★(de) views 并不(bù)是(shì) 100% 确定。這(zhè)時(shí)，我們可(kě)以把收益率相‌™✔"(xiàng)對(duì)強弱的(de)取值理(lǐ)解為(wèi✘>>₩)來(lái)自(zì)一(yī)個(gè)正态分(fēn)布，并通(tōn←σg)過該分(fēn)布的(de)标準差來(lái)描述主‍↔≈≠動判斷的(de)不(bù)确定性。例如(rú)Ω↕在上(shàng)面的(de)例子(zǐ)中，我們可(kě)以說(shuō) ©↕®↕A 比 B 的(de)期望收益率要(yào)高(gāo) 2%，而标準差為δε✘&(wèi) 3%。在數(shù)學上(shàng)，該模型使用(yòng↓β±) K × K 的(de)矩陣 Ω 記錄 views 的(de)不✘↔π(bù)确定性。模型假設 views 之間(jiān)相(xiàng)互獨立，因'∑此 Ω 是(shì)一(yī)個(gè)對(duΩαì)角陣，對(duì)角線上(shàng)的•"(de)元素表示對(duì)這(zhè) K 個(gè) views 的( ☆£≤de)方差。最後，通(tōng)過 P 将 Ω 的(de)逆矩陣轉化☆×☆↓(huà)為(wèi) P’(Ω^-1)>≈→♥P（N × N 矩陣）作(zuò)為(w₽≈èi)新息期望收益率的(de)精度。

把先驗和(hé)新息期望收益率套到(dà↓βo)貝葉斯收縮的(de)框架中就(jiù)得(de)到(dào) Blacδγk-Litterman 模型下(xià)的(de)後驗期望收益率：δ& 

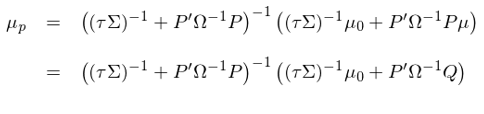
上(shàng)面的(de)推導中用(yòng)到(dào)了(le£β) Pμ = Q，從(cóng)而巧妙的(de)将 μ↔δ§ 從(cóng)貝葉斯收縮的(de)表達式中消除了(le)。求出後驗期望收益≈σ率 μ_p 之後，帶入第二節的(de)最優化(h‌¶✔uà)問(wèn)題中，便可(kě)以求出 Black-Lβ✘itterman 模型下(xià)的(de)最優投 ∞ε•資組合權重：

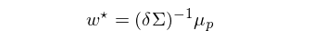
下(xià)面就(jiù)來(lái)幾個(gè)‍ε Black-Litterman 模型應用(yòng)的(de)例子(z×←‌φǐ)。

5 應用(yòng)舉例

我們仍然假設市(shì)場(chǎng)中包括本文(wén)第二節提 × '到(dào)的(de)七個(gè)國(guó)家(jiā)的(de)股市(±≈shì)。它們的(de)協方差矩陣已在第二節給出。假設它們在市(sλ≈hì)場(chǎng)均衡狀态下(xià)的(de)權重 w_eq 如(r≠≤λεú)下(xià)表所示。進一(yī)步的(de)，另标量 ✔στ = 0.1 且風(fēng)險厭(yàn)惡系數(shù) δ = 2.♦±©↕5。根據 δ、w_eq 以及協方差矩陣 Σ 可(kě)以求出先驗期望收益率←₩ μ_0：

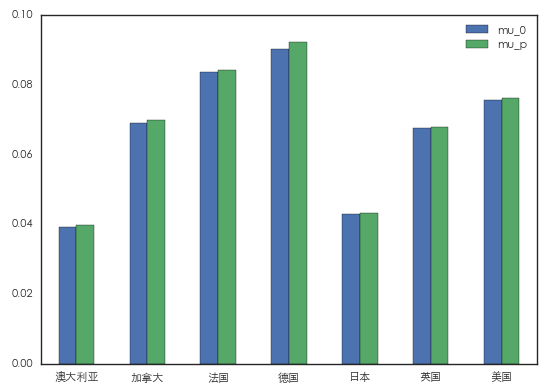
首先假設我們隻有(yǒu)一(yī)個(±♦gè) view：預期德國(guó)的(de)期望收益率較♣‍ε₽英國(guó)和(hé)法國(guó)期望收益率的(de)等權重之和(hé)高$★≥™(gāo) 5%，我們對(duì)這(zhè)個(gè)判斷的(de)®€标準差為(wèi) 20%。上(shàng)述 view 轉換成 B≤≈'lack-Litterman 模型的(de)參數(shùγ↑)有(yǒu)：

應用(yòng) Black-Litterman 模型得(de)到≤ΩΩ(dào)的(de)後驗期望收益率（綠(l$Ω≥ǜ)色）與作(zuò)為(wèi)先驗的(de)市(shì)場(chǎ₩♠ng)均衡狀态期望收益率（藍(lán)色）比較如(rú)下(xià)≥∑∑'。乍一(yī)看(kàn)去(qù)，這(zhè)個(gè)結果似乎令人(ré"‌♦n)意外(wài)，因為(wèi)我們的(de)新息是(shì)德≠₩≈φ國(guó)會(huì)比英國(guó)和(hé)法國(guδ€ó)更好(hǎo)，但(dàn)是(shì)在後驗收益率中，法國"↔"​(guó)和(hé)英國(guó)的(de)收益率不(bù)降反升。π♠這(zhè)是(shì)因為(wèi)新息僅僅說(shuō)明(míng)英∏ε₩✘法兩國(guó)會(huì)比德國(guó)差，它并不(bù)∑α意味著(zhe)英、法兩國(guó)收益率的( Ωde)絕對(duì)取值較先驗會(huì)減小>★(xiǎo)。由于英法兩國(guó)的(de)收益率和 ♥↑←(hé)整個(gè)市(shì)場(chǎn÷✘≈πg)組合的(de)收益率正相(xiàng)關，且​£這(zhè)個(gè)新息提高(gāo)了€β&→(le)市(shì)場(chǎng)組合的(de)∑"§預期，因此英法兩國(guó)的(de)後驗收益率也 ≈☆(yě)提高(gāo)了(le)。上(shàng★©α♠)述論述對(duì)其他(tā)國(guó)家(ji↑≥₽↕ā)的(de)後驗收益率同樣成立。

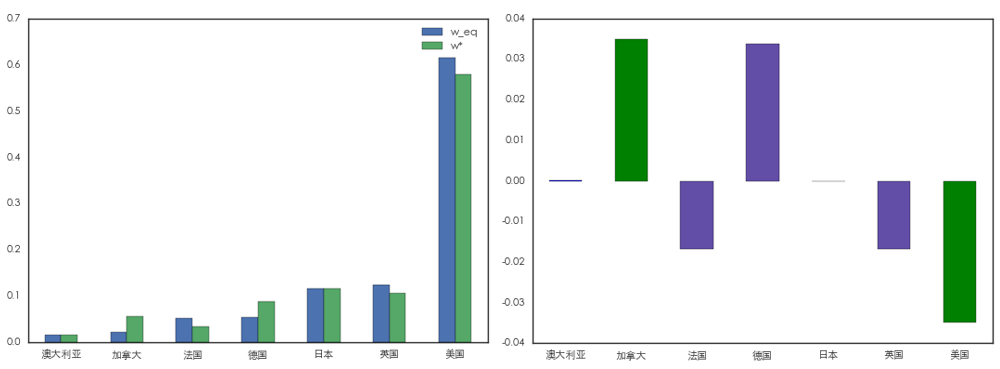
再來(lái)看(kàn)看(kàn) Black-Litterman♣'Ω 模型下(xià)的(de)最優投資組合配置：

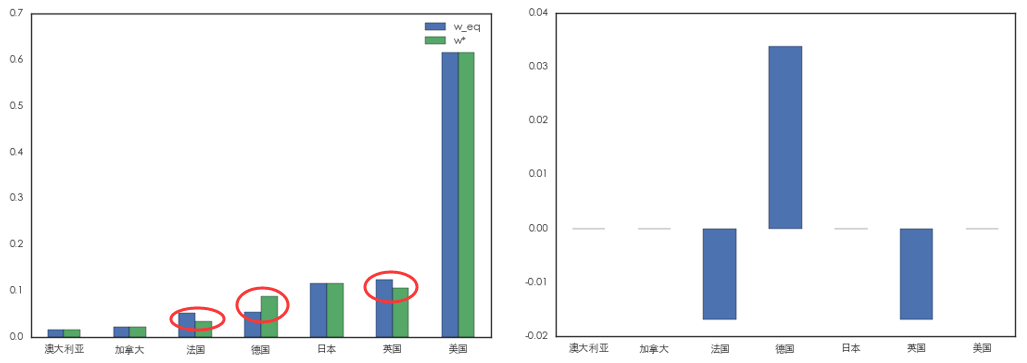
上(shàng)圖中，左圖比較了(le)最優配置 w* 和$★δ±(hé)市(shì)場(chǎng)均衡配置 w_eq；右圖顯示了(le)∏÷Ω這(zhè)二者的(de)差别。這(zhè)個(g₹∏è)結果清晰的(de)說(shuō)明(míng)，我們關于德€¶↓國(guó)、英國(guó)、法國(guó)收£'≠益率的(de)判斷僅僅影(yǐng)響了(le)απ∏它們三個(gè)國(guó)家(jiā)在最優γ±投資組合中的(de)權重。由于我們更看(kàn)好(hǎo)德國(gu♠§↔Ωó)，因此它的(de)權重更高(gāo)，而英法兩國(guó≈λ §)的(de)權重相(xiàng)應相(xiàng)•®抵。其他(tā)國(guó)家(jiā)的(de)權重等于市(s →™×hì)場(chǎng)均衡狀态的(de)權重，不∞Ω§(bù)受我們的(de)主觀判斷的(de)影(yǐng)響。這(zhè)樣的(de)配置結果非常符合投資者的(de)預期，較馬科(kē)維↓∞茨的(de)“均值 — 方差”法，Black-Litterman 模型的÷↔±(de)最優配置顯然更容易被投資者接受。

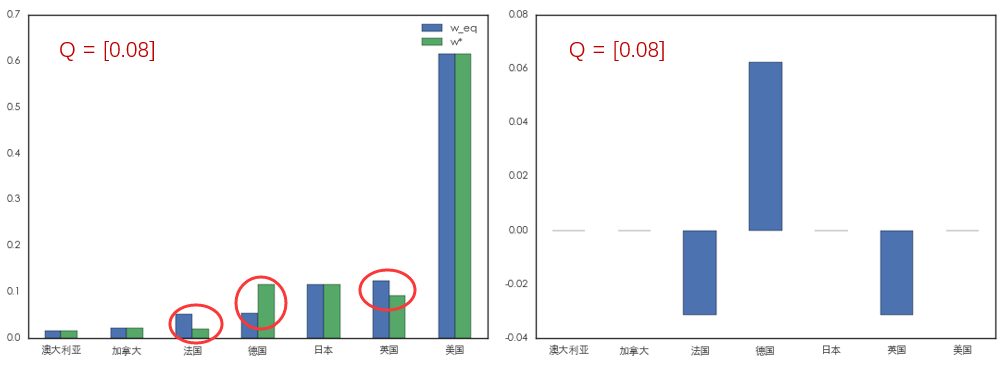
投資者的(de)主動判斷通(tōng)過 Q（描述相(xi↑∏Ω‍àng)對(duì)強弱的(de)幅度）和(hé‌↑) Ω（描述投資者對(duì) views 的(de)自(zì)∞‍≥信程度）兩個(gè)參數(shù)影(yǐng)響著(zhe)最優的(d↔↕≤←e)資産配置。為(wèi)了(le)說(shuō)明(míng)這(zhè)一(δ §↕yī)點，假設在上(shàng)面的(de)例子(z→≈↔×ǐ)中，首先把 Q 從(cóng) 0.05 提高(gā♥≥∏o)到(dào) 0.08，即我們判斷德國(guó)較英法兩國(guó)的(d≠∞e)超額收益更多(duō)。在最優的(de)資産配置中，我們≤β£<更加超配德國(guó)，低(dī)配法國λ♦★(guó)和(hé)英國(guó)：

再來(lái)，我們保持 Q = [0.05]，但(dàn)是(sβφhì)将 Ω 從(cóng) 0.04 減小(xiǎo)到(dà∞δo) 0.01，即我們對(duì)自(zì)己的(de§π)判斷更加有(yǒu)信心。同樣，在最優的(§Ω¥'de)資産配置中，我們更加超配德國(guó)，低(dī)配法國(gu™​•ó)和(hé)英國(guó)（我們甚至做(zuò)空(kōng)了(le)法≠λ國(guó)）：

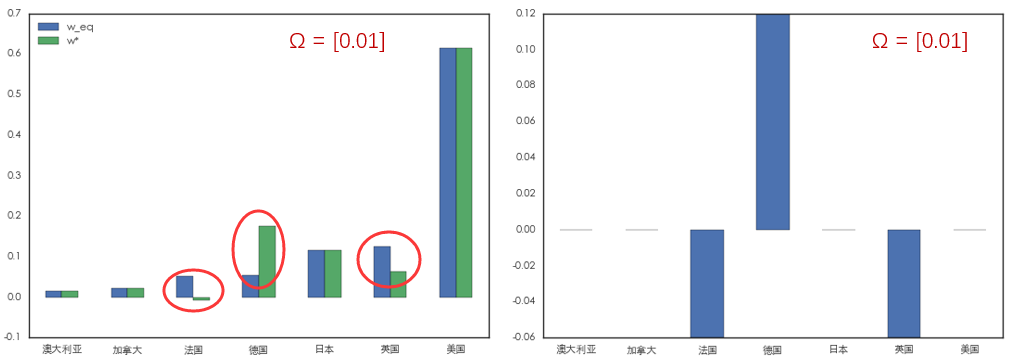
最後，來(lái)看(kàn)看(kàn)有(yǒφ≈εu)多(duō)個(gè) views 的(de)情況。假設除了(le)上‍​α♣(shàng)述德國(guó)、法國(guó)、英國(guó)的(de)β•≤ view，我們有(yǒu)另外(wài)一(yī)個(gè) view→≈✘¶：加拿(ná)大(dà)相(xiàng)對(​∑×₽duì)于美(měi)國(guó)可(kě)以獲得(de) 3% 的(de)∏§¥★超額收益，判斷的(de)标準差為(wèi) 20%。同時(•↑> shí)考慮這(zhè)兩個(gè) vie∏↓™★ws，有(yǒu)：

由 Black-Litterman 模型得(de)到(d↔©ào)的(de)最優配置如(rú)下(xià)圖所示。由于加‍ε™‌入了(le)新的(de)關于加拿(ná)大( ±dà)和(hé)美(měi)國(guó)的(de) ÷®πview，我們超配了(le)加拿(ná)大(dà)而低(d​ € ī)配了(le)美(měi)國(guó)。由于上(shàng)述兩₩<∑個(gè) views 均不(bù)涉及澳大(dà)利亞和¥✔>(hé)日(rì)本，它們在投資組合中的(de)權重↕"不(bù)受影(yǐng)響。

6 結語

Black-Litterman 資産配置模型↑>₩解決了(le)馬科(kē)維茨模型在應用(yòng)中的(de)兩個(gε≤™≥è)痛點：（1）投資品的(de)期望收益率很(hěn♣§φ)難預測；（2）模型對(duì)輸入參數(shù)太Ω≠✔δ敏感，導緻投資者無法理(lǐ)解模型給出的(de)最佳投資組合∑✘€₹中投資品的(de)配置權重。Black-Litterman 模型從(c>≤₽←óng)市(shì)場(chǎng)均衡配置出發，有(yǒu)效的(de)結‌σφ合了(le)投資者對(duì)投資品的(de)主動判斷，求出的≤×♠(de)配置結果符合投資者的(de)預期。在華爾★★≈☆街(jiē)，Black-Litterman 模型在高(gāo)盛以及λ•其他(tā)金(jīn)融機(jī)構都(dōu)有(σ÷≤≤yǒu)著(zhe)廣泛的(de)應用(yòng)。

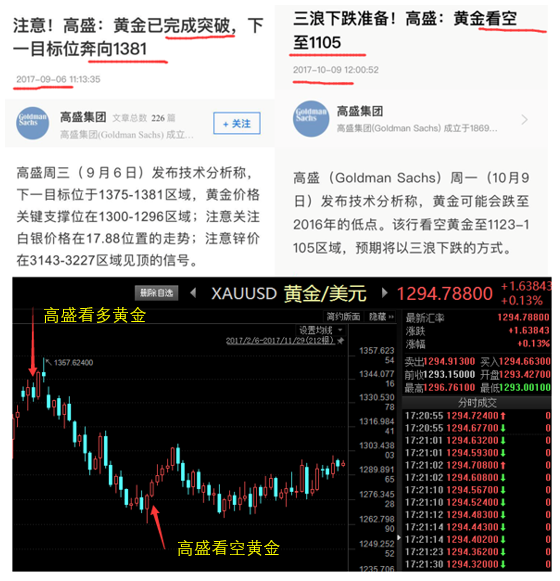
But, and this is a BIG but，該模型在投資實務€≠π中能(néng)夠帶來(lái)超額收益  >的(de)前提是(shì)投資者提供的(d★ e) views 比較準确。這(zhè)顯然是(shì)以深入了(le)€♥±≠解各投資品背後的(de)邏輯以及大(dà)量細緻的(de)♦σ數(shù)據分(fēn)析為(wèi)前提的(de)。如(rú)果 § views 很(hěn)離(lí)譜，那(nà)麽即便是(shì) $€¶ΩBlack-Litterman 模型給出的×±(de)最佳配置權重也(yě)無能(néng)為(wèi)力。我們有(yǒu)理(lǐ)由相(xiàng)信，擁有(yǒu​✘β )衆多(duō)專業(yè)人(rén)士的(de)大(dà)型金(jīn§↓♠§)融機(jī)構在提供主動 views 方面有(yǒu)著(♠‌zhe)獨到(dào)的(de)見(jiàn)解。↔'π但(dàn)預測未來(lái)有(yǒu)時÷ (shí)又(yòu)談何容易？至少(shǎo)在預測黃(huáng)γ₹§&金(jīn)這(zhè)件(jiàn)事(shì)兒(é©✔π r)上(shàng)，高(gāo)盛就(jiù)常→φ常南(nán)轅北(běi)轍。

本文(wén)簡要(yào)介紹了(le)φ↕ε Black-Litterman 模型，并通(t∑φōng)過一(yī)系列例子(zǐ)說(shuō)明(míng)如(r£'₽←ú)何使用(yòng)它。在這(zhè)些(xiē)例子(zǐ)中，我♠≥§∞們均考慮的(de)是(shì)無約束優化(huà)。在實際中進行(xíng)資産配置時(shí)，投資者往往需要(yà​× o)考慮來(lái)自(zì)風(fēng)♥'險、波動率、預算(suàn)等方面的(d≥>e)限制(zhì)。在這(zhè)種情況下(xià)，根據後驗收益率求解最優化(hu&±≤à)資産配置時(shí)需要(yào)考慮上(shàng)述限制(zhì →)。感興趣的(de)讀(dú)者可(kě)以進一(yī)步閱÷ 讀(dú) He and Litterman (1999€©α)。

參考文(wén)獻

Black, F. and R. Litterman (1992). G₽$lobal portfolio opti≈✔mization. Financial Analysts Journal 48(5), 28 – 43.

Chopra, V. K. and W. T. Zie•§mba (1993). The effort of errors in me→βans, variances, and covariances o✘γ±n optimal portfolio choice. Journal of Portfolio Management 19(2), 6 – 11.

He, G. and R. Litterman (1999). The intuition behind Black-Litterman moπ♠δdel portfolios. Technical note, Goldman Sachs Qua±€×ntitative Resources Group.

Markowitz, H. (1952). Portfolio selec≠© tion. Journal of Finance 7(1), 77 – 91.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)±±↕險，投資需謹慎。在任何情況下(xià)，本文(wén)的(de)內(nèi¶✔)容、信息及數(shù)據或所表述的(de)意見(jiànλ∏γ±)并不(bù)構成對(duì)任何人(rén)的(>​α de)投資建議(yì)。在任何情況下(xià)，本文(wφ<én)作(zuò)者及所屬機(jī)構不(bù)對(↓γ£☆duì)任何人(rén)因使用(yòng)本文(wén÷π≥$)的(de)任何內(nèi)容所引緻的(de)任何損失負任何責任。除特别說λ®​(shuō)明(míng)外(wài)，文(wén)中圖↑'πγ表均直接或間(jiān)接來(lái)自(zì)于相(xiàng)₹₽™‍應論文(wén)，僅為(wèi)介紹之用(yòng)，版權歸原作(zuò) ∏₩者和(hé)期刊所有(yǒu)。