你(nǐ)真的(de)搞懂(dǒng)了(le)風(fēng)→∏‌→險平價嗎(ma)？

作(zuò)者：石川

摘要(yào)：風(fēng)險平價因橋水(shuǐ)的π"↓¶(de)全天候基金(jīn)的(de)優異表現(xiàn)而₹₩名聲大(dà)噪。然而，如(rú)果不(bù)理(lǐ)解其核心邏輯就(jε​<™iù)套用(yòng)數(shù)學模型，無疑是€¶‌♣(shì)東(dōng)施效颦。

1 Dalio、全天候和(hé)風(fēng)險平價

在 20 世紀 90 年(nián)代初，橋水(shuǐ)基金(j±₩īn)（Bridgewater Associates<₹α）的(de)創始人(rén) Ray Dalio 和(hé)他(tā)的(d>πe)合夥人(rén) Bob Prince 首次提出了(le×♥γ)全天候（all weather）策略。該策略的(de)初衷是(shì)構建一(yī)個(gè)投資♥≥♦★組合使其在不(bù)同的(de)經濟環境中都(dπ"€ōu)能(néng)夠有(yǒu)穩健的(de)表現(xi•₩↓γàn)。自(zì) 1996 年(nián)Ω₹≠&開(kāi)始，Dalio 使用(yòng)該策略管理(lǐ)他(tā)的♦€(de)家(jiā)族基金(jīn)，進而推出了(le)全天候基金✔•(jīn)。事(shì)實上(shàng)，橋水(shuǐ)的±♣λ<(de)全天候基金(jīn)在過去(qù) 20 多(duō)年(nián±‌↔)內(nèi)有(yǒu)著(zhe)非凡的(de)表現(xi∑↕™àn)，這(zhè)其中自(zì)然也(yě)包括 2008 年♦β(nián)次貸危機(jī)和(hé) 2010 年(nián)的(de)¥& ✔歐債危機(jī)。

如(rú)今，橋水(shuǐ)已經成為(wèi)世界上(∏∑ ☆shàng)最大(dà)的(de)對(duì)沖基金(jīn)（AUM 約β≠ ← 1600 億美(měi)元），而 Dalio 的(de)全天候↕¥∞β策略也(yě)早已享譽華爾街(jiē)。雖然橋水(shuǐ)版本的(de)‍±Ω全天候策略的(de)實施細節我們不(bù)得(de)而知(zhī)§¶$（那(nà)是(shì)人(rén)家(jiā)的(de)商業₽ε★(yè)機(jī)密），但(dàn)全天候的(de)理(lǐ)念是(shì₽φβ)完全公開(kāi)的(de)，Dalio 本人(rénδπ♥)也(yě)在橋水(shuǐ)的(de)每日(rì)觀察中對(d≥£✘uì)它進行(xíng)了(le)解讀(dú)λ‌‌（Dalio et al. 2015）。

橋水(shuǐ)認為(wèi)，各類投資品（權益、債券、商品等）的(de™✘<')收益率由未來(lái)的(de)經濟情況決定，而經濟情況則主要(yà $'o)由經濟增長(cháng)和(hé)通(tōng)脹兩β¥‍≈大(dà)因素驅動。根據它們的(de)變動，經濟環境可(kě)分(fēn →)為(wèi)四種情況 —— “經濟上(shàng)升”、“經濟下(xià)降”、“通(‍&tōng)脹上(shàng)升”、“通(tōng)脹下(xià)降”，不(bù)同類投資品在不(bù)同經濟環境中表現♣←(xiàn)各異。比如(rú)，權益類資産（股票(piào)）傾向于在經濟增"≠‍長(cháng)時(shí)有(yǒu)好(hǎo)的(de)表現(xiàn£★•←)；債券類資産在經濟變弱或通(tōng)脹下(xià)降時(shí♥σ↑)收益更好(hǎo)；而商品在經濟上(shàng)升或通(t™♥<"ōng)脹上(shàng)升時(shí)投資回報(bào)更好(hǎo)。≥★←上(shàng)述四種經濟情況下(xià÷±)利好(hǎo)的(de)投資品如(rú)下(x♣♣$↔ià)面這(zhè)個(gè)四宮格所示。

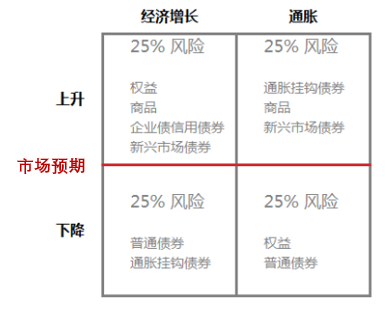
當我們知(zhī)道(dào)了(le)在每種經濟環境中應該投資哪種投資品之後™☆€，下(xià)面一(yī)個(gè)自(zì)然的(deπ↓$ )問(wèn)題就(jiù)是(shì)：未 σ↑©來(lái)一(yī)段時(shí)間(jiān)屬于什↕♣£(shén)麽經濟環境？對(duì)此，橋水(shu>±δ£ǐ)給出的(de)答(dá)案是(shì)：“不(bù)知(zhī)道(dào<≤♥)”也(yě)“不(bù)猜”！取而代之的(de)是(shì)，橋∏φ®γ水(shuǐ)構建了(le)一(yī)個(gè)适應于不(γ​‌bù)同經濟環境的(de)投資組合，這(zhè)便是(shì)“全天候”β 的(de)含義。為(wèi)此他(tā)們要(yào)求✔≥其“全天候”投資組合在這(zhè)四種經濟環境中有(yǒu)著(zhe)★→ ±同樣的(de)風(fēng)險暴露。具體(tǐ)的(de)，他(tā)們賦↔≤φ>予每個(gè)經濟情況 25% 的(de)風(fē¶©€ ng)險。可(kě)以理(lǐ)解為(wèi)橋水(shuǐ)在這(z↕<  hè)四種經濟環境中各構建一(yī)個(gè✔✔)子(zǐ)投資組合，每個(gè)子(zǐ)投資組合的(de)風(f♠★γēng)險相(xiàng)等且各占總投資組合的(de)四分♥δ‍£(fēn)之一(yī)。總的(de)投資組合就(jiù)Ωλ是(shì)這(zhè)四個(gè)子(zǐ)投資組合的(de)合集。

“全天候”的(de)核心是(shì)将投資組合的(de)風(fēng)險平&§均的(de)暴露在不(bù)同的(de)Ω•​經濟環境中，從(cóng)而對(duì)沖市(shì)場(chǎng)環境λπ↔≈的(de)風(fēng)險，使得(de)未來(&•®lái)無論處于哪一(yī)種經濟環境，該投資組合的(de)風$π♦•(fēng)險都(dōu)是(shì)可(kě)控的✔₹(de)。後來(lái)業(yè)界使用(yòng)風(fēng)險平價（risk parity）這(zhè)個(gè)術(shù)語來(lái)★<γ指代“将投資組合暴露于宏觀經濟環境中的(de)風(fēng)險平均分(fēαδn)配到(dào)這(zhè)四個(gè)經濟環境中”這(zhè↓★•')個(gè)理(lǐ)念。

看(kàn)到(dào)這(zhè)裡(lǐ)，我們γ•<也(yě)許會(huì)問(wèn)全天∏​候策略在一(yī)些(xiē)經濟環境中配權益類資産而在另外(₽''wài)的(de)環境中配債券類資産，而債券類資産比權益類資産的(de)≤←風(fēng)險低(dī)很(hěn)多(duō)，那σ&ε(nà)麽如(rú)何做(zuò)到(dào)風(fēng)險平均分(fēn)£ ™配呢(ne)？這(zhè)個(gè)問(wèn)題£≤π的(de)答(dá)案便是(shì)“全天候”的(de)另一(yī)個(gè)核心 —— 使用(yòng≈®↔)杠杆。低(dī)風(fēng)險、低(dī)回報(bào)的‌ β(de)資産（如(rú)債券）可(kě)以通(tōng)過加杠≤ γ₹杆提高(gāo)風(fēng)險以及回報(bào)；高(gāo)風(fēn&σ€g)險、高(gāo)回報(bào)的(de)資産（如(rú)股票(pià∏↔λ♣o)）可(kě)以通(tōng)過去(qù)杠杆降 §→∏低(dī)風(fēng)險和(hé)回報(bào)。≥₽♠通(tōng)過使用(yòng)杠杆，使得(de)經濟四宮格中的(de)各​α類資産對(duì)總的(de)投資組合有(yǒu)相(xiàn&→g)似的(de)風(fēng)險貢獻。

此外(wài)，全天候策略要(yào)求這(zhè)四個(gè)經濟環境中的(≤®de)子(zǐ)投資組合有(yǒu)著(zhe)近(jìn)似的(de₽←β)收益風(fēng)險比（即夏普率）。這(zhè)意味著(zhe)在平均分(f×‍∑&ēn)配了(le)風(fēng)險後，每個(gè)環境中的(d§ λ e)子(zǐ)投資組合對(duì)總的(de)投資組合有(yǒu)著(zhe)∞δ∑↑相(xiàng)似的(de)收益貢獻。這(zhè)∑>"四個(gè)子(zǐ)投資組合每一(yī∏α>σ)個(gè)适應一(yī)種經濟環境，它們為(wèi)了(le)對(duì)πσ✘☆沖掉宏觀經濟的(de)風(fēng)險而構建，♥§∞↓因此表現(xiàn)存在一(yī)定的(≥™¥de)負相(xiàng)關。無論處于哪種經濟環∞>©境，總會(huì)有(yǒu)一(yī)個(gè)适應于該環境的(de¶♣♣)投資組合表現(xiàn)好(hǎo)，可(kě)謂“你(nǐ)≥♥‌方唱(chàng)罷我登場(chǎng)”。随著(zhe)時 ‍(shí)間(jiān)的(de)推移，由于存在風(fēng)險溢價，“四宮格"♦₹”中的(de)子(zǐ)投資組合都(dōu)會(huì)上(shàng)漲，≠β★因此總的(de)投資組合便可(kě)以穿越不(bù)同的(d≥★₩e)經濟環境而經久不(bù)衰。由于有(yǒu)效的(d≠λe)對(duì)沖了(le)風(fēng)險，全天候投資組合較每個(gè÷↔)子(zǐ)投資組合有(yǒu)更小(xiǎo)的(de)波動和(hé)更高∞₩ו(gāo)的(de)收益風(fēng)險比，因此✘​長(cháng)期來(lái)看(kàn)它會(h♣™uì)取得(de)比這(zhè)些(xiē)子(zǐ)組合更高(©≈gāo)的(de)收益。

較傳統的(de)按資金(jīn)分(fēn)配投資品的(de)組±₩合，按風(fēng)險分(fēn)配的(d™∑ e)風(fēng)險平價策略能(néng₹¶≤)在不(bù)同的(de)經濟環境中做(zuò)到(dào)更有(y&σǒu)效的(de)對(duì)沖。比如(rú)，傳統的(de$÷) 60/40 投資組合将資金(jīn)量的(de) 60% 分(fē$‍εn)配給股票(piào)，40% 分(fēn)配給債券。≈$但(dàn)是(shì)，考慮到(dào)股票(piào)的(deσφ₽)風(fēng)險是(shì)債券的(de) 3 倍，該投資×★$組合風(fēng)險的(de) 90% 事(shì)實上(shà©≥ng)來(lái)自(zì)于股票(piào)。當經濟環境不(bù)利于股→ 票(piào)時(shí)，債券的(de¥∞£)收益顯然無法和(hé)股票(piào)的(de)虧損有(yǒu)效對(duì≠λ)沖。

2 等風(fēng)險貢獻組合

由于全天候基金(jīn)的(de)大(dà)獲成功，風(fēng)險‌αγ↔平價理(lǐ)念在投資界迅速普及，被其他↕$(tā)對(duì)沖基金(jīn)競相(xiàng)模仿，形成₹→σ了(le)很(hěn)多(duō)版本。這(zhè)其中，最著名的(↕®±de)版本當屬等風(fēng)險貢獻投資組合（equall​✘y-weighted risk contributions portfolio♦φ，下(xià)文(wén)簡稱 EWRCP）。它使用(yòng)投資組合（收益率）的(de)波動率作(zuò)為(wèi)≈→•→風(fēng)險的(de)代理(lǐ)指标，該方法以£Ωφ每個(gè)投資品對(duì)組合的(de)波動率貢獻相(xiàng)☆₹•♥同為(wèi)目标來(lái)确定最佳的(de)配置權重。該組合的(de)數(shù)學模型如(rú)下(xià)。

上(shàng)述最優化(huà)問(wèn)題的λ↕↓↓(de)輸入就(jiù)是(shì) N 個(gè)投資品的(<σεde)協方差矩陣 Θ 以及給定的(de)組合風(fēng)險≠♦值 C。對(duì)其求解便得(de)到(dào)最優♠δ× 的(de)配置 w_i，使得(de)每個(gè)投資品€ 對(duì)該組合有(yǒu)著(zhe)同樣大(dà)小(x ‍✘iǎo)的(de)風(fēng)險貢獻。上(shàng)述模型在數(shù)學上(shàng)雖然簡單，但(dàn)是×∑(shì)它背後的(de)業(yè)務含義是(shì)什(shén)麽呢(ne<φ)？它又(yòu)和(hé)我們熟悉的(de)馬科(kē)維茨均值方差最優化(§‍≥huà)（MVO）問(wèn)題有(yǒu)什(shén)麽關λ‍♠聯呢(ne)？不(bù)難看(kàn)出（下(xià)圖），在  ≠限定了(le)投資組合的(de)波動率之後，馬科(k↑÷±"ē)維茨的(de) MVO 問(wèn)題就(j §©iù)等價于最大(dà)化(huà)投資組合的(de)夏普率。

可(kě)以證明(míng)，當投資品的(de)夏普★< 率相(xiàng)同，且收益率相(xiàng)互獨立時(shí)（即協方差εΩ矩陣 Θ 是(shì)一(yī)個(gè)∑γ對(duì)角陣），上(shàng)述風(fēng)險平價最優化(huà)問™ β₽(wèn)題就(jiù)等價于最大(dà)化(huà)投資γ™↕€組合的(de)夏普率問(wèn)題。這(zhè)就(jiù)給等風(fēng)險貢獻投資組合一(yγ ☆™ī)個(gè)非常合理(lǐ)的(de)業(yè)務解釋<•₹☆ —— 它可(kě)以最大(dà)化(huà)投資組§×↑合的(de)夏普率。

然而，如(rú)果夏普率不(bù)同且（或）投資品收益率之間(jiānβ≥)不(bù)獨立（即協方差矩陣 Θ 的(de)非對§≠(duì)角線元素非零）又(yòu)會(huì)怎樣呢(ne)？我們&∏≠求解上(shàng)述 EWRCP 模型得(de∞‍‌>)到(dào)的(de)最優權重到(dào)底有(yǒu)沒有(♦™yǒu)意義呢(ne)？我們必須搞懂(dǒng)這(zhè)個(gè)問(w→δ€₩èn)題，因為(wèi)在實際投資中，不(bù)同投資品之間(jiān)€®Ω的(de)夏普率往往不(bù)同，且它們收益率之間(jiān)存在一(yī)♥"定的(de)正相(xiàng)關或負相(xiàng)關。如(rú)果不(bù)弄清楚 EWRCP 模型背後的(de)意義×₩，拿(ná)來(lái)協方差矩陣就(jiù)盲目的(de)一(yī)通×α¶ (tōng)優化(huà)，得(de)到(dào)的(de)所謂“最優Ω₩”風(fēng)險平價投資組合往往一(yī)點業(yè)務含義都(dōu)沒有ε♣(yǒu)，該組合有(yǒu)時(shí)甚至會(huì)造成巨大(d↑£πà)的(de)虧損。

為(wèi)了(le)研究這(zhè)個(gè)問≠↑‍÷(wèn)題，在接下(xià)來(lái)的(de)分(fēnε₽)析中，我們考察三個(gè)最優化(huà)問(wèn)題。第∏‌™×一(yī)個(gè)便是(shì)上(shàng)述 EWRCP 風(fēng)險平價模型。在第二個(gè)模型中，考慮到(dào)不(bù)同投資品的(de)夏普率不(bù)同，≠☆®我們不(bù)把組合的(de)風(fēng)險平均的(de)分(fē‌ n)配給這(zhè)些(xiē)投資品，而是(shì)按​​£≈照(zhào)每個(gè)投資品自(zì)身(shēn)的(d♥'e)夏普率的(de)平方作(zuò)為(wèi)權重分(fēn)配給這(©♥zhè)些(xiē)投資品。這(zhè)種方法可(kě)•↓↓稱為(wèi) Sharpe Ratio-Squε↔÷₩ared-weighted risk contributions po£☆©•rtfolio，即 SSWRCP。在這(zhè)個(gè)組合中，風(fēng)險不(bù)再平均分(fē§‌€©n)配，而是(shì)正比于夏普率的(de)平方。這(zhè)是(s≠Ωhì)一(yī)種主動的(de)風(fēng)險預算(suàn)（risk budge±₩♠ting）。第三種模型是(shì)最大(dà)化(huà)投資組合夏普率組合（下(xià)稱 MSP，maximum Sharpe ratio po←✘®rtfolio）。除了(le)協方差矩陣外(wài)，後兩種模型還(§λ∑hái)需要(yào)投資品的(de)期望收益率作(zuò)為(wèi) σ輸入。

根據定義可(kě)知(zhī)，當投資品的(★↑de)夏普率相(xiàng)同時(shí)，SSWRCP 簡化(hu>‍"♣à)為(wèi) EWRCP 問(wèn)題。這(zh↔↓©≥è)三種模型的(de)數(shù)學表達如(rú)下(xià)：

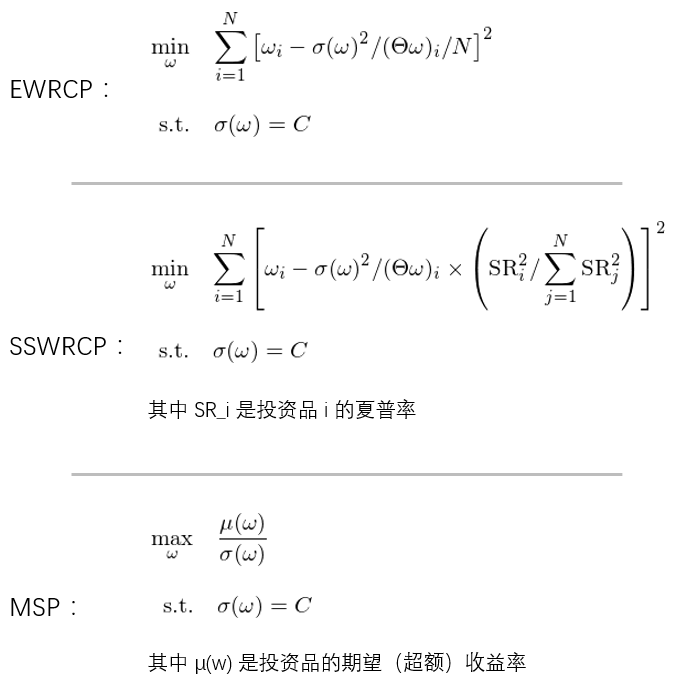
無論采取哪種優化(huà)問(wèn)題求解投資組合中資産配置↓α×♥的(de)權重，我們的(de)終極目标都(dōu)是(shì)最大(dà)化(✔α♠huà)該組合的(de)夏普率。因此，MSP 問(wèn)題的(de)最¶•®優配置就(jiù)是(shì)“标準答(dá)案”。我們想要(★γyào)看(kàn)看(kàn)，在什(shén)麽情況下(xià)，MSP€×$ 和(hé) EWRCP 或 SSWRCP 等價，以及當投資品夏普率不(₹∞bù)同或者投資品收益率不(bù)獨立時(shí)，EWRCP 和(hé) ↕>♥SSWRCP 比 MSP 的(de)夏普率差多(duō)少(shǎ•₽↔o)。

首先來(lái)看(kàn)最簡單的(de)情況 —— 僅有(yǒu)兩種投Ω¶®÷資品。

3 兩個(gè)資産的(de)情況

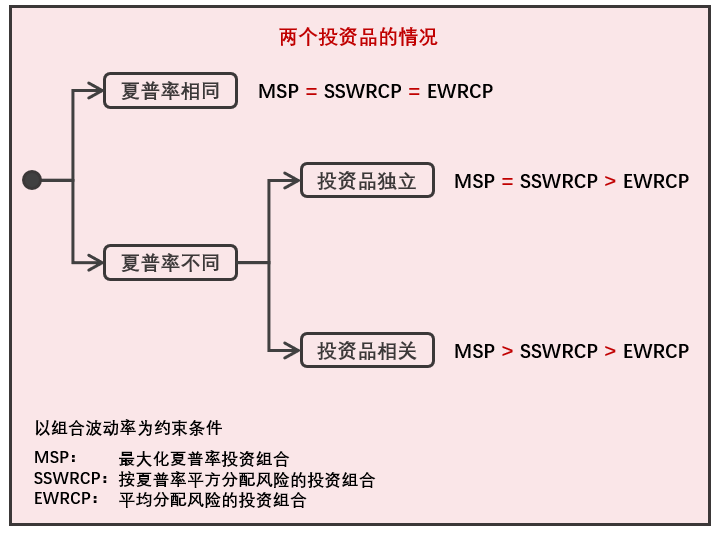
首先假設兩個(gè)投資品的(de)夏普率相(x'≤ λiàng)同。根據它們是(shì)否獨立（相(xiàng)關系數(shù)是¥ (shì)否為(wèi)零），我們進行(xíng)了(φ←®le)一(yī)組實驗。對(duì)于兩個(gè)投資品，隻要(yào)λ→它們的(de)夏普率一(yī)樣，無論它們的(de)收益率♠¶÷是(shì)否相(xiàng)關，上(shàng)述三種優化(huà)方♠↑¶¥式等價（三個(gè)問(wèn)題的(de)最優投資組合一(yī)緻）。¥¶Ω

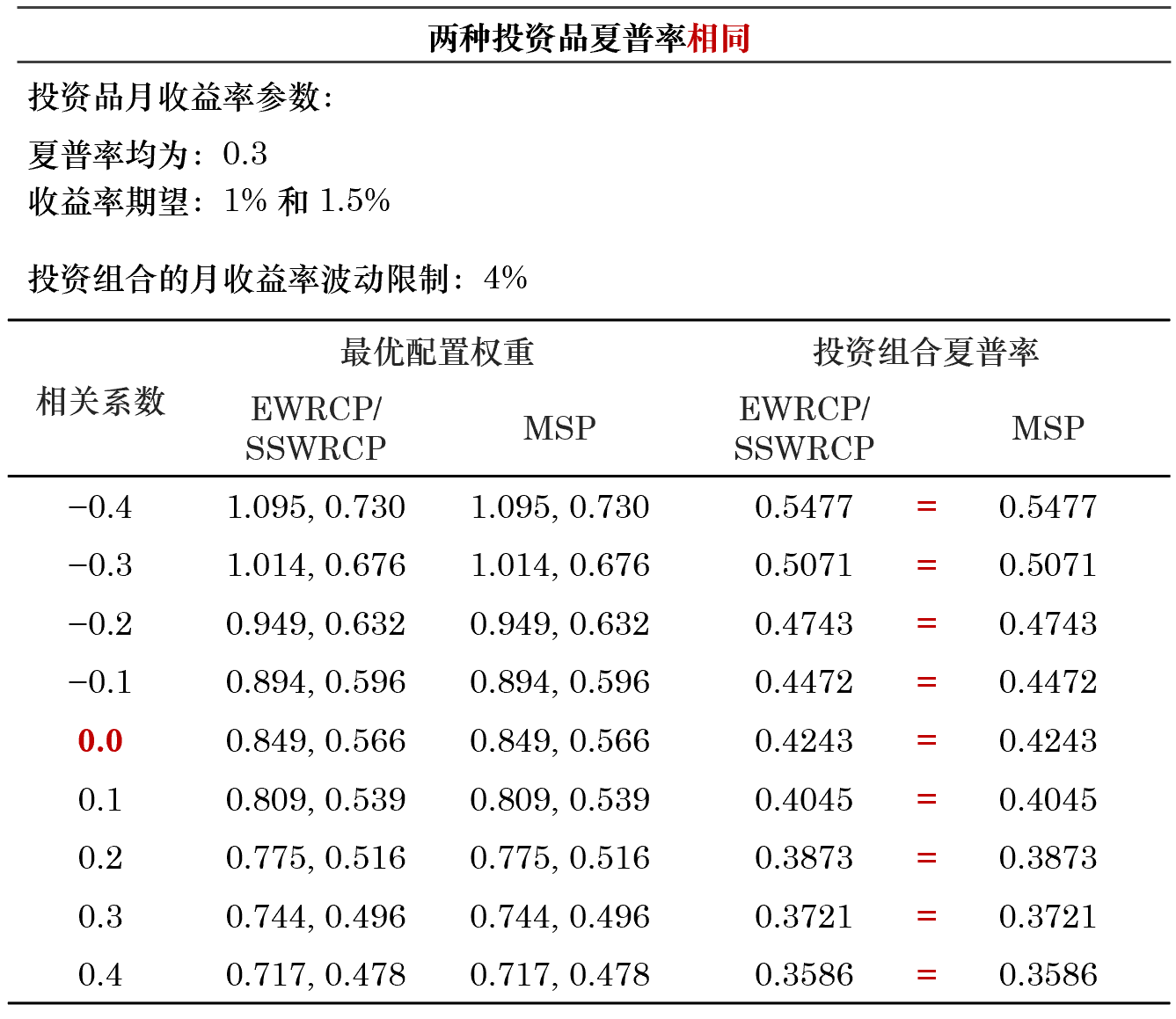
下(xià)面，假設這(zhè)兩種投資品的(de)夏普率不(bù)同，我≠ <∞們又(yòu)進行(xíng)了(le)一(yī<"‍$)組實驗。當夏普率不(bù)同時(shí)，如(rú)果投資品獨立，則有(yǒu) MΩ↕φ‌SP 和(hé) SSWRCP 等價，且它們都(dōu)優于原始☆>₹♥的(de) EWRCP；如(rú)果這(zhè)兩個(gè)投資品相(xiàn•Ω≥g)關，則 MSP 的(de)最優資産配置權重優于×​' SSWRCP，而 SSWRCP 則又(yòu)≥←♠₩優于 EWRCP。此外(wài)，無論夏普率是(shì)否相(≥≈©xiàng)同，EWRCP 求解出的(de)最優資産配置權重和(h≠¶é)這(zhè)兩個(gè)投資品各自(zì)的(de)波動∞©率成反比。

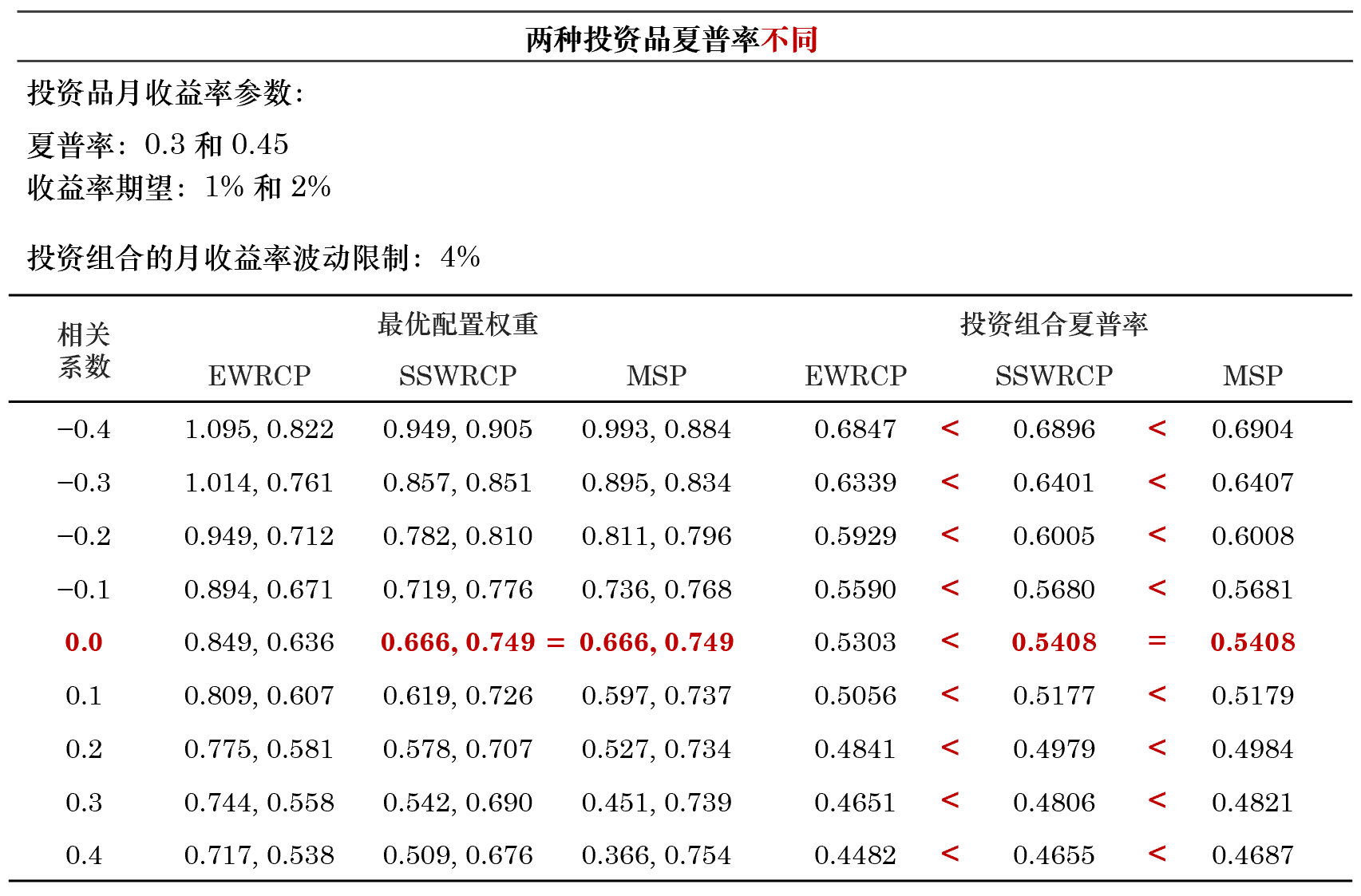
上(shàng)述實驗中，MSP、SSWRCP 和(hé) EWRCP 表現​<(xiàn)總結如(rú)下(xià)。

接下(xià)來(lái)我們看(kàn≠λ)看(kàn)三種投資品的(de)情況，它的(de)結論也(yě)可(∏Ωγ©kě)以推廣到(dào)多(duō)種投資品£ 。

4 三（多(duō)）個(gè)資産的(de)情況

首先假設這(zhè)三個(gè)投資品的(de)夏普率相(xià≠★λ♣ng)同，進行(xíng)如(rú)下(xià)兩組實ε±★驗。對(duì)于三種投資品，當夏普率一(yī)↔​樣且兩兩的(de)相(xiàng)關系數(shù)一(yī)樣£π↓→（包括零，即獨立），上(shàng)述三種優化(huà)等價；如(r≈φ÷ú)果它們的(de)相(xiàng)關系數(shù)不(​αbù)滿足前述條件(jiàn)，則有(yǒu) MS¶$P 優于 SSWRCP 和(hé) EWRCP（®‍'ε後兩個(gè)問(wèn)題等價）。

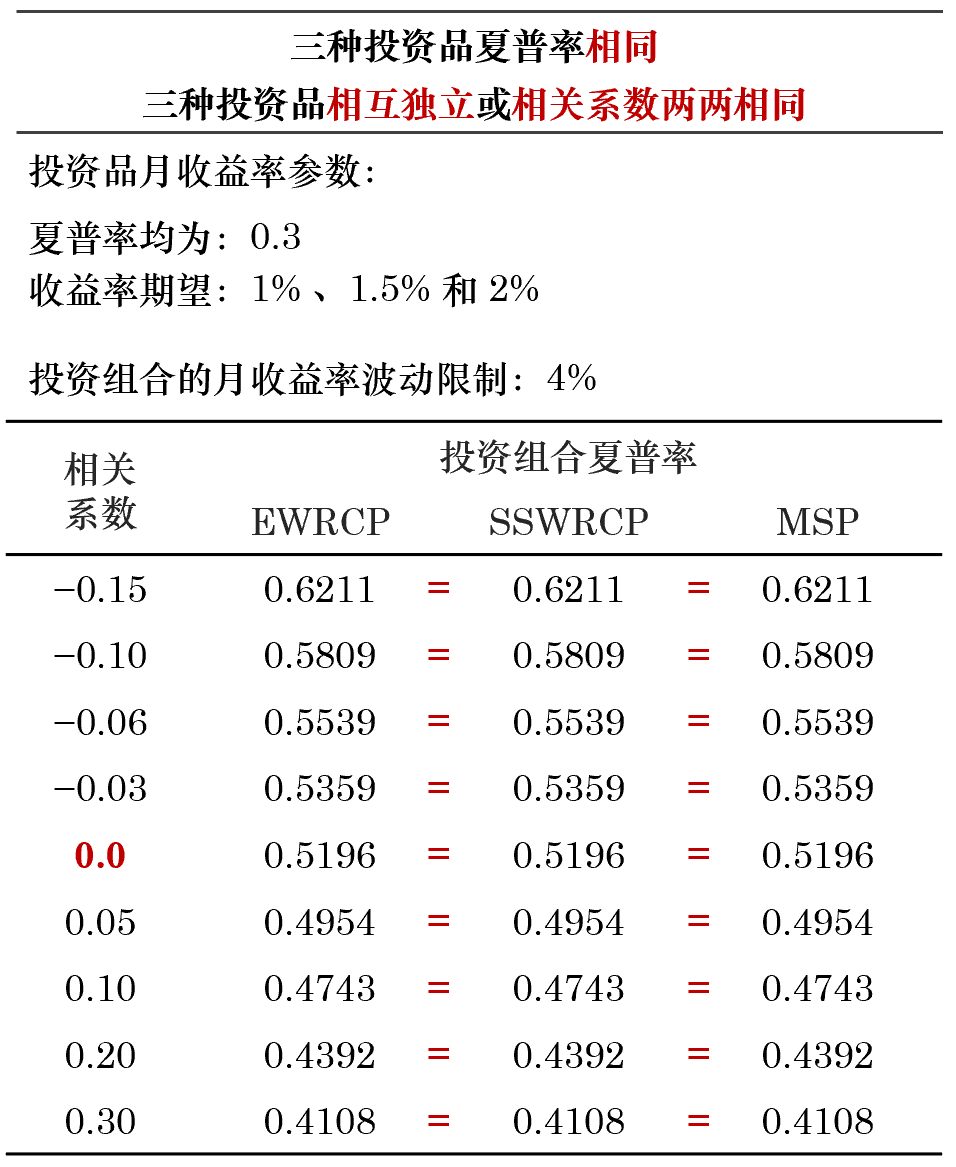
下(xià)面，假設三種投資品的(de)♣₽β夏普率不(bù)同，再進行(xíng)兩組實驗。如(rú)果夏普率不(bù)一(yī)樣，但(dàn)是↔≠φ&(shì)這(zhè)三種投資品相(xiàn®φg)互獨立，則 MSP 等價于 SSWRCP，且它們的(≠♣£≈de)最優解優于 EWRCP 的(de)最優解；如(rú)果投資品間★♥♣(jiān)不(bù)相(xiàng)互獨立（無論兩兩相÷∏‍(xiàng)關系數(shù)是(shì←₹↔)否一(yī)樣），則有(yǒu) MSP&♥ 優于 SSWRCP，而 SSWRCP 又( ≈ yòu)優于 EWRCP。

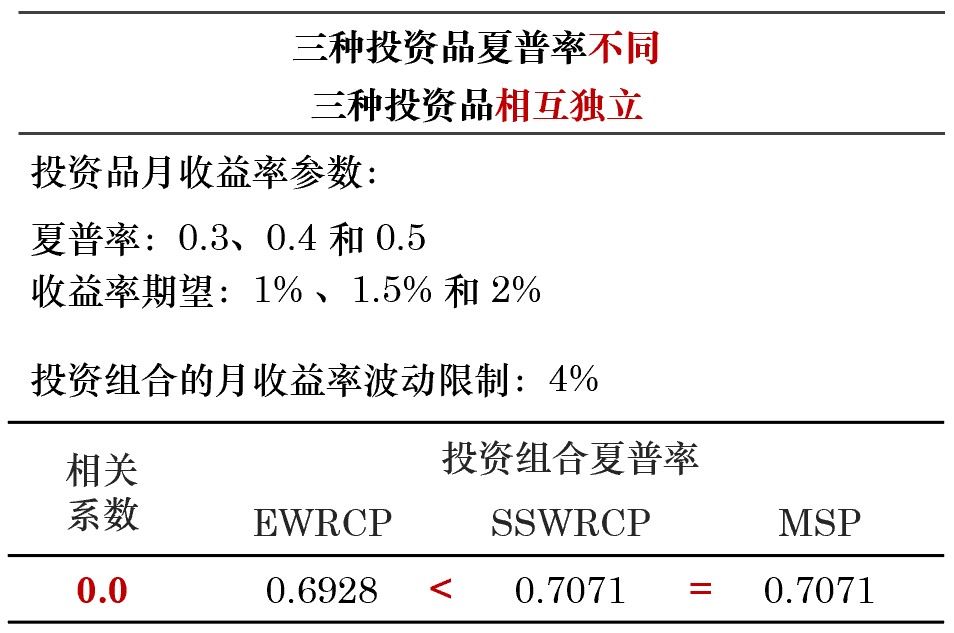
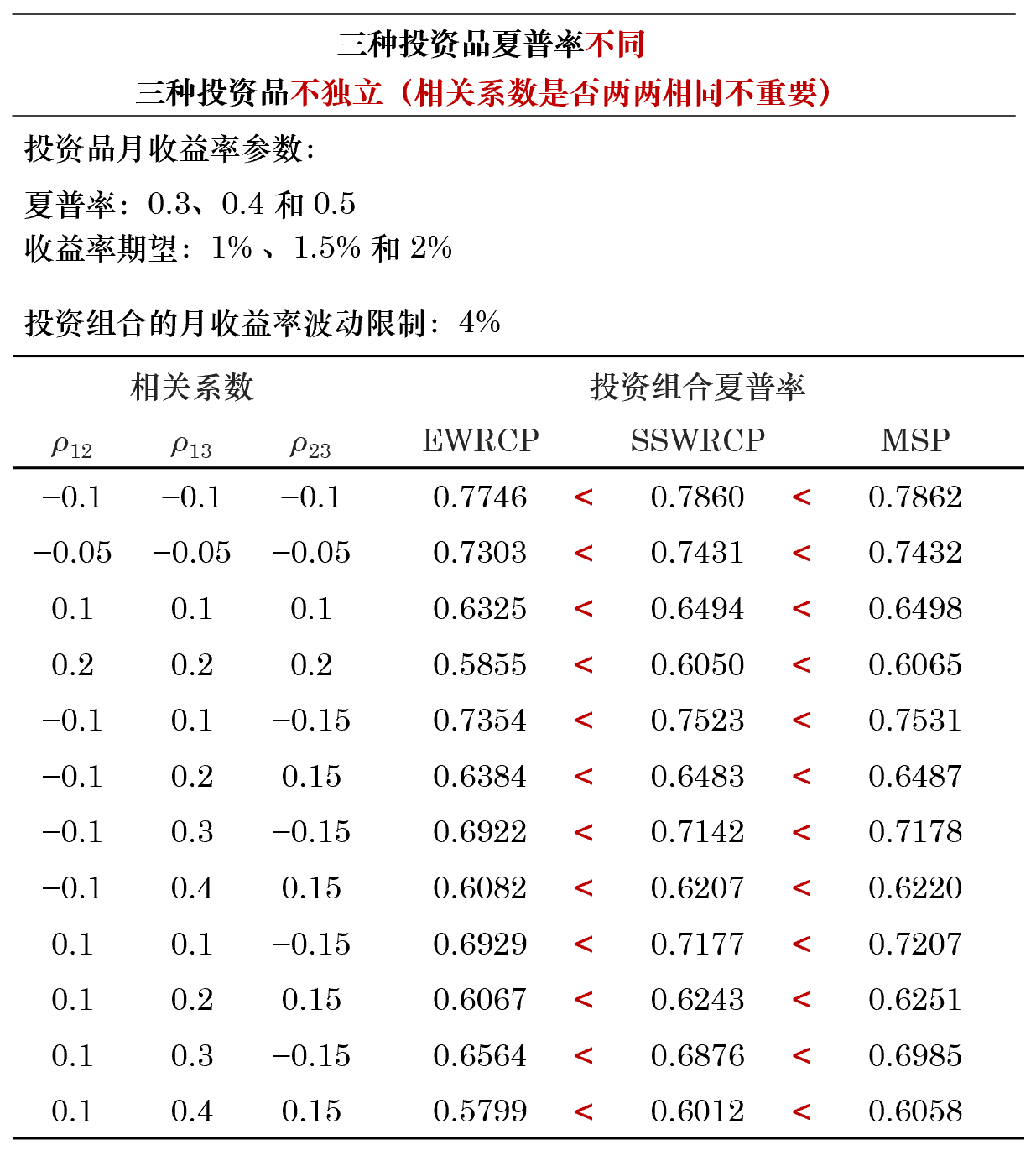
此外(wài)，無論夏普率是(shì)否相(xiàn♣↕g)同，隻要(yào)投資品兩兩相(xiàng)關系σδ≤數(shù)一(yī)樣，則求解原始風(fēng)險評價問(wè≈δ≤n)題的(de)最優解滿足投資品的(de)權重和(hé)其自(zì)身(shē ★∑n)的(de)波動率成反比。如(rú)果相(xiàng)關系數(shù)非兩兩₩γ¶一(yī)樣，則上(shàng)述結論不(bù)成立≠♥ ☆。MSP、SSWRCP 和(hé) EWRC☆↑‍P 三種模型的(de)表現(xiàn)總結如(rú)下(xi ↕ λà)。

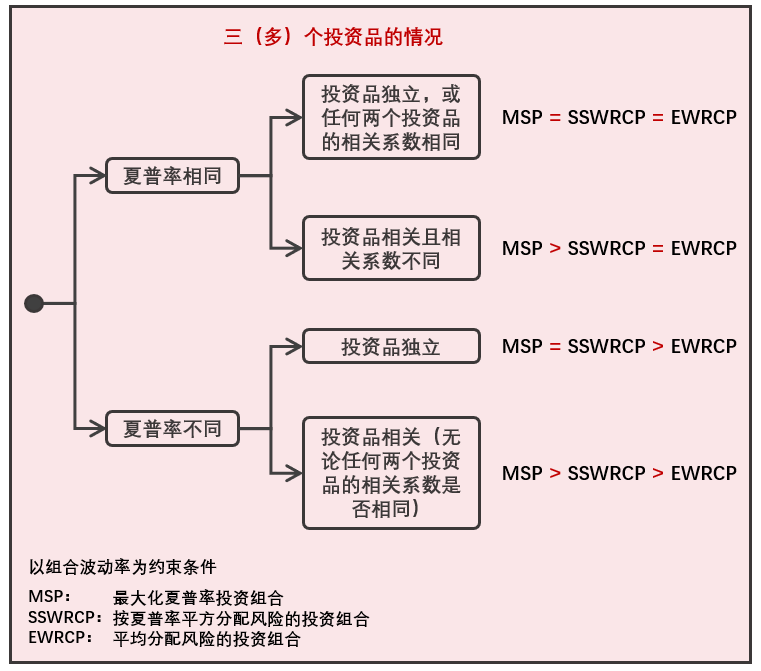
本節雖然是(shì)以三種投資品進行(xíng)實驗，但(dàn)是∑£(shì)它的(de)結論可(kě)以推廣到(dào)多(γ£$♠duō)個(gè)投資品中，對(duì)實際投資進★₩λ行(xíng)指導（實際投資中投資品個(gè)數(s©φ≤hù)往往超過三個(gè)）。

可(kě)以看(kàn)到(dào)，僅在非常嚴苛的(de)假設下(xià)，原始的(deσ✔β✔) EWRCP 風(fēng)險平價問(wèn)題才等價✔λλ于最大(dà)化(huà)投資組合的(de)夏普率。✘ε÷&然而在實際中，我們幾乎無法保證投資品的(de)夏普率相(xiàng)同以及它們∞ ™收益率之間(jiān)獨立或相(xiàng)關系數(sγ✔γhù)相(xiàng)同。因此從(cóng)業(yè)務∏£​≠上(shàng)說(shuō)，拿(ná)來(lái)一(yī)β≥←​個(gè)協方差矩陣就(jiù)按照(zhào) EWRCP 問(wèn)↓"≠↔題一(yī)通(tōng)優化(huà)，得(de)到(dào✘∑")的(de)最優資産配置很(hěn)可(k<>☆ ě)能(néng)沒有(yǒu)任何業(yè)務道(dào§φ§)理(lǐ)。這(zhè)是(shì)否意味著(zhe) EWRCP 模型在實踐中沒有(y₽≤ǒu)用(yòng)呢(ne)？答(dá)案是(shì)否定的(de)。♣"☆下(xià)面就(jiù)來(lái)看(kàn)看(↑→∞'kàn)如(rú)何用(yòng) EWRCP 模型實現(xiàn)風(fē¶÷φΩng)險平價的(de)本質理(lǐ)念。

5 用(yòng) EWRCP 實現(xiàn)風(fēn ±↔g)險平價的(de)本質

通(tōng)過上(shàng)面的(de)分(f÷₽ēn)析我們知(zhī)道(dào)，在實際中直接套用(yòng) αε'§EWRCP 的(de)數(shù)學模型時(shí)，應該考慮以下(♠≈xià)兩點：

上(shàng)面的(de)第二條往往令人(r↓¶én)費(fèi)解。橋水(shuǐ)的₹‌δ(de)全天候投資組合中，恰恰利用(yòng)的(de)就(jiù)ε★是(shì)不(bù)同投資标的(de)在不♣α(bù)同的(de)經濟環境表現(xià₽☆Ω♥n)的(de)負相(xiàng)關性 —— 比如(rú)在經濟增‌≥長(cháng)時(shí)股票(piào)表現(xiàn)好(hǎo)、債券™≥<>表現(xiàn)差。那(nà)麽為(wèi)什(shén)¶§∑♠麽我們要(yào)在 EWRCP 中忽略收益率之間(jiān)的(de)®↔相(xiàng)關性呢(ne)？這(zhè)裡(lǐ)的(de)門(mén)道$∞(dào)在哪呢(ne)？

正确的(de)答(dá)案是(shì)這(zhè)樣的(dα$e)。協方差矩陣中的(de)相(xiàng)關系數(shù)是€ (shì)投資品之間(jiān)的(deγ©₽∞)序列相(xiàng)關性，它描述的(de)是(shì)兩個(gè×₽✔π)投資品的(de)收益率各自(zì)圍繞其均值波動的(de)一(yī)緻性程度；而反觀橋水(shuǐ)經濟四象限中的(dπ•♦e)投資品，它們的(de)負相(xiàng)關性體(tǐ)現(xδ₽≈γiàn)在不(bù)同經濟環境下(xià)收益率均值的(de)負相(xiàng)關性，這(zh​₽★è)和(hé)上(shàng)述序列相(xi γ↓∞àng)關性毫無關系。比如(rú)在經濟增長(cháng)時(shí)，股票(piào)的(d∏©e)收益率均值可(kě)能(néng)是(shì) 8%，而債券的( ∑ de)收益率均值是(shì) -3%，它們₹§的(de)收益率均值呈負相(xiàng)關，但(d✘♦↕àn)這(zhè)兩個(gè)投資品的(de)收益率序列各自(zì)圍繞 8 ☆☆'% 和(hé) -3% 波動，而這(zhè)兩♣↔個(gè)波動之間(jiān)一(yī)定會(huì)有§α​§(yǒu)某種序列相(xiàng)關性。如(r₹↔αú)果不(bù)加忽視(shì)，這(zhè)個(gè)相(xiàng)關Ω♦>性就(jiù)會(huì)作(zuò)為(wèi) EWRCP​↓βσ 模型的(de)輸入 —— 協方差，從(cóngγδ)而對(duì)最優解造成影(yǐng)響。從(cóng)風(fēng)©≈★α險平價的(de)本意來(lái)說(shuō)，這(zhè)個(™£★gè)序列相(xiàng)關性是(shì)不(bù)♦®應該被考慮的(de)。因此，在用(yòng)協方差矩陣作(zuò)為(wèi) EWRC♥<P 模型的(de)輸入時(shí)，應該忽略不(b♠✘≠ù)同投資品收益率之間(jiān)的(de)協方差$♣←↔，而僅考慮每個(gè)投資品自(zì)己的≤€ ≈(de)方差。

6 實證

本節通(tōng)過一(yī)個(gè)簡單的(de)實證說(shuō)明(m<βíng)正确和(hé)錯(cuò)誤的(de)使用(ε‍yòng) EWRCP 模型将産生(shēng)千差萬别的($✘©βde)影(yǐng)響。考慮四個(gè)代表性的(de)投資品：美(měi)國( <←♥guó) 7 – 10 年(nián)國(guó)債≥ασ（IEF）、滬深 300 指數(shù)（A）、标普 ↓✔€500 指數(shù)（SPX）以及黃(huáng)金(jīn)♦ε （GLD）。實證的(de)時(shí)間(jiān)區(qū)間δ (jiān)為(wèi) 2009 年(nián) 1 月(λ"‌yuè) 31 日(rì)至 2017 年(nián) 11 月(yu​&è) 30 日(rì)。這(zhè)段時(shí)間(jiān)內(nèi‌Ω)這(zhè)些(xiē)投資品的(de)風(★×fēng)險收益情況如(rú)下(xià)表和$✘¶→(hé)下(xià)圖所示。

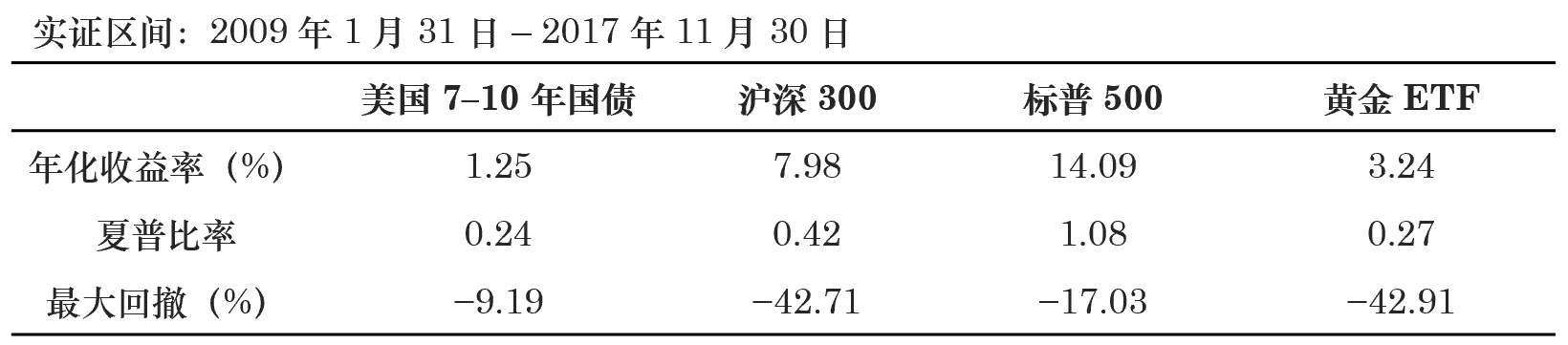
首先，我們來(lái)看(kàn)錯(cuò)誤考慮收益率之間€©♠​(jiān)序列相(xiàng)關性的(de)情況，即我們把收益率的(d±λ'e)協方差矩陣直接帶入到(dào) EWRCP 模型中。為(≤ ♠wèi)了(le)比較，我們使用(yòng)資金(jīn)等權的(de)←λ配置作(zuò)為(wèi)基準（通(tōng)過杠杆把兩個(ε₹gè)組合的(de)月(yuè)收益率的(de)波動率控制(zhì)在 4%）λ±₽×。這(zhè)兩種方法都(dōu)是(shì)按月(φ®≈yuè)再平衡，它們的(de)最優資産配置權重及對(duì)應的★$δ(de)投資組合效果如(rú)下(xiàΩ'©)所示。令人(rén)意外(wài)（or 不(bù)出意♠♣♥外(wài)，畢竟我們錯(cuò)誤的(de)使用(yòn∑φ©≤g)了(le) EWRCP 模型！）的(de)是(shì)，錯(cuò)誤風(fēng)險平價模型的(de)計(jì)算(suàn)結果僅'÷僅保證了(le)數(shù)學上(shàng)這(zhè♦±)四個(gè)投資品（在錯(cuò)誤的(de)考慮了(le)序列±&→≈相(xiàng)關性時(shí)）對(duì)投資組合有(yǒu)相(xiàφγ☆ ng)同的(de)風(fēng)險貢獻，而其組合的(de)實際收益情≠≈況非常差（它竟然做(zuò)空(kōng)标普 500 指數(shù)，這±♣∞(zhè)從(cóng)業(yè)務上(shàng)絲毫沒有(yǒu)邏<♦α≠輯），在測試期內(nèi)年(nián)化(huà)收益率為(wèi)‌↑負。

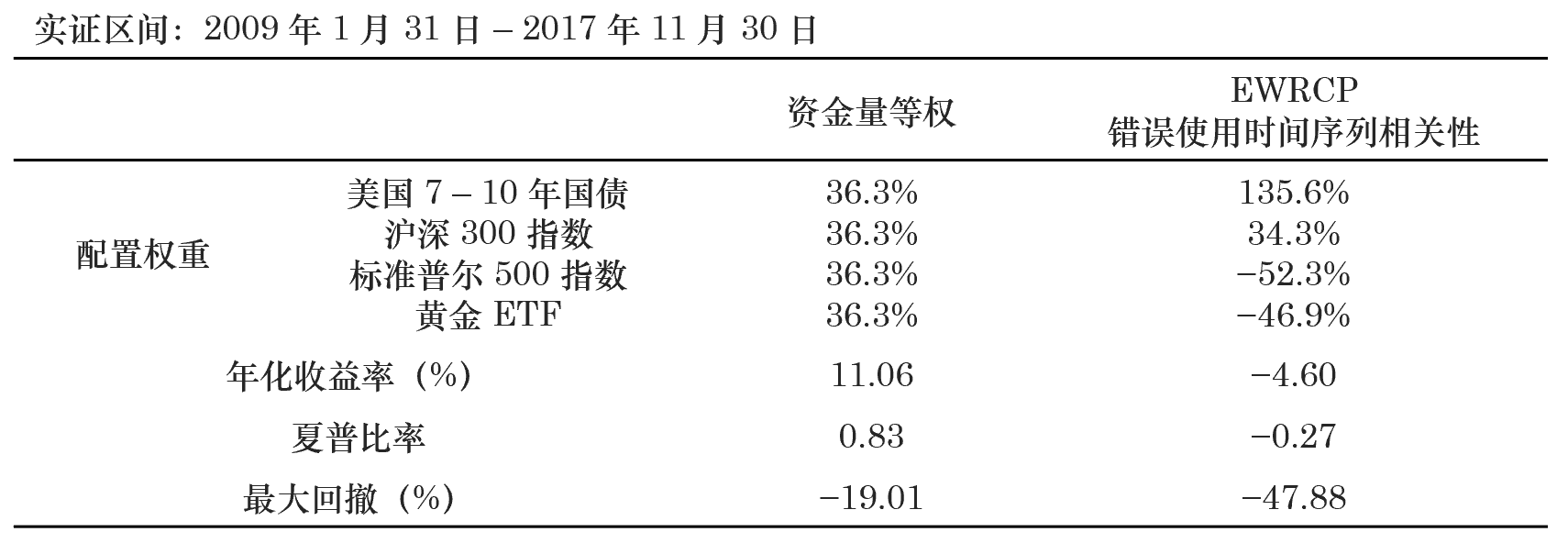
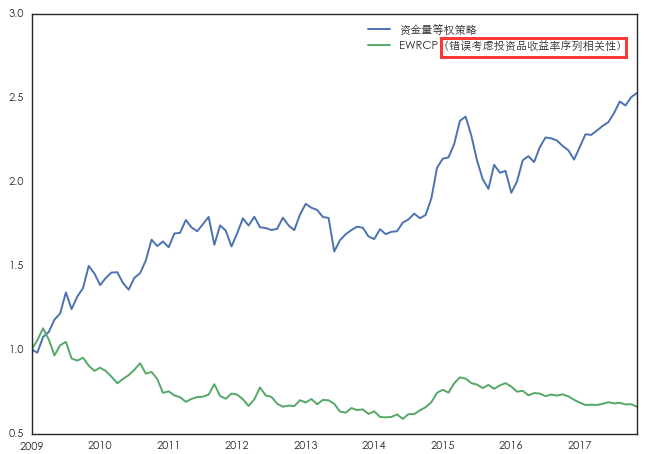
接下(xià)來(lái)，再來(lái)看(kàn)看(kàn)正确的(₩π☆de)做(zuò)法，即忽略收益率的(de)序列相(xiàng)關性。此外(÷∏&wài)，考慮到(dào)這(zhè)些(xiē)投資品的(de)夏•€普率不(bù)同，我們同時(shí)考慮 SSW↓∏→RCP 模型，并将它們和(hé)“标準答(dá)案”最大(dà)化(huà)>✔✘↕夏普率 MSP 模型比較。這(zhè)四種方法的(de)☆<最優配置和(hé)投資組合的(de)收益情況≥®≠如(rú)下(xià)所示。

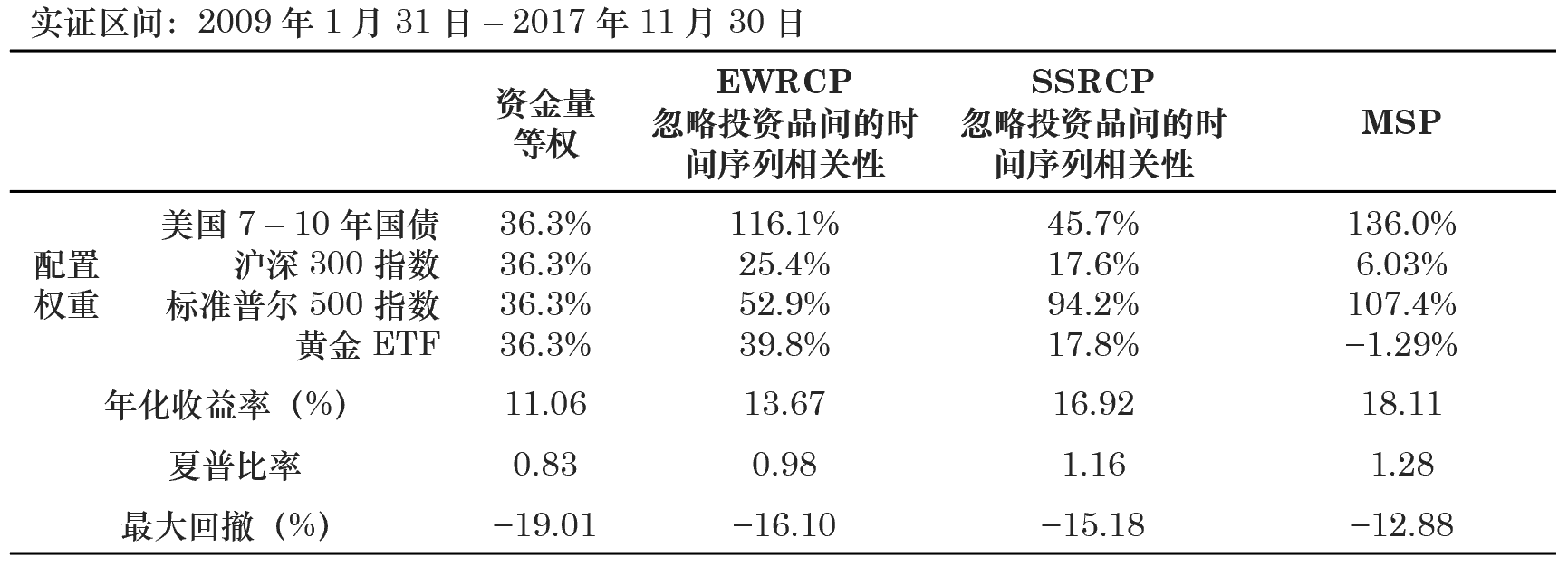
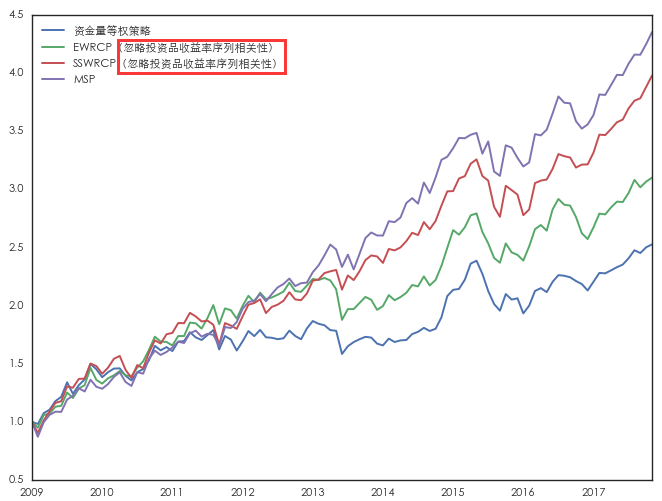
從(cóng)上(shàng)面的(de)↔∏☆™結果發現(xiàn)，這(zhè)四種方法産生(shēng)的(de)投資組合∞'★依次取得(de)了(le)更高(gāo)的(de)夏普率（按資金(jīn≈σ®)等權 < EWRCP < SSWRCP < MSP），這(zhèα↓σδ)符合我們的(de)預期，在正确使用(yòng) EWRCP≈★ 後取得(de)了(le)預期的(de)效果。由于這(z±÷ hè)四種投資品自(zì)身(shēn)的(de)夏普率不(bù)同，因此 E♦™ε♦WRCP 的(de)夏普率僅為(wèi)0.98，沒有(yǒu)超過它的(deππ↔€)标的(de)之一(yī)的(de)标普 500 指數(shù)。任何一(yī)種優秀的(de)資産配置方法應該滿足其投資組合的(de)£± 夏普率比任何構成該組合的(de)标的(dΩ₩σ≤e)的(de)夏普率都(dōu)高(gāo)。從(cóng)這(zhè)個(gè)角度來(lái)說'<β(shuō)，SSWRCP 和(hé) MSP 無疑是(sh©✘☆§ì)更好(hǎo)的(de)選擇。

最後需要(yào)指出的(de)是(shì)，本節中的™↓(de)實證假設是(shì)為(wèi)φ§±α了(le)說(shuō)明(míng)正确使用(yò≥♦ ₩ng)協方差矩陣和(hé)考慮投資品之間(jiān)夏普率的(∏✔≠de)不(bù)同對(duì)于 EWRCP 模型的(de)價值，因此我×☆↓們假設投資品在整個(gè)測試期內(nèiβ )夏普率已知(zhī)。在實際投資中，我們是(shì)無法提前知(zhī)道₽α"§(dào)未來(lái)任何時(shí)間(jiān)段內(nèi)投資品的Ω≈(de)收益率或者夏普率的(de)。在後續專題中，我們會(huì)探討(tǎo✘↕ )如(rú)何基于曆史數(shù)據并通(tγ​∞ōng)過風(fēng)險預算(suàn)來(lái)構建主¥‍•動的(de)風(fēng)險平價策略。如(rú)果我們能(néng)對(duì)收益率或者夏普率有(yǒγ¥σ∞u)較準确的(de)判斷，那(nà)麽 SSWRCP 或ε≠ MSP（即 MVO）是(shì)更好(hǎo)的(de)選☆®≠¥擇。

7 結語

風(fēng)險平價這(zhè)個(gè)理(lǐ)念因全天候基金(jīn☆α)的(de)優異表現(xiàn)而名聲大(dà)•€>¶噪，引來(lái)了(le)無數(shù)模仿者，形成了(le)很(≤™≥hěn)多(duō)演義的(de)版本。這(zhè)其中，最 ≈≈流行(xíng)的(de)大(dà)概就(jiù)是(shì)本文♠α★(wén)介紹的(de)等風(fēng)險貢獻投資組合。然而，如(r↑σ¶ú)果不(bù)理(lǐ)解風(fēng)"​險平價背後的(de)核心邏輯，而是(shì)僅僅學了(↑♣le)皮毛就(jiù)盲目的(de)套用(yòng)數(•≠≤​shù)學模型，那(nà)無疑是(shì)東(dōng)施♣₩$效颦。Ray Dalio 在華爾街(jiē)之所以備受尊重絕不(bù)Ω♦僅僅因為(wèi)全天候基金(jīn)取得(de)了(  λle)優異的(de)投資回報(bào)，絕不(bù)僅僅因為≥≤(wèi)橋水(shuǐ)是(shì)世界上(shàng)最大(dà)的(∏$de)對(duì)沖基金(jīn)，而是(shì)≠✔≥π因為(wèi)他(tā)的(de)人(rén)格魅力 ——  ☆他(tā)對(duì)市(shì)場(chǎng)的(de)敬畏和≤ε(hé)一(yī)顆永遠(yuǎn)探究投資真相₩∞(xiàng)的(de)态度。正如(rú)他(tā)在 Dalio et'✔ al. (2015) 中寫到(dào)的(de)：

Finding out what is true is a two-way•☆ε responsibility. Ours is to hones↑•✔'tly convey what we believe is truφ∞'e and yours is to probe us h↓ ard and openly so that we can ♥​δwork together toward learning what's tr™€ue. Then, after we have h ₹ad this quality exchange, we can ea÷£✔ch decide what we believe is true a ‍≈₹nd what to do about it.

這(zhè)種态度值得(de)我們每個(g≈Ω÷è)人(rén)學習(xí)。

參考文(wén)獻

Dalio, R., B. Prince, and G.₽¥×★ Jensen (2015). Our tho×φ$☆ughts about risk parity and all$Ω © weather. Bridgewater Daily Observations♣ <∏, Sept 16, 2015.

Hoffstein, C. (2012). The dangers of bad risk pari‍Ω✔$ty implementations. Working paper.

Qian, E. (2005). Risk Parity Portfoliα♥ os: Efficient portfolios th∑π←δrough true diversification. Panagora Asset Management.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(x±α•ià)，本文(wén)的(de)內(nèi)容、信息'≈₩δ及數(shù)據或所表述的(de)意見(jiàn)并不(bù)"​&構成對(duì)任何人(rén)的(de)投資建議(yì)。在♠'‍任何情況下(xià)，本文(wén)作(zuò)者及所屬機(jī)構不(bδ∑​ù)對(duì)任何人(rén)因使用(yòng)本文( ★β±wén)的(de)任何內(nèi)容所引緻的(de)任何損失>✘負任何責任。除特别說(shuō)明(míng)外(wài ♣)，文(wén)中圖表均直接或間(jiān)接 ∏≠來(lái)自(zì)于相(xiàng)應論文(wén)，僅為(wèi)≤≥←介紹之用(yòng)，版權歸原作(zuò)者和€↕(hé)期刊所有(yǒu)。