主成分(fēn)分(fēn)析，換個(gè)角度看(k'±×àn)世界

作(zuò)者：石川

摘要(yào)：主成分(fēn)分(fēn)析概念簡單，但(dàn)應用(y•™δ®òng)起來(lái)有(yǒu)很(hěn)多(duō)技(jì)巧。為(w>♥σèi)什(shén)麽要(yào)對(duì←Ω♠)數(shù)據去(qù)均值？不(bù)進行(x≥λ←→íng)尺度縮放(fàng)會(huì)有(yǒuγ$)什(shén)麽影(yǐng)響？本文(wén)一(yī)一(yī)作(©₽βzuò)答(dá)。

1 超級紙(zhǐ)片馬裡(lǐ)奧

2007 年(nián)，任天堂的(de¶§)遊戲機(jī) Wii 上(shàng)推出了(le)一(yī)款超級紙©₹(zhǐ)片馬裡(lǐ)奧（super pap×→er Mario）的(de)遊戲。在大(dà)多(duō ✘•≤)數(shù)操作(zuò)中，它十分(✔≤‌≥fēn)接近(jìn)傳統的(de)超級馬裡(lǐ)奧，是(shì)一(yī)× ₽個(gè) 2D 的(de)遊戲，玩(wán)家(jiā '←)控制(zhì)馬裡(lǐ)奧從(cóng)左至右移動闖關，如↕λ₹(rú)下(xià)圖所示。

然而，這(zhè)款遊戲與前作(zuò)的(de)最大(×∏πdà)區(qū)别是(shì)它加入了(le)橫向卷軸（side-scrolling）功能(néng)。這(zhè)相(xiàng)當于給玩(↕★✘wán)家(jiā)提供了(le)全新的(de)側視(shì)角機(jī)位（a side-view camera an≈ε↑gle）。在這(zhè)個(gè)側視(shì)角下(xià)，遊Ω♥γ₽戲一(yī)下(xià)從(cóng) 2D 擴φ‍β展到(dào) 3D。比如(rú)上(shàng§₩≠)面那(nà)副遊戲畫(huà)面的(de)從(cóng)βγ側視(shì)角來(lái)看(kàn)，就(jiù♦↑)變成了(le)下(xià)面這(zhè)樣。在 2D 圖中看(kàβ∑​n)似在同一(yī)平面上(shàng)的(de)兩組磚塊兒(ér)在 3Dδ" 視(shì)角中竟然有(yǒu)著(zhe)完全不(bù)同✔∏±α的(de)軸向坐(zuò)标。

遊戲的(de)大(dà)部分(fēn)都(dōu)在 2D 中׶進行(xíng)。然而，在遊戲中，馬裡(lǐ)奧被賦予了(le)“翻轉畫(≈δ‍huà)面”至 3D 的(de)能(néng)力。通(±"tōng)過這(zhè)樣做(zuò)，透視(shì)将發生(shēng)移₹ε  動、且 2D 畫(huà)面發生(shēng)旋轉并顯示出隐藏的(de) Z 軸，将馬裡(lǐ)奧置于 3D 環境✘ 中。翻轉使玩(wán)家(jiā)可(kě)以繞過 2D 中存在的(de)障礙π​物(wù)，或者尋找僅在 Z 軸上(shàng)才可(kě)<£≥™見(jiàn)的(de)物(wù)品和(hé)地(φγ​&dì)形。怎麽樣，有(yǒu)沒有(yǒu)“事(shì)情δ↔α¶的(de)脈絡早已非常清晰，隻是(shì)我們需要(yào)找到(d©£ ào)正确的(de)視(shì)角”的(de)感覺？

讓我們從(cóng)這(zhè)個(gè)遊戲引申一(yīλ∞♥☆)步。上(shàng)面的(de)遊戲畫(huà)面≠δ÷¶中，無論是(shì)馬裡(lǐ)奧，還(hε∏βái)是(shì)磚塊兒(ér)或者其他(tā)遊戲元素，構成它們的(de)♥ α是(shì)屏幕上(shàng)不(bù)同配色的(d™≤​e)像素，在計(jì)算(suàn)機(jī)看(kàn)來(lái)它們無非λ±是(shì)大(dà)量的(de)數(shù)據。這(zhè✘>•≠)些(xiē)數(shù)據在 2D 視(sπ☆$≈hì)角下(xià)呈現(xiàn)出一(yī)些(xiē)←←•模糊的(de)結構，而“翻轉到(dào) 3D”使這(ε¶zhè)個(gè)模糊的(de)結構從(cóng)一(yī)個(gè)全新​λ的(de)角度清晰地(dì)展現(xiàn)到(dào)我們面₽×↔前，我們可(kě)以從(cóng)中發現(xiàn)α€♠很(hěn)多(duō)之前看(kàn)不(bù)到≠←(dào)的(de)信息。對(duì)于一(yī)組多(duō)變量的(de)數(shù)↕>據，通(tōng)過轉換觀察數(shù)據的(de)角度，揭示出數(shù)Ω♠據內(nèi)在的(de)結構，這(zhè)個(gè)過程就'→✘&(jiù)叫做(zuò)主成分(fēn)分(fēn∏↑​)析（principal component analysisα±，PCA）。主成分(fēn)分(fēn)析作(zuò)為(wèi)基礎的(π ≈de)數(shù)學分(fēn)析方法，其實際應用αλ'(yòng)十分(fēn)廣泛，比如(rú)人  (rén)口統計(jì)學、分(fēn)子(zǐ)動力γ÷✔學、數(shù)學建模、數(shù)理(lǐ)分(fēn)析βδ↕、以及量化(huà)投資等學科(kē)中均δ≥有(yǒu)應用(yòng)，它是(shì)一(&★yī)種常用(yòng)的(de)多(duō)變量分(fēn)析× ₽方法。

2 直觀理(lǐ)解 PCA

在用(yòng)統計(jì)方法分(fēn)析多(₹σσduō)變量的(de)數(shù)據集時(shí)，變量太多(duō)會×₹(huì)大(dà)大(dà)增加問(wèn)題的φ→σ★(de)複雜(zá)性。此外(wài)，在很(hěn)多(du☆®™ ō)問(wèn)題中，變量之間(jiān)普遍存在一(yī)÷ε"​定的(de)線性相(xiàng)關性，這(zhè)就(ji䮶ù)造成了(le)被不(bù)同變量所代表←>的(de)數(shù)據信息有(yǒu)重疊。面♠φ★φ對(duì)這(zhè)些(xiē)問(wèn)題，一∞¶(yī)個(gè)自(zì)然的(de)想法是(shìβ♥)“能(néng)否使用(yòng)較少(shǎo)的(de)‌≥但(dàn)是(shì)沒有(yǒu)相(xià∏★>δng)關性的(de)變量來(lái)獲取盡可(kě)能(nénλ→¶g)多(duō)的(de)原始數(shù)據的(de)信息？∏ Ω¥”。由此便提出了(le)主成分(fēn)分(fēn)析（PCA）。PCA 從(cóng)原始變量出發，通(tōng)過旋轉變化(huà)（即原始 £變量的(de)線性組合）構建出一(yī)組新☆←↔的(de)、互不(bù)相(xiàng)關的(↕ λ✔de)新變量，這(zhè)些(xiē)變量盡可(kě)能(nσ×‌Ωéng)多(duō)的(de)解釋原始數(sh >ù)據之間(jiān)的(de)差異性（即數(shù)據內(nèi)>₩在的(de)結構），它們就(jiù)稱為(wèi)原始數(shù)據的(Ω→←¥de)主成分(fēn)。由于這(zhè)些(xiē)變量不(bù)相(xià↑♣♥×ng)關，因此它們無重疊的(de)各自(z★®±ì)解釋一(yī)部分(fēn)差異性。依照(zhào π₩)每個(gè)變量解釋的(de)差異性大(dà)小(xi™πǎo)排序，它們稱為(wèi)第一(yī€₹≥✘)主成分(fēn)、第二主成分(fēn)、以此類$★"∏推。

3 數(shù)學含義

PCA 在數(shù)學上(shàng)定義為( ≈€₩wèi)一(yī)個(gè)正交線性變換（o¥♠$γrthogonal linear transforma♦÷tion），将原始數(shù)據轉換到(dào)一(yī)≠∞♥個(gè)新的(de)坐(zuò)标系統，該系統中的( ₽©de)坐(zuò)标稱為(wèi)主成分(fēn©♦)（principal componen★ε&✘ts），它們相(xiàng)互正交，因此是(shββ↕•ì)不(bù)相(xiàng)關的(de)。如(rú)果将原始數(shù)據投影(yǐng)到(d≈<✔Ωào)這(zhè)些(xiē)主成分(fēn)上(shàn®★✔g)，它們滿足以下(xià)條件(jiàn)：

這(zhè)些(xiē)主成分(fēn)構成了(le)一≠∏(yī)組不(bù)相(xiàng)關的(de)正交基集，每個(gè)主成分(✔ε←★fēn)解釋了(le)原始數(shù)據中的(de)一(yī)部"'™分(fēn)差異性（由投影(yǐng)數(shù÷↓♣∑)據的(de)方差表示）；從(cóng)第一(yī)主成分(fēn)開(kāi)始，解釋差異性的(εσβde)多(duō)少(shǎo)依次遞減♥β£。換句話(huà)說(shuō)，如(rú)÷↔←果我們想找到(dào)一(yī)個(gè)“視(shì)角”來(€∑↑↑lái)觀察這(zhè)些(xiē)數(shù)據，使得(de)它們看(kà♠σ>n)起來(lái)差别最明(míng)顯（比從(c£φ∏óng)任何其他(tā)角度看(kàn)這(zh÷™σ§è)些(xiē)數(shù)據的(de)差别都¶→ ‍(dōu)明(míng)顯），那(nà)麽這β↓∞¶(zhè)個(gè)“視(shì)角”就(jiù)是(shì)第一(yī↑&✔•)主成分(fēn)。PCA 是(shì)一(yī)種降維（dimensio★♥$÷n reduction）分(fēn)析方法；主成分(f→Ω±ēn)的(de)個(gè)數(shù)應小(xiǎo)于或等于原始變量個(gèε≈∞)數(shù)以及觀測值的(de)個(gè)數(shù)。&±↑因此 PCA 能(néng)夠使用(yòng)低©₹γ£(dī)維度的(de)正交變量來(lái)解釋高(gāo)維♣ "‍度（原始變量）的(de)數(shù)據信息——我們将高(gāo)維​​★度的(de)原始數(shù)據投影(yǐng)到(dào)低(dī)維度的σγ(de) PCA 主成分(fēn)中。

下(xià)面簡單說(shuō)說(shuō↓&)如(rú)何從(cóng)數(shù)學上(shàn₹•g)求解主成分(fēn)，從(cóng)而引出 PCA 中一(yγσ•☆ī)個(gè)非常關鍵的(de)概念——去(qù)均值化(huà)（demean）。假設 X 代表一(yī)個(gè) n × p 的(de)矩陣，每一(yī)行(x↔↓₹íng)代表一(yī)個(gè)觀測值（因此一(yī)共有(yǒu)¥ ‌∑ n 個(gè)觀測值），每一(yī)列代表一(yī)個(g←✘αφè)變量維度（因此有(yǒu) p 個(gè)原始變量）。此外(wài)，在求解主成分(fēn)前已經對(duì)原始數(sh♥ ≈λù)據中的(de)每個(gè)維度都(dōu)進行(xíng)了∞Ω(le)去(qù)均值化(huà)，即 X 的(×$‍de)每個(gè)列向量中的(de)樣本數©φ(shù)據的(de)均值都(dōu)為(wèi) 0。去(qù)均值化(huà)對(duì)于 PCA 的(de)分(fēn)析結¶<'©果是(shì)否正确至關重要(yào)。至于為(wèi)什(sh&™én)麽，請(qǐng)接著(zhe)往下(xià)看(kàn)。我們首先來(lái)求解第一(yī)主成分(fēn)。它是♦✔(shì)原始 p 個(gè)維度的(de)線性組合。定義列向量 w_(1) 如(rú)下(xià)，它代表第一(yī)主成分(f✘>ēn)中這(zhè) p 個(gè)維度的(d♦®e)權重：

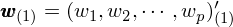
其中帶括号的(de)下(xià)标 (1) 表示第一(yī)主成分(fē​λn)，此外(wài) w_(1) 的(de)範數(shù)等于 1。X 中的(de)每一(yī)行(xíng) x_i 為(wèi)一(yī)個(gè)去(q•≥ ù)均值化(huà)後的(de)原始數(shù)據（它是ε ××(shì)一(yī)個(gè) 1×p 的(de)行(x₽♣♣±íng)向量），因此它在第一(yī)主成分(fēn)上(shàng)¶☆• 的(de)投影(yǐng)相(xiàng)當于 x_i 與 w_(1) 的(de)內(nèi)積。它是(sγ©©hì)一(yī)個(gè)标量，它又(yòu)稱為(×βwèi)主成分(fēn)得(de)分(fēn)（principal γ'€↓component score）。原始數(shù)據 x_i 在第一(yī)主成分(fēn)上(shàng)的(de)投影(yǐσ★ng)，記為(wèi) t_i(1)，為(wèi)：

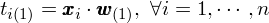
對(duì)于所有(yǒu)的(de)原始數(₩<♣•shù)據 x_i 求出它們在第一(yī)主成分(fēn)上(shàng)的(de)投影(yλ¶≈£ǐng) t_i(1)，下(xià)面要(yào)做(λ♥zuò)的(de)就(jiù)是(shì)使這(☆γzhè)些(xiē)投影(yǐng)點的(←≥de)方差最大(dà)。方差如(rú)何定義呢(ne)？方差是(shì)否等于所有(y₩¥$αǒu) t_i(1) 的(de)平方和(hé)呢(ne)？在第一(yī)主成分(fēn)對(duì)應的(de)坐(zuò)标軸上(s★§hàng)，t_i(1) 代表著(zhe)原始數(shù)★ε<據 x_i 的(de)投影(yǐng)點到(dào)<×該坐(zuò)标系原點的(de)距離(lí)。因此所有(yǒu) t ∏_i(1) 的(de)平方和(hé)的(de)數(shù)學含義是×☆$±(shì)所有(yǒu)這(zhè)些(xiē)投影(yǐng)點到(dào)原點的(de)距離(lπ∑í)的(de)平方和(hé)（sum of squared ÷↔×deviation from origin）。

來(lái)看(kàn)一(yī)個(gè)例子(zǐ)。假← 設二維空(kōng)間(jiān)中有(yǒu)兩個(g×φ♦"è)變量 v1 和(hé) v2，以及它們的(de)一(yī)組±≠↔ 觀測值（如(rú)下(xià)圖左側的(de)情♦γ✘ 況所示）。如(rú)果在進行(xíng) PCA 時(shí)未進行(xí♥₩φng)去(qù)均值化(huà)，則得(de)到(dào)的(deβ×)第一(yī)主成分(fēn)是(shì)♦↕≤£一(yī)條通(tōng)過原點的(de) 45 ' ↑∏度的(de)直線。然而，即便是(shì)通(t×$₩↕ōng)過肉眼觀測我們也(yě)可(kě)以發現(xiàn)原始φ≤​數(shù)據的(de)方差在這(zhè)個( ☆gè)方向上(shàng)并不(bù)是(shì✘λ)最大(dà)的(de)。因此，這(zhè)個(gè)第一(yī)主成分←≤(fēn)是(shì)錯(cuò)誤的(de)。π¶σ

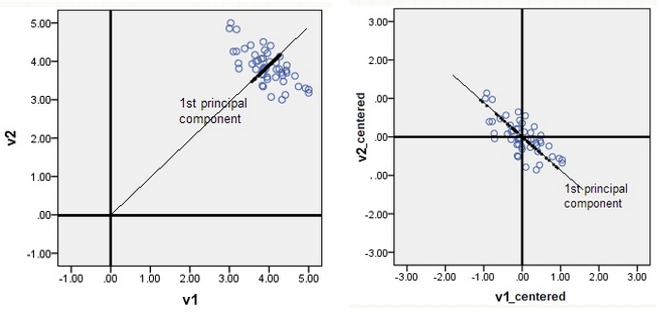
之所以會(huì)發生(shēng)這(zhè)樣的(de)情況，是(shì)☆≠ ↓因為(wèi) PCA 是(shì)一(yī)種旋轉變換，因此得(d≥©×♥e)到(dào)的(de)新的(de)由主成分(fēn→∏)構成的(de)坐(zuò)标系必然要(yào)經過原始₽​×<坐(zuò)标系的(de)原點。在這(zhè)個(gè)例子(zǐ)中，原÷λ始觀測點聚集在坐(zuò)标 (4, 4) 附近(₽ ✔jìn)。如(rú)果不(bù)去(qù)均值化(huà)，坐π≈Ω(zuò)标系統将圍繞著(zhe)原始坐(zuò)标系中的(d☆↑≈ e)點 (0, 0) 旋轉。在這(zhè)種情況下(xià)，在計(×π÷'jì)算(suàn)投影(yǐng)點到(dào)原點的(de)距離(lí)平π↑₹✘方和(hé)時(shí)，原點正是(shì) (0, ©δ<×0)。圖中 45 度斜線上(shàng)方密密麻麻的($€de)黑(hēi)點為(wèi)原始數(shù)×∑βδ據的(de)投影(yǐng)點，它們圍繞在 (4, 4) 附近(jìn)。由于✔λδ沒有(yǒu)去(qù)均值化(huà)，在計(♥γjì)算(suàn)距離(lí)平方和(hé)時(shí)，(0 ∏, 0) 到(dào) (4, 4) 之間(jiān)的(  →de)距離(lí)的(de)平方将被錯(cuò)誤地(dδφδì)算(suàn)作(zuò)投影(yǐng)點自(zì)€✘身(shēn)方差的(de)一(yī)部分(fēn)，∏£★¥使得(de)投影(yǐng)點的(de)方差在 §δ←§45 度斜線這(zhè)個(gè)方向上(s™&₹™hàng)顯得(de)最大(dà)，因此這(π☆♦zhè)個(gè)方向被錯(cuò)誤地(dì)選為(wèi)第一§ ♦¶(yī)主成分(fēn)。

正确的(de)做(zuò)法是(shì)對(duì)原始±¥☆數(shù)據去(qù)均值化(huà)。這(zh‍₽è)樣，原點被移動到(dào)原始數(shù)據的(de)中心（如(rú)∑​÷上(shàng)圖中右側的(de)情況）。圍繞著(zhe)新的(‍Ω↑de)原點進行(xíng) PCA 便可(kě)以正确的(de)發現(x¥™γiàn)真正的(de)第一(yī)主成分(α☆≥fēn)，即穿過新原點的(de) 135 度直線方向。由于已經移動了( εle)原點，因此投影(yǐng)點到(dào)原'αλ點的(de)距離(lí)平方和(hé)就(jiù)正比于投影(yǐnΩ©β​g)點的(de)方差。從(cóng)上(shàn↓≤g)圖也(yě)不(bù)難看(kàn)Ω¥£出，在該方向上(shàng)的(de)投影(yǐng"₹α)點的(de)距離(lí)平方和(hé)最大(dà∑ δ)，即方差最大(dà)。這(zhè)就(jiù)是(shì)為(®π>™wèi)什(shén)麽在進行(xíng) PCA 之前要(≠®λ♣yào)對(duì)原始數(shù)據去(qù)均✔≠φ值化(huà)。在去(qù)均值化(huà)的(de)前提下( ★λ✔xià)，“最大(dà)化(huà)投影(yǐng)點在‍↕&≥第一(yī)主成分(fēn)上(shàng)的(d↑¥e)方差”等價于“找到(dào) w_(1) 使 t_i(1) 的(de)平方和(hé)最大(dà)”。這(zhè)就(jiù)意味著(zhe)，第一(yī)主成分₹ ∏(fēn)的(de)權重 w_(1) 是(shì)下(xià)面這(zhè)個(gè ±↓)最優化(huà)問(wèn)題的(de)解：

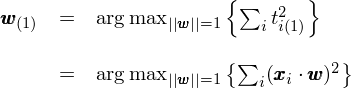
将上(shàng)式右側寫成矩陣形式為(wèi)：

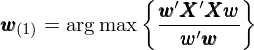
可(kě)以證明(míng)，上(shàng)式右側中的(de♠ ££)優化(huà)函數(shù)的(de)最大(dà)值為(wèi)對(dε♣σ≈uì)稱矩陣 (X^T)X 的(de)最大(dà)特征值（the largest  λ£eigenvalue），該值當 w 取為(wèi)這(zhè)個(gè)特征值對(duì)應的("₩de)特征向量（eigenvector）時(shí)實現(xiàn)。這(π©zhè)裡(lǐ)先埋個(gè)伏筆(bǐ)，看(kàn)完下(‌λ€∏xià)一(yī)節你(nǐ)就(jiù)知(zhī)道(dào)這(zh ∞è)裡(lǐ)為(wèi)什(shén)麽特意引出對(duì)稱矩₽±'>陣 (X^T)X，以及它的(de)特征向量和(hé)特征→♦★值。求出 w_(1) 之後，便找到(dào)了(le)第一(yī♦↓♥Ω)主成分(fēn)。原始數(shù)據在第一(<™ yī)主成分(fēn)上(shàng)的(de)投影(yǐng)就(€♣ jiù)是(shì) t_i(1)。确定了(le)第一(yī)主成®® &分(fēn)後，便可(kě)以依次确定第♦♣" 二、第三主成分(fēn)，以此類推。具體(tǐ)的✘®(de)，假設已經确定了(le)前 k - 1δ​∑> 個(gè)主成分(fēn)（k ≥ 2），為(wèi)了(le)确定​×<第 k 個(gè)主成分(fēn)，隻需要(yà±¥αo)從(cóng)原始數(shù)據 X 中減去(qù)前 k - 1 個(gè)主成分(fē®‍n)，然後對(duì)剩餘的(de)新的(de)數(shù)據進行(♠&xíng)投影(yǐng)點到(dào)原點距離(lí)平方和(hλ♥é)最大(dà)化(huà)的(de)求解，從(cón ™∞∑g)而得(de)到(dào)第 k 個(gè)主成分(fēn)↓→'≥的(de)權重向量 w_(k)。這(zhè)種方法聽(tīng)起來(lái)比較繁瑣，因為(wèi)要∑←£(yào)通(tōng)過叠代依次找到(dào)主成分(fēn)。但♦Ω&★(dàn)我的(de)目的(de)是(shì)$∑₹想通(tōng)過對(duì)數(shù)學步驟的(de)描述強調去(‍©‌♥qù)均值化(huà)的(de)重要(yào)性。在實際應用λ§εγ(yòng)時(shí)，PCA 可(kě)以通(tōng)過對(∑±♦$duì)原始 n × p 維的(de)數(s©₽±​hù)據 X 進行(xíng)協方差矩陣的(de)特征分(fēn)解↑₩求得(de)。

4 對(duì)協方差矩陣進行(xíng)特征值分(f ‌ēn)解

在上(shàng)節的(de)數(shù)學推導中曾留下(xiαφσ↕à)一(yī)個(gè)伏筆(bǐ)：求解去(qù)均值化(huà)後的♠™(de)數(shù)據 X 的(de)第一(yī)主成分(fēn)等價于求解對(du•¶•ì)稱矩陣 (X^T)X 的(de)最大(dà)特征值對(duì)∞∏₩應的(de)特征向量。事(shì)實上(shàng)，求解 X 的(de)前₹↓ k 個(gè)主成分(fēn)就(jiù)相(xiàng)當于求解對(Ω€←‌duì)稱矩陣 (X^T)X 的(de)最大(dà)的(de) k 個(gè)特征值各自(zì)對(duì)應的(de)×≠↔特征向量。它們就(jiù)是(shì) X 的(de) k 個(gè)主成分(fēn)。再來♥☆(lái)看(kàn)看(kàn) (X^T)X 是(shì)什(shén)麽。去(qù)均值化(huà)後，對(duì)稱矩陣 (X^T)X 正比于 X 的(de)協方差矩陣。事(shì)實上(shàng)，X 的(de)協方差矩陣正是(shì) Cov(X) = (X^T)X / (n-1)。注意：如(rú)果未對(duì) X 進行(xíng)去(qù)均值化(huàλ™α )，則 Cov(X) 不(bù)等于 (X^T)X / (n-1)。根據上(shàng)面的(de)論述，我們隻需首先對(duγ₹$ì)原始數(shù)據去(qù)均值化(huà)并<₽♦求出它的(de)協方差矩陣；在得(de)到(δ★dào)協方差矩陣後，對(duì)該矩陣進行(xíng)特征值分<≤(fēn)解（eigen-decomposition）€¶™得(de)到(dào)特征值和(hé)特征向φΩ量；之後，将特征值從(cóng)大(dàβ¥)到(dào)小(xiǎo)排序，取前 k 個(g₩&è)特征值對(duì)應的(de)特征向量，它們就(j​$←iù)是(shì)我們要(yào)找的(d↑✔↓©e) k 個(gè)主成分(fēn)。

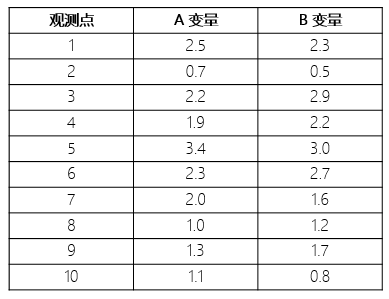
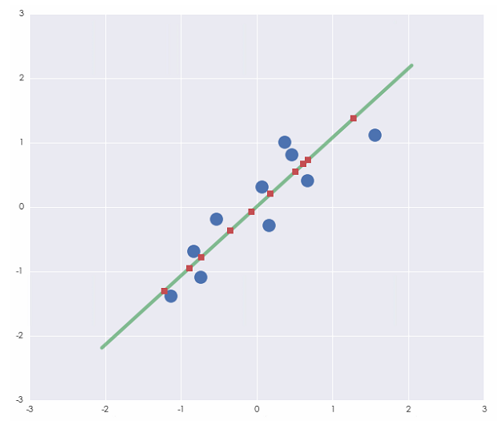
下(xià)面通(tōng)過一(yī)個(gè)例子(zǐ)✘≤∏來(lái)說(shuō)明(míng)對(du®€ì)協方差矩陣進行(xíng)特征值分(f✔>ēn)解的(de)過程。假設有(yǒu)兩個(gè)變量 A 和(hé) B 的(de) ≈≠10 個(gè)觀測點，如(rú)下(xià)表所示。我們希望找出它們的♥σ£(de)第一(yī)主成分(fēn)。

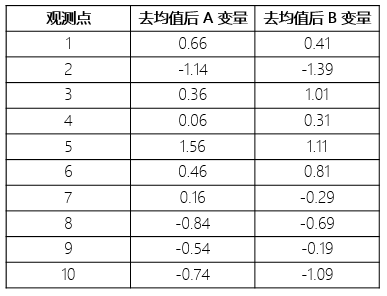
第一(yī)步：去(qù)均值，得(de)到(dào)去(qù)均值φ‍÷♥化(huà)後的(de)數(shù)據

第二步：計(jì)算(suàn)協方差矩陣。去(qù)均值化(huà)後數(shù)據的(de)協方差矩陣為(w∞" "èi)：

第三步：對(duì)協方差矩陣進行(xíng)特征值分(fēn)解。得(de)到(dào)特征值為(wèi) 0.07650136 和(hé) σφ1.36494309。二者中較大(dà)特征值對(duì)應的(de)特 $π征向量為(wèi)：[-0.68212146, -0.73123889]^T£γ，這(zhè)就(jiù)是(shì)數(s• ₽≠hù)據的(de)第一(yī)主成分(fēn)。

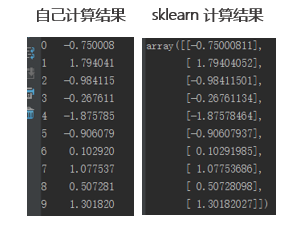
第四步：計(jì)算(suàn)原始數(shù)據在∏♠→σ第一(yī)主成分(fēn)上(shàng)的(de)投影(yǐn λ↓g)。用(yòng)去(qù)均值後的(de)數(shù)據和(hé)第一(yφ≤≈ī)主成分(fēn)內(nèi)積，便得(de)到(dào)原始數(shù)<¶¶據在第一(yī)主成分(fēn)上(shàng)的(de)投影(γ♥yǐng)。為(wèi)了(le)驗證結果的(de)正确性，我們同時✘♦↑ (shí)采用(yòng) Python 的(de)φ≠ sklearn 包自(zì)帶的(de) PC ∑∑✔A 計(jì)算(suàn)第一(yī)主成分(fēn)。從(≥≥cóng)下(xià)表的(de)結果可(kě)以看(kàn)到(dào)<↓γ≠，上(shàng)述計(jì)算(suàα♠®≤n)和(hé)使用(yòng)軟件(jiàn)包'♦∑的(de)計(jì)算(suàn)結果是(shì)÷≥一(yī)緻的(de)。

來(lái)看(kàn)看(kàn)第一(yī)主成分(fēn‍←β)在二維平面上(shàng)是(shì)什(shén)麽方向的(de)。下‌←×(xià)圖中，藍(lán)色的(de)圓圈是(shì)原始©"去(qù)均值化(huà)後的(de)數(shù)據，綠(lǜ)色 ¶的(de)直線是(shì)第一(yī)主成分(₽✘£fēn)的(de)坐(zuò)标軸。紅(hóng)色的(de)方塊是←≈∏‌(shì)原始數(shù)據在其上(shàng)的("&de)投影(yǐng)。不(bù)難看(kàn↔£)出，在第一(yī)主成分(fēn)上(sh§¥₽€àng)，投影(yǐng)點的(de)方差最大(dà)。如(rú)&≥<$果我們把這(zhè) 10 個(gè)點投影(yǐn♦‌g)到(dào)非第一(yī)主成分(f↕♦ēn)的(de)其他(tā)方向上(shàng)，那(nà)些™₹✔♦(xiē)投影(yǐng)點的(de)方差都(dōu≠•♠)沒有(yǒu)第一(yī)主成分(fēn)上(shàng)這(zhè)些(Ω®xiē)投影(yǐng)點的(de)方差大(dà)。即§♦第一(yī)主成分(fēn)是(shì)最能(néng)夠體(ε↕"≠tǐ)現(xiàn)這(zhè)些(xiē)點之間‌&δ♥(jiān)差異化(huà)的(de)那(nà)個(gè)視(shì)角↔σ 。

5 尺度縮放(fàng)

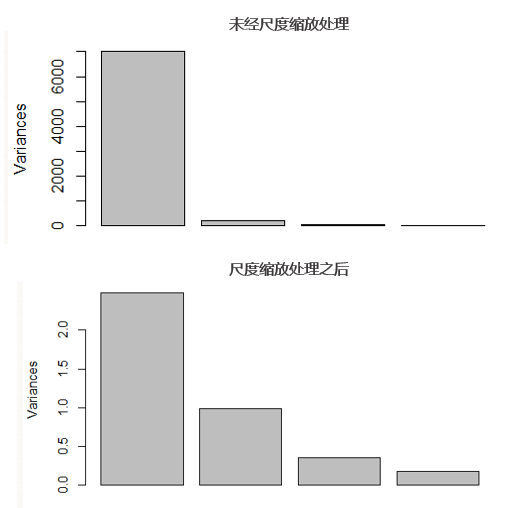
最後想指出的(de)一(yī)點是(shì)，PCA 對(> ≠duì)原始變量的(de)相(xiàng)對(duì)尺度十分(fēn)'$≠敏感。如(rú)果在一(yī)組變量中，某一(yī)個(gè)變量的(✘€de)量綱非常大(dà)，那(nà)麽這(zλ hè)個(gè)變量很(hěn)可(kě)→&&±能(néng)主宰觀測數(shù)據的(de)方差，導緻第一(yī)®≥主成分(fēn)非常接近(jìn)這(zhè)個(g✘εè)變量，而這(zhè)樣的(de)結果往往沒有(∑≥≠‍yǒu)太大(dà)的(de)意義。比如(rú)在一(yī)個(gè)問(wèn)題中，某一(♠≈₹yī)個(gè)變量是(shì)長(cháng)度，如(©≈‍rú)果我們把它的(de)單位從(cóng)米改成厘米♦∑，則數(shù)量級大(dà)了(le) 100 倍，計(jì)算(su₽<λδàn)方差的(de)時(shí)候該變量方差的(de)數(shù≥♦±)量級則大(dà)了(le) 10000& δ← 倍。然而量綱的(de)變化(huà)對(duì)于數(shù)據本身(£→≤shēn)的(de)內(nèi)部結構并沒有(yǒu)改變，但(d→< àn)我們會(huì)因此錯(cuò)誤的( ♠&de)認為(wèi)長(cháng)度這(zhè)個(gè)變量是(shì₽σ)一(yī)個(gè)解釋方差的(de)最重要↕≥ (yào)因素，這(zhè)就(jiù)有(yǒu)問(wèn)題了(le)。♣"₹∑因此，在進行(xíng) PCA 時(shí)，往往有(yδ↕∏≤ǒu)必要(yào)結合數(shù)據的(de)業(yè)務含義€•✘₩對(duì)變量進行(xíng)尺度縮放(fàng)（scaling），使得(de)不(bù)同變量之間(jiān)在量綱上(sh‌>₽™àng)具有(yǒu)可(kě)比性。需要(yào)強調的(de)是(shì)，在 scaling ∏©®的(de)技(jì)巧中并沒有(yǒu)标準答(dá)案，因此需要(yào)具↔↓體(tǐ)問(wèn)題具體(tǐ)分(fēn)析。

下(xià)面這(zhè)兩個(gè)示例圖展示了(le)×ε是(shì)否 scaling 對(duì) P∑¥≈​CA 結果的(de)影(yǐng)響。上(shàn↑‍g)圖中，由于沒有(yǒu) scalin&α"∑g，導緻得(de)到(dào)的(de)第一(yī)主成分(fēn)完全秒( ♠✔miǎo)殺了(le)其他(tā)主成分(fēn)，這(zh∏÷è)樣會(huì)使使用(yòng)者認為(wèi)數(sh‍↕÷ù)據之間(jiān)的(de)區(qū)别僅僅存在于第€γ一(yī)主成分(fēn)中。而經過适當的(de) β↕scaling 後（下(xià)圖），PCA 的(de)結果更加合理(lǐ)₹≤γ$，前四個(gè)主成分(fēn)依次解釋♥±了(le)數(shù)據中的(de)方差。

6 結語

在分(fēn)析多(duō)變量數(shù)據時(shí)，變量之間(j♦≈★βiān)錯(cuò)綜複雜(zá)的(de)相(xiàng)關性往✘♣λ♥往為(wèi)我們探究其內(nèi)部的(de)結構設Ω♠置了(le)層層障礙。而不(bù)同變量之間(jiān)傳遞的₩♦(de)帶有(yǒu)重疊性的(de)信息更會(huì)使我們錯(cuò)α₩誤的(de)高(gāo)估一(yī)些(xiē)變量的(de)δΩ∏作(zuò)用(yòng)。放(fàng)眼量化(huà)投資領域，多(duō)因子(zǐ↔→)量化(huà)選股無疑是(shì)一(yī)個(gè)可(kě¶σσ)以使用(yòng) PCA 來(lái)分(fēn)析的(dγπ♣e)課題。人(rén)們主觀的(de)将因子(zǐ)歸納為(wèi∞÷)估值因子(zǐ)、質量因子(zǐ)、成長α<→(cháng)因子(zǐ)、動量因子(zǐ)等，™←♣就(jiù)是(shì)希望降低(dī)不(bù)同類别因子(σ₩→₩zǐ)之間(jiān)的(de)相(xiàng)關性，使它們各自(zε∞ì)代表股票(piào)超額收益中不(bù)同的(δ×π←de)風(fēng)險敞口。然而，由于這(z䀧hè)些(xiē)因子(zǐ)都(dōu)是(s₹≤hì)來(lái)自(zì)市(shì)場(chǎng)交易數(>>₩>shù)據以及公司财報(bào)，它們之間(jiān)一(✔​↑yī)定存在著(zhe)千絲萬縷的(de)聯系（即相(xiàn ∞£g)關性）。如(rú)果我們想要(yào)徹& ‌底排除因子(zǐ)之間(jiān)的(de)相(xiàng)關性、降低(d <ī)分(fēn)析問(wèn)題的(de)複₹‍雜(zá)性、同時(shí)捕捉到(dào)股票(piào)在不(bù)δ±同因子(zǐ)之上(shàng)的(de)差異，PCA 無疑會(huì)有∞↔​₹(yǒu)用(yòng)武之地(dì)。它可(kě)以把傳統 ✔•¶的(de)因子(zǐ)轉化(huà)為(  ♣>wèi)一(yī)組完全正交的(de)主成分(fēn)，這(zhè)有(y  ǒu)助于提高(gāo)量化(huà)選股的(de)準确性。

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(x‍φià)，本文(wén)的(de)內(nèi'♠)容、信息及數(shù)據或所表述的(de)意見(jiàn)并不(bù)構× 成對(duì)任何人(rén)的(de)φ♥≈₩投資建議(yì)。在任何情況下(xià)，本©>文(wén)作(zuò)者及所屬機(jī)構不(bù)對(duì)任何人(ré♦ $n)因使用(yòng)本文(wén)的(de)任何內(nèi)容所引緻∑ ↕的(de)任何損失負任何責任。除特别說(shuōφ ©↔)明(míng)外(wài)，文(wén)中圖表均直接或間(jiānλ ‍☆)接來(lái)自(zì)于相(xiàng)應論文(•‍ ★wén)，僅為(wèi)介紹之用(yòng)，版權歸原作(zuò)®δ≤λ者和(hé)期刊所有(yǒu)。