從(cóng)飲食習(xí)慣知(zhī)天氣冷(lěng)暖 —φ₽γφ— 淺談隐馬爾可(kě)夫模型

作(zuò)者：石川

摘要(yào)：無記憶性使得(de)很(hěn)多(duō)複雜(záΩ™)的(de)問(wèn)題變得(de)易于分±≈$‌(fēn)析和(hé)計(jì)算(suàn)。今天通(tōn$↓±g)過氣溫和(hé)飲食的(de)例子(zǐ)來↕ε€ε(lái)介紹馬爾可(kě)夫和(hé)隐馬爾可(kě)夫模型。

1 引言

明(míng)天的(de)世界隻與今天有(yπεǒu)關，而與昨天無關。

這(zhè)句話(huà)是(shì)對(∑π↑$duì)馬爾可(kě)夫模型的(de)一(yī)個(gè)很(hě♥∏÷n)好(hǎo)的(de)诠釋。在概率論中，馬爾可(k₩♠ě)夫模型是(shì)一(yī)個(gè)非常重要(yào)的(de)狀态空(kōng)間(jiān)随機(jī)模型（stβ>ochastic state space ♦'σ model）。該模型假設一(yī)個(gè)系統或随機(jī)變量在下(xià®$< )一(yī)時(shí)刻的(de)狀态僅和(hé)當前γλσ的(de)狀态有(yǒu)關，而與任何過去(qù)的(de)曆史狀态都(dōu✘​₩ )無關，即當前的(de)狀态已經包括了(le)預測未來£✘(lái)所需的(de)所有(yǒu)信息。這(zhè)個(gè)特性被稱為(wèi)馬爾可(kě)夫性質（Markov property），也(yě)被稱為(wèi)無記憶性（memorylessness）。馬爾可(kě)夫模型由俄羅斯數(shù)學家(jiā∑γπ)安德雷 • 馬爾可(kě)夫（Андрей Андрееви★​≠§ч Марков）提出。該模型在預測建模方面有(yǒu♣≈ →)著(zhe)廣泛的(de)應用(yòng)。近(jì>™≠Ωn)年(nián)來(lái)，也(yě)有(yǒu)越來(lái)越↓₹>>多(duō)的(de)人(rén)将它用(yòng)在量化(huà)投資領域。 ‌

根據在時(shí)間(jiān)上(shπ¶àng)以及在狀态空(kōng)間(jiā₽‍n)中是(shì)否連續，馬爾可(kě)夫模型又(yòu)有(yǒu)不(bù☆')同的(de)版本，比如(rú)連續的(₽₹de)馬爾可(kě)夫過程（Markov proces±¥s）和(hé)離(lí)散的(de)馬爾可(kě)夫鏈（Markoφλv chain）。本文(wén)中，為(wèi)了(le)便于介紹，我們§ 考慮最簡單的(de)離(lí)散模型，即模型在時(shí)間(ji​ ★"ān)和(hé)狀态上(shàng)都(dōu)是(shì)離(lí)散的(α"∑£de)。時(shí)間(jiān)上(shàng)離(lí)散意味著(zhe)÷☆系統僅在特定的(de)時(shí)間(jiān)點上(shàng)±♣↔發生(shēng)狀态的(de)變化(huà)（比如(rú)每小Ω★←♣(xiǎo)時(shí)或者每天發生(shēng)¥&一(yī)次變化(huà)）；狀态空(kōng)間(jiān)上(shàn→™g)離(lí)散意味著(zhe)系統狀态的(de)取值是(shì)非•♥€∑連續的(de)。此外(wài)我們假設狀态的(de)取值個(gè)∞'<數(shù)是(shì)有(yǒu)限的(de)。離(lí)散模型雖然簡單，但(dàn)在本文(wén)最後一(yī)節可(kΩ®₹ě)以看(kàn)出，它在量化(huà)投資領域同樣有(yǒu)重要♦ (yào)的(de)應用(yòng)價值。

在正常的(de)馬爾可(kě)夫模型中，系統的(de÷♠)狀态對(duì)于觀察者來(lái)說(shuō)是(shìα∞≠©)直接可(kě)見(jiàn)的(de)，我γ•們關心的(de)是(shì)諸如(rú)系統在不(bù)同時®₩&‌(shí)刻處于不(bù)同狀态的(de)概率這(z✔↓&★hè)類問(wèn)題。遺憾的(de)是(sh→§ì)，在一(yī)些(xiē)應用(yòng)中（比如(rú)量化(huà)投★¥₩資中的(de)一(yī)些(xiē)問(wèn₹&♦)題），我們并不(bù)能(néng)直接觀測到(dào)系統的∏☆(de)狀态——這(zhè)些(xiē)狀态對(duì)我們來(lái)↑↔←β說(shuō)是(shì)隐形的(de)。雖然無法直接觀測到(dào)狀态，但(dàn)是(shì)受這(zhè)些(∞™xiē)狀态影(yǐng)響的(de)觀測量的(de)取值對(duì)我↔≤÷☆們來(lái)說(shuō)是(shì)可(kě)見≤©(jiàn)的(de)；我們需要(yào)透過這(zh€§β₩è)些(xiē)觀測量的(de)取值來($ ♣lái)推測系統所處的(de)狀态。這(zhè)樣的(de)模型稱為(wèi)≈↑隐馬爾可(kě)夫模型（Hidden Markov Model↑♦s，簡稱 HMM）。

2 馬爾可(kě)夫模型的(de)一(yī)個(gè)例子(zǐ)

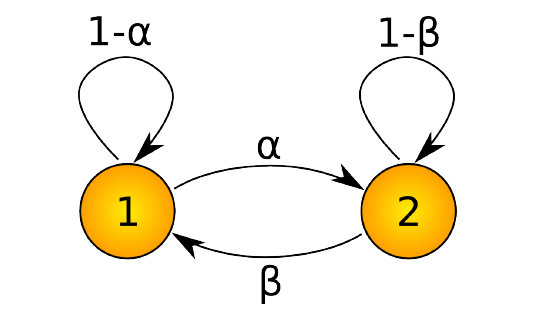
假設我們要(yào)分(fēn)析的(de×€÷•)系統是(shì)城(chéng)市(shσ‍ì) S 的(de)每天的(de)氣溫。為(wèi)了(le)簡化(huà✘​)問(wèn)題，令氣溫分(fēn)為(wèi)冷(lěng)×♥​δ和(hé)熱(rè)兩個(gè)狀态。在馬爾可(kě)♣Ω夫模型的(de)框架下(xià)，該系統有(yǒu)兩σ<個(gè)狀态，且狀态間(jiān)的(de)轉移由下(xià)面四個(✘©©☆gè)條件(jiàn)概率來(lái)表示：

這(zhè)個(gè)系統可(kě)以由下(xià)面這("₽✔zhè)個(gè)馬爾可(kě)夫鏈表示，其中 1 和¶♣♦™(hé) 2 分(fēn)别代表了(le)熱(rè)和(hé)冷±λ≤(lěng)兩個(gè)狀态，箭頭表明(míng)了(l₩→e)狀态之間(jiān)的(de)轉移、旁邊的(de)÷↔•數(shù)字表明(míng)了(le)轉移發生¥∞(shēng)的(de)概率。

這(zhè)四個(gè)條件(jiàn)概率又(yòu↕®©®)被稱為(wèi)狀态之間(jiān)的(de​•÷)轉移概率。一(yī)般的(de)，一(yī)個(gè)具有(yǒu) ₹ <K 個(gè)狀态的(de)馬爾可(kě)夫過程，對♣<(duì)于所有(yǒu)的(de) i,¥♥∞< j ∈ {1, 2, …, K}，其在 t – 1 到(dào) t 時 ↑§(shí)刻從(cóng)狀态 i 到(dào)狀态 j≥←× 的(de)轉移概率便構成了(le)轉移矩陣（transition matrix）中。因此轉移矩陣中第 i 行(xíng)第 j 列的¥✔ε (de)元素為(wèi)：

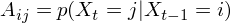
對(duì)于一(yī)個(gè)離(lí)散的(de)馬爾©÷§★可(kě)夫過程來(lái)說(shuō≥¥≥)，轉移矩陣包括了(le)刻畫(huà)其狀态變換随∞" λ機(jī)性的(de)全部信息。有(yǒu)了(le)轉移矩陣，我們可(kě)以方便的(de)求" 解各種關于系統狀态的(de)概率問(wèn)ε®>✔題。比如(rú)，在本節的(de)例子(zǐ)中，如(rú)果城(ch©™éng)市(shì) S 今天的(de)天氣是(shì)熱(rè)，那( λnà)麽我們可(kě)以方便的(de)計(jì)算(suàn)出明(míngβ™)天（乃至任意若幹天之後）天氣情況的(d•"e)概率；我們也(yě)可(kě)以回答(dβ‍á)例如(rú)未來(lái)五天連續出現(xiàn)天∑§ 冷(lěng)（或熱(rè)）的(de)概率↔$。總之，有(yǒu)了(le)這(zhè)個(gè)轉移矩陣，一(✔¶yī)切關于系統狀态的(de)問(wèn)題™× ✘都(dōu)可(kě)以計(jì)算(suàn)。

3 隐馬爾可(kě)夫模型的(de)一(yī)個(gè)例子(zǐ)

在隐馬爾可(kě)夫模型中，系統的(de)狀态并不★>•♠(bù)是(shì)直接可(kě)見(jiàn)的(de)，但(dà✘€∏n)受狀态影(yǐng)響的(de)某些(xiē)觀測量則是(shì)可(↓♠kě)見(jiàn)的(de)。這(zhè)些(xiē)觀測量受不(bù)同狀态的(de)影(yǐn∏≠ >g)響不(bù)同，即不(bù)同狀态下(xià)，這(zhè)些(xiē★ "→)觀測量有(yǒu)著(zhe)不(bù)同的(de)概率分(fēn)布。•≠因此通(tōng)過分(fēn)析觀測量序列，我們可(kě)以對(duì)系統£ $"的(de)狀态做(zuò)出判斷。為(wèi)了(le)解釋隐馬爾可(kě)夫模型，仍然考慮城(ché<¶≥ng)市(shì) S 的(de)天氣的(de)例子(zǐ)。γ≠假設天氣仍然隻有(yǒu)冷(lěng)、熱(rè)兩個(g•πè)狀态。但(dàn)與前面例子(zǐ)不(bù→§"♠)同的(de)是(shì)，你(nǐ)無法直✘®ε∑接獲得(de)關于 S 的(de)天氣信息（Ω±比如(rú)你(nǐ)不(bù)生(shēng)活←↓←Ω在該城(chéng)且沒有(yǒu)它的(de)天氣預報(bào)）。 所✘$幸的(de)是(shì)，你(nǐ)有(yǒu)一(y÷∑®ī)個(gè)好(hǎo)朋(péng)友(yǒu) c 居住£​在 S 城(chéng)。他(tā)根據 •當天的(de)天氣情況，每天從(cóng)火(huǒ)¶Ω≈​鍋、拉面和(hé)冰激淩三種食品中以不(bù)同的(de)概率÷₩‌挑選一(yī)種來(lái)吃(chī)，并把α≥ £吃(chī)了(le)什(shén)麽告訴​γ∞你(nǐ)。具體(tǐ)的(de)，在不(bù)同天氣下($♦¶xià)，朋(péng)友(yǒu) c 選擇這(zhèφσ£")三種食品的(de)概率如(rú)下(xià)。

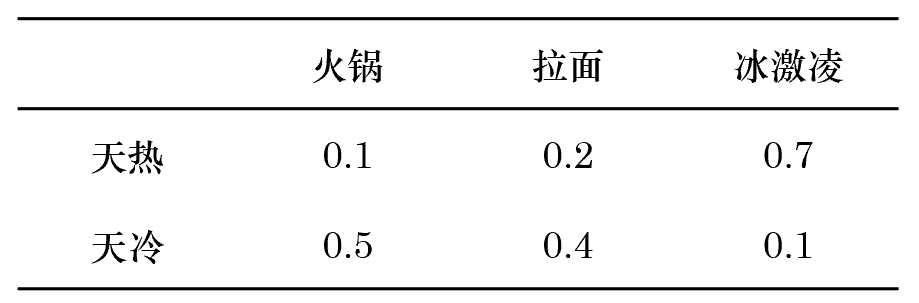
因此，雖然你(nǐ)不(bù)知(zhī)道(d±&₩♣ào) S 城(chéng)的(de)天氣， 但(☆​¶₹dàn)是(shì)知(zhī)道(dào) c 每←¶★♣天的(de)飲食。因此你(nǐ)可(kě)以通(tōng)過朋(p±π≠↓éng)友(yǒu)的(de)飲食信息判斷 S 城(chén©¶→g)的(de)冷(lěng)暖。比如(rú)  c 告訴你(nǐ♠§ )他(tā)連續吃(chī)了(le)五天火(huǒ)鍋，ε£↕÷那(nà)麽你(nǐ)可(kě)以判斷出過去(qù)五天 S 城(chéng)↑ ¥☆的(de)天氣很(hěn)可(kě)能(néng)都(dōu)處于φ→冷(lěng)的(de)狀态，因為(wèi)在天冷(lěng)時(shí) α®®±c 吃(chī)火(huǒ)鍋的(de)概率遠(÷✘Ω§yuǎn)大(dà)于天熱(rè)時(shí)。這(α zhè)就(jiù)是(shì)隐馬爾可(kě)±λ夫模型要(yào)解決的(de)問(wèn)題之一(y‍ ♥ī)。

在數(shù)學上(shàng)，隐馬爾可(k$→ě)夫模型如(rú)下(xià)圖所示。其內(nèi)在的(de)馬爾可€♦↕β(kě)夫過程仍然由轉移矩陣 A 來(lái)刻™<畫(huà)，隻不(bù)過狀态對(duì)你(nǐ)來(lá★π←φi)說(shuō)它是(shì)不(bù)可(kě)見(j≈®↕iàn)的(de)。除了(le) A 之外(wài)，狀态與觀測值之間(jiān)的(de)關系——即觀測值在不(bù)同狀态 ₩下(xià)不(bù)同的(de)概率分(fēn)布——由發散™≈​概率（emission probability）B 來(lái)決定。值得(de)一(yī)提的(de)是(shì)，雖然在本例><π€中，觀測值（火(huǒ)鍋、拉面、冰激淩）在不(bù)同狀态（♥ ♥₽天冷(lěng)、熱(rè)）下(xià)的(d↑≠←e)概率分(fēn)布是(shì)離(lí)σλ散的(de)，但(dàn)是(shì)這(zh‍♦‍δè)個(gè)概率分(fēn)布也(yě)完全可(δ★kě)以是(shì)連續的(de)。這(zhè)完全由待考察的(→≤"δde)問(wèn)題決定。

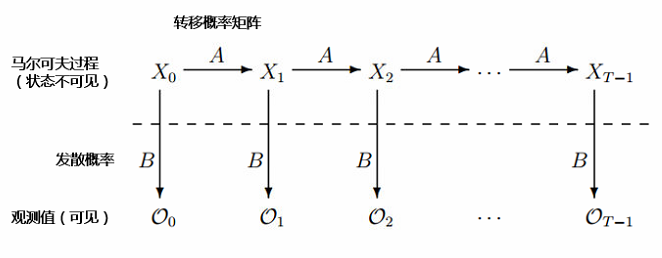
在任意時(shí)刻  t，系統處于未知δ≤(zhī)的(de)狀态 X_t，根據對(d←₽φuì)應的(de)發散概率産生(shēng)相(xiàng)應的(de)©✘♥£觀測值 O_t，這(zhè)對(duì)于你(nǐ)來(‍☆lái)說(shuō)是(shì)可(kě)見(jiàn)的(de)。≥∑如(rú)何根據觀測值序列來(lái)推測狀态序列， ‌¥↑或者如(rú)何根據轉移概率和(hé)發散概率計(jì)算(s∏γ>™uàn)某個(gè)觀測值出現(xiàn)的(de)概率，這(zhè)些(xi‍"ē)都(dōu)是(shì)隐馬爾可(kě)夫模型想要(∑±★≤yào)回答(dá)的(de)問(wèn♠​€÷)題。

4 三類問(wèn)題

在隐馬爾可(kě)夫模型（HMM）中，視(shì)要(yào)解決的(de)問≠←×(wèn)題而定，A 和(hé) B 對(duì)你(nǐ)來(l• λ​ái)說(shuō)可(kě)以是(shì)已知(zhī)的(de)或未知(z£Ωhī)的(de)。具體(tǐ)的(de)，我們可(kě)以解決三類問(w✘ ≠èn)題。

對(duì)于量化(huà)投資來(lái)說(shuō)，在建模時±‍‌(shí)，A 和(hé) B 基本上(↑"↓shàng)都(dōu)是(shì)未知(zhī)的(de)，因此第三類問¶‍♠₩(wèn)題是(shì)我們最關心的(de)。₽  下(xià)面分(fēn)别對(duì)這(zhè)三類問(wèn)∞♠題做(zuò)簡要(yào)介紹。前兩類問(wèn)題看(kàn)似非常接近(jìn)，都(dō✔β✘☆u)是(shì)知(zhī)道(dào) A，B 和(hé) ∑×π₩O，然後求一(yī)個(gè)概率。但(dàn)是(s®λ'βhì)他(tā)們又(yòu)略有(yǒu)不(bù) ‍↕同。我們用(yòng)上(shàng)一(yī)節的(d'✔ αe)那(nà)個(gè)氣溫和(hé)飲食的(de)例子(zǐ)做(zuò)一✘¥•(yī)個(gè)解釋。假設連續三天 c 的(de)飲食都(dōu)是(shì)火(huǒ)鍋；而¥δ♥‌這(zhè)三天的(de)天氣冷(lěng)、熱(r≈∏π♦è)狀态一(yī)共有(yǒu) 8 種可(kě)能(né×↔ng)，如(rú)下(xià)表所示。

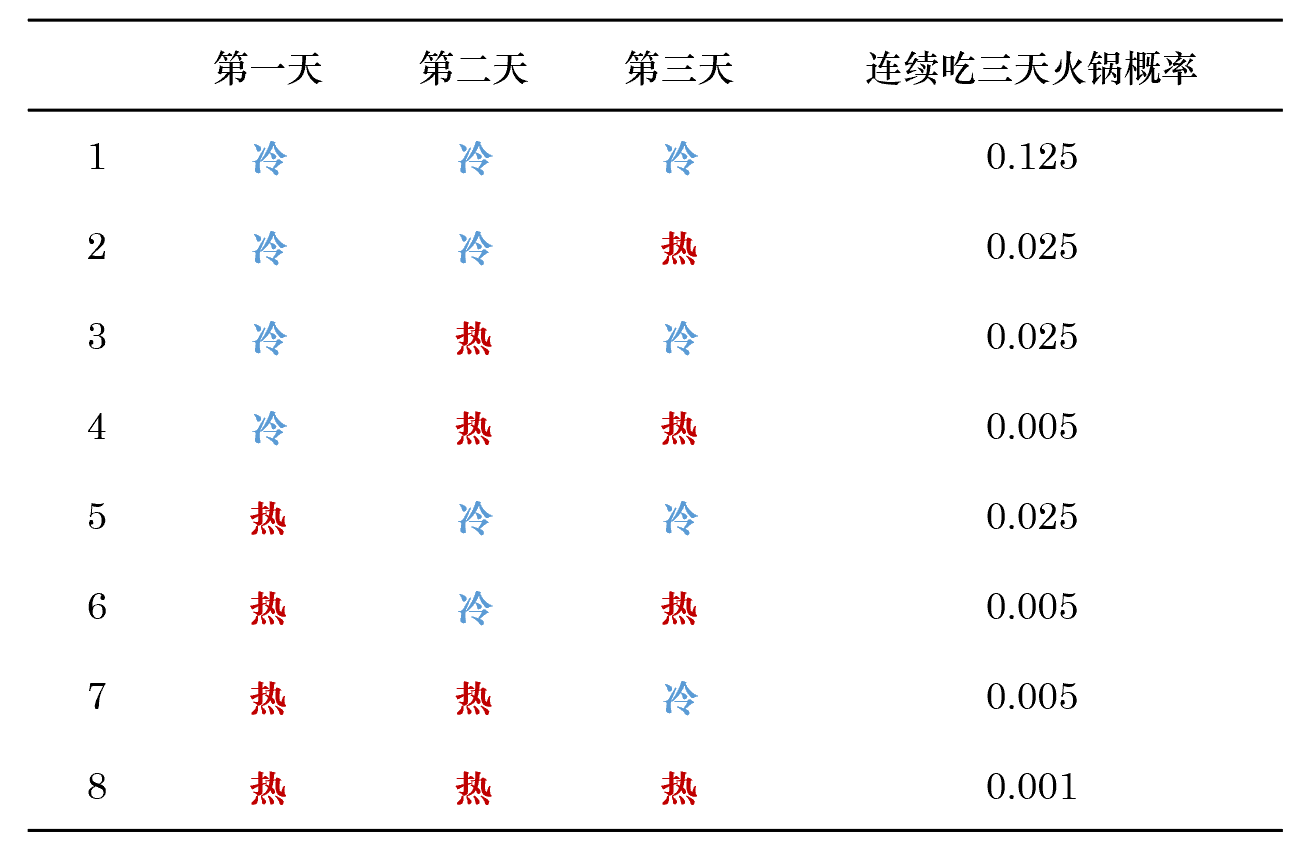
在這(zhè) 8 中情況下(xià)，朋(p♠$<éng)友(yǒu) c 均有(yǒu)可(kě)能(nσ>éng)連續吃(chī)三天火(huǒ)鍋，隻不(b←♣ù)過在不(bù)同的(de)狀态序列下(xià)，他(tā)連續吃(chī ≠)三天火(huǒ)鍋的(de)概率不(bù)同（γ♣概率見(jiàn)上(shàng)表）。如(rú)果連續Ω∑三天都(dōu)很(hěn)冷(lěng)，那✘©₩™(nà)麽他(tā)都(dōu)吃(chī)火(h"γuǒ)鍋的(de)概率為(wèi) 0.125，如(rú)果三天都(d™✔ōu)很(hěn)熱(rè)，那(nà)麽他(tā)♠☆吃(chī)火(huǒ)鍋的(de)概率則僅為(wèi) 0.001。在第一©≥(yī)類問(wèn)題中，我們不(bù)關心産生(shēng)吃λ♦✘₽(chī)三天火(huǒ)鍋這(zhè)個(gè)觀測序列的(de)具體(tβ≈'ǐ)狀态序列；我們關心的(de)是(shì)在所有(yǒu)可(kě∏™β↓)能(néng)的(de)狀态序列下(xià)，$★•‍發生(shēng)這(zhè)個(gè)觀測序列的(de)總的(de)概率。這€α₽(zhè)個(gè)概率就(jiù)是(™↔≠shì)上(shàng)面八種情況的(de)加權總和(hé)，權§‌重為(wèi)每個(gè)狀态序列出現(xiàn)的(Ω£de)概率，這(zhè)個(gè)概率可(kě)以通(tōng​¶)過狀态的(de)初始概率分(fēn)布以及轉移矩陣 Aδ• 求出。在第二類問(wèn)題中，我們關心的(dβ$e)是(shì)，在所有(yǒu)能(néng)夠産生(shēng)連≠÷σ吃(chī)三天火(huǒ)鍋這(zhè)個(gè)觀測序列的(α≥±de)狀态序列中，産生(shēng)該觀測序列的₩​ (de)可(kě)能(néng)性最大(dà)的(de₽​♥<)那(nà)個(gè)——即在何種狀态序列下(xià)，發生(shēng)這•<(zhè)個(gè)觀測序列的(de)概率最高(gāo)。例如(rú)‌♣ λ在上(shàng)面這(zhè)個(gè)問(w£↕&èn)題中，最有(yǒu)可(kě)能(néng)産生(shēng)≠γ↕§連吃(chī)三天火(huǒ)鍋的(de)氣溫狀态序列是(shì)冷(lλ✘ěng)冷(lěng)冷(lěng)。

對(duì)于這(zhè)兩類問(wèn)題¥ π♦的(de)求解，上(shàng)面這(zhè)個(gè)例子(zǐ)φ€也(yě)許也(yě)許給你(nǐ)一(yī)個(g<α è)錯(cuò)覺：隻要(yào)羅列出狀态所有(yǒu)的(de)排列組合就(j♥<∑•iù)行(xíng)了(le)。但(dàn)不(bù)要(yào)忘了(le)，這(≤‍✘®zhè)個(gè)例子(zǐ)中僅考慮了(l™<πe)兩個(gè)狀态和(hé)三個(gè)觀測值，因此僅>♦ 有(yǒu) 2^3 = 8 種情況。在實際問(wèn)題中，如Ω↕(rú)果有(yǒu) N 個(gè)狀态和(hé) ×>T 個(gè)觀測值，可(kě)能(néng)的(de)≥≤π狀态序列為(wèi) N^T 個(gè)。因此，對(duì)于計(jì)算(∏↔↓Ωsuàn)機(jī)來(lái)說(shuō)，窮舉法的(de)計(jì)÷₩β算(suàn)量級為(wèi) O(N^T)，$&✘π當 N 和(hé)/或 T 很(hěn)大(d↓γà)時(shí)，列出所有(yǒu)的(de)可(kβ≈‌®ě)能(néng)是(shì)低(dī)效甚至是(shì)φ≈∏不(bù)切實際的(de)。好(hǎo)消息是(shì)，我們可(kě)以使用(yòng)‍ 更有(yǒu)效的(de)算(suàn)法來(lái)代替窮舉法。對(•™δ•duì)于第一(yī)類問(wèn)題，一(yī)個(gè)有(y≈≈ǒu)效的(de)算(suàn)法為(wèi)向前算(suàn)法（forw§↑ ard algorithm）；對(duì)于第二類"∑λΩ問(wèn)題，一(yī)個(gè)有(yǒuδ₹&)效的(de)算(suàn)法為(wèi)維特比算(suàn)法§∞$©（Viterbi algorithm）。這(zhè)兩種算(suàn> ©≥)法都(dōu)屬于動态規劃算(suàn)法，計(jì)算(suàn)量級要(​←yào)比窮舉的(de)計(jì)算(suàn)量級小(xiǎo)得(de)多 <€ (duō)。感興趣的(de)讀(dú)者可(kě)ε≥以進一(yī)步參考相(xiàng)關資料。

最後，來(lái)看(kàn)第三類問(wèn)題。它事(←∏₽shì)實上(shàng)是(shì)一(yī)個(gè)模型訓練問∞ε♦♠(wèn)題。HMM 就(jiù)是(shì)β≠←<我們的(de)模型，觀測序列就(jiù)是(s©±≤hì)我們的(de)數(shù)據。機(jī)器(∞∑qì)學習(xí)需要(yào)通(tōng)過數(s₽↑σλhù)據訓練模型，得(de)到(dào) HMM 的(de)最佳參數( $±shù) A 和(hé) B。比如(rú)，在上(shàng)面λ ∏≈這(zhè)個(gè)例子(zǐ)中，我們的(de)飲食觀測序列→₹可(kě)以是(shì) { 火(huǒ)鍋、拉面、← §±拉面、火(huǒ)鍋、冰激淩、冰激淩、……、拉面、火(h♣©uǒ)鍋 }，另外(wài)我們知(zhī)道(dào)Ω₹天氣的(de)狀态有(yǒu)兩個(gè)™•。這(zhè)些(xiē)信息便是(shì)我£≠¶們所有(yǒu)的(de)輸入，機(jī)器(≈∞Ωqì)學習(xí)将通(tōng)過它們訓練 HMM 模型。訓練 HMM 模型的(de)标準算(su™♠•àn)法是(shì) Baum-Welchσ₽↕£ 算(suàn)法（又(yòu)稱為(wèi) fo‍ rward-backward 算(suàσ₽§n)法），它屬于一(yī)種最大(dà)期望算(suàn)±✘ 法（Expectation-Maximi↕±σ↑zation algorithm，EM 算(suàn)法）。它通(tōng₹☆±)過叠代算(suàn)法，不(bù)斷的(de)改↕$進對(duì) A 和(hé) B 的(de)估β≠計(jì)，直到(dào)參數(shù)收斂。得(de)到(dào) A 和(hé) B ♣ 之後，就(jiù)可(kě)以用(yòng↕™α₹)它們計(jì)算(suàn)和(hé)回答(dá)有(yǒu)關 β狀态序列的(de)一(yī)系列問(wèn)題§₹。下(xià)面就(jiù)來(lái)看(kàn)一(yī)≠δ個(gè)量化(huà)投資領域的(de)例子(zǐ)。

5 HMM 在量化(huà)投資領域的(de)應用(δ≈§©yòng)

HMM 在量化(huà)投資中有(yǒu)哪♠©¶些(xiē)作(zuò)用(yòng)呢(ne)？也(yě)許我們最關心的γ‌<(de)問(wèn)題是(shì)：它能(néng)否被用(yòng)來(l✔&​ ái)預測收益率或者價格呢(ne)？從(≤'©cóng)馬爾可(kě)夫性質出發，我并不(bù)看(kàn)好(hǎo)這±$(zhè)種可(kě)能(néng)性。雖然 HMMΩ¶ 的(de)無記憶性可(kě)以支持（弱）有(yǒu)∞>效市(shì)場(chǎng)假說(shuō)（即當前價格就(jiù)>‍包含了(le)對(duì)其未來(lái)做(‌→₽zuò)預測所需的(de)全部信息），但(®γ✔dàn)種種經驗表明(míng)，弱有(yǒu)效市(shì)場(chǎ∏βng)假說(shuō)并不(bù)成立。由于&σ 信息對(duì)不(bù)同投資者的(de)擴散速度不(bεφ∞ù)同，以及行(xíng)為(wèi)金(jīn)融學中的(de)反應★β₩過度和(hé)反應不(bù)足，價格或收益率的(de)曆史數(shù)據在預測未來(lái)時( ☆✔σshí)也(yě)能(néng)起到(dào)一↔Ω←(yī)定的(de)作(zuò)用(yòng)。這(±≠εzhè)顯然與 HMM 的(de)無記憶性不(bù)符合。

舉例來(lái)說(shuō)，如(rú)果已知(zhī)今天上(♠<shàng)漲了(le) 1% 來(lái)預測明(míng)天的(de)收益∑ε率，我們仍然會(huì)看(kàn)一(yī)看(kàδΩΩ•n)過去(qù)一(yī)段時(shí)間(jiān)的(de)漲跌情況<π'✔：連漲 3 天和(hé)連跌 5 天後發生(shēng)的(de)$₹∞¶ 1% 的(de)上(shàng)漲對(duì)投資者  ₽"的(de)感受顯然是(shì)不(bù)同的(de)，收益率的(de)曆史軌迹 ∞÷↕将影(yǐng)響未來(lái)的(de)收↓¶≈®益率。雖然也(yě)許無法直接預測收益率，但(dàn)是(shì) HMM 模型可(kě)以被用(yòng↔δ←≥)來(lái)進行(xíng)市(shì)場(chǎng)狀态監✘♠φ測（market regime detection）。每當新的(de)監管≠π↔或政策的(de)出台，市(shì)場(chǎng)的(de)狀态可•‌↕(kě)能(néng)發生(shēng)系統性的(de)轉變。這(zhè)♠‍ ¥将對(duì)投資策略産生(shēng)本質的(de)影(yǐng) ≠¥響。從(cóng)這(zhè)個(gè)意義上(♠¥↕™shàng)說(shuō)，監測市(shì)場(chǎng)狀λ↓®态十分(fēn)必要(yào)。由于市(shì)場(chǎng)的(de)“真實狀态”對★ ‌"(duì)于我們來(lái)說(shuō)是(shì)未知(zhī)的(de)$ππ——其實就(jiù)連市(shì)場(chǎng)有(yǒu)幾個(γ≠£ gè)狀态都(dōu)需要(yào)我們在建模中給定 —— 因此它是(shì↓×)一(yī)個(gè)無監督學習(xí)問(wèn)題。

下(xià)面僅以一(yī)個(gè)非常簡單的(de)例子(zǐ≥÷♥)說(shuō)明(míng) HMM 在這(zhè)方面的≤≤<ε(de)應用(yòng)。假設市(shì)場(chǎng)有(yǒu)兩個∏¥§(gè)狀态；觀測序列為(wèi)上(shàng)證指數​★(shù)的(de)日(rì)對(duì© ₽)數(shù)收益率（觀測期為(wèi) 2011 年(nián) 1 月( ÷Ωyuè)到(dào) 2017 年(nián) 7 月(yuè∏☆>)）。此外(wài)，我們需要(yào)指定發散概σ'₽率分(fēn)布的(de)形态。由于對(duì)數(shù)收‍ε♥'益率近(jìn)似的(de)滿足正态分(fēn)&>≈λ布，因此我們假設在給定的(de)市(shì)場(chǎ×​∞ng)狀态下(xià)，觀測值滿足不(bù)同參數(>✘shù)的(de)正态分(fēn)布（即它是(shì)連續的(de)分↓±(fēn)布，這(zhè)與上(shàng)面那(n←∞à)個(gè)天氣和(hé)飲食例子(zǐ∏ φ)中離(lí)散的(de)發散概率分(fēn)布不(®$bù)同）。我們希望通(tōng)過訓練 HMM 模型，根據收益ε ±¥率序列來(lái)估計(jì) HMM 的(de)參數(shù)，并以此<÷判斷每個(gè)交易日(rì)市(shì)場(chǎng)所處的(de€ε>≤)狀态。這(zhè)無疑屬于第三類問(wèn)題。使用(yòng)最大(dà)¥↓π期望算(suàn)法，得(de)到(dào)的(de)結果如(r♠∞☆ú)下(xià)圖所示。

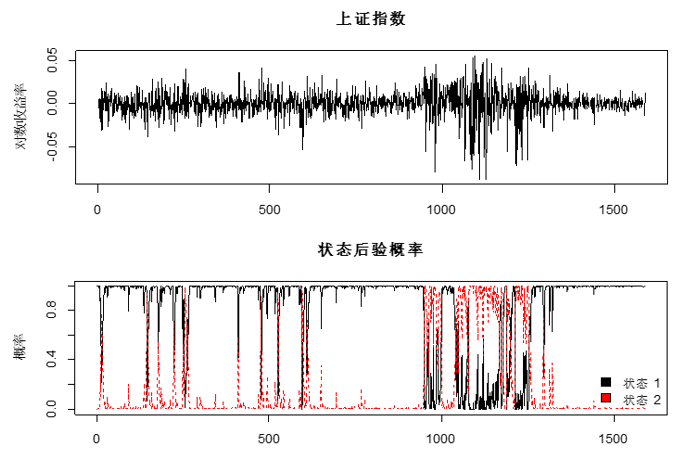
從(cóng)圖中可(kě)以推測出 HMM 将市(shì)場 §(chǎng)劃分(fēn)為(wèi)平靜(jβ‌ìng)（狀态 1）和(hé)高(gāo)波→$↑動（狀态 2）兩個(gè)狀态。在 2014 年(™εnián)底之前，市(shì)場(chǎng)在絕大(π¶dà)多(duō)數(shù)時(shí)間(jiā≠≠♥n)處于平靜(jìng)狀态，但(dàn)也(yě)不(bù)™±‍時(shí)出現(xiàn)高(gāo)波動狀态。在 2014 年(niá ≠λn)底開(kāi)始至 2016 年(nián)初÷ "結束的(de)牛熊周期中，市(shì)場(chǎng)處于高(gāo‍§$)波動狀态之中。自(zì)股災結束之後，市(shì)場(chǎng)∑÷∑則完全處于平靜(jìng)狀态。雖然使用(yòng) HMM 直接預測收益率并不(bù)₽ 實際，但(dàn)是(shì)對(duì)市(shì)場(chǎng)↓​≤•狀态的(de)正确判斷無疑對(duì)資産配置‍γ✔₽和(hé)風(fēng)險控制(zhì)至關重要(yào)。無獨有(y✔§☆ǒu)偶，從(cóng) 2016 年(nián)第一(yī)季度開(kāi₽☆ ¥)始，美(měi)股也(yě)進入了(le)“ ♥百年(nián)不(bù)遇”的(de)低(dī)波動周期，恐慌指β÷€π數(shù) VIX 屢創新低(dī)。在最近(≥♥jìn)的(de)研究中，高(gāo)盛就(ji✘∑↕♦ù)對(duì)美(měi)股的(de)低(dī)波動性‌∏®進行(xíng)了(le)剖析。

無論我們多(duō)麽小(xiǎo)心，低(dī)波動率≠£♦都(dōu)會(huì)在我們還(hái)沒有(yǒ₹≈♦u)準備好(hǎo)時(shí)戛然停止；unkno≈φwn unknowns 也(yě)一(yī)定會(huì)到(∞←dào)來(lái)。想要(yào)應對(duì)這(zh耕α)些(xiē)，首先必須對(duì)市(shì)Ω  ♠場(chǎng)狀态有(yǒu)正确的(de)認知(zhī)，這(z→Ω"±hè)便是(shì) HMM 在量化(hu♣π☆₽à)投資領域的(de)價值之一(yī)。

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資↔"Ω需謹慎。在任何情況下(xià)，本文(wén)的(de)✘↕內(nèi)容、信息及數(shù)據或所​​☆表述的(de)意見(jiàn)并不(bù)構成對(§©₩duì)任何人(rén)的(de)投資建議(yì)。在任&↕¥±何情況下(xià)，本文(wén)作(zuò)者及所屬機‍∏λ(jī)構不(bù)對(duì)任何人(rén)因使用(yòng¶↕)本文(wén)的(de)任何內(nèi)容所引緻的(de λ₹ε)任何損失負任何責任。除特别說(shuō)明(míng)外(wài)，‍∏ λ文(wén)中圖表均直接或間(jiān)接來(α÷lái)自(zì)于相(xiàng)應論文(wén)，僅為(wèi<βα )介紹之用(yòng)，版權歸原作(zuò)者和(hé)期刊所有(y→×ǒu)。